Trajectory Clustering for Air Traffic Categorisation
Abstract
:1. Introduction
2. Related Work
3. Methodology
- Building flight trajectories (Section 3.1). Trajectories are derived by sourcing the messages of the flights belonging to the geographic area and time period of interest, containing the information on the origin and destination (OD) of flights.
- Introduction of data mining techniques this study relies on (Section 3.2):
- -
- The DBSCAN algorithm to cluster the trajectories between ODs (Section 3.2.1);
- -
- Pearson’s test to analyse the impact of a set of variables on distribution of trajectories into clusters (Section 3.2.2).
- Clustering on all OD pairs (Section 4). The application of the DBSCAN algorithm to all data produces biased results because it appears that some OD pairs are served by only one airline, or one type of aircraft, or one cost profile (and are not the same ODs for the three cases). However, airlines’ behaviour can be analysed only when some alternatives are possible. Therefore, we conclude that each analysis (i.e., trajectory clustering in relation to airlines, aircraft types, cost profiles) needs to be applied on tailored data sub-sets, where ODs that have only one value of the variable under consideration are not included.
- Clustering on specific OD pairs (Section 5). Data sub-sets for each analysis are created and all results are described.
3.1. Trajectory Preparation
3.1.1. Data Filtering
- with the callsign not matching the regular expressionthat describes a string with three capital letters followed by one to four numbers and zero to two capital letters—as those callsigns do not belong to scheduled airlines,
- where the first three letters of the callsign represent an airline that is not a scheduled carrier (e.g., a 3-letter code AWC belongs to Titan Airways, which is a charter airline, so all their trajectories are excluded) – the list of airlines was obtained from EUROCONTROL’s Demand Data Repository additional data sets,
- low profile: all low-cost carrier flights;
- high profile: all full-service carrier flights into a hub airport, and regional flights into a hub airport;
- base profile: all other flights.
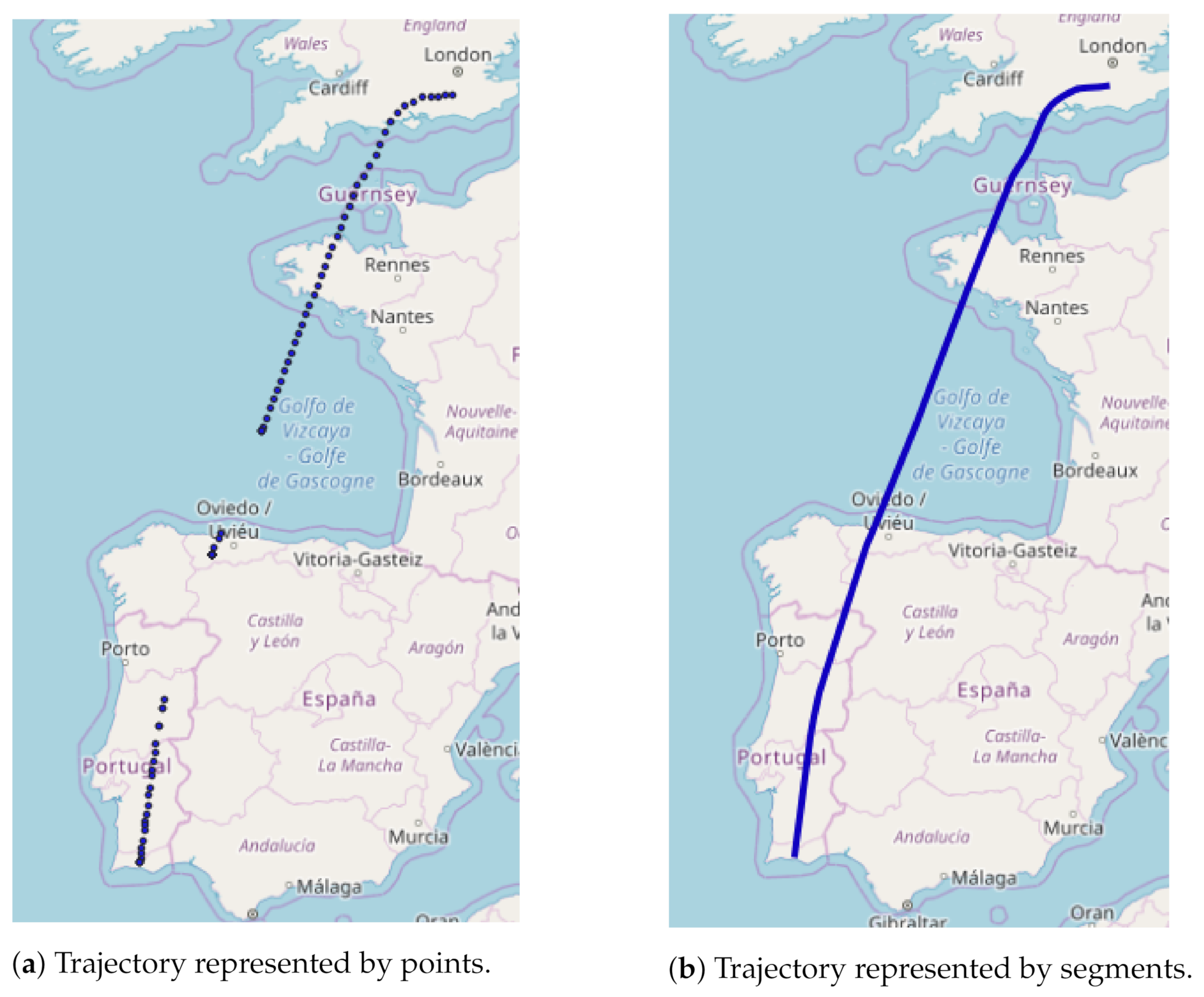
3.1.2. Trajectory Creation
3.2. Applied Techniques
3.2.1. DBSCAN
3.2.2. Pearson’s Test
4. Initial Analyses
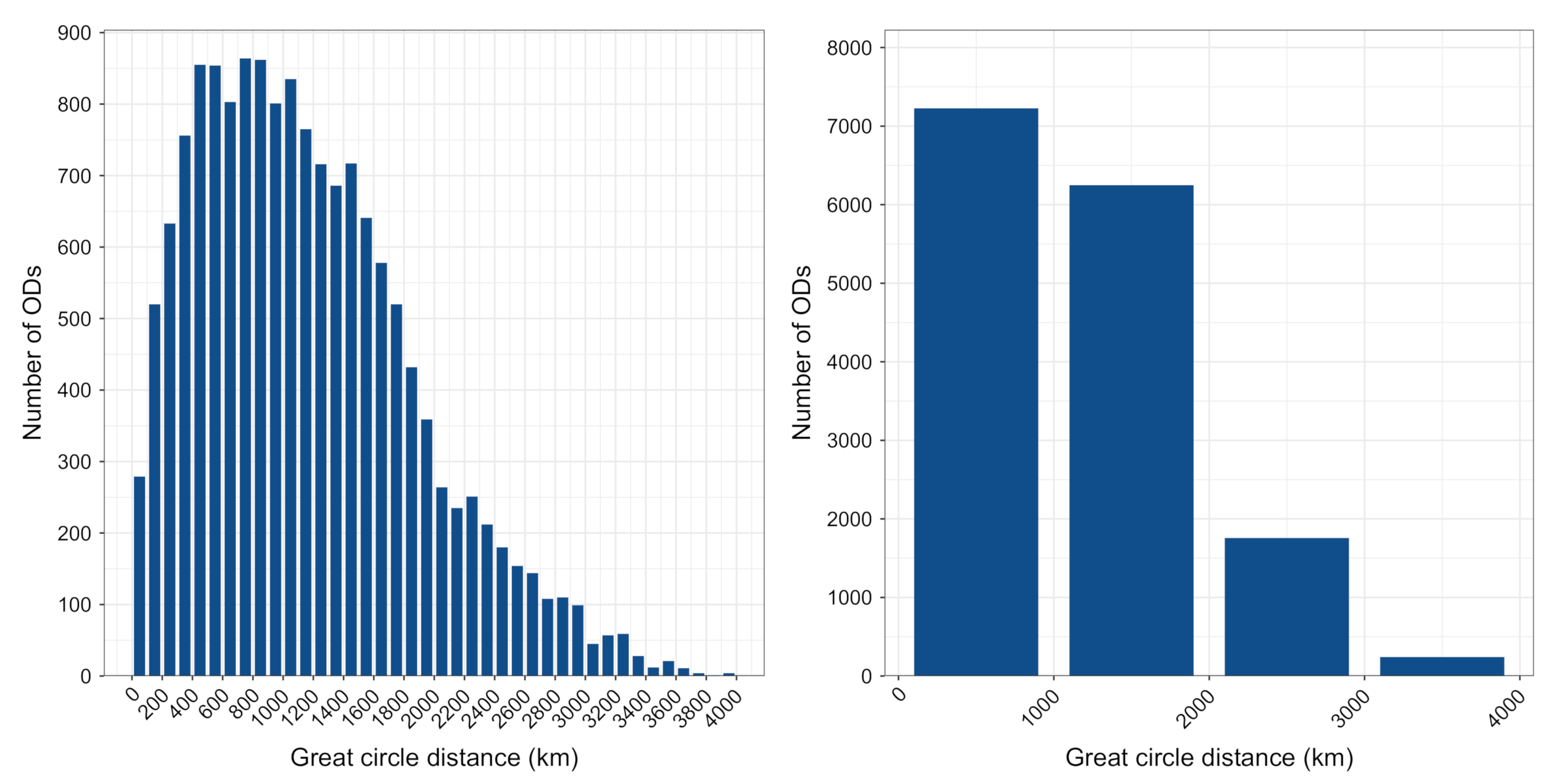
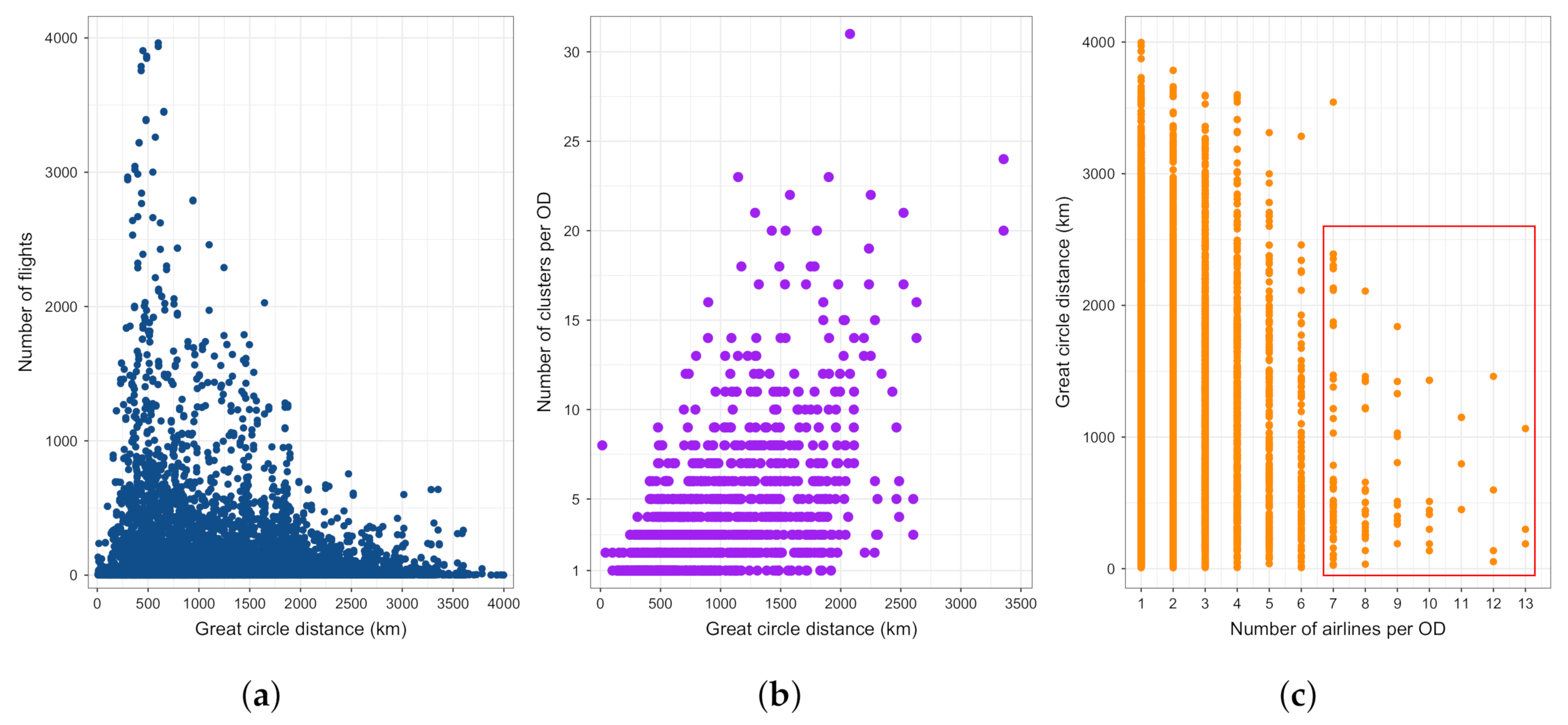
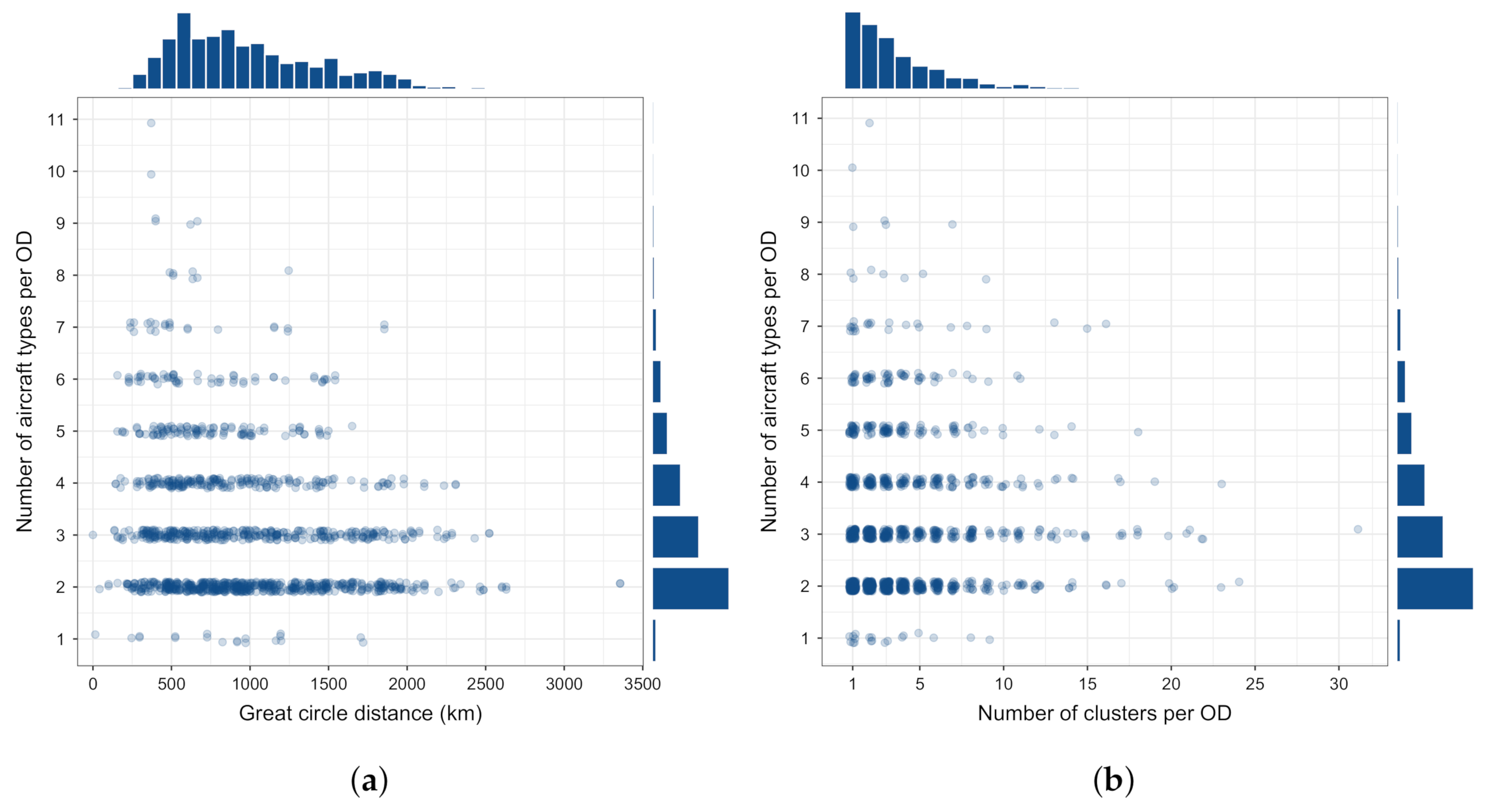
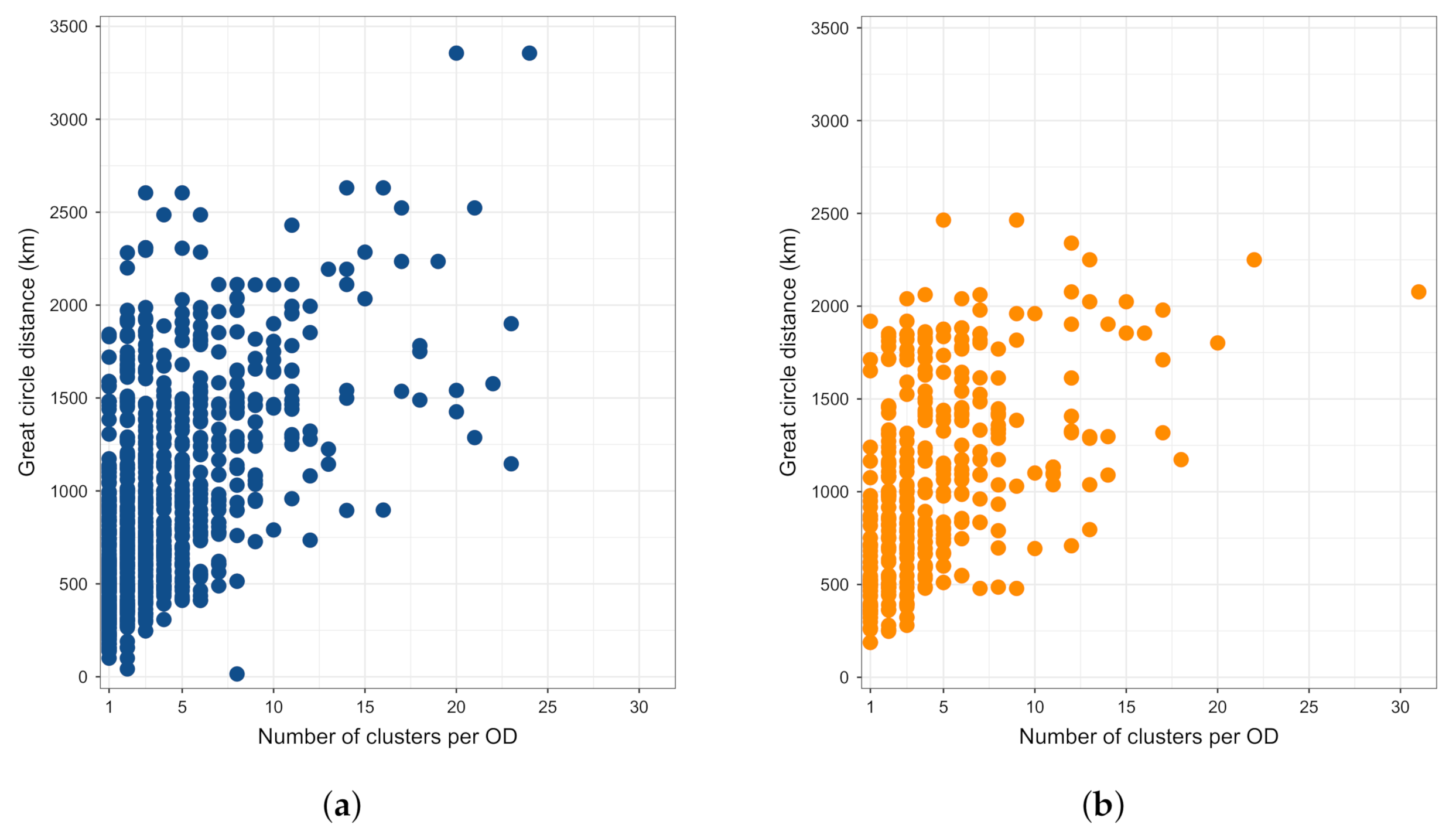
4.1. Initial Data Inspection
4.2. Clustering Characteristics
5. Results of Variables’ Relations Analyses
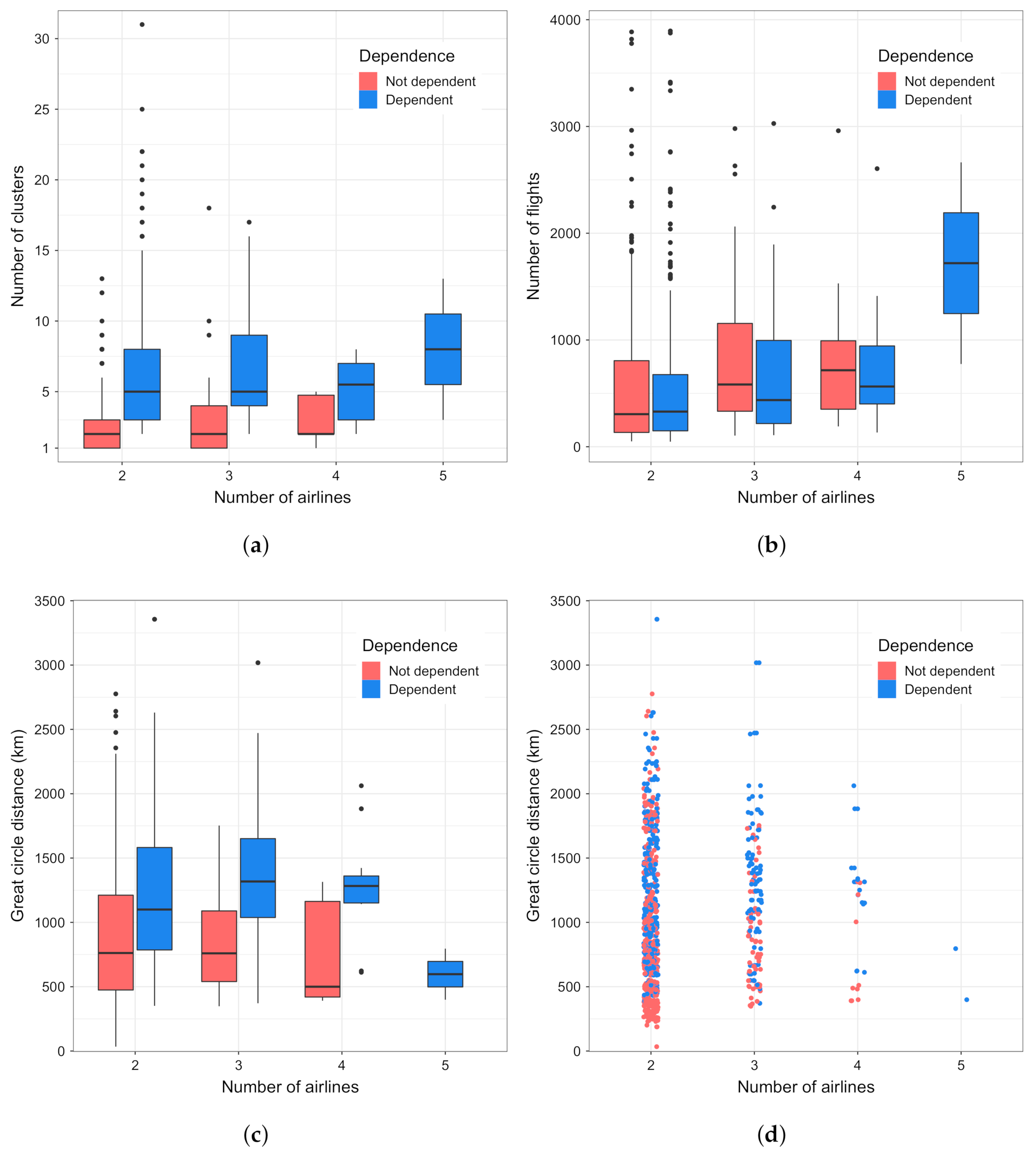
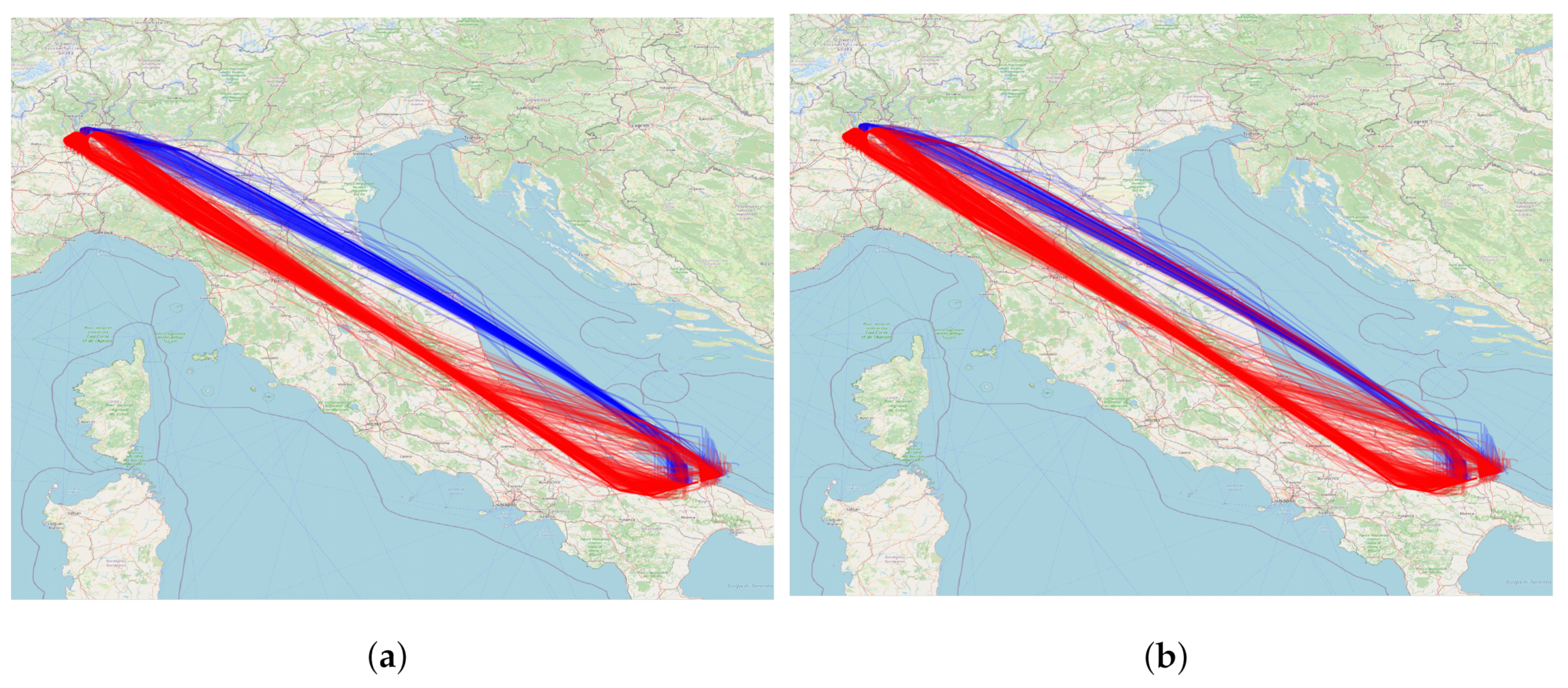
5.1. Relation between Clusters and Airlines
- the OD pairs served by only one airline;
- the OD pairs with less than 30 flights;
- and, for each OD, flights by an airline that had less than 30 flights in the season between that OD.
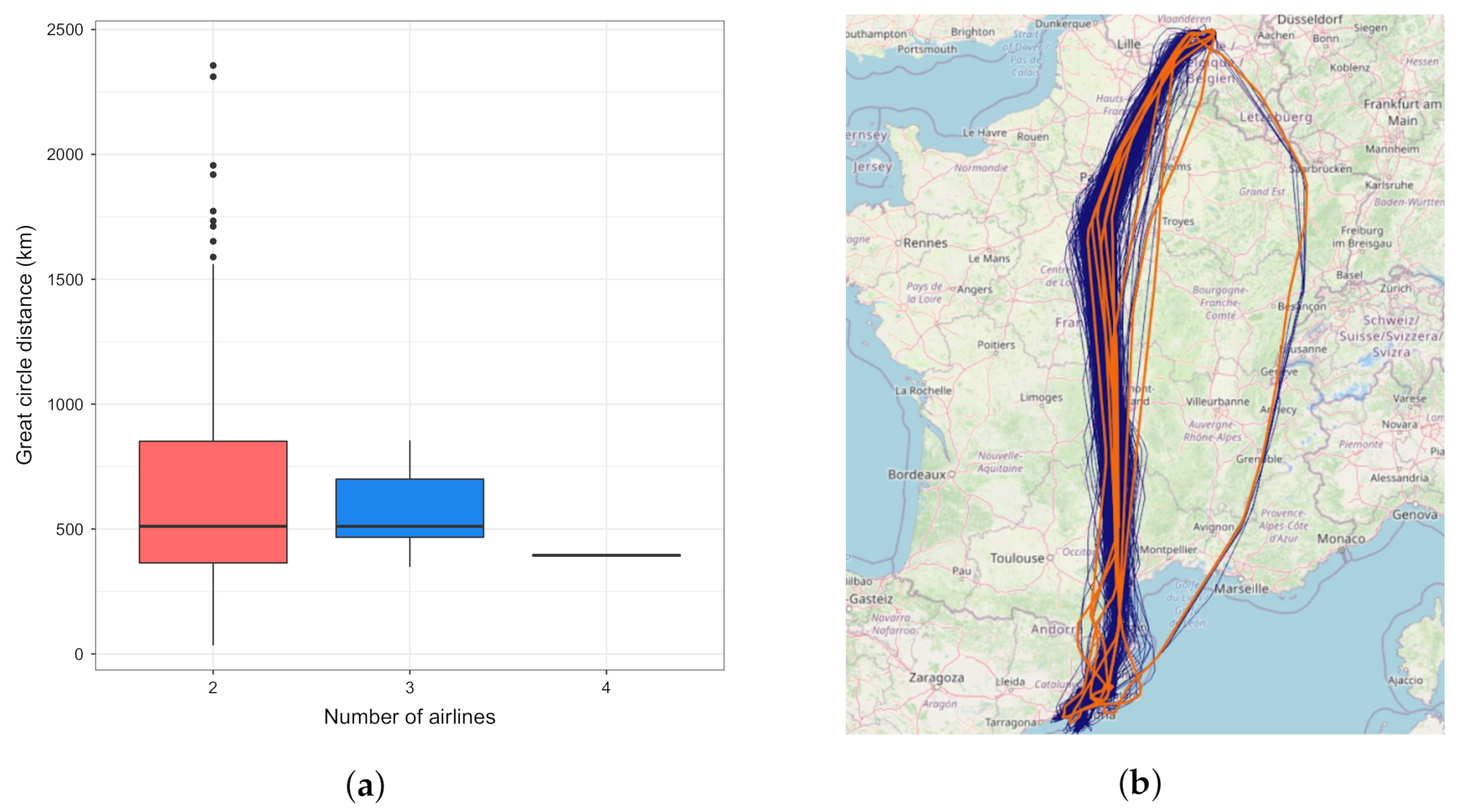
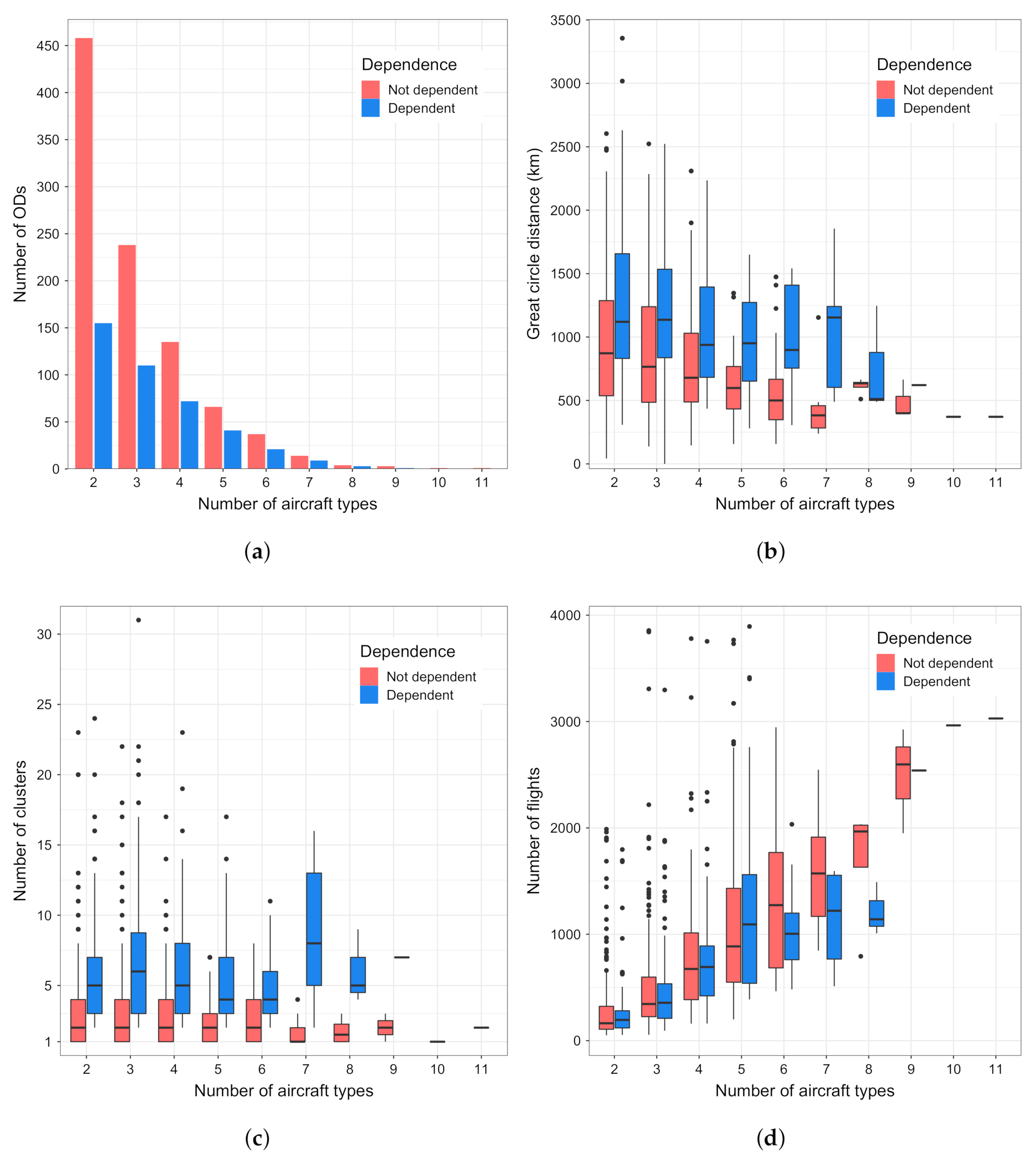
5.2. Relation between Clusters and Aircraft Types
- the OD pairs served by only one aircraft type;
- the OD pairs with less than 30 flights;
- and, for each OD, flights by an aircraft type that had less than 30 flights in the season between that OD,
5.3. Relation between Clusters and the Cost Profile
- the OD pairs with one cost type;
- the OD pairs with less than 30 flights.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACI | Airports Council International |
| ADS-B | Automatic Dependent Surveillance-Broadcast |
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
| ECAC | European Civil Aviation Conference |
| GCD | Great-Circle Distance |
| MTOW | Maximum Take-off Weight |
| OD | Origin-Destination |
| TMA | Terminal Manoeuvring Area |
References
- Bourgois, M.; Sfyroeras, M. Open data for air transport research: Dream or reality? In Proceedings of the International Symposium on Open Collaboration, Berlin, Germany, 27–29 August 2014; p. 17. [Google Scholar]
- Spinielli, E.; Koelle, R.; Barker, K.; Korbey, N. Open Flight Trajectories for Reproducible ANS Performance Review. In Proceedings of the SIDs 2018, 8th SESAR Innovation Days, Salzburg, Austria, 4–6 December 2018. [Google Scholar]
- Schafer, M.; Strohmeier, M.; Smith, M.; Fuchs, M.; Pinheiro, R.; Lenders, V.; Martinovic, I. OpenSky report 2016: Facts and figures on SSR mode S and ADS-B usage. In Proceedings of the 2016 IEEE/AIAA 35th Digital Avionics Systems Conference (DASC), Sacramento, CA, USA, 25–29 September 2016; pp. 1–9. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. Berkeley Symp. Math. Stat. Probab. 1967, 1, 281–297. [Google Scholar]
- Murtagh, F.; Contreras, P. Algorithms for hierarchical clustering: An overview. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2012, 2, 86–97. [Google Scholar] [CrossRef]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. ACM Sigmod Rec. 1999, 28, 49–60. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. Kdd 1996, 96, 226–231. [Google Scholar]
- Gariel, M.; Srivastava, A.N.; Feron, E. Trajectory clustering and an application to airspace monitoring. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1511–1524. [Google Scholar] [CrossRef] [Green Version]
- Basora, L.; Morio, J.; Mailhot, C. A Trajectory Clustering Framework to Analyse Air Traffic Flows. In Proceedings of the SIDs 2017, 7th SESAR Innovation Days, Belgrade, Serbia, 28–30 November 2017. [Google Scholar]
- Nicol, F.; Puechmorel, S. Unsupervised aircraft trajectories clustering: A minimum entropy approach. In Proceedings of the ALLDATA 2016, Lisbonne, Portugal, 21–25 February 2016; pp. 35–41. [Google Scholar]
- Puechmorel, S.; Nicol, F. Entropy minimizing curves with application to flight path design and clustering. Entropy 2016, 18, 337. [Google Scholar] [CrossRef] [Green Version]
- Olive, X.; Basora, L. Identifying Anomalies in past en-route Trajectories with Clustering and Anomaly Detection Methods. In Proceedings of the Thirteenth USA/Europe Air Traffic Management Research and Development Seminar (ATM2019), Vienna, Austria, 17–21 June 2019. [Google Scholar]
- Olive, X.; Basora, L.; Viry, B.; Alligier, R. Deep Trajectory Clustering with Autoencoders. In Proceedings of the International Conference for Research in Air Transportation (ICRAT 2020), Virtual Event, 15 September 2020. [Google Scholar]
- Corrado, S.J.; Puranik, T.G.; Pinon, O.J.; Mavris, D.N. Trajectory Clustering within the Terminal Airspace Utilizing a Weighted Distance Function. Proceedings 2020, 59, 7. [Google Scholar] [CrossRef]
- Poppe, M.; Buxbaum, J. Clustering Climb Profiles for Vertical Trajectory Analysis. In Proceedings of the SIDs 2020, 10th SESAR Innovation Days, Virtual Event, 7–10 December 2020. [Google Scholar]
- Chen, G.; Rosenow, J.; Schultz, M.; Okhrin, O. Using Open Source Data for Landing Time Prediction with Machine Learning Methods. Proceedings 2020, 59, 5. [Google Scholar] [CrossRef]
- Jesse, C.; Liu, H.; Smart, E.; Brown, D. Analysing flight data using clustering methods. In Proceedings of the International Conference on Knowledge-Based and Intelligent Information and Engineering Systems, Zagreb, Croatia, 3–5 September 2018; Springer: Berlin/Heidelberg, Germany, 2008; pp. 733–740. [Google Scholar]
- Ayhan, S.; Samet, H. Time series clustering of weather observations in predicting climb phase of aircraft trajectories. In Proceedings of the 9th ACM SIGSPATIAL International Workshop on Computational Transportation Science, Burlingame, CA, USA, 31 October–3 November 2016; pp. 25–30. [Google Scholar]
- Annoni, R.; Forster, C.H. Analysis of aircraft trajectories using fourier descriptors and kernel density estimation. In Proceedings of the 2012 15th International IEEE Conference on Intelligent Transportation Systems, Anchorage, AK, USA, 16–19 September 2012; pp. 1441–1446. [Google Scholar]
- Mcfadyen, A.; O’Flynn, M.; Martin, T.; Campbell, D. Aircraft trajectory clustering techniques using circular statistics. In Proceedings of the 2016 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2016; pp. 1–10. [Google Scholar]
- Marcos, R.; Ros, O.G.C.; Herranz, R. Combining Visual Analytics and Machine Learning for Route Choice Prediction. In Proceedings of the SIDs 2017, 7th SESAR Innovation Days, Belgrade, Serbia, 28–30 November 2017. [Google Scholar]
- Evans, A.D.; Lee, P.U. Using machine-learning to dynamically generate operationally acceptable strategic reroute options. In Proceedings of the Thirteenth USA/Europe Air Traffic Management Research and Development Seminar (ATM2019), Vienna, Austria, 17–21 June 2019. [Google Scholar]
- Rehm, F. Clustering of flight tracks. In Proceedings of the AIAA Infotech@ Aerospace 2010, Atlanta, GA, USA, 20–22 April 2010; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2010; p. 3412. [Google Scholar]
- Atev, S.; Miller, G.; Papanikolopoulos, N.P. Clustering of vehicle trajectories. IEEE Trans. Intell. Transp. Syst. 2010, 11, 647–657. [Google Scholar] [CrossRef]
- Chen, J.; Wang, R.; Liu, L.; Song, J. Clustering of trajectories based on Hausdorff distance. In Proceedings of the 2011 International Conference on Electronics, Communications and Control (ICECC), Ningbo, China, 9–11 September 2011; pp. 1940–1944. [Google Scholar]
- Cook, A.J.; Tanner, G. European Airline Delay Cost Reference Values; Technical report; EUROCONTROL Performance Review Unit: Brussels, Belgium, 2015. [Google Scholar]
- Bolić, T.; Castelli, L.; Corolli, L.; Rigonat, D. Reducing ATFM delays through strategic flight planning. Transp. Res. Part E Logist. Transp. Rev. 2017, 98, 42–59. [Google Scholar] [CrossRef] [Green Version]
- Bolić, T.; Castelli, L.; Rigonat, D. Peak-load pricing for the European Air Traffic Management system using modulation of en-route charges. Eur. J. Transp. Infrastruct. Res. 2017, 17. [Google Scholar] [CrossRef]
- ACI Europe. Top 30 European Airports 2017; Technical Report; Airports Council International: Montréal, QC, Canada, 2017. [Google Scholar]
- Olive, X.; Basora, L. A python toolbox for processing air traffic data: A use case with trajectory clustering. In Proceedings of the 7th OpenSky Workshop 2019, Zurich, Switzerland, 21–22 November 2019. [Google Scholar]
- Olive, X.; Basora, L. Detection and identification of significant events in historical aircraft trajectory data. Transp. Res. Part C Emerg. Technol. 2020, 119, 102737. [Google Scholar] [CrossRef]
- Taha, A.A.; Hanbury, A. An efficient algorithm for calculating the exact Hausdorff distance. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 2153–2163. [Google Scholar] [CrossRef] [PubMed]


| Cluster | ||||
|---|---|---|---|---|
| Airline | 0 | 1 | 2 | 3 |
| Airline 1 | 0 | 4 | 0 | 169 |
| Airline 2 | 198 | 12 | 3 | 0 |
| Cluster | ||
|---|---|---|
| Airline | 0 | 1 |
| Airline 1 | 20 | 346 |
| Airline 2 | 118 | 2 |
| Cluster | |||
|---|---|---|---|
| Airline | Cost Type | 0 | 1 |
| Airline 1 | Low | 105 | 161 |
| Airline 2 | High | 154 | 1 |
| Airline 3 | High | 176 | 6 |
| Airline 4 | High | 176 | 0 |
| Aircraft Type | |||
|---|---|---|---|
| Airline | A | B | C |
| Airline 1 | 187 | 64 | 0 |
| Airline 2 | 0 | 0 | 144 |
| Airline 3 | 0 | 176 | 0 |
| Airline 4 | 0 | 0 | 164 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bolić, T.; Castelli, L.; De Lorenzo, A.; Vascotto, F. Trajectory Clustering for Air Traffic Categorisation. Aerospace 2022, 9, 227. https://doi.org/10.3390/aerospace9050227
Bolić T, Castelli L, De Lorenzo A, Vascotto F. Trajectory Clustering for Air Traffic Categorisation. Aerospace. 2022; 9(5):227. https://doi.org/10.3390/aerospace9050227
Chicago/Turabian StyleBolić, Tatjana, Lorenzo Castelli, Andrea De Lorenzo, and Fulvio Vascotto. 2022. "Trajectory Clustering for Air Traffic Categorisation" Aerospace 9, no. 5: 227. https://doi.org/10.3390/aerospace9050227








