A Modal Interpretation for Aeroelastic Stability Enhancement of Mistuned Bladed Disks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Problem Formulation
2.2. Dynamic Model of the Mistuned Bladed Disk
2.3. Interpretation to the Aerodynamic Damping of the Mistuned Bladed Disk
2.3.1. Level 1: Interpret the Mistuned Aeroelastic Damping
2.3.2. Level 2: Evaluate a Given Mistuned Pattern
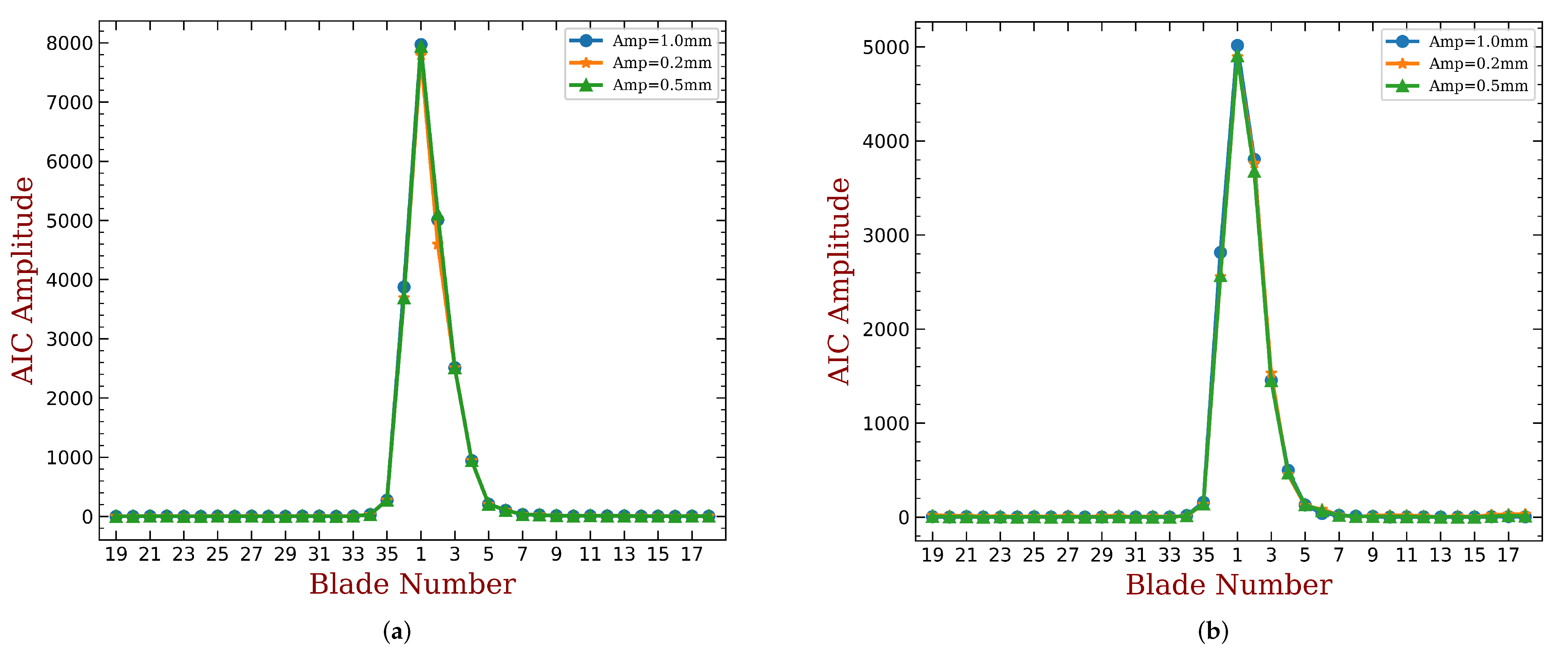
3. Results
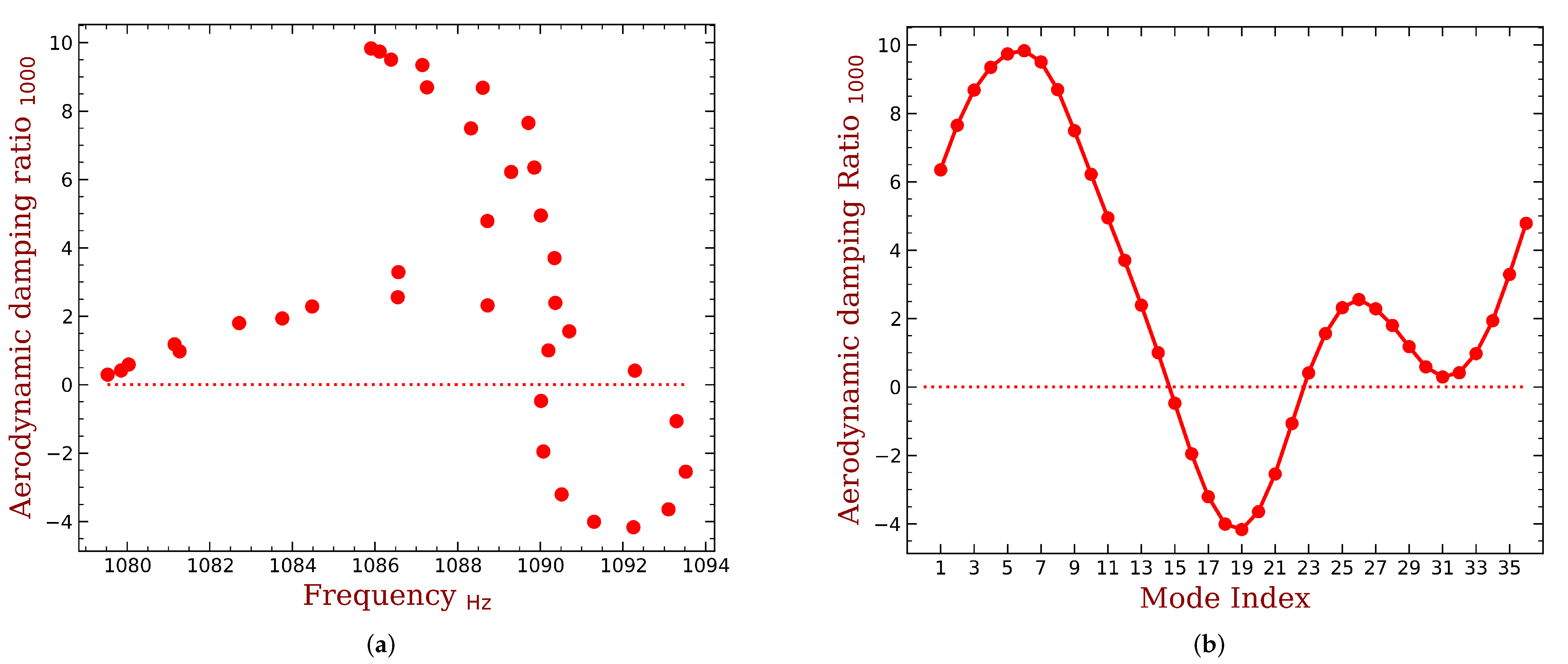
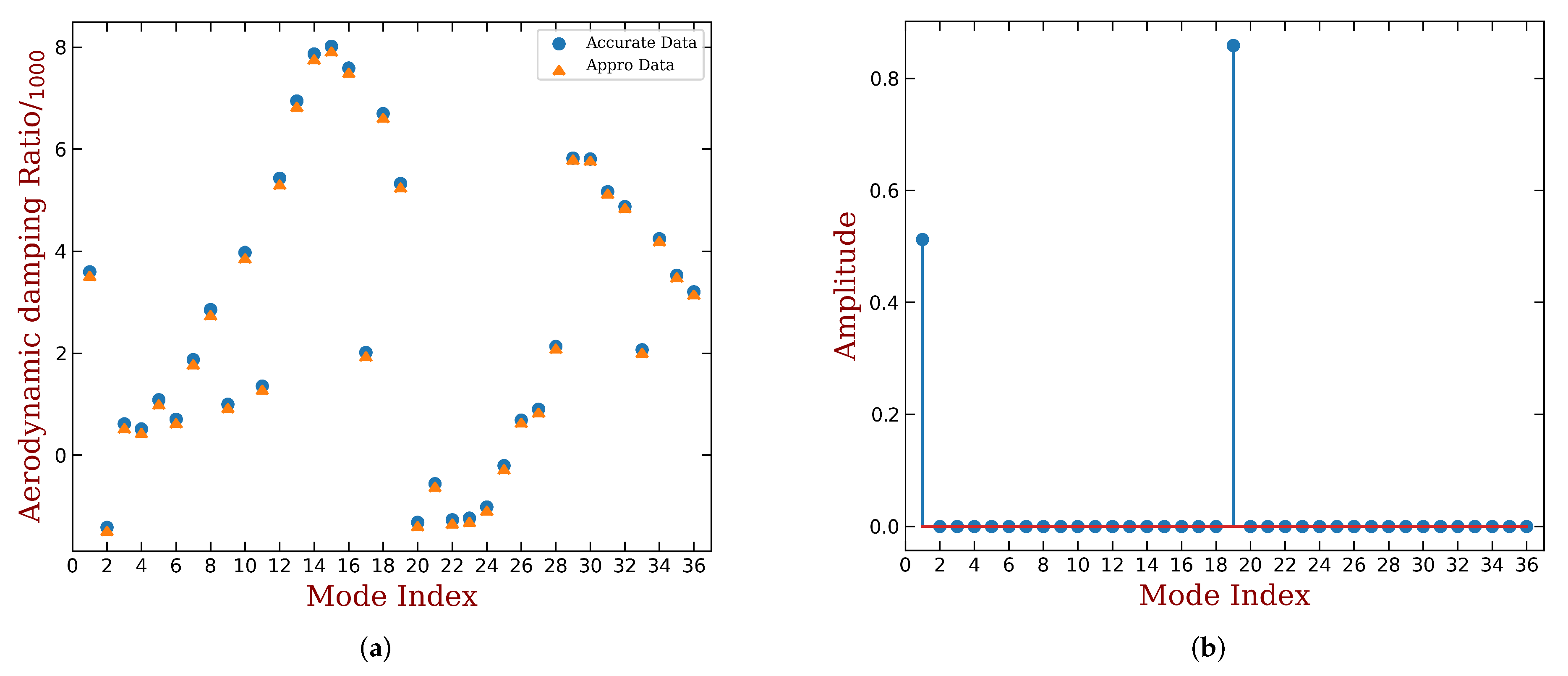
3.1. Aeroelastic Damping of the Tuned Blade Disk
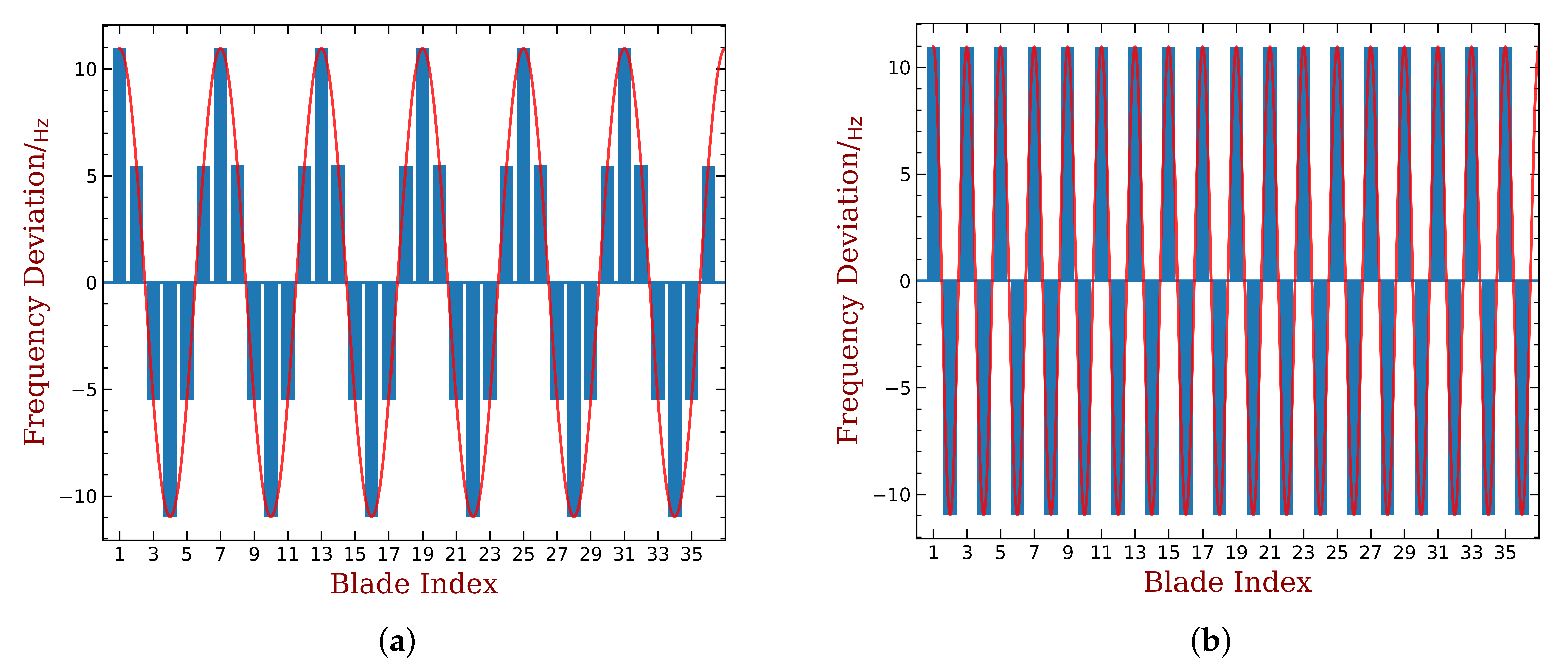
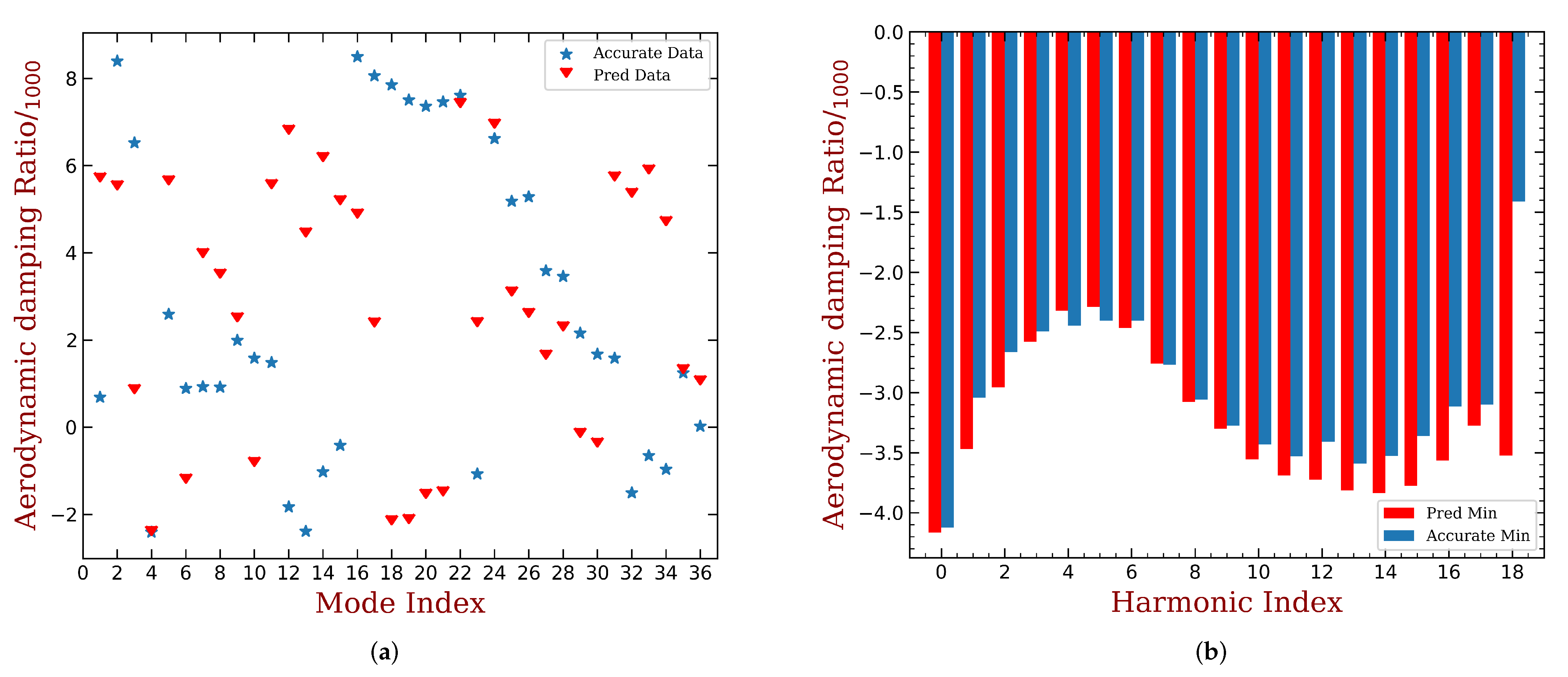
3.2. Interpreting the Aeroelastic Damping of Mistuned Bladed Disk
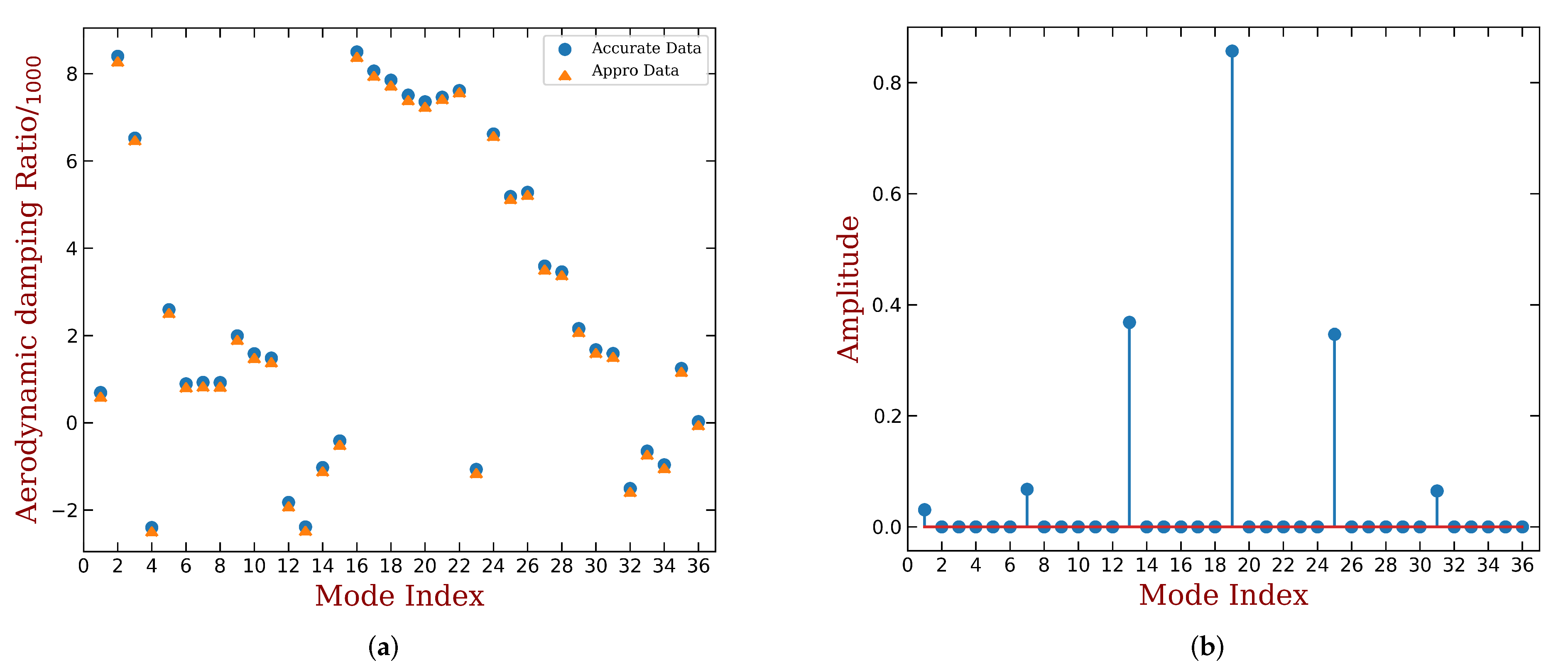
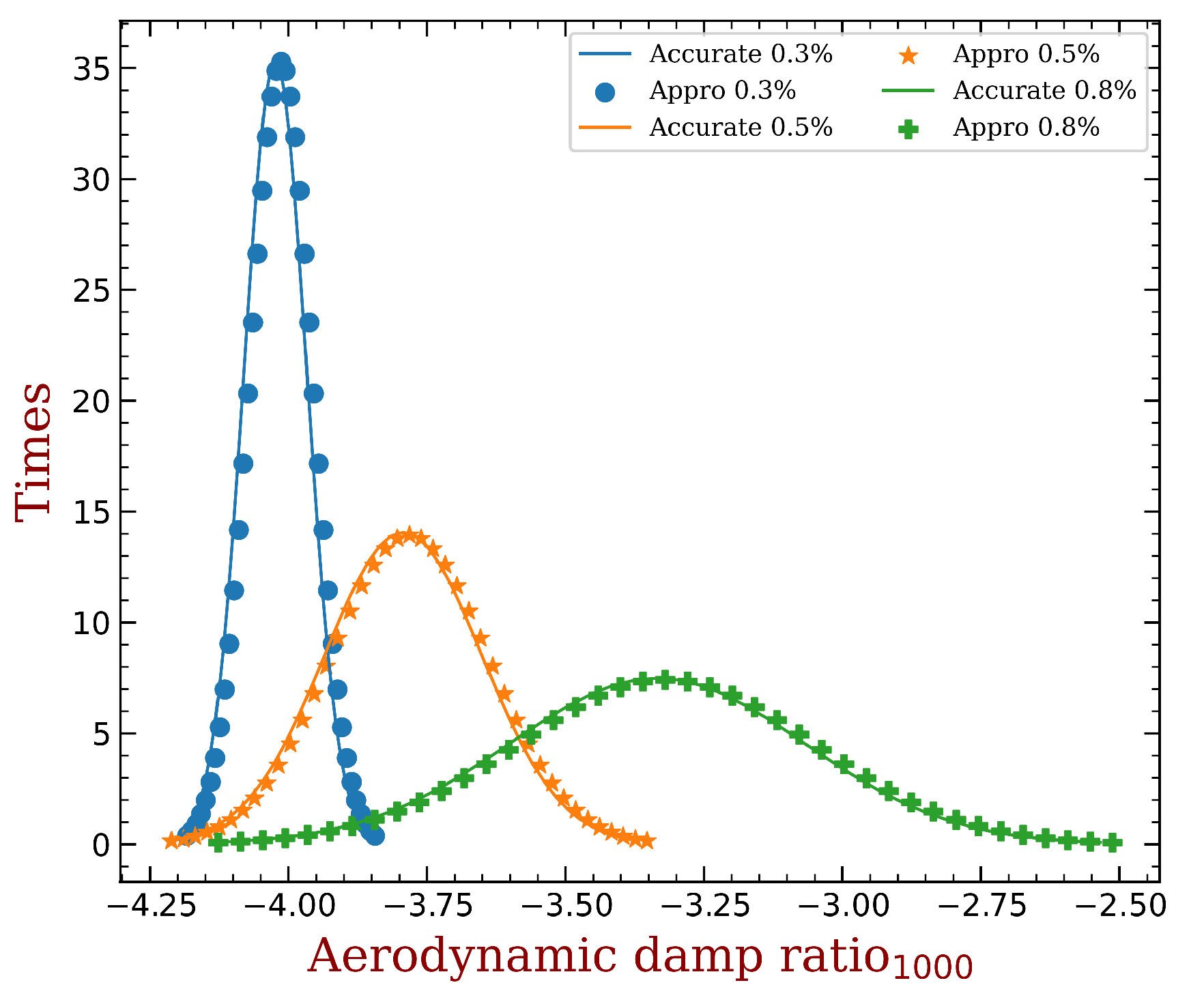
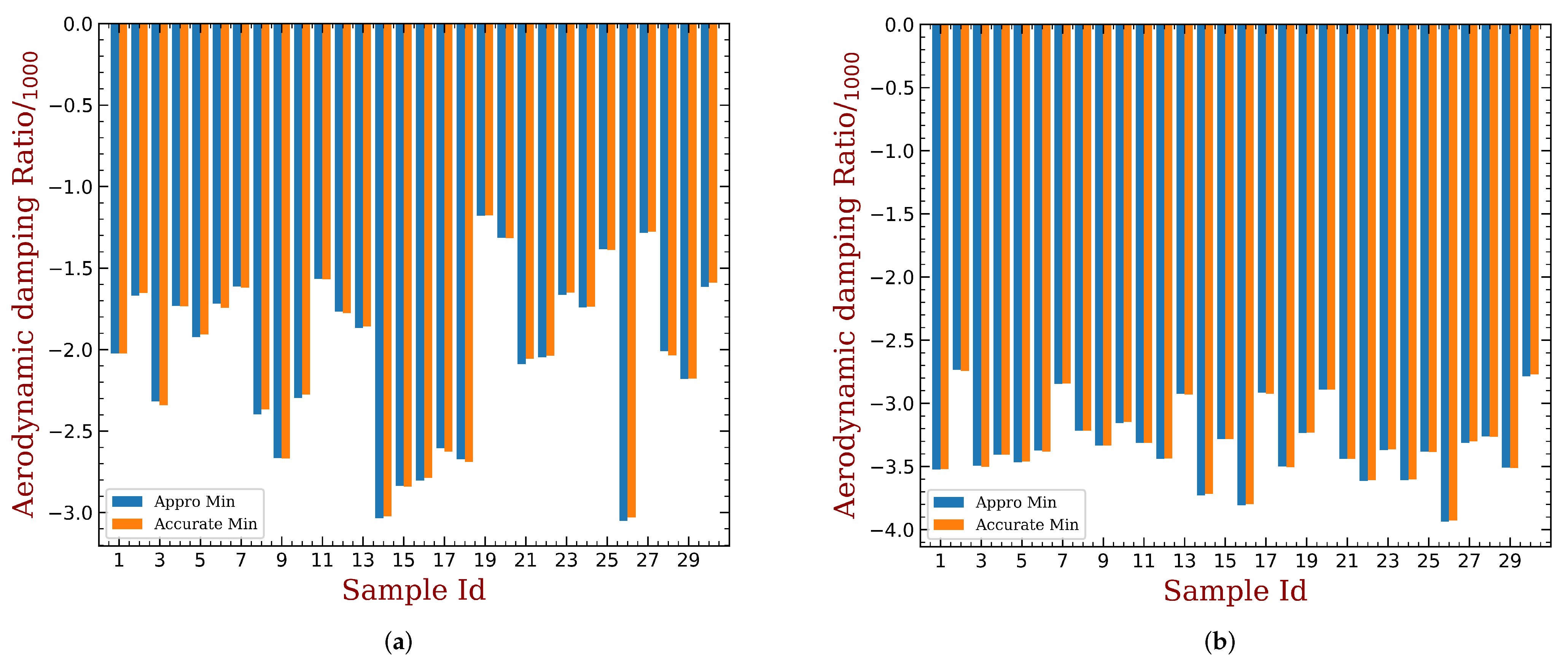
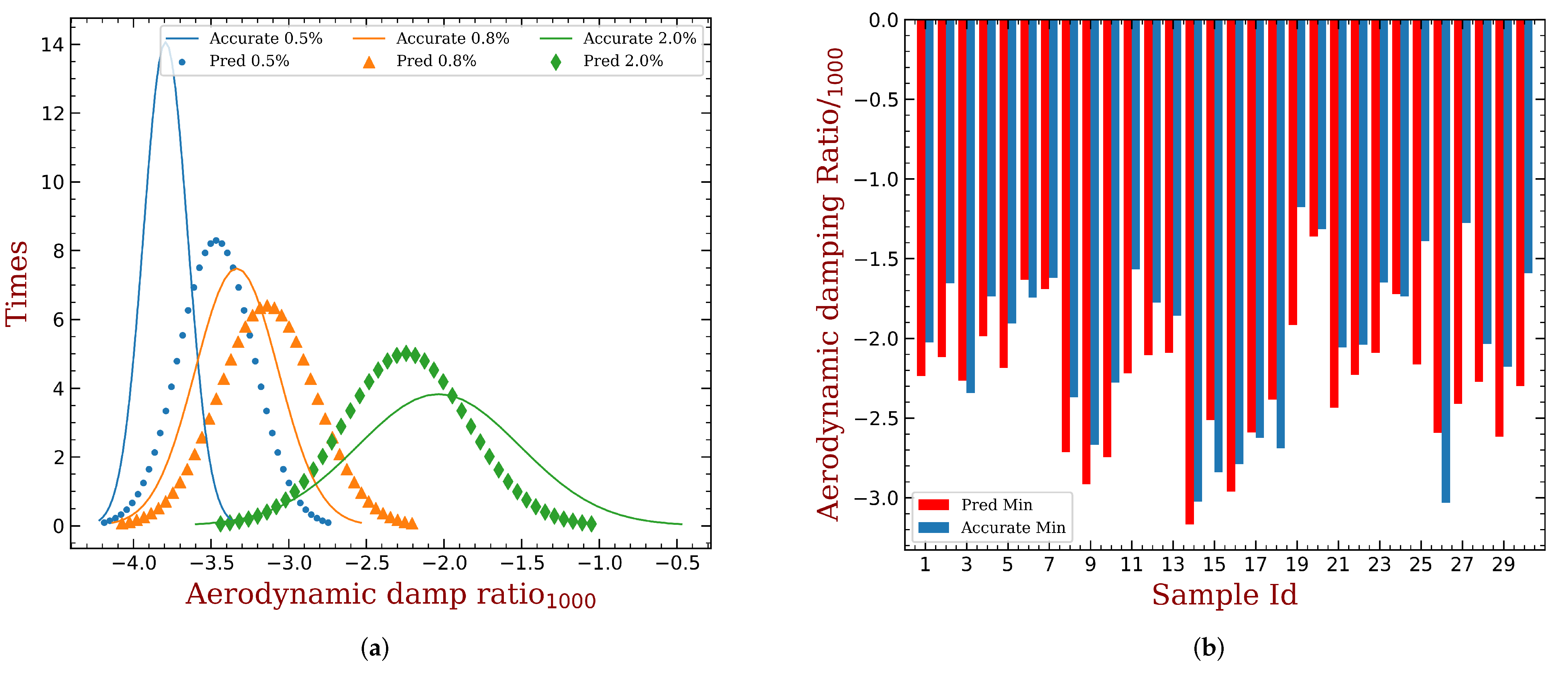
3.3. Predicting the Aeroelastic Enhancement of a Given Mistuning Pattern
4. Discussion
- Mistuning cannot increase and would rather decrease the largest aeroelastic damping ratio. It can be demonstrated that if the kth tuned mode has the largest aeroelastic damping ratio. This happens only when and . It is unlikely to perfectly satisfy this condition if mistuning is presented. However, when the mistuning strength is slight, it is more likely to have mistuned modal shapes dominated by the kth tuned mode, namely . In this case, the difference between and is minor. However, with the increase of mistuning strength, the mistuned modes tend to have a more significant contribution from multiple tuned modes. In this case, the difference between and will also be enlarged.
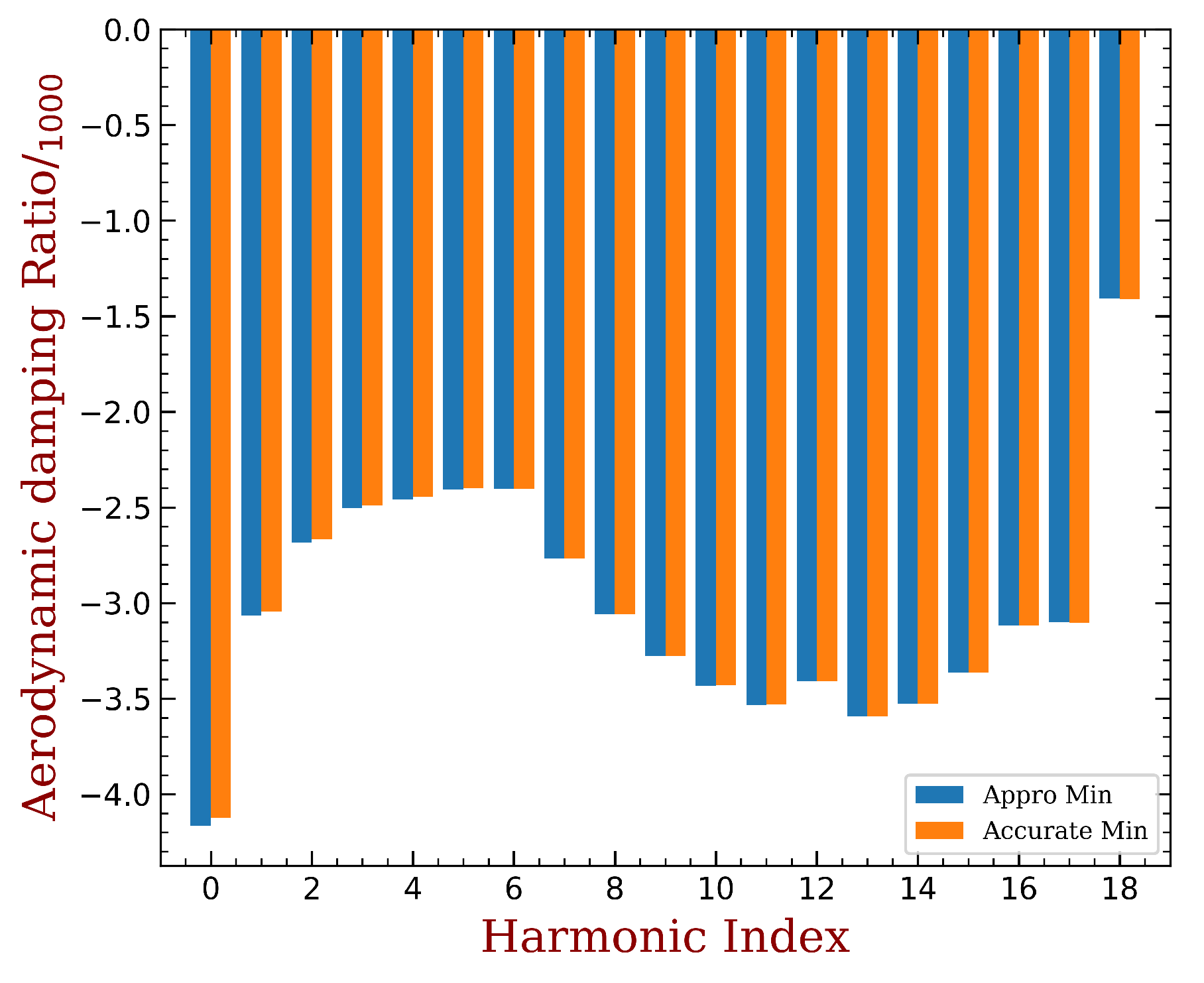
- Mistuning cannot further decrease the smallest aeroelastic damping ratio; thus, it is always beneficial to the aeroelastic stability. It can be demonstrated that if the lth tuned mode has the smallest aeroelastic damping ratio. This happens only when and . As noted earlier, will always be larger than with the presence of mistuning, and this gap is enlarged by the increase of mistuning strength. This remark is illustrated by comparing Figure 8a and Figure 9a with Figure 6b.
- A mistuned mode has higher aeroelastic damping ratio than another, only if its modal has more contribution from the tuned modes with higher aeroelastic damping ratio. The best mistuning pattern is the one who tends to produce modal shapes constructed by the tuned modes with relatively high aeroelastic damping ratio. This remark is illustrated by comparing Figure 8b and Figure 9b with Figure 6b.
5. Conclusions
- (1)
- The aeroelastic damping ratio of a mode in the mistuned bladed disk can be interpreted as follows: it is determined by the contribution of each tuned mode in the associated modal shape. Derivations are given in detail, and the accuracy is validated by numerical investigation. The proposed interpretation is applicable for various mistuning patterns, including the alternate, wave, and random patterns.
- (2)
- Several general conclusions are drawn, confirming the frequently reported trends in the literature [14,15,16,18,31]. First, mistuning cannot increase and would rather decrease the largest aeroelastic damping ratio. Second, mistuning cannot further decrease the smallest aeroelastic damping ratio; thus, it is always beneficial to the aeroelastic stability. Third, a mistuned mode has higher aeroelastic damping ratio than another only if its modal has more contribution from the tuned modes with higher aeroelastic damping ratio.
- (3)
- A prediction method is also proposed, providing an acceptable approximation of the least aeroelastic damping of a given mistuning pattern. This is done with the mistuning and aeroelastic effects analyzed separately. The advantages are two-fold. First, the design of mistuning pattern is accelerated. Second, this allows one to introduce more accurate data or models of aeroelastic damping.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Srinivasan, A.V. Flutter and Resonant Vibration Characteristics of Engine Blades: An IGTI Scholar Paper. In Proceedings of the ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition, Orlando, FL, USA, 2–5 June 1997. [Google Scholar] [CrossRef] [Green Version]
- Whitehead, D.S. Effect of Mistuning on the Vibration of Turbo-Machine Blades Induced by Wakes. J. Mech. Eng. Sci. 1966, 8, 15–21. [Google Scholar] [CrossRef]
- Bendiksen, O.O. Flutter of mistimed turbomachinery rotors. J. Eng. Gas Turbines Power 1984, 106, 25–33. [Google Scholar] [CrossRef]
- Groth, P.; Mårtensson, H.; Andersson, C. Design and Experimental Verification of Mistuning of a Supersonic Turbine Blisk. J. Turbomach. 2010, 132, 011012. [Google Scholar] [CrossRef]
- Figaschewsky, F.; Kuhhorn, A.; Beirow, B.; Nipkau, J.; Giersch, T.; Power, B. Design and analysis of an intentional mistuning experiment reducing flutter susceptibility and minimizing forced response of a jet engine fan. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017; Volume 7B-2017, pp. 1–13. [Google Scholar] [CrossRef]
- Biagiotti, S.; Pinelli, L.; Poli, F.; Vanti, F.; Pacciani, R. Numerical Study of Flutter Stabilization in Low Pressure Turbine Rotor with Intentional Mistuning. Energy Procedia 2018, 148, 98–105. [Google Scholar] [CrossRef]
- Corral, R.; Khemiri, O.; Martel, C. Design of mistuning patterns to control the vibration amplitude of unstable rotor blades. Aerosp. Sci. Technol. 2018, 80, 20–28. [Google Scholar] [CrossRef]
- Kaza, K.R.V.; Kielb, R.E. Flutter and response of a mistuned cascade in incompressible flow. AIAA J. 1982, 20, 1120–1127. [Google Scholar] [CrossRef]
- Kielb, R.E.; Kaza, K.R.V. Aeroelastic Characteristics of a Cascade of Mistuned Blades in Subsonic and Supersonic Flows. J. Vib. Acoust. 1983, 105, 425–433. [Google Scholar] [CrossRef] [Green Version]
- Kielb, R.E.; Kaza, K.R.V. Effects of Structural Coupling on Mistuned Cascade Flutter and Response. J. Eng. Gas Turbines Power 1984, 106, 17–24. [Google Scholar] [CrossRef] [Green Version]
- Crawley, E.F.; Hall, K.C. Optimization and Mechanisms of Mistuning in Cascades. J. Eng. Gas Turbines Power 1985, 107, 418–426. [Google Scholar] [CrossRef]
- Shapiro, B. Symmetry approach to extension of flutter boundaries via mistuning. J. Propuls. Power 1998, 14, 354–366. [Google Scholar] [CrossRef] [Green Version]
- Kielb, R.E.; Hall, K.C.; Hong, E.; Pai, S.S. Probabilistic Flutter Analysis of a Mistuned Bladed Disks. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; pp. 1145–1150. [Google Scholar] [CrossRef]
- Li, L.; Yu, X.; Wang, P. Research on aerodynamic damping of bladed disk with random mistuning. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017; Volume 7B-2017, p. V07BT36A010. [Google Scholar] [CrossRef]
- Liu, X.; Li, L.; Fan, Y.; Deng, P. Improving the Aero-Elastic Stability of Bladed Disks through Parallel Piezoelectric Network. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y. Mistuning Effects on Aero-elastic Stability of Contra-Rotating Turbine Blades. Int. J. Aeronaut. Space Sci. 2019, 20, 100–113. [Google Scholar] [CrossRef]
- Fang, M.; Wang, Y. Intentional Mistuning Effect on the Blisk Vibration with Aerodynamic Damping. AIAA J. 2022, 1–10. [Google Scholar] [CrossRef]
- Liu, X.; Fan, Y.; Li, L.; Yu, X. Improving Aeroelastic Stability of Bladed Disks with Topologically Optimized Piezoelectric Materials and Intentionally Mistuned Shunt Capacitance. Materials 2022, 15, 1309. [Google Scholar] [CrossRef] [PubMed]
- Martel, C.; Corral, R.; Llorens, J.M. Stability Increase of Aerodynamically Unstable Rotors Using Intentional Mistuning. J. Turbomach. 2008, 130, 011006. [Google Scholar] [CrossRef]
- Bleeg, J.M.; Yang, M.T.; Eley, J.A. Aeroelastic Analysis of Rotors With Flexible Disks and Alternate Blade Mistuning. J. Turbomach. 2009, 131, 1–9. [Google Scholar] [CrossRef]
- Martel, C.; Sánchez, J.J. Intentional Mistuning with Predominant Aerodynamic Effects. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018; Volume 7C, pp. 1–11. [Google Scholar] [CrossRef]
- Hsu, K.; Hoyniak, D. A fast influence coefficient method for aerodynamically mistuned disks aeroelasticity analysis. J. Eng. Gas Turbines Power 2011, 133, 1–10. [Google Scholar] [CrossRef]
- Panovsky, J.; Kielb, R.E. A design method to prevent low pressure turbine blade flutter. In Proceedings of the ASME 1998 International Gas Turbine and Aeroengine Congress and Exhibition, Stockholm, Sweden, 2–5 June 1998; Volume 5. [Google Scholar] [CrossRef] [Green Version]
- Campobasso, M.S.; Giles, M.B. Analysis of The Effect of Mistuning on Turbomachinery Aeroelasticity. In Proceedings of the 9th International Symposium on Unsteady Aerodynamics, Aeroacoustics and Aeroelasticity of Turbomachines, Lyon, France, 4–8 September 2000; pp. 885–896. [Google Scholar]
- Ewins, D.J. Vibration Modes of Mistuned Bladed Disks. J. Eng. Power 1976, 98, 349–355. [Google Scholar] [CrossRef]
- Slater, J.C.; Minkiewicz, G.R.; Blair, A.J. Forced Response of Bladed Disk Assemblies—A Survey. Shock Vib. Dig. 1999, 31, 17–24. [Google Scholar] [CrossRef]
- Castanier, M.P.; Pierre, C. Modeling and Analysis of Mistuned Bladed Disk Vibration: Current Status and Emerging Directions. J. Propuls. Power 2006, 22, 384–396. [Google Scholar] [CrossRef]
- Srinivasan, A.V. Vibrations of Bladed-Disk Assemblies—A Selected Survey (Survey Paper). J. Vib. Acoust. 1984, 106, 165–168. [Google Scholar] [CrossRef]
- Feiner, D.M.; Griffin, J.H. A Fundamental Model of Mistuning for a Single Family of Modes. J. Turbomach. 2002, 124, 597. [Google Scholar] [CrossRef]
- Hanamura, Y.; Tanaka, H.; Yamaguchi, K. A Simplified Method to Measure Unsteady Forces Acting on the Vibrating Blades in Cascade. Bull. JSME 1980, 23, 880–887. [Google Scholar] [CrossRef] [Green Version]
- Fu, Z.; Wang, Y. Aeroelastic Analysis of a Transonic Fan Blade with Low Hub-to-Tip Ratio including Mistuning Effects. J. Power Energy Eng. 2015, 3, 362–372. [Google Scholar] [CrossRef]
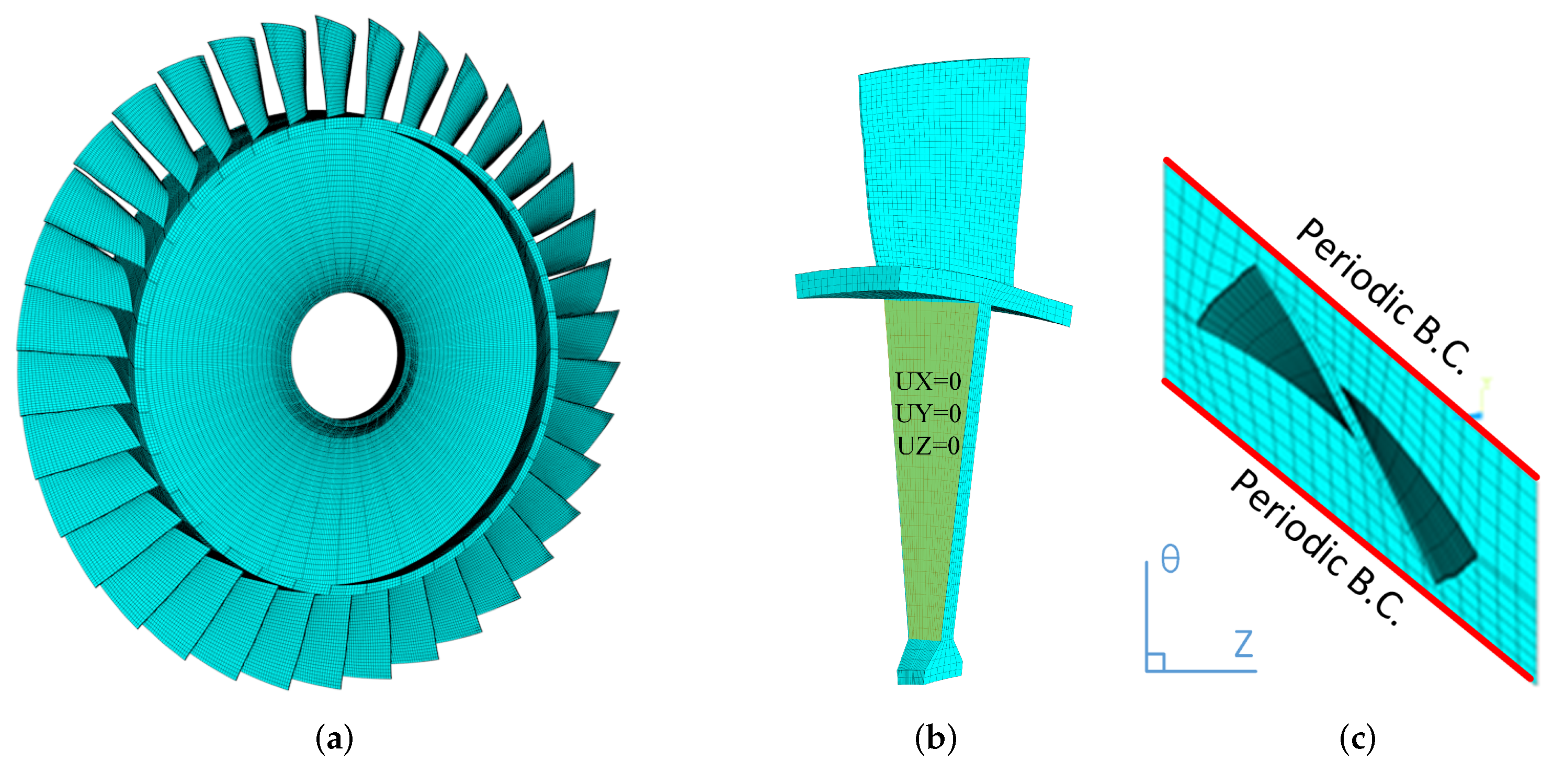
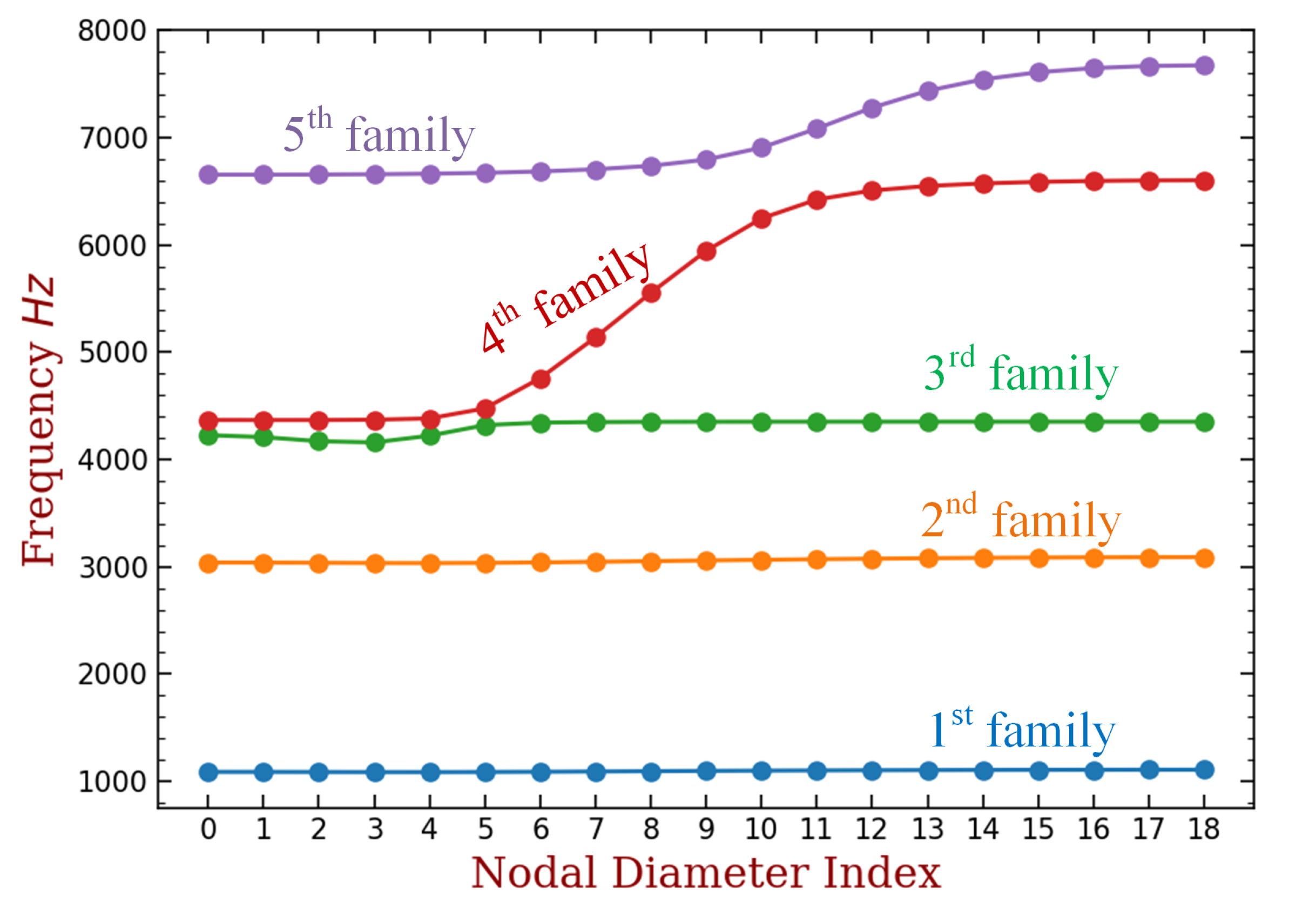
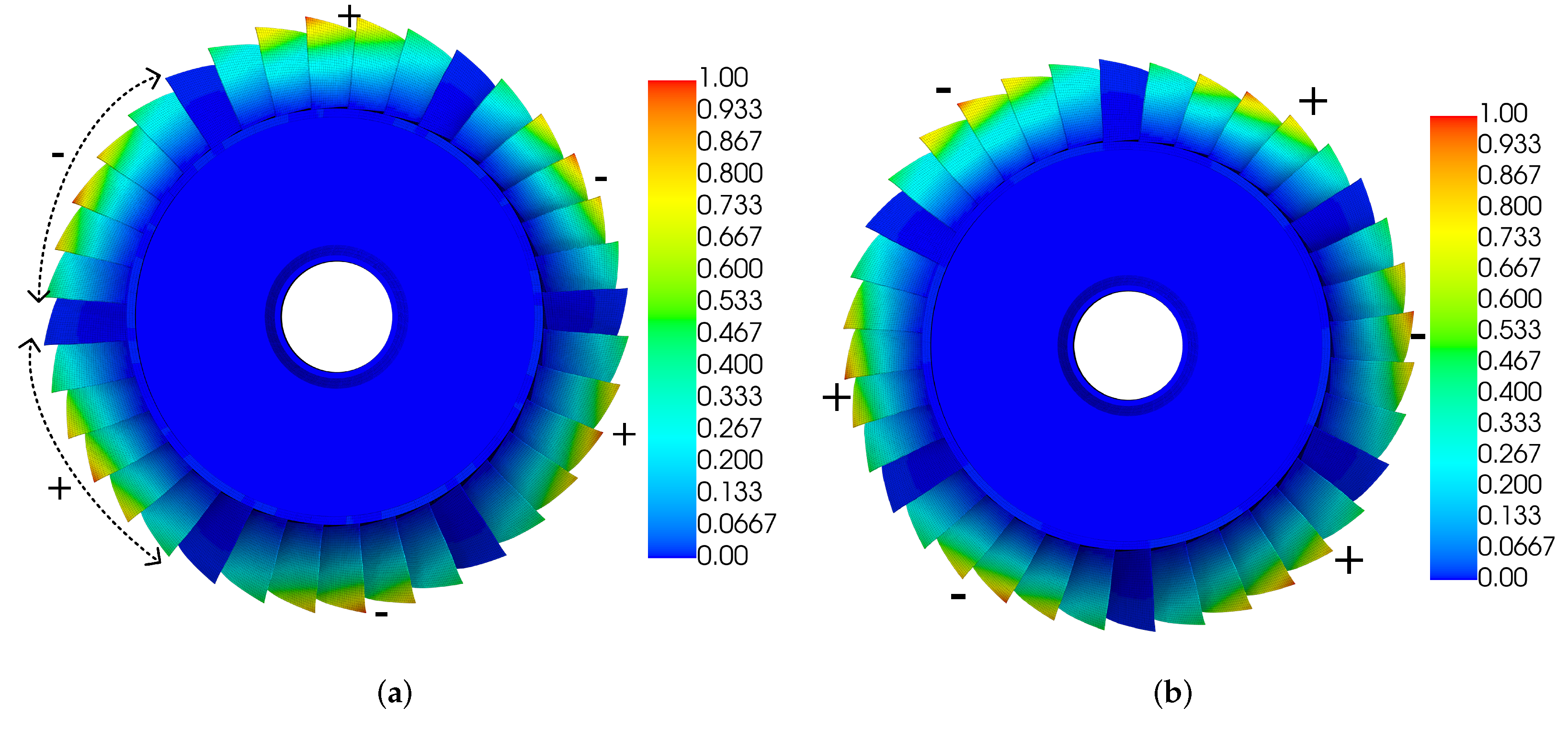
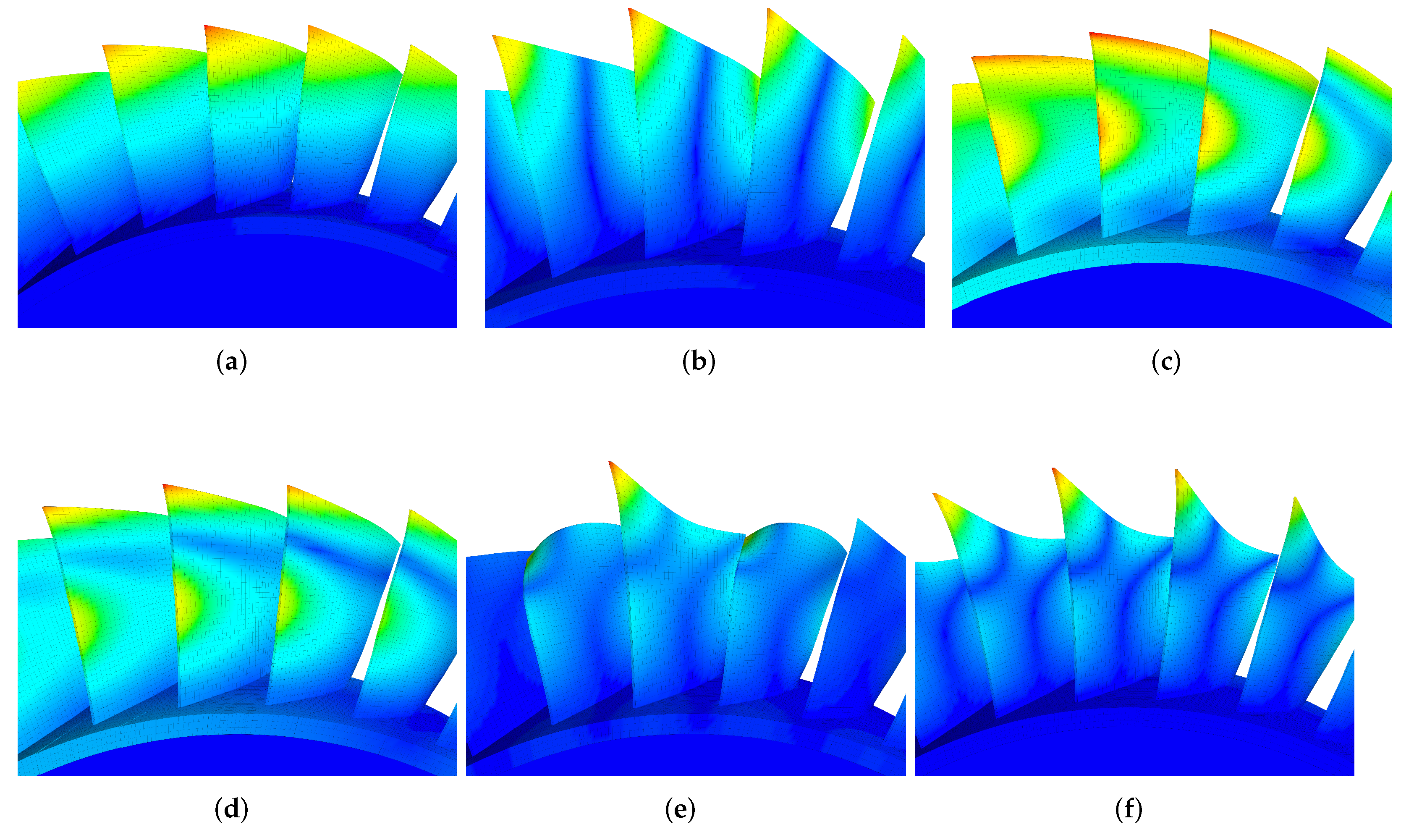
| Parameter | Value (Design Point) | Value (Unstable) |
|---|---|---|
| Number of blades | 36 | unchanged |
| Designed speed (rpm) | 17,188.7 | unchanged |
| Designed pressure ratio | 2.1 | 2.4 |
| Blade tip speed (m/s) | 454 | unchanged |
| Average blade tip clearance (mm) | 0.356 | unchanged |
| Aspect ratio | 1.1 | unchanged |
| Inlet hub ratio | 0.7 | unchanged |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Fan, Y.; Li, L.; Yu, X. A Modal Interpretation for Aeroelastic Stability Enhancement of Mistuned Bladed Disks. Aerospace 2022, 9, 265. https://doi.org/10.3390/aerospace9050265
Liu X, Fan Y, Li L, Yu X. A Modal Interpretation for Aeroelastic Stability Enhancement of Mistuned Bladed Disks. Aerospace. 2022; 9(5):265. https://doi.org/10.3390/aerospace9050265
Chicago/Turabian StyleLiu, Xin, Yu Fan, Lin Li, and Xiaoping Yu. 2022. "A Modal Interpretation for Aeroelastic Stability Enhancement of Mistuned Bladed Disks" Aerospace 9, no. 5: 265. https://doi.org/10.3390/aerospace9050265







