Simultaneous Pressure and Displacement Measurement on Helicopter Rotor Blades Using a Binocular Stereophotogrammetry PSP System
Abstract
:1. Introduction
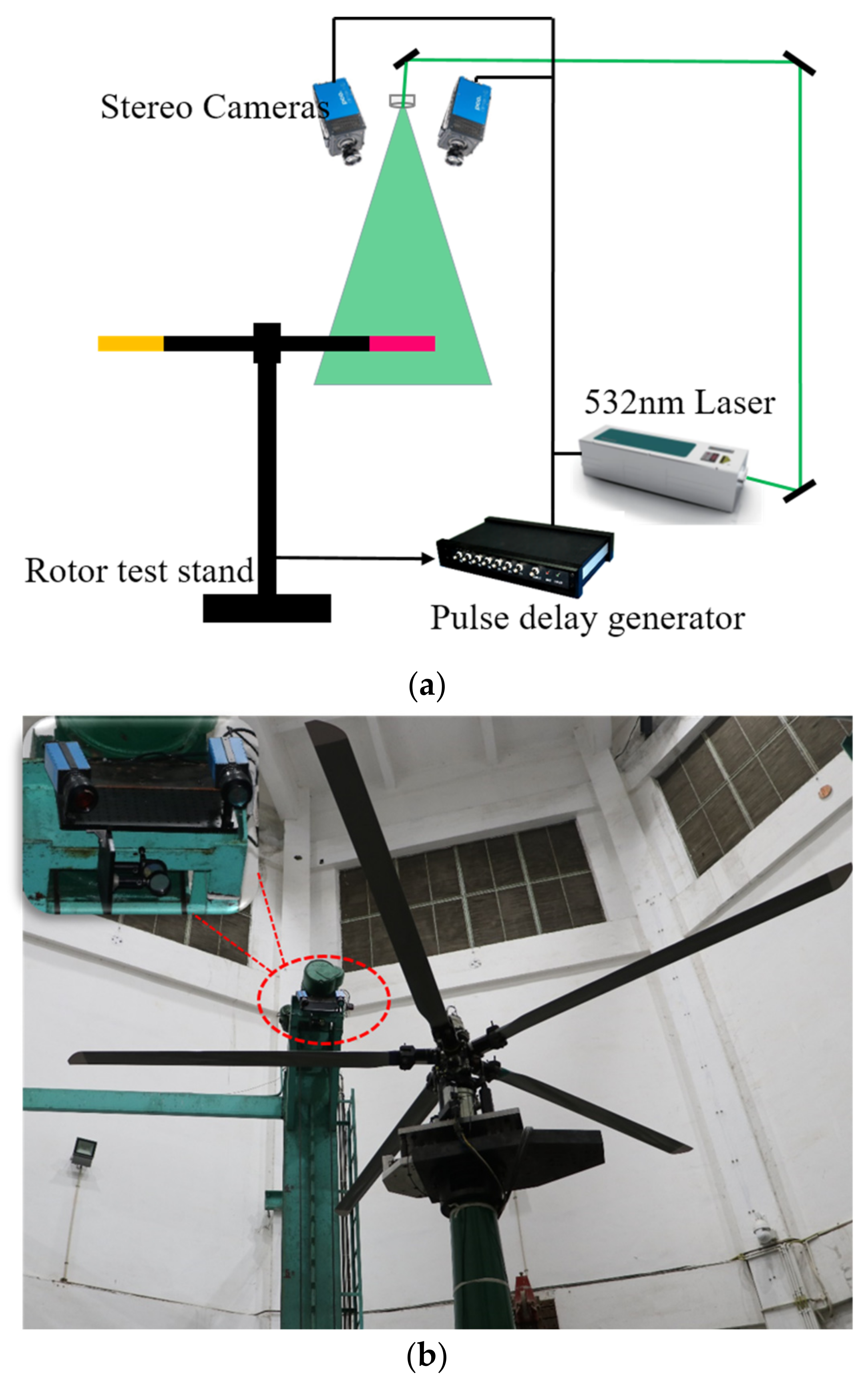
2. Experimental Setup
2.1. Rotor Test Stand and Model
2.2. Measurement Setup
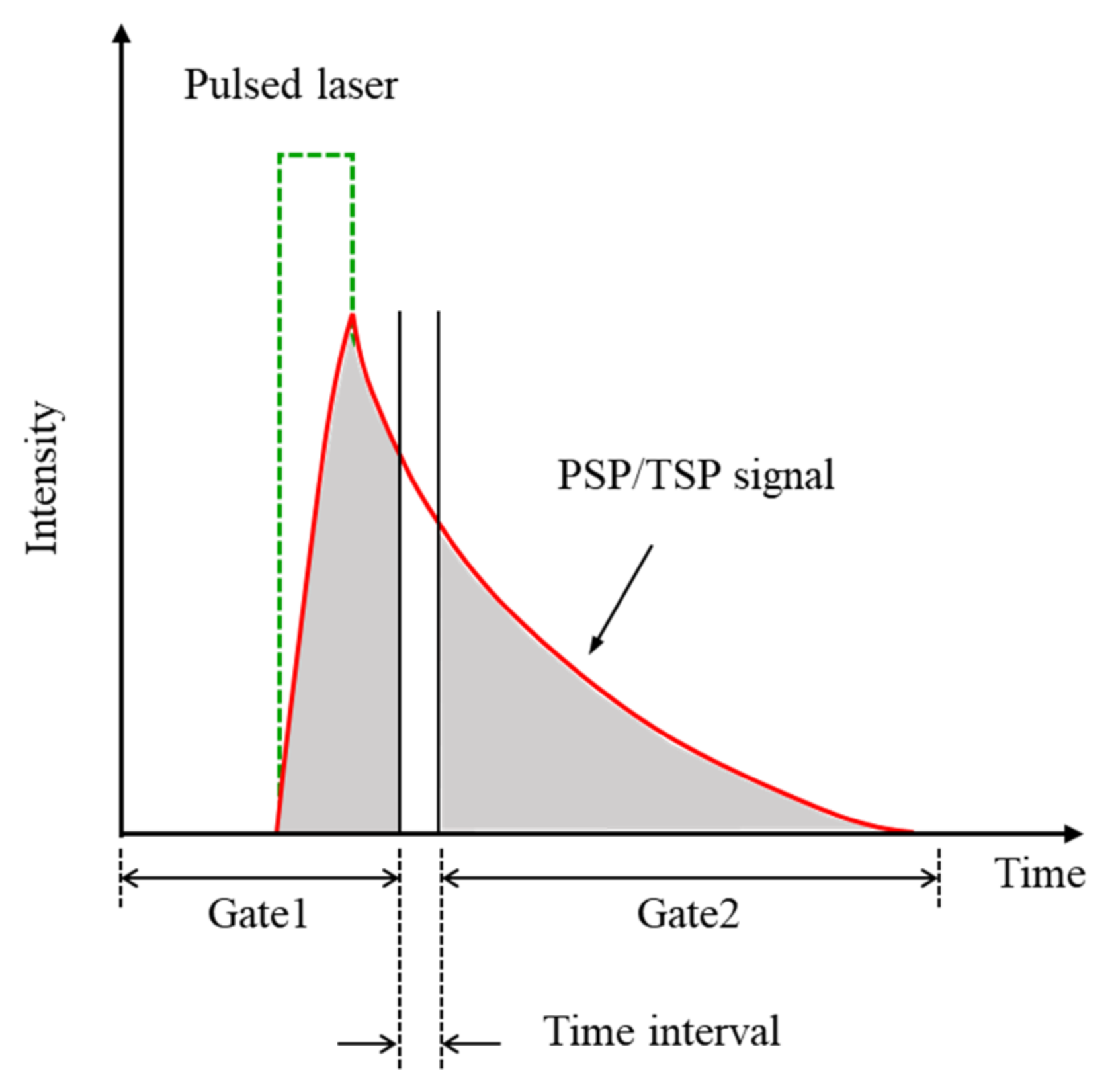
2.3. Data Acquisition
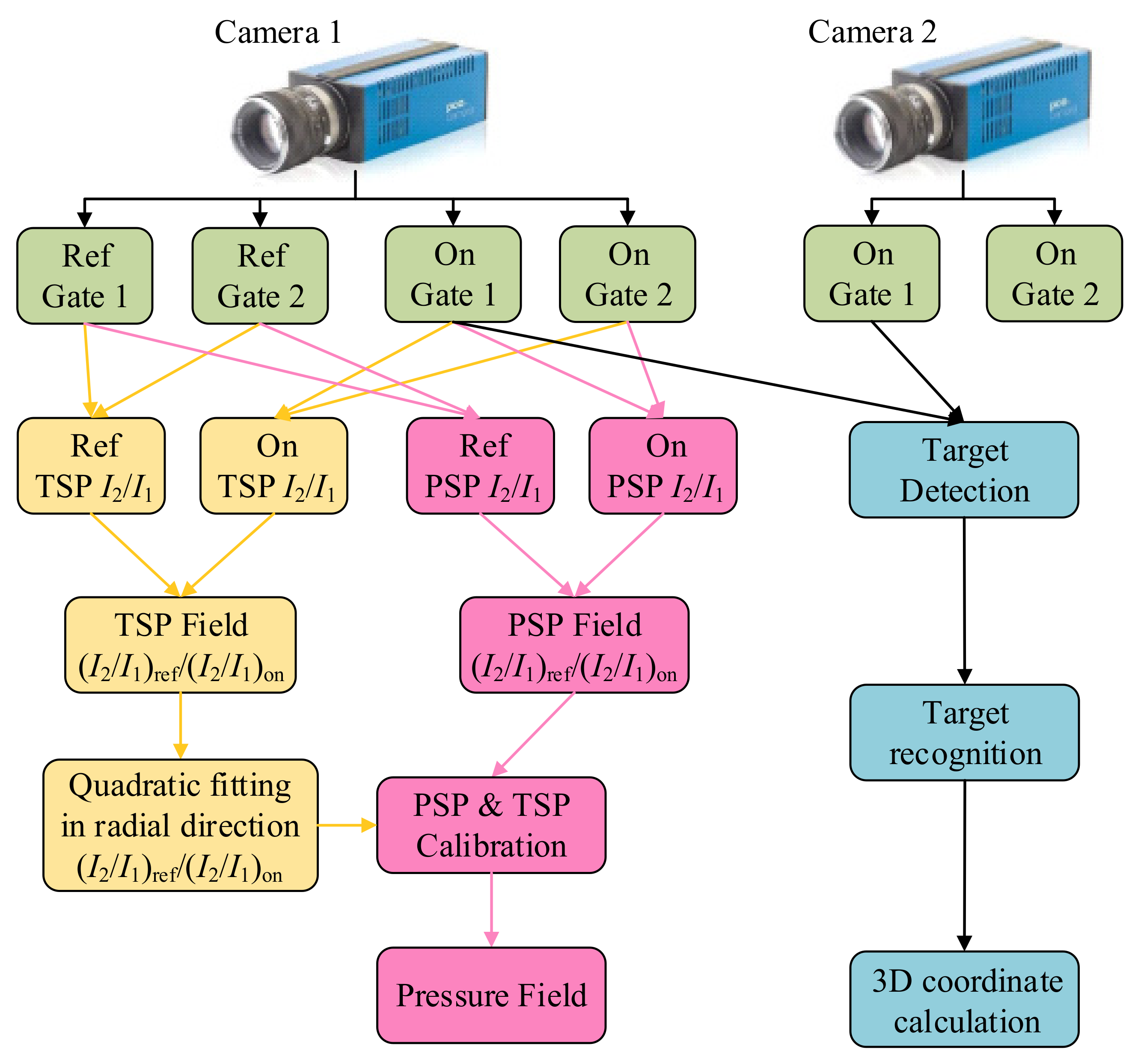
3. Data Processing
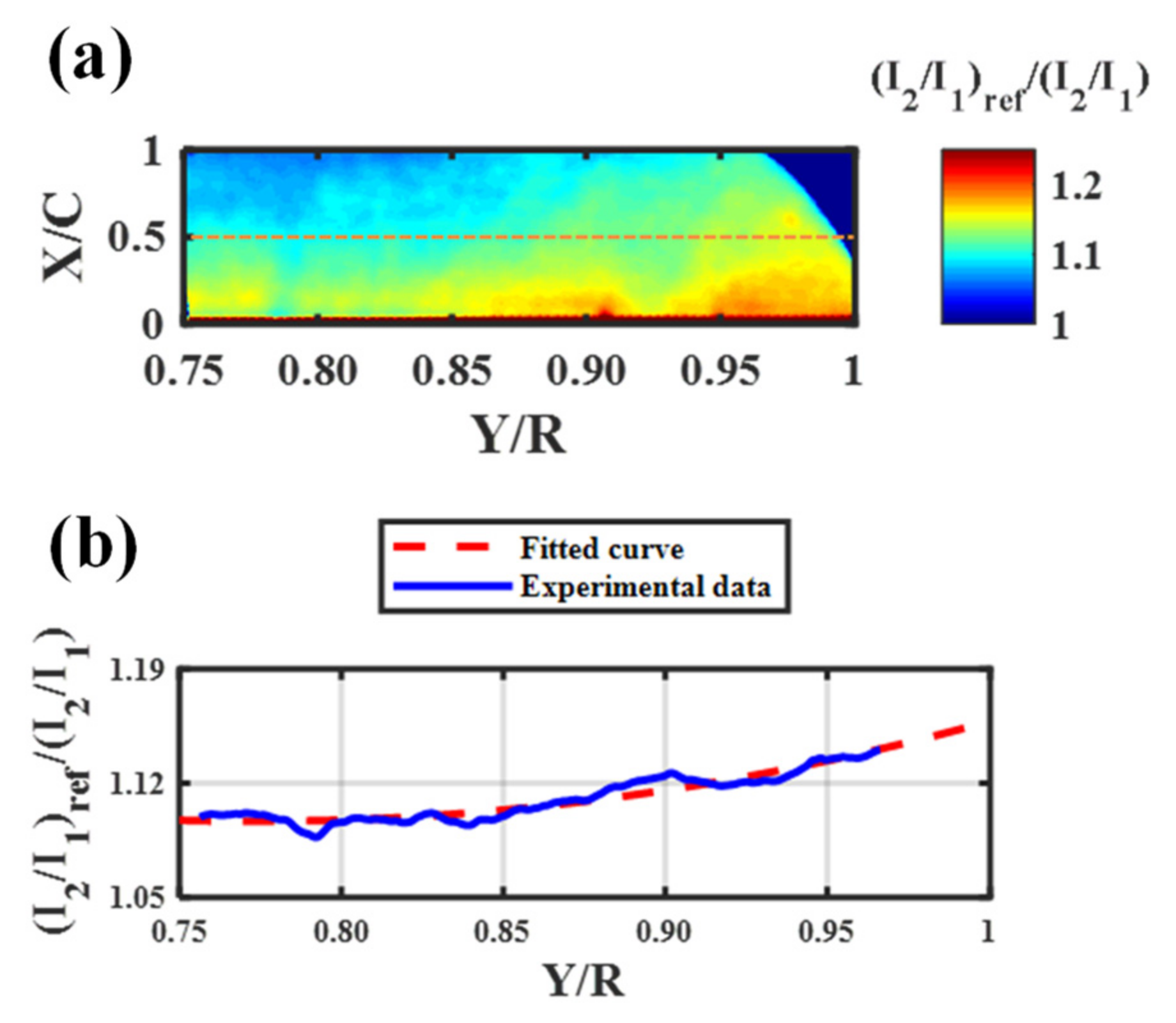
3.1. PSP Paint Calibration
3.2. PSP Temperature Correction
3.3. Binocular Stereophotogrammetry
4. Results and Discussion
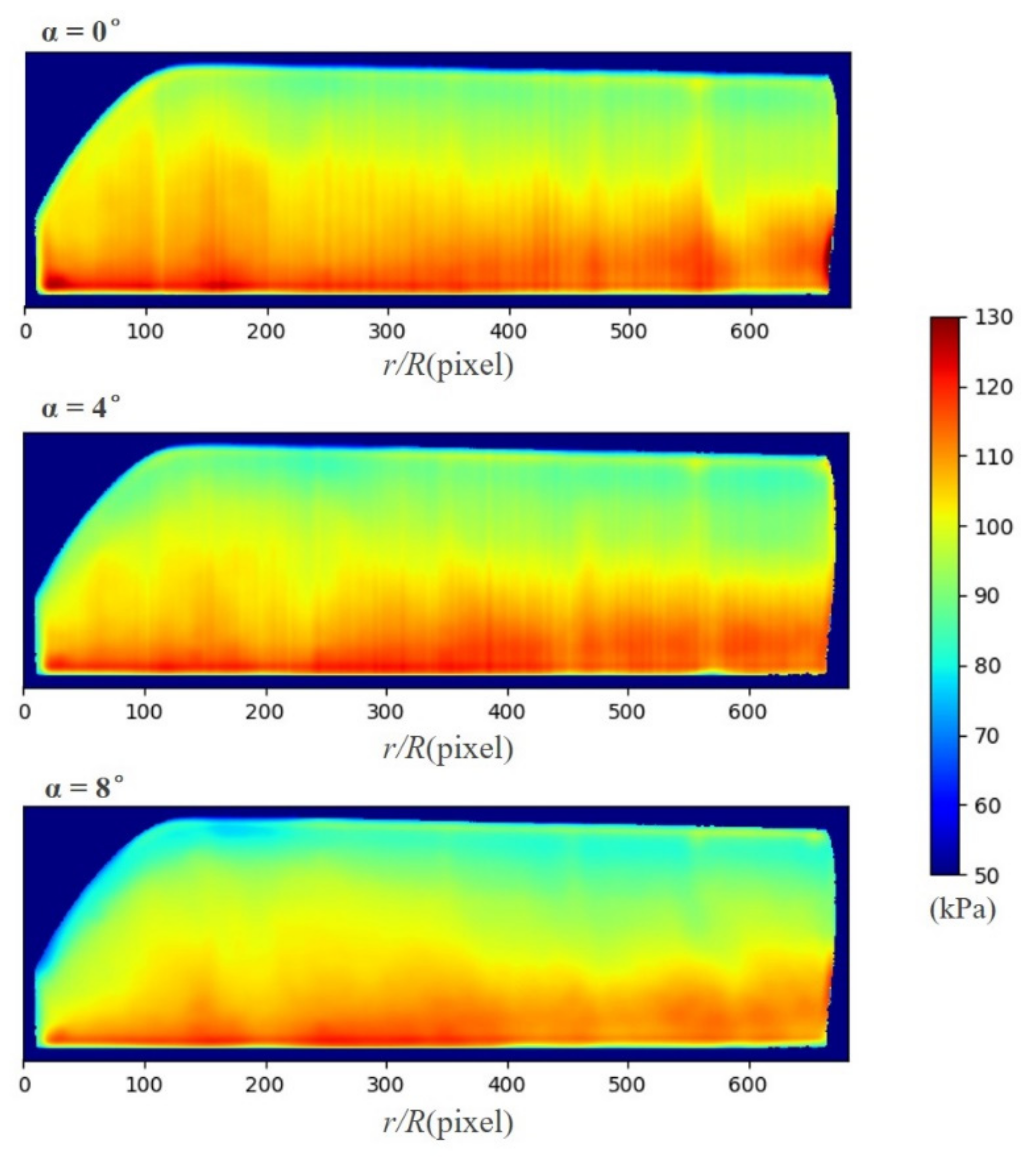
4.1. Results of Surface Pressure Measurement
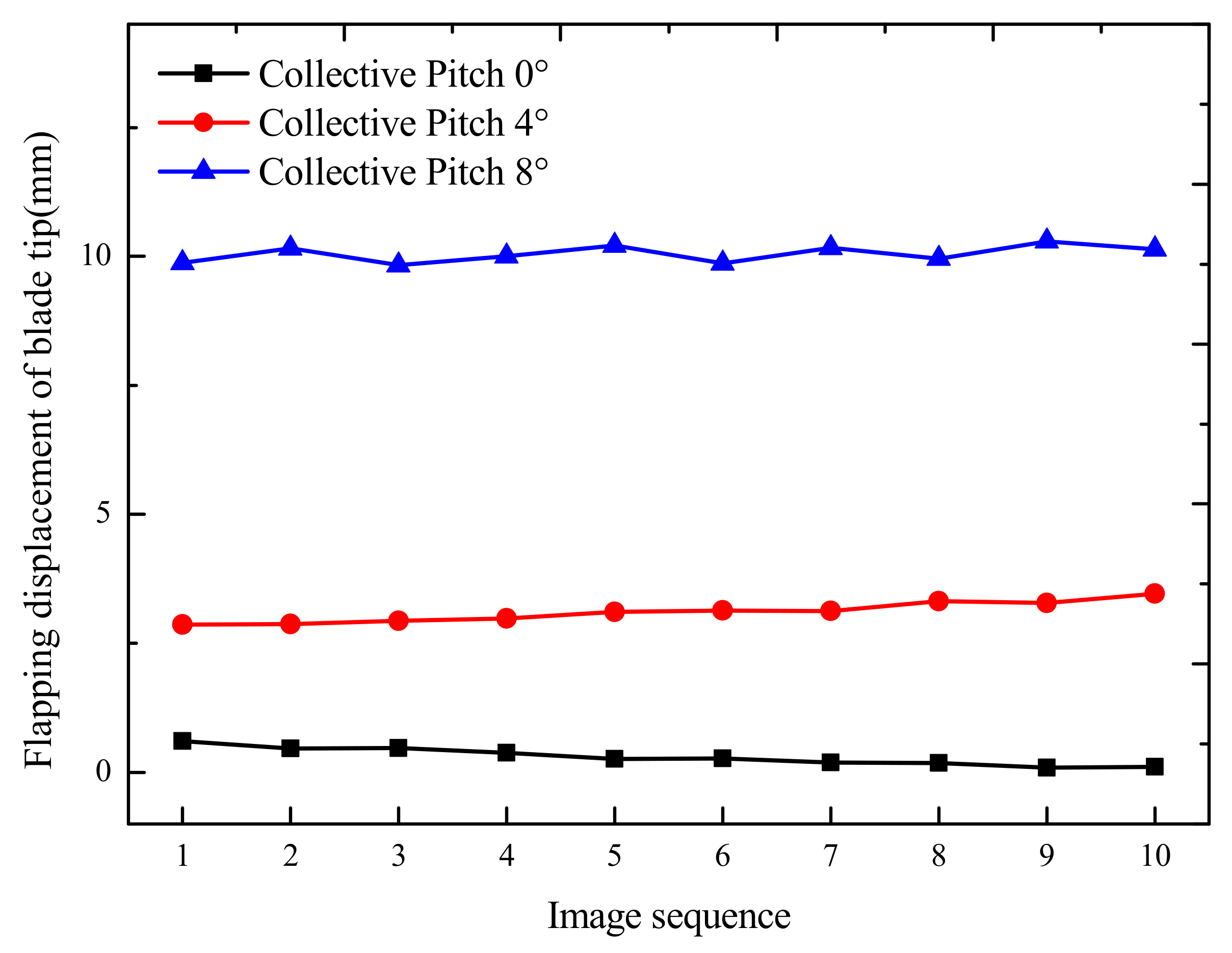
4.2. Results of Blade Displacement Measurement
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schneider, O. Analysis of SPR measurements from HART II. Aerosp. Sci. Technol. 2005, 9, 409–420. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, L.; Wang, S.; Zhou, X. Numerical Investigations of the Influence of Unsteady Vane Trailing Edge Shock Wave on Film Cooling Effectiveness of Rotor Blade Leading Edge. J. Therm. Sci. 2018, 27, 135–145. [Google Scholar] [CrossRef]
- Shi, J.; Xu, T.; Schafer, S.; Chen, C. Adaptive Control of Shock Waves with a Passively Morphing Layer for Rotating Blades. J. Aerosp. Eng. 2015, 28, 1040140701. [Google Scholar] [CrossRef]
- Castells, C.; Richez, F.; Costes, M. A Numerical Investigation of the Influence of the Blade-Vortex Interaction on the Dynamic Stall Onset. J. Am. Helicopter Soc. 2021, 66, 1–13. [Google Scholar] [CrossRef]
- Weiss, A.; Geisler, R.; Müller, M.; Klein, C.; Henne, U.; Braukmann, J.; Letzgus, J. Dynamic-stall measurements using time-resolved pressure-sensitive paint on double-swept rotor blades. Exp. Fluids. 2022, 63, 15. [Google Scholar] [CrossRef]
- Johannes, N.; Braukmann, C.; Andreas, G.; Markus, R. Blade Tip Vortex System of a Rotor with Cyclic Pitch. AIAA J. 2020, 58, 2869–2880. [Google Scholar]
- Wu, J.; Stalnov, O.; Chen, W.; Yang, Z.; Huang, X. Transient analysis of blade-vortex interaction noise. Aerosp. Sci. Technol. 2022, 120, 107294. [Google Scholar] [CrossRef]
- Bauknecht, A.; Ewers, B.; Wolf, C.; Leopold, F.; Yin, J.; Raffel, M. Three-dimensional reconstruction of helicopter blade–tip vortices using a multi-camera BOS system. Exp. Fluids 2015, 56, 1866. [Google Scholar] [CrossRef]
- Zuo, C.; Wei, C.; Ma, J.; Yue, T.; Liu, L.; Shi, Z. Full-Field Displacement Measurements of Helicopter Rotor Blades Using Stereophotogrammetry. Int. J. Aerosp. Eng. 2021, 2021, 8811601. [Google Scholar] [CrossRef]
- Hammond, C. Higher Harmonic Control: A Historical Perspective. J. Am. Helicopter Soc. 2021, 66, 1–14. [Google Scholar] [CrossRef]
- Ma, J.; Lu, Y.; Qin, Y.; Xu, X. Tilt-rotor aircraft fuselage wall aeroacoustics radiation suppression using Higher harmonic control. Appl. Acoust. 2022, 188, 108548. [Google Scholar] [CrossRef]
- Saptarshi, S.; Breiffni, F.; Biswajit, B. Individual Blade Pitch Control of Floating Offshore Wind Turbines for Load Mitigation and Power Regulation. IEEE Trans. Control. Syst. Technol. 2021, 29, 305–315. [Google Scholar]
- Vedulla, M.; Wang, C. Active Flow Control of Flapping Airfoil Using Openfoam. J. Mech. 2021, 36, 361–372. [Google Scholar]
- Tan, J.; Sun, Y.; Wang, H.; Lin, C. New Approach for Aerodynamic and Aeroacoustic Analysis of Actively Controlled Flaps Roto. J. Aircraft. 2018, 55, 2191–2202. [Google Scholar] [CrossRef]
- Juliano, T.; Kumar, P.; Peng, D.; Gregory, J.; Crafton, J.; Fonov, S. Single shot, lifetime based pressure sensitive paint for rotating blades. Mea. Sci. Technol. 2011, 22, 085403. [Google Scholar] [CrossRef]
- Disotell, K.; Peng, D.; Juliano, T.; Crafton, J.; Komerath, N. Single shot temperature and pressure sensitive paint measurements on an unsteady helicopter blade. Exp. Fluids. 2014, 55, 1671. [Google Scholar] [CrossRef] [Green Version]
- Jiao, L.; Shi, Z.; Zhang, W.; Liang, L.; Chen, X.; Zhao, Q.; Peng, D.; Liu, Y. A two-dimensional temperature correction method for pressure-sensitive paint measurement on helicopter rotor blades. Exp. Fluids. 2020, 61, 104. [Google Scholar] [CrossRef]
- Davidson, T.; Stokes, N.; Roberts, D.; Quinn, M. Time-resolved surface pressure and model deformation measurements in an industrial transonic wind tunnel. In Proceedings of the AIAA Aviation 2019 Forum, AIAA 2019–2905, Dallas, TX, USA, 17–21 June 2019. [Google Scholar]
- Ogg, D.; Rice, B.; Peltier, S.; Staines, J.; Claucherty, S.; Combs, C. Simultaneous Stereo Digital Image Correlation and Pressure-Sensitive Paint Measurements of a Compliant Panel in a Mach 2 Wind Tunnel. In Proceedings of the 2018 Fluid Dynamics Conference, AIAA 2018-3869, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef] [Green Version]
- Gao, S.; Zhao, M.; Zhang, L.; Zou, Y. Improved algorithm about subpixel edge detection of image based on Zernike orthogonal moments. Acta Autom. Sin. 2008, 34, 1163–1168. [Google Scholar] [CrossRef]





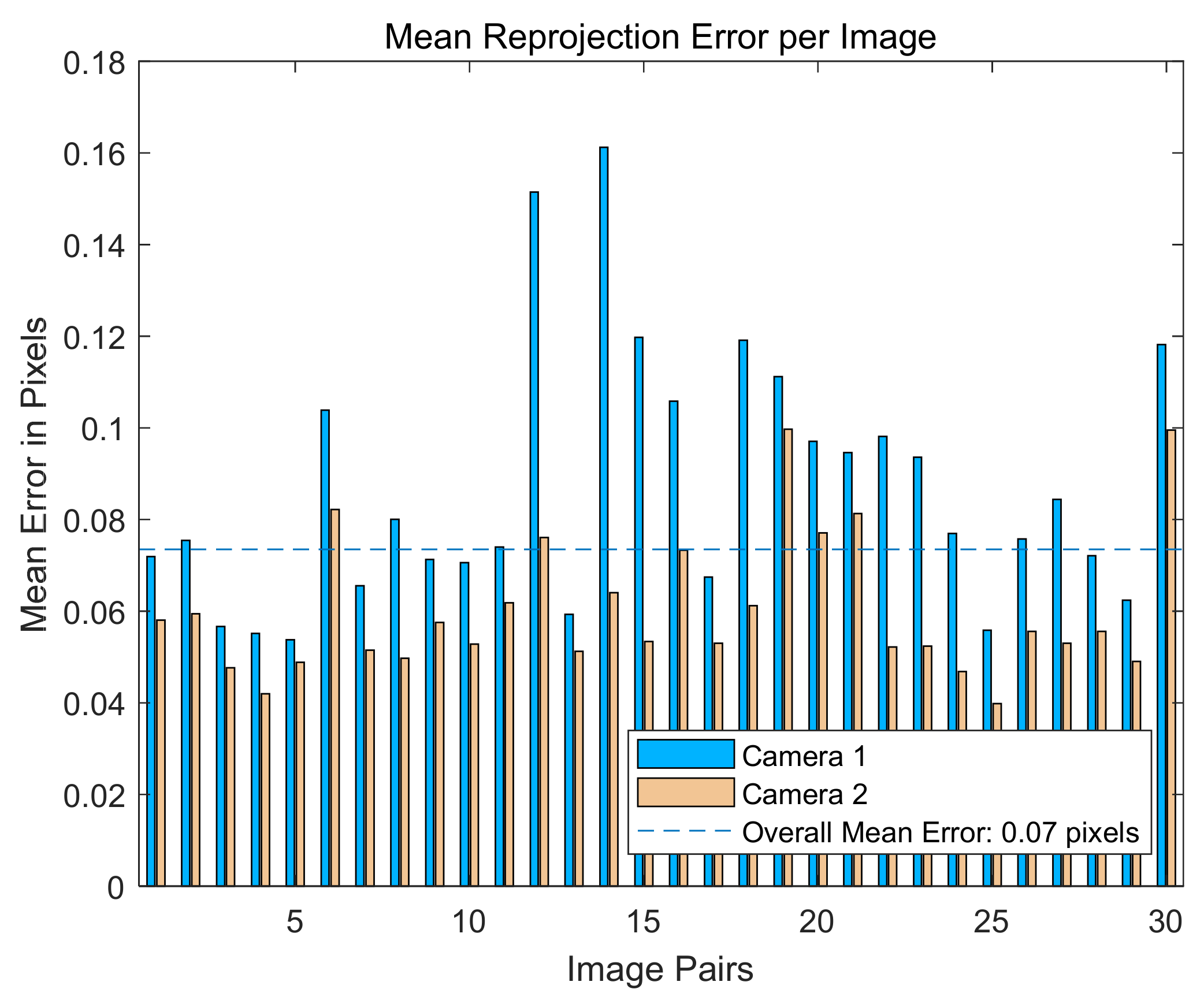



| Collective Pitch (°) | Accuracy of Blade Targets (mm) |
|---|---|
| 0 | 0.152 |
| 4 | 0.174 |
| 8 | 0.197 |
| Average | 0.174 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, C.; Zuo, C.; Liao, X.; Li, G.; Jiao, L.; Peng, D.; Liang, L. Simultaneous Pressure and Displacement Measurement on Helicopter Rotor Blades Using a Binocular Stereophotogrammetry PSP System. Aerospace 2022, 9, 292. https://doi.org/10.3390/aerospace9060292
Wei C, Zuo C, Liao X, Li G, Jiao L, Peng D, Liang L. Simultaneous Pressure and Displacement Measurement on Helicopter Rotor Blades Using a Binocular Stereophotogrammetry PSP System. Aerospace. 2022; 9(6):292. https://doi.org/10.3390/aerospace9060292
Chicago/Turabian StyleWei, Chunhua, Chenglin Zuo, Xianhui Liao, Guoshuai Li, Lingrui Jiao, Di Peng, and Lei Liang. 2022. "Simultaneous Pressure and Displacement Measurement on Helicopter Rotor Blades Using a Binocular Stereophotogrammetry PSP System" Aerospace 9, no. 6: 292. https://doi.org/10.3390/aerospace9060292
APA StyleWei, C., Zuo, C., Liao, X., Li, G., Jiao, L., Peng, D., & Liang, L. (2022). Simultaneous Pressure and Displacement Measurement on Helicopter Rotor Blades Using a Binocular Stereophotogrammetry PSP System. Aerospace, 9(6), 292. https://doi.org/10.3390/aerospace9060292






