Nonlinear Control of a Single Tail Tilt Servomotor Tri-Rotor Ducted VTOL-UAV
Abstract
:1. Introduction
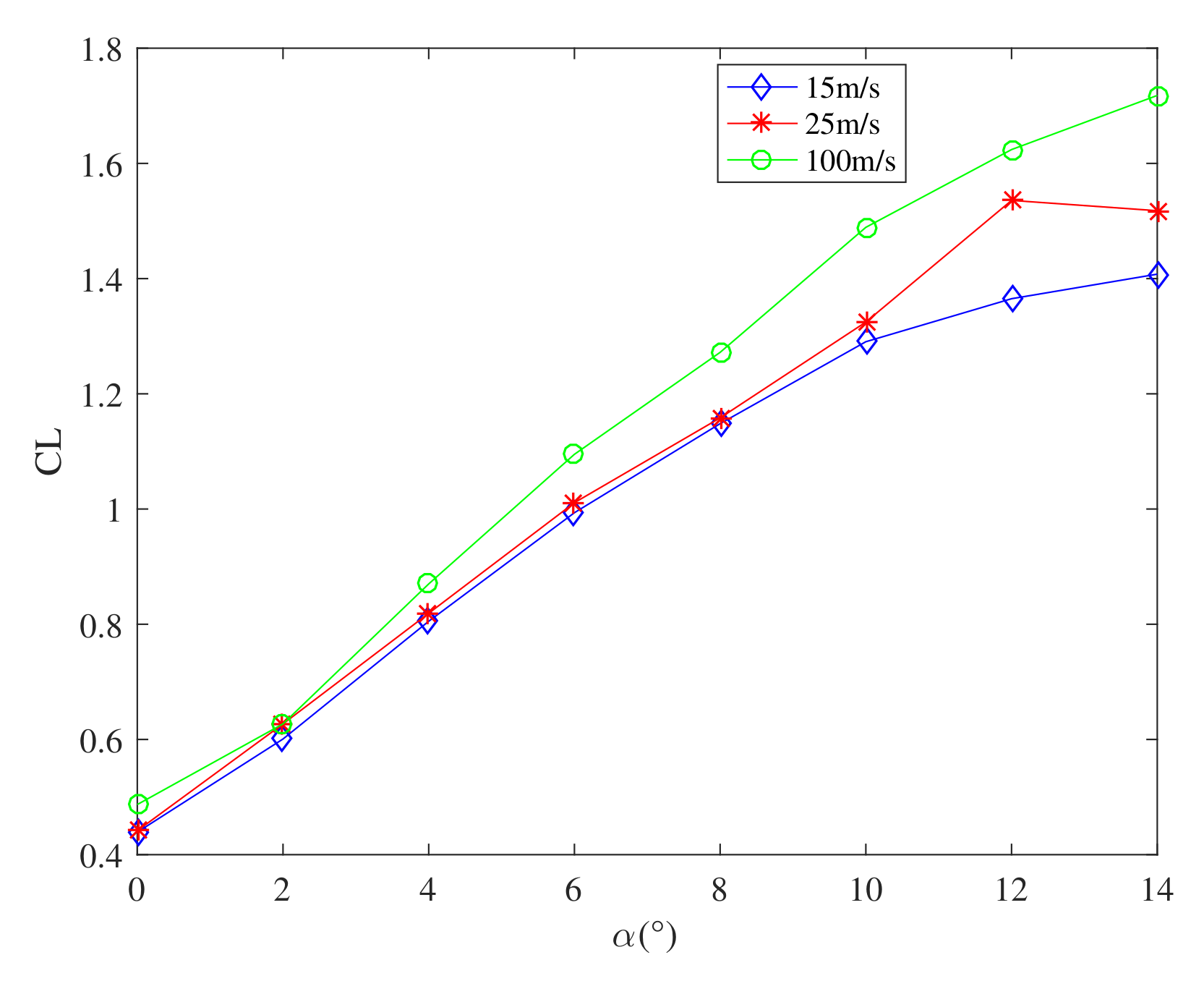
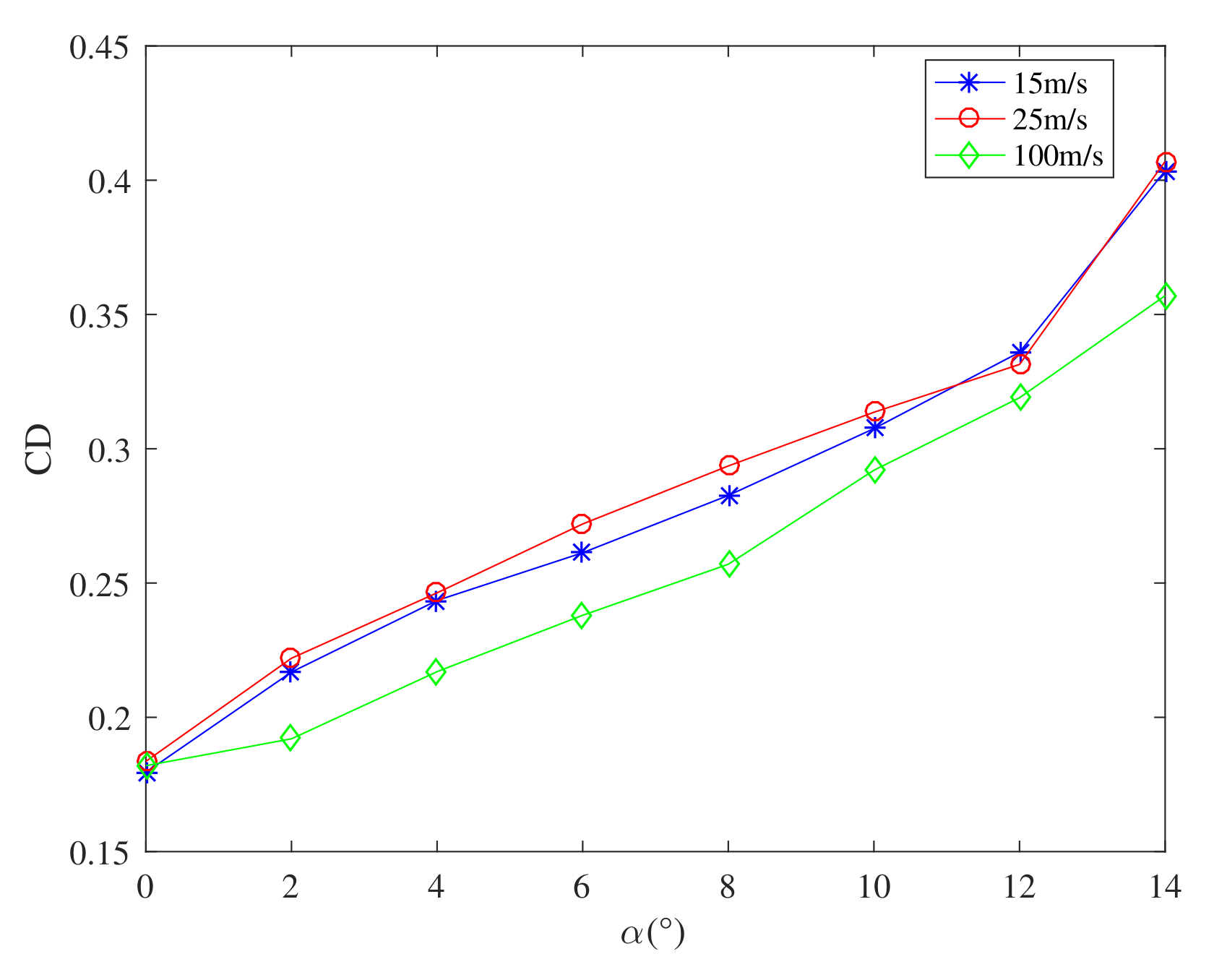
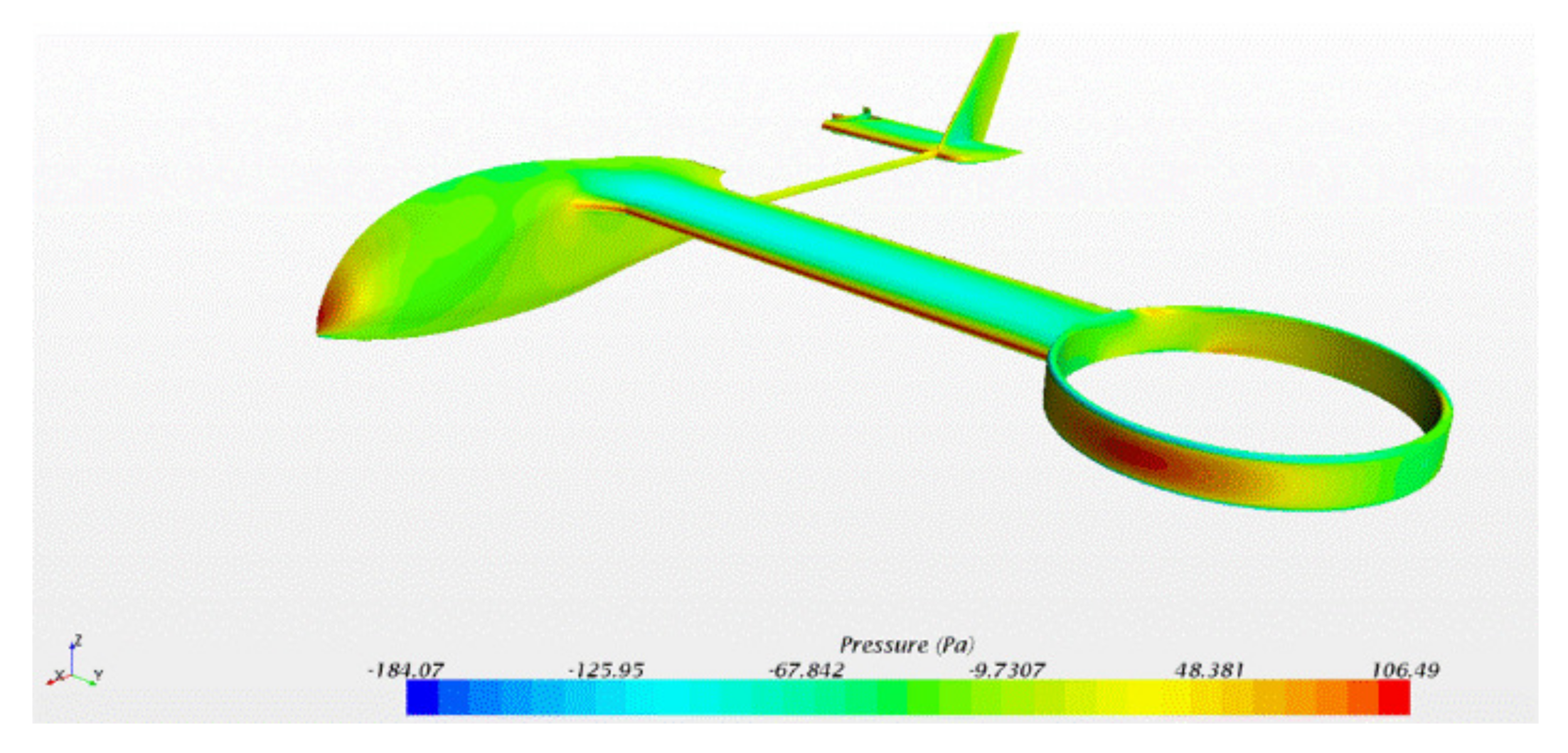
2. Flight Dynamic Model
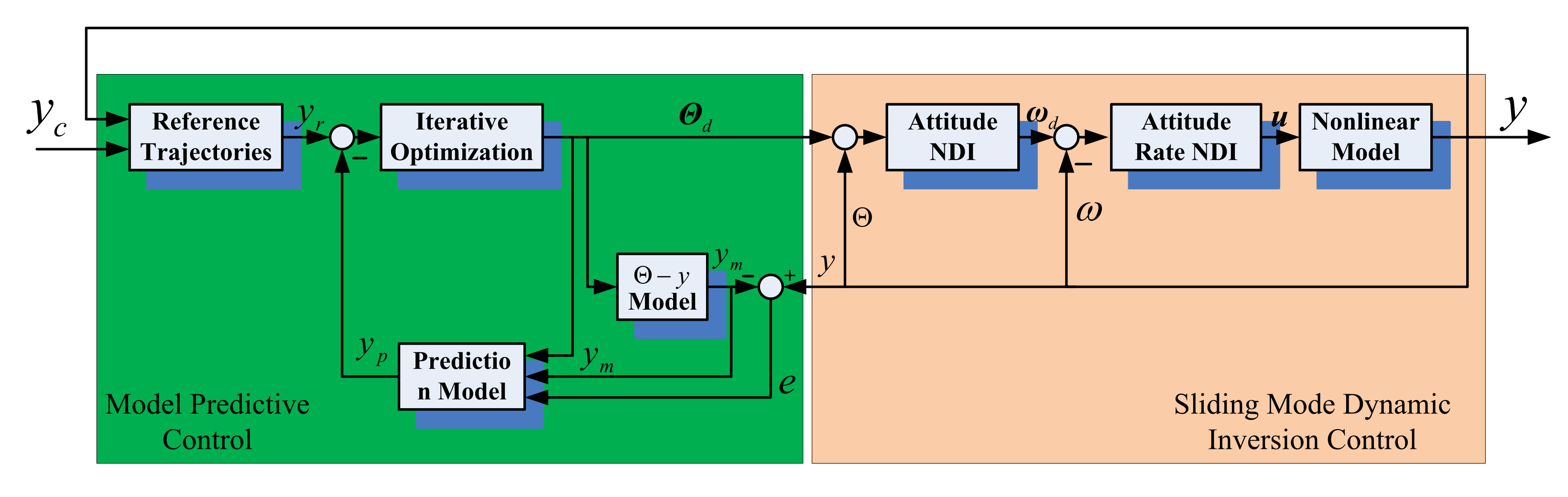
3. Controller Design
3.1. Attitude Dynamic Inverse Controller Design
3.1.1. Attitude Angle Rate Loop Controller Design
3.1.2. Attitude Angle Loop Controller Design
3.2. Model Predictive Position Controller Design
3.2.1. Prediction Model
3.2.2. Optimal Control Law
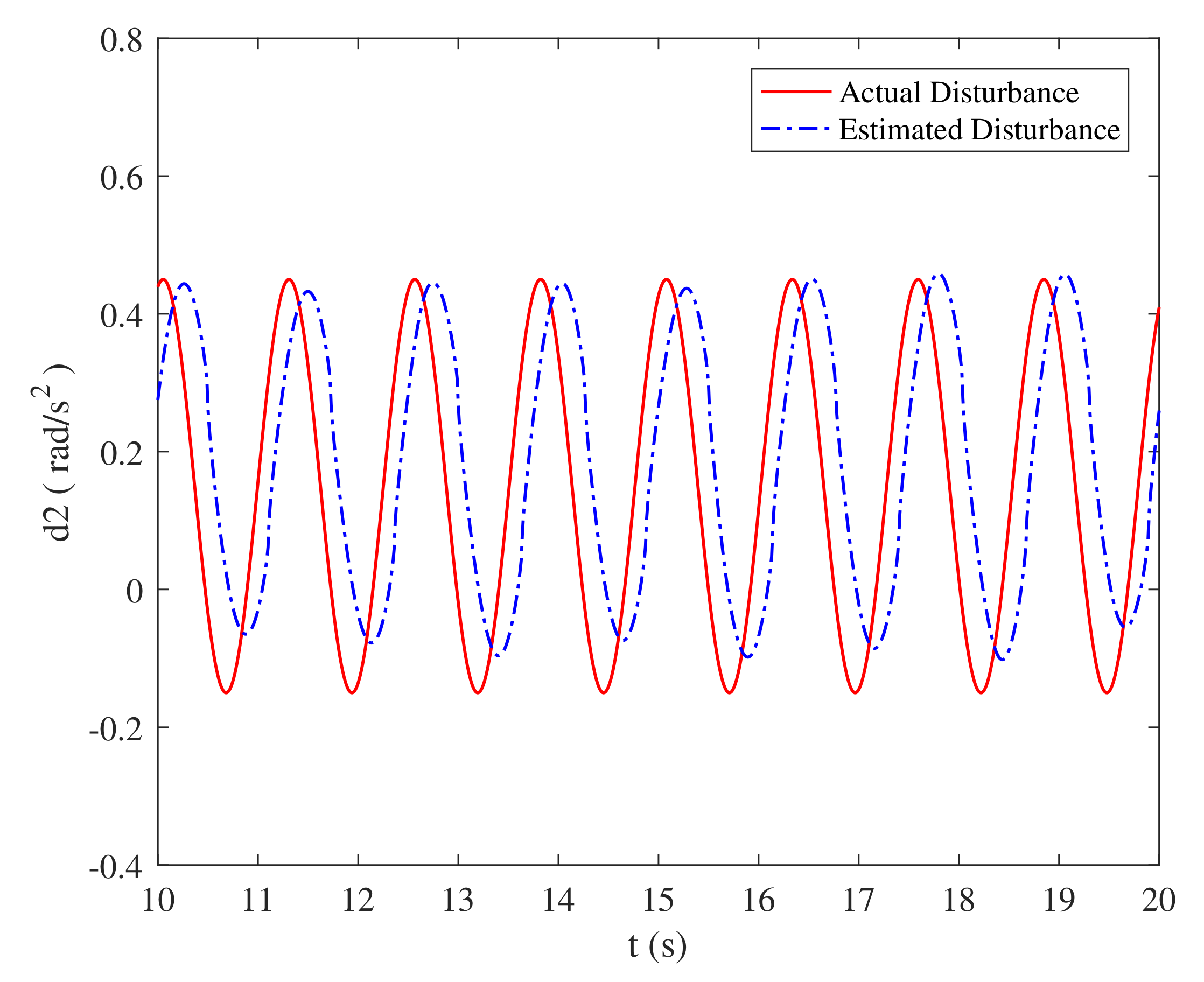
3.2.3. Sliding Mode Disturbance Observer Design
4. Numerical Simulation and Flight Test
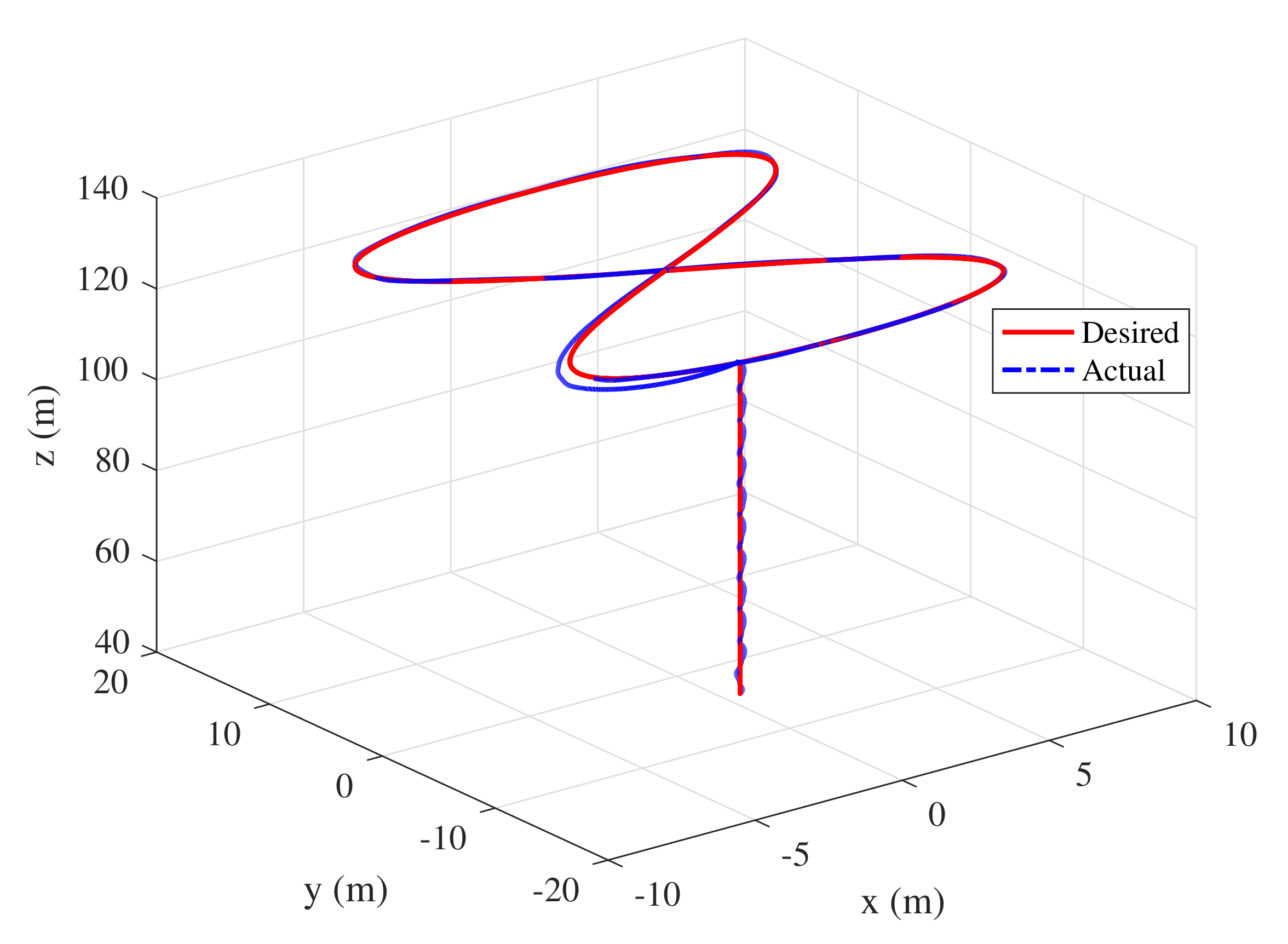
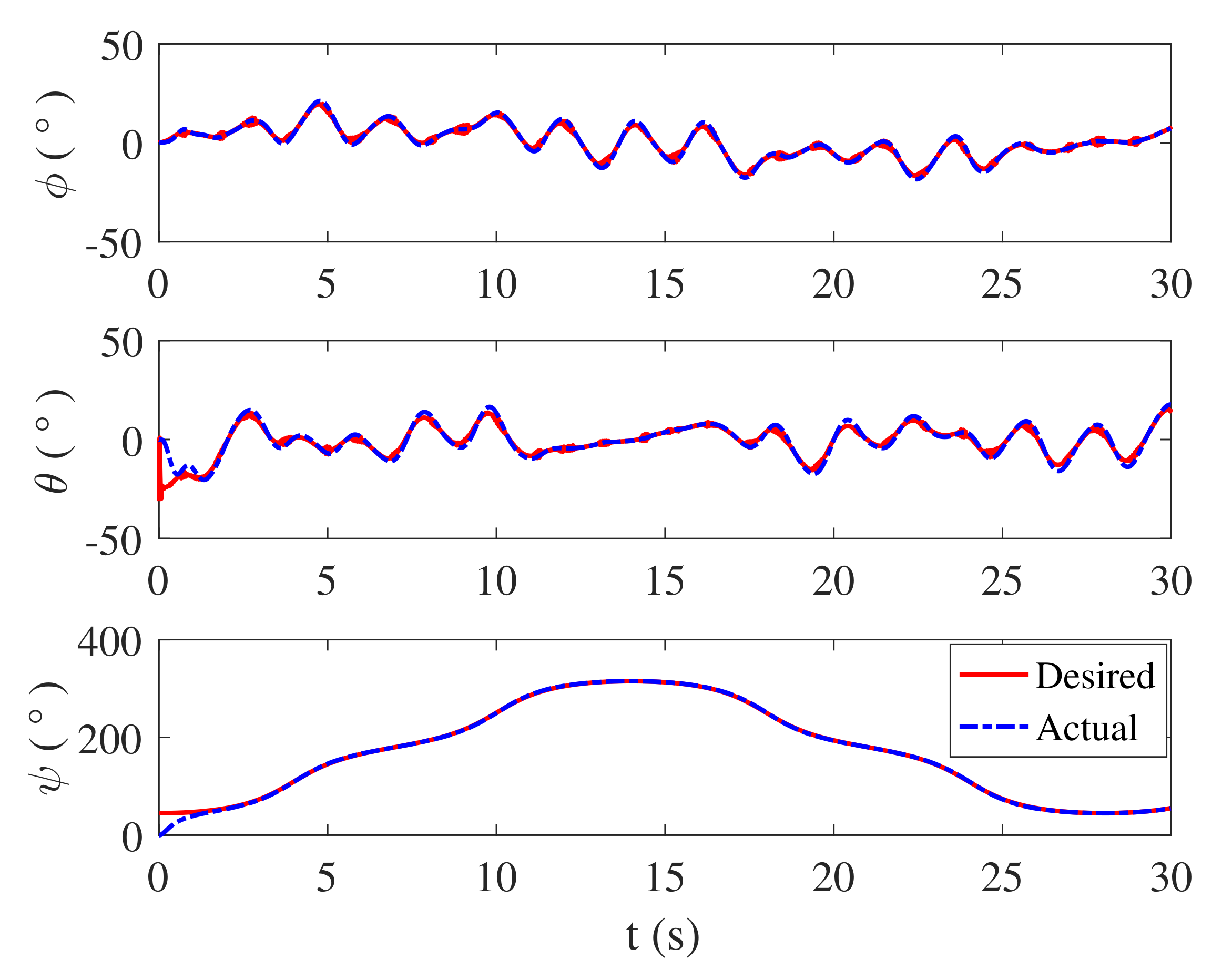
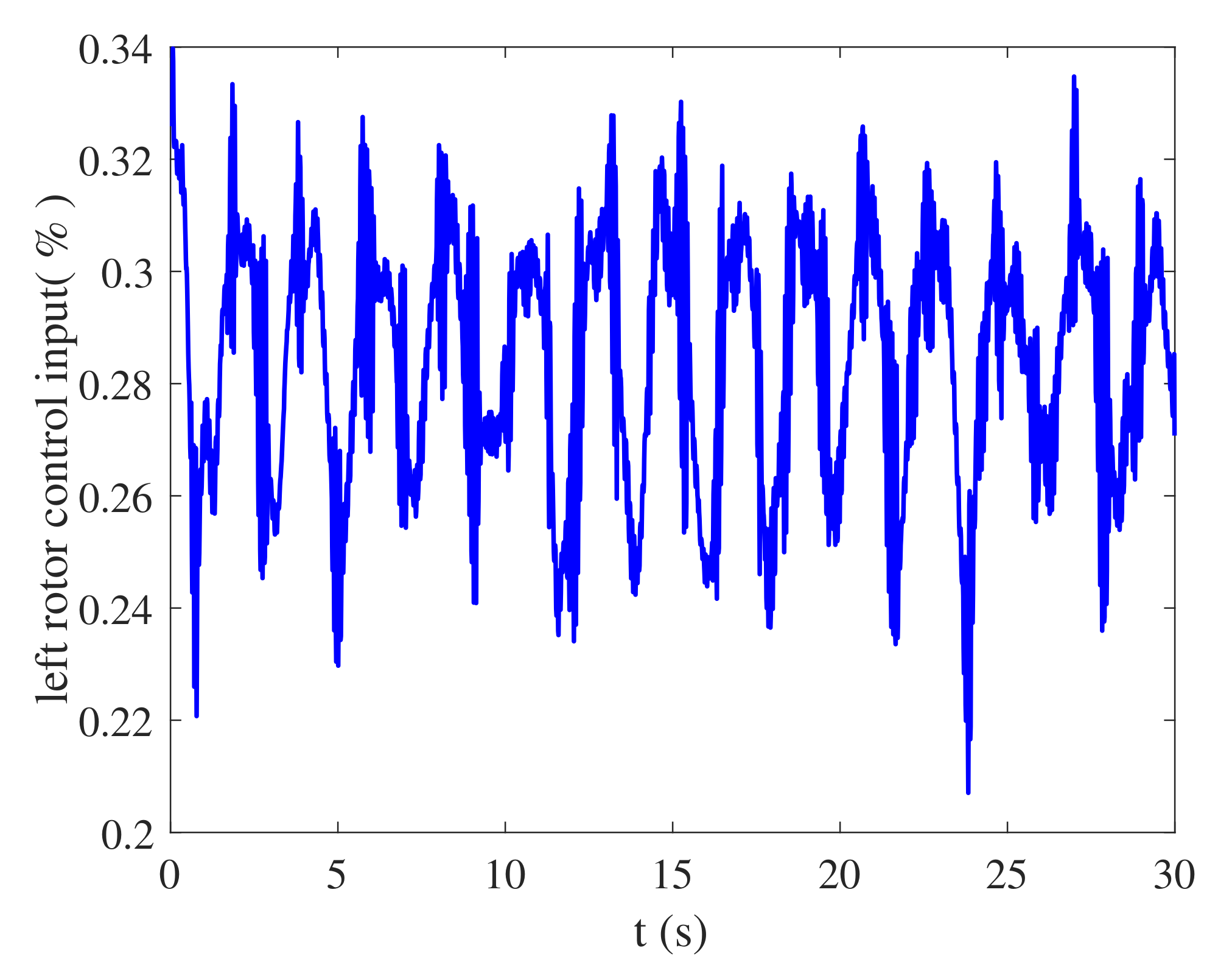
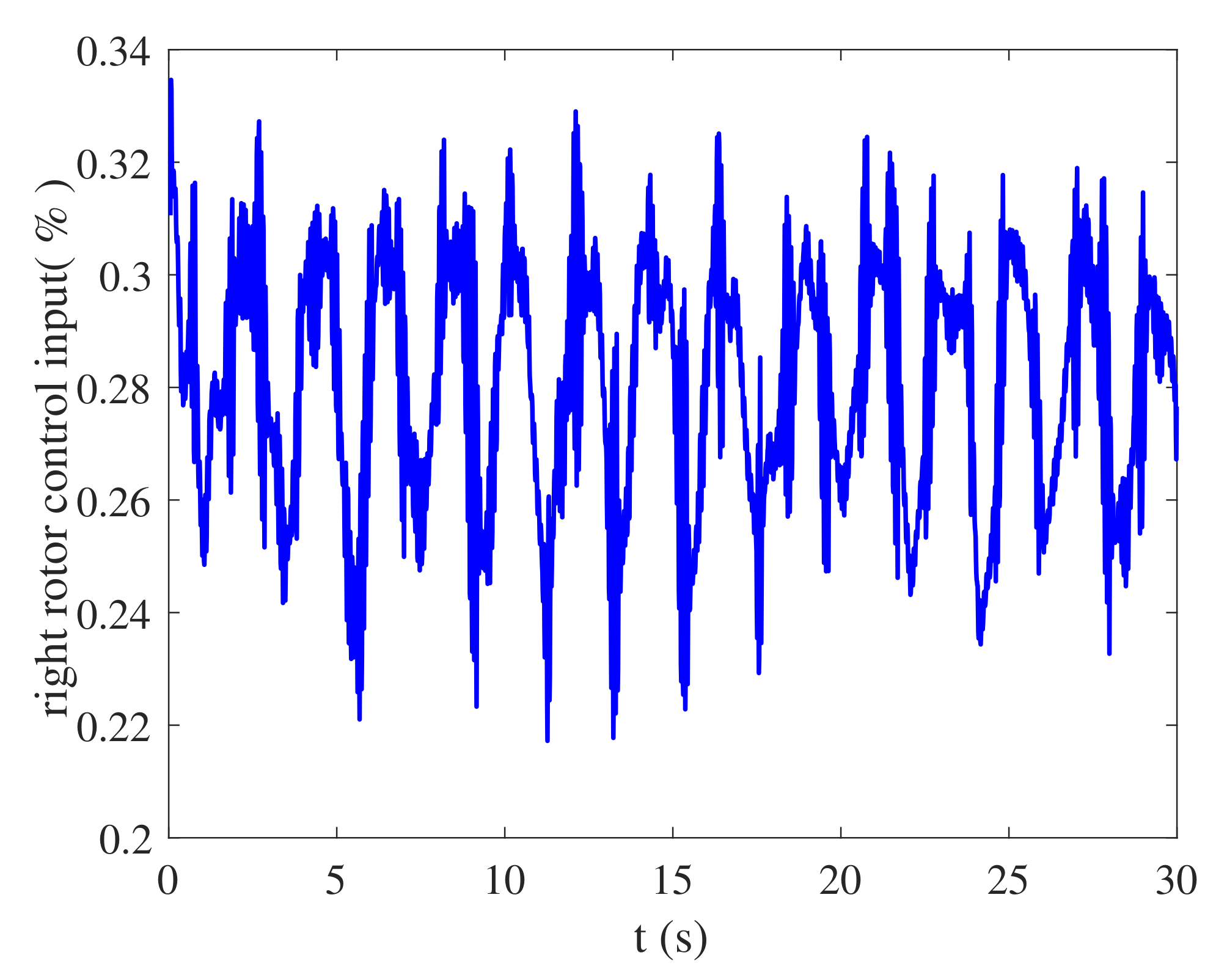
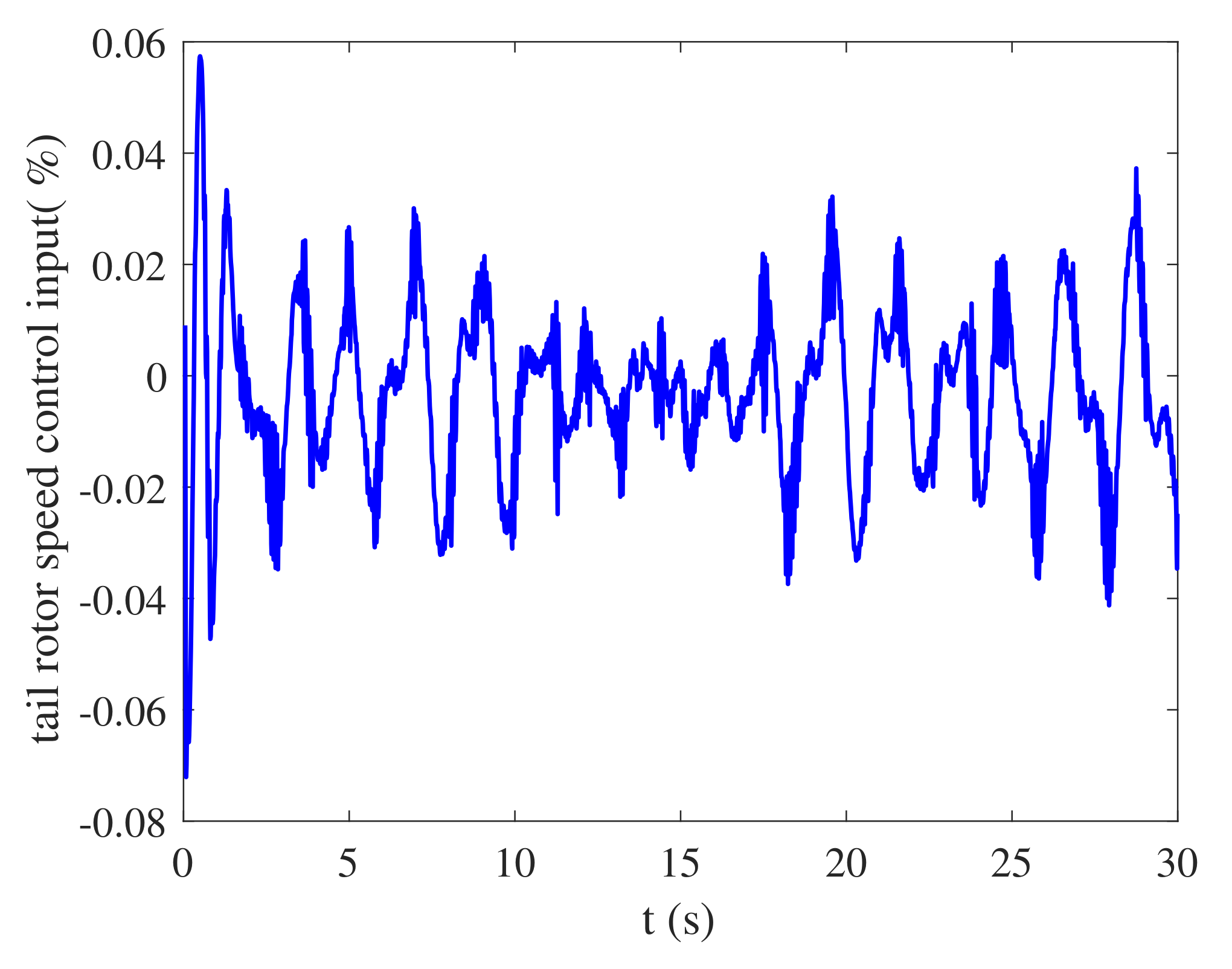
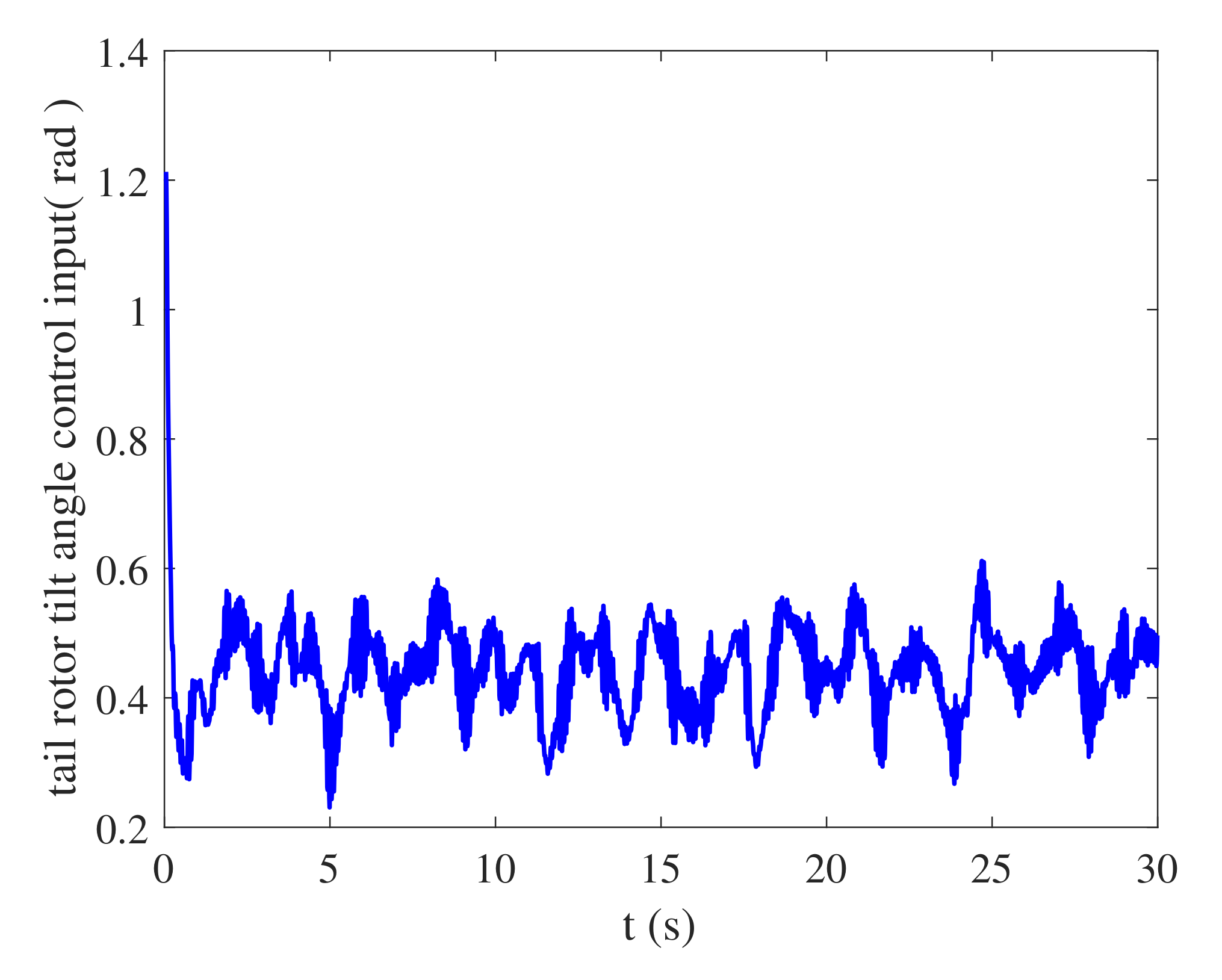
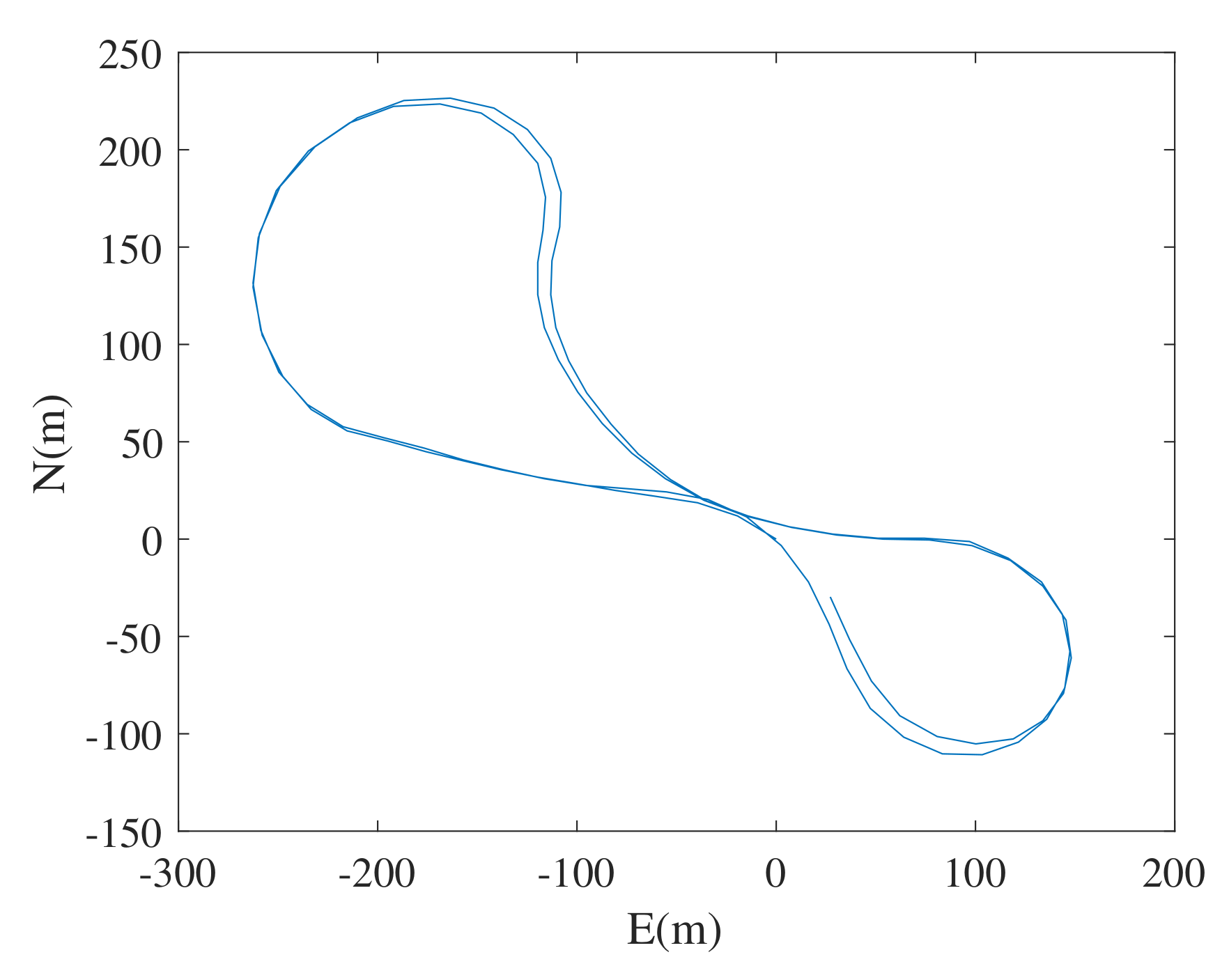
4.1. Simulation
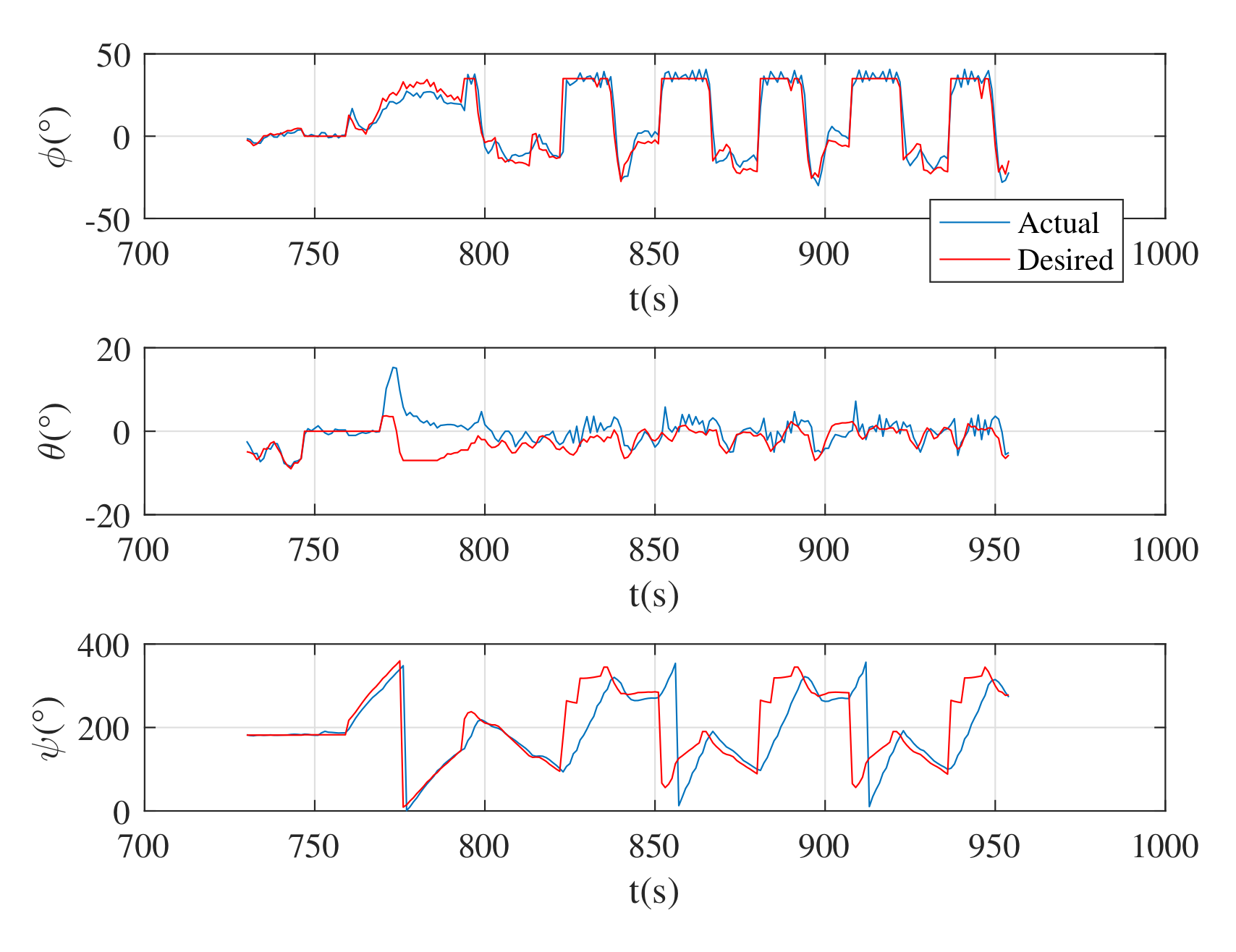
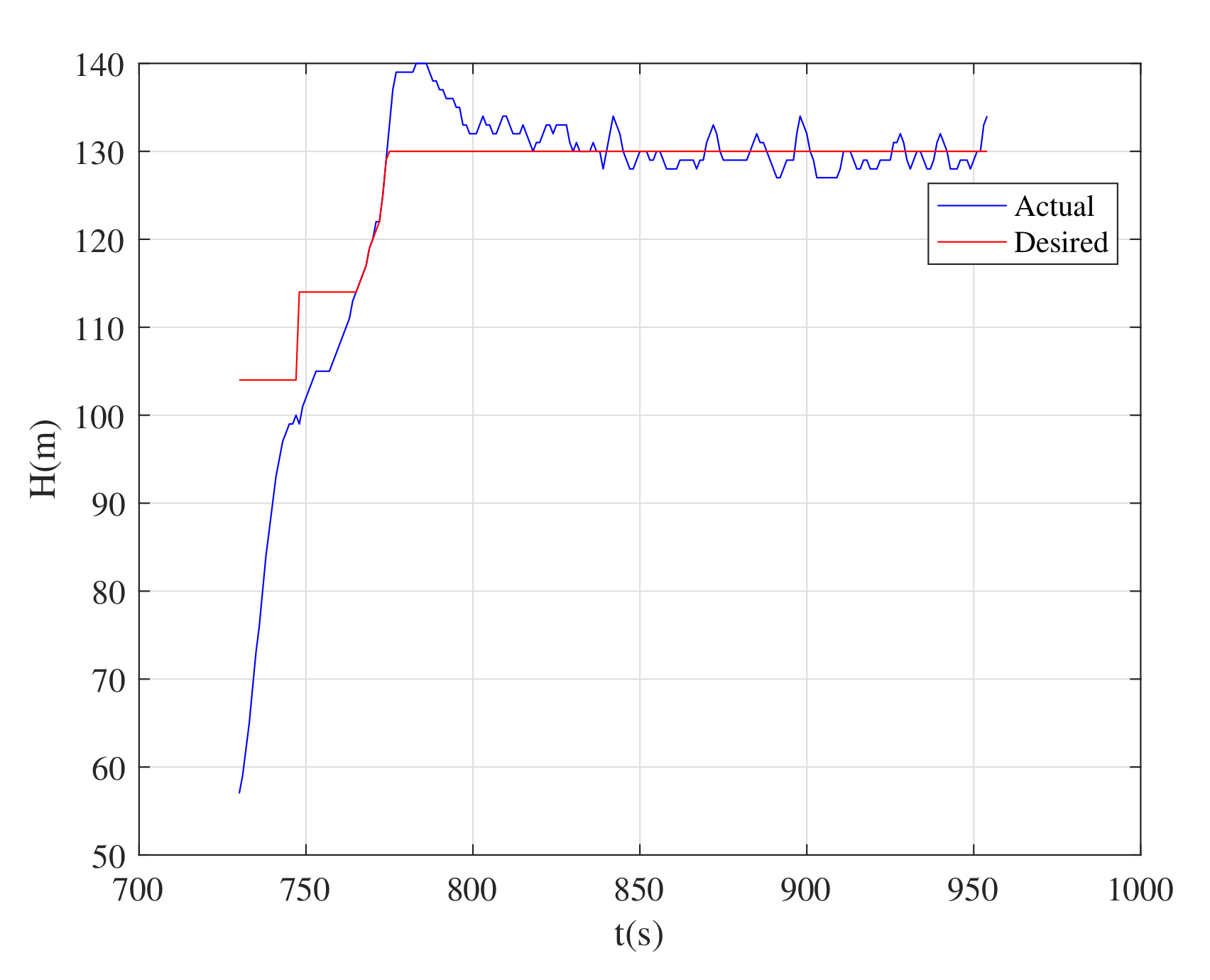
4.2. Flight Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Future Long Range Assault Aircraft. Available online: https://www.boeing.com/defense/future-long-range-assault-aircraft/index.page{#}/videos/defiant-x-exceeds-230-knots (accessed on 21 March 2022).
- Helicopters History. Available online: https://www.airbus.com/en/who-we-are/our-history/helicopters-history/x3 (accessed on 21 March 2022).
- Yang, K.; Han, D.; Shi, Q. Study on the lift and propulsive force shares to improve the flight performance of a compound helicopter. Chin. J. Aeronaut. 2021, 35, 365–375. [Google Scholar] [CrossRef]
- Yan, K.; Chen, M.; Wu, Q.; Zhu, R. Robust adaptive compensation control for unmanned autonomous helicopter with input saturation and actuator faults. Chin. J. Aeronaut. 2019, 32, 2299–2310. [Google Scholar] [CrossRef]
- Xian, B.; Guo, J.; Zhang, Y.; Zhao, B. Sliding mode tracking control for miniature unmanned helicopters. Chin. J. Aeronaut. 2015, 28, 277–284. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Wang, X. Design of a controller for hypersonic vehicle based on sliding mode disturbance observer. Electron. Opt. Control. 2020, 27, 90–94. [Google Scholar]
- Tan, S.; Guo, J.; Zhao, Y.; Zhang, J. Adaptive control with saturation-constrainted observations for drag-free satellites—A set-valued identification approach. Sci. China Inf. Sci. 2021, 64, 182–193. [Google Scholar] [CrossRef]
- Li, Y.; Liu, X.; He, Q. An adaptive dynamic inversion control method based on improved piecewise constant for flight control system. J. Northwestern Polytech. Univ. 2021, 39, 167–174. [Google Scholar] [CrossRef]
- Lu, B. Research on High-Bandwidth/High-Precision Longitudinal Control for a Hypersonic Vehicle; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2008. [Google Scholar]
- Zhou, H. Small-Scale Unmanned Helicopter Modeling and Controller Design; South China University of Technology: Guangzhou, China, 2011. [Google Scholar]
- Wang, X.; Meng, X.; Li, C. Design of trajectory tracking controller for UAV based on MPC. Syst. Eng. Electron. 2021, 43, 191–198. [Google Scholar]
- Chen, J.; Sun, R.; Zhu, B. Disturbance observer-based control for small nonlinear UAV systems with transient performance constraint. Aerosp. Sci. Technol. 2020, 105, 106028. [Google Scholar] [CrossRef]
- Li, Y.; Chen, M.; Ge, S.S.; Li, D. Anti-disturbance control for attitude and altitude systems of the helicopter under random disturbances. Aerosp. Sci. Technol. 2019, 96, 105561. [Google Scholar] [CrossRef]
- Wang, Q. A Numerical Analysis of the Aerodynamic Performance of the Ducted-Fan UAV; National University of Defense Technology: Changsha, China, 2008. [Google Scholar]
- Wang, S. Theory and Simulation on Overall Design and Control System of the Saucer Ducted Unmanned Aerial Vehicle; Fudan University: Shanghai, China, 2011. [Google Scholar]
- Kong, W. Research on some Key Technical Issues of Composed High Speed Helicopter; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2011. [Google Scholar]
- Hu, Y. Research on System-Identification-Based Dynamic Modelling and Control Technology for High-Speed Helicopter; Beihang University: Beijing, China, 2020. [Google Scholar]
- Shen, H. Research in the Interaction Flow Field of Compound High-Speed Helicopter Rotor/Fuselage/Auxiliary Propulsor; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2015. [Google Scholar]
- Wang, Q.; Chen, M.; Xu, G. Control strategy for compound coaxial helicopter under conversion mode. J. Aerosp. Power 2014, 29, 458–466. [Google Scholar]
- Chen, N. Research on Nonlinear Robust Control Technology for Unmanned Helicopter; Beihang University: Beijing, China, 2018. [Google Scholar]
- Bai, Y.; Shi, X.; Wang, S. Auv attitude control system design with robust nonlinear dynamic inversion. Tactical Missile Technol. 2016, 2, 93–97. [Google Scholar]
- Dávila, A.; Moreno, J.A.; Fridman, L. Variable gains super-twisting algorithm: A lyapunov based design. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 968–973. [Google Scholar]
- Evangelista, C.; Puleston, P.; Valenciaga, F. Lyapunov-designed super-twisting sliding mode control for wind energy conversion optimization. IEEE Trans. Ind. Electron. 2013, 60, 538–545. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. Strict lyapunov functions for the super-twisting algorithm. IEEE Trans. Autom. Control. 2012, 57, 1035–1040. [Google Scholar] [CrossRef]
- Tan, J.; Zhou, Z.; Zhu, X.; Xu, X. Fast super twisting algorithm and its application to attitude control of flying wing UAV. Control. Decis. 2016, 31, 143–148. [Google Scholar]
- Yang, F.; Tan, S.; Xue, W.; Guo, J.; Zhao, Y. Extended state filtering with saturation-constrainted observations and active disturbance rejection control of position and attitude for drag-free satellites. Acta Autom. Sin. 2020, 46, 2337–2349. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Guo, J.; Ying, P.; Zeng, G.; Chen, N. Nonlinear Control of a Single Tail Tilt Servomotor Tri-Rotor Ducted VTOL-UAV. Aerospace 2022, 9, 296. https://doi.org/10.3390/aerospace9060296
Hu Y, Guo J, Ying P, Zeng G, Chen N. Nonlinear Control of a Single Tail Tilt Servomotor Tri-Rotor Ducted VTOL-UAV. Aerospace. 2022; 9(6):296. https://doi.org/10.3390/aerospace9060296
Chicago/Turabian StyleHu, Yanpeng, Jin Guo, Pei Ying, Guannan Zeng, and Nanyu Chen. 2022. "Nonlinear Control of a Single Tail Tilt Servomotor Tri-Rotor Ducted VTOL-UAV" Aerospace 9, no. 6: 296. https://doi.org/10.3390/aerospace9060296
APA StyleHu, Y., Guo, J., Ying, P., Zeng, G., & Chen, N. (2022). Nonlinear Control of a Single Tail Tilt Servomotor Tri-Rotor Ducted VTOL-UAV. Aerospace, 9(6), 296. https://doi.org/10.3390/aerospace9060296




