Capture Dynamics and Control of a Flexible Net for Space Debris Removal
Abstract
:1. Introduction
2. Dynamics of the Capture System
2.1. Constitutive Model of the Flexible Net
2.2. Dynamics Model of the Debris
2.3. Contact Dynamics between the Debris and the FNR
3. Active Control Scheme for the Flexible Net
4. Results and Discussion
4.1. Design of Simulations
4.2. Critical Variables for Evaluating the Capture Process
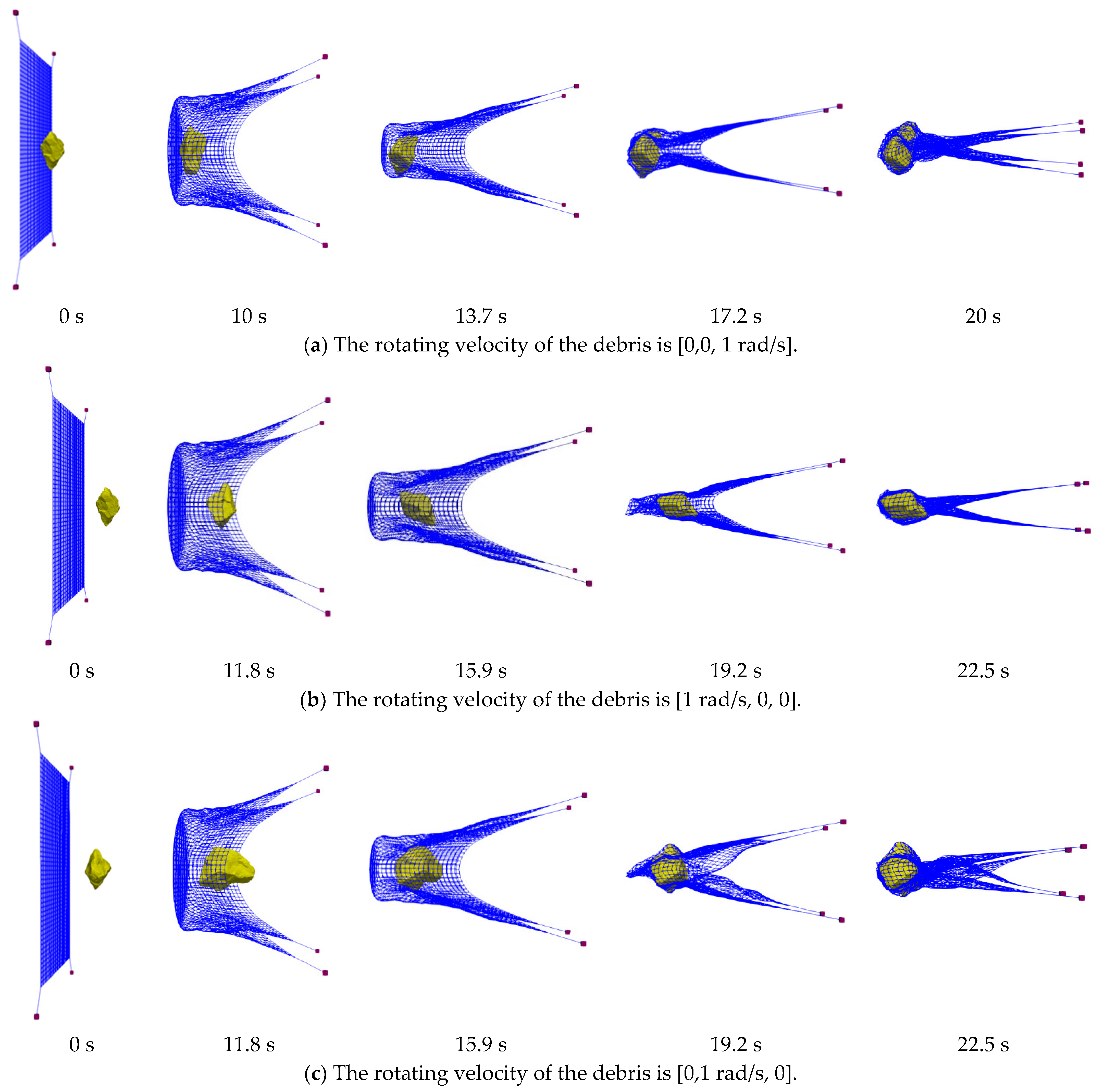
4.3. Simulations and Analysis of the Contact Process
4.4. Simulations and Analysis of the Control Process
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Shan, M.H.; Guo, J.; Gill, E. Review and comparison of active space debris capturing and removal methods. Prog. Aerosp. Sci. 2016, 80, 18–32. [Google Scholar] [CrossRef]
- Kessler, D.J.; Burton, G.C.P. Collision frequency of artificial satellites: The creation of a debris belt. J. Geophys. Res. Space Phys. 1978, 83, 2637–2646. [Google Scholar] [CrossRef]
- Tarran, B. Prepare for impact: Space debris and statistics. Significance 2021, 18, 18–23. [Google Scholar] [CrossRef]
- Houman, H.; Bazzocchi, M.C.F.; Emami, M.R. A deorbiter CubeSat for active orbital debris removal. Adv. Space Res. 2018, 61, 2377–2392. [Google Scholar]
- Peters, T.V.; Valero, J.F.B.; Olmos, D.E.; Lappas, V.; Jakowski, P.; Gray, I.; Tsourdos, A.; Schaub, H.; Biesbroek, R. Attitude control analysis of tethered de-orbiting. Acta Astronaut. 2018, 146, 316–331. [Google Scholar] [CrossRef] [Green Version]
- Shan, M.H.; Shi, L.L. Post-capture control of a tumbling space debris via tether tension. Acta Astronaut. 2021, 180, 317–327. [Google Scholar] [CrossRef]
- Shan, M.H.; Shi, L.L. Comparison of Tethered Post-Capture System Models for Space Debris Removal. Aerospace 2022, 9, 33. [Google Scholar] [CrossRef]
- Markus, W.; Clark, C.; Romano, M. Historical survey of kinematic and dynamic spacecraft simulators for laboratory experimentation of on-orbit proximity maneuvers. Prog. Aerosp. Sci. 2019, 110, 100552. [Google Scholar]
- Castronuovo, M.M. Active space debris removal—A preliminary mission analysis and design. Acta Astronaut. 2011, 69, 848–859. [Google Scholar] [CrossRef]
- Liu, X.-F.; Zhang, X.-Y.; Cai, G.-P.; Chen, W.-J. Capturing a Space Target Using a Flexible Space Robot. Appl. Sci. 2022, 12, 984. [Google Scholar] [CrossRef]
- Colmenarejo, P.; Graziano, M.; Novelli, G.; Mora, D.; Serra, P.; Tomassini, A.; Seweryn, K.; Prisco, G.; Gil Fernandez, J. On ground validation of debris removal technologies. Acta Astronaut. 2019, 158, 206–219. [Google Scholar] [CrossRef]
- Flores-Abad, A.; Ma, O.; Pham, K.; Ulrich, S. A review of space robotics technologies for on-orbit servicing. Prog. Aerosp. Sci. 2014, 68, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Huang, P.; Zhang, F.; Meng, Z. Contact dynamics and control for tethered space net robot. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 918–929. [Google Scholar] [CrossRef]
- Botta, E.M.; Sharf, I.; Misra, A.K. Contact dynamics modeling and simulation of tether nets for space-debris capture. J. Guid. Control Dyn. 2017, 40, 110–123. [Google Scholar] [CrossRef]
- Dudziak, R.; Tuttle, S.; Barraclough, S. Harpoon technology development for the active removal of space debris. Adv. Space Res. 2015, 56, 509–527. [Google Scholar] [CrossRef]
- Sizov, D.A.; Aslanov, V.S. Space debris removal with harpoon assistance: Choice of parameters and optimization. J. Guid. Control Dyn. 2020, 44, 767–778. [Google Scholar] [CrossRef]
- Huang, P.; Zhang, F.; Chen, L.; Meng, Z.; Zhang, Y.; Liu, Z.; Hu, Y. A review of space tether in new applications. Nonlinear Dyn. 2018, 94, 1–19. [Google Scholar] [CrossRef]
- Lim, J.; Chung, J. Dynamic analysis of a tethered satellite system for space debris capture. Nonlinear Dyn. 2018, 94, 2391–2408. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, Y.; Baoyin, H. Dynamical behavior of flexible net spacecraft for landing on asteroid. Astrodynamics 2021, 5, 249–261. [Google Scholar] [CrossRef]
- Sharf, I.; Thomsen, B.; Botta, E.M.; Misra, A.K. Experiments and simulation of a net closing mechanism for tether-net capture of space debris. Acta Astronaut. 2017, 139, 332–343. [Google Scholar] [CrossRef]
- Shan, M.; Guo, J.; Gill, E. Contact dynamics on net capturing of tumbling space debris. J. Guid. Control Dyn. 2018, 41, 2063–2072. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Huang, P.; Zhang, F. Capture dynamics and net closing control for tethered space net robot. J. Guid. Control Dyn. 2019, 42, 199–208. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, F.; Huang, P.F. Capture dynamics and control of tethered space net robot for space debris capturing in unideal capture case. J. Frankl. Inst. 2020, 357, 12019–12036. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, F.; Huang, P.F. Dynamic Closing Point Determination for Space Debris Capturing via Tethered Space Net Robot. IEEE Trans. Aerosp. Electron. Syst. 2022. [Google Scholar] [CrossRef]
- Riccardo, B.; Salvi, S.; Lavagna, M. Dynamics analysis and GNC design of flexible systems for space debris active removal. Acta Astronaut. 2015, 110, 247–265. [Google Scholar]
- Si, J.; Pang, Z.; Du, Z.; Cheng, C. Dynamics modeling and simulation of self-collision of tether-net for space debris removal. Adv. Space Res. 2019, 64, 1675–1687. [Google Scholar] [CrossRef]
- Endo, Y.; Kojima, H.; Trivailo, P.M. Study on acceptable offsets of ejected nets from debris center for successful capture of debris. Adv. Space Res. 2020, 66, 450–461. [Google Scholar] [CrossRef]
- Botta, E.M.; Miles, C.; Sharf, I. Simulation and tension control of a tether-actuated closing mechanism for net-based capture of space debris. Acta Astronaut. 2020, 174, 347–358. [Google Scholar] [CrossRef]
- Shan, M.; Guo, J.; Gill, E. An analysis of the flexibility modeling of a net for space debris removal. Adv. Space Res. 2020, 65, 1083–1094. [Google Scholar] [CrossRef]
- Hou, Y.; Liu, C.; Hu, H.; Yang, W.; Shi, J. Dynamic computation of a tether-net system capturing a space target via discrete elastic rods and an energy-conserving integrator. Acta Astronaut. 2021, 186, 118–134. [Google Scholar] [CrossRef]
- Si, J.; Pang, Z.; Du, Z.; Fu, J. Dynamics modeling and simulation of a net closing mechanism for tether-net capture. Int. J. Aerosp. Eng. 2021, 2021, 8827141. [Google Scholar] [CrossRef]
- Shan, M.; Guo, J.; Gill, E. Deployment dynamics of tethered-net for space debris removal. Acta Astronaut. 2017, 132, 293–302. [Google Scholar] [CrossRef]
- Gardsback, M.; Tibert, G. Deployment control of spinning space webs. J. Guid. Control Dyn. 2009, 32, 40–50. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, P.; Meng, Z.; Zhang, Y.; Liu, Z. Dynamics analysis and controller design for maneuverable tethered space net robot. J. Guid. Control Dyn. 2017, 40, 2828–2843. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, R.; Yu, Y.; Liu, J.; Baoyin, H. Asteroid Capture Dynamics and Control using a Large-scale Flexible Net. IEEE Trans. Aerosp. Electron. Syst. 2022. [Google Scholar] [CrossRef]
- Zhong, R.; Xu, S. Neural-network-based terminal sliding-mode control for thrust regulation of a tethered space-tug. Astrodynamics 2018, 2, 175–185. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, Z.; Baoyin, H. Timeline Club: An optimization algorithm for solving multiple debris removal missions of the time-dependent traveling salesman problem model. Astrodynamics 2022, 6, 219–234. [Google Scholar] [CrossRef]
- Schwartz, S.R.; Richardson, D.C.; Michel, P. An implementation of the soft-sphere discrete element method in a high-performance parallel gravity tree-code. Granul. Matter 2012, 14, 363–380. [Google Scholar] [CrossRef]
- Ferellec, J.F.; McDowell, G.R. A method to model realistic particle shape and inertia in DEM. Granul. Matter 2010, 12, 459–467. [Google Scholar] [CrossRef]
- Bierhaus, E.B.; Clark, B.C.; Harris, J.W.; Payne, K.S.; Dubisher, R.D.; Wurts, D.W.; Hund, R.A.; Kuhns, R.M.; Linn, T.M.; Wood, J.L.; et al. The OSIRIS-REx spacecraft and the touch-and-go sample acquisition mechanism (TAGSAM). Space Sci. Rev. 2018, 214, 107. [Google Scholar] [CrossRef] [Green Version]
- Yoshikawa, K.; Sawada, H.; Kikuchi, S.; Ogawa, N.; Mimasu, Y.; Ono, G.; Takei, Y.; Terui, F.; Saiki, T.; Yasuda, S.; et al. Modeling and analysis of Hayabusa2 touchdown. Astrodynamics 2020, 4, 119–135. [Google Scholar] [CrossRef]
- Biele, J.; Kesseler, L.; Grimm, C.D.; Schröder, S.; Mierheim, O.; Lange, M.; Ho, T.M. Experimental determination of the structural coefficient of restitution of a bouncing asteroid lander. arXiv 2017, arXiv:1705.00701. [Google Scholar]
- Abd, E.; Afaf, M.; Abdel, Y.A. Aluminium Alloys in Space Applications: A Short Report. J. Appl. Sci. Eng. 2021, 22, 1–7. [Google Scholar]













| Comparison Indicators | Literature [21] | Literature [22,23,24] | Literature [25] | Literature [26] | Literature [29] | Literature [28] | Literature [29] | Literature [30] | Literature [31] | Our Study |
|---|---|---|---|---|---|---|---|---|---|---|
| Modeling method of the net | Kelvin–Voigt method | Kelvin–Voigt method | Kelvin–Voigt method | Kelvin–Voigt method | Kelvin–Voigt method | Kelvin–Voigt method | Kelvin–Voigt method & the ANCF method | The discrete elastic rods method | Kelvin–Voigt method | Kelvin–Voigt method |
| Consider the post-capture process? | no | no | yes | no | no | yes | no | no | no | yes |
| Consider the translational dynamics of the debris? | yes | no | yes | no | no | yes | no | no | no | yes |
| Consider the rotational dynamics of the net? | yes | no | yes | no | no | yes | no | no | no | yes |
| Net closing mechanism | Mechanical mechanism (e.g., spring) | Active control scheme | Mechanical mechanism (e.g., spring) | No mechanism | No mechanism | Mechanical mechanism (e.g., spring) | Mechanical mechanism (e.g., spring) | No mechanism | The split closing mechanism | Active control scheme |
| Can the net be reopened? | no | yes | no | no | no | no | no | no | no | yes |
| Can many pieces of debris be removed in one mission? | no | yes | no | no | no | no | no | no | no | yes |
| Consider the self-collision of the net? | no | no | no | yes | no | no | no | no | no | no |
| Consider the capture robustness? | no | no | no | no | yes | no | no | no | no | no |
| Simulation software | no | no | no | no | no | Vortex Studio | no | no | no | no |
| Parameter | Value |
|---|---|
| Mass mT | 308.7747 g |
| Material | Aluminum alloy [43] |
| Dimensions | 5 cm × 13 cm × 10 cm |
| Restitution coefficient | 0.5 [42] |
| Frictional angle | 45° [35] |
| Parameter | Value |
|---|---|
| Mass of each actuator mk | 10 kg |
| Maximum deployment area | 3600 cm2 |
| Material | Zylon fiber |
| Density | 1440 kg/m3 |
| Thread diameter | 2 mm |
| Initial thread length | 4 cm |
| Young’s modulus | 180 GPa |
| Damping ratio | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ru, M.; Zhan, Y.; Cheng, B.; Zhang, Y. Capture Dynamics and Control of a Flexible Net for Space Debris Removal. Aerospace 2022, 9, 299. https://doi.org/10.3390/aerospace9060299
Ru M, Zhan Y, Cheng B, Zhang Y. Capture Dynamics and Control of a Flexible Net for Space Debris Removal. Aerospace. 2022; 9(6):299. https://doi.org/10.3390/aerospace9060299
Chicago/Turabian StyleRu, Man, Ying Zhan, Bin Cheng, and Yu Zhang. 2022. "Capture Dynamics and Control of a Flexible Net for Space Debris Removal" Aerospace 9, no. 6: 299. https://doi.org/10.3390/aerospace9060299
APA StyleRu, M., Zhan, Y., Cheng, B., & Zhang, Y. (2022). Capture Dynamics and Control of a Flexible Net for Space Debris Removal. Aerospace, 9(6), 299. https://doi.org/10.3390/aerospace9060299





