Attitude Maneuver and Stability Control of Hyper-Agile Satellite Using Reconfigurable Control Moment Gyros
Abstract
:1. Introduction
- (a)
- A detailed modeling of the hyper-agile satellite ACS is established.
- (b)
- An octagonal cone-type SGCMGs is designed as an actuator, and the momentum characteristics are analyzed in detail. Based on this design, norm and norm are introduced to define evaluation metrics for SGCMGs to analyze the configuration benefits, respectively.
- (c)
- The disturbance mechanism of SGCMGs is analyzed, and the disturbance torque is fitted by experimental data to be applied to the later ACS disturbance model. According to the real flying results of the Jilin-1 hyper-agile satellite, two practical engineering problems are faced. In the first place, unknown frictional disturbances of the low-cost miniaturized SGCMG are difficult to eliminate. In the second place, it is difficult to balance the trade-off between ultra-fast maneuverability and high stability during the attitude maneuver. The concept of reconfigurable SGCMGs is proposed to address the above problems: by switching between octagonal cone-type SGCMGs and pyramid-type SGCMGs to allocate the torque that meets the attitude control requirements of different maneuver segments.
- (d)
- The overall design of the hyper-agile satellite ACS is completed that includes the modeling of the steering law and controller. The simulations demonstrate the feasibility and superiority of the reconfigurable octagonal cone-type SGCMGs system.
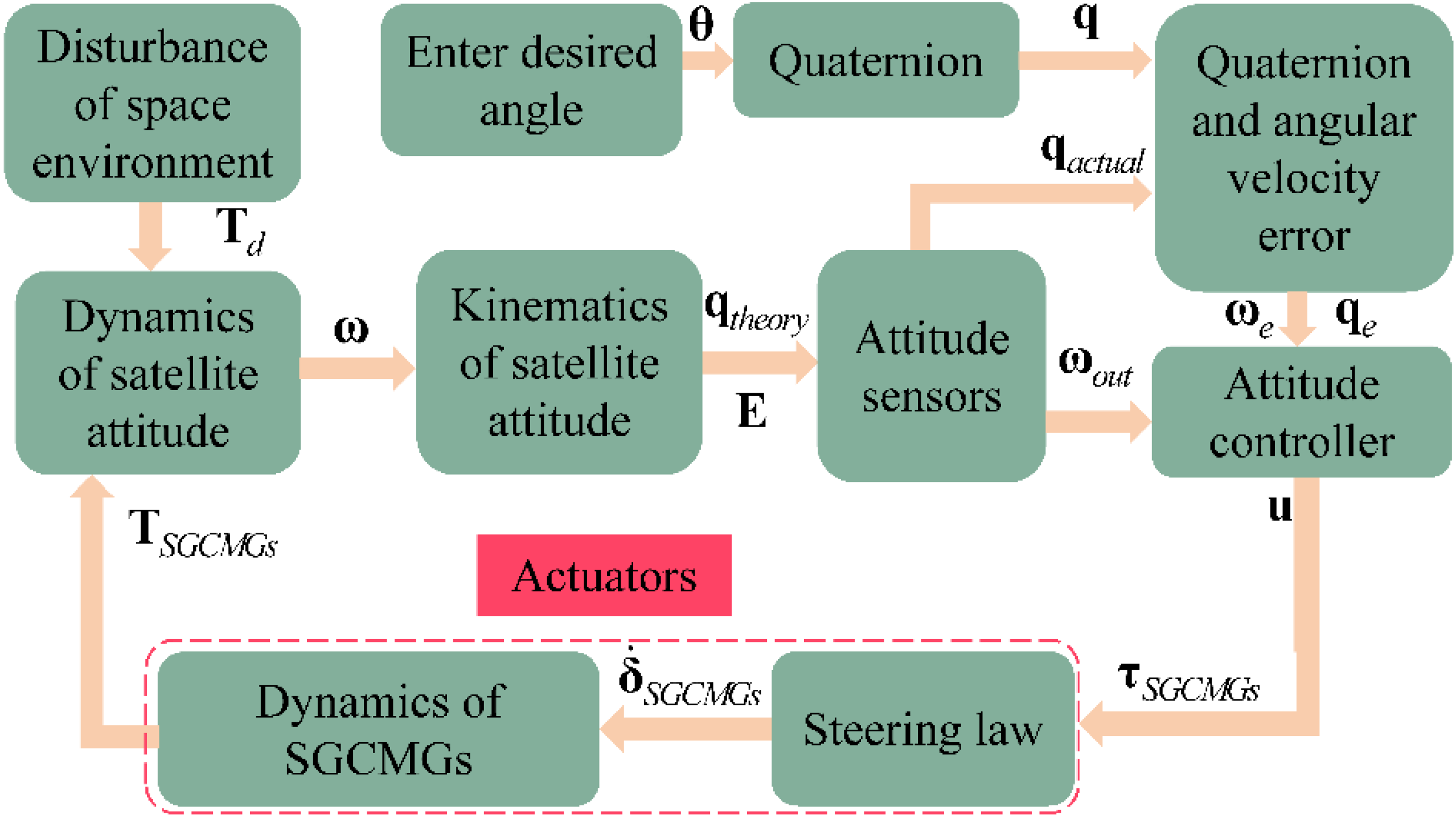
2. Mathematical Model
2.1. Kinematics
2.1.1. Kinematic Characterization of Euler Angle
2.1.2. Kinematic Characterization of Quaternion
2.2. Dynamics of Hyper-Agile Satellite Attitude
2.3. Environment Disturbance Torques
2.3.1. Gravity Gradient Torque
2.3.2. Aerodynamic Torque
2.3.3. Sunlight Pressure Torque
2.3.4. Magnetic Torque
2.4. Attitude Sensors
2.4.1. Stellar Sensor Model
2.4.2. Fiber Optic Gyro Model
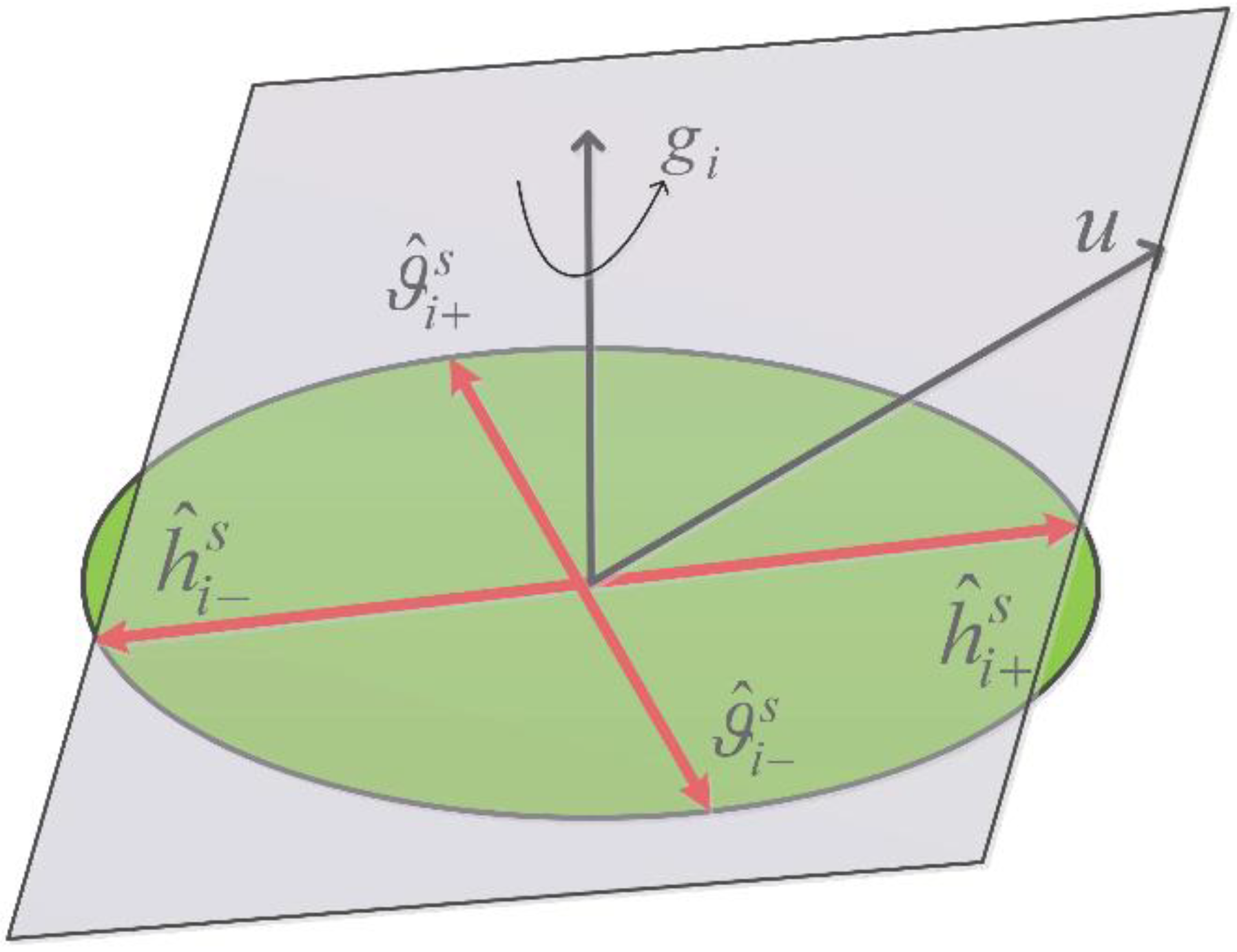
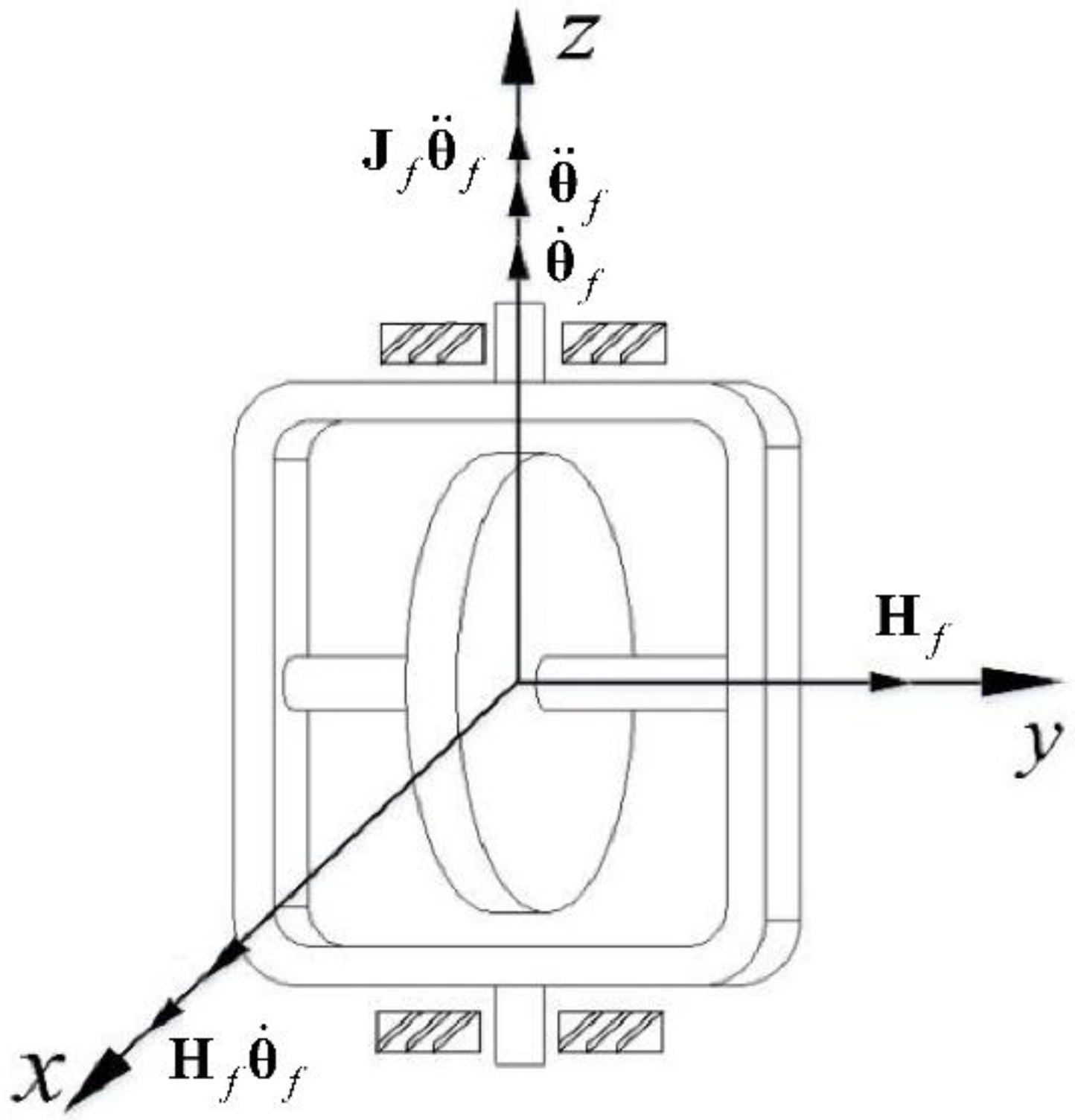
3. Configuration Design and Benefit Analysis of SGCMGs
3.1. Problem Formulation
3.2. Dynamics of 8-SGCMGs
3.3. Benefit Analysis of 8-SGCMGs
3.3.1. Momentum Envelope
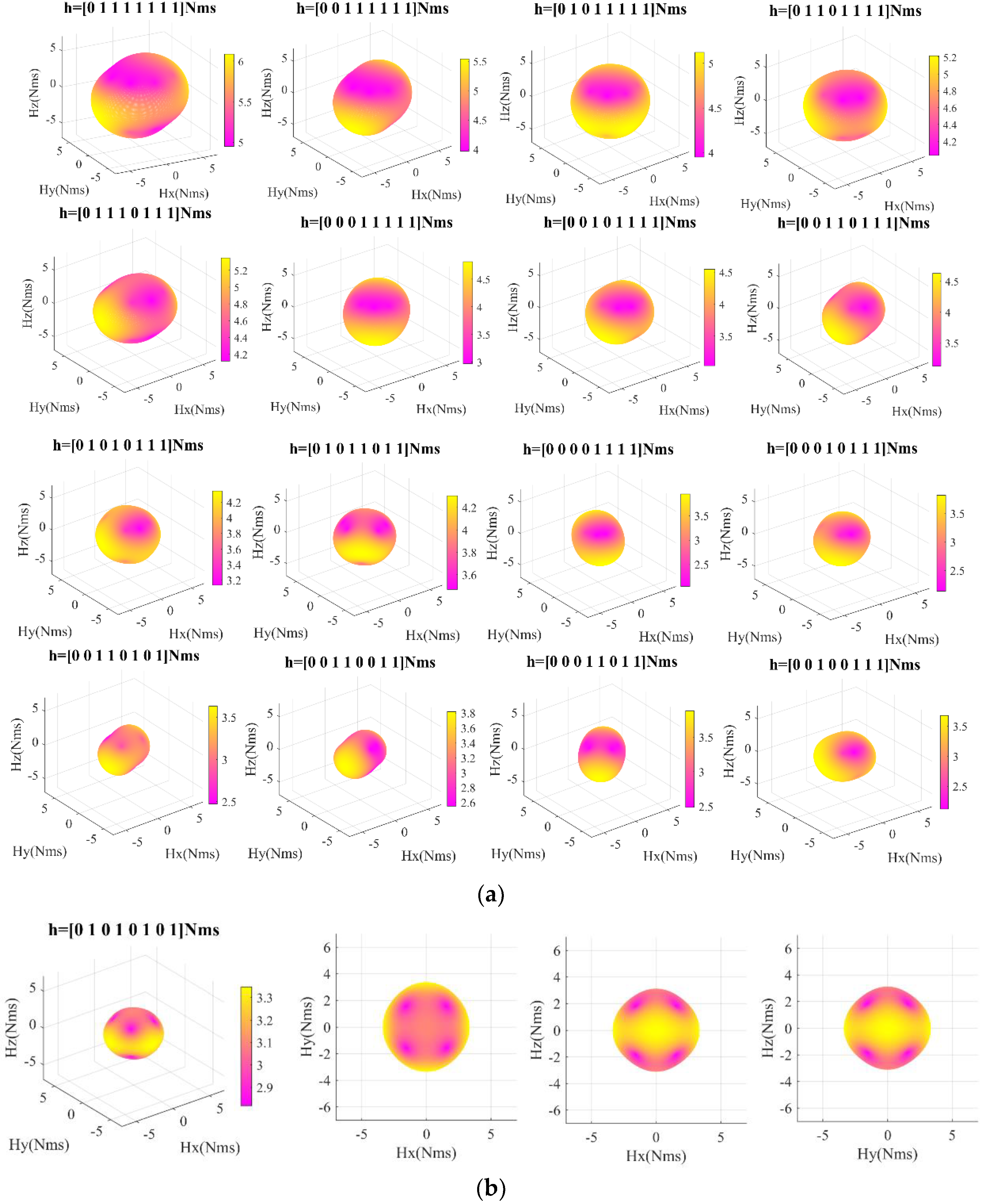
3.3.2. Failure Momentum Envelopes
3.3.3. Singular Momentum Envelopes
4. Reconfigurable SGCMGs System Design
4.1. Problem Formulation
4.2. Disturbance Torque Analysis of 8-SGCMGs
4.3. Reconfiguration of 8-SGCMGs into 4-SGCMGs
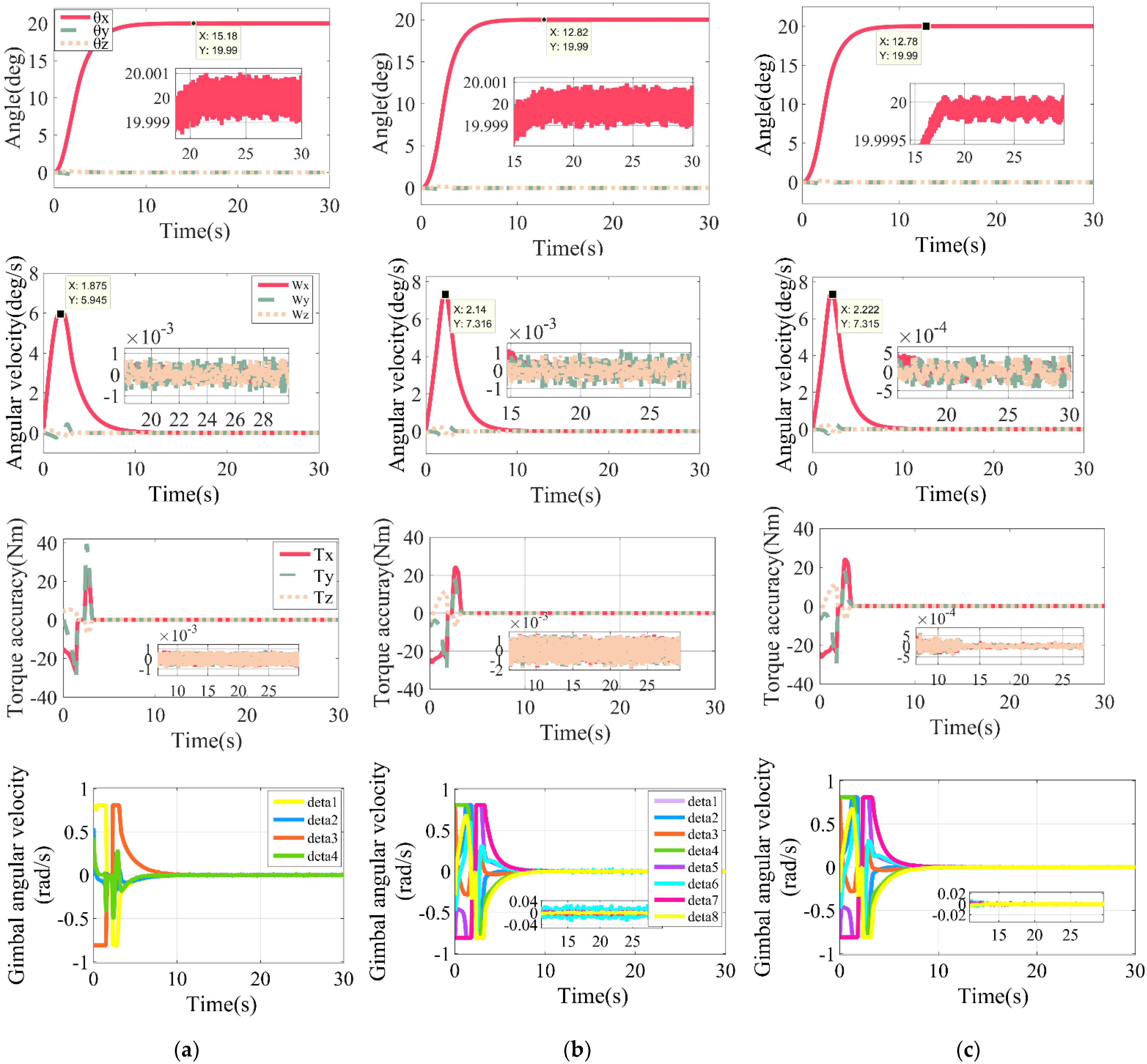
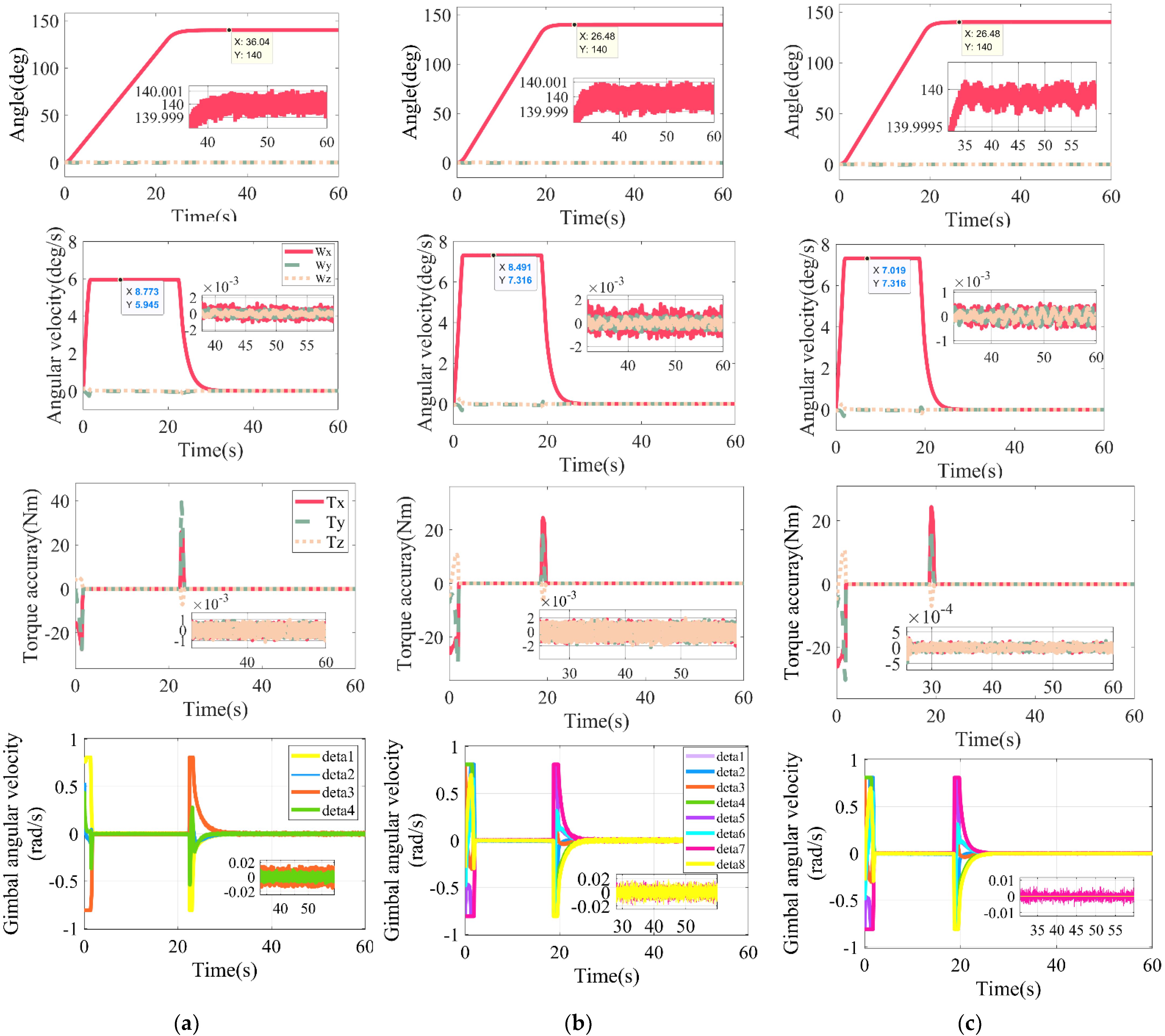
5. Simulation and Analysis
- Case 1, a small angle of 20 deg around the x-axis attitude maneuver;
- Case 2, a large angle of 140 deg around the x-axis attitude maneuver.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
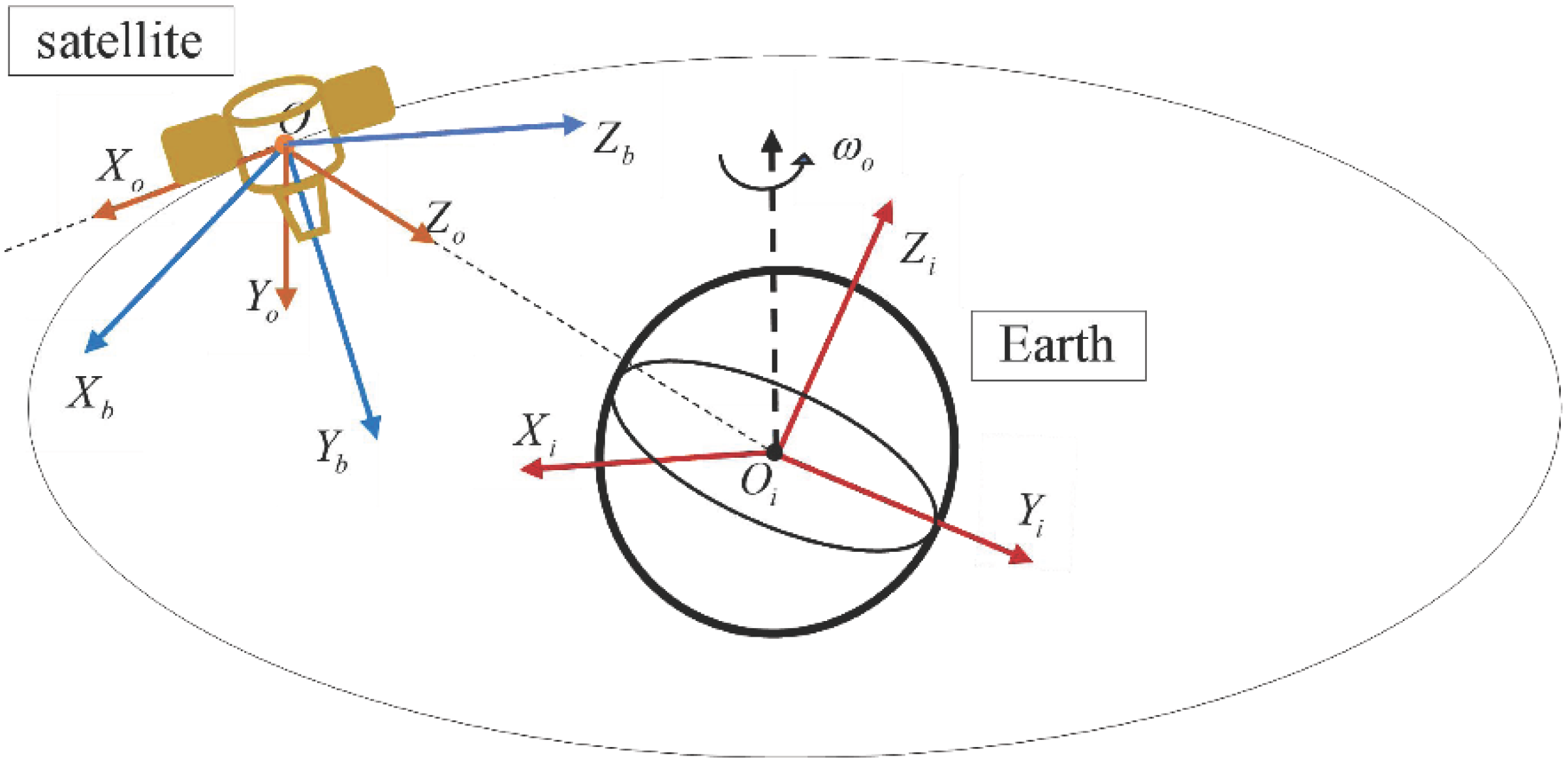
- Inertial Coordinate System
- 2.
- Orbital Coordinate System
- 3.
- Body Coordinate System
References
- Xie, Y.; Lei, Y.; Guo, J.; Meng, B. Spacecraft Dynamics and Control; Space Science and Technologies; Springer: Singapore, 2022; ISBN 978-981-336-447-9. [Google Scholar]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Berger, M.; Aschbacher, J. Preface: The Sentinel Missions—New Opportunities for Science. Remote Sens. Environ. 2012, 120, 1–2. [Google Scholar] [CrossRef]
- ESA Earth Observation Portal. Copernicus: Sentinel-1—The SAR Imaging Constellation for Land and Ocean Services. Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/c-missions/copernicus-sentinel-1 (accessed on 26 May 2022).
- Thieuw, A.; Marcille, H. Pleiades-Hr CMGs-Based Attitude Control System Design, Development Status and Performances. IFAC Proc. Vol. 2007, 40, 834–839. [Google Scholar] [CrossRef]
- Kruse, F.A.; Baugh, W.M.; Perry, S.L. Validation of DigitalGlobe WorldView-3 Earth Imaging Satellite Shortwave Infrared Bands for Mineral Mapping. J. Appl. Remote Sens. 2015, 9, 096044. [Google Scholar] [CrossRef]
- Xu, S.; Lu, Z.; Zhang, X.; Liao, W. Attitude Stability Control of Micro-Nano Satellite Orbit Maneuver Based on Bias Momentum. J. Phys. Conf. Ser. 2021, 2083, 022060. [Google Scholar] [CrossRef]
- Lappas, V.J.; Steyn, W.H.; Underwood, C.I. Attitude Control for Small Satellites Using Control Moment Gyros. Acta Astronaut. 2002, 51, 101–111. [Google Scholar] [CrossRef] [Green Version]
- Mkrtychyan, A.R.; Bashkeev, N.I.; Yakimovskii, D.O.; Akashev, D.I.; Yakovets, O.B. Control Moment Gyroscopes for Spacecraft Attitude Control Systems: Current Status and Prospects. Gyroscopy Navig. 2015, 6, 236–240. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J. Disturbance Characteristics Analysis of CMG Due to Imbalances and Installation Errors. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1017–1026. [Google Scholar] [CrossRef]
- Cui, P.; Zhang, D.; Yang, S.; Li, H. Friction Compensation Based on Time-Delay Control and Internal Model Control for a Gimbal System in Magnetically Suspended CMG. IEEE Trans. Ind. Electron. 2017, 64, 3798–3807. [Google Scholar] [CrossRef]
- Lee, S.; Jung, S. Experimental Verification of Singularity-Robust Torque Control for a 1.2-Nm–5-Hz SGCMG. IEEE Trans. Ind. Electron. 2018, 65, 4871–4879. [Google Scholar] [CrossRef]
- Kojima, H. Singularity Analysis and Steering Control Laws for Adaptive-Skew Pyramid-Type Control Moment Gyros. Acta Astronaut. 2013, 85, 120–137. [Google Scholar] [CrossRef]
- Takada, K.; Kojima, H.; Matsuda, N. Control Moment Gyro Singularity-Avoidance Steering Control Based on Singular-Surface Cost Function. J. Guid. Control Dyn. 2010, 33, 1442–1450. [Google Scholar] [CrossRef]
- Kawajiri, S.; Matunaga, S. A Low-Complexity Attitude Control Method for Large-Angle Agile Maneuvers of a Spacecraft with Control Moment Gyros. Acta Astronaut. 2017, 139, 486–493. [Google Scholar] [CrossRef]
- Hu, Q.; Guo, C.; Zhang, J. Singularity and Steering Logic for Control Moment Gyros on Flexible Space Structures. Acta Astronaut. 2017, 137, 261–273. [Google Scholar] [CrossRef]
- Hou, Z.; Geng, Y.; Wu, B.; Huang, S. Spacecraft Angular Velocity Trajectory Planning for SGCMG Singularity Avoidance. Acta Astronaut. 2018, 151, 284–295. [Google Scholar] [CrossRef]
- Leeghim, H.; Lee, C.-Y.; Jin, J.; Kim, D. A Singularity-Free Steering Law of Roof Array of Control Moment Gyros for Agile Spacecraft Maneuver. Int. J. Control Autom. Syst. 2020, 18, 1679–1690. [Google Scholar] [CrossRef]
- Seo, H.-H.; Bang, H.; Cheon, Y.-J. Steering Law of Control Moment Gyros Using Artificial Potential Function Approach. Acta Astronaut. 2019, 157, 374–389. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, K.; Meng, G.; Tian, S. Spacecraft Maneuvers via Singularity-Avoidance of Control Moment Gyros Based on Dual-Mode Model Predictive Control. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2546–2559. [Google Scholar] [CrossRef]
- Elkhayat, M.A.; Elhalwagy, Y.; ElRaffie, A.Y.; Elnashar, G.A. Robust Nonlinear Combined Attitude Control Algorithm Using Control Moment Gyro for Agile Satellites. In Proceedings of the AIAA SPACE 2016, Long Beach, CA, USA, 13–16 September 2016. [Google Scholar]
- Ozawa, R.; Takahashi, M. Agile Attitude Maneuver via SDRE Controller Using SGCMG Integrated Satellite Model. In Proceedings of the 2018 AIAA Guidance, Navigation and Control Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Hu, Q.; Tan, X. Dynamic Near-Optimal Control Allocation for Spacecraft Attitude Control Using a Hybrid Configuration of Actuators. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1430–1443. [Google Scholar] [CrossRef]
- Yu, X.; Zhu, Y.; Qiao, J.; Guo, L. Antidisturbance Controllability Analysis and Enhanced Antidisturbance Controller Design with Application to Flexible Spacecraft. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3393–3404. [Google Scholar] [CrossRef]
- Kristiansen, R.; Nicklasson, P.J.; Gravdahl, J.T. Satellite Attitude Control by Quaternion-Based Backstepping. IEEE Trans. Control Syst. Technol. 2009, 17, 227–232. [Google Scholar] [CrossRef]
- Giuseppi, A.; Pietrabissa, A.; Cilione, S.; Galvagni, L. Feedback Linearization-Based Satellite Attitude Control with a Life-Support Device without Communications. Control Eng. Pract. 2019, 90, 221–230. [Google Scholar] [CrossRef]
- Verbin, D.; Lappas, V.J. Rapid Rotational Maneuvering of Rigid Satellites with Hybrid Actuators Configuration. J. Guid. Control Dyn. 2013, 36, 532–547. [Google Scholar] [CrossRef]
- Yamada, K.; Jikuya, I.; Kwak, O. Rate Damping of a Spacecraft Using Two Single-Gimbal Control Moment Gyros. J. Guid. Control Dyn. 2013, 36, 1606–1623. [Google Scholar] [CrossRef]
- Yoshimura, Y. Optimal Fault-Tolerant Configurations of Control Moment Gyros. J. Guid. Control Dyn. 2015, 38, 2460–2467. [Google Scholar] [CrossRef]
- Yue, C.; Kumar, K.D.; Shen, Q.; Goh, C.H.; Lee, T.H. Attitude Stabilization Using Two Parallel Single-Gimbal Control Moment Gyroscopes. J. Guid. Control Dyn. 2019, 42, 1353–1364. [Google Scholar] [CrossRef]
- Yue, C.; Wu, F.; Wang, F.; Cao, X.; Shen, Q.; Kumar, K.D. Two Parallel Single-Gimbal Control Moment Gyros Actuated Spacecraft Attitude Maneuver. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4112–4123. [Google Scholar] [CrossRef]
- Geshnizjani, R.; Kornienko, A.; Ziegler, T.; Löhr, J.; Fichter, W. Torque Optimal Steering of Control Moment Gyroscopes for Agile Spacecraft. J. Guid. Control Dyn. 2021, 44, 629–640. [Google Scholar] [CrossRef]
- Lei, Y.; Yuan, L.; Zhu, Q.; Wang, Z.; Liu, J. A Steering Method with Multiobjective Optimizing for Nonredundant Single-Gimbal Control Moment Gyro Systems. IEEE Trans. Ind. Electron. 2022, 69, 4177–4184. [Google Scholar] [CrossRef]
- Karpenko, M.; King, J.T.; Dennehy, C.J.; Ross, I.M. Agility Analysis of the James Webb Space Telescope. J. Guid. Control Dyn. 2019, 42, 810–821. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, C.; Zhang, S.; Cai, H. Optimal Attitude Trajectory Planning Method for CMG Actuated Spacecraft. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 131–142. [Google Scholar] [CrossRef]
- Markley, F.L.; Reynolds, R.G.; Liu, F.X.; Lebsock, K.L. Maximum Torque and Momentum Envelopes for Reaction Wheel Arrays. J. Guid. Control Dyn. 2010, 33, 1606–1614. [Google Scholar] [CrossRef]
- Chen, S.; Xuan, M.; Xin, J.; Liu, Y.; Gu, S.; Li, J.; Zhang, L. Design and Experiment of Dual Micro-Vibration Isolation System for Optical Satellite Flywheel. Int. J. Mech. Sci. 2020, 179, 105592. [Google Scholar] [CrossRef]
- Qu, Z.; Jia, H.; Xu, K.; He, X.; Yang, F.; Li, F.; Liu, M. Reconfigurability Analysis of Distributed Control Moment Gyro for Jilin-1 Super Agile Satellite. In Proceedings of the 2020 3rd International Conference on Electron Device and Mechanical Engineering (ICEDME), Suzhou, China, 1–3 May 2020. [Google Scholar]
- Inumoh, L.; Pechev, A.; Horri, N.; Forshaw, J. Three-Axis Attitude Control of a Satellite in Zero Momentum Mode Using a Tilted Wheel Methodology. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar]
- Powell, B.K. Gravity-Gradient Momentum Management. J. Spacecr. Rockets 1972, 9, 385–386. [Google Scholar] [CrossRef]
- Frik, M.A. Attitude Stability of Satellites Subjected to Gravity Gradient and Aerodynamic Torques. AIAA J. 1970, 8, 1780–1785. [Google Scholar] [CrossRef]
- Stuck, B.W. Solar Pressure Three-Axis Attitude Control. J. Guid. Control 1980, 3, 132–139. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, L.; Zhu, Y.; Huang, H.; Cai, W. Angular-Momentum Management of Spacecraft Electromagnetic Docking Considering the Earth’s Magnetic Field. J. Guid. Control Dyn. 2013, 36, 860–869. [Google Scholar] [CrossRef]
- Lefferts, E.J.; Markley, F.L.; Shuster, M.D. Kalman Filtering for Spacecraft Attitude Estimation. J. Guid. Control Dyn. 1982, 5, 417–429. [Google Scholar] [CrossRef]
- Xiong, K.; Liang, T.; Yongjun, L. Multiple Model Kalman Filter for Attitude Determination of Precision Pointing Spacecraft. Acta Astronaut. 2011, 68, 843–852. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, M.; Song, Z.; Shan, J.; Guan, X.; Tang, L. Design and Analysis of a Moment Control Unit for Agile Satellite with High Attitude Stability Requirement. Acta Astronaut. 2016, 122, 90–105. [Google Scholar] [CrossRef]
- Kawak, B.J. Development of a Low-Cost, Low Micro-Vibration CMG for Small Agile Satellite Applications. Acta Astronaut. 2017, 131, 113–122. [Google Scholar] [CrossRef]
- Hamilton-Jacobi Perturbation Theory. In Orbital and Celestial Mechanics; Progress in Astronautics and Aeronautics, 23 August 2012; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012. [CrossRef]
- Kurokawa, H. Survey of Theory and Steering Laws of Single-Gimbal Control Moment Gyros. J. Guid. Control Dyn. 2007, 30, 1331–1340. [Google Scholar] [CrossRef]
- Sands, T.A.; Kim, J.J.; Agrawal, B.N. Nonredundant Single-Gimbaled Control Moment Gyroscopes. J. Guid. Control Dyn. 2012, 35, 578–587. [Google Scholar] [CrossRef] [Green Version]
- Yamada, K.; Jikuya, I. Directional Passability and Quadratic Steering Logic for Pyramid-Type Single Gimbal Control Moment Gyros. Acta Astronaut. 2014, 102, 103–123. [Google Scholar] [CrossRef]

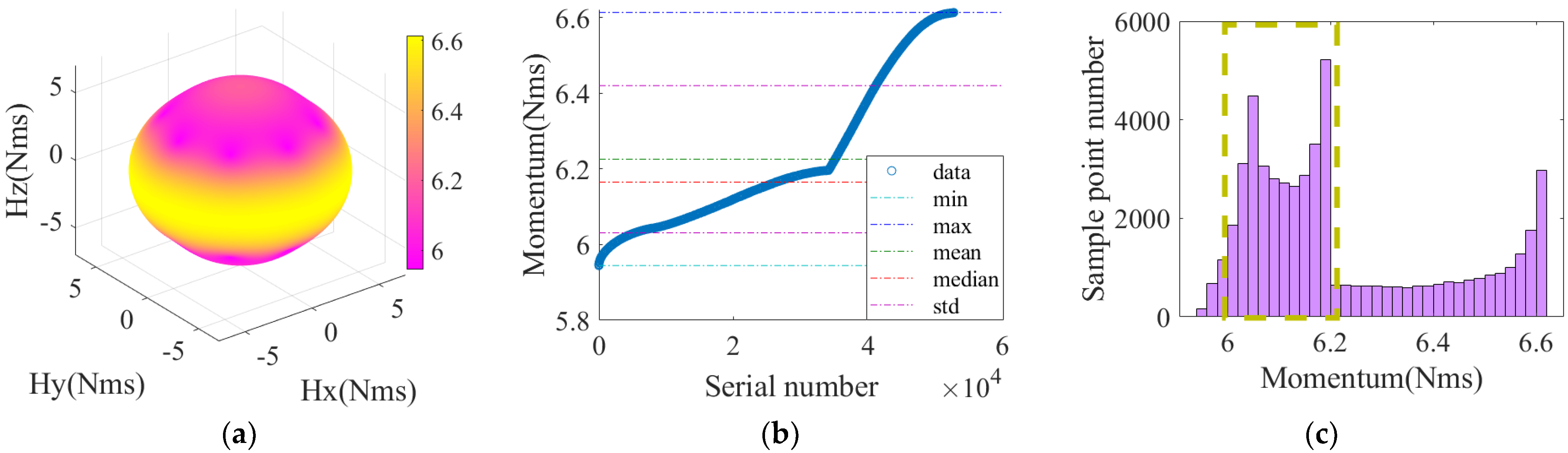



| Statistical Parameters (h0 = 1 Nms) | Value Interval | Mean | Median | |||
|---|---|---|---|---|---|---|
| Value | No failure | 6.226 | 6.165 | 0.195 | ||
| 1 failed unit | 5.426 | 5.447 | 0.269 | |||
| 2 failed units | 4.641 | 4.663 | 0.391 | |||
| 4.699 | 4.666 | 0.301 | ||||
| 4.673 | 4.668 | 0.255 | ||||
| 4.641 | 4.669 | 0.254 | ||||
| 3 failed units | 3.821 | 3.823 | 0.449 | |||
| 3.907 | 3.862 | 0.353 | ||||
| 3.833 | 3.870 | 0.308 | ||||
| 3.914 | 3.861 | 0.249 | ||||
| 3.871 | 3.873 | 0.178 | ||||
| 4 failed units | 3.113 | 3.070 | 0.481 | |||
| 3.110 | 3.093 | 0.377 | ||||
| 3.099 | 3.108 | 0.227 | ||||
| 3.089 | 3.089 | 0.304 | ||||
| 3.057 | 3.098 | 0.336 | ||||
| 3.142 | 3.087 | 0.349 | ||||
| 3.089 | 3.114 | 0.116 | ||||
| Statistical Parameters (h0 = 1 Nms) | Value Interval | Mean | Median | Standard Deviation | ||
|---|---|---|---|---|---|---|
| Value | 8H | 2.872 | 3.083 | 2.103 | ||
| 6H | 2.358 | 2.535 | 1.617 | |||
| 4H | 2.081 | 1.972 | 1.127 | |||
| 2H | 1.432 | 1.328 | 0.668 | |||
| 0H | 0.388 | 0.595 | 0.577 | |||
| Typical Configuration | ME | FME | SME | Evaluation Metric | ||||
|---|---|---|---|---|---|---|---|---|
| 4-SGCMGs | 0.7078 | 0.7879 | 0 | 0 | 0.6566 | 0.3254 | 1.3644 | 1.1133 |
| 5-SGCMGs | 0.7165 | 0.7949 | 0.3173 | 0.4015 | 0.6891 | 0.2699 | 1.7229 | 1.4663 |
| 6-SGCMGs | 0.6463 | 0.8217 | 0.2475 | 0.3242 | 0.7487 | 0.3051 | 1.6425 | 1.4510 |
| 8-SGCMGs | 0.7434 | 0.7787 | 0.3712 | 0.4444 | 0.5251 | 0.2831 | 1.6397 | 1.5062 |
| Parameter Name | Value |
|---|---|
| Equatorial rotational inertia of the flywheel | |
| Rotational inertia of pole | |
| Maximum gimbal angular acceleration of | |
| Maximum gimbal angular velocity | |
| Rated speed of flywheel | |
| Rated angular momentum of flywheel | |
| Rated torque of SGCMG |
| Output Torque | Gimbal Angular Velocity | Flywheel Disturbance Torque |
|---|---|---|
| 0.2611 | 0.0373 | 0.00511 |
| 0.861 | 0.123 | 0.01122 |
| 1.4609 | 0.2087 | 0.01299 |
| 2.0608 | 0.2944 | 0.01353 |
| 2.6607 | 0.3801 | 0.01448 |
| 3.2606 | 0.4658 | 0.01599 |
| 3.8605 | 0.5515 | 0.01671 |
| 4.4604 | 0.6372 | 0.01780 |
| 5.0603 | 0.7229 | 0.01896 |
| 5.6602 | 0.8086 | 0.02163 |
| Function for Determining 8-SGCMGs Control Allocation |
|---|
 |
| Parameter | Value |
|---|---|
| Momentum of inertia | |
| Initial angle | |
| Initial angular velocity | |
| Mass of satellite | 1000 kg |
| SGCMG flywheel momentum (large size 4-SGCMGs) | 14 Nms |
| SGCMG flywheel momentum (8-SGCMGs) | 7 Nms |
| Maximum gimbal rate | |
| Orbit inclination | 90 deg |
| Orbit altitude | 560 km |
| Proportional gain | |
| Derivative gain | |
| Factor of the null motion | 0.3 |
| Singularity parameter , , , | 0.01, 0.3, 20, 1 |
| Periodic perturbation parameter | 0.01 |
| Parameter | Value |
|---|---|
| Stellar sensitive noise | |
| Fiber optic gyro initial zero bias | |
| Fiber optic gyro angle random wandering | |
| Fiber optic gyro angular rate random wandering | |
| Characteristic area of windward | |
| Drag coefficient of aerodynamic | 2.6 |
| Position vector of the center of pressure concerning the center of satellite mass | |
| Sunlight pressure area | |
| Reflectivity of the surface | 0.5 |
| Transmissibility of the surface | 0.2 |
| Force arm of sunlight pressure | |
| Remanent magnetic moment |
| Metrics | Case1 (20 deg) | Case2 (140 deg) | ||||
|---|---|---|---|---|---|---|
| Large 4-SGCMGs | 8-SGCMGs | Reconfiguration of 8-SGCMGs into 4-SGCMGs | Large 4-SGCMGs | 8-SGCMGs | Reconfiguration of 8-SGCMGs into 4-SGCMGs | |
| Maneuver time | 15.18 | 12.82 | 12.78 | 36.04 | 26.48 | 26.48 |
| Angle error | ||||||
| Maximum angular velocity | 5.945 | 7.316 | 7.316 | 5.945 | 7.316 | 7.316 |
| Angular velocity error | ||||||
| Torque accuracy | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, Z.; Zhang, G.; Meng, Z.; Xu, K.; Xu, R.; Di, J. Attitude Maneuver and Stability Control of Hyper-Agile Satellite Using Reconfigurable Control Moment Gyros. Aerospace 2022, 9, 303. https://doi.org/10.3390/aerospace9060303
Qu Z, Zhang G, Meng Z, Xu K, Xu R, Di J. Attitude Maneuver and Stability Control of Hyper-Agile Satellite Using Reconfigurable Control Moment Gyros. Aerospace. 2022; 9(6):303. https://doi.org/10.3390/aerospace9060303
Chicago/Turabian StyleQu, Zhi, Gaofei Zhang, Ziyang Meng, Kai Xu, Ruiqin Xu, and Jiaojiao Di. 2022. "Attitude Maneuver and Stability Control of Hyper-Agile Satellite Using Reconfigurable Control Moment Gyros" Aerospace 9, no. 6: 303. https://doi.org/10.3390/aerospace9060303
APA StyleQu, Z., Zhang, G., Meng, Z., Xu, K., Xu, R., & Di, J. (2022). Attitude Maneuver and Stability Control of Hyper-Agile Satellite Using Reconfigurable Control Moment Gyros. Aerospace, 9(6), 303. https://doi.org/10.3390/aerospace9060303






