Water Surface Flight Control of a Cross Domain Robot Based on an Adaptive and Robust Sliding Mode Barrier Control Algorithm
Abstract
:1. Introduction
- A CDR that can work in three environments is designed. The dynamic model for the CDR flying on the water surface is presented;
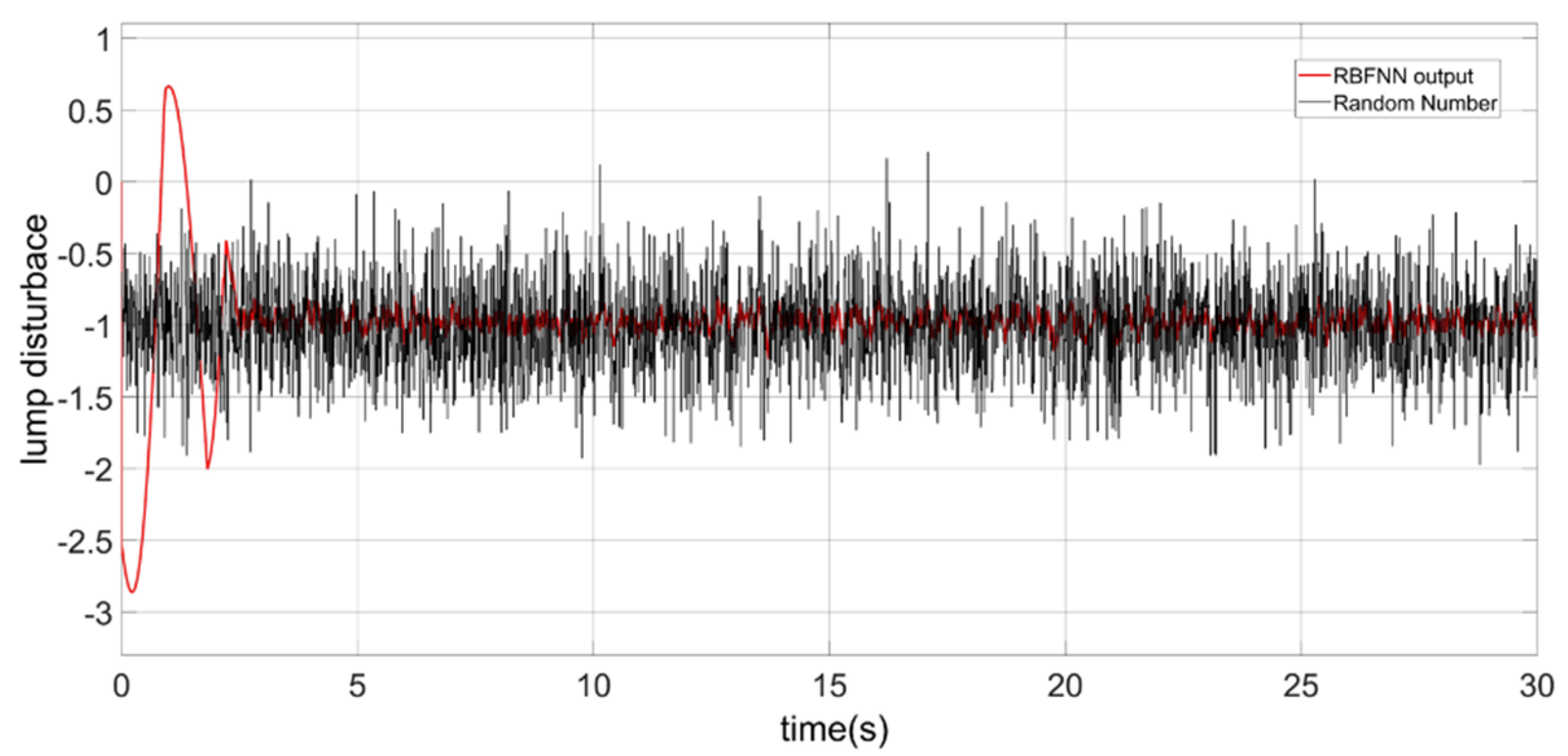
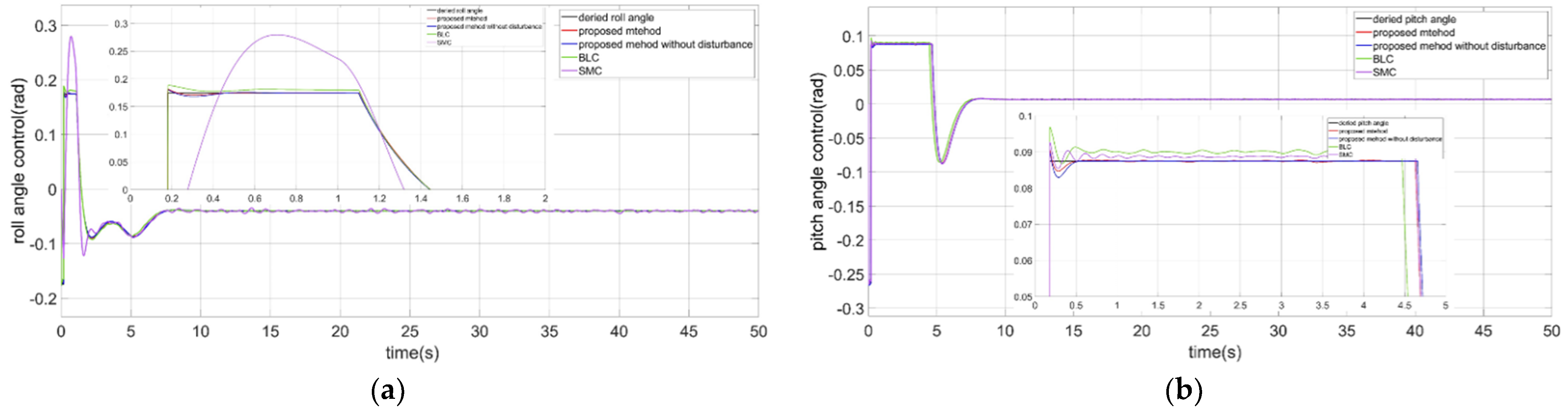
- Based on the traditional BC [16], a nonsingular terminal sliding mode asymmetric barrier control (NTSMABC) algorithm is proposed to constrain the pitch angle and roll angle of CDR on the water surface. Since the robot has an asymmetric structure which is similar with a small USV, the roll angle is controlled by NTSMBC, but the pitch angle is controlled by NTSMABC. To handle the lumped disturbance including uncertain model parameters and time-vary external disturbances, a RBFNN is adopted to compensate for the controller. Moreover, an adaptive law of neural network weight is designed with the Lyapunov function. The proposed method combines NTSMC with BC, which improves the convergence speed of the state errors and robustness;
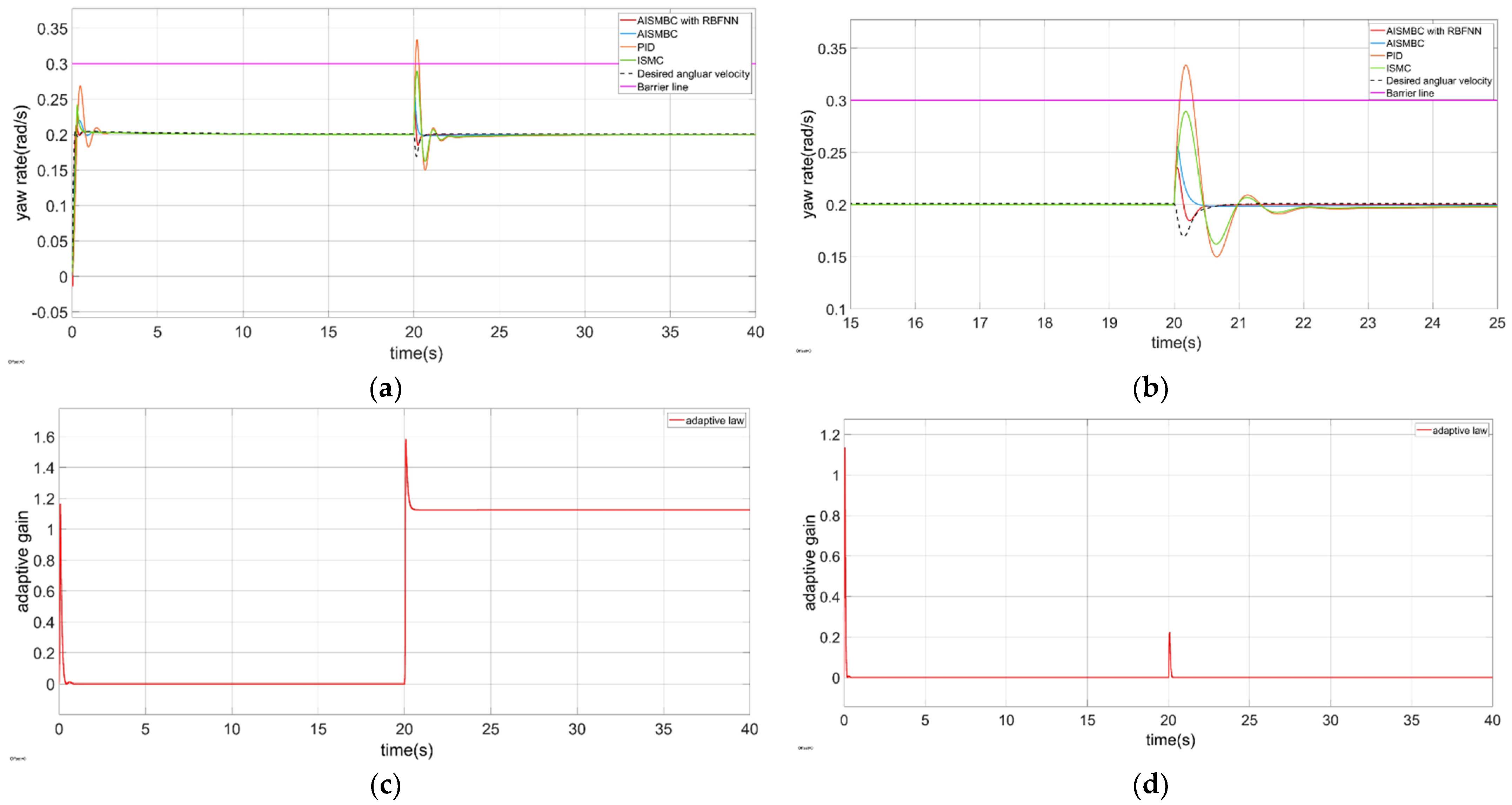
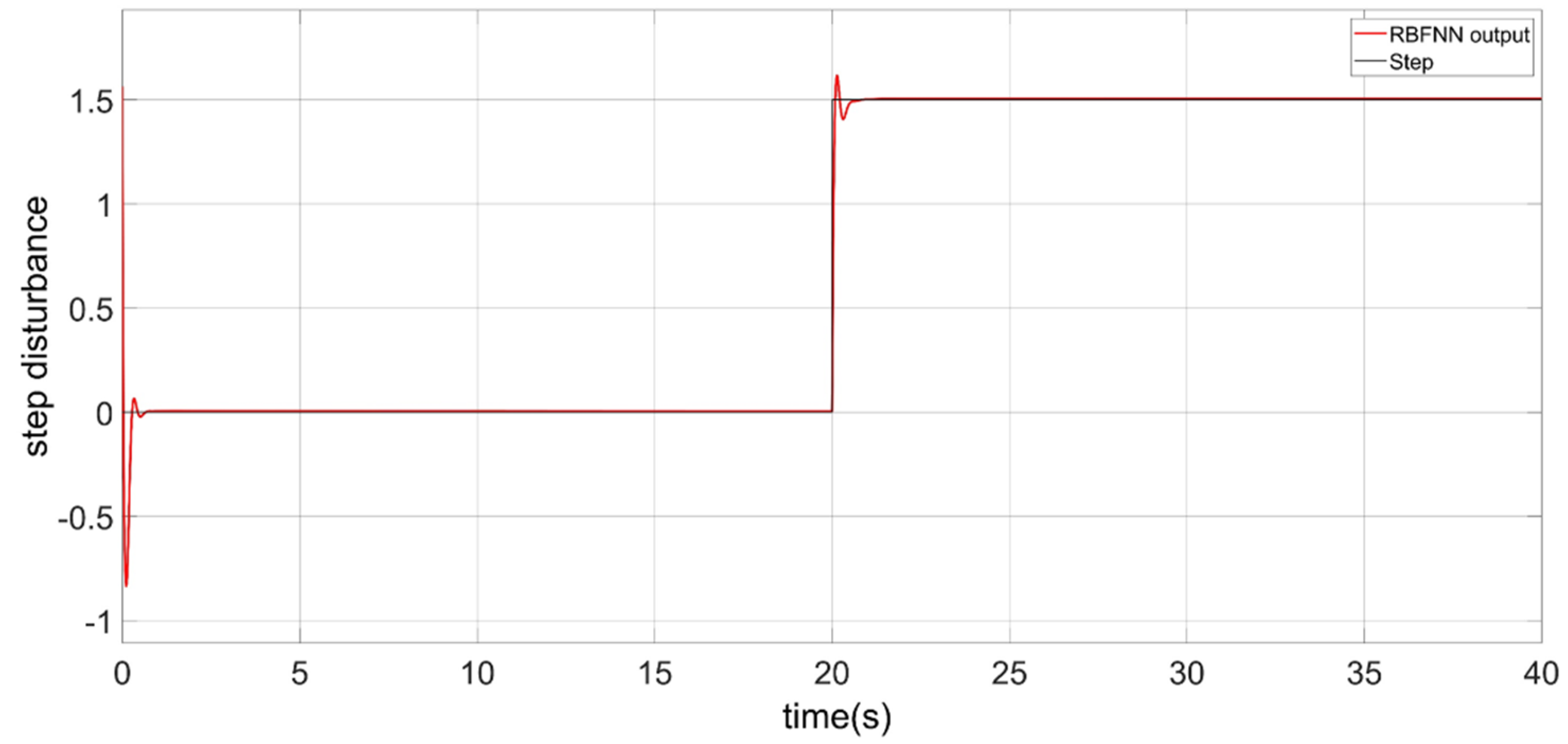
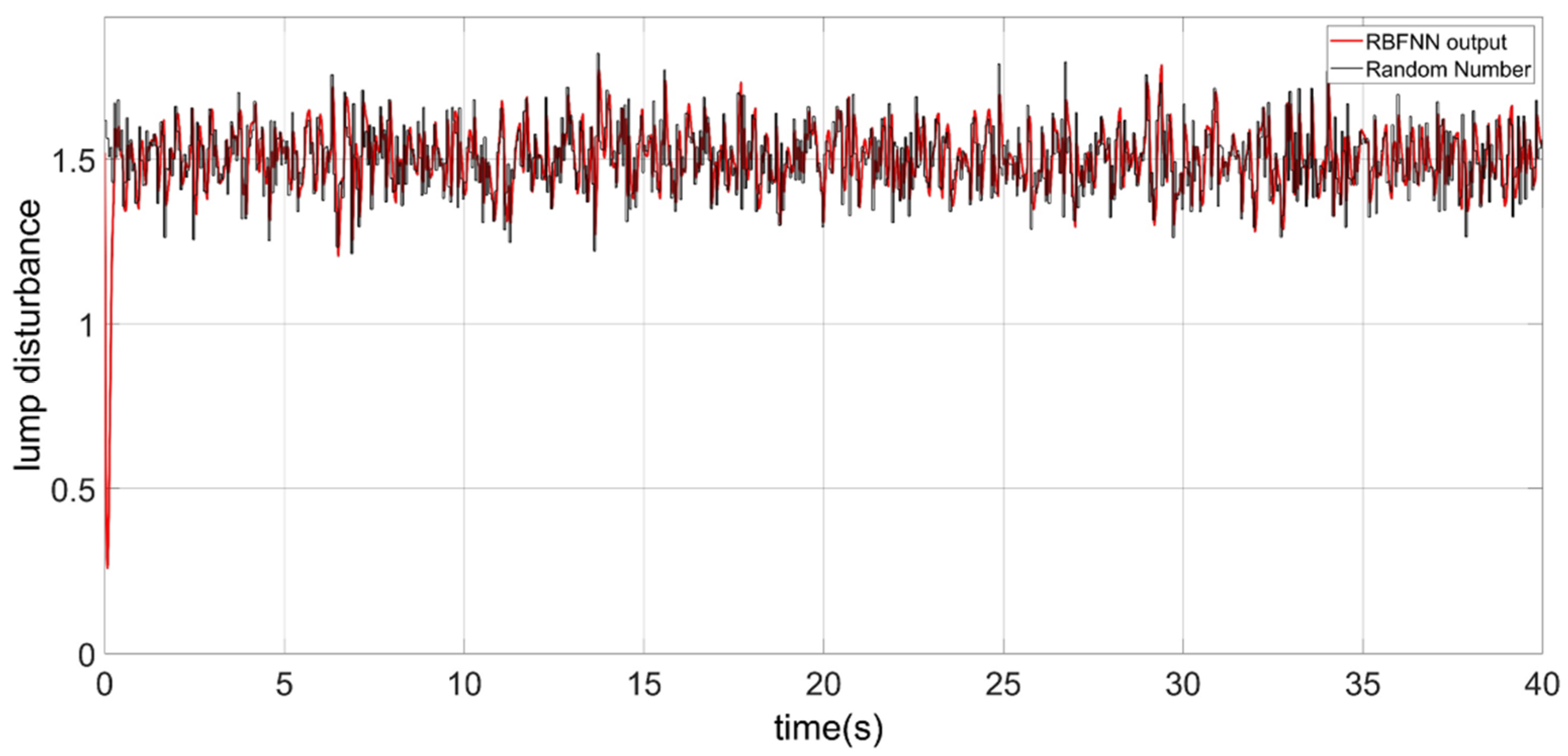
- Inspired by references [35,36], an adaptive integral sliding mode barrier control (AISMBC) is proposed to constrain the yaw angular velocity. The sliding mode surface we designed only includes the angular velocity state error, and the gain of sliding mode is adaptively adjusted according to the difference between the actual state and the barrier value. RBFNN is also designed to obtain the uncertain lump disturbance. The weights of the neural network are adjusted by the adaptive rate.
2. Preliminary Work and the Mathematic Model
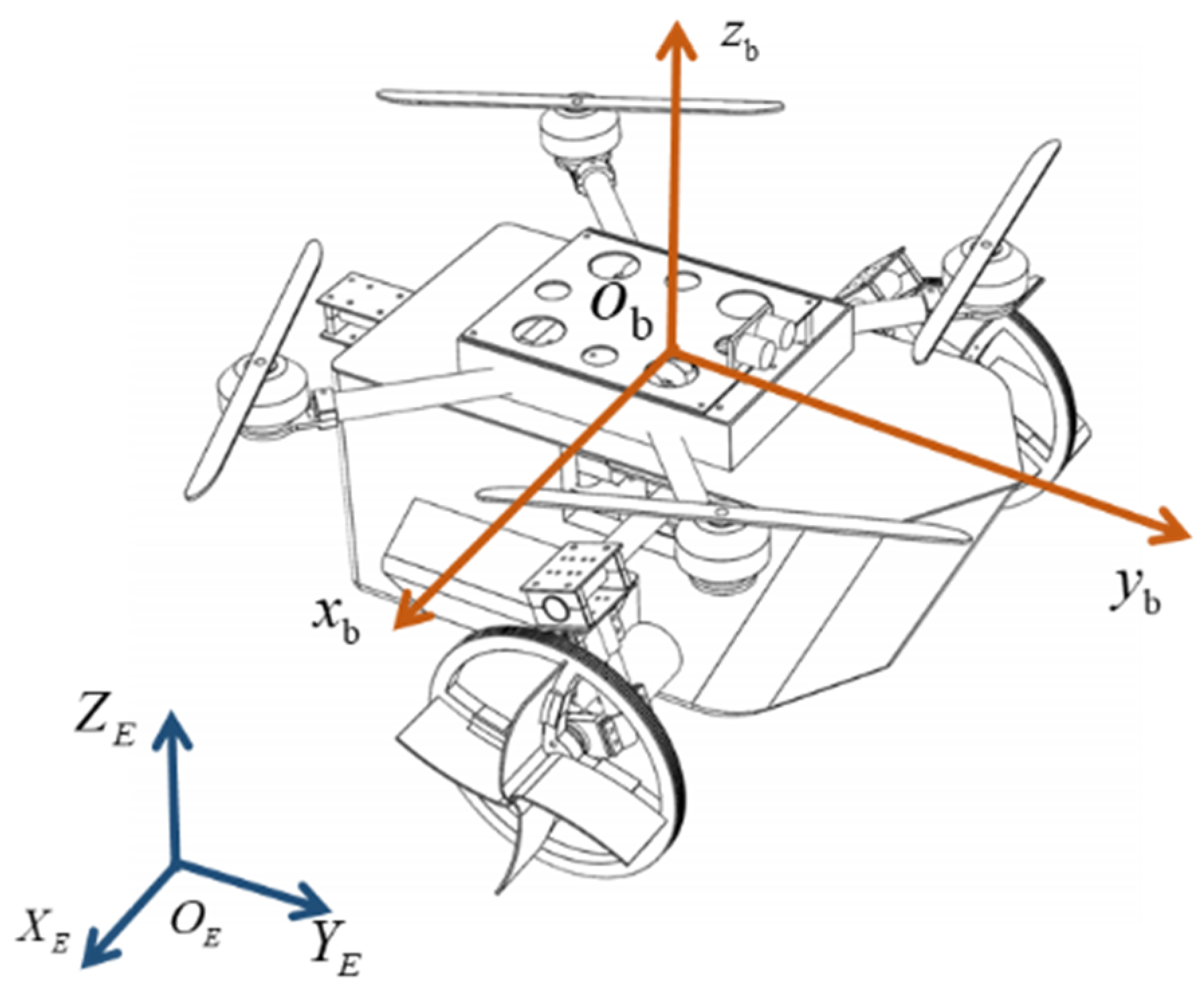
2.1. The Introduction of the Cross-Domain Robot
2.2. Dynamic Model of the Cross-Domain Robot
2.3. Motivation and Problem Statement
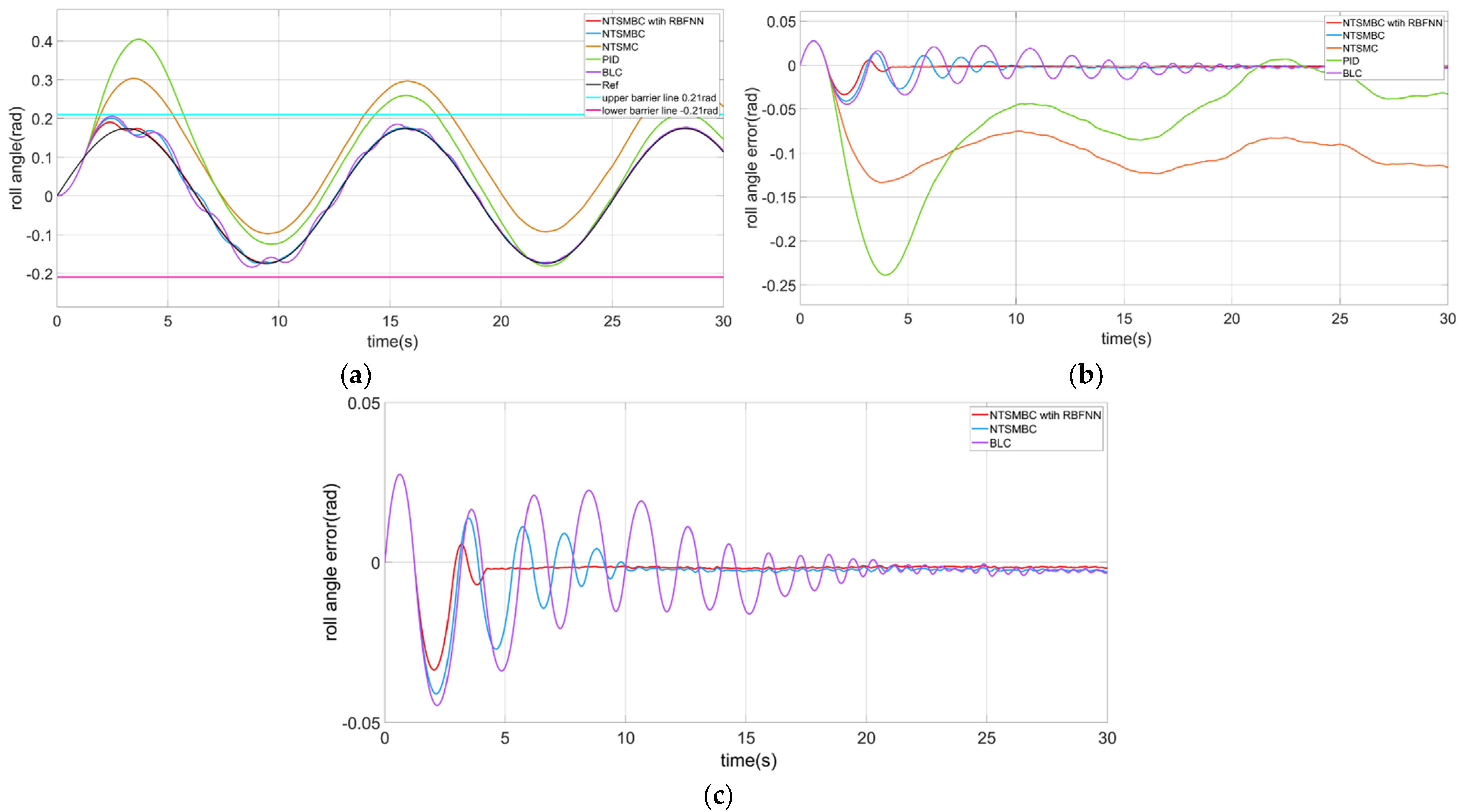
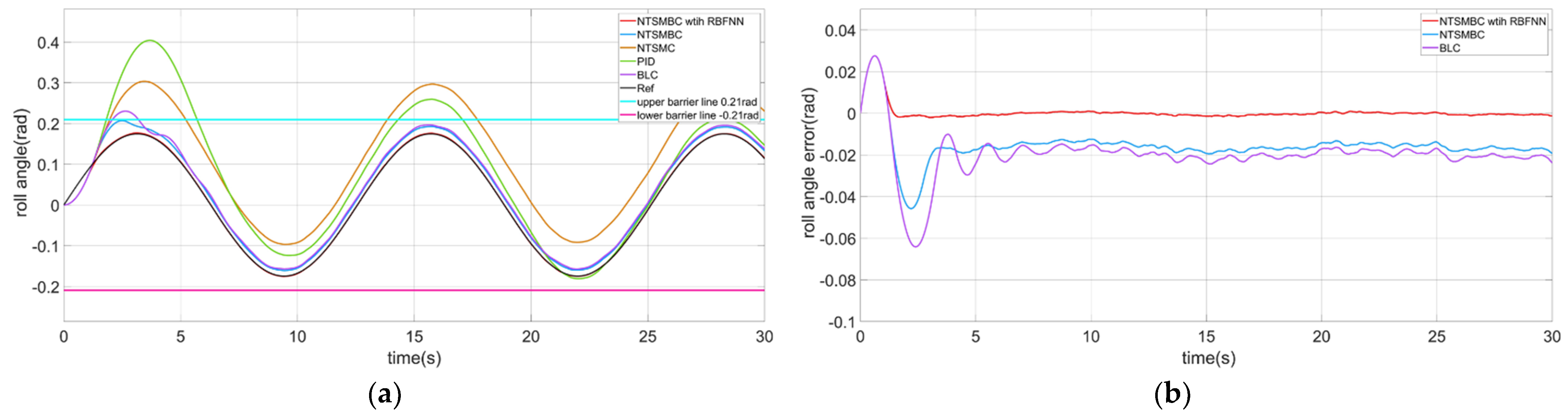
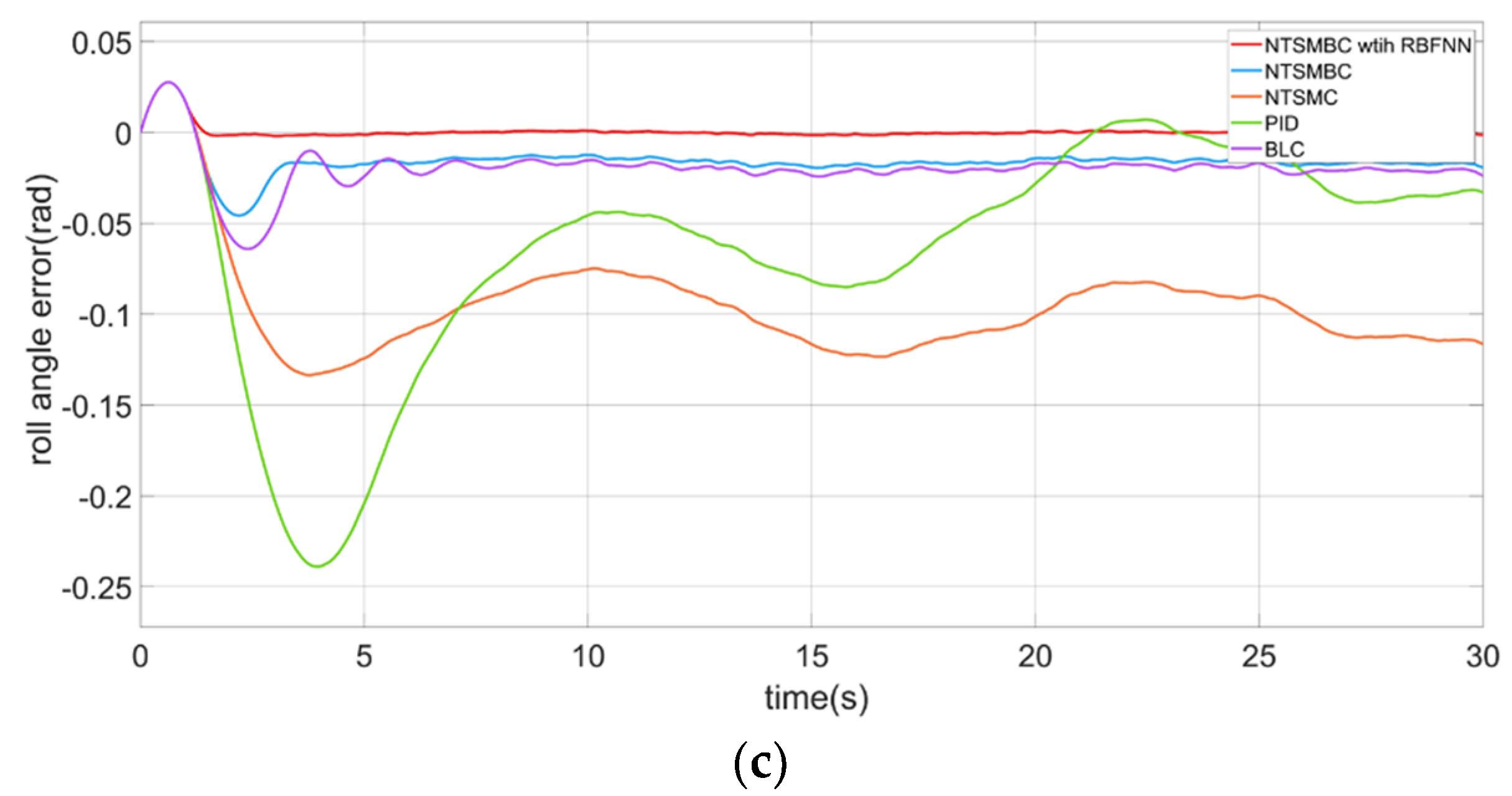
- When the CDR flies on the water surface, the large attitude angle leads to the water flooding into the cabin or even overturning. Therefore, it is necessary to constrain the attitude angle of the robot. The left and right sides of the robot structure are symmetrical, and a small roll angle can help balance the robot. Thus, the roll angle is constrained symmetrically. The pitch angle is constrained asymmetrically because the front and rear structures of the robot are asymmetric;
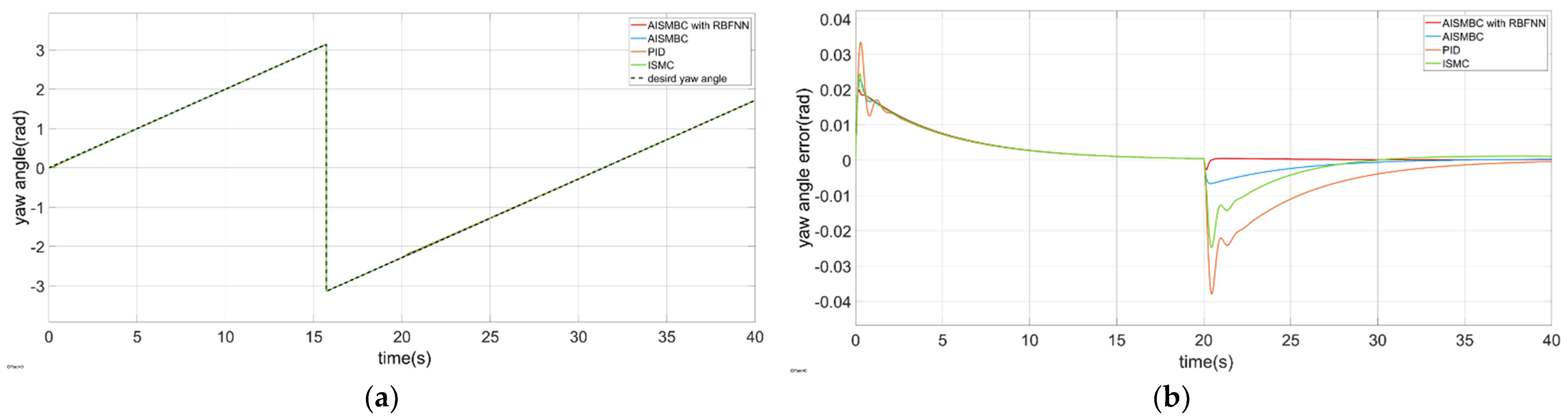
- When the yaw angular velocity reaches the maximum, even if the motor speed continues to increase, the yaw angular velocity cannot be increased. In addition, a large yaw angular velocity causes the robot roll over. Therefore, the yaw angular velocity is controlled by ISMBC algorithm, directly;
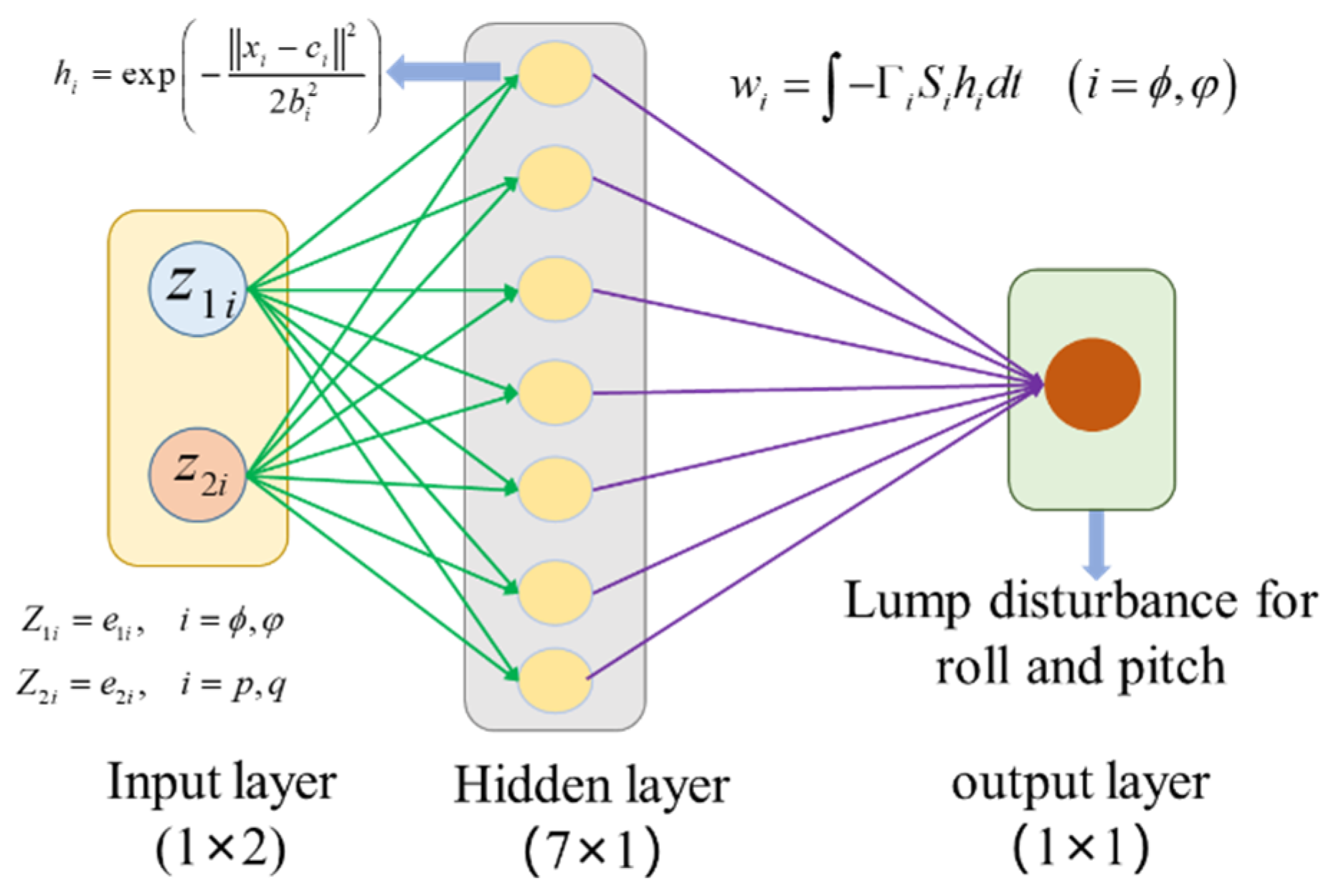
- There are uncertain parameters and coupling in the dynamic model of the robot attitude. Besides, the attitude of the robot is influenced by the unknown and time-varying water resistance, wind, and current. Thus, the RBFNN is designed for the uncertain lumped disturbances.
3. The Design of the CDR Attitude Controllers
3.1. Non-Singular Terminal Sliding Mode Asymmetric Barrier Control (NTSMABC)
3.2. Adaptive Integral Sliding Mode Barrier Control
4. Simulation Results and Discussion
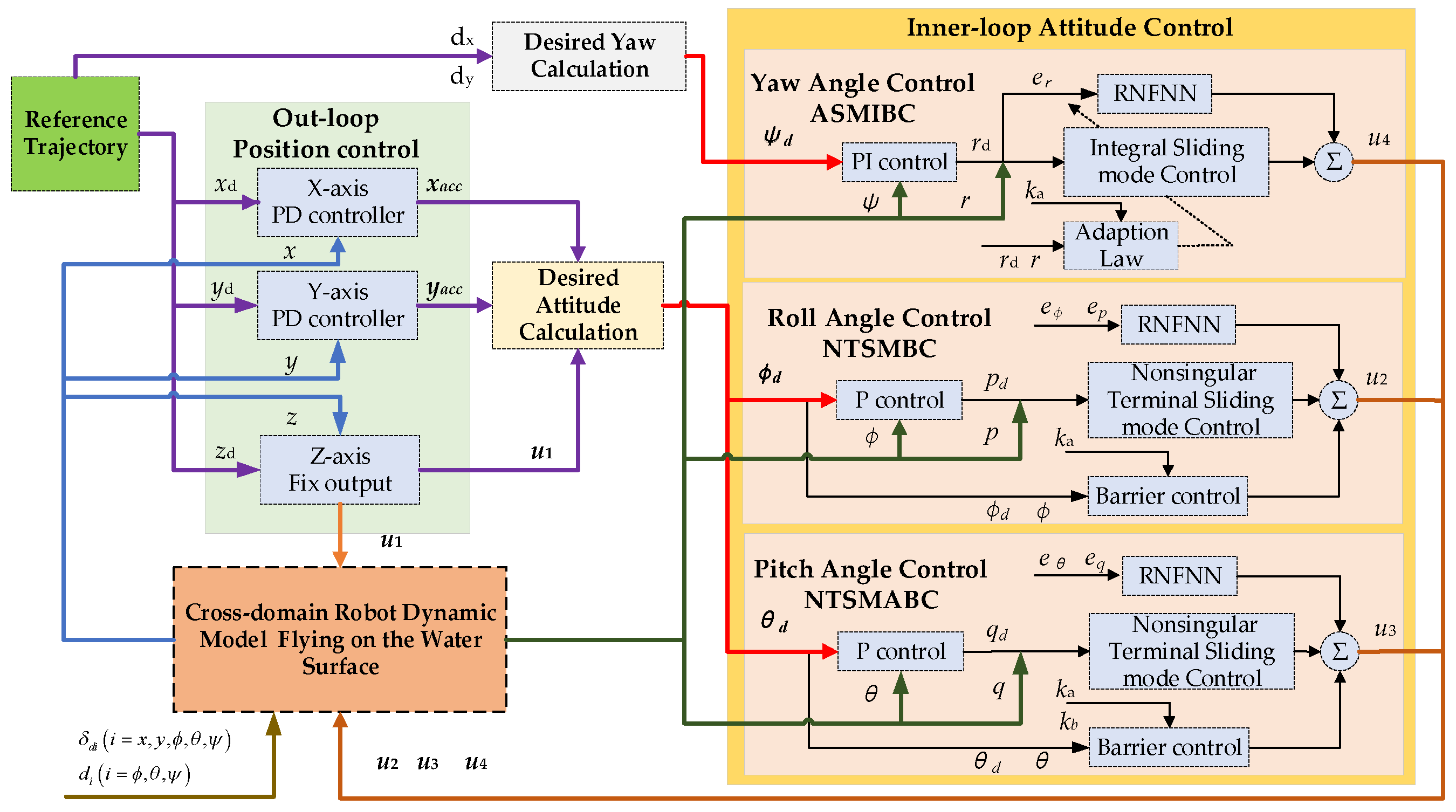
4.1. Design for the Controllers for CDR Flying on the Water Surface
4.2. Simulation Results of the CDR Flying on Water Surface
4.2.1. The Roll Angle Control of the CDR
4.2.2. The Pitch Angle Control of the CDR
4.2.3. The Yaw Angle Control of the CDR
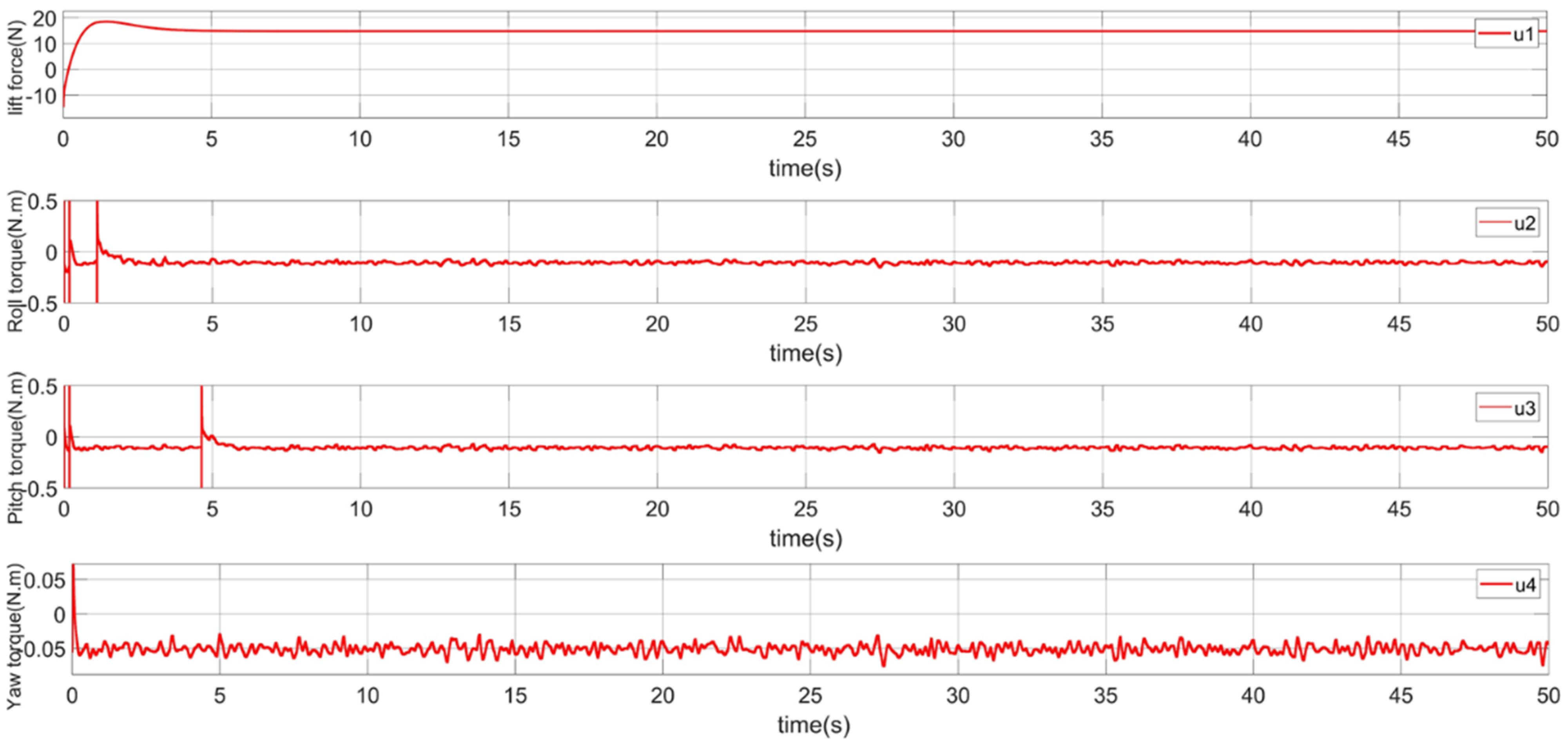
4.2.4. The CDR Tracks the Circular Desired Trajectory on the Water Surface
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbol | Description | Unit |
| x, y, z | longitudinal, lateral, and altitude motions in Earth-coordinate frame, respectively. | m |
| ϕ, θ, ψ | roll, pitch, and yaw angles in Earth-coordinate frame, respectively. | rad |
| p, q, r | roll, pitch, and yaw rotational velocities in body-coordinate frame, respectively. | rad/s |
| Ix, Iy, Iz | roll, pitch, and yaw inertia moments. | Kg·m2 |
| g | gravity acceleration | m/s2 |
| l | distance between quadrotor center mass and the axis of the propeller | M |
| u2, u3, u4 | aerodynamic roll, pitch, and yaw moments, respectively | N·m |
| u1 | lift force | N |
| ωi | rotor i velocity, i = {1, 2, 3, 4} | rad/s |
| b | distance between the left wheel with the right wheel | m |
| ωl, ωr | motor velocity of the left wheel and the right wheel | rad/s |
References
- Guo, J.; Zhang, K.; Guo, S.; Li, C.; Yang, X. Design of a New Type of Tri-habitat Robot. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019; pp. 1508–1513. [Google Scholar] [CrossRef]
- Li, Y.; Yang, M.; Sun, H.; Liu, Z.; Zhang, Y. A Novel Amphibious Spherical Robot Equipped with Flywheel, Pendulum, and Propeller. J. Intell. Robot. Syst. 2017, 89, 485–501. [Google Scholar] [CrossRef]
- Xing, H.; Shi, L.; Hou, X.; Liu, Y.; Hu, Y.; Xia, D.; Li, Z.; Guo, S. Design, modeling and control of a miniature bio-inspired amphibious spherical robot. Mechatronics 2021, 77, 102574. [Google Scholar] [CrossRef]
- Yao, Y.; Deng, Z.; Zhang, X.; Lv, C. Design and Implementation of a Quadrotor-Based Spherical Robot. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; pp. 2430–2434. [Google Scholar] [CrossRef]
- Zheng, L.; Piao, Y.; Ma, Y.; Wang, Y. Development and control of articulated amphibious spherical robot. Microsyst. Technol. 2019, 26, 1553–1561. [Google Scholar] [CrossRef]
- Sun, Y.; Jing, Z.; Dong, P.; Chen, W.; Huang, J. Locomotion Control for a Land-Air Hexapod Robot. In Proceedings of the 2021 6th IEEE International Conference on Advanced Robotics and Mechatronics (ICARM), Chongqing, China, 3–5 July 2021; pp. 887–892. [Google Scholar] [CrossRef]
- Guo, S.; He, Y.; Shi, L.; Pan, S.; Xiao, R.; Tang, K.; Guo, P. Modeling and experimental evaluation of an improved amphibious robot with compact structure. Robot. Comput.-Integr. Manuf. 2017, 51, 37–52. [Google Scholar] [CrossRef]
- Liu, Z.; Song, M.; Liu, Y.; Bai, B. Design, Modeling and Simulation of a Reconfigurable Land-Air Amphibious Robot. In Proceedings of the 2021 IEEE 11th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Jiaxian, China, 27–31 July 2021; pp. 346–352. [Google Scholar] [CrossRef]
- Xiao, F.; Zheng, P.; di Tria, J.; Kocer, B.B.; Kovac, M. Optic Flow-Based Reactive Collision Prevention for MAVs Using the Fictitious Obstacle Hypothesis. IEEE Robot. Autom. Lett. 2021, 6, 3144–3151. [Google Scholar] [CrossRef]
- McGuire, K.; de Croon, G.; De Wagter, C.; Tuyls, K.; Kappen, H. Efficient Optical Flow and Stereo Vision for Velocity Estimation and Obstacle Avoidance on an Autonomous Pocket Drone. IEEE Robot. Autom. Lett. 2017, 2, 1070–1076. [Google Scholar] [CrossRef] [Green Version]
- Poultney, A.; Gong, P.; Ashrafiuon, H. Integral backstepping control for trajectory and yaw motion tracking of quadrotors. Robotica 2018, 37, 300–320. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, Y.; Ahn, C.K.; Cheng, J.; Chen, C. Adaptive Fuzzy Backstepping-Based Formation Control of Unmanned Surface Vehicles With Unknown Model Nonlinearity and Actuator Saturation. IEEE Trans. Veh. Technol. 2020, 69, 14749–14764. [Google Scholar] [CrossRef]
- Li, Z.; Yang, C.; Su, C.-Y.; Deng, J.; Zhang, W. Vision-Based Model Predictive Control for Steering of a Nonholonomic Mobile Robot. IEEE Trans. Control Syst. Technol. 2015, 24, 1. [Google Scholar] [CrossRef]
- Zhao, Y.; Qi, X.; Ma, Y.; Li, Z.; Malekian, R.; Sotelo, M.A. Path following Optimization for an Underactuated USV Using Smoothly-Convergent Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2020, 22, 6208–6220. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Khooban, M.H. An Intelligent Non-Integer PID Controller-Based Deep Reinforcement Learning: Implementation and Experimental Results. IEEE Trans. Ind. Electron. 2021, 68, 3609–3618. [Google Scholar] [CrossRef]
- Tee, K.P.; Ge, S.S.; Tay, E.H. Barrier Lyapunov Functions for the control of output-constrained nonlinear systems. Automatica 2009, 45, 918–927. [Google Scholar] [CrossRef]
- Tee, K.P.; Ge, S.S. Control of state-constrained nonlinear systems using Integral Barrier Lyapunov Functionals. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3239–3244. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Tong, S. Barrier Lyapunov Functions-based adaptive control for a class of nonlinear pure-feedback systems with full state constraints. Automatica 2016, 64, 70–75. [Google Scholar] [CrossRef]
- Liu, L.; Gao, T.; Liu, Y.-J.; Tong, S.; Chen, C.P.; Ma, L. Time-varying IBLFs-based adaptive control of uncertain nonlinear systems with full state constraints. Automatica 2021, 129, 109595. [Google Scholar] [CrossRef]
- Wang, C.; Wu, Y.; Wang, F.; Zhao, Y. TABLF-based adaptive control for uncertain nonlinear systems with time-varying asymmetric full-state constraints. Int. J. Control. 2021, 94, 1238–1246. [Google Scholar] [CrossRef]
- Dasgupta, R.; Roy, S.B.; Bhasin, S. Non-singular Trajectory Tracking Control of a Pitch-Constrained Quad-Rotorcraft using Integral Barrier Lyapunov Function. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 3788–3795. [Google Scholar] [CrossRef]
- Zhang, Z.; Cheng, W.; Wu, Y. Trajectory Tracking Control Design for Nonholonomic Systems with Full-state Constraints. Int. J. Control Autom. Syst. 2021, 19, 1798–1806. [Google Scholar] [CrossRef]
- Liu, B.; Hou, M.; Ni, J.; Li, Y.; Wu, Z. Asymmetric integral barrier Lyapunov function-based adaptive tracking control considering full-state with input magnitude and rate constraint. J. Frankl. Inst. 2020, 357, 9709–9732. [Google Scholar] [CrossRef]
- Qin, H.; Li, C.; Sun, Y. Adaptive neural network-based fault-tolerant trajectory-tracking control of unmanned surface vessels with input saturation and error co nstraints. IET Intell. Transp. Syst. 2020, 14, 356–363. [Google Scholar] [CrossRef]
- Li, S.; Wang, Q.; Ding, L.; An, X.; Gao, H.; Hou, Y.; Deng, Z. Adaptive NN-based finite-time tracking control for wheeled mobile robots with time-varying full state constraints. Neurocomputing 2020, 403, 421–430. [Google Scholar] [CrossRef]
- Zhang, S.; Dong, Y.; Ouyang, Y.; Yin, Z.; Peng, K. Adaptive Neural Control for Robotic Manipulators With Output Constraints and Uncertainties. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5554–5564. [Google Scholar] [CrossRef]
- Elmokadem, T.; Zribi, M.; Youcef-Toumi, K. Trajectory tracking sliding mode control of underactuated AUVs. Nonlinear Dyn. 2016, 84, 1079–1091. [Google Scholar] [CrossRef] [Green Version]
- Eliker, K.; Zhang, W. Finite-time Adaptive Integral Backstepping Fast Terminal Sliding Mode Control Application on Quadrotor UAV. Int. J. Control. Autom. Syst. 2020, 18, 415–430. [Google Scholar] [CrossRef]
- Ali, N.; Tawiah, I.; Zhang, W. Finite-time extended state observer based nonsingular fast terminal sliding mode control of autonomous underwater vehicles. Ocean. Eng. 2020, 218, 108179. [Google Scholar] [CrossRef]
- Castañeda, H.; Rodriguez, J.; Gordillo, J.L. Continuous and smooth differentiator based on adaptive sliding mode control for a quad-rotor MAV. Asian J. Control 2021, 23, 661–672. [Google Scholar] [CrossRef]
- Gonzalez-Garcia, A.; Castaeda, H. Guidance and Control Based on Adaptive Sliding Mode Strategy for a USV Subject to Uncertainties. IEEE J. Ocean. Eng. 2021, 46, 1144–1154. [Google Scholar] [CrossRef]
- Guerrero-Sanchez, M.-E.; Hernandez-Gonzalez, O.; Valencia-Palomo, G.; Lopez-Estrada, F.-R.; Rodriguez-Mata, A.-E.; Garrido, J. Filtered Observer-Based IDA-PBC Control for Trajectory Tracking of a Quadrotor. IEEE Access 2021, 9, 114821–114835. [Google Scholar] [CrossRef]
- Xie, W.; Ma, B.; Fernando, T.; Iu, H.H.-C. A simple robust control for global asymptotic position stabilization of underactuated surface vessels. Int. J. Robust. Nonlinear Control. 2017, 27, 5028–5043. [Google Scholar] [CrossRef]
- Cruz-Ortiz, D.; Chairez, I.; Poznyak, A. Non-singular terminal sliding-mode control for a manipulator robot using a barrier Lyapunov function. ISA Trans. 2021, 121, 268–283. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.; Fan, W.; Wang, C.; Ma, P. Finite-time control for quadrotor based on composite barrier Lyapunov function with system state constraints and actuator faults. Aerosp. Sci. Technol. 2021, 119, 107063. [Google Scholar] [CrossRef]
- Deepika, D.; Kaur, S.; Narayan, S. Integral terminal sliding mode control unified with UDE for output constrained tracking of mismatched uncertain non-linear systems. ISA Trans. 2020, 101, 1–9. [Google Scholar] [CrossRef]
- Rath, J.J.; Defoort, M.; Sentouh, C.; Karimi, H.R.; Veluvolu, K.C. Output Constrained Robust Sliding Mode Based Nonlinear Active Suspension Control. IEEE Trans. Ind. Electron. 2020, 67, 10652–10662. [Google Scholar] [CrossRef]
- Liu, X.; Liang, X. Integrated Guidance and Control of Interceptor Missile Based on Asymmetric Barrier Lyapunov Function. Int. J. Aerosp. Eng. 2019, 2019, 8531584. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Wu, Y. Adaptive Fuzzy Tracking Control of Autonomous Underwater Vehicles with Output Constraints. IEEE Trans. Fuzzy Syst. 2021, 29, 1311–1319. [Google Scholar] [CrossRef]
- Wu, Z.; Albalawi, F.; Zhang, Z.; Zhang, J.; Durand, H.; Christofides, P.D. Control Lyapunov-Barrier function-based model predictive control of nonlinear systems. Automatica 2019, 109, 108508. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Wang, K.; Xiao, Z. Modeling and Hybrid Powers Control of Cross-domain Robot on the Water. In Proceedings of the 2021 IEEE 11th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Jiaxian, China, 27–31 July 2021; pp. 334–339. [Google Scholar] [CrossRef]











| Controller | Parameter | Value |
|---|---|---|
| PID | k1 | 1 |
| k2, I2 | 5, 0.5 | |
| NTSMC | k1 | 1 |
| k2, k3, β, index | 5, 1.5, 2,3 | |
| BLC | k1 | 1 |
| k2, kb | 5, 0.035 | |
| NTSMBC | k1 | 1 |
| k2, k3, β, index, kb | 5, 1.5, 2, 3, 0.035 |
| Controller | Parameter | Value |
|---|---|---|
| PID | k1 | 1 |
| k2, I2 | 5, 0.5 | |
| NTSMC | k1 | 1 |
| k2, k3, β, index | 5, 1.5, 2,3 | |
| BLC | k1 | 1 |
| k2, ka, kb | 5, 0.035, 0.054 | |
| NTSMBC | k1 | 1 |
| k2, k3, β, index, ka, kb | 5, 1.5, 2, 3, 0.035, 0.054 |
| Controller | Parameter | Value |
|---|---|---|
| PID | k1, I1 | 10, 2 |
| k2 | 5 | |
| ISMC | k1 I1 | 10, 2 |
| k2, k3, β, index | 5, 0.5, 2, 3 | |
| AISMBC | k1 I1 | 10, 2 |
| k2, k3, ksh, β, index | 5, 5, 0.1, 2, 3 |
| Model Parameter | Value | Unit |
|---|---|---|
| m | 3 | kg |
| Ix | 0.083 | kg·m2 |
| Iy | 0.074 | kg·m2 |
| Iz | 0.113 | kg·m2 |
| l | 0.25 | m |
| b | 0.25 | m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Liu, Y.; Huang, C.; Bao, W. Water Surface Flight Control of a Cross Domain Robot Based on an Adaptive and Robust Sliding Mode Barrier Control Algorithm. Aerospace 2022, 9, 332. https://doi.org/10.3390/aerospace9070332
Wang K, Liu Y, Huang C, Bao W. Water Surface Flight Control of a Cross Domain Robot Based on an Adaptive and Robust Sliding Mode Barrier Control Algorithm. Aerospace. 2022; 9(7):332. https://doi.org/10.3390/aerospace9070332
Chicago/Turabian StyleWang, Ke, Yong Liu, Chengwei Huang, and Wei Bao. 2022. "Water Surface Flight Control of a Cross Domain Robot Based on an Adaptive and Robust Sliding Mode Barrier Control Algorithm" Aerospace 9, no. 7: 332. https://doi.org/10.3390/aerospace9070332
APA StyleWang, K., Liu, Y., Huang, C., & Bao, W. (2022). Water Surface Flight Control of a Cross Domain Robot Based on an Adaptive and Robust Sliding Mode Barrier Control Algorithm. Aerospace, 9(7), 332. https://doi.org/10.3390/aerospace9070332






