Novel Approach to Fault-Tolerant Control of Inter-Turn Short Circuits in Permanent Magnet Synchronous Motors for UAV Propellers

Abstract

This paper deals with the development of a novel fault-tolerant control technique aiming at the diagnosis and accommodation of inter-turn short circuit faults in permanent magnet synchronous motors for lightweight UAV propulsion. The reference motor is driven by a four-leg converter, which can be reconfigured in case of a phase fault by enabling the control of the central point of the motor Y-connection. A crucial design point entails the development of fault detection and isolation (FDI) algorithms capable of minimizing the failure transients and avoiding the short circuit extension. The proposed fault-tolerant control is composed of two sections: the first one applies a novel FDI algorithm for short circuit faults based on the trajectory tracking of the motor current phasor in the Clarke plane; the second one implements the fault accommodation, by applying a reference frame transformation technique to the post-fault commands. The control effectiveness is assessed via nonlinear simulations by characterizing the FDI latency and the post-fault performances. The proposed technique demonstrates excellent potentialities: the FDI algorithm simultaneously detects and isolates the considered faults, even with very limited extensions, during both stationary and unsteady operating conditions. In addition, the proposed accommodation technique is very effective in minimizing the post-fault torque ripples.

1. Introduction

The design of next-generation long-endurance UAVs is undoubtedly moving towards the full-electric propulsion. Though immature today, full-electric propulsion systems are expected to obtain large investments in the forthcoming years, to replace conventional internal combustion engines, as well as hybrid or hydrogen-based solutions. Full-electric propulsion would guarantee smaller CO₂-emissions, lower noise, a higher efficiency, a reduced thermal signature (crucial for military applications), and simplified maintenance. However, several reliability and safety issues are still open, especially for long-endurance UAVs flying in unsegregated airspaces.

In this context, the Italian Government and the Tuscany Regional Government co-funded the project TERSA (Tecnologie Elettriche e Radar per Sistemi aeromobili a pilotaggio remoto Autonomi) [1], led by Sky Eye Systems (Italy) in collaboration with the University of Pisa and other Italian industries. The TERSA project aims to develop an Unmanned Aerial System (UAS) with a fixed-wing UAV, Figure 1, having the following main characteristics:

• Take-off weight: from 35 to 50 kg;
• Endurance: >6 h;
• Range: >3 km;
• Take-off system: pneumatic launcher;
• Landing system: parachute and airbags;
• Propulsion system: Permanent Magnet Synchronous Motor (PMSM) powering a twin-blade fixed-pitch propeller;
• Innovative sensing systems:

  ○

  Synthetic aperture radar, to support surveillance missions in adverse environmental conditions;

  ○

  Sense-and-avoid system, integrating a camera with a miniaturised radar, to support autonomous flight capabilities in emergency conditions.

With reference to the activities related to the TERSA UAV propulsion system development (which this work refers to), a special attention has been devoted to the architecture definition for obtaining fault-tolerant capabilities. In particular, propulsion systems based on three-phase PMSMs driven by conventional three-leg converters typically have failure rates from 100 to 200 per million flight hours [2], which are not compatible with the reliability and safety levels required for the airworthiness certification [3]. The failure rate of PMSMs is mostly driven by motor phase faults and converter faults (open-switch in a converter leg, open-phase, inter-turn, phase-to-leg, phase-to-ground, or capacitor short-circuits [4]), which cover from 60% to 70% of the total fault modes [5]. Provided that the weight and envelopes required by UAV applications impede the extensive use of hardware redundancy (e.g., redundant motors), the reliability enhancement of full-electric propulsion systems can be achieved only through the redundancy of phases or stator modules [6] or by unconventional converters. By reducing design complexity, weight and envelopes, the use of four-leg converters [7,8,9], Figure 2, could represent a suitable solution for UAV applications.

In this converter topology, a couple of power switches are added, as stand-by devices, to the conventional three-leg bridge, enabling the control of the central point of the “star” connection (often Y-connection) of the motor. Nevertheless, to benefit from their fault-tolerance capability, these devices must be promptly reconfigured when a fault occurs, and extremely fast Fault-Detection and Isolation (FDI) algorithms must be developed. Especially for PMSMs operating at high speeds (such as the ones used for aircraft propellers), phase faults can generate abnormal torque ripples and the related failure transients can potentially cause unsafe conditions [10,11].

Many pieces of research on the development of FDI algorithms for PMSMs have been carried out in the last decades, and a special attention has been recently addressed to the Inter-Turn Short Circuit (ITSC) fault [12,13,14,15], which typically contributes to 10% of the PMSM failure rate [5,9,16].

Faiz [12] carried out a comprehensive literature review on FDI methods for ITSC faults in PMSMs. Depending on the measurements processed by the algorithms, they can be categorized as torque-based [17,18], flux-based [19,20], electromagnetic parameters-based [21], voltage-based, and current-based.

The most common strategy is given by the voltage-based methods. Immovilli and Bianchini [22] propose reconstructing harmonic patterns of the voltage components in the Clarke plane. The technique works very well in transient conditions, but it is not able to identify the shorted phase. The FDI algorithm proposed in [23], implements an estimator of back electromotive force and detects the ITSC by comparing the estimates to a reference model. The method is very robust against load disturbances, but it requires a very accurate model of the Back Electromotive Force (BEMF). Other approaches use as fault symptoms the harmonic components of the Zero Sequence Voltage Component (ZSVC) signal. Urresty et al. [24] proposes a Vold–Kalman Filtering Order Tracking (VKF-OT) algorithm to track the ZSVCs first harmonic component. The method offers reliable indicators, which are applicable in transient phases too, but it needs to be extended in terms of fault isolation. A robust algorithm is proposed by Hang et al., in [25], where the fault indicators are defined to remove the influence of rotor speed variation and a frequency tracking algorithm based on reference frame transformation is used to extract the fault symptoms. A possible drawback is the dependency of the fault indicator on the PMSM parameters, which may vary with environmental temperature. Boileau [26] considered as a fault indicator the amplitude of the positive voltage sequence while Meinguet [27] used as an indicator the ratio between the amplitudes of negative and positive voltage sequences. These methods are not able to locate the shorted phase, neither.

Concerning the current-based methods, the most relevant one is based on the so-called Park Vector Approach (PVA) [28,29,30,31]. When the PMSM is operating in normal conditions, the current phasor in the Clarke plane draws a circular trajectory, while it follows an elliptic one if a stator fault occurs. In PVAs, the fault index is thus defined by a geometrical distortion factor, obtained by currents measurements. Though demonstrating to be excellent for online ITSC FDI, the PVA is not able to locate the shorted phase.

All the current methods have in common the observation that in case of ITSCs, the stator currents are not balanced, and higher harmonic components in the signals can be used as fault symptoms. Different signal processing methods are employed to extract these symptoms (or patterns). Frequency-domain transforms such as Fast-Fourier Transforms (FFT) are applied in [13,32,33,34], while mixed frequency/time-domain transforms such as Short-Time Fourier Transform (STFT) are used in [14], Wavelet Transform (WT) in [15,35,36], and Hilbert–Huang Transform (HHT) in [37,38]. Frequency-domain transforms entail the loss of transient events such as speed or loads variations, so FFT analyses, though effective in stationary conditions, must be avoided if the FDI is required during transients. By requiring a higher computational effort, STFT analyses partially compensate the FFT limits, but FDI capabilities are still limited in unsteady conditions. On the other hand, WT methods permit to decompose time domain signals into stationary and non-stationary contributions, but the appropriate choice of wavelets is a drawback. Many limits of WT techniques are removed by HHT techniques, even if they are effective when applied to signals characterised by a narrow frequency content.

Other methods, based on artificial intelligence applications (Convolutional Neural Networks are used in [39]) have been also explored, but, though the results are remarkable, these techniques are not preferred for airworthiness certification [40].

Within this research context, this paper aims to develop an innovative Fault-Tolerant Control (FTC), capable of prompt FDI and accommodation of ITSC faults in three-phase PMSMs for lightweight UAVs propulsion, in both stationary and transient conditions. The proposed FTC is composed of two sections: the first one addresses the FDI problem via an original current-based method (here referred as Advanced-PVA, APVA), the second is dedicated to the fault accommodation, obtained by activating the stand-by leg of a four-leg converter and controlling the central point of the motor Y-connection. It is worth noting that the ITSC accommodation is developed by applying the Rotor Current Frame Transformation Control (RCFTC) technique, already applied by the authors in [9] for the FTC of open-circuit faults.

The paper is articulated as follows: in the first part, the nonlinear model of the propulsion system is presented; successively, the FDI algorithms and the fault accommodation technique are described by highlighting their basic design criteria; finally, a summary of the simulation results is proposed, by characterizing the failure transients and the post-fault behaviours after the injection of ITSC faults.

2. Materials and Methods

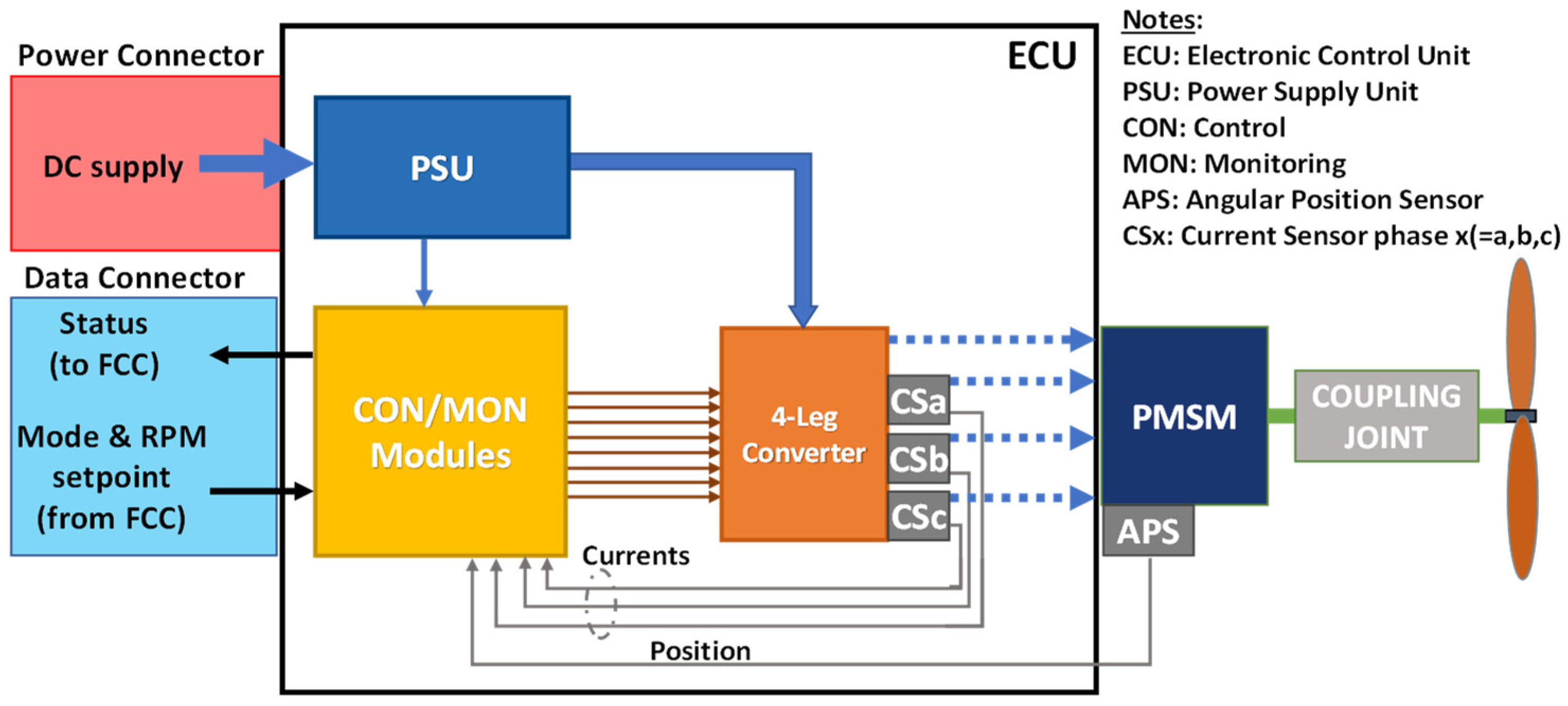
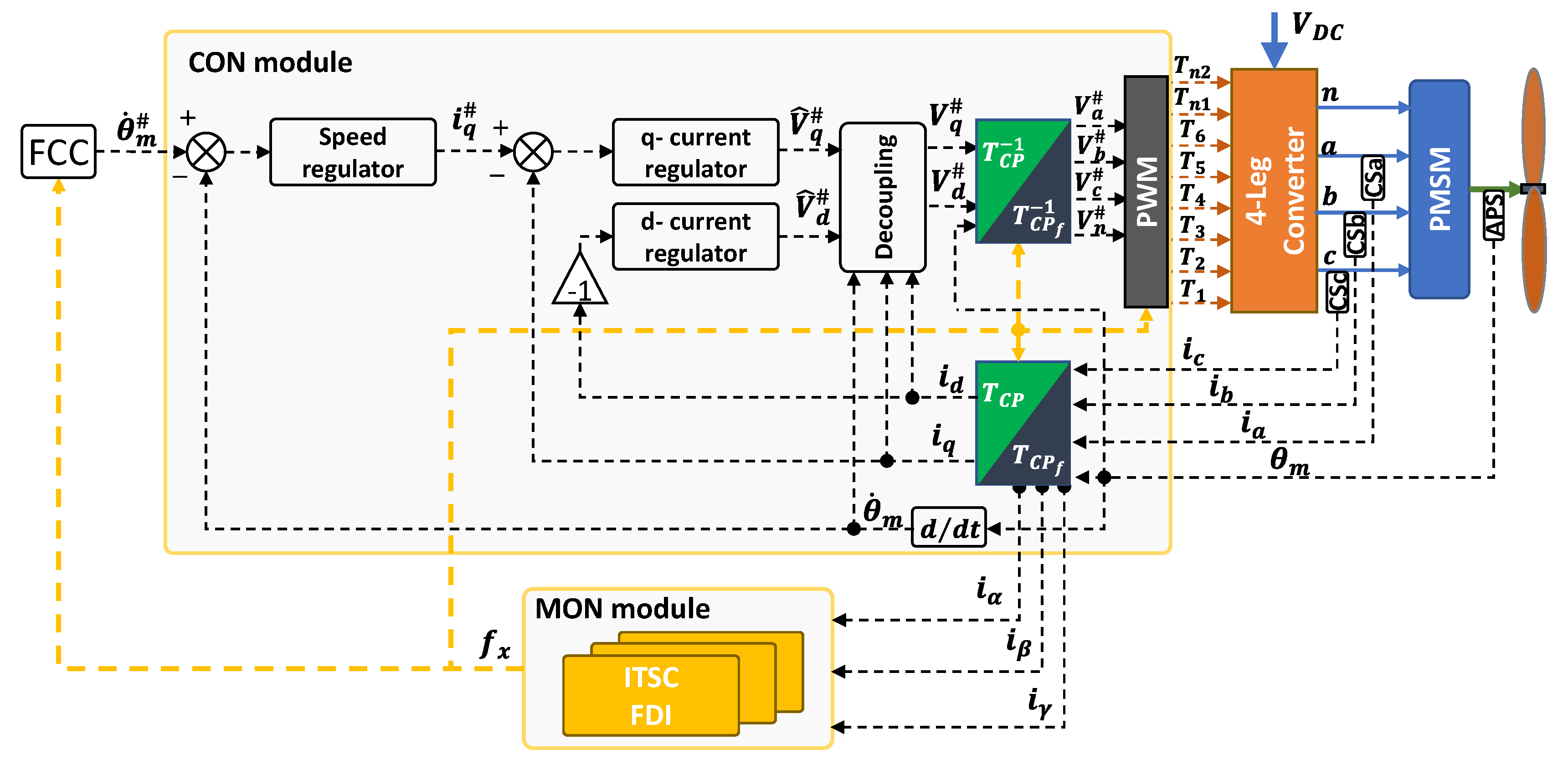
2.1. System Description

The reference propulsion system, designed for the full-electric propulsion of a lightweight UAV, is composed of (Figure 3):

• An electromechanical section, with:

  ○

  Three-phase surface-mounted PMSM with phase windings in Y-connection;

  ○

  Twin-blade fixed-pitch propeller [41];

  ○

  Mechanical coupling joint.

• An Electronic Control Unit (ECU), including:

  ○

  CONtrol/MONitoring (CON/MON) module, for the implementation of the closed-loop control and health-monitoring functions;

  ○

  Four-leg converter;

  ○

  Three current sensors (CSa, CSb, CSc), one per each motor phase;

  ○

  One Angular Position Sensor (APS), measuring the motor angle;

  ○

  A Power Supply Unit (PSU), converting the power input coming from the UAV electrical power storage system to all components and sensors;

  ○

  Data and power connectors for the interface with the Flight Control Computer (FCC) and the UAV electrical system.

The CON module operates the closed-loop control of the system by implementing two nested loops on propeller speed and motor currents (via Field-Oriented Control, FOC). All the regulators implement proportional/integral actions on the tracking error signals, plus anti-windup functions with back-calculation algorithms to compensate for commands saturation. The MON module executes the health-monitoring algorithms, including the FTC proposed in this work.

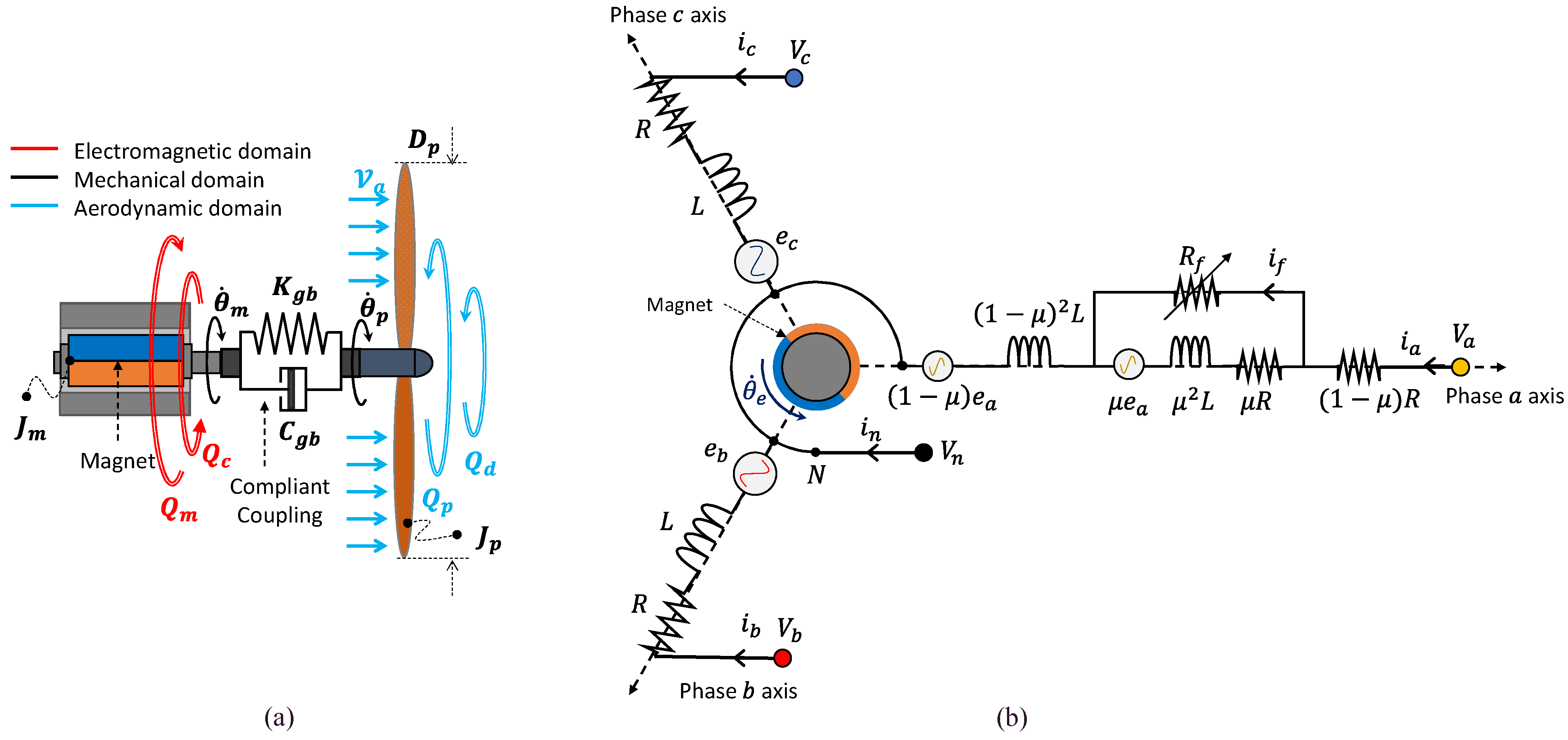
2.2. Model of the Aero-Mechanical Section

The dynamics of the aero-mechanical section of the propulsion system, providing the UAV with the thrust is schematically depicted in Figure 4a and is modelled by [7,9]:

$$\left\{\begin{array}{c}{J}_p{\ddot{\theta }}_p=-Q_p-C_{gb}\left({\dot{\theta }}_p-{\dot{\theta }}_m\right)-K_{gb}\left({\theta }_p-{\theta }_m\right)+Q_d\\ J_m{\ddot{\theta }}_m=Q_m+C_{gb}\left({\dot{\theta }}_p-{\dot{\theta }}_m\right)+K_{gb}\left({\theta }_p-{\theta }_m\right)+Q_c\\ Q_p=C_{Q_p}\left({\dot{\theta }}_p,AR\right)\rho D_p^5{\dot{\theta }}_p^2\\ AR={\mathcal{V}}_a/D_p{\dot{\theta }}_p\\ Q_c=Q_c{}_{max}sin\left(n_h{n}_d{\theta }_m\right)\end{array},\right.$$

(1)

where $J_p$ and ${\theta }_p$, $J_m$, and ${\theta }_m$ are the inertia and the angular position of the propeller and the motor, respectively, $Q_p$ is the propeller-resistant torque, $Q_d$ is a gust-induced disturbance torque, $Q_m$ is the motor torque, $Q_c$, is the cogging torque, and $Q_c{}_{max}$ is the maximum cogging torque, $n_d$ is the pole pairs number, $n_h$ is the harmonic index of the cogging disturbance, $C_{Q_p}$ is the nondimensional torque coefficient of the propeller, $AR$ is the propeller advance ratio, $D_p$ is the propeller diameter, $\rho$ is the air density, ${\mathcal{V}}_a$ is the UAV forward speed, while $K_{gb}$ and $C_{gb}$ are the stiffness and the damping of the mechanical coupling joint.

2.3. Model of the PMSM with ITSC Fault

The mathematical modelling of PMSM with ITSC faults that will be used for this work has been previously presented and applied in literature, demonstrating it to be very accurate [13,42,43,44].

The occurrence of a short circuit in a stator phase causes an asymmetry in the motor magnetic flux, due to an additional circuit with insulation resistance $R_f$, in which the shorted current $i_f$ flows, Figure 4b:

Once indicated, the fault extension along the winding with the parameter $\mu =N_f/N$ (defined as the ratio of the number of shorted turns to the total one), the winding affected by ITSC can be split into an undamaged and a damaged part, Figure 4b. Hence, the electrical equations can be written as:

$${\mathit{V}}_{xn}=ℝ\mathit{I}+\mathbb{L}\frac{d}{dt}\mathit{I}+\mathit{e}.$$

(2)

In Equation (2), ${\mathit{V}}_{xn}={\left[V_a-V_n, V_b-V_n, V_c-V_n, 0 \right]}^{\mathrm{T}}$ is the applied voltages vector, $\mathit{I}={\left[i_a, i_b, i_c, i_f\right]}^{\mathrm{T}}$ is the currents vector, e is the BEMF vector, which can be expressed as in Equation (3) (in Equation (3) and in the following equations, “s” and “c” briefly indicates “sine” and “cosine” functions):

$$\mathit{e}=\left[\begin{array}{c}\left(1-\mu \right)e_a\\ e_b\\ e_c\\ \mu e_a\end{array}\right]=-{\lambda }_m{\dot{\theta }}_e\left[\begin{array}{c}\left(1-\mu \right)\mathrm{s}\left({\theta }_e\right)\\ \mathrm{s}\left({\theta }_e-2/3\pi \right)\\ \mathrm{s}\left({\theta }_e+2/3\pi \right)\\ \mu \mathrm{s}\left({\theta }_e\right)\end{array}\right],$$

(3)

where ${\theta }_e=n_d{\theta }_m$ is the electrical angle of the motor and ${\lambda }_m$ is the rotor magnet flux linkage. The resistance and inductance matrixes are:

$$ℝ=\left[\begin{array}{cccc}\left(1-\mu \right)R& 0& 0& R_f\\ 0& R& 0& 0\\ 0& 0& R& 0\\ \mu R& 0& 0& -\left(\mu R+R_f\right)\end{array}\right], \mathbb{L}=\left[\begin{array}{cccc}{\left(1-\mu \right)}^{2}L& 0& 0& 0\\ 0& L& 0& 0\\ 0& 0& L& 0\\ {\mu }^{2}L& 0& 0& -{\mu }^{2}L\end{array}\right],$$

(4)

in which $R$ is the phase resistance, $L$ is the phase self-inductance, and $R_f$ is the insulation resistance, given by:

$$R_f=k_{R_f}R\left(1-\mu \right),$$

(5)

with $k_{R_f}$ a factor depending on the insulation material.

By considering an inter-turn fault, the PMSM torque can be calculated as [44]:

$$Q_m=\left(\left(1-\mu \right)e_a{i}_a+e_b{i}_b+e_c{i}_c-\mu e_a{i}_f\right)/{\dot{\theta }}_m,$$

(6)

Since the neutral point voltage $V_n$ is not null when a short circuit occurs, it is convenient to reformulate the electrical equations by extrapolating $V_n$. Hence, by applying Kirchhoff laws to the circuit in Figure 4b and by substituting in Equation (2), we have:

$$\mathit{V}=\mathcal{R}\mathit{I}+\mathcal{L}\frac{d}{dt}\mathit{I}+\mathit{E},$$

(7)

where the reformulated BEMF vector $\mathit{E}$ is:

$$\mathit{E}=\frac{1}{3}\left[\begin{array}{c}2e_{a_f}-\left(e_b+e_c\right)\\ 2e_b-\left(e_{a_f}+e_c\right)\\ 2e_c-\left(e_{a_f}+e_b\right)\\ 3e_f\end{array}\right],$$

(8)

The new resistance and inductance matrixes are:

$$\mathcal{R}=\left[\begin{array}{cccc}\left(1-2/3\mu \right)R& 0& 0& 2/3R_f\\ \mu R/3& R& 0& -R_f/3\\ \mu R/3& 0& R& -R_f/3\\ \mu R& 0& 0& -\left(\mu R+R_f\right)\end{array}\right], \mathcal{L}=\left[\begin{array}{cccc}\left(1-4/3\mu +2/3{\mu }^2\right)L& 0& 0& 0\\ \left(2-\mu \right)\mu L/3& L& 0& 0\\ \left(2-\mu \right)\mu L/3& 0& L& 0\\ {\mu }^{2}L& 0& 0& -{\mu }^{2}L\end{array}\right],$$

(9)

while $V={\left[V_a, V_b, V_c, 0 \right]}^{\mathrm{T}}$ is a vector defining the voltage commands sent by the converter to the motor terminals (first three components) and the voltage on the shorted turns. Finally, since the PMSM is controlled via FOC technique, it is convenient to express the voltage vector via the Clarke–Park transformation, as a function of direct and quadrature voltages $V_d$ and $V_q$, generated by the closed-loop control algorithms:

$$\left[\begin{array}{c}{V}_a\\ V_b\\ V_c\\ V_n\end{array}\right]=\sqrt{\frac{2}{3}}\left[\begin{array}{c}\begin{array}{cc}\mathrm{c}\left({\theta }_e\right)& -\mathrm{s}\left({\theta }_e\right)\end{array}\\ \begin{array}{cc}\mathrm{c}\left({\theta }_e-2/3\pi \right)& -\mathrm{s}\left({\theta }_e-2/3\pi \right)\end{array}\\ \begin{array}{cc}\mathrm{c}\left({\theta }_e+2/3\pi \right)& -\mathrm{s}\left({\theta }_e+2/3\pi \right)\end{array}\\ \begin{array}{cc}0 & 0\end{array}\end{array}\right]\left[\begin{array}{c}{V}_d\\ V_q\end{array}\right],$$

(10)

3. Fault-Tolerant Control System

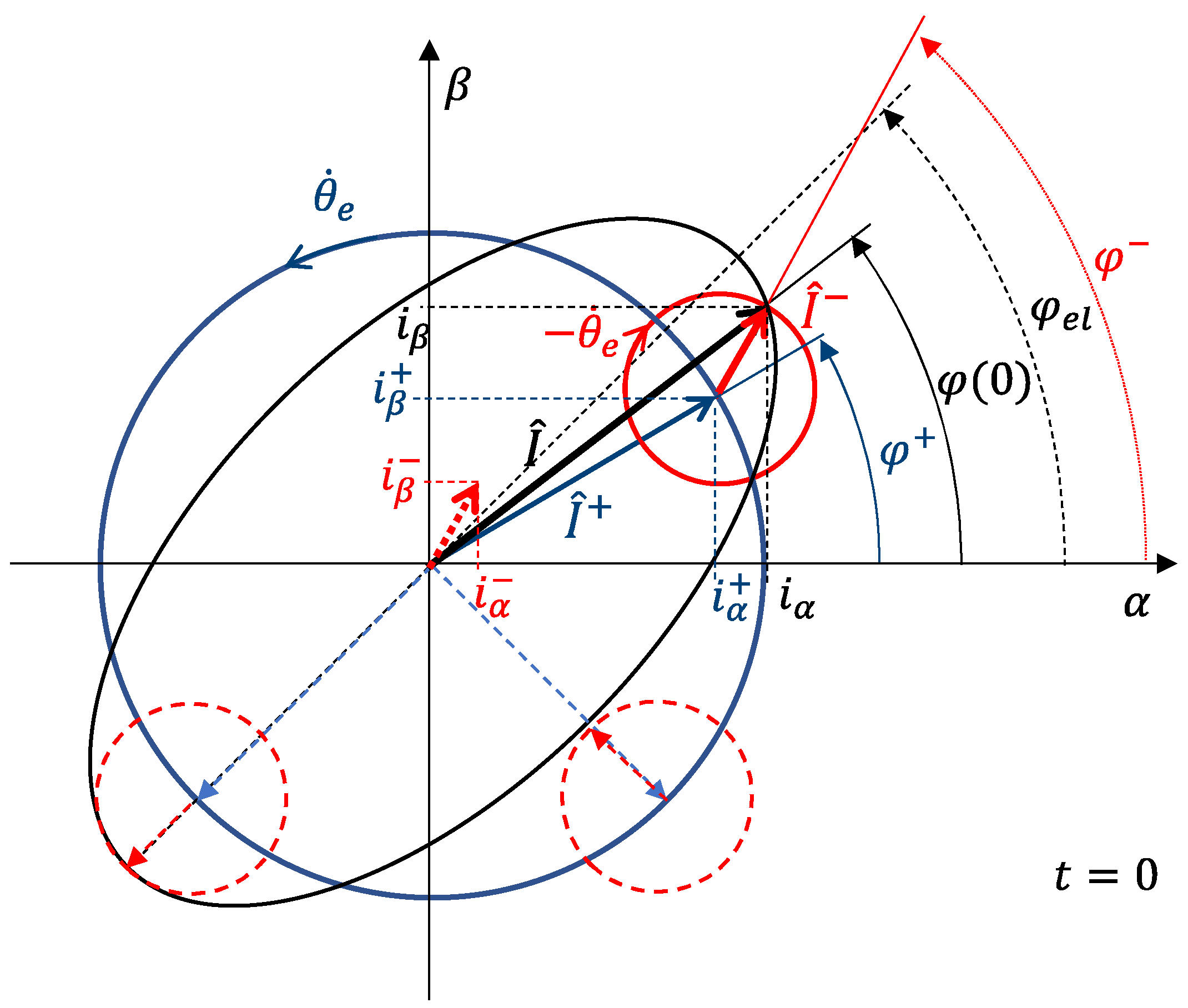
3.1. FDI Algorithm Conceptualization

When a PMSM operates at constant speed without faults, the current phasor in the Clarke plane draws a circular trajectory, while it follows an elliptical trajectory when an ITSC fault occurs [28,29,30,31]. Torque oscillations appear, at the motor level, with amplitudes that depend on the short-circuit extension.

This section aims to demonstrate that the geometrical parameters of this elliptical trajectory (major, minor axes length, and axes inclination) are univocally related to the location and extension of the ITSC. In particular, we will demonstrate that:

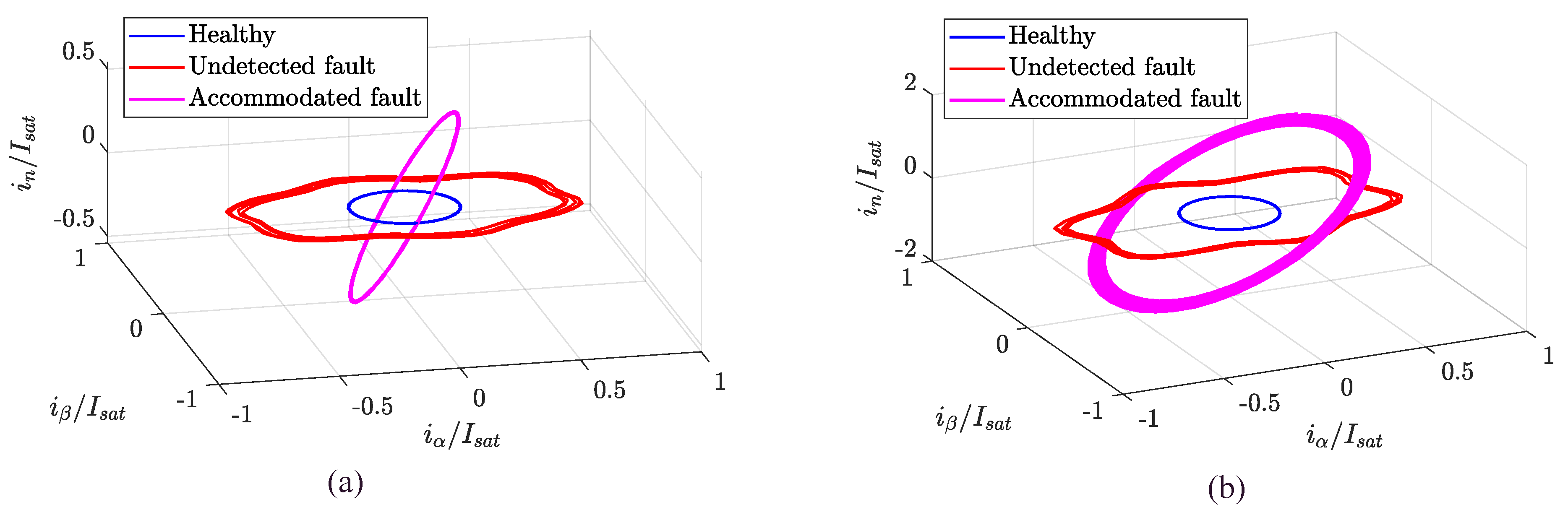
• An ITSC fault can be detected by measuring the difference between the lengths of major and minor axes of the ellipse;
• An ITSC fault can be isolated by measuring the inclination of the major axis of the ellipse.

It is worth noting that, during constant speed operations, any elliptical trajectory of the motor current phasor in the Clarke plane (including the circular one, as a special case) can be reconstructed via the Fortescue decomposition [45], as the sum of three symmetrical and balanced rotating systems: positive-, negative-, and zero-sequence systems.

When an ITSC fault occurs, the central point of the Y-connection is isolated, so the zero-sequence current is zero, and the ellipse tracked by the current phasor ($\widehat{I}$) can be considered as the sum of two counter-rotating phasors: positive- (${\widehat{I}}^{+}$) and negative-sequence phasors (${\widehat{I}}^{-}$), as given by:

$$\widehat{I}=\left|\widehat{I}\left(t\right)\right|e^{j\phi \left(t\right)}=\left|{\widehat{I}}^{+}\right|e^{j\left({\dot{\theta }}_{e}t+{\phi }^{+}\right)}+\left|{\widehat{I}}^{-}\right|e^{-j\left({\dot{\theta }}_{e}t-{\phi }^{-}\right)},$$

(11)

where $\phi$, ${\phi }^{+}$, and ${\phi }^{-}$ are the phase angles of the resultant, positive-, and negative-sequence current phasors, respectively. As illustrated in Figure 5, the semi major and semi minor axis lengths are obtained by:

$$s_{M,m}=\left|{\widehat{I}}^{+}\right|\pm \left|{\widehat{I}}^{-}\right|.$$

(12)

While the inclination of the ellipse major axis corresponds to the angle that maximizes the current phasor amplitude, up to:

$$max\left(\left|\widehat{I}\right|\right)=\left|{\widehat{I}}^{+}\right|+\left|{\widehat{I}}^{-}\right|.$$

(13)

The condition in Equation (13) is reached when the positive- and negative-sequence phasors have the same angular orientation:

$${\phi }_{el}={\dot{\theta }}_e{\left.t\right|}_{max\left(\left|\widehat{I}\right|\right)}+{\phi }^{+}=-{\dot{\theta }}_e{\left.t\right|}_{max\left(\left|\widehat{I}\right|\right)}+{\phi }^{-},$$

(14)

which leads to:

$${\phi }_{el}=\left({\phi }^{-}+{\phi }^{+}\right)/2.$$

(15)

To identify the ellipse inclination, it is thus crucial to evaluate the phase angles of the positive- and negative-sequence phasors, expressed by:

$${\phi }^{*}=\mathrm{atan}\left(i_{\beta }^{*}/i_{\alpha }^{*}\right),$$

(16)

where “$*$” stands for “$+$” or “$-$”, and $i_{\alpha }^{*}$ and $i_{\beta }^{*}$ are the projections of the phasor ${\widehat{I}}^{*}$ on the $\alpha$ and $\beta$ axes in the Clarke plane.

By introducing a complex analysis notation, the phasor ${\widehat{I}}^{*}$ can be also represented in terms of a balanced three-phase space vector system, as:

$${\widehat{I}}^{*}=\sqrt{2/3}\left(Re\left({\widehat{I}}_a^{*}\right)+Re\left({\widehat{I}}_b^{*}\right)e^{j2\pi /3}+Re\left({\widehat{I}}_c^{*}\right)e^{j4\pi /3}\right),$$

(17)

Then, by expressing the space vector ${\widehat{I}}^{*}$ into its real ($i_{\alpha }^{*}$) and imaginary ($i_{\beta }^{*}$) components, we have:

$$\begin{gathered} i_{\alpha }^{*}=\sqrt{2/3}\left[Re\left({\widehat{I}}_a^{*}\right)-1/2\left(Re\left({\widehat{I}}_b^{*}\right)+Re\left({\widehat{I}}_c^{*}\right)\right)\right]=\sqrt{3/2}Re\left({\widehat{I}}_a^{*}\right), \\ {i}_{\beta }^{*}=\sqrt{2/3}\left[\sqrt{3}/2\left(Re\left({\widehat{I}}_b^{*}\right)-Re\left({\widehat{I}}_c^{*}\right)\right)\right]=*-\sqrt{3/2}Im\left({\widehat{I}}_a^{*}\right), \end{gathered}$$

(18)

The phase angles of the positive- and negative-sequence phasors with ITSC faults can be thus calculated via the positive- and negative-sequence phasors related to phase a only (${\widehat{I}}_a^{+}$ and ${\widehat{I}}_a^{-}$), given by the Fortescue transform:

$$\left[\begin{array}{c}{\widehat{I}}_a^{+}\\ {\widehat{I}}_a^{-}\\ 0\\ {\widehat{I}}_f\end{array}\right]=\frac{1}{3}\left[\begin{array}{cccc}1& e^{j2\pi /3}& e^{j4\pi /3}& 0\\ 1& e^{j4\pi /3}& e^{j2\pi /3}& 0\\ 1& 1& 1& 0\\ 0& 0& 0& 3\end{array}\right]\left[\begin{array}{c}{\widehat{I}}_a\\ {\widehat{I}}_b\\ {\widehat{I}}_c\\ {\widehat{I}}_f\end{array}\right],$$

(19)

The vector of phasors $\widehat{\mathit{I}}=\left[{\widehat{I}}_a, {\widehat{I}}_b, {\widehat{I}}_c, {\widehat{I}}_f\right]$ can be obtained from:

$$\widehat{\mathit{I}}={\left(\mathcal{R}+j{\dot{\theta }}_e\mathcal{L}\right)}^{-1}\left(\widehat{\mathit{V}}-\widehat{\mathit{E}}\right),$$

(20)

where the voltage and BEMF phasors are:

$$\widehat{\mathit{V}}=\sqrt{\frac{2}{3}}\left(V_d+j{V}_q\right)\left[\begin{array}{c}1\\ \left(-1/2-j\sqrt{3}/2\right)\\ \begin{array}{c}\left(-1/2+j\sqrt{3}/2\right)\\ 0\end{array}\end{array}\right],$$

(21)

$$\widehat{\mathit{E}}=j{\lambda }_m{\dot{\theta }}_e\left[\begin{array}{c}1-2/3\mu \\ \mu -1/2-j\sqrt{3}/2\\ \begin{array}{c}\mu -1/2+j\sqrt{3}/2\\ \mu \end{array}\end{array}\right],$$

(22)

The solution of Equation (20) in terms of current phasors are presented by the polar-coordinate plot in Figure 6a, in which, given along the radius the ITSC fault extension ($\mu =N_f/N$), the inclination of the ellipse major axis of the current phasor trajectory is reported along the phase angle for each motor phase. In addition, Figure 6b shows the ratio of ellipse semi-axes lengths as a function of the ITSC fault extension parameter $\mu$. It is worth noting that, if an ITSC fault occurs on phase a (b, c), the ellipse inclination will be 0° (240°, 120°) ±15°.

The above-mentioned discussion thus supports the development of an FDI algorithm based on the estimation of the geometrical characteristics of (generic) elliptical trajectories of current phasors in the Clarke plane, so that:

• The difference between the lengths of major and minor axes of the ellipse provides a symptom about the ITSC extension (fault detection);
• The inclination of the major axis of the ellipse provides a symptom about the ITSC location (fault isolation).

The FDI concept essentially entails the identification of geometrical properties of an ellipse. Clearly, at a single monitoring time, a single point of the ellipse is known ($i_{\alpha }, i_{\beta }$ Figure 5); therefore, the fitting problem is under-determined. On the other hand, the problem becomes over-determined if a sufficient number of measurements are used. The over-determined problem of fitting an ellipse to a set of data points arises in many applications such as computer graphics [46], hydraulic engineering [47], and statistics [48]. Many different methods are proposed in literature for fitting the geometric primitives of an ellipse: voting/clustering methods (e.g., the Hough transform [49] and the RANSAC technique [50]) are robust but they have poor accuracy and require large computing resources, optimization methods and direct least-square methods [51] are accurate, but, in case of nonlinear applications such as an ellipse fitting, they apply iterative techniques.

Here we instead use a direct least-square method, as proposed by Halìř and Flusser [52], who, starting from the quadratically-constrained least-squares minimization postulated by Fitzgibbon [53], reformulated the problem via partitioning techniques, by obtaining a very robust and computationally-effective algorithm.

Once given the vectorial conic definition of an ellipse,

$$\Gamma ·\mathit{\gamma }=0,$$

(23)

in which $\Gamma =\left[{\alpha }^2, \alpha \beta ,{\beta }^2,\alpha ,\beta ,1\right]$ and $\mathit{\gamma }={\left[A, B,C,D,E,F\right]}^{\mathrm{T}}$ are vectors defining the Cartesian coordinates of the ellipse points and the ellipse coefficients, respectively, the over-determined fitting problem to a set of coordinate points ${\alpha }_i$ and ${\beta }_i$ (where $i=1,\dots , n$, and $n$ is greater than the number of ellipse coefficients, i.e., $n$ > 6) can be solved by the following eigenvalues problem (for more details, see Appendix A):

$$\left\{\begin{array}{c}M{\mathit{\gamma }}_1=\lambda {\mathit{\gamma }}_1\\ {\mathit{\gamma }}_1^{\mathrm{T}}{ℂ}_1{\mathit{\gamma }}_1=1\\ {\mathit{\gamma }}_2=-{\mathbb{S}}_3^{-1}{\mathbb{S}}_2^{\mathrm{T}}{\mathit{\gamma }}_1\\ \mathit{\gamma }={\left({\mathit{\gamma }}_1 {\mathit{\gamma }}_2\right)}^{\mathrm{T}}\end{array}\right.,$$

(24)

where $\mathbb{M}$ is the reduced scatter matrix,

$$\mathbb{M}={ℂ}_1^{-1}\left({\mathbb{S}}_1-{\mathbb{S}}_2{\mathbb{S}}_3^{-1}{\mathbb{S}}_2^{\mathrm{T}}\right),$$

(25)

$${\mathbb{S}}_1={\mathbb{D}}_1^{\mathrm{T}}{\mathbb{D}}_1, {\mathbb{S}}_2={\mathbb{D}}_1^{\mathrm{T}}{\mathbb{D}}_2, {\mathbb{S}}_3={\mathbb{D}}_2^{\mathrm{T}}{\mathbb{D}}_2,,$$

(26)

$${\mathbb{D}}_1=\left[\begin{array}{ccc}{\alpha }_1^2& {\alpha }_1{\beta }_1& {\beta }_1^2\\ ⋮& ⋮& ⋮\\ {\alpha }_n^2& {\alpha }_n{\beta }_n& {\beta }_n^2\end{array}\right],{\mathbb{D}}_2=\left[\begin{array}{ccc}{\alpha }_1& {\beta }_1& 1\\ ⋮& ⋮& ⋮\\ {\alpha }_n& {\beta }_n& 1\end{array}\right],$$

(27)

$${ℂ}_1=\left[\begin{array}{ccc}0& 0& 2\\ 0& -1& 0\\ 2& 0& 0\end{array}\right],$$

(28)

$$\mathit{\gamma }={\left[{\mathit{\gamma }}_1 {\mathit{\gamma }}_2\right]}^{\mathrm{T}},$$

(29)

with the ellipse coefficient vector segmented in ${\mathit{\gamma }}_1={\left[\begin{array}{ccc}A& B& C\end{array}\right]}^{\mathrm{T}}$ and ${\mathit{\gamma }}_2={\left[\begin{array}{ccc}D& E& F\end{array}\right]}^{\mathrm{T}}$. The solution of Equation (24) corresponds to the eigenvector $\mathit{\gamma }$ yielding a minimal non-negative eigenvalue $\lambda$. Once obtained $\mathit{\gamma }$, the lengths of major and minor semi-axes $s_M$ and $s_m$ are given by [54]:

$$s_{M,m}=\frac{\sqrt{\frac{2\left(A{E}^2+C{D}^2-BDE+\left(B^2-4AC\right)F\right)}{{\left(A+C\pm \sqrt{{\left(A-C\right)}^2+B^2}\right)}^{-1}}}}{4AC-B^2},$$

(30)

while the major axis inclination ${\phi }_{el}$ is [54]:

$${\phi }_{el}=\left\{\begin{array}{cc}0& for B=0, A<C\\ \pi /2& for B=0, A>C\\ 1/2{\cot }^{-1}\left((A-C) /B\right)& for B\ne 0, A<C\\ \pi /2+1/2{\cot }^{-1}\left((A-C) /B\right)& for B\ne 0, A>C\end{array}\right.,$$

(31)

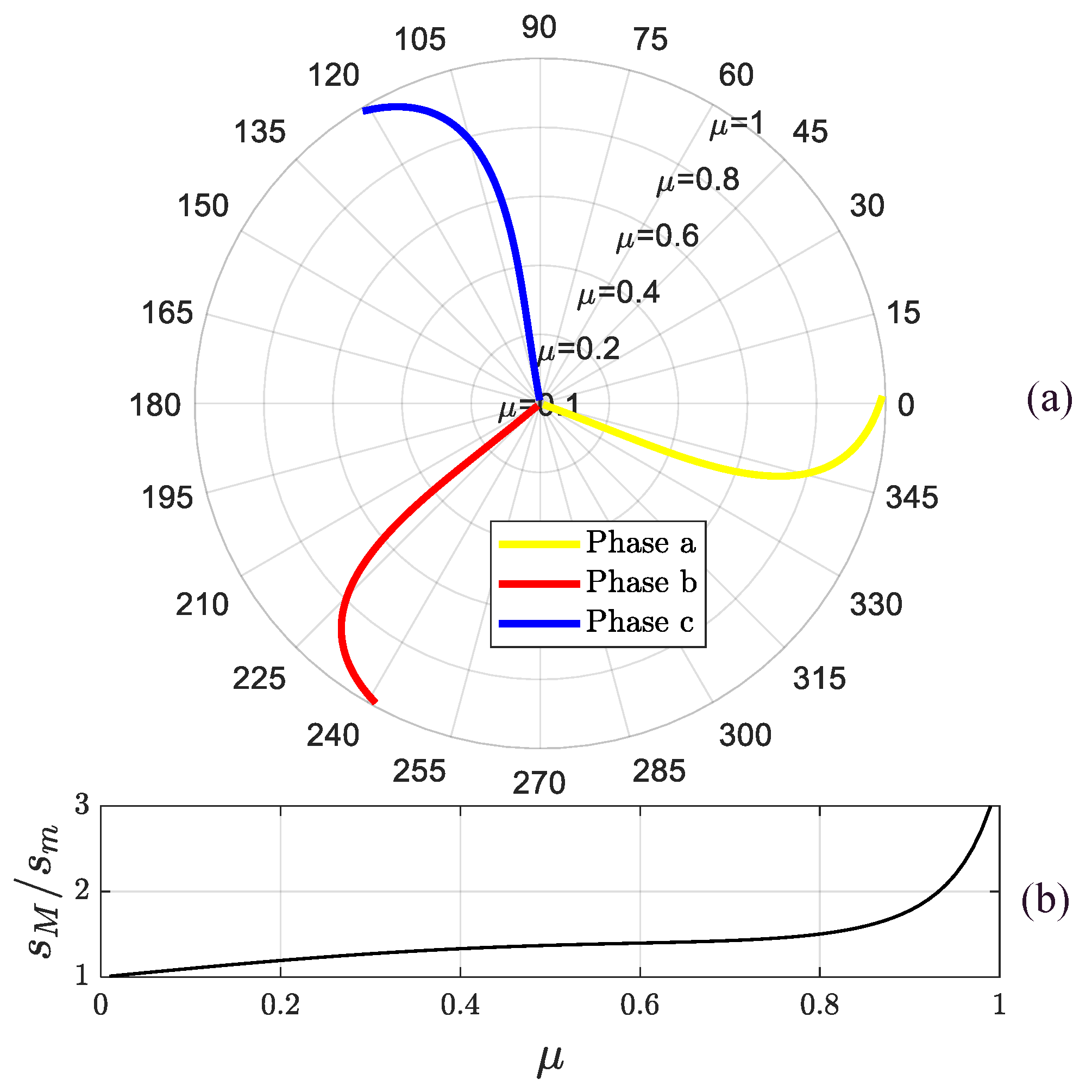
3.2. FDI Algorithm Design and Implementation

One of the basic limitations of the proposed FDI concept is that the technique is defined by assuming constant speed motor operations. During unsteady conditions, the current phasor changes its amplitude while rotating in the Clarke plane. Consequently, the ellipse identification does not work appropriately, and it could cause false alarms.

To overcome the problem, it is worth noting that, differently from the constant speed operations with ITSC faults, the axes of the ellipse reconstructed in unsteady conditions rotate. For this reason, the developed FDI algorithm detects an ITSC fault only if the value of the ellipse major axis is constant and stationary. This FDI logic has been implemented as represented by the flow chart in Figure 7: at each k-th monitoring sample, if the Boolean variable $mo{n}^{\left(k\right)}$ is true (Equation (32)), a fault counter $n_c^{\left(k\right)}$ is increased by two, otherwise it is reduced by one. When the fault counter reaches a predefined maximum value ($n_{th}$), the algorithm outputs a true Boolean fault flag $f_x$, which indicates that a fault on the phase $x \left(=a,b,c\right)$ is detected and isolated.

$$mo{n}^{\left(k\right)}=\left({\mathsf{\Delta }}_d^{\left(k\right)}\ge {\epsilon }_d{}_{th} \wedge {\mathsf{\Delta }}_i^{\left(k\right)}\le {\epsilon }_i{}_{th}\right),$$

(32)

where:

$${\mathsf{\Delta }}_d^{\left(k\right)}=\left|s_M^{\left(k\right)}-s_m^{\left(k\right)}\right|,$$

(33)

$${\mathsf{\Delta }}_i^{\left(k\right)}=\min \left({\left.{\mathsf{\Delta }}_i^{\left(k\right)}\right|}_a,{\left.{\mathsf{\Delta }}_i^{\left(k\right)}\right|}_c,{\left.{\mathsf{\Delta }}_i^{\left(k\right)}\right|}_b\right),$$

(34)

$${\left.{\mathsf{\Delta }}_i^{\left(k\right)}\right|}_a=\left|{\phi }_{el}^{\left(k\right)}\right|, {\left.{\mathsf{\Delta }}_i^{\left(k\right)}\right|}_b=\left|{\phi }_{el}^{\left(k\right)}\right|-\frac{2\pi }{3}, {\left.{\mathsf{\Delta }}_i^{\left(k\right)}\right|}_c=\left|{\phi }_{el}^{\left(k\right)}\right|+\frac{2\pi }{3},$$

(35)

The details and a dedicated discussion about the FDI parameters design are proposed in Section 4, while tables reporting the FDI parameters are reported in Appendix B.

3.3. Fault Accommodation Algorithm

After the FDI algorithm detects and isolates the ITSC fault, the motor still has two active phases. To maintain the performances after the fault, the FTC should accommodate the system by restoring the operation of the current phasor in the Clarke plane as it was in healthy conditions. This is here achieved by enabling the control of the central point of the motor Y-connection, via the stand-by leg of the four-leg converter, and by applying an RCFTC technique [9,55].

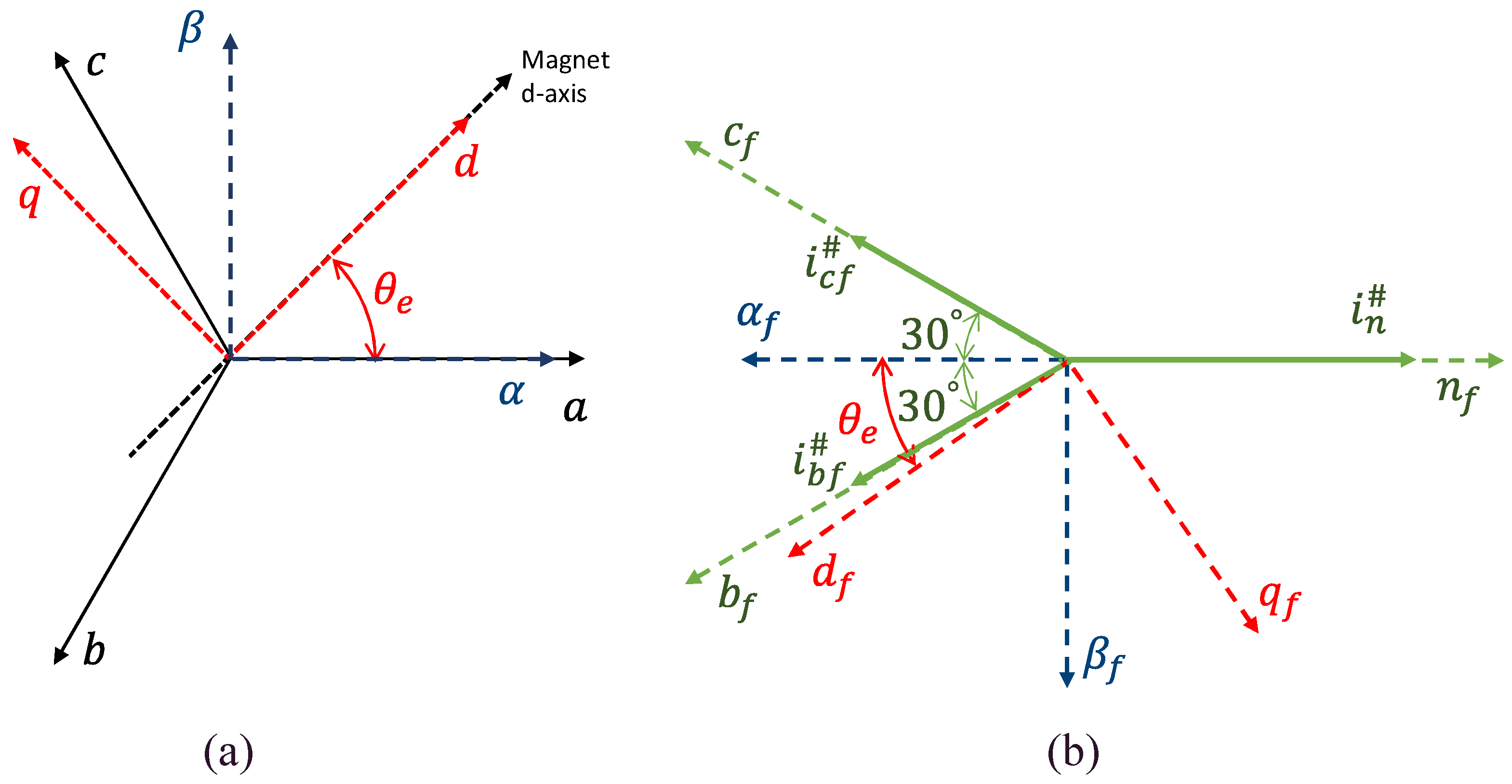
To maintain the torque performances with only two phases, the currents amplitudes in the healthy phases in the rotor reference frame ($i_{xf}^{\#},$ $i_{yf}^{\#}$) must increase by $\sqrt{3}$ w.r.t. those before the fault, and they must shift by 60° along the electrical angle. In addition, the amplitude of the current flowing into the central point ($i_n^{\#}$) must be $\sqrt{3}$ times those in the healthy phases:

$$\left\{\begin{array}{c}{i}_{xf}^{\#}=\sqrt{2}\left(i_d^{\#}\mathrm{c}\left[{\theta }_e+\frac{2\pi }{3}\left(m+\frac{7}{4}\right)\right]-i_q^{\#}\mathrm{s}\left[{\theta }_e+\frac{2\pi }{3}\left(m+\frac{7}{4}\right)\right]\right)\\ i_{yf}^{\#}=\sqrt{2}\left(i_d^{\#}\mathrm{c}\left[{\theta }_e+\frac{2\pi }{3}\left(m+\frac{5}{4}\right)\right]-i_q^{\#}\mathrm{s}\left[{\theta }_e+\frac{2\pi }{3}\left(m+\frac{5}{4}\right)\right]\right)\\ i_{wf}^{\#}=0\\ i_n^{\#}=\sqrt{6}\left(i_d^{\#}\mathrm{c}\left({\theta }_e+\frac{2\pi }{3}m\right)-i_q^{\#}\mathrm{s}\left({\theta }_e+\frac{2\pi }{3}\right)\right)\end{array}\right.$$

(36)

In Equation (36), $i_d^{\#}, i_q^{\#}$ are the current demands in the Park frame before the fault. The subscripts $xf$, $yf$, and $wf$ indicate the healthy and the isolated phases, while $m$ is an integer number defined by the values in

Table 1. Reconfiguration parameters.

Isolated Phase (w)	x	y	m
a	b	c	0
b	c	a	2
c	a	c	1

.

Since all the current demands in the stator frame are synchronous with the rotor motion, they can be expressed into a rotating frame by applying two new Clarke–Park transformations [9,55] (Figure 8):

• From the planar reference $\left(n_f, b_f, c_f\right)$ to a planar reference frame $({\alpha }_f,{\beta }_f,{\mathit{\gamma }}_f)$, in which the ${\alpha }_f$ axis has an opposite direction w.r.t. the neutral current axis $n_f$;
• From the planar reference $({\alpha }_f,{\beta }_f,{\mathit{\gamma }}_f)$ to a planar rotating frame $(d_f,q_f,z_f)$ that maintains the same commands after the isolation ($i_d{}_f=i_d^{*}$ and $i_q{}_f=i_q^{*})$.

$$\left[\begin{array}{c}{i}_{df}^{\#}\\ i_{qf}^{\#}\\ i_{zf}^{\#}\end{array}\right]={\mathit{R}}_{PCf}\left(m\right){\mathit{T}}_{PCaf}\left({\theta }_e\right)\left[\begin{array}{c}\begin{array}{c}{i}_{xf}^{\#}\\ i_{yf}^{\#}\end{array}\\ i_n^{\#}\end{array}\right],$$

(37)

where ${\mathit{R}}_{CPf}\left(m\right)$ is a rotation matrix that generalizes the transformation matrix ${\mathit{T}}_{CPaf}\left({\theta }_e\right)$ related to the case of isolation of phase a [9]:

$$\begin{gathered} {\mathit{T}}_{CPaf}\left({\theta }_e\right)=\left[\begin{array}{ccc}{k}_2\mathrm{s}\left({\theta }_e\right)-k_1\mathrm{c}\left({\theta }_e\right)& -k_2\mathrm{s}\left({\theta }_e\right)-k_1\mathrm{c}\left({\theta }_e\right)& k_3\mathrm{c}\left({\theta }_e\right)\\ k_1\mathrm{s}\left({\theta }_e\right)+k_2\mathrm{c}\left({\theta }_e\right)& k_1\mathrm{s}\left({\theta }_e\right)-k_2\mathrm{c}\left({\theta }_e\right)& -k_3\mathrm{s}\left({\theta }_e\right)\\ 0& 0& -1/\sqrt{3}\end{array}\right], \\ {\mathit{R}}_{CPf}\left(m\right)=\left[\begin{array}{ccc}\mathrm{c}\left(m2\pi /3\right)& -\mathrm{s}\left(m2\pi /3\right)& 0\\ \mathrm{s}\left(m2\pi /3\right)& \mathrm{c}\left(m2\pi /3\right)& 0\\ 0& 0& 1\end{array}\right], \end{gathered}$$

(38)

$$k_1=\sqrt{6}/\left(6+4\sqrt{3}\right), k_2=1/\sqrt{2}, k_3=2/\sqrt{3},$$

(39)

The RCFTC accommodation is finally completed by inverting the direct transformation matrix to calculate the reference voltages for the converter:

$$\left[\begin{array}{c}\begin{array}{c}{V}_{xnf}^{\#}\\ V_{ynf}^{\#}\end{array}\\ V_{nof}^{\#}\end{array}\right]={\left({\mathit{T}}_{CPaf}\left({\theta }_e\right)\right)}^{-1}{\left({\mathit{R}}_{PCf}\left(m\right)\right)}^{\mathrm{T}} \left[\begin{array}{c}{V}_{df}^{\#}\\ V_{qf}^{\#}\\ V_{zf}^{\#}\end{array}\right],$$

(40)

where

$${\left(T_{CPaf}\left({\theta }_e\right)\right)}^{-1}=\left[\begin{array}{ccc}\frac{\mathrm{s}\left({\theta }_e\right)}{2k_2}-\frac{\mathrm{c}\left({\theta }_e\right)}{2k_1}& \frac{\mathrm{s}\left({\theta }_e\right)}{2k_1}+\frac{\mathrm{c}\left({\theta }_e\right)}{2k_2}& -1\\ -\frac{\mathrm{s}\left({\theta }_e\right)}{2k_2}-\frac{\mathrm{c}\left({\theta }_e\right)}{2k_1}& \frac{\mathrm{s}\left({\theta }_e\right)}{2k_1}-\frac{\mathrm{c}\left({\theta }_e\right)}{2k_2}& -1\\ 0& 0& -\sqrt{3}\end{array}\right],$$

(41)

The integration of the proposed FTC strategy within the motor closed-loop system is schematically depicted in Figure 9.

When the system is in normal condition, the conventional Clarke–Parke transformations are employed ($T_{CP}, T_{CP}^{-1}$) and the central point of the Y-connection is isolated ($T_{n1}$ and $T_{n2}$ are not used). Once an ITSC is detected and isolated, the reference frame transformations of the RCFTC are employed ($T_{C{P}_f}, T_{C{P}_f}^{-1}$), and the reconfigured voltage references are sent to the four-leg converter to signal the central point ($T_{n1}$ and $T_{n2}$).

4. Results and Discussion

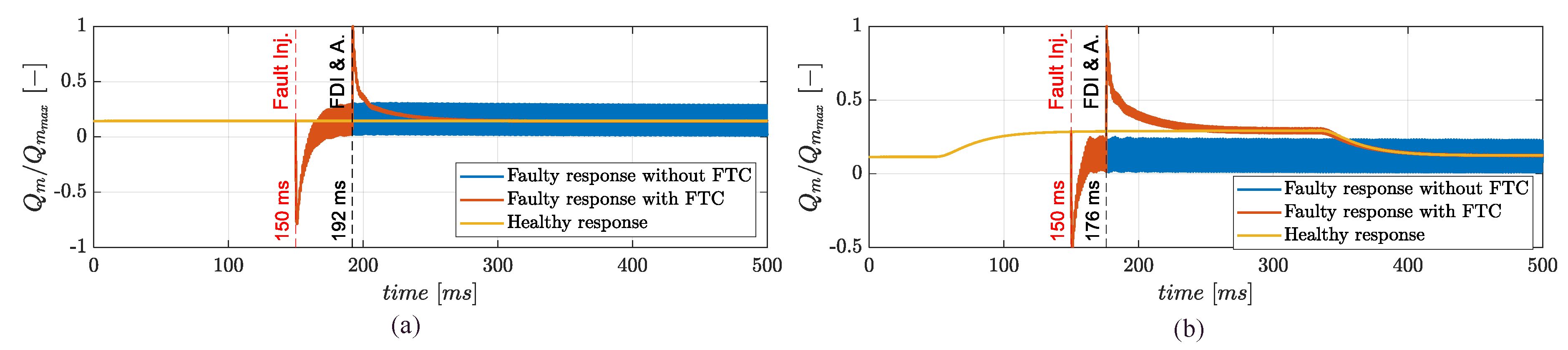
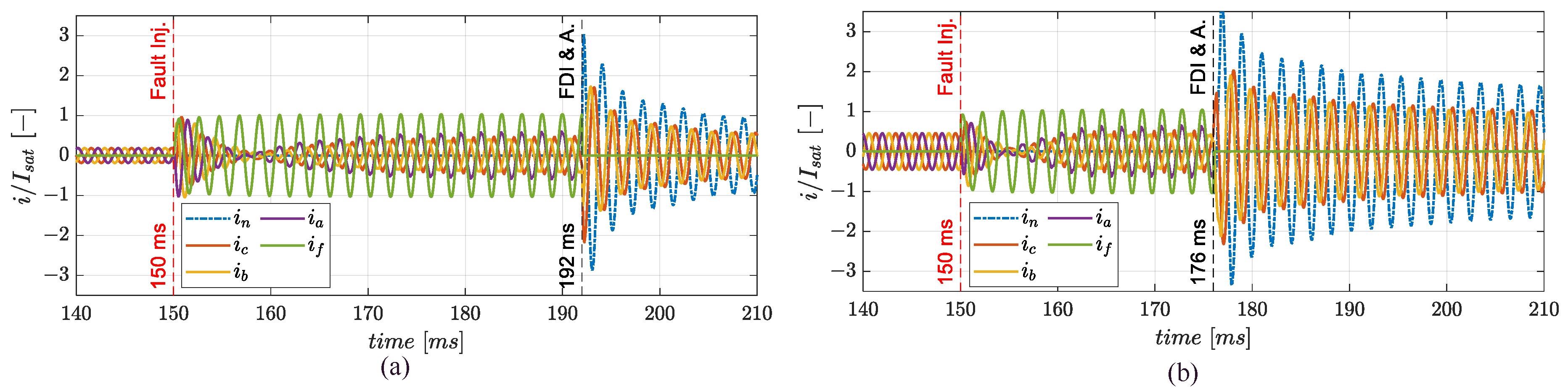
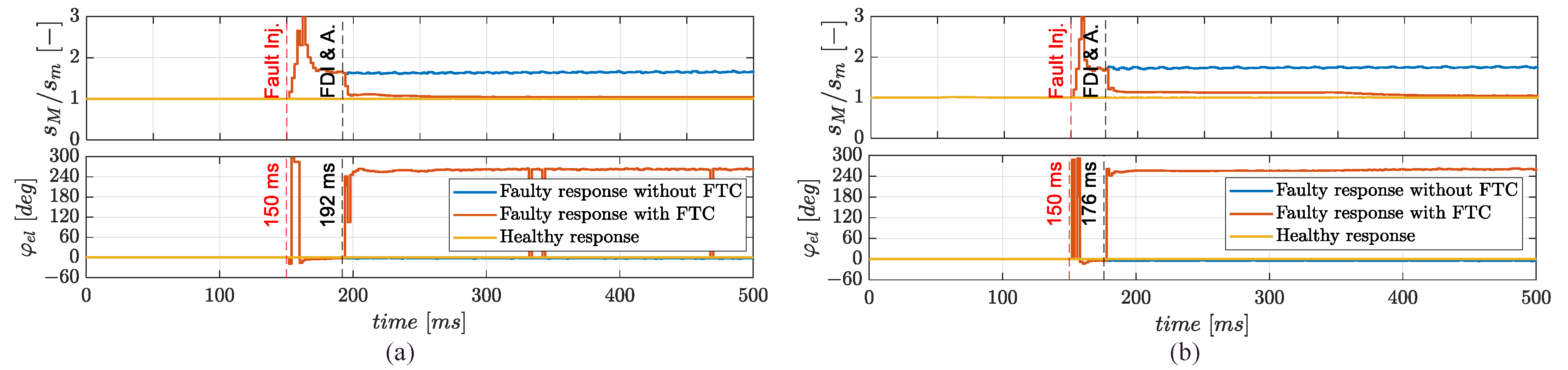
4.1. Failure Transient Characterization

The effectiveness of the presented FTC strategy has been tested by using the nonlinear model of the propulsion system. The model is entirely developed in the MATLAB/Simulink environment, and its numerical solution is obtained via the fourth order Runge–Kutta method, using a 10⁻⁶ s integration step. It is worth noting that the choice of a fixed-step solver is not strictly related to the objectives of this work (in which the model is used for “off-line” simulations testing the FTC), but it has been selected for the next step of the project, when the FTC system will be implemented in the ECU boards via the automatic MATLAB compiler and executed in “real-time”.

The closed-loop control is executed at a 20 kHz sampling rate and the maximum allowable fault latency has been set to 50 ms (for details, see Section 4.2). All the simulations started (t = 0 s) with a healthy PMSM, driving the propeller at 5800 rpm (UAV in straight-and-level flight at sea level

Table A1. APC 22 × 10E Propeller data.

Definition	Symbol	Value	Unit
Cruise speed	${\dot{\theta }}_p$|cruise	5800	rpm
Cruise power	Pp|cruise	1100	W
Climb speed	${\dot{\theta }}_p$|climb	7400	rpm
Climb power	Pp|climb	3238	W

).

The FTC strategy has been assessed by simulating the occurrence of an ITSC fault with $\mu =0.5$ on phase a at t = 150 ms. The failure transient is characterized by applying or not the proposed FTC and by comparing the responses with those in healthy conditions. As shown by Figure 10, though its relevant extension, the ITSC fault implies minor impacts on the propeller speed response during stationary operations (Figure 10a), even if the FTC application assures a faster recovery of the pre-fault speed value. On the other hand, the failure transient during unsteady operations is much more limited with FTC, even if small-amplitude ripples (at approximately 100 Hz) appear immediately after the accommodation (Figure 10b). These responses highlight the importance of applying the FTC for ITSC faults: since the fault effects are minor during stationary operations, its detection is very difficult, but the ITSC is typically unstable, and it progressively spreads along the phase windings if the coil is not isolated.

The failure transient in terms of motor torque is then reported in Figure 11. It can be noted that, if the FTC is not applied, the post-fault behaviour is characterized, during both stationary and unsteady operations, by relevant high-frequency ripples (at approximately 1 kHz, i.e., twice the electrical frequency of the motor). In particular, during stationary operations, the FTC permits to rapidly restore the pre-fault torque level, by eliminating high-frequency loads that would inevitably cause damages at mechanical and electrical parts (Figure 11a). The failure transients in terms of phase currents are then reported in Figure 12, when the FTC is applied. The fault generates a short circuit current ($i_f$, Figure 12) causing the loss of symmetry of the three-phase system. Thanks to the RCFTC accommodation, the phase a is disengaged and the fourth leg of the converter is activated: this action stops the short circuit current and opens a current path through the central point ($i_n$, Figure 12).

The current phasor trajectories in the Clarke space are shown in Figure 13. It can be noted that, when an ITSC fault is injected in phase a, the trajectories are not strictly elliptical. This depends on the fact that the faulty currents are not perfectly sinusoidal, but they also contain higher harmonic contents. The phenomenon is caused by the phase voltages saturation. Despite the presence of these higher harmonic contents, the ellipse fitting technique successfully operates by demonstrating the relevant robustness of the FDI algorithm. On the other hand, when the fault is accommodated, the trajectory involves the neutral axis too, in such a way that, its projection on the $\alpha ,\beta$ plane overlaps the healthy circular trajectory. Finally, the geometrical parameters of the current phasor elliptical trajectory (semi-axes lengths and major axis inclination) are plotted in Figure 14. It can be noted that, when the FTC intervenes, the projection of the current trajectory on the $\alpha ,\beta$ plane becomes circular ($s_M/s_m=1$) and the ellipse inclination returns to zero.

4.2. FDI Parameters Definition

As described in Section 3.2, the design of the FDI algorithm requires the definition of four parameters, i.e., ${\epsilon }_d{}_{th}$, ${\epsilon }_i{}_{th}$, $n_{th}$, and $n$. Concerning the ellipse fitting samples $n$, this parameter has been defined by pursuing a good balance between the trajectory reconstruction accuracy and the FDI latency, both increasing when $n$ increases. Considering that the propeller speed tracking bandwidth is approximately 15 Hz, the maximum allowable FDI latency has been set to 50 ms, which could be reasonably targeted by an equivalent monitoring frequency of 500 Hz. Being the sampling rate of the sensor system at 20 kHz, $n=40$ has been imposed. The values of the remaining parameters (${\epsilon }_d{}_{th}$, ${\epsilon }_i{}_{th}$, $n_{th}$) have been instead defined via time domain simulations, aiming to obtain correct ITSC FDI with very limited extension ($\mu =0.1$). Two FDI design simulations have been performed, Figure 15:

• Simulation 1: cruise speed hold,
• Simulation 2: maximum speed ramp demand.

The FDI parameter plotted in Figure 16 shows that low values of ${\epsilon }_d{}_{th}$ would clearly imply a too-sensitive algorithm, with high counts $n_c$ during unsteady operations and in turn high values of $n_{th}$ to avoid false alarms. On the other hand, high values of ${\epsilon }_d{}_{th}$ will make the algorithm too robust to false alarms but it will reduce the effectiveness in detecting ITSC at an early stage. In the proposed case study, a good balance between the robustness against false alarms and the effectiveness in diagnosing ITSC higher than $\mu =0.1$ can be obtained by selected ${\epsilon }_d{}_{th}=0.6 \mathrm{A}$ and $n_{th}=20$, which guarantees an FDI latency lower than the 50 ms among the two cases reported in Figure 15.

4.3. Critical Comparison with Other ITSC FDI Methods

A comparative analysis of the proposed FDI method with the most relevant ones developed in the literature (

Table 2. Relevant FDI methods for ITSC faults.

Acronym	Method	Reference
M1	FFT	[13]
M2	HHT transforms	[38]
M3	PVA	[31]
M4	CNN	[39]
M5	APVA	Present work

) has been carried out by using the list of capabilities given in

Table 3. FDI capabilities for ITSC faults.

Acronym	Method
C1	Able to detect the faulty phase.
C2	Insensitive to operating loads.
C3	Robust against speed changes.
C4	Robust against current waveform.
C5	Minimum number of detected shorted turns.
C6	Electrical periods for FDI (latency time).
C7	Real-time computation.
C8	Tuning simplicity.

. The results are reported in

Table 4. Comparison of FDI methods for ITSC faults.

	Method
Capability	M1	M2	M3	M4	M5
C1	Yes	No	No	Yes	Yes
C2	No	No	Yes	No	Yes
C3	No	Yes	No	Not provided	Yes
C4	Not provided	Not provided	Not provided	Not provided	Yes
C5	2	1	4	1	4
C6	Not provided	Not provided	Not provided	10 (200 ms)	20 (40 ms)
C7	No	No	No	Yes	Yes
C8	Yes	No	Yes	No	Yes

.

The FFT methods are robust against noise, but they are not applicable in unsteady operations. They can be enhanced by applying HHT transforms, but the capability to detect the faulty phase is lost. Similarly, the main disadvantage of the PVA methods is the inability to locate the fault. The CNN method is competitive in terms of the ITSC location, but their robustness in unsteady operations has not been proved; furthermore, the design of the neural detector requires a complex design and training process. On the other hand, the proposed APVA method demonstrates excellent capabilities in unsteady operations, it succeeds in fault location and detects ITSC faults with a very limited extension (10%, less than four turns) independently from the load level. All the methods considered are capable of detecting incipient faults, but many of them lack enough information for a comparison in terms of detection and isolation latency.

5. Conclusions

A novel FTC strategy for a high-speed PMSM with a four-leg converter employed for UAV propulsion is developed and characterized in terms of FDI and fault accommodation capabilities. The FTC performances are assessed via dynamic simulation by using a detailed nonlinear model of the electric propulsion system, which includes a physically based modelling of ITSC faults. For the proposed FTC, an original FDI algorithm is developed and applied, based on an innovative current signature technique, which uses as fault symptoms the geometrical parameters of the elliptical trajectory of the currents phasor in the Clarke plane (e.g., major and minor axes lengths, and major axis inclination). In addition, a theoretical analysis is carried out to support the FDI algorithms, by demonstrating that the major axis inclination can be used as a symptom for the faulty phase identification.

A comparative analysis with other ITSC FDI methods from the literature is also carried out. If compared with neural networks methods, which exhibit the best sensibility to incipient faults (a shorted turn is isolated within 10 electrical periods), the proposed technique behaves slightly worse (four shorted turns, corresponding to a 10% extension along the coil, and are isolated within 20 electrical periods). Nevertheless, the neural methods are more complicated to be tuned (due to the training process), while the proposed method only requires tuning four parameters. Finally, the paper demonstrates that a fault accommodation based on the RCFTC technique succeeds in minimizing the failure transient and eliminates the high-frequency torque ripples induced by the fault.