A Thermo-Mechanical Properties Evaluation of Multi-Directional Carbon/Carbon Composite Materials in Aerospace Applications
Abstract
:1. Introduction
2. Yarn Architectures of Multi-Directional C/C Composites
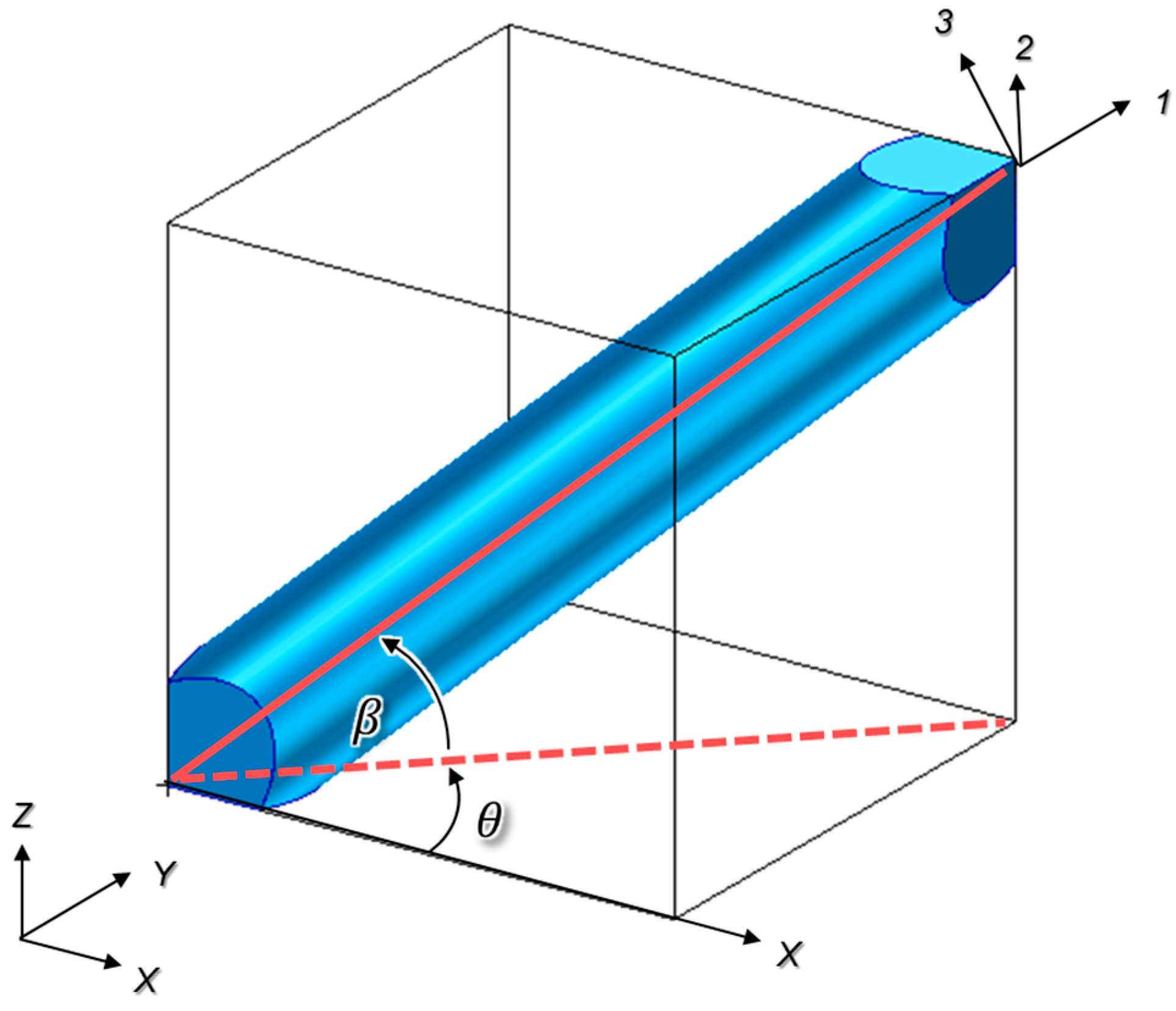
3. Geometric Model of Repeating Unit Cell (RUC)
Geometric Modelling
4. Thermo-Mechanical Properties Prediction of C/C Composites
4.1. Effective Stiffness Prediction Method
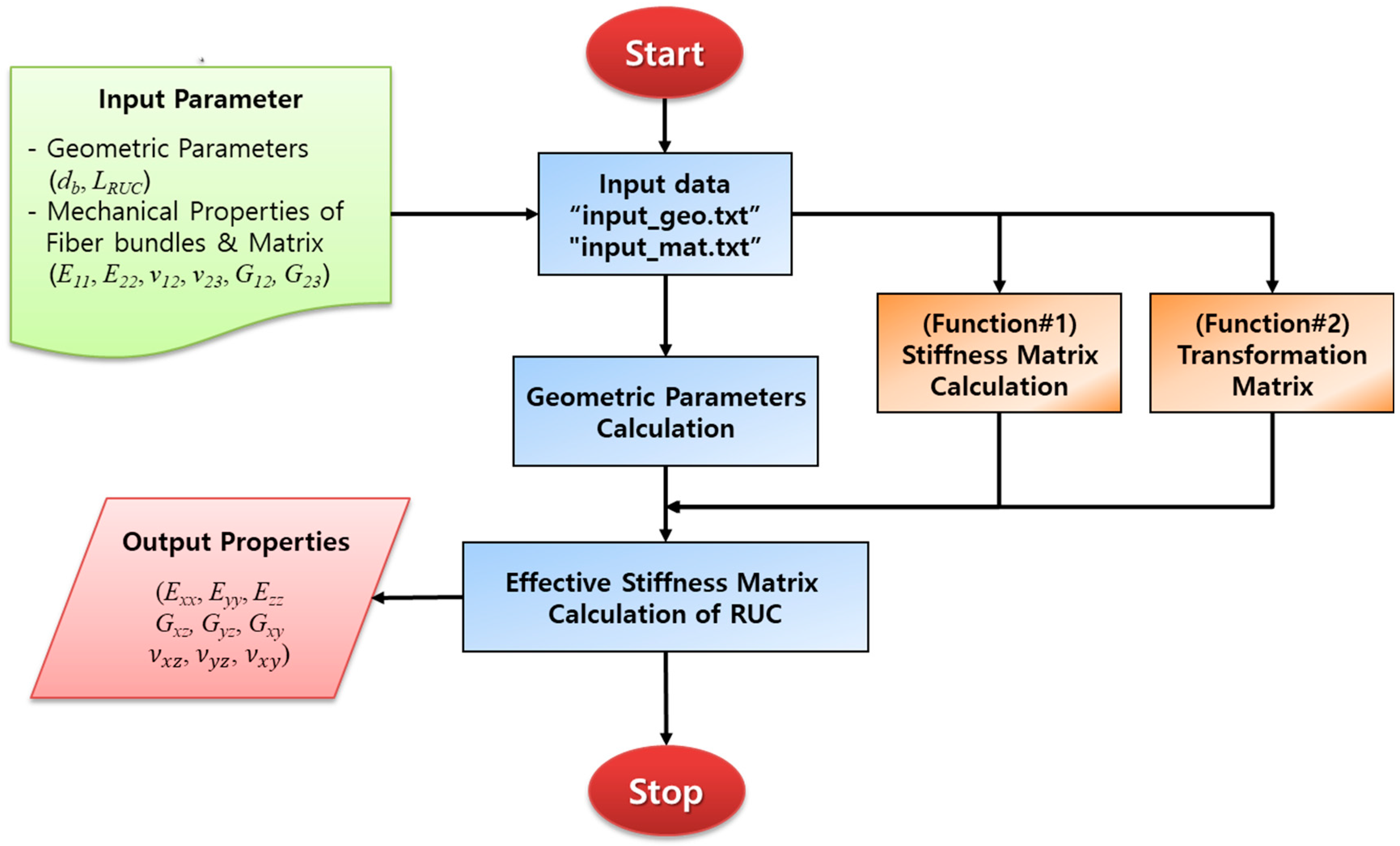
4.2. In-House Code
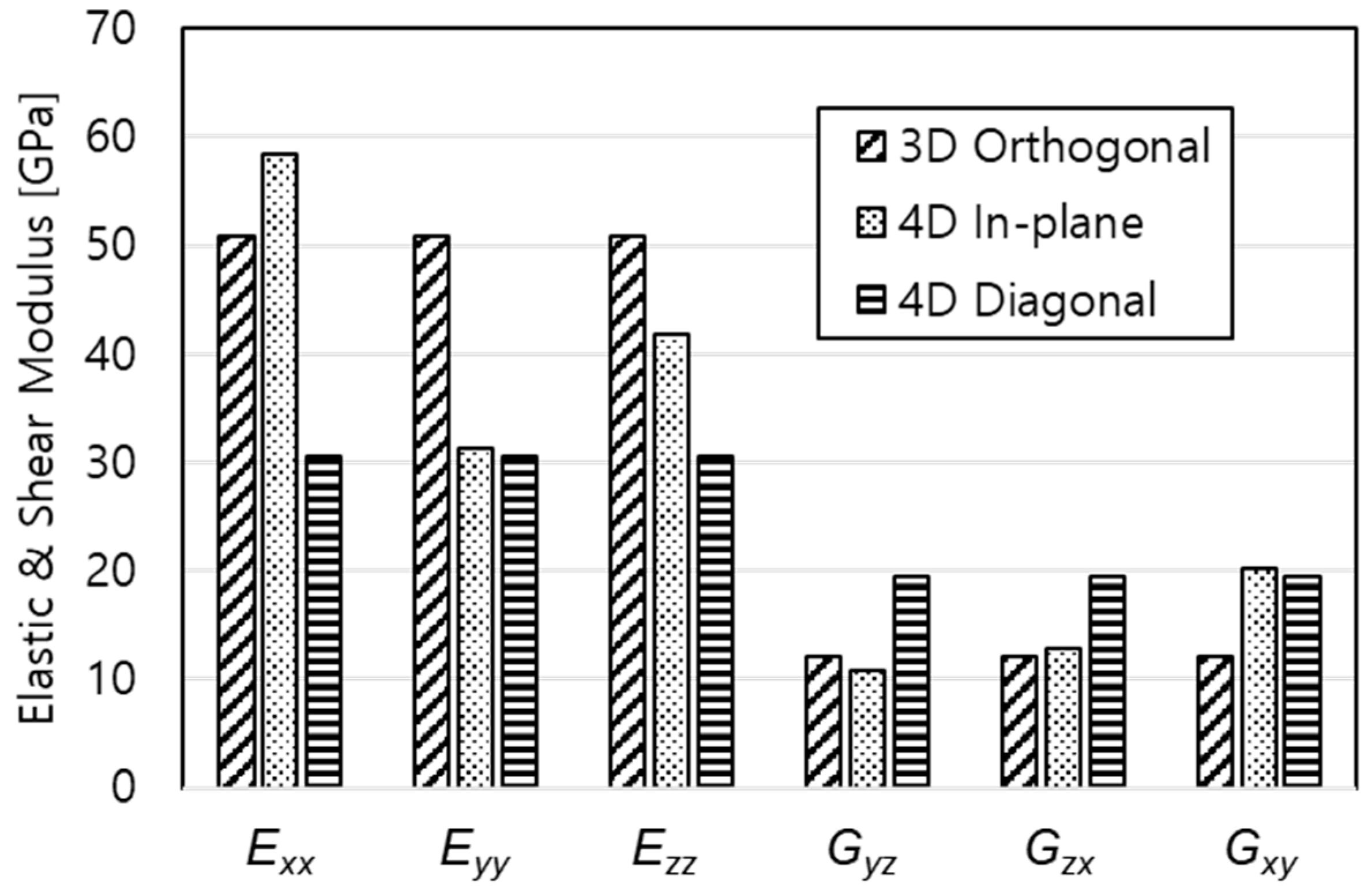
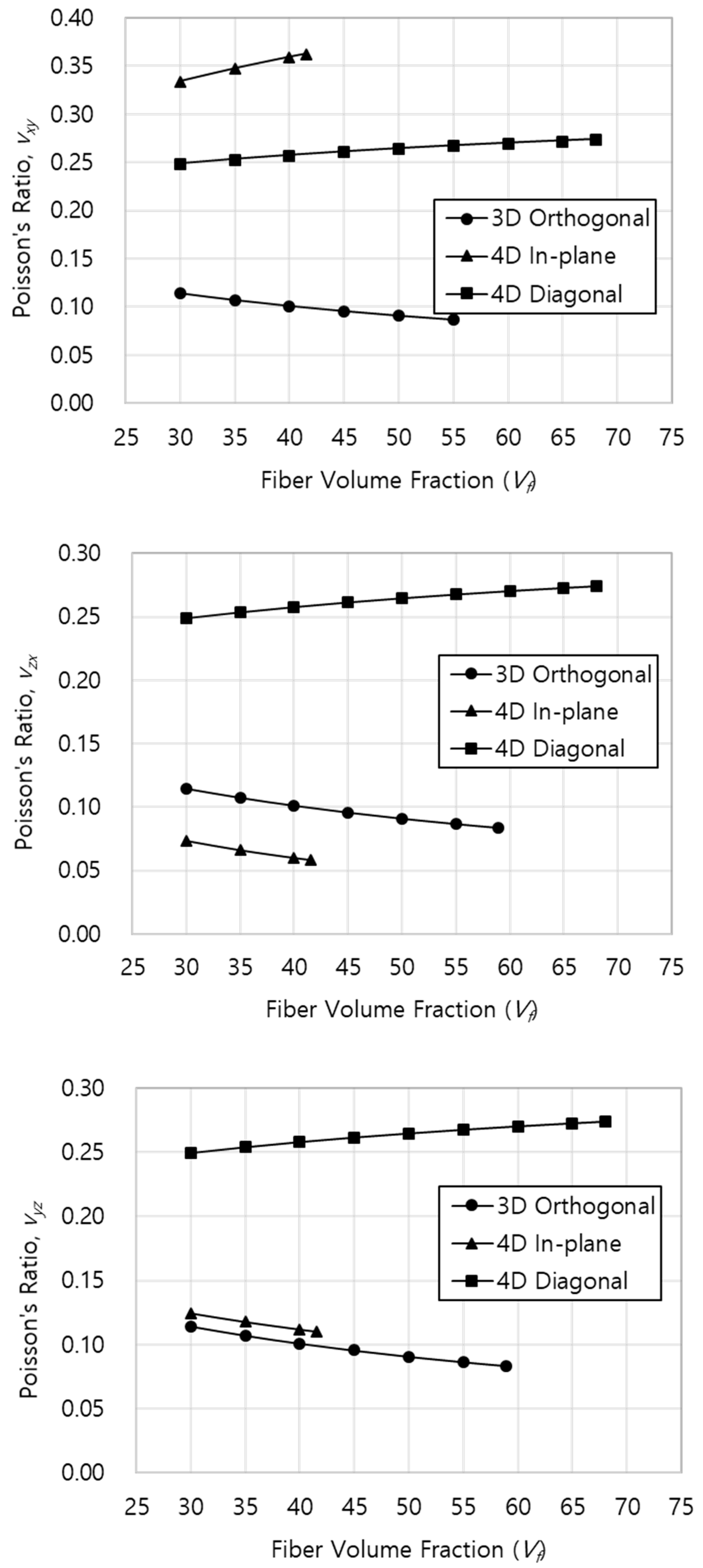
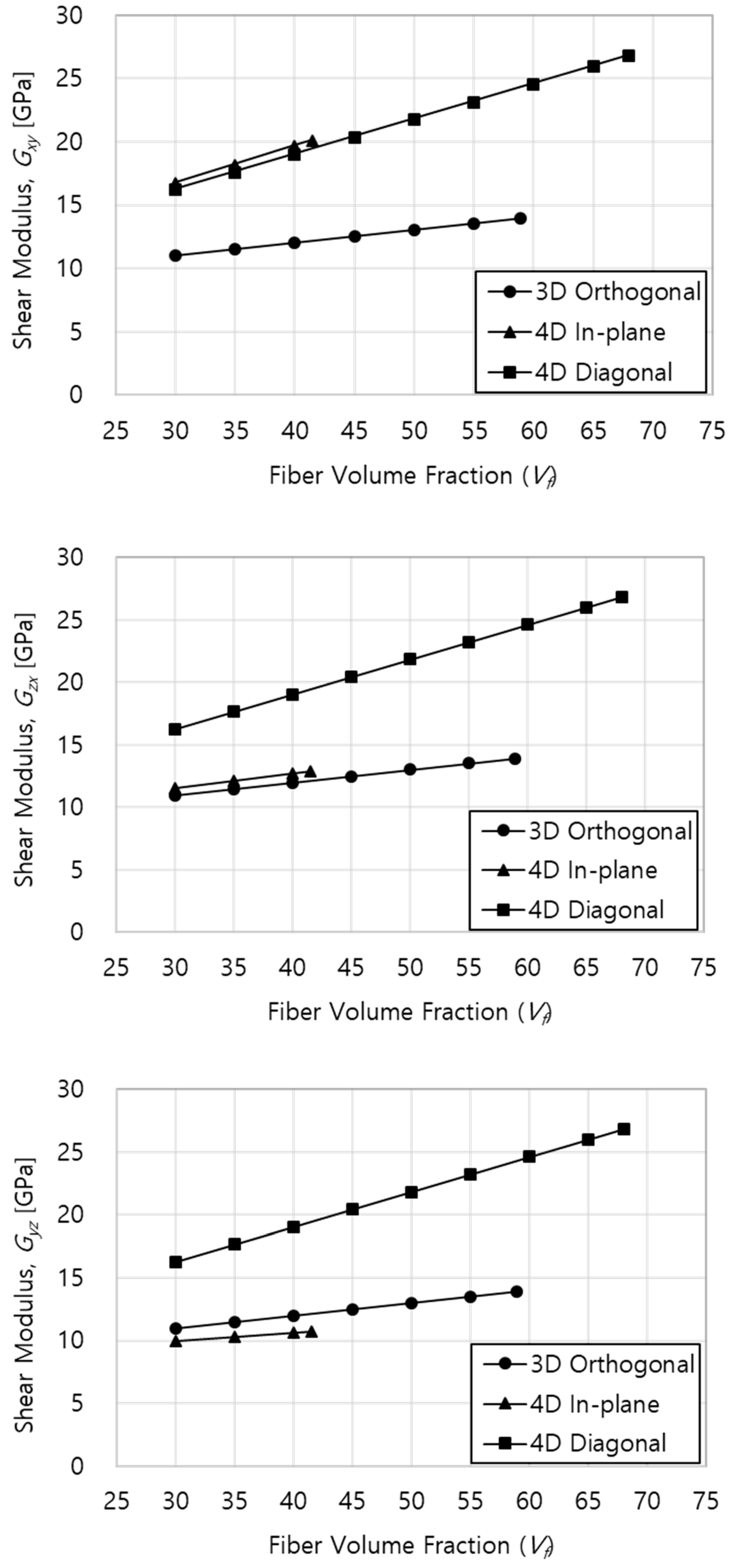
4.3. Thermo-Mechanical Properties Prediction
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| m | Constituents | Vm [%] | |
|---|---|---|---|
| 1 | Fiber bundle | 0.139 | 13.9 |
| 2 | Fiber bundle | 0.139 | 13.9 |
| 3 | Fiber bundle | 0.139 | 13.9 |
| 4 | Interstitial Matrix | 0.584 | 58.4 |
| Total | RUC | 1.000 | 100.0 |
References
- Herakovich, C.T. Mechanics of Fibrous Composite; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1998. [Google Scholar]
- Niu, M.C. Composite Airframe Structures; Conmilit Press Ltd.: Hong Kong, 1992. [Google Scholar]
- Buckley, J.D.; Edie, D.D. Carbon-Carbon Materials and Composites; Noyes Publications: Park Ridge, NJ, USA, 1993. [Google Scholar]
- Devi, G.R.; Rao, K.R. Carbon-Carbon Composites—An Overview. Def. Sci. J. 1993, 43, 369–383. [Google Scholar] [CrossRef]
- Naik, N.K. Woven Fabric Composites; Technomic Publishing Co., Inc.: Lancaster, PA, USA, 1994. [Google Scholar]
- Chou, T.-W.; Ko, F.K. Textile Structural Composites; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Cox, B.N. Handbook of Analytical Methods for Textile Composites; NASA Contractor Report 4750, Contract NAS1-19243; NASA: Washington, DC, USA, 1997.
- Chou, T.-W.; Ishikawa, T. Analysis and Modeling of Two-Dimensional Fabric Composites. In Composite Materials Series 3, Textile Structural Composites; Elsevier Science Publishers: Amsterdam, The Netherlands, 1989; pp. 210–264. [Google Scholar]
- Ko, F.K.; Pastore, C.M.; Lei, C.; Whyte, D.W. A Fabric Geometry Model for 3-D Braid Reinforced FP/AI-Li Composites. In Proceedings of the International SAMPE Metals Conference: Competitive Advances in Metals/Metal Processing, Cherry Hill, NJ, USA, 18–20 August 1987. [Google Scholar]
- Johnson, W.; Masters, J.; O’Brien, T.; Pastore, C.; Gowayed, Y. A Self-Consistent Fabric Geometry Model: Modification and Application of a Fabric Geometry Model to Predict the Elastic Properties of Textile Composites. J. Compos. Technol. Res. 1994, 16, 32–36. [Google Scholar] [CrossRef]
- Ma, C.-L.; Yang, J.-M.; Chou, T.-W. Elastic Stiffness of Three-Dimensional Braided Textile Structural Composites. In Composite Materials: Testing and Design; ASTM STP 893; ASTM: Philadelphia, PA, USA, 1986; pp. 404–421. [Google Scholar]
- Foye, R.L. Finite Element Analysis of the Stiffness of Fabric Reinforced Composites; NASA CR-189597; National Aeronautics and Space Administration: Hampton, VA, USA, 1992.
- Xu, L.; Kim, S.J.; Ong, C.-H.; Ha, S.K. Prediction of material properties of biaxial and triaxial braided textile composites. J. Compos. Mater. 2012, 46, 2255–2270. [Google Scholar] [CrossRef]
- Naik, R.A.; Ifju, P.G.; Masters, J.E. Effect of Fiber Architecture Parameters on Deformation Fields and Elastic Moduli of 2-D Braided Composites. J. Compos. Mater. 1994, 28, 656–681. [Google Scholar] [CrossRef]
- Naik, R.A. Analysis of Woven and Braided Fabric Reinforced Composites; NASA Contractor Report 194930, Contract NAS1-19399; NASA: Washington, DC, USA, 1994.
- Naik, R.A. TEXCAD—Textile Composite Analysis for Design; NASA Contractor Report 4639, Contract NAS1-19708; NASA: Washington, DC, USA, 1994.
- Delneste, L.; Pérez, B. An inelastic finite element model of 4D carbon-carbon composite. AIAA J. 1983, 21, 1143–1149. [Google Scholar] [CrossRef]
- Sharma, R.; Bhagat, A.R.; Mahajan, P. Finite element analysis for mechanical characterization of 4D inplane carbon/carbon composite with imperfect microstructure. Lat. Am. J. Solids Struct. 2014, 11, 170–184. [Google Scholar] [CrossRef]
- Wang, C.; Cao, P.; Tang, M.; Tian, W.; Liu, K.; Liu, B. Study on Properties Prediction and Braiding Optimization of Axial Braided Carbon/Carbon Composite. Materials 2020, 13, 2588. [Google Scholar] [CrossRef] [PubMed]
- Rao, M.V.; Mahajan, P.; Mittal, R. Effect of architecture on mechanical properties of carbon/carbon composites. Compos. Struct. 2008, 83, 131–142. [Google Scholar] [CrossRef]
- Xia, Z.; Zhou, C.; Yong, Q.; Wang, X. On selection of repeated unit cell model and application of unified periodic boundary conditions in micro-mechanical analysis of composites. Int. J. Solids Struct. 2006, 43, 266–278. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.-J.; Park, J.-S. Mechanical Properties Prediction by Geometric Modeling of Plain Weave Composites. J. Korean Soc. Aeronaut. Space Sci. 2016, 44, 941–948. [Google Scholar]
- Kim, M.J. Mechanical Properties Prediction by Manufacturing Parameters for Braided Composites. J. Aerosp. Syst. Eng. 2020, 14, 26–32. [Google Scholar]
- Kim, M.; Park, J. Stiffness Prediction of Triaxial Braided Composites Accounting for Manufacturing Parameters. Int. J. Aeronaut. Space Sci. 2021, 22, 602–612. [Google Scholar] [CrossRef]
- Liao, X.; Li, H.; Xu, W.; Li, K. Study on the thermal expansion properties of C/C composites. J. Mater. Sci. 2007, 42, 3435–3439. [Google Scholar] [CrossRef]
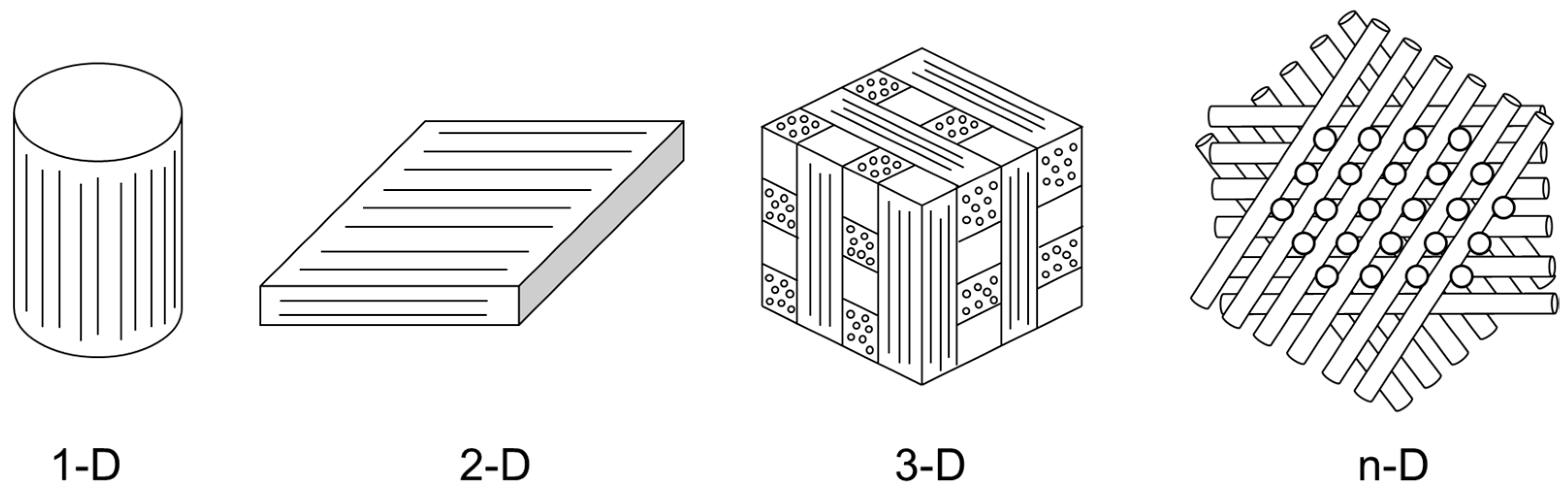



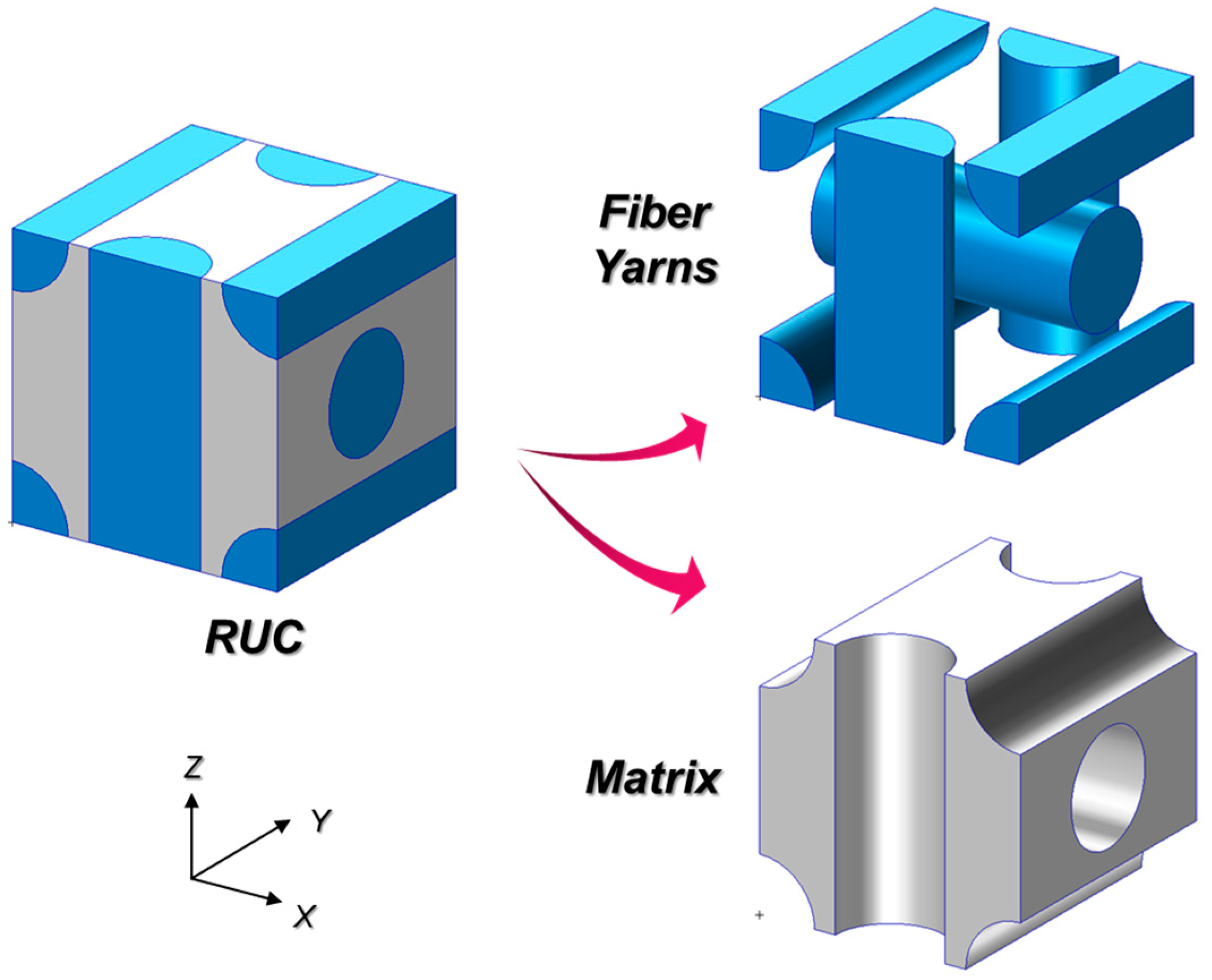
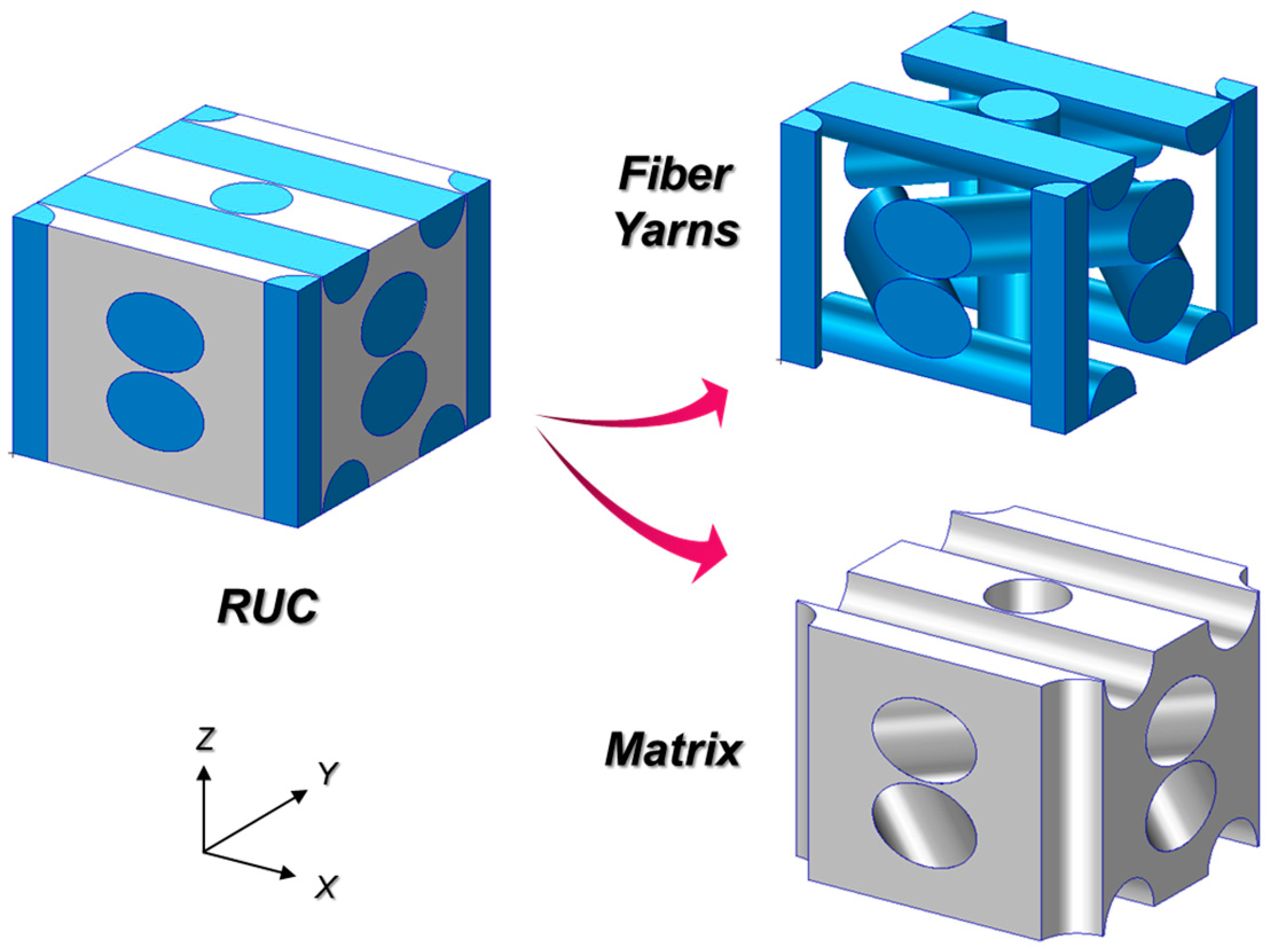
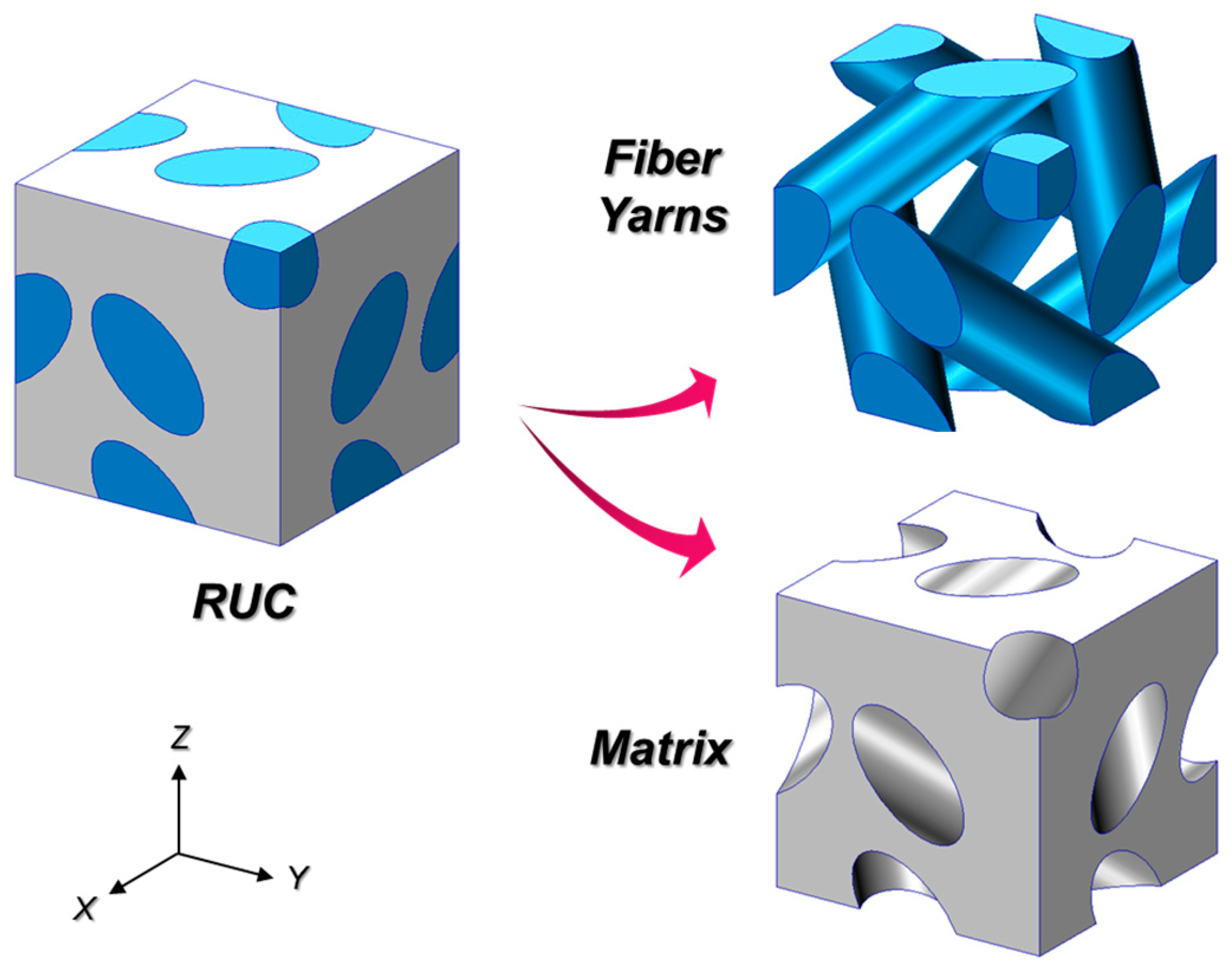
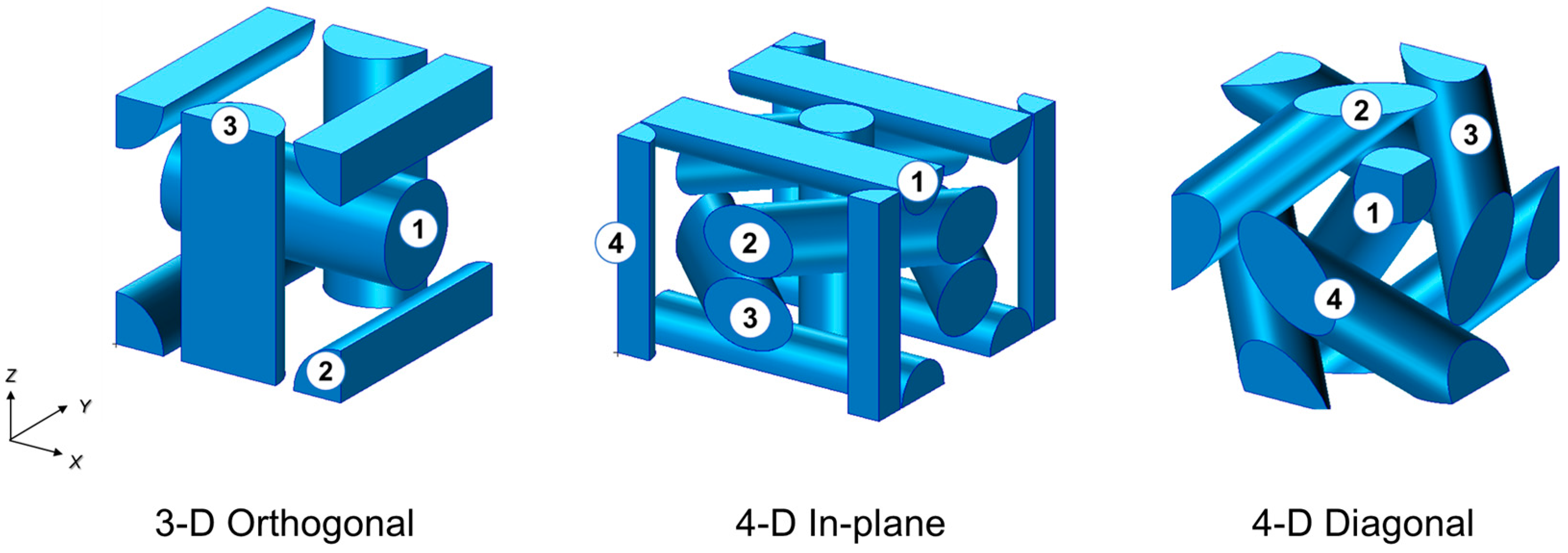



| Yarn Architecture | Fiber Bundle ID | Complete Yarn Count | Length [mm] | [deg] | [deg] |
|---|---|---|---|---|---|
| 3-D Orthogonal | 1 | 1 | 1.000 | 0 | 0 |
| 2 | 1 | 1.000 | 90 | 0 | |
| 3 | 1 | 1.000 | 0 | 90 | |
| 4-D In-plane | 1 | 2 | 1.000 | 0 | 0 |
| 2 | 2 | 0.707 | 45 | 0 | |
| 3 | 2 | 0.707 | −45 | 0 | |
| 4 | 2 | 0.750 | 0 | 90 | |
| 4-D Diagonal | 1 | 1 | 1.732 | 45 | 35.3 |
| 2 | 2 | 0.866 | 135 | 35.3 | |
| 3 | 2 | 0.866 | 225 | 35.3 | |
| 4 | 2 | 0.866 | 315 | 35.3 |
| Property | Constituents | |
|---|---|---|
| Carbon Fiber Bundle | Carbon Matrix | |
| E11 [MPa] | 240,900 | 19,000 |
| E22 [MPa] | 19,000 | 19,000 |
| E33 [MPa] | 19,000 | 19,000 |
| ν23 | 0.34 | 0.2 |
| ν31 | 0.20 | 0.2 |
| ν12 | 0.20 | 0.2 |
| G23 [MPa] | 7060 | 7917 |
| G31 [MPa] | 23,630 | 7917 |
| G12 [MPa] | 23,630 | 7917 |
| α11 [10−6/K] | −0.84 | 8 |
| α22 [10−6/K] | 7.2 | 1.8 |
| α33 [10−6/K] | 7.2 | 1.8 |
| Property | FEM [20] | In-House Code | Difference |
|---|---|---|---|
| Exx [GPa] | 54.32 | 51.97 | −4.3% |
| Eyy [GPa] | 54.32 | 51.97 | −4.3% |
| Ezz [GPa] | 54.32 | 51.97 | −4.3% |
| νyz | 0.094 | 0.10 | +3.8% |
| νzx | 0.094 | 0.10 | +3.8% |
| νxy | 0.094 | 0.10 | +3.8% |
| Gyz [GPa] | 10.40 | 12.30 | +18.3% |
| Gzx [GPa] | 10.40 | 12.30 | +18.3% |
| Gxy [GPa] | 10.40 | 12.30 | +18.3% |
| Property | Yarn Architecture | ||
|---|---|---|---|
| 3-D Orthogonal | 4-D In-Plane | 4-D Diagonal | |
| Exx [MPa] | 50,890 | 58,313 | 30,569 |
| Eyy [MPa] | 50,890 | 31,306 | 30,569 |
| Ezz [MPa] | 50,890 | 41,880 | 30,576 |
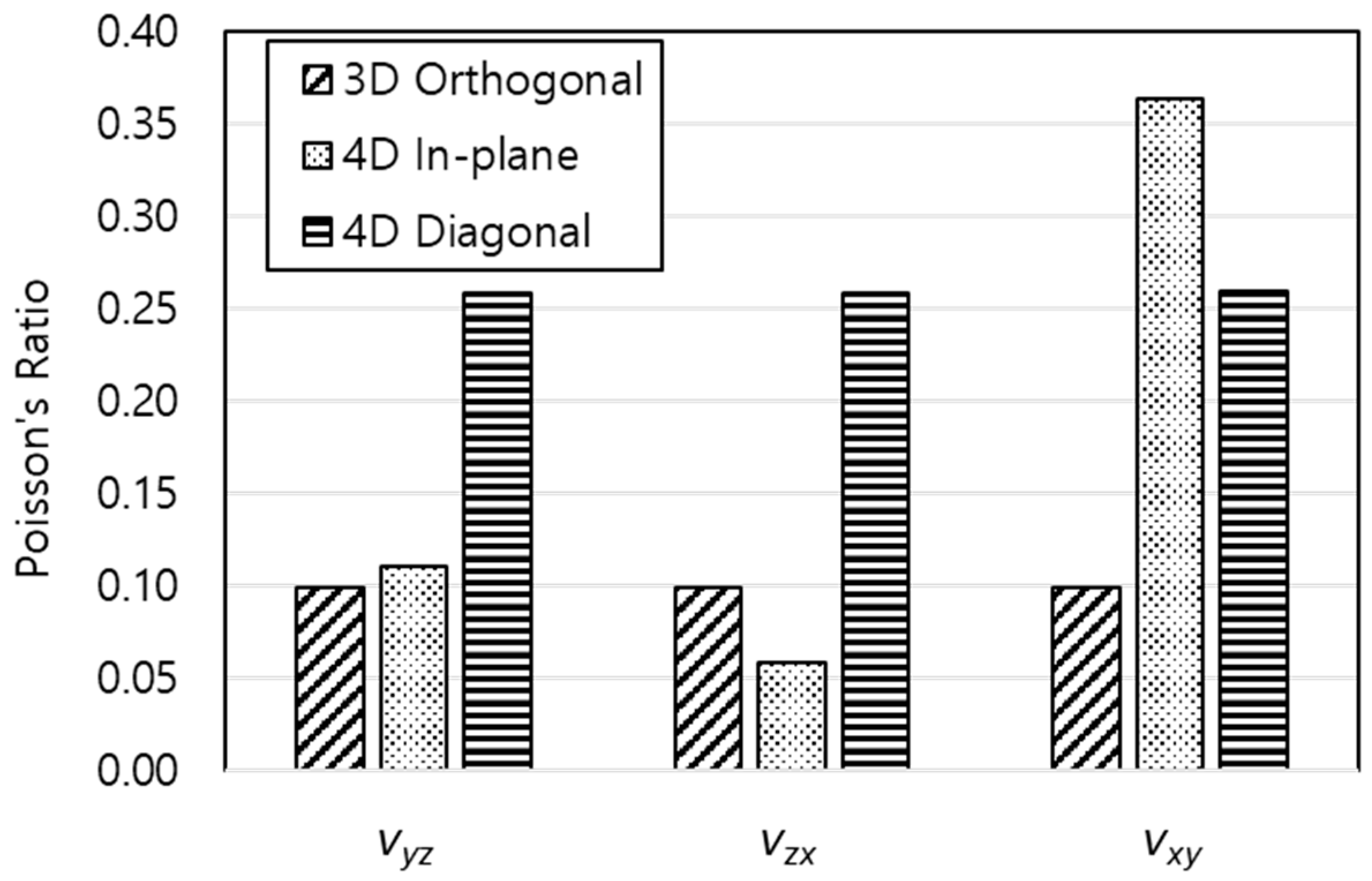
| νyz | 0.10 | 0.11 | 0.26 |
| νzx | 0.10 | 0.06 | 0.26 |
| νxy | 0.10 | 0.36 | 0.26 |
| Gyz [MPa] | 12,152 | 10,722 | 19,450 |
| Gzx [MPa] | 12,152 | 12,891 | 19,450 |
| Gxy [MPa] | 12,152 | 20,143 | 19,454 |
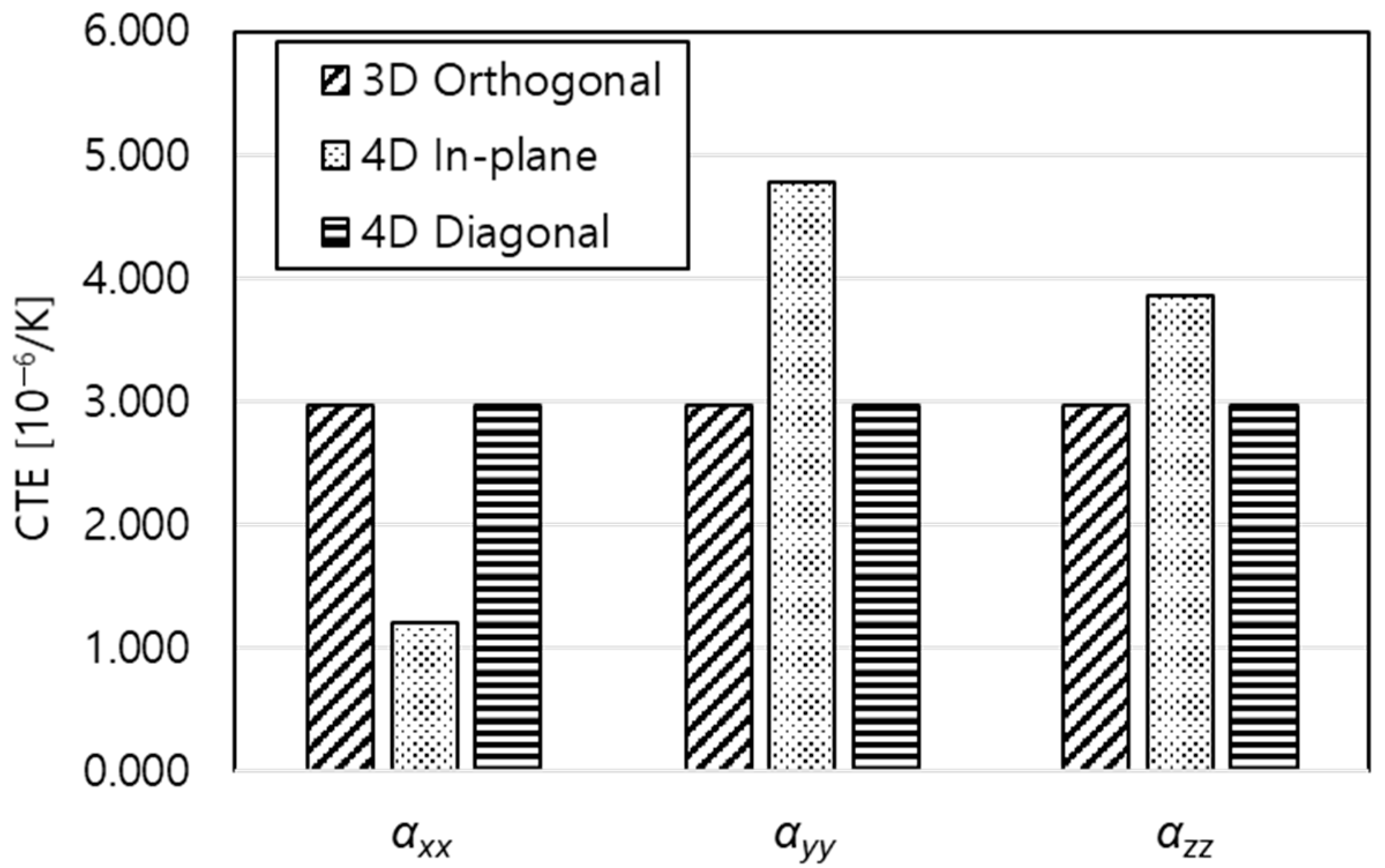
| αxx [10−6/K] | 2.961 | 1.205 | 2.968 |
| αyy [10−6/K] | 2.961 | 4.774 | 2.968 |
| αzz [10−6/K] | 2.961 | 3.862 | 2.968 |
| Property | Yarn Architecture | ||
|---|---|---|---|
| 3-D Orthogonal (Vf = 58.9%) | 4-D In-Plane (Vf = 41.5%) | 4-D Diagonal (Vf = 68.0%) | |
| Exx [MPa] | 63,937 | 58,313 | 37,837 |
| Eyy [MPa] | 63,937 | 31,306 | 37,837 |
| Ezz [MPa] | 63,937 | 41,880 | 37,848 |
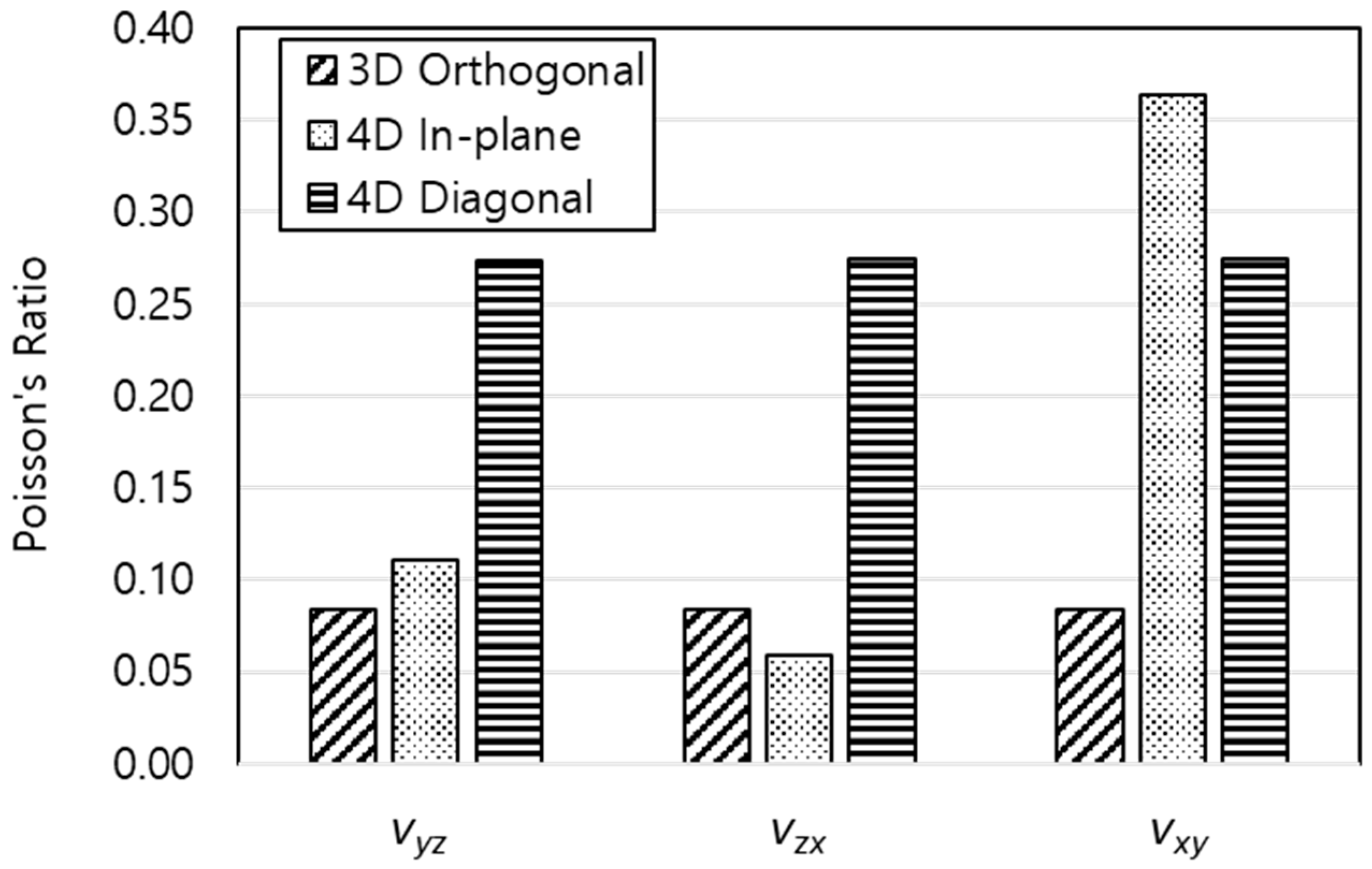
| νyz | 0.08 | 0.11 | 0.27 |
| νzx | 0.08 | 0.06 | 0.27 |
| νxy | 0.08 | 0.36 | 0.27 |
| Gyz [MPa] | 13,919 | 10,722 | 26,842 |
| Gzx [MPa] | 13,919 | 12,891 | 26,842 |
| Gxy [MPa] | 13,919 | 20,143 | 26,848 |
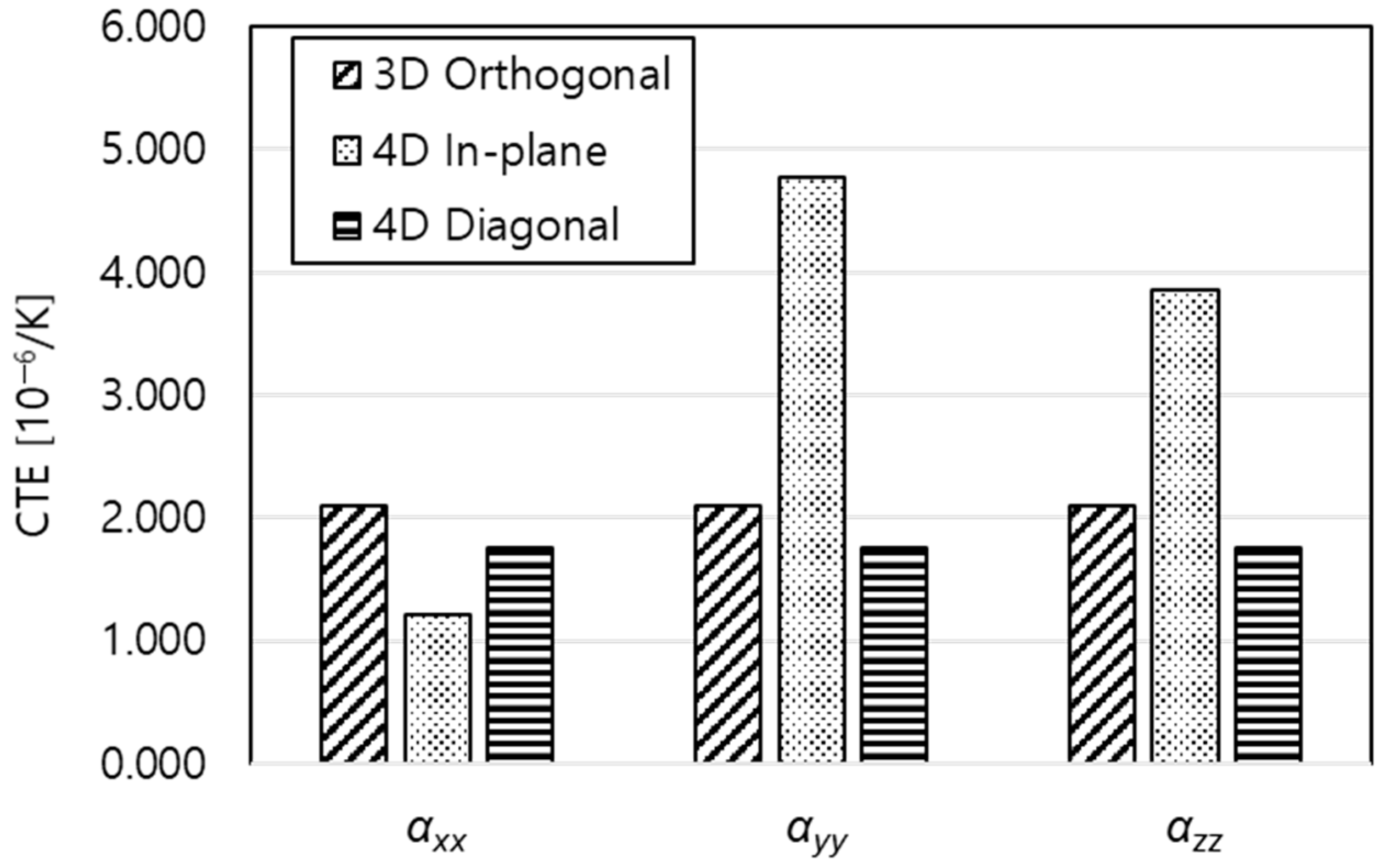
| αxx [10−6/K] | 2.094 | 1.205 | 1.748 |
| αyy [10−6/K] | 2.094 | 4.774 | 1.748 |
| αzz [10−6/K] | 2.094 | 3.862 | 1.748 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.; Kim, Y. A Thermo-Mechanical Properties Evaluation of Multi-Directional Carbon/Carbon Composite Materials in Aerospace Applications. Aerospace 2022, 9, 461. https://doi.org/10.3390/aerospace9080461
Kim M, Kim Y. A Thermo-Mechanical Properties Evaluation of Multi-Directional Carbon/Carbon Composite Materials in Aerospace Applications. Aerospace. 2022; 9(8):461. https://doi.org/10.3390/aerospace9080461
Chicago/Turabian StyleKim, Myungjun, and Yongha Kim. 2022. "A Thermo-Mechanical Properties Evaluation of Multi-Directional Carbon/Carbon Composite Materials in Aerospace Applications" Aerospace 9, no. 8: 461. https://doi.org/10.3390/aerospace9080461
APA StyleKim, M., & Kim, Y. (2022). A Thermo-Mechanical Properties Evaluation of Multi-Directional Carbon/Carbon Composite Materials in Aerospace Applications. Aerospace, 9(8), 461. https://doi.org/10.3390/aerospace9080461






