Will Gold Prices Persist Post Pandemic Period? An Econometric Evidence
Abstract
:1. Introduction
2. Literature Review
Indian Gold Market
3. Discussion
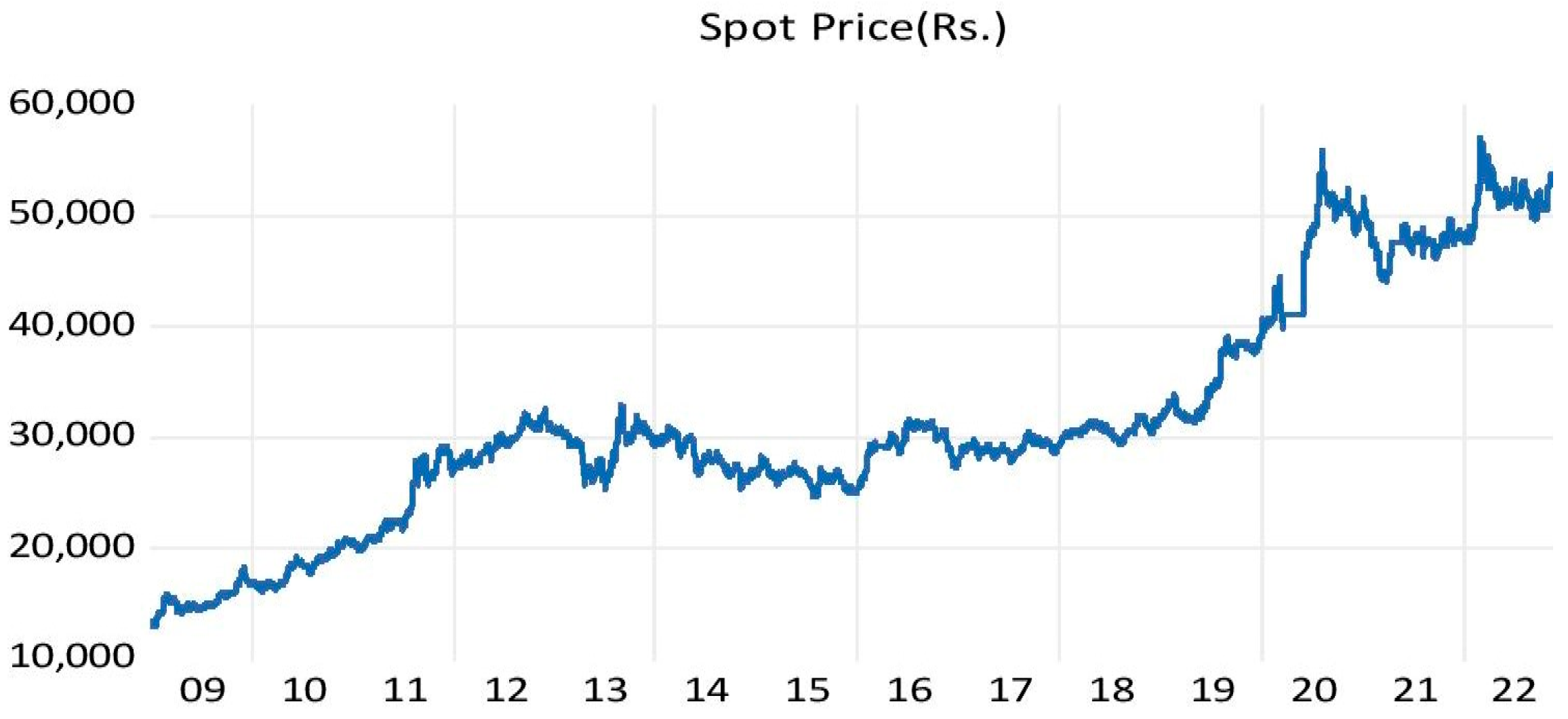
3.1. Sample Data
3.2. Preliminary Diagnostics
3.2.1. Stationarity
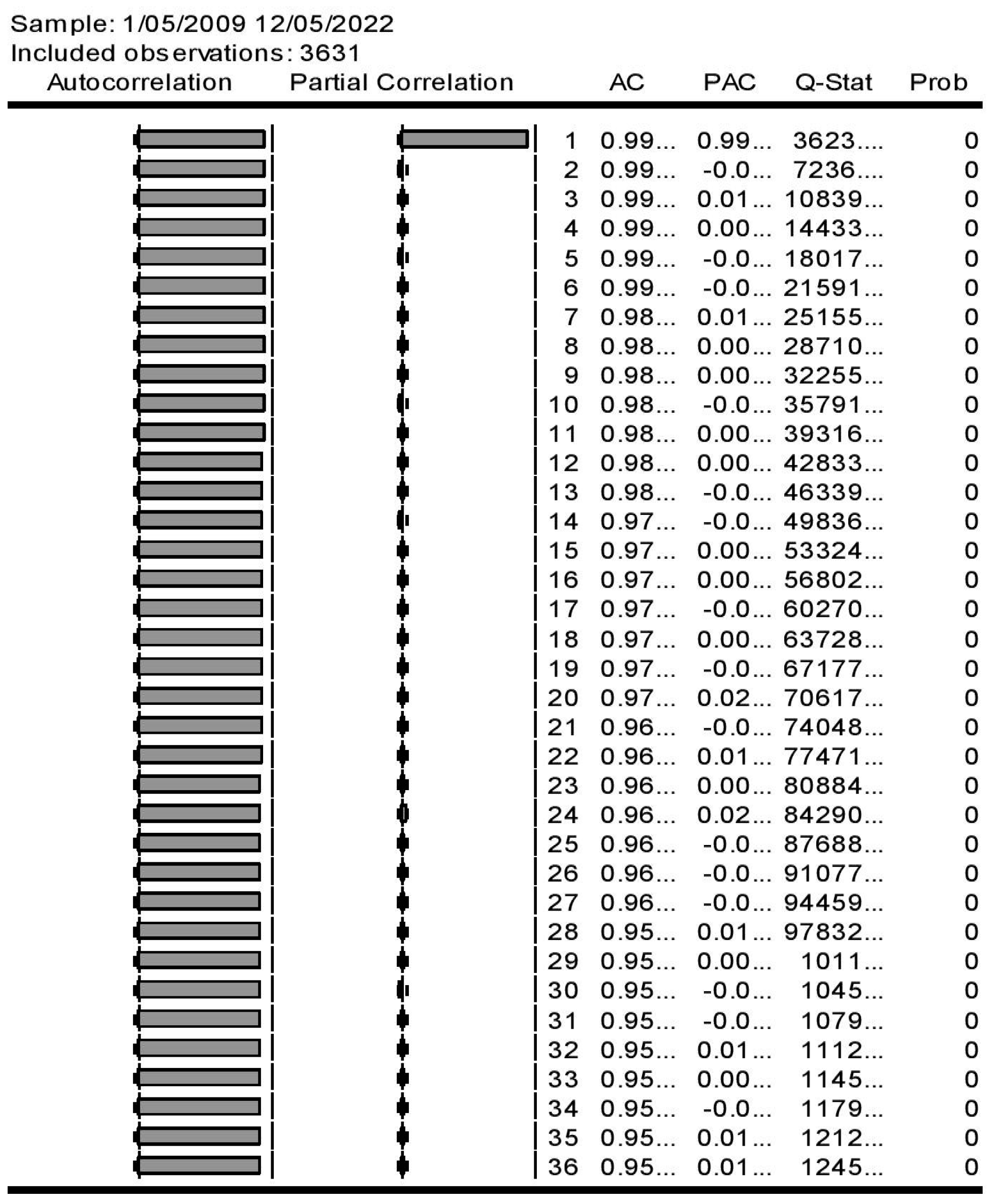
3.2.2. Autocorrelation
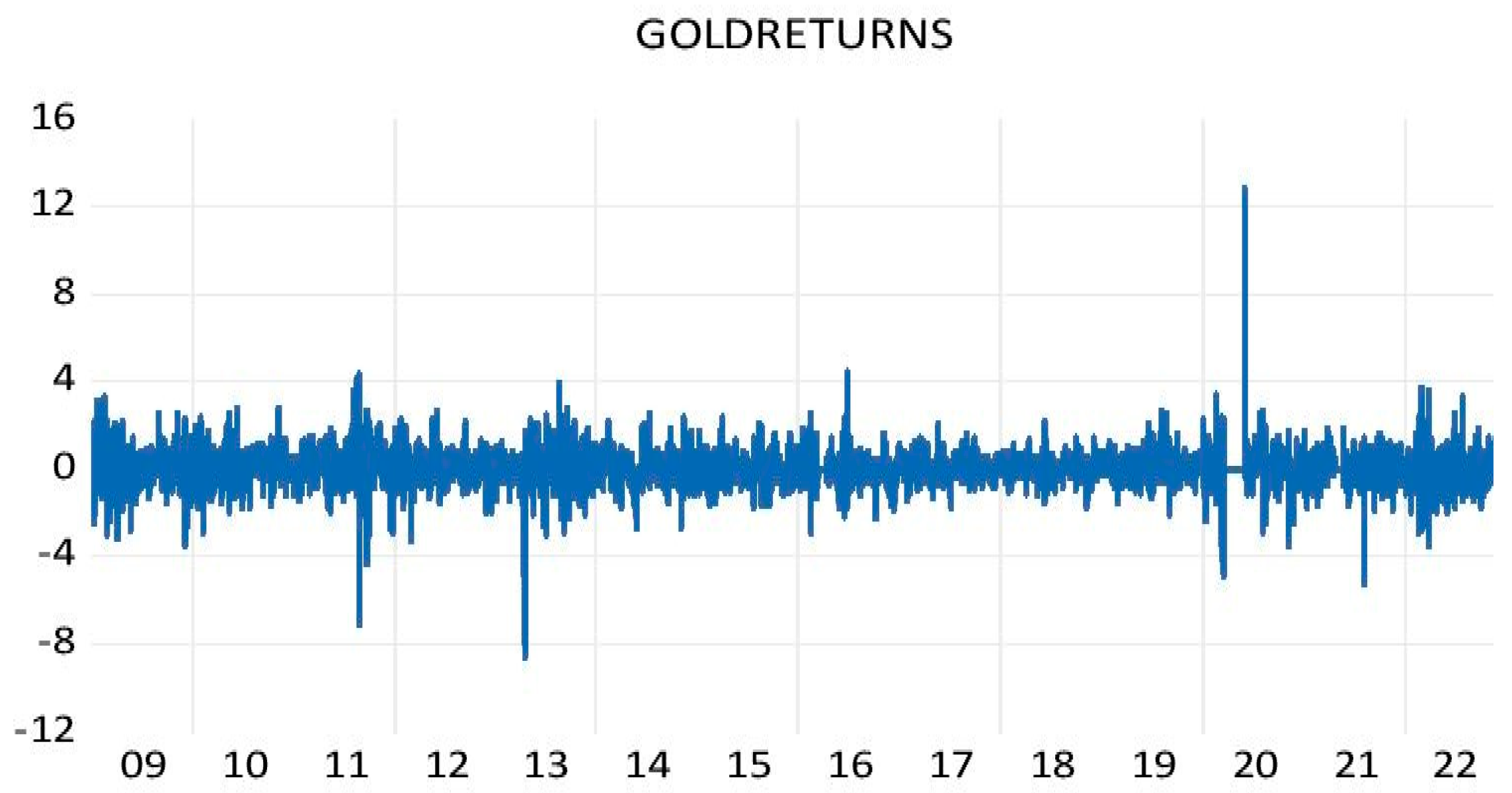
3.2.3. Volatility Clustering
3.2.4. Leptokurtic Distribution
3.3. Empirical Model
4. Results and Discussion
4.1. Descriptive Statistics
4.2. Preliminary Diagnostics Results
4.3. Stationarity Results of Gold Spot Price
4.4. Empirical Model Results
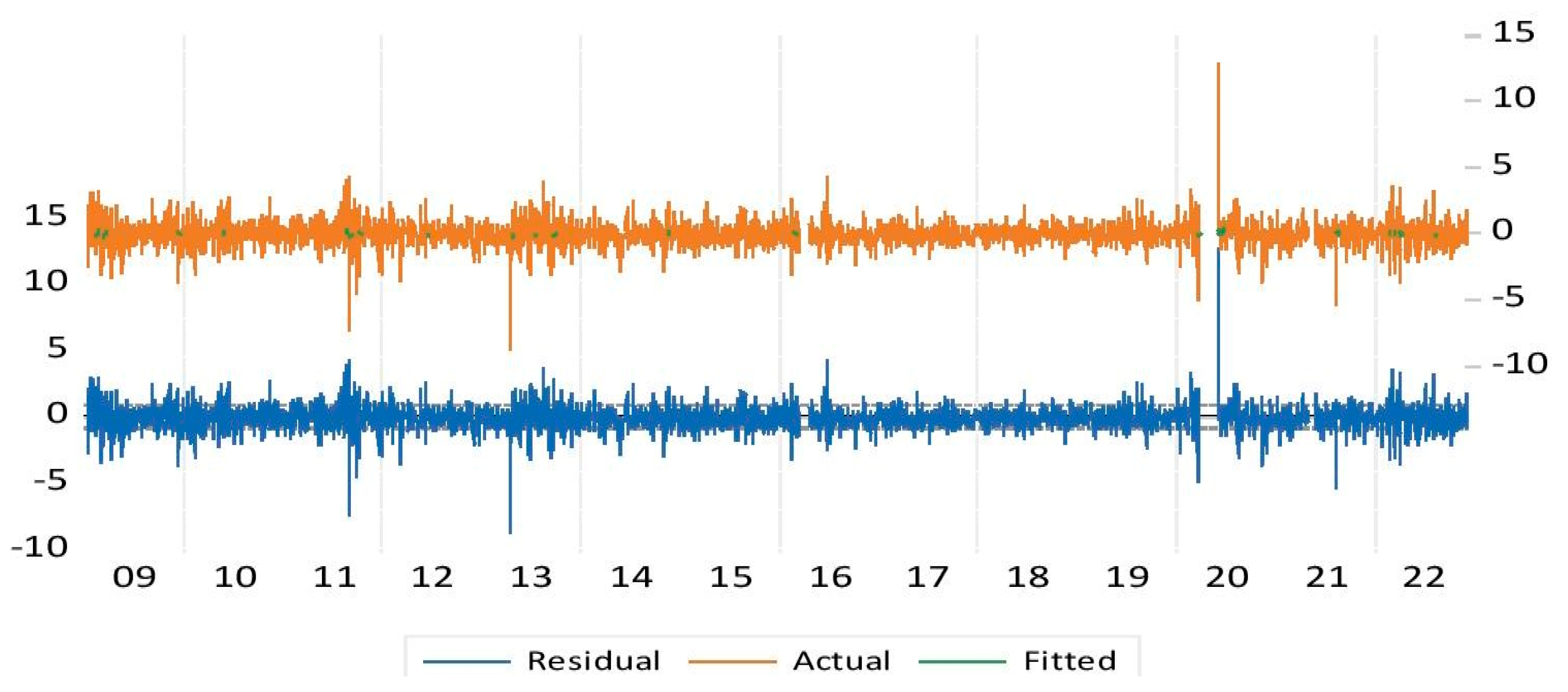
4.5. Residual Diagnostics of the Empirical Model
4.6. Engle-Ng Sign-Bias Test
4.7. Coefficient Diagnostics of the Empirical Model
4.8. Forecasting of Gold Price Using Empirical Model
5. Conclusions
5.1. Conclusion
5.2. Practical Implication
5.3. Limitations and Future Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Agung, Gusti Ngurah. 2011. Time Series Data Analysis Using EViews. Singapore: John Wiley & Sons. [Google Scholar]
- Akhtaruzzaman, Md, Sabri Boubaker, Brian M. Lucey, and Ahmet Sensoy. 2021. Is gold a hedge or a safe-haven asset in the COVID–19 crisis? Economic Modelling 102: 105588. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef] [Green Version]
- Bouri, Elie, Anshul Jain, Pratap Chandra Biswal, and David Roubaud. 2017. Cointegration and nonlinear causality amongst gold, oil, and the Indian stock market: Evidence from implied volatility indices. Resources Policy 52: 201–6. [Google Scholar] [CrossRef]
- Brooks, Chris. 2008. RATS Handbook to Accompany Introductory Econometrics for Finance. Cambridge: Cambridge University Press. [Google Scholar]
- Cao, Guangxi, Yingchao Zhao, and Yan Han. 2015. Asymmetric statistical features of the Chinese domestic and international gold price fluctuation. International Journal of Modern Physics B 29: 1550113. [Google Scholar] [CrossRef]
- Čermák, Michal, Karel Malec, and Mansoor Maitah. 2017. Price Volatility Modelling–Wheat: GARCH Model Application. AGRIS On-Line Papers in Economics and Informatics 9: 15–24. [Google Scholar] [CrossRef] [Green Version]
- Cheema, Muhammad A., Robert Faff, and Kenneth R. Szulczyk. 2022. The 2008 global financial crisis and COVID-19 pandemic: How safe are the safe haven assets? International Review of Financial Analysis 83: 102316. [Google Scholar] [CrossRef]
- Dey, Shubhasis, and Aravind Sampath. 2020. Returns, volatility and spillover–A paradigm shift in India? The North American Journal of Economics and Finance 52: 101110. [Google Scholar] [CrossRef]
- Dey, Shubhasis, and Aravind Sampath. 2018. Dynamic linkages between gold and equity prices: Evidence from Indian financial services and information technology companies. Finance Research Letters 25: 41–6. [Google Scholar] [CrossRef]
- Francq, Christian, and Jean-Michel Zakoian. 2020. Virtual Historical Simulation for estimating the conditional VaR of large portfolios. Journal of Econometrics 217: 356–80. [Google Scholar] [CrossRef] [Green Version]
- Gharib, Cheima, Salma Mefteh-Wali, and Sami Ben Jabeur. 2021. The bubble contagion effect of COVID-19 outbreak: Evidence from crude oil and gold markets. Finance Research Letters 38: 101703. [Google Scholar] [CrossRef]
- Gokmenoglu, Korhan, and Negar Fazlollahi. 2015. The interactions among gold, oil, and stock market: Evidence from S&P500. Procedia Economics and Finance 25: 478–88. [Google Scholar]
- Gujarati, Damodar. 2011. Econometrics by Example. New York: Palgrave Macmillan, vol. 1. [Google Scholar]
- Handika, Rangga, and Dony Abdul Chalid. 2018. The predictive power of log-likelihood of GARCH volatility. Review of Accounting and Finance 17: 482–97. [Google Scholar] [CrossRef]
- Hansen, Peter Reinhard, and Asger Lunde. 2006. Consistent ranking of volatility models. Journal of Econometrics 131: 97–121. [Google Scholar] [CrossRef]
- He, Xie, Tetsuya Takiguchi, Tadahiro Nakajima, and Shigeyuki Hamori. 2020. Spillover effects between energies, gold, and stock: The United States versus China. Energy & Environment 31: 1416–47. [Google Scholar] [CrossRef]
- Irene, Yanne, Madona Yunita Wijaya, and Aisyah Muhayani. 2020. World Gold Price Forecast using APARCH, EGARCH and TGARCH Model. InPrime: Indonesian Journal of Pure and Applied Mathematics 2: 71–78. [Google Scholar] [CrossRef]
- Jain, Anshul, and Pratap Chandra Biswal. 2016. Dynamic linkages among oil price, gold price, exchange rate, and stock market in India. Resources Policy 49: 179–85. [Google Scholar] [CrossRef]
- Ji, Qiang, Dayong Zhang, and Yuqian Zhao. 2020. Searching for safe-haven assets during the COVID-19 pandemic. International Review of Financial Analysis 71: 101526. [Google Scholar] [CrossRef]
- Kumar, Dilip, and S. Maheswaran. 2013. Correlation transmission between crude oil and Indian markets. South Asian Journal of Global Business Research 2: 211–29. [Google Scholar] [CrossRef]
- Li, Yong, Wei-Ping Huang, and Jie Zhang. 2013. Forecasting volatility in the Chinese stock market under model uncertainty. Economic Modelling 35: 231–34. [Google Scholar] [CrossRef]
- Liu, Guo-Dong, and Chi-Wei Su. 2019. The dynamic causality between gold and silver prices in China market: A rolling window bootstrap approach. Finance Research Letters 28: 101–6. [Google Scholar] [CrossRef]
- Lucey, Brian M., and Edel Tully. 2006. The evolving relationship between gold and silver 1978–2002: Evidence from a dynamic cointegration analysis: A note. Applied Financial Economics Letters 2: 47–53. [Google Scholar] [CrossRef]
- Meister, Alexander, and Jens-Peter Kreiß. 2016. Statistical inference for nonparametric GARCH models. Stochastic Processes and Their Applications 126: 3009–40. [Google Scholar] [CrossRef]
- Mishra, Bibhuti Ranjan, Ashis Kumar Pradhan, Aviral Kumar Tiwari, and Muhammad Shahbaz. 2019. The dynamic causality between gold and silver prices in India: Evidence using time-varying and non-linear approaches. Resources Policy 62: 66–76. [Google Scholar] [CrossRef]
- Mishra, Ashwini Kumar, Kshitish Ghate, Jayashree Renganathan, Joushita Kennet, and Nilay Pradeep Rajderkar. 2022. Rolling, recursive evolving and asymmetric causality between crude oil and gold prices: Evidence from an emerging market. Resources Policy 75: 102474. [Google Scholar] [CrossRef]
- Mroua, Mourad, and Lotfi Trabelsi. 2020. Causality and dynamic relationships between exchange rate and stock market indices in BRICS countries: Panel/GMM and ARDL analyses. Journal of Economics, Finance and Administrative Science 25: 395–412. [Google Scholar] [CrossRef]
- Ping, Pung Yean, Nor Hamizah Miswan, and Maizah Hura Ahmad. 2013. Forecasting Malaysian gold using GARCH model. Applied Mathematical Sciences 7: 2879–84. [Google Scholar] [CrossRef]
- Pradhan, Ashis Kumar, Bibhuti Ranjan Mishra, Aviral Kumar Tiwari, and Shawkat Hammoudeh. 2020. Macroeconomic factors and frequency domain causality between gold and silver returns in India. Resources Policy 68: 101744. [Google Scholar] [CrossRef] [PubMed]
- Qin, Meng, Chi-Wei Su, Ran Tao, and Muhammad Umar. 2020. Is factionalism a push for gold price? Resources Policy 67: 101679. [Google Scholar] [CrossRef]
- Rastogi, Shailesh, Adesh Doifode, Jagjeevan Kanoujiya, and Satyendra Pratap Singh. 2021. Volatility integration of gold and crude oil prices with the interest rates in India. South Asian Journal of Business Studies. [Google Scholar] [CrossRef]
- Salisu, Afees A., Xuan Vinh Vo, and Adedoyin Lawal. 2021. Hedging oil price risk with gold during COVID-19 pandemic. Resources Policy 70: 101897. [Google Scholar] [CrossRef]
- Sami, Janesh. 2021. Has the long-run relationship between gold and silver prices really disappeared? Evidence from an emerging market. Resources Policy 74: 102292. [Google Scholar] [CrossRef]
- Sharma, Prateek. 2015. Forecasting stock index volatility with GARCH models: International evidence. Studies in Economics and Finance 32: 445–63. [Google Scholar] [CrossRef]
- Singhal, Shelly, Sangita Choudhary, and Pratap Chandra Biswal. 2019. Return and volatility linkages among International crude oil price, gold price, exchange rate and stock markets: Evidence from Mexico. Resources Policy 60: 255–61. [Google Scholar] [CrossRef]
- Sopipan, Nop, Pairote Sattayatham, and Bhusana Premanode. 2012. Forecasting volatility of gold price using markov regime switching and trading strategy. Journal of Mathematical Finance 2: 121. [Google Scholar] [CrossRef] [Green Version]
- Su, Chi-Wei, Meng Qin, Ran Tao, and Xiaoyan Zhang. 2020. Is the Status of Gold Threatened by Bitcoin. Ekonomska Istrazivanja-Economic Research 33: 420–37. [Google Scholar] [CrossRef]
- Teräsvirta, Timo. 2009. An introduction to univariate GARCH models. In Handbook of Financial Time Series. Berlin and Heidelberg: Springer, pp. 17–42. [Google Scholar]
- Trabelsi, Nader, Giray Gozgor, Aviral Kumar Tiwari, and Shawkat Hammoudeh. 2021. Effects of price of gold on Bombay stock exchange sectoral indices: New evidence for portfolio risk management. Research in International Business and Finance 55: 101316. [Google Scholar] [CrossRef]
- Wilhelmsson, Anders. 2006. GARCH forecasting performance under different distribution assumptions. Journal of Forecasting 25: 561–78. [Google Scholar] [CrossRef] [Green Version]
- Yousaf, Imran, Elie Bouri, Shoaib Ali, and Nehme Azoury. 2021. Gold against asian stock markets during the COVID-19 outbreak. Journal of Risk and Financial Management 14: 186. [Google Scholar] [CrossRef]
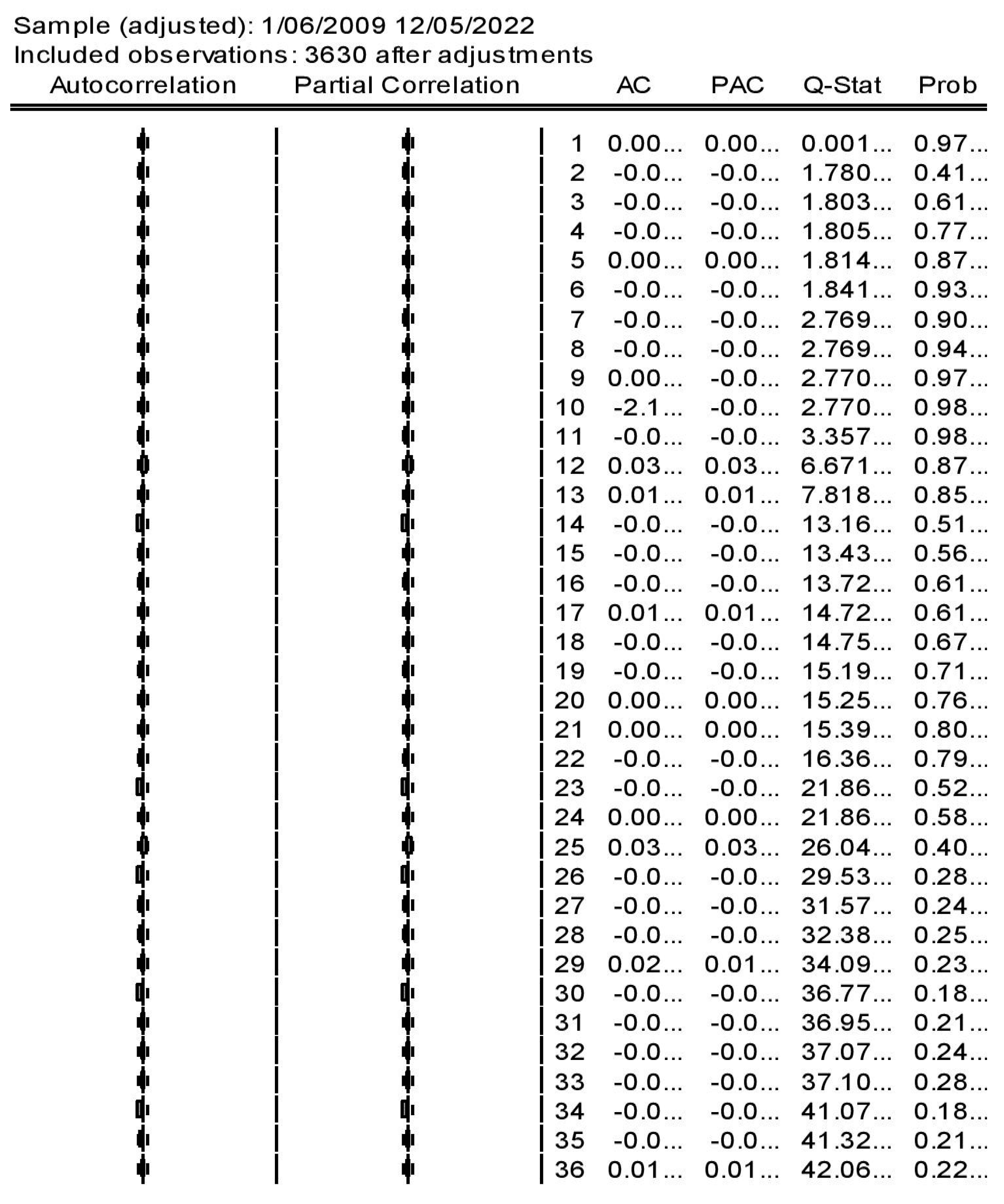

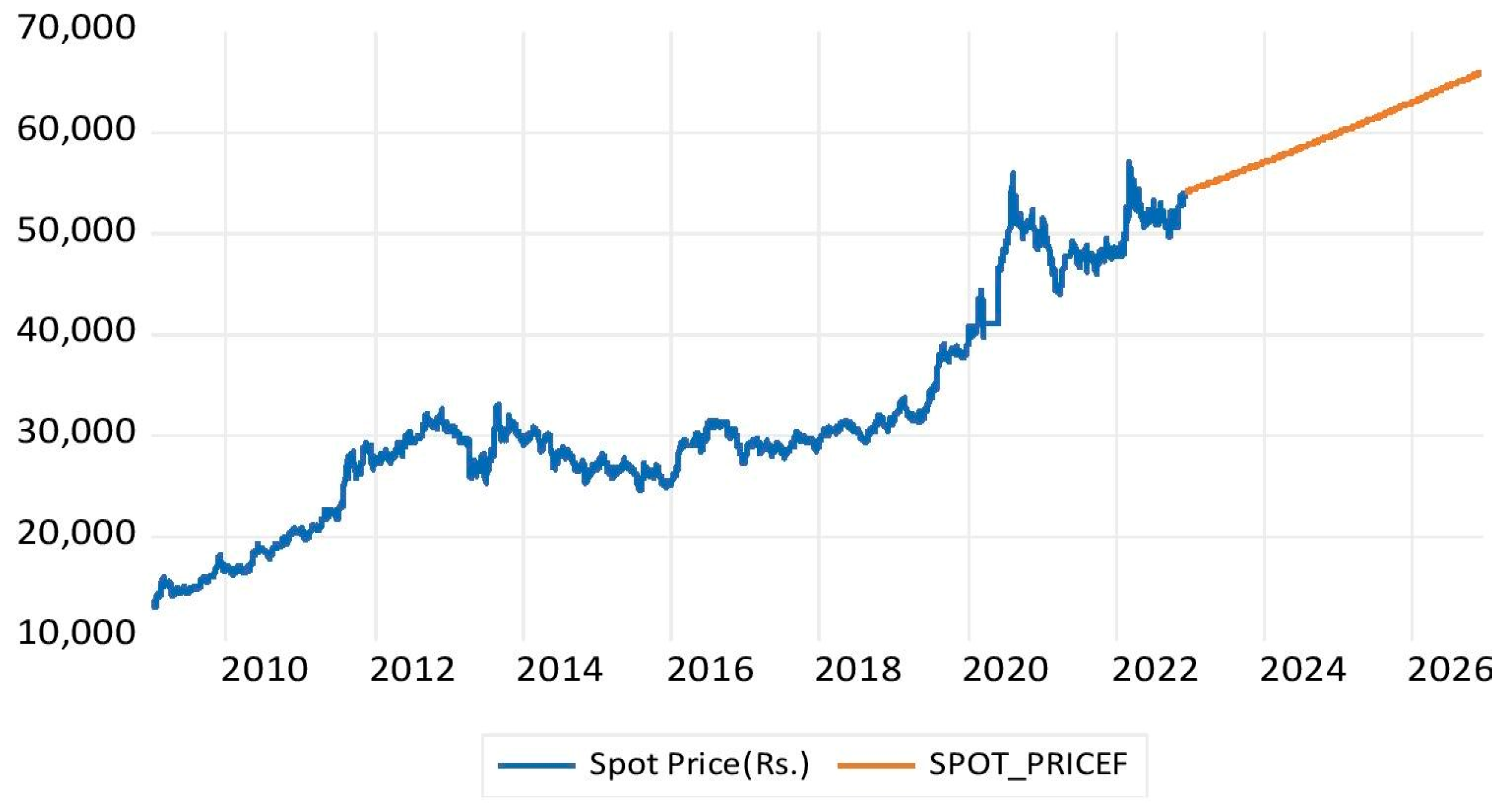
| Parameter | SPOT_PRICE | GOLD RETURNS |
|---|---|---|
| Mean | 31,321.15 | 0.038384 |
| Median | 29,442.00 | 0.000000 |
| Maximum | 57,006.00 | 12.84899 |
| Minimum | 12,935.00 | −8.65765 |
| Std. Dev. | 10,289.30 | 0.864064 |
| Skewness | 0.615776 | 0.465281 |
| Kurtosis | 2.713009 | 22.87019 |
| Jarque-Bera | 241.9281 | 59,848.19 |
| Probability | 0.000000 | 0.000000 |
| Sum | 1.14 × 108 | 139.33 |
| Sum Sq. Dev. | 3.84 × 1011 | 2709.43 |
| Observations | 3631 | 3630 |
| Parameter | t-Statistic | Prob. |
|---|---|---|
| ADF test statistic | −1.6560 | 0.7704 |
| Parameter | t-Statistic | Prob. |
|---|---|---|
| Augmented Dickey-Fuller test statistic | −59.12637 | 0.0000 |
| Variable | Coefficient | Std.Error | t-Statistics | Prob. |
|---|---|---|---|---|
| C | 0.038332 | 0.016436 | 2.332276 | 0.01974 |
| AR (1) | 0.018191 | 0.011694 | 1.555674 | 0.11987 |
| AR (4) | 0.040725 | 0.012808 | 1.555674 | 0.00148 |
| AR (5) | 0.021245 | 0.012962 | 1.639034 | 0.10129 |
| AR (9) | 0.032531 | 0.013796 | 2.358085 | 0.01842 |
| SIGMASQ | 7.44 × 10−1 | 5.32 × 10−3 | 139.6852 | 0 |
| Log likelihood | −4613.19 | |||
| Durbin-Watson stat | 1.997477 |
| Parameter | t-Statistic | Prob. |
|---|---|---|
| Augmented Dickey-Fuller test statistic | −60.23087 | 0.0000 |
| Parameter | Values |
|---|---|
| F-statistic | 8.796150 |
| Obs*R-squared | 8.779708 |
| Prob. F (1,3627) | 0.00 |
| Prob. Chi-Square (1) | 0.00 |
| Parameter | ARCH (1,1) | GARCH (1,1) | T-GARCH (1,1) | E-GARCH (1,1) | A-PARCH (1,1) | GARCH-M (1,1) | |
|---|---|---|---|---|---|---|---|
| Mean Equation | Cons | 0.000366 [2.91848] (0.0035) ** | 0.000357 [0.87258] (0.3829) | 0.000219 [1.980607] (0.0476) ** | 0.000194 [1.74757] (0.0805) | 2.14 × 10−13 [6.53 × 10−7] (1.000) | 9.85 × 10−5 [0.492086] (0.6227) |
| AR (L1) | 0.024542 [1.539131] (0.1238) | 0.018674 [0.42552] (0.6705) | 0.01406 [0.865835] (0.3866) | 0.015211 [0.98299] (0.3256) | 0.017636 [1.2269] (0.2198) | 0.014491 [0.887448] (0.3748) | |
| AR (L4) | 0.034794 [2.99912] (0.0027) | 0.038414 [0.96437] (0.3349) | 0.022871 [1.45061] (0.1469) | 0.018913 [1.2608] (0.2074) | 0.012163 [0.90949] (0.3631) | 0.022869 [1.443366] (0.1489) | |
| AR (L5) | 0.010359 [0.90528] (0.3653) | 0.02040 [0.52539] (0.5593) | 0.01724 [1.12007] (0.2627) | 0.016810 [1.12483] (0.2607) | 0.013325 [1.00919] (0.3129) | 0.018663 [1.202983] (0.2290) | |
| AR (L9) | 0.016263 [1.45578] (0.1455) | 0.02222 [0.61043] (0.5416) | 0.00784 [0.54424] (0.5863) | 0.008814 [0.61103] (0.5412) | −1.52 × 10−9 [−2.79 × 10−6] (1.000) | 0.008001 [0.553063] (0.5802) | |
| Returns | 0.016565 [0.564349] (0.5725) | ||||||
| Variance Equation | Cons ω0 | 4.29 × 10−5 [40.6538] (0.0000) *** | 6.40 × 10−5 [3.17916] (0.0015) ** | 3.45 × 10−6 [5.28347] (0.0000) *** | −0.65087 [−6.04593] (0.0000) *** | 0.000509 [1.65126] (0.0987) | 3.55 × 10−6 [5.2739] (0.0000) *** |
| ARCH (L1) α | 0.17139 [10.7971] (0.0000) *** | 0.14999 [2.82679] (0.0047) ** | 0.157632 [6.51693] (0.0000) *** | 0.17014 [9.236451] (0.000) *** | 0.137593 [11.04234] (0.0000) *** | 0.13040 [7.2246] (0.0000) *** | |
| GARCH(L1) β | 0.59999 [4.9962] (0.0000) *** | 0.842684 [47.00552] (0.0000) ** | 0.944671 [92.81759] (0.0000) *** | 0.893304 [96.8589] (0.0000) *** | 0.83816 [45.7931] (0.0000) *** | ||
| Leverage γ | −0.065202 [−2.601464] (0.0093) ** | 0.007397 [0.588514] (0.5704) | −0.1749490 [−2.73399] (0.0063) ** | ||||
| POWER δ | 0.690901 [8.134186] (0.0000) ** | ||||||
| Model Selection Indicators | Loglikelihood | 12,397.89 | 12,669.57 | 12,672.84 | 12,679.88 | 1,2749.71 | 12,669.81 |
| AIC | −6.843353 | −6.4439 | −6.994115 | −6.998001 | −7.036018 | −6.99244 | |
| SC | −6.829667 | −6.42859 | −6.977008 | −6.998089 | −7.017200 | −6.97533 | |
| HQ | −6.838477 | −6.43850 | −6.988020 | −6.991906 | −7.029314 | −6.98634 | |
| DW | 2.00 | 1.99 | 1.98 | 1.98 | 1.99 | 1.99 | |
| T-DIST.OFF | 3.23 (0.00) *** | 19.99 (0.00) *** | 3.75 (0.00) *** | 3.69 (0.0000) *** | 3.34 (0.0000) *** | 3.73 (0.0000) *** |
| F-statistic | 0.092139 | Prob. F (1,3618) | 0.7615 |
| Obs*R-squared | 0.092188 | Prob.Chi-Square (1) | 0.7614 |
| Parameter | t-Statistic | Prob. |
|---|---|---|
| Sign-Bias | 1.052600 | 0.2926 |
| Negative-Bias | −0.785975 | 0.4319 |
| Positive-Bias | 0.874395 | 0.3820 |
| Joint-Bias | 3.057096 | 0.3830 |
| Variable | Statistic | 1% Crit | 5%Crit |
|---|---|---|---|
| Cons | 0.276755 | 0.748 | 0.470 |
| AR (L1) | 0.094857 | 0.748 | 0.470 |
| AR (L4) | 0.438079 | 0.748 | 0.470 |
| AR (L5) | 0.375021 | 0.748 | 0.470 |
| AR (L9) | 0.275547 | 0.748 | 0.470 |
| Cons ω0 | 457.8123 | 0.748 | 0.470 |
| RESID (−1)2 | 142.5651 | 0.748 | 0.470 |
| DIST-PARAM | 25.6157 | 0.748 | 0.470 |
| Joint | 578.3226 | 2.820 | 2.320 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumaraswamy, S.; Abdulla, Y.; Panigrahi, S.K. Will Gold Prices Persist Post Pandemic Period? An Econometric Evidence. Int. J. Financial Stud. 2023, 11, 8. https://doi.org/10.3390/ijfs11010008
Kumaraswamy S, Abdulla Y, Panigrahi SK. Will Gold Prices Persist Post Pandemic Period? An Econometric Evidence. International Journal of Financial Studies. 2023; 11(1):8. https://doi.org/10.3390/ijfs11010008
Chicago/Turabian StyleKumaraswamy, Sumathi, Yomna Abdulla, and Shrikant Krupasindhu Panigrahi. 2023. "Will Gold Prices Persist Post Pandemic Period? An Econometric Evidence" International Journal of Financial Studies 11, no. 1: 8. https://doi.org/10.3390/ijfs11010008
APA StyleKumaraswamy, S., Abdulla, Y., & Panigrahi, S. K. (2023). Will Gold Prices Persist Post Pandemic Period? An Econometric Evidence. International Journal of Financial Studies, 11(1), 8. https://doi.org/10.3390/ijfs11010008






