Microcredit Pricing Model for Microfinance Institutions under Basel III Banking Regulations †
Abstract
:1. Introduction
2. Data and Variables
2.1. Sample Selection
2.2. Dependent Variable
2.3. Independent Variables
- ∆VMi,j: rate of change of the macroeconomic variable under consideration.
- VM: macroeconomic variable under consideration.
- i: m time of granting the loan.
- j: duration of the microcredit.
3. Research Methodology and Experimental Design
3.1. Binary Logistic Regression Model
3.2. Artificial Neural Network Model
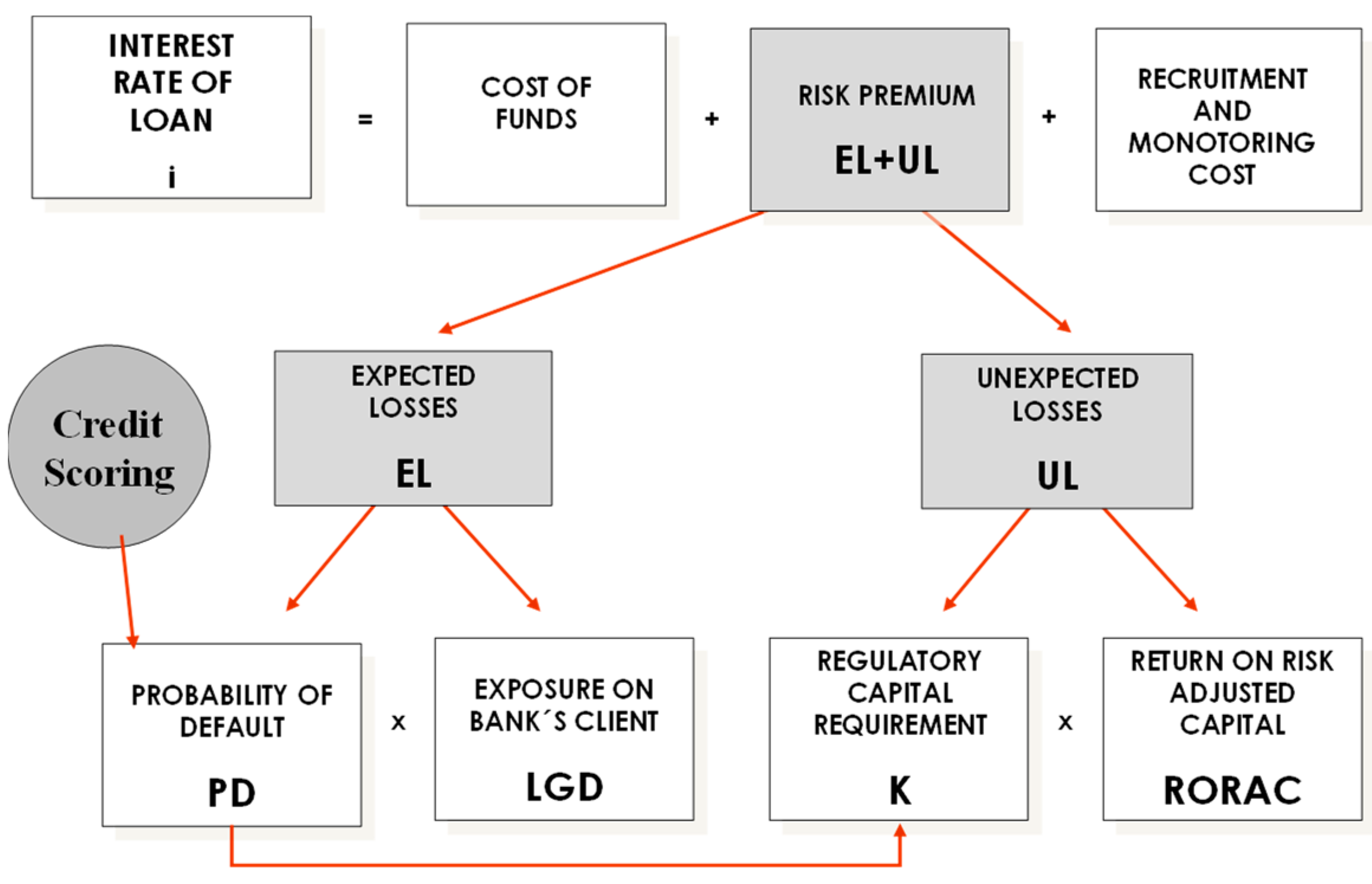
3.3. Internal Rating Based Model Design
- K: Capital requirement.
- PD: Probability of default, derived from the credit rating.
- ρ (PD): Correlation coefficient.
- LGD: Loss given default
- EAD: Exposure at default.
- RWA: Risk-weighted assets.
- EL: Expected loss.
- G (0.999): Inverse of the normally cumulative distribution function = −3.090.
- G (PD): Inverse of the normally cumulative distribution function in PD.
- EL: Expected loss (covered by provision)
- UL: Unexpected loss (covered by the capital requirement)
- K: Capital requirement
- r: Risk-adjusted return on equity for the sector
- FR: Financial income
- FC: Financial costs
- OC: Operational costs
- EL: Expected loss
- IC: Capital income
- K: Capital requirement
- i: Interest rate
- TR: Tax rate
- EAD: Exposure at default
- Rf: Risk-free interest rate
4. Results and Discussion
4.1. Comparison of Default Probability Models Accuracy
4.2. Application of Pricing Strategy
4.3. Practical and Policy Implications
4.4. Limitations of the Research
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abdullah, Shahnaz, and Shakil Quayes. 2016. Do women borrowers augment financial performance of MFIs? Applied Economics 48: 5593–604. [Google Scholar] [CrossRef]
- Aguilar, Giovanna, and Jhonatan Portilla. 2019. Technical change in the Peruvian regulated microfinance sector. Latin American Business Review 20: 5–35. [Google Scholar] [CrossRef]
- Al-Azzam, Moh’d, and Christopher Parmeter. 2021. Competition and microcredit interest rates: International evidence. Empirical economics 60: 829–68. [Google Scholar] [CrossRef]
- Altinbas, Hazar, and Goktug Cenk Akkaya. 2017. Improving the performance of statistical learning methods with a combined meta-heuristic for consumer credit risk assessment. Risk Management 19: 255–80. [Google Scholar] [CrossRef]
- Asencios, Rodrigo, Christian Asencios, and Efrain Ramos. 2023. Profit scoring for credit unions using the multilayer perceptron, XGBoost and TabNet algorithms: Evidence from Peru. Expert Systems with Applications 213: 119201. [Google Scholar] [CrossRef]
- Badr El Din, A. Ibrahim. 2022. Lessons for African microfinance providers and regulators in the aftermath of COVID-19. Enterprise Development & Microfinance 33: 182–91. [Google Scholar] [CrossRef]
- Balushi, Yasmeen Al, Stuart Locke, and Zakaria Boulanouar. 2018. Islamic financial decision-making among SMEs in the Sultanate of Oman: An adaption of the theory of planned behaviour. Journal of Behavioral and Experimental Finance 20: 30–38. [Google Scholar] [CrossRef]
- Bank of Guatemala. 2021. Desempeño Macroeconómico Reciente y Perspectivas. December 3. Available online: https://www.banguat.gob.gt/sites/default/files/banguat/Publica/conferencias/cbanguat787.pdf (accessed on 20 April 2024).
- Basel Committee on Banking Supervision, BCBS. 2017. Basel III: Finalising Post-Crisis Reforms. Bank for International Settlements. Available online: https://www.bis.org/bcbs/publ/d424.pdf (accessed on 15 April 2024).
- Beisland, Leif Atle, Bert D’Espallier, and Roy Mersland. 2019. The Commercialization of the MicrofinanceIndustry: Is There a “Personal Mission Drift’ Among Credit Officers? Journal of Business Ethics 158: 119–34. [Google Scholar] [CrossRef]
- Bettoni, Luis, Marcelo Santos, and Gilberto Oliveira Filho. 2023. The impact of microcredit on small firms in Brazil: A potential to promote investment, growth and inclusion. Journal of Policy Modeling 45: 592–608. [Google Scholar] [CrossRef]
- Bishop, Christopher Michael. 1995. Neural Networks for Pattern Recognition, 1st ed. New York: Oxford University Press. [Google Scholar]
- Blanco, Antonio, Rafael Pino-Mejías, Juan Lara, and Salvador Rayo. 2013. Credit scoring models for the microfinance industry using neural networks: Evidence from Peru. Expert Systems with Applications 40: 356–64. [Google Scholar] [CrossRef]
- Blanco-Oliver, Antonio, Ana Irimia-Diéguez, and María Dolores Oliver-Alfonso. 2016. Hybrid model using logit and nonparametric methods for predicting micro-entity failure. Investment Management and Financial Innovations 13: 35–46. [Google Scholar] [CrossRef] [PubMed]
- Blanco-Oliver, Antonio, Antonio Samaniego, and María José Palacin-Sanchez. 2024. How do loan officer-borrower gender-driven behavioural differences impact on the microfinance lending market? Borsa Istanbul Review 24: 435–48. [Google Scholar] [CrossRef]
- Brau, James C., Shon Hiatt, and Warner Woodworth. 2009. Evaluating impacts of microfinance institutions using Guatemalan data. Managerial Finance 35: 953–74. [Google Scholar] [CrossRef]
- Castro, José Antonio Morales, Patricia Margarita Espinosa Jiménez, and Marcela Rojas Ortega. 2022. Efecto de las variables macroeconómicas en los índices de morosidad de los bancos en México, durante el periodo COVID-19 versus el periodo previo. RAN-Revista Academia & Negocios 8: 55–70. [Google Scholar] [CrossRef]
- Cepeda, Isabel, Maricruz Lacalle-Calderon, and Miguel Torralba. 2021. Microfinance and Violence Against Women in Rural Guatemala. Journal of Interpersonal Vilolence 36: 1391–413. [Google Scholar] [CrossRef]
- Concha, Emerson Toledo. 2009. Microfinanzas: Diagnóstico del sector de la micro y pequeña empresa y su tecnología crediticia. Contabilidad y Negocios 4: 23–32. [Google Scholar] [CrossRef]
- Cozarenco, Anastasia, and Ariane Szafarz. 2018. Gender biases in bank lending: Lessons from microcredit in France. Journal of Business Ethics 147: 631–50. [Google Scholar] [CrossRef]
- Cubiles-De-La-Vega, María Dolores, Antonio Blanco-Oliver, Rafael Pino-Mejías, and Juan Lara-Rubio. 2013. Improving the management of microfinance institutions by using credit scoring models based on Statistical Learning techniques. Expert Systems with Applications 40: 6910–17. [Google Scholar] [CrossRef]
- DGRV. 2022. Datos y ranking de Cooperativas de Ahorro y Crédito en América Latina y el Caribe. Available online: https://www.dgrv.coop/es/publication/datos-y-ranking-de-cacs-en-america-latina-y-el-caribe/ (accessed on 3 May 2024).
- Durango, María Patricia, Juan Lara-Rubio, Andrés Navarro Galera, and A. Blanco-Oliver. 2022. The effects of pricing strategy on the efficiency and self-sustainability of microfinance institutions: A case study. Applied Economics 54: 2032–47. [Google Scholar] [CrossRef]
- Durango-Gutiérrez, María Patricia, Juan Lara-Rubio, and Andrés Navarro-Galera. 2023. Analysis of default risk in microfinance institutions under the Basel III framework. International Journal of Finance & Economics 28: 1261–78. [Google Scholar] [CrossRef]
- ECLAC (Economic Commission for Latin America and the Caribbean). 2009. Equality at the Center of Sustainable United Nations. Available online: https://repositorio.cepal.org/server/api/core/bitstreams/b1da0f9d-3746-43f8-9bb3-fa7b31f7ca4d/content (accessed on 6 April 2024).
- EIU (Economist Intelligence Unit). 2020. Microscopio Global de 2020: El papel de la inclusión financiera en la respuesta frente a la COVID-19. New York: Inter-American Development Bank Invest. [Google Scholar]
- Elloumi, Awatef, and Aïda Kammoun. 2013. Les déterminants de la performance de remboursement des microcrédits en Tunisie. Annals of Public and Cooperative Economics 84: 267–87. [Google Scholar] [CrossRef]
- Financial Stability Board (FSB). 2023. Promoting Global Financial Stability. 2023 FSB Annual Report. Available online: https://www.fsb.org/wp-content/uploads/P111023.pdf (accessed on 10 April 2024).
- Findevgateway. 2022. Portal FinDev un programa de CGAP. Guatemala, América Latina y el Caribe. Available online: https://www.findevgateway.org/es/pais/guatemala (accessed on 15 May 2024).
- Gutiérrez-Nieto, Begoña, Carlos Serrano-Cinca, and Juan Camón-Cala. 2016. A credit score system for socially responsible lending. Journal of Business Ethics 133: 691–701. [Google Scholar] [CrossRef]
- Hastie, Trevor, Robert Tibshirani, and Jerome Friedman. 2009. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. New York: Springer. [Google Scholar]
- IDB. 2020. El Microscopio Global de 2020 El Papel de la Inclusión Financiera en la Respuesta Frente a la COVID-19. Available online: https://idbinvest.org/es/publications/el-microscopio-global-de-2020-el-papel-de-la-inclusion-financiera-en-la-respuesta (accessed on 22 May 2024).
- Ince, Huseyin, and Bora Aktan. 2009. A comparison of data mining techniques for credit scoring in banking: A managerial perspective. Journal of Business Economics and Management 10: 233–40. [Google Scholar] [CrossRef]
- Irimia-Dieguez, Ana Isabel, A. Blanco-Oliver, and María José Vazquez-Cueto. 2015. A comparison of classification/regression trees and logistic regression in failure model. Procedia Economics and Finance 23: 9–14. [Google Scholar] [CrossRef]
- Kalita, Alakesh, Chiranjeeb Biswas, Anil Kumar Saikia, and Swabera Islam. 2022. Impact of Microfinance on Agriculture Sector: An Analysis. International Journal of Early Childhood Special Education 14: 2301–6. [Google Scholar] [CrossRef]
- Karlan, Dean, and Jonathan Zinman. 2011. Microcredit in Theory and Practice: Using Randomized Credit Scoring for Impact Evaluation. Science 332: 1278–84. [Google Scholar] [CrossRef] [PubMed]
- Kim, Kyoung-Jae. 2003. Financial time series forecasting using support vector machines. Neurocomputing 55: 307–19. [Google Scholar] [CrossRef]
- Lara-Rubio, Juan, Antonio Blanco-Oliver, and Rafael Pino-Mejías. 2017. Promoting entrepreneurship at the base of the social pyramid via pricing systems: A case study. Intelligent Systems in Accounting, Finance and Management 24: 12–28. [Google Scholar] [CrossRef]
- Lara-Rubio, Juan, Francisco Jesús Gálvez-Sánchez, Valentín Molina-Moreno, and Andrés Navarro-Galera. 2024. Analysing credit risk in persons with disabilities as an instrument of financial inclusion. Journal of Social and Economic Development, 1–23. [Google Scholar] [CrossRef]
- Lepetit, Laetitia, Emmanuelle Nys, Philippe Rous, and Amine Tarazi. 2008. The Expansion of Services in European Banking: Implications for Loan Pricing and Interest Margins. Journal of Banking & Finance 32: 2325–35. [Google Scholar] [CrossRef]
- Lin, Xuchen, Xiaolong Li, and Zhong Zheng. 2017. Evaluating borrower’s default risk in peer-to-peer lending: Evidence from a lending platform in China. Applied Economics 49: 3538–45. [Google Scholar] [CrossRef]
- Maes, Jan P., and Larry R. Reed. 2012. State of the Microcredit Summit Campaign Report 2012. Washington, DC: Microcredit Summit Campaign. [Google Scholar]
- Maudos, Joaquín, and Juan Fernandez De Guevara. 2004. Factors explaining the interest margin in the banking sectors of the European Union. Journal of Banking & Finance 28: 2259–81. [Google Scholar] [CrossRef]
- Mohamed, Toka S., and Mohammed M. Elgammal. 2023. Does the extent of branchless banking adoption enhance the social and financial performance of microfinance institutions? Applied Economics 56: 1671–88. [Google Scholar] [CrossRef]
- Montevechi, André Aoun, Rafael de Carvalho Miranda, André Luiz Medeiros, and José Arnaldo Barra Montevechi. 2024. Advancing credit risk modelling with Machine Learning: A comprehensive review of the state-of-the-art. Engineering Applications of Artificial Intelligence 137: 109082. [Google Scholar] [CrossRef]
- Mustapa, Wan Nurulasiah binti Wan, Abdullah Al Mamun, and Mohamed Dahlan Ibrahim. 2018. Development initiatives, micro-enterprise performance and sustainability. International Journal of Financial Studies 6: 74. [Google Scholar] [CrossRef]
- Newman, Alexander, Susan Schwarz, and Daniel Borgia. 2014. How does microfinance enhance entrepreneurial outcomes in emerging economies? The mediating mechanisms of psychological and social capital. International Small Business Journal 32: 158–79. [Google Scholar] [CrossRef]
- Okello Candiya Bongomin, George, and John C. Munene. 2020. Financial inclusion of the poor in developing economies in the twenty-first century: Qualitative evidence from rural Uganda. Journal of African Business 21: 355–74. [Google Scholar] [CrossRef]
- Pietrapiana, Fabio, José Manuel Feria-Dominguez, and Alicia Troncoso. 2021. Applying wrapper-based variable selection techniques to predict MFIs profitability: Evidence from Peru. Journal of Development Effectiveness 13: 84–99. [Google Scholar] [CrossRef]
- Rahayu, Ninik Sri. 2020. The intersection of Islamic microfinance and women’s empowerment: A case study of Baitul Maal wat Tamwil in Indonesia. International Journal of Financial Studies 8: 37. [Google Scholar] [CrossRef]
- Rayo, Salvador, Juan Lara Rubio, and David Camino Blasco. 2010. A credit scoring model for institutions of microfinance under the Basel II Normative. Journal of Economics, Finance and Administrative Science 15: 89–124. [Google Scholar]
- Roa, María José, Alejandra Villegas, and Ignacio Garrón. 2022. Interest rate caps on microcredit: Evidence from a natural experiment in Bolivia. Journal of Development Effectiveness 14: 125–42. [Google Scholar] [CrossRef]
- Ruthenberg, David, and Yoram Landskroner. 2008. Loan pricing under Basel II in an imperfectly competitive banking market. Journal of Banking & Finance 32: 2725–33. [Google Scholar] [CrossRef]
- Saunders, Anthony, and Liliana Schumacher. 2000. The determinants of bank interest rate margins: An international study. Journal of international Money and Finance 19: 813–32. [Google Scholar] [CrossRef]
- Schreiner, Mark. 2002. Aspects of outreach: A framework for discussion of the social benefits of microfinance. Journal of International Development 14: 591–603. [Google Scholar] [CrossRef]
- Shahriar, Abu Zafar M., and Mukesh Garg. 2017. Lender-entrepreneur relationships and credit risk: A global analysis of microfinance institutions. International Small Business Journal 35: 829–54. [Google Scholar] [CrossRef]
- Shahriar, Abu Zafar M., Susan Schwarz, and Alexander Newman. 2016. Profit orientation of microfinance institutions and provision of financial capital to business start-ups. International Small Business Journal 34: 532–52. [Google Scholar] [CrossRef]
- Tang, Zaiyong, and Paul A. Fishwick. 1993. Feedforward neural nets as models for time series forecasting. ORSA Journal on Computing 5: 374–85. [Google Scholar] [CrossRef]
- UN (United Nations). 2019. Ocho Amenazas a la Economía Mundial. Departamento de asuntos económicos y sociales. Available online: https://www.un.org/es/desa/world-economic-situation-and-prospects-wesp-2019 (accessed on 5 May 2024).
- Van Gool, Joris, Wouter Verbeke, Piet Sercu, and Bart Baesens. 2012. Credit scoring for microfinance: Is it worth it? International Journal of Finance and Economics 17: 103–23. [Google Scholar] [CrossRef]
- Vellido, Alfredo, Paulo J. G. Lisboa, and Karon Meehan. 1999. Segmentation of the on-line shopping market using neural networks. Expert systems with applications 17: 303–14. [Google Scholar] [CrossRef]
- Viswanathan, P. Karthiayani, and Srikant K. Shanthi. 2017. Modelling credit default in microfinance-an Indian case study. Journal of Emerging Market Finance 16: 246–58. [Google Scholar] [CrossRef]
- Vogelgesang, Ulrike. 2003. Microfinance in times of crisis: The effects of competition, rising indebtness, and economic crisis on repayment behavior. World Development 31: 2085–114. [Google Scholar] [CrossRef]
- Wennekers, Sander, André Van Wennekers, Roy Thurik, and Paul Reynolds. 2005. Nascent entrepreneurship and the level of economic development. Small Business Economics 24: 293–309. [Google Scholar] [CrossRef]
- West, David. 2000. Neural network credit scoring models. Computer and Operational Research 27: 1131–52. [Google Scholar] [CrossRef]
- Wong, Felix S., Pei-Zhuang Wang, Thong H. Goh, and Boon Kiat Quek. 1992. Fuzzy neural systems for stock selection. Financial Analysts Journal 48: 47–52. [Google Scholar] [CrossRef]
- Wulandari, Permata, and Muthia Pramesti. 2021. Designing sustainable Islamic Microfinance to enhance the accessibility of poor borrowers in Indonesia: An appreciative intelligence approach. IOP Conference Series: Earth and Environmental Science 716: 012065. [Google Scholar] [CrossRef]
- Zeballos, Eliana, Alessandra Cassar, and Bruce Wydick. 2014. Do risky microfinance borrowers really invest in risky projects? Experimental evidence from Bolivia. Journal of Development Studies 50: 276–87. [Google Scholar] [CrossRef]
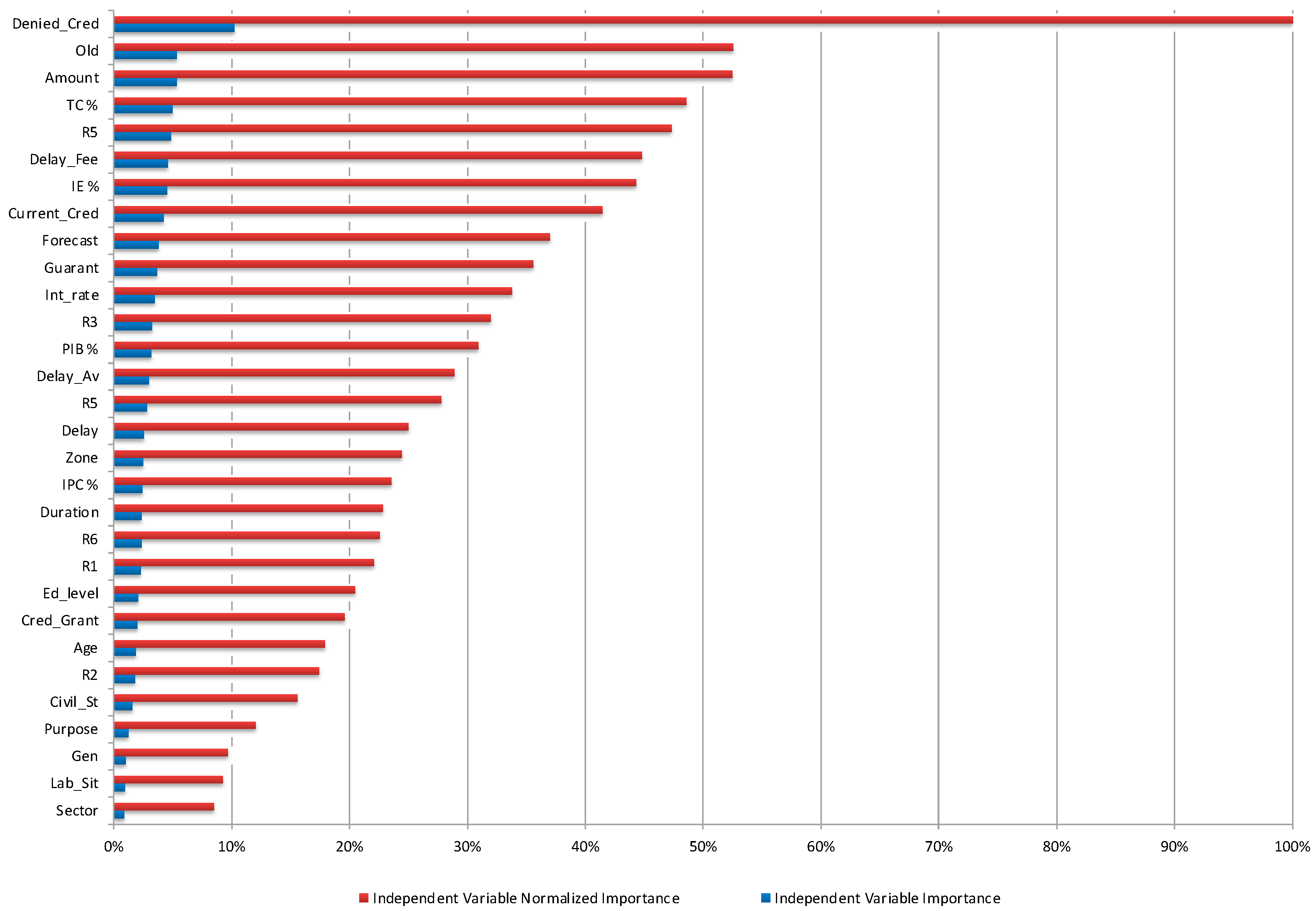
| Variable | Acronim | Concept | Expected Sign (B) |
|---|---|---|---|
| Idiosyncratic Variables | |||
| Non-financial variables | |||
| Gender | Gen | 0 = Male 1 = Female | - |
| Marital status | Civil_St | 0 = Single 1 = Family unit | - |
| Zone | Zone | 0 = Central zone 1 = Outskirts | - |
| Employment status | Lab-Sit | 0 = Owner 1 = Dependent | - |
| Age | Age | Age at the time of application | +/− |
| Sector | Sector | 0 = Commerce 1 = Production 2 = Services | +/− |
| Educational Level | Ed_ Level | 0 = Bachelor 1 = Technician 2 = Professional | - |
| Duration as a borrower of MFI | Old | Number of months as a client in the MFI | - |
| Previously granted loans | Cred_Grant | Number of loans granted in the MFI | - |
| Credit denied | Denied_Cred | Number of loans denied in the MFI | + |
| Number of current credits | Current_Cred | Number of current loans in the MFI | + |
| Credit arrears | Delay | Number of loans in arrears | + |
| Average arrears | Delay_Av | Average arrears | + |
| Fees on a defaulted loan (%) | Arrears | Percentage of arrears to total fees | + |
| Financial Ratios | |||
| Asset Rotation | R1 | Income sales/total assets | - |
| Liquidity | R2 | ability to pay/liquid assets (%) | - |
| Leverage 1 | R3 | Total liabilities/Shareholders’ equity (%) | - |
| Leverage 2 | R4 | Total liabilities/(Total liabilities + shareholders’ total equity) (%) | + |
| ROA | R5 | Net income/Total assets (%) | - |
| ROE | R6 | Net income/Shareholders’ equity (%) | - |
| Loan Variables | |||
| Purpose/Destination | Purpose | 0 = Fixed asset 1 = Work capital | + |
| Duration | Duration | Number of monthly fees for applied loan. | + |
| Amount | Amount | Amount of microcredit (USD) | + |
| Interest rate | Int_Rate | Annual interest rate applied | + |
| Garantía | Guarant | 0 = Personal 1 = Pledge | + |
| Credit analyst forecast | Forecast | 0 = no payment problems 1 = with payment problems | + |
| Sistematic Variables | |||
| Gross Domestic Product | GDP | Rate of annual change of Gross Domestic Product during loan term | - |
| Consumer Price Index | CPI | Rate of annual change of Consumer Price Index during loan term | - |
| Exchange rate | ER | Rate of annual change of variation in exchange rate during loan term | + |
| Unemployment rate | UR | Rate of annual change of variation in unemployment rate during loan term | + |
| B | S.E. | Wald | Exp(B) | |
|---|---|---|---|---|
| Gen (1) | −0.099 *** | 0.061 | 2.642 | 0.906 |
| Civil_St (1) | −0.060 *** | 0.060 | 1.011 | 0.942 |
| Zone (1) | −0.057 *** | 0.060 | 0.903 | 0.945 |
| Lab_Sit (1) | −0.047 *** | 0.060 | 0.631 | 0.954 |
| Old | −0.082 ** | 0.011 | 1.326 | 0.988 |
| Cred_Grant | −0.180 *** | 0.013 | 2.139 | 0.982 |
| Denied_Cred | 0.147 *** | 0.060 | 0.623 | 1.048 |
| Current_Cred | 0.083 *** | 0.060 | 0.050 | 1.013 |
| Delay_Fee | 0.557 *** | 1.128 | 0.797 | 2.737 |
| Delay_Av | 0.006 *** | 0.007 | 0.756 | 1.006 |
| R1 | −0.098 *** | 0.251 | 0.151 | 0.907 |
| R2 | −0.307 ** | 0.248 | 1.531 | 0.736 |
| R3 | 0.124 *** | 0.332 | 0.138 | 1.132 |
| R5 | −3.407 *** | 2.116 | 2.592 | 0.033 |
| Duration | 0.011 *** | 0.011 | 0.882 | 1.011 |
| Amount | 0.002 *** | 0.002 | 0.834 | 1.002 |
| Int_rate | 1.735 *** | 3.019 | 0.330 | 5.669 |
| Guarant (1) | 0.437 *** | 0.191 | 5.244 | 1.548 |
| Forecast (1) | 0.041 * | 0.116 | 0.124 | 1.042 |
| Constant | −1.248 *** | 0.777 | 0.102 |
| Logistic Regression | |||
| Observ. | Prediction | ||
| 0 | 1 | PCC | |
| 0 | 1809 | 559 | 76.39% |
| 1 | 590 | 1592 | 72.96% |
| PCC | 74.75% | ||
| AUC: 0.8433 | |||
| Neural Network | |||
| Observ. | Prediction | ||
| 0 | 1 | PCC | |
| 0 | 2019 | 349 | 85.26% |
| 1 | 320 | 1862 | 85.33% |
| PCC | 85.30% | ||
| AUC: 0.8917 | |||
| Acronim | Borrower 1 | Borrower 2 | Borrower 3 |
|---|---|---|---|
| Gen | 1 | 0 | 0 |
| Civil_St | 1 | 0 | 1 |
| Zone | 1 | 0 | 0 |
| Lab-Sit | 1 | 1 | 0 |
| Age | 45 | 27 | 60 |
| Sector | 1 | 1 | 0 |
| Ed_Level | 2 | 0 | 0 |
| Old | 36 | 10 | 18 |
| Cred_Grant | 5 | 1 | 2 |
| Denied_Cred | 0 | 0 | 2 |
| Current_Cred | 1 | 0 | 0 |
| Delay | 0 | 0 | 2 |
| Delay_Av | 0 | 0 | 6 |
| Arrears | 0 | 0 | 0.1111 |
| R1 | 0.8405 | 0.6493 | 0.4367 |
| R2 | 0.2793 | 0.12 | 0.0821 |
| R3 | 0.1262 | 0 | 0.0995 |
| R4 | 0.1121 | 0 | 0.0905 |
| R5 | 0.1348 | 0.0655 | 0.08654 |
| R6 | 0.1676 | 0.0947 | 0.1037 |
| Purpose | 0 | 0 | 0 |
| Duration | 12 | 18 | 12 |
| Amount | 1.45 | 1 | 1.2 |
| Int_Rate | 0.12 | 0.15 | 0.115 |
| Guarant | 0 | 0 | 1 |
| Forecast | 0 | 0 | 1 |
| PIB | 0.2156 | 0.0566 | 0.0348 |
| IPC | 0.0219 | 0.0207 | 0.0080 |
| TC | −0.0697 | −0.0815 | −0.1374 |
| IE | 0.1014 | 0.0729 | 0.0215 |
| PD (LR) | 0.39% | 10.36% | 24.50% |
| PD (MLP) | 0.12% | 2.55% | 29.02% |
| Concept | Amount |
|---|---|
| Microcredit amount | USD 1500 |
| Maturity (years) | 1 |
| Interest rate (the same for all 3 customers) | 12.32% |
| Cost of Debt | 2.25% |
| Operating Cost | 5.24% |
| Tax Rate | 25% |
| RORAC Objetive | 17.14% |
| Risk-free rate (Government bond) | 1.75% |
| Borrower 1 | Borrower 2 | Borrower 3 | Borrower 1 | Borrower 2 | Borrower 3 | ||
|---|---|---|---|---|---|---|---|
| Before the Rate Adjustment | After the Rate Adjustment | ||||||
| Interest rate | 12.32% | 12.32% | 12.32% | 7.90% | 10.01% | 23.70% | |
| Basel III IRB Approach | Borrower 1 | Borrower 2 | Borrower 3 | Borrower 1 | Borrower 2 | Borrower 3 | |
| PD | 0.12% | 2.55% | 29.02% | 0.12% | 2.55% | 29.02% | |
| LGD | 45.00% | 45.00% | 45.00% | 45.00% | 45.00% | 45.00% | |
| Expected Loss (EL) | 0.81 | 17.21 | 195.89 | 0.81 | 17.21 | 195.89 | |
| Weight | 21.89% | 83.15% | 191.36% | 21.89% | 83.15% | 191.36% | |
| RWA | 328.42 USD | 1247.32 USD | 2870.34 USD | 328.42 USD | 1247.32 USD | 2870.34 USD | |
| Basel III—IRB Coefficient | 8.00% | 8.00% | 8.00% | 8.00% | 8.00% | 8.00% | |
| Stockholders’ Equity | 26.27 USD | 99.79 USD | 229.63 USD | 26.27 USD | 99.79 USD | 229.63 USD | |
| Liabilities | 1473.73 USD | 1400.21 USD | 1270.37 USD | 1473.73 USD | 1400.21 USD | 1270.37 USD | |
| Total | 1500.00 USD | 1500.00 USD | 1500.00 USD | 1500.00 USD | 1500.00 USD | 1500.00 USD | |
| Interest income | 184.80 USD | 184.80 USD | 184.80 USD | 184.80 USD | 184.80 USD | 184.80 USD | |
| Interest expenses | 33.16 USD | 31.50 USD | 28.58 USD | 33.16 USD | 31.50 USD | 28.58 USD | |
| Operating cost | 78.60 USD | 78.60 USD | 78.60 USD | 78.60 USD | 78.60 USD | 78.60 USD | |
| RORAC | 206.19% | 43.20% | −38.63% | 17.14% | 17.14% | 17.14% | |
| RORAC target | 17.14% | 17.14% | 17.14% | 17.14% | 17.14% | 17.14% | |
| Price (Interest Rate) | 12.32% | 12.32% | 12.32% | 7.90% | 10.01% | 23.70% | |
| Borrower 1 | Borrower 2 | Borrower 3 | Borrower 1 | Borrower 2 | Borrower 3 | ||
|---|---|---|---|---|---|---|---|
| Before the Rate Adjustment | After the Rate Adjustment | ||||||
| Interest rate | 12.32% | 12.32% | 12.32% | 8.40% | 14.30% | 21.67% | |
| Basel III IRB Approach | Borrower 1 | Borrower 2 | Borrower 3 | Borrower 1 | Borrower 2 | Borrower 3 | |
| PD | 0.39% | 10.36% | 24.50% | 0.39% | 10.36% | 24.50% | |
| LGD | 45.00% | 45.00% | 45.00% | 45.00% | 45.00% | 45.00% | |
| Expected Loss (EL) | 2.62 | 69.90 | 165.38 | 2.62 | 69.90 | 165.38 | |
| Weight | 44.33% | 130.27% | 191.36% | 44.33% | 130.27% | 191.36% | |
| RWA | 664.99 USD | 1954.08 USD | 2870.34 USD | 664.99 USD | 1954.08 USD | 2870.34 USD | |
| Basel III—IRB Coefficient | 8.00% | 8.00% | 8.00% | 8.00% | 8.00% | 8.00% | |
| Stockholders’ Equity | 53.20 USD | 156.33 USD | 229.63 USD | 53.20 USD | 156.33 USD | 229.63 USD | |
| Liabilities | 1446.80 USD | 1343.67 USD | 1270.37 USD | 1446.80 USD | 1343.67 USD | 1270.37 USD | |
| Total | 1500.00 USD | 1500.00 USD | 1500.00 USD | 1500.00 USD | 1500.00 USD | 1500.00 USD | |
| Interest income | 184.80 USD | 184.80 USD | 184.80 USD | 125.93 USD | 214.46 USD | 325.04 USD | |
| Interest expenses | 33.16 USD | 31.50 USD | 28.58 USD | 32.55 USD | 30.23 USD | 28.58 USD | |
| Operating cost | 78.60 USD | 78.60 USD | 78.60 USD | 78.60 USD | 78.60 USD | 78.60 USD | |
| RORAC | 206.19% | 43.20% | −38.63% | 17.14% | 17.14% | 17.14% | |
| RORAC target | 17.14% | 17.14% | 17.14% | 17.14% | 17.14% | 17.14% | |
| Price (Interest Rate) | 12.32% | 12.32% | 12.32% | 8.40% | 14.30% | 21.67% | |
| Risk Category | Provision (%) |
|---|---|
| A. Normal risk | 0.00% |
| B. Above normal risk | 5.00% |
| C. Expected loss | 20.00% |
| D. With significant expected losses | 50.00% |
| E. High risk of irrecoverability. | 100.00% |
| Credit-Scoring Method | Borrower 1 | Borrower 2 | Borrower 3 | |
|---|---|---|---|---|
| Neural Network | Before rate adjustment | 12.32% | 12.32% | 12.32% |
| After rate adjustment | 7.90% | 10.01% | 23.70% | |
| Difference | −4.42% | −2.31% | 11.38% | |
| Logistic Regression | Before the rate adjustment | 12.32% | 12.32% | 12.32% |
| After the rate adjustment | 8.40% | 14.30% | 21.67% | |
| Gap | −3.92% | 1.98% | 9.35% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Durango-Gutiérrez, P.; Lara-Rubio, J.; Navarro-Galera, A.; Buendía-Carrillo, D. Microcredit Pricing Model for Microfinance Institutions under Basel III Banking Regulations. Int. J. Financial Stud. 2024, 12, 88. https://doi.org/10.3390/ijfs12030088
Durango-Gutiérrez P, Lara-Rubio J, Navarro-Galera A, Buendía-Carrillo D. Microcredit Pricing Model for Microfinance Institutions under Basel III Banking Regulations. International Journal of Financial Studies. 2024; 12(3):88. https://doi.org/10.3390/ijfs12030088
Chicago/Turabian StyleDurango-Gutiérrez, Patricia, Juan Lara-Rubio, Andrés Navarro-Galera, and Dionisio Buendía-Carrillo. 2024. "Microcredit Pricing Model for Microfinance Institutions under Basel III Banking Regulations" International Journal of Financial Studies 12, no. 3: 88. https://doi.org/10.3390/ijfs12030088
APA StyleDurango-Gutiérrez, P., Lara-Rubio, J., Navarro-Galera, A., & Buendía-Carrillo, D. (2024). Microcredit Pricing Model for Microfinance Institutions under Basel III Banking Regulations. International Journal of Financial Studies, 12(3), 88. https://doi.org/10.3390/ijfs12030088







