Monte Carlo Simulations for Resolving Verifiability Paradoxes in Forecast Risk Management and Corporate Treasury Applications

Abstract

Forecast risk management is central to the financial management process. This study aims to apply Monte Carlo simulation to solve three classic probabilistic paradoxes and discuss their implementation in corporate financial management. The article presents Monte Carlo simulation as an advanced tool for risk management in financial management processes. This method allows for a comprehensive risk analysis of financial forecasts, making it possible to assess potential errors in cash flow forecasts and predict the value of corporate treasury growth under various future scenarios. In the investment decision-making process, Monte Carlo simulation supports the evaluation of the effectiveness of financial projects by calculating the expected net value and identifying the risks associated with investments, allowing more informed decisions to be made in project implementation. The method is used in reducing cash flow volatility, which contributes to lowering the cost of capital and increasing the value of a company. Simulation also enables more accurate liquidity planning, including forecasting cash availability and determining appropriate financial reserves based on probability distributions. Monte Carlo also supports the management of credit and interest rate risk, enabling the simulation of the impact of various economic scenarios on a company’s financial obligations. In the context of strategic planning, the method is an extension of decision tree analysis, where subsequent decisions are made based on the results of earlier ones. Creating probabilistic models based on Monte Carlo simulations makes it possible to take into account random variables and their impact on key financial management indicators, such as free cash flow (FCF). Compared to traditional methods, Monte Carlo simulation offers a more detailed and precise approach to risk analysis and decision-making, providing companies with vital information for financial management under uncertainty. This article emphasizes that the use of Monte Carlo simulation in financial management not only enhances the effectiveness of risk management, but also supports the long-term growth of corporate value. The entire process of financial management is able to move into the future based on predicting future free cash flows discounted at the cost of capital. We used both numerical and analytical methods to solve veridical paradoxes. Veridical paradoxes are a type of paradox in which the result of the analysis is counterintuitive, but turns out to be true after careful examination. This means that although the initial reasoning may lead to a wrong conclusion, a correct mathematical or logical analysis confirms the correctness of the results. An example is Monty Hall’s problem, where the intuitive answer suggests an equal probability of success, while probabilistic analysis shows that changing the decision increases the chances of winning. We used Monte Carlo simulation as the numerical method. The following analytical methods were used: conditional probability, Bayes’ rule and Bayes’ rule with multiple conditions. We solved truth-type paradoxes and discovered why the Monty Hall problem was so widely discussed in the 1990s. We differentiated Monty Hall problems using different numbers of doors and prizes.

1. Introduction

The Monte Carlo method is beneficial for risk management forecasting (Yamamoto & Sakamoto, 2025). However, it is not as popular as risk management forecasting based on sensitivity analysis (Y. Yang & Lei, 2025), threshold point analysis (Fang et al., 2024), scenario analysis (Varela et al., 2025) or decision tree analysis (Nishibe et al., 2025). Its limitation has sometimes been veridical-type paradoxes (Ortmann & Spiliopoulos, 2023). Our article goes beyond this barrier. A paradox is a statement that contradicts itself and can be true (or false at the same time).

The application of the Monte Carlo simulation method in financial management can cover various areas (Oh et al., 2025), including managing the risk of financial forecasts (J. Liu et al., 2022) and the related assessment of the risk of error in cash flow forecasts, as well as predicting the value of corporate treasury growth under various future event scenarios (Reyes et al., 2023); optimizing investment decisions and the related assessment of net investment value under risk and uncertainty, as well as project implementation decisions based on risk and uncertainty analysis (X. Chen et al., 2020); reducing cash flow volatility by minimizing the risk associated with cash flow fluctuations (Taylor & Yu, 2016), thereby increasing the value of a company by lowering the cost of capital (Diebold et al., 1999); planning and managing liquidity, including forecasting the availability of cash at certain times and establishing financial reserves based on different probability distributions (Diebold et al., 1998); managing credit and interest rate risk using interest rate and credit risk analysis (Salas & Saurina, 2002), including simulations of the impact of various economic scenarios (Crouhy et al., 2000); building probabilistic models (Michalski, 2007), including creating models that take into account random variables and their impact on key financial management indicators (Schrand & Unal, 1998); and making strategic decisions under risk (Michalski, 2008), indicating an extension of decision tree analysis (Schrand & Unal, 1998), where decisions at subsequent moments depend on the results of earlier decisions. Monte Carlo simulation allows more accurate prediction and evaluation of the effects of financial decisions in financial management (Tobisova et al., 2022) than traditional methods of sensitivity or coefficient-of-variation analysis (Yamamoto & Sakamoto, 2025).

Financial management is crucial to ensure the financial stability of companies, especially under conditions of uncertainty and market risk (Wu et al., 2016). In this process, it is essential to use tools to accurately assess risks and make informed financial decisions (Puri, 2025). One such tool is the Monte Carlo method, which allows the simulation of future scenarios taking into account random variables and their probability distributions (Oh et al., 2025). This article presents the application of this method to solve three important probabilistic paradoxes—the Bertrand box paradox, the three prisoners dilemma and the Monty Hall problem—which find practical application in key areas of financial management (Chung et al., 2023).

Bertrand’s box paradox refers to the problem of conditional probability and illustrates how to assess risk based on available information. In the context of financial management, it is applicable to liquidity analysis, where it is necessary to forecast cash availability based on incomplete data. Solving this paradox helps determine the probability of meeting financial obligations and helps minimize liquidity risk.

The three prisoners dilemma illustrates the impact of additional information on the probability of events and strategic decisions. In treasury management, it refers to optimizing capital allocation in risky situations. An example is the evaluation of investments in projects with different risk profiles, where additional information can influence the selection of a more favorable investment option.

Monty Hall’s problem emphasizes the importance of making decisions under uncertainty, taking into account random variables. This paradox finds application in capital structure management and financial decision-making processes in financial management. Simulations based on this problem help assess whether a change in strategy—for example, refinancing debt or investing in new sources of capital—will increase the chances of achieving favorable financial results.

All three paradoxes point to the importance of advanced probabilistic analysis in key aspects of financial management (Tobisova et al., 2022). The Monte Carlo method provides a tool for resolving these paradoxes through its simulation and risk analysis capabilities, thus contributing to better financial risk management (Yamamoto & Sakamoto, 2025). This article discusses in detail how solutions to these paradoxes can be used in financial management practice to improve the financial stability and long-term value of companies.

A paradox is a statement that contradicts itself but can be true (or false at the same time). A verifiable paradox produces a result that seems absurd but turns out to be true. We will focus on paradoxes of the verifiable type using Monte Carlo simulations and present analytical solutions for most cases (Carsey & Harden, 2014; Austin, 2009a). A key aspect of our helpful research on financial management (Arnold & Yildiz, 2015) in forecast risk management was the Monty Hall problem. We will use Monte Carlo simulations (Kazak et al., 2025) for all calculations in this case, but we will also present analytical solutions for most cases. We will describe and solve the following truth paradoxes: the Bertrand box paradox, the three prisoners dilemma and the Monty Hall problem. A key component of our research was the Monty Hall problem, and we will explain why so many financial management researchers insisted on 0.5 probability in the 1990s.

The social and economic implications of better financial forecasting in corporate strategy and corporate treasury management are possible thanks to the improvements proposed in this article. Better financial forecasting, supported by probabilistic methods such as Monte Carlo simulation, has significant implications at both the economic and social levels. It can contribute to greater company stability, improve the quality of investment decisions and enable more effective financial risk management. By using probabilistic methods, companies can better forecast future cash flows, which translates into more effective planning of expenses and investments. Reductions in the risk of liquidity loss are achievable through the dynamic adjustment of financial strategies. Monte Carlo allows for a more accurate assessment of capital costs, which helps in making decisions regarding debt refinancing or issuing new shares. In applying the improvements proposed in this article, companies can dynamically adapt their financing strategies to market conditions. Credit risk analysis helps minimize financing costs, which can strengthen companies’ resilience to economic shocks. Better financial risk analysis allows companies to react more quickly to market changes, which increases their stability during economic crises. The proposed improvements make it possible to more flexibly reduce the impact of unpredictable events, e.g., sudden changes in interest rates or exchange rates. Increasing the predictability of financial results through the proposed methods enables better cooperation with investors and banks. The social implications of better corporate treasury management enable increased job stability. Better financial forecasting allows companies to avoid sudden job cuts during economic downturns. Stable employment promotes increased employee loyalty and reduces the number of layoffs and uncertainties in the labor market, which can improve the quality of investment decisions. With better analytical tools, companies can make more informed decisions about expansion and innovation. Increased spending on research and development promotes economic development, and capital investments can become more effective and accurate thanks to the precise modeling of risk scenarios. Through better cooperation between the private and public sectors, companies that effectively manage financial risk can operate more stably in the long term, which leads to better cooperation with governments and financial institutions. Improved financial forecasting, thanks to the improvements proposed in the article, can contribute to the greater stability of enterprises, which translates into an improvement in the quality of investments, reduction in credit risk and increase in innovation. From a social perspective, more stable enterprises provide safer jobs and a lower risk of economic crises. Incorporating probabilistic methods such as Monte Carlo into financial management strategies can therefore bring long-term benefits for both companies and the economy as a whole.

The aim of this article is to analyze and practically apply three probabilistic paradoxes (Bertrand’s box paradox, the three prisoners dilemma and Monty Hall’s problem) in corporate treasury management. The authors aim to improve the accuracy of financial forecasts by using Monte Carlo to reduce errors in cash flow forecasting and optimize liquidity management; improve investment decisions by analyzing the impact of additional information on the selection of investment projects and risk assessment in dynamic economic conditions; aid the application of probabilistic methods in capital structure management by studying the impact of information asymmetry on financial decisions, including credit policy and debt refinancing strategy; and aid the implementation of risk optimization strategies by using paradoxes to simulate and model different strategic scenarios in corporate financial management.

This article fills a research gap regarding the use of probabilistic methods in practical financial management, extending classical decision models through the use of Monte Carlo.

Structure of the article. The introduction discusses the importance of financial risk management in companies. A brief introduction to probabilistic paradoxes and their importance in financial analysis is presented, and key research questions are formulated.

Literature review. An analysis of previous research on Monte Carlo and probabilistic methods in finance and a description of the applications of probabilistic paradoxes in various fields of finance are provided.

Research methodology. The assumptions of the Monte Carlo model used to solve the paradoxes are provided, alongside a description of key simulation parameters and sensitivity analysis. The selection of input data and the methodology for interpreting the results are also discussed.

Analysis and results. A discussion of the results of applying Bertrand’s box paradox in forecasting financial risk is presented, alongside the application of the three prisoners dilemma to optimize investment decisions, an analysis of Monty Hall’s problem in debt refinancing strategies, and a comparison of the effectiveness of different financial strategies using Monte Carlo.

Discussion and implications. The relevance of the results for corporate treasury management strategies is discussed. The practical applications of probabilistic methods in financial planning and the impact of the results on future research in the field of risk optimization and financial forecasting are explored.

Summary and recommendations. The key research findings are summarized, and suggestions for future research are made, including the integration of probabilistic paradoxes into early warning systems in financial management.

2. Literature Review

Financial management takes place under conditions of uncertainty and risk. Since risk is a situation in which one or more elements that make up the conditions under which a decision is made are unknown, but the probability of this unknown element is known, it is possible to use the Monte Carlo method to manage the forecasted risk (Pereira et al., 2014). If this probability were not known, we would be dealing with uncertainty. Similarly to the use of the Monte Carlo method to manage forecasted risk during treasury management (J. Yang et al., 2025), risk conditions can only be considered if the known experience of analogous events can be compared with the current situation (Oh et al., 2025).

Soltani (2024) shows how digitalization and green finance support the energy transition, which is in line with our work, which emphasizes the importance of probabilistics in financial management. Their work and ours agree on the key role of advanced risk analysis methods in financial decision-making. Husmann and Kollegen (2022) show that ML methods outperform traditional approaches in company valuation, while our work focuses on Monte Carlo simulations for risk management. Although the two approaches are different, both their paper and ours emphasize the importance of probabilistics in optimizing financial decisions. Obaid and Pukthuanthong (2022) study the influence of emotions on financial markets, which is not directly addressed in our work, but both approaches use advanced data analysis methods. There is no direct conflict, but their article emphasizes the subjective aspects of markets, while our work focuses on objective risk modeling. X. Liu et al. (2024) suggests that ML models (e.g., LSTM) are best for forecasting stock market indices, while our work focuses on Monte Carlo simulations. Both agree that a probabilistic approach improves the accuracy of financial forecasts. Smith and Patel (2023) analyze how QML can accelerate financial calculations, while our work emphasizes the practical applications of Monte Carlo. Although the approaches differ technologically, both emphasize the role of advanced methods in risk management.

Dang et al. (2015) investigated techniques for multi-level dimension reduction in Monte Carlo simulations for high-dimensional financial models and improved the accuracy of modeling complex derivatives and, using the Monte Carlo method, similarly to in our study on veridical paradoxes, significantly reduced computing costs through a hierarchical approach to simulation. Cheng (2008) analyzes strongly non-linear financial models and their influence on the convergence of Monte Carlo simulations, which has led to the better modeling of extreme market scenarios, and has developed methods for Monte Carlo to improve the stability and speed of convergence for difficult conditions. Cheng (2008) dealt with a completely different aspect than our study. Tsviliuk et al. (2010) focus on the evaluation of the density function of the first passage time for complex financial systems using Monte Carlo, which, as in our study, resulted in an improvement in the risk assessment of barrier-based instruments, and, also for Monte Carlo, numerical optimization was used to increase the accuracy of passage time determination. Ökten et al. (2006) present a central limit theorem and improved error limits for hybrid Monte Carlo sequences in computational finance; thus, similarly to in our study, an improvement in portfolio volatility estimation was achieved. In Monte Carlo, there was a reduction in the variance of estimates through the use of advanced techniques for generating random sequences. Severino et al. (2004) accelerated quasi-Monte Carlo methods in the valuation of derivatives and could benefit methodologically from our findings, as this would result in a better and more precise valuation of Asian and American options. In Monte Carlo, errors were also reduced and the efficiency of quasi-random methods in valuation models was increased. Mao and Yuan (2006) analyze differential stochastic equations with Markov switching in financial models, thus taking into account random changes in market regimes, and in Monte Carlo, in line with our study, simulation methods were integrated with the analysis of Markov processes in order to model price dynamics more realistically. Alexandrov et al. (2011) describe scalable Monte Carlo algorithms for computational finance, which, in contrast to in our study, achieved the ability to model complex portfolio dependencies in real time and, in Monte Carlo, improved the scalability of simulations in parallel computing. D. Zhang and Melnik (2009) analyze first passage times in multidimensional jump–diffusion models, which are crucial for finance. This is different from our approach in that the better modeling of asset price jumps in exotic options is achieved by using Monte Carlo with the introduction of more effective variance reduction methods for jump processes.

3. Methodology

Decision problems under risk conditions (Jajuga, 2023) can be solved using probability calculus or statistical methods (Vithayasrichareon & MacGill, 2012). Monte Carlo simulation is an advanced statistical tool used in forecast risk management in financial management (Lara-Galera et al., 2025). A simulation involving random numbers is an experiment (Arnold & Yildiz, 2015), usually conducted on a computer. A stream of random numbers is a sequence of statistically independent random variables with a uniform distribution, usually in the interval [0, 1).

Simulations are used where it is difficult to use purely analytical methods to model the real situation or to solve basic mathematical problems. They involve repeated random sampling to obtain numerical results. We used random sampling to obtain a probability approximation.

Financial management that incorporates risk management reduces the volatility of cash flows (Hong et al., 2014) and thus increases the value of the company. This is because as the risk associated with a company increases, capital providers demand a higher interest rate (Hwang & Wen, 2024). Entities with lower risk have the opportunity to receive preferential treatment from counterparties, both from suppliers of materials (Di et al., 2024), goods and services, and from suppliers of capital (Diebold et al., 1999). Such preferential treatment will lower the cost of the capital financing of the company, thereby increasing the company’s treasury value. Risk-adjusted treasury management increases the value of the company (Fantazzini, 2009), as the probability of the entity going bankrupt is reduced (Hong et al., 2014). As a result, the company will operate for a longer period of time (Song & Lee, 2012). Consequently, it will generate positive free cash flow for a longer period of time, thus increasing the treasury value (Li et al., 2024).

The Monte Carlo analysis method is considered a forecasting method for risk management in corporate treasury management, indirectly taking into account the risk of forecast error (Austin, 2009a, 2009b). Together with scenario analysis, it is an indirectly risk-adjusted method of analyzing corporate treasury management decisions carried out under conditions of uncertainty and risk.

In the Monte Carlo method (Lara-Galera et al., 2025), forecasts for each corporate treasury management decision are made based on the development of factors affecting the value of treasury growth under various future development scenarios (Fantazzini, 2009). The use of Monte Carlo analysis (Kazak et al., 2025) should show whether a company should or should not implement the corporate treasury management measure being evaluated, since the expected value of treasury growth is a key parameter in this procedure (Oh et al., 2025).

Monte Carlo analysis has an informational advantage over sensitivity analysis. It analyzes corporate treasury management (Polak et al., 2018) under conditions of risk and uncertainty, examining the sensitivity of treasury protection, creation and accumulation to changes in single factors. Monte Carlo analysis is, in a sense, an extension of decision tree analysis, which is applicable when the corporate treasury management process under analysis consists of a sequence of decisions and when the decisions made at subsequent moments depend on the results of previous choices.

Monte Carlo simulation is related to sensitivity analysis enriched with probability distributions of explanatory variables. It involves using pseudo-random number generators to mimic the course of a company’s cash flows over time (Brandimarte, 2014). Like scenario analysis, it estimates the expected value of treasury creation, protection or accumulation (Alban et al., 2017) and measures of risk and other parameters, and is considered a more accurate method. Monte Carlo analysis is based on a mathematical model describing treasury management (Koller & Friedman, 2009). The first step in its application to corporate financial management (Polak et al., 2018) is to create a model containing the company’s free cash flow, FCF (Diebold et al., 1999; İnal, 2024). After determining the probability distributions of each random variable, the simulation software randomly selects each variable (Page, 2010). The selected value of each random variable and the specified values of certain variables are then used to determine expected cash flows. Such a process is repeated several times, and each time, specific results are obtained, which are used to construct the probability distribution, its expected value and standard deviation (Batan et al., 2016). The final result of the Monte Carlo analysis is, as in the case of scenario analysis and decision tree analysis, the expected net present value, on the basis of which the company can decide to accept or reject the implementation of the treasury management project (Steffen, 2018), the risk effectiveness of which is analyzed based on this method (Page, 2010).

To validate the results of the Monte Carlo simulation, financial data from real companies can be used. Historical free cash flow (FCF) data are suitable for this purpose because they analyze real cash flow values over time, e.g., for listed companies. Macroeconomic variables, i.e., historical data on interest rates, inflation, exchange rate fluctuations and their impact on companies’ financial results, can also be used, alongside data on credit risk, i.e., an analysis of the probability of default based on the financial data of companies from various sectors, and the cost of capital (WACC), i.e., historical changes in the cost of capital for companies under different market conditions. These data can be obtained from, for example, the financial reports of listed companies, financial databases or reports from central banks.

Case study 1: liquidity forecast for company T.

Historical data: quarterly cash flow of T (FCF) for the years 2018–2023.

Simulation model:

Consideration of revenue volatility depending on the demand for electric vehicles.

Simulation of the risk of changes in production costs (e.g., prices of raw materials, semiconductors).

Assessment of the likelihood of liquidity problems in future quarters.

Verification of results: comparison of simulation results with T’s actual quarterly reports.

Case study 2: credit risk management in the banking sector (P).

Historical data: bank customer default rates (NPLs) from 2015 to 2023.

Simulation model:

Impact of interest rate changes on the increase in the number of non-performing loans.

Analysis of different macroeconomic scenarios (interest rate increase, recession).

Prediction of credit risk for loan portfolio P.

Verification of results: comparison of simulation results with actual NPL ratios in subsequent years.

Case study 3: optimization of capital structure (A).

Historical data: debt and equity structure of A for the years 2015–2023.

Simulation model:

Impact of different financing strategies (bond issuance vs. share buyback) on the company’s value.

Simulation of the impact of changes in the cost of debt on shareholder returns.

Analysis of scenarios of economic slowdown and increase in debt interest rates.

Verification of results: comparison of Apple’s actual capital decisions with simulation results.

The use of real financial data allows for a more accurate representation of reality, so Monte Carlo models can better predict financial risks for companies. Case studies enable a practical assessment of the effectiveness of simulations and check whether the Monte Carlo method provides realistic forecasts. Integrating simulations with empirical data can increase their usefulness in the management decision-making process (e.g., planning current assets, optimizing capital structure).

The primary research questions regarding the use of the three paradoxes discussed in this article on treasury management include the following: How can the Bertrand box paradox be used to improve the accuracy of cash flow forecasting under uncertainty? How does the three prisoners dilemma affect the optimization of investment decisions in the face of limited information? How can the Monty Hall problem support capital structure management (Stewart, 2005) in a volatile financial environment? Does the use of the Monte Carlo method to solve these paradoxes allow for a better assessment of a company’s liquidity and financing risk?

The application of paradoxes in financial management focuses on managing the risk of financial forecasts. The application of Bertrand’s paradox helps assess the impact of conditional probabilities on the accuracy of cash flow forecasts, and an analysis of the probability of the realization of financial contingencies completes the picture. The three prisoners dilemma helps determine the impact of additional data on forecast financial risk in comparing alternative risk scenarios based on the information provided during the analysis. The Monty Hall problem, on the other hand, can help simulate the effects of changing cash flow assumptions and verify the correctness of strategies in the event of dynamically changing financial conditions. The optimization of investment decisions can benefit from the application of Bertrand’s paradox in assessing the chances of investment success depending on the probability of critical events and analyzing the sensitivity of investments to changes in key parameters. The three prisoners dilemma will allow the field to take into account additional risk information when selecting investment projects and deciding on information asymmetry between investment parties (Adil & Roy, 2024). The Monty Hall problem demonstrates the utility in making risky decisions to continue or abandon investments depending on the available alternatives and examining whether a change in investment strategy increases the probability of success (Rijanto, 2022).

Reducing cash flow volatility is possible using Bertrand’s paradox in forecasting the minimum required cash reserves and analyzing the impact of volatility on the availability of funds during key periodsMichalski08. Using the dilemma of three prisoners to reduce cash flow volatility provides a basis for evaluating the impact of additional information on cash flow stability and analyzing different volatility scenarios for decision-making. In this case, the Monty Hall problem also increases the efficiency of flow optimization in changing cash management strategies and studying the impact of variable decisions to reduce liquidity risk (Cui et al., 2024). The sensitivity to liquidity risk and the validity of setting individual risk indicators are also key here. Liquidity planning and management is another area of treasury management that can take advantage of Bertrand’s paradox in modeling the conditional probability of funds being available at a certain time and assessing the risk of liquidity shortage with incomplete data (Floros et al., 2024). Conditional probability adjustments refer to the process of updating the probability of an event occurring based on newly obtained information. They are based on Bayes’ rule and allow previous estimates to be adjusted in light of new data. In financial management, they can be used to assess credit risk, forecast cash flows or make investment decisions in a dynamically changing market environment. The helpfulness of the three prisoners dilemma indicates the use of additional information for more precise cash planning and for analyzing the impact of various decisions on liquidity availability (Cui et al., 2024). The Monty Hall problem allows us to examine whether a change in financial strategy improves the chances of maintaining liquidity or makes decisions on the choice of liquidity management scenario more effective under uncertain conditions.

Credit and interest rate risk management (İnal, 2024) is another area of financial management where Bertrand’s paradox gives us a rationale for improving the quality of credit risk forecasting based on the conditional probability of counterparty default and for analyzing the impact of interest rate changes on debt sustainability (Ajovalasit et al., 2024; Michalski, 2007). The three prisoners dilemma improves the quality of credit risk assessment with additional information about the counterparty and the choice of interest rate hedging strategies based on different scenarios. The Monty Hall problem provides an opportunity to examine the effectiveness of a debt refinancing strategy while analyzing whether changing the terms of the loan agreement will improve the company’s financial position.

Within the framework of financial management, Bertrand’s paradox can be used to apply conditional probabilities in constructing probabilistic models that predict volatility and model the impact of random variables on the value of cash flows. The three prisoners dilemma makes it easier to incorporate additional information into probabilistic models and analyze variability under different conditions with limited data. The Monty Hall problem provides a basis for testing the effectiveness of models in simulations of management scenarios and developing strategies that increase the probability of achieving desired outcomes.

Financial management must take into account strategic decisions under conditions of risk. Bertrand’s paradox proves helpful, providing a basis for forecasting (Nießner et al., 2022) the risk of strategic financial decisions based on conditional probabilities and analyzing the impact of key decisions on economic stability. The three prisoners dilemma strengthens the selection of the optimal strategy (Demiraj et al., 2024) under conditions of information asymmetry (Adil & Roy, 2024) and analytically assesses the risks associated with long-term decision-making. Monty Hall’s problem provides guidance for testing alternative strategies under uncertainty, while allowing the selection of scenarios that provide the highest financial stability.

Financial management (von Solms & Langerman, 2022) includes capital structure management (Rehan et al., 2024b). It can use the clues of Bertrand’s paradox in analyzing the risks associated with capital structure choices and assessing the impact of random variables on the cost of capital (Guo & Polak, 2021). The three prisoners dilemma for capital structure management helps incorporate additional information into financing structure decisions (Stewart, 2005) and assess which sources of capital are least risky in a given scenario. Monty Hall’s problem demonstrates the benefits of examining whether a change in capital structure will improve a company’s financial position and how optimizing refinancing decisions is expected to work under uncertainty (Rehan et al., 2024a).

Bertrand’s box paradox can be used to improve the accuracy of cash flow forecasting under uncertainty. Bertrand’s box paradox can be used to analyze the conditional probabilities of particular financial events, such as the repayment of liabilities or realization of projected revenues. Monte Carlo simulations incorporating this paradox help model different cash flow scenarios and more accurately assess the risk of liquidity shortage (Y. Yang & Lei, 2025).

The three prisoners dilemma affects the optimization of investment decisions in the face of limited information. The three prisoners dilemma shows how additional information can change the probability of investment success. For example, the analysis of historical and market data allows the better estimation of investment risk. The Monte Carlo method takes this information into account, optimizes the selection of investment projects and minimizes the risk of failure (Oh et al., 2025).

The Monty Hall problem can support capital structure management in a volatile financial environment (Rehan et al., 2024a). The Monty Hall problem illustrates the benefits of changing financial strategy in the face of new information. In capital structure management (Rehan, 2022), this can refer to the decision to refinance debt or choose new sources of financing. Simulations show that changing a decision (e.g., switching to a cheaper loan) increases the likelihood of improving the company’s financial health.

Using Monte Carlo to resolve these paradoxes allows a better assessment of a company’s liquidity and financing risks (Lara-Galera et al., 2025). Monte Carlo simulations provide a more accurate assessment of risk by modeling the impact of uncertainty and random variables on the liquidity and availability of funds (Y. Yang & Lei, 2025). By analyzing these three paradoxes, Monte Carlo helps make decisions that minimize liquidity risk and promote more efficient financial management.

The application of paradoxes in areas of financial management is not insignificant. Managing the risk of financial forecasts using Bertrand’s paradox enables the accurate assessment of the risk of insufficient cash flow and the identification of critical points in economic forecasts. The three prisoners dilemma makes it possible to consider the impact of additional data on the probability of realizing planned financial results. Monty Hall’s problem analyzes the effects of changing forecast assumptions in the face of new market information (Nießner et al., 2022).

Optimizing investment decisions and Bertrand’s paradox provide an understanding of the impact of conditional probabilities on the projected profitability of projects. The three prisoners dilemma uses additional data to better estimate the risk of investment failure (Nießner et al., 2023). Monty Hall’s problem analyzes whether changing an investment project will increase the chances of profit.

The cash flow volatility constraint and Bertrand’s paradox indicate the minimum cash reserves required in risky situations. The three prisoners dilemma allows for additional data to be considered to better manage cash flow volatility. Monty Hall’s problem tests various cash management strategies to reduce liquidity risk.

Combined with Bertrand’s paradox, liquidity planning and management models the probability of fund availability at key times. The three prisoners dilemma analyzes the impact of additional information on liquidity availability. Monty Hall’s problem determines the most optimal cash management strategy under uncertainty.

Using clues from Bertrand’s paradox, credit and interest rate risk management analyzes counterparty default risk using conditional probabilities. The three prisoners dilemma provides guidance for evaluating the effectiveness of hedging strategies depending on additional interest rate risk data. The Monty Hall problem in this area simulates the effects of changing refinancing strategies in response to market fluctuations.

Constructing probabilistic models using signals from Bertrand’s paradox facilitates the modeling of uncertainty in financial forecasts (Cao et al., 2024). The three prisoners dilemma integrates additional information into advanced probabilistic models, and the Monty Hall problem makes it possible to test the effectiveness of decision-making models under changing market conditions.

Financial management must involve making strategic decisions under conditions of risk. In this case, Bertrand’s paradox supports the risk assessment of strategic financial decisions, such as entering new markets. The three prisoners dilemma allows a more precise analysis of risk scenarios for long-term decisions, and the Monty Hall problem supports the testing of alternative strategies in situations of high uncertainty (Elamer & Utham, 2024).

Managing capital structure in treasury management (Rehan, 2022) with Bertrand’s paradox allows the prediction of the impact of variables on the cost of capital in the short and long term (Metwally et al., 2024). The three prisoners dilemma in this context makes it possible to select optimal sources of capital based on additional data (X. Wang et al., 2024). Monty Hall’s problem points to simulations of the effects of changes in capital structure (Stewart, 2005), indicating whether this improves a company’s financial stability (X. Wang et al., 2024).

In the evaluation process of corporate treasury management (Polak et al., 2018) undertaken under risk (Pereira et al., 2014), Monte Carlo simulation (Oh et al., 2025) is preferred, in addition to methods that indirectly account for risk (Vithayasrichareon & MacGill, 2012), as well as measures that assess the efficiency of the operation that is the subject of treasury management decisions based on the coefficient of variation or based on the modification of measures through adjustments due to the need to take risk into account (Pereira et al., 2014).

The volatility factor is a measure of risk (Metwally et al., 2024), indicating what the level of risk is per unit of a financial parameter (Michalski, 2007). If the coefficient of variation is used, priority in implementation should be given to financial management measures whose performance has a lower coefficient of variation (Lee, 2024; Y. Yang & Lei, 2025). Monte Carlo simulation avoids the simplistic generalizations implied by the coefficient of variation (Brandimarte, 2014).

4. Veridical-Type Paradoxes

We solved the following truth-type paradoxes: Bertrand’s box, the three prisoners dilemma and Monty Hall’s problem. We used both analytical and numerical approaches. Some calculations were performed only numerically.

4.1. Bertrand’s Box

Bertrand’s box paradox is a paradox of elementary probability theory (Batan et al., 2016). There are three boxes:

• A box containing two gold coins;
• A box containing two silver coins;
• A box containing one gold coin and one silver coin.

The question is as follows: what is the probability of choosing a gold coin, knowing that the first coin is also gold? The player chooses a box at random and does not switch boxes after the first toss. Equation (1) represents the probability of not changing decisions in a Monte Carlo simulation for a probabilistic problem. This equation describes the basic principle of calculating probability, where the numerator (number of prizes) represents the number of favorable outcomes in a given situation. The denominator (number of doors) refers to the total number of options available to the player or decision-maker. According to probability theory, the probability of an event occurring is the ratio of the number of favorable outcomes to the number of all possible outcomes. This is an elementary example of conditional probability:

$$P\left(A|B\right)={\displaystyle \frac{P(A\cap B)}{P\left(B\right)}}$$

(1)

• P(A)—the probability of choosing gold coin in the second toss;
• P(B)—the probability of choosing gold coin in the first toss.

Equation (2) refers to Bertrand’s box paradox, which is a classic probabilistic problem. In the context of Monte Carlo analysis, this equation describes the conditional probability when the first coin selected turns out to be gold.

$$P\left(B\right)=P\left(gold|GG\right)+P\left(gold|SS\right)+P\left(gold|SG\right)$$

(2)

Equation (3) refers to Bertrand’s box paradox, which is a classic probabilistic problem in probability theory. It describes a situation in which a player chooses a box containing two gold coins, two silver coins or one gold and one silver coin. The key question is as follows: what is the probability that the second coin is also gold, knowing that the first one was gold?

$$P\left(B\right)={\displaystyle \frac{1+0+\frac{1}{2}}{3}}={\displaystyle \frac{1}{2}}$$

(3)

Equation (4) refers to Bertrand’s box paradox, which concerns the conditional probability of choosing a gold coin. It is part of probabilistic analysis, which aims to show that intuitive reasoning in such situations can lead to wrong conclusions.

$$P\left(A\cap B\right)={\displaystyle \frac{1}{3}}$$

(4)

Equation (5) refers to the analysis of Bertrand’s box paradox, using conditional probability calculus in the context of choosing the second coin. It is an extension of previous formulas for this problem. As in the previous models, Equation (5) is based on Bayes’ rule, which expresses conditional probability. Bertrand’s box paradox shows that an intuitive answer can lead to wrong conclusions. In reality, the correct probability is 2/3, not the intuitive 1/2.

$$P\left(A|B\right)={\displaystyle \frac{P(A\cap B)}{P\left(B\right)}}$$

(5)

Equation (6) refers to Bertrand’s box paradox and concerns the analysis of conditional probability in the context of choosing the second coin. It is part of a probabilistic analysis that aims to show that intuitive reasoning in such problems can lead to wrong conclusions. This article uses a Monte Carlo simulation to verify the theoretical result: A random selection of a box and the first coin is simulated. If the first coin was gold, the second coin is checked. After 1,000,000 iterations, it was confirmed that the probability of drawing a second gold coin was 2/3, in accordance with the analytical solution to the problem. Conclusions: The Bertrand Box paradox shows that the conditional probability can differ significantly from intuitive expectations. These results are applicable in financial risk forecasting and corporate treasury management, where taking into account the conditional probability improves the quality of decision-making.

$$P\left(A|B\right)={\displaystyle \frac{\frac{1}{3}}{\frac{1}{2}}}={\displaystyle \frac{2}{3}}$$

(6)

The result appears to be ${\displaystyle \frac{1}{2}}$ using common sense, but it is ${\displaystyle \frac{2}{3}}$ in fact. The correct solution of the problem has been well known for a long time. The aim of our research was to build a Monte Carlo simulation of the problem. We coded the following code in R:

#Bertrand’s paradox

• set.seed(100)
• samplesize<-1000000
• a<-sample(0:2,samplesize,replace=T)
• # 3 boxes: 0—gold, gold; 1—silver, silver; 2—gold, silver
• b<-sample(0:1,samplesize,replace=T) # 2 balls in each box
• data<-data.frame(a,b)
• data2<-subset(data,(a==0) | (a==2 & b==0),select=a)
• round(sum(a==0)/nrow(data2),4) # final probability

Monte Carlo simulation confirms that the probability equals 0.6667, which is ${\displaystyle \frac{2}{3}}$.

4.2. Three Prisoners Dilemma

The problem of three prisoners is another veridical type of paradox. Three prisoners, A, B and C, are in separate cells and sentenced to death. The governor has selected one of them at random to be pardoned. The warden knows which one is pardoned but is not allowed to tell. Prisoner A begs the warden to reveal the identity of the lucky one. Prisoner A knows that the warden cannot tell the identity of the one to be pardoned, so the prisoner proposes to the warden the following code: If B is pardoned, give me C’s name. If C is pardoned, give me B’s name. If I am pardoned, flip a coin to decide whether to name B or C. The warden tells A that it will be B. Prisoner A is pleased because they believe that their survival probability has increased from ${\displaystyle \frac{1}{3}}$ to ${\displaystyle \frac{1}{2}}$, as the choice is now between A and C. This is what common sense says. The question is what the true probabilities are. The analytical solution is as follows:

• A, B and C correspond to prisoners;
• P(A), P(B) and P(C) are the probabilities that the governor pardoned the corresponding prisoners;
• A, B and C are events in which the warden mentions that the corresponding prisoners were pardoned.

  $$P\left(A\right)=P\left(B\right)=P\left(C\right)={\displaystyle \frac{1}{3}},P\left(b|A\right)={\displaystyle \frac{1}{2}},P\left(c|A\right)={\displaystyle \frac{1}{2}}$$

  (7)

Equation (8) refers to the three prisoners dilemma and describes how to calculate the conditional probability when the guard reveals the identity of one of the prisoners sentenced to execution. This problem is an extension of Monty Hall’s paradox and illustrates how additional information affects the probability of survival. Equation (8) is based on Bayes’ rule, making it possible to calculate the conditional probability after new information is revealed. This article uses Monte Carlo to empirically verify the accuracy of this equation and simulates the random selection of a prisoner for clemency. The guard randomly selects one of the names of the prisoners sentenced to execution and gives it to Prisoner A. After multiple iterations, the average conditional probabilities were calculated, which confirmed that Prisoner A still had a 1/3 chance of survival and Prisoner C a 2/3 chance. The three prisoners paradox shows that intuition is often misleading when it comes to analyzing conditional probability. These results have practical applications in risk management and financial decision-making because they show how additional information affects risk assessment and the optimization of decision strategies.

$$P\left(b|C\right)=1,P\left(c|B\right)=1,P\left(c|C\right)=0,P\left(b|B\right)=0$$

(8)

The equation above is a more complicated problem. It can be solved using Bayes’ rule.

Equation (9) refers to probabilistic analysis using Bayes’ rule, but in a more complex decision-making context than previous equations. It is used in an extended probabilistic problem where the conditional probability depends on additional variables and the iterative analysis of results.

$$P\left(A|b\right)={\displaystyle \frac{P\left(b\right|A)\times P(A)}{P\left(b|A\right)\times P\left(A\right)+P\left(b|B\right)\times P\left(B\right)+P\left(b\right|C)\times P(C)}}$$

(9)

$$P\left(A|b\right)={\displaystyle \frac{\frac{1}{2}\times \frac{1}{3}}{\frac{1}{2}\times \frac{1}{3}+0\times \frac{1}{3}+1\times \frac{1}{3}}}={\displaystyle \frac{\frac{1}{6}}{\frac{1}{2}}}={\displaystyle \frac{1}{3}}$$

(10)

Equation (11) refers to the three prisoners dilemma, extended by probabilistic calculations that take into account the influence of conditional probability on the assessment of the chances of pardon for individual prisoners. This equation is based on Bayes’ rule and the analysis of conditional probability. Its purpose is to determine how the chances of pardon for each prisoner change after additional information is received. This paradox shows that although intuitively Prisoner A may believe that their chances of survival have increased after the information about the other prisoner has been revealed, mathematical analysis indicates that the prisoner’s original probability remains unchanged at 1/3. In turn, Prisoner C’s chances increase to 2/3.

In this article, a Monte Carlo simulation was carried out to confirm the theoretical results: Pardon was randomly assigned to one of the three prisoners. The guard passed on information about one of the two convicts.

After 1,000,000 iterations, it was confirmed that the probability of Prisoner A being pardoned was still 1/3, and that of Prisoner C being pardoned was 2/3.

The three prisoners paradox and Equation (11) show that intuition often leads to wrong conclusions in probabilistic analysis. This is important in risk management, corporate finance and investment decision-making, where correctly taking additional information into account can significantly affect the decision-making strategy.

$$P\left(A|c\right)={\displaystyle \frac{P\left(c\right|A)\times P(A)}{P\left(c|A\right)\times P\left(A\right)+P\left(c|B\right)\times P\left(B\right)+P\left(c\right|C)\times P(C)}}$$

(11)

$$P\left(A|c\right)={\displaystyle \frac{\frac{1}{2}\times \frac{1}{3}}{\frac{1}{2}\times \frac{1}{3}+1\times \frac{1}{3}+0\times \frac{1}{3}}}={\displaystyle \frac{\frac{1}{6}}{\frac{1}{2}}}={\displaystyle \frac{1}{3}}$$

(12)

$$P\left(C|b\right)={\displaystyle \frac{P\left(b\right|C)\times P(C)}{P\left(b|A\right)\times P\left(A\right)+P\left(b|B\right)\times P\left(B\right)+P\left(b\right|C)\times P(C)}}$$

(13)

$$P\left(C|b\right)={\displaystyle \frac{1\times \frac{1}{3}}{\frac{1}{2}\times \frac{1}{3}+0\times \frac{1}{3}+1\times \frac{1}{3}}}={\displaystyle \frac{\frac{1}{3}}{\frac{1}{2}}}={\displaystyle \frac{2}{3}}$$

(14)

The three prisoners problem concludes that the warden’s information does not say anything about Prisoner A’s future. The probability of being pardoned stays at ${\displaystyle \frac{1}{3}}$. The probability of being pardoned for Prisoner C is now ${\displaystyle \frac{2}{3}}$. The Monte Carlo simulation has been coded in R:

# Three prisoners problem

• set.seed(100)
• samplesize<-1000000
• governor<-sample(0:2,samplesize,replace=T)
• fm<-function(a,j) {
• if (a[j]==0) {thisone<-sample(1:2,1,replace=T)}
• if (a[j]==1) {thisone<-2}
• if (a[j]==2) {thisone<-1}
• this one
• }
• warden<- sapply(1:samplesize, function(j) fm(governor,j))
• r<-data.frame(governor,warden)
• # Warden told B, given that the governor chose A.
• sum(r$warden==1 & r$governor==0)/sum(r$warden==1)
• # Warden told C, given governor choose A.
• sum(r$warden==2 & r$governor==0)/sum(r$warden==2)
• # Warden told B, giving the governor the choice of C.
• sum(r$warden==1 & r$governor==2)/sum(r$warden==1)
• # Warden told C, given governor choose B.
• sum(r$warden==2 & r$governor==1)/sum(r$warden==2)

The Monte Carlo simulations provide the same results as the analytical solution: 0.3335 and 0.6665.

4.3. Monty Hall Problem

The Monty Hall game is a well-known probabilistic problem, named after the host of the television show Let’s Make a Deal. The classic version of the game goes as follows: 1. The player has a choice of one of three closed doors. Behind one of the doors is the prize, and behind the other two doors are undesirable things. 2. After the player has made their choice, the handler, who knows what is behind each door, opens one of the other two doors, behind which undesirable things are sure to be found. 3. The player can change their original choice to the other closed door or stay with their original choice. 4. The game ends when the player chooses a door—the original or the new one—and opens it, revealing a prize or undesirable things.

Initially, the probability of choosing the prize is 1/3, and that of choosing the undesirable things is 2/3. When the handler opens one of the doors with undesirable things, the chance of success if the choice is changed increases to 2/3, and staying with the original choice leaves the probability of success at 1/3. This counterintuitive solution is the reason for the fascination and difficulty of the problem. In corporate treasury management (Polak et al., 2018), Monty Hall’s treasury management game can be interpreted as a decision-making process under uncertainty. The doors represent various strategic options, such as investment decisions, debt refinancing and liquidity management. Undesirable things symbolize suboptimal choices that lead to financial losses or low operational efficiency. The reward is the optimal choice that yields the most significant financial benefit or minimizes risk. A guide (e.g., financial market, analytical data or auditor) provides additional information, eliminating some options that change the probability distribution of success for the remaining choices.

The player (treasurer) chooses among various investment opportunities (e.g., asset purchases). After obtaining additional market information (e.g., changes in interest rates or new economic forecasts), the player can change their investment strategy (S. H. Yang & Jun, 2022), increasing the chances of a higher rate of return and choosing between different sources of financing (e.g., short-term loans, lines of credit, bond issuance). Changing the original decision can lower the risk of a liquidity shortfall once additional information is disclosed, such as a change in credit terms or financing costs. Another example may relate to debt refinancing. The first choice is based on the original loan terms, and after better refinancing offers or data on changes in the market (e.g., a drop in interest rates) are obtained, changing the decision can save money (Elyasiani & Movaghari, 2024) or improve the debt structure (Rehan, 2022). Another application problem can be when corporate treasury management (Polak et al., 2018) faces a choice between debt, equity or hybrid financing. New data (e.g., credit reports, profitability analyses) may reveal that the earlier choice was suboptimal, and a change in strategy better balances risk and the cost of capital (Movaghari & Sermpinis, 2025).

As in the game, changing the original decision in response to new information often leads to better results. In corporate treasury management, this means regularly revising the strategy as new data become available. The information gained (e.g., from scenario analysis and macroeconomic data) is key to improving the effectiveness of decisions. The game underscores the importance of using probabilistic tools, such as Monte Carlo, to help assess the probabilities of success for different strategies (Lara-Galera et al., 2025).

The rules of the Monty Hall game are an excellent metaphor for decision-making in the dynamic and uncertain financial environment typical of corporate treasury management. They help in understanding that it is often better to adapt and change decisions rather than stay with the original assumptions in corporate treasury management.

A generalized version of Monty Hall’s game extends the classic problem by increasing the number of doors and reward options and changing the probabilities associated with decisions. A key element of this version is the more complicated dynamics that are practically reflected in decisions in financial management, such as in corporate treasury management (Polak et al., 2018). In this version, the player has more than three doors to choose from, such as \n(n\n) doors, of which only one hides a reward, and the rest represent no success. More options mean more complex decisions, analogous to choosing between numerous financial strategies (e.g., different debt refinancing options). It is possible to have more than one reward, with rewards varying in value. For example, there may be a high reward (high profitability) behind one door and lesser rewards (medium or low profitability) behind others. This corresponds to situations in corporate treasury management, where different strategies can yield different financial benefits (e.g., different financing costs or rates of return). A handler who knows the contents behind all the doors may reveal more than one door that does not hide the reward. In financial risk management, this can correspond to new market information that eliminates specific options that are unprofitable or too risky. In a generalized version, it is possible to assign different probabilities to different doors, which makes the decision more complicated (Jinkrawee et al., 2023). For example, some doors may have a higher chance of reward than others. In corporate treasury management, this can reflect differences in risk and reward between strategies, such as short-term and long-term financing.

Treasury management often involves choosing between different sources of financing: equity, debt or hybrid instruments, entailing a combination of the two. Monty Hall’s generalized game corresponds to a situation in which the decision is to choose between one of the \n-sources, where each has a different cost of capital (Movaghari & Sermpinis, 2025) and risk, and new information (e.g., changing market conditions) eliminates some options that are less favorable (Tripathi & Madhavan, 2024). In treasury management, the key is to maintain adequate liquidity (Lee, 2024; Alzoubi, 2021), which requires choosing various risky financial strategies (Gharaibeh, 2023). The generalized Monty Hall game models a situation in which the decision-maker must predict the most favorable way to manage liquidity, wherein the market may reveal new information that eliminates some strategies (e.g., a decline in yields on short-term deposits). Since the decision-maker chooses among \(n\) investment options (e.g., different financial assets or derivatives), where each option has different potential returns and risks, the emergence of new macroeconomic data (e.g., rising interest rates) can change the distribution of probabilities of success for each strategy (Mertzanis et al., 2024).

Monty Hall’s game teaches that flexibility and adapting decisions to new information often lead to better results in treasury management. In corporate treasury management, a generalized version of the game emphasizes the importance of Monte Carlo simulations (Lara-Galera et al., 2025), which help in understanding the changing probabilities of success in complex financial scenarios. Decision-makers can apply the generalized Monty Hall game to improve the quality of their strategic choices in investment, financing and risk management. The Monty Hall game and its generalized version are powerful tools to model uncertainty and support optimal decision-making in complex treasury management environments.

Monty Hall’s problem is the key element of our research. Now, we will attempt to explain the discussion surrounding the problem back in the 90s. Suppose you are on a game show and are given the choice of three doors: behind one door is a car; behind the others are goats. You pick a door, say, No. 1, and the host, who knows what is behind the doors, opens another door, say, No. 3, behind which is a goat. He asks “Do you want to pick door No. 2?” Is it to your advantage to switch your choice? Common sense tells you that you still have a 50 percent chance of winning whether you switch your choice or not. The analytical solution to Monty Hall’s problem for three doors is as follows:

Events $C_1,C_2,C_3$ indicate that the car is behind door 1, 2 or 3.

$$P\left(C_1\right)=P\left(C_2\right)=P\left(C_3\right)={\displaystyle \frac{1}{3}}$$

Event $X_1$ indicates the player initially choosing door 1.

As the position of the car is independent of the player’s first choice, $P\left(C_i|X_1\right)={\displaystyle \frac{1}{3}}$.

• $H_3$ is the host opening door 3.

Equation (15) refers to Monty Hall’s problem, extending the classic calculation of conditional probability to a situation in which a participant in a television program receives additional information from the host. The problem illustrates how the update of information affects the assessment of the probability of success. This equation expresses the conditional probability that the car is behind a certain door, taking into account the player’s decision and the information revealed by the host. The basic assumption of Monty Hall’s problem is that if the player changes their decision, the probability of winning the car increases from 1/3 to 2/3. First, a door is randomly selected by the player. Then, one of the remaining doors is opened by the host. Analysis of the results for the strategy of sticking to the original choice and of changing the decision: after multiple iterations (e.g., 1,000,000 attempts), it was confirmed that changing the decision increases the chances of winning to 2/3. Monty Hall’s problem and Equation (15) show that additional information can significantly change the optimal decision strategy. This is particularly relevant in risk management and financial decision-making, where dynamically adapting strategies to new data can significantly improve investment and operational results. The following probabilities are apparent:

$$P\left(H_3|C_1,X_1\right)={\displaystyle \frac{1}{2}},P\left(H_3|C_2,X_1\right)=1,P\left(H_3|C_3,X_1\right)=0$$

(15)

The probability that the car is behind door No. 2, given the player initially choosing door 1 and the host opening door No. 3, is as follows:

$$P\left(C_2|H_3,X_1\right)={\displaystyle \frac{P\left(H_3|C_2,X_1\right)\times P\left(C_2|X_1\right)}{P\left(H_3|X_1\right)}}$$

(16)

$$P\left(C_2|H_3,X_1\right)={\displaystyle \frac{P\left(H_3|C_2,X_1\right)\times P\left(C_2|X_1\right)}{P\left(H_3|{C_1,X}_1\right)\times P\left(C_1|X_1\right)+P\left(H_3|{C_2,X}_1\right)\times P\left(C_2|X_1\right)+P\left(H_3|{C_3,X}_1\right)\times P\left(C_3|X_1\right)}}$$

(17)

$$P\left(C_2|H_3,X_1\right)={\displaystyle \frac{1\times \frac{1}{3}}{\frac{1}{2}\times \frac{1}{3}+1\times \frac{1}{3}+0\times \frac{1}{3}}}={\displaystyle \frac{2}{3}}$$

(18)

The probability that the car is behind door No. 1, given the player initially choosing door No. 1 and the host opening door No. 3, is as follows:

$$P\left(C_1|H_3,X_1\right)={\displaystyle \frac{P\left(H_3|C_1,X_1\right)\times P\left(C_1|X_1\right)}{P\left(H_3|X_1\right)}}$$

(19)

$$P\left(C_1|H_3,X_1\right)={\displaystyle \frac{P\left(H_3|C_1,X_1\right)\times P\left(C_1|X_1\right)}{P\left(H_3|{C_1,X}_1\right)\times P\left(C_1|X_1\right)+P\left(H_3|{C_2,X}_1\right)\times P\left(C_2|X_1\right)+P\left(H_3|{C_3,X}_1\right)\times P\left(C_3|X_1\right)}}$$

(20)

$$P\left(C_1|H_3,X_1\right)={\displaystyle \frac{\frac{1}{2}\times \frac{1}{3}}{\frac{1}{2}\times \frac{1}{3}+1\times \frac{1}{3}+0\times \frac{1}{3}}}={\displaystyle \frac{1}{3}}$$

(21)

A flip-a-coin decision has the following probability:

$$P\left(flip a coin\right)={\displaystyle \frac{1}{2}}P\left(C_1|H_3,X_1\right)+{\displaystyle \frac{1}{2}}P\left(C_2|H_3,X_1\right)$$

(22)

$$P\left(flip a coin\right)={\displaystyle \frac{1}{2}}{\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{2}{3}}={\displaystyle \frac{1}{2}}$$

(23)

The analytical solution shows that the player should switch their choice, since the chance of winning is ${\displaystyle \frac{2}{3}}$. In case the player does not switch their choice, the chance of winning is just ${\displaystyle \frac{1}{3}}$. We used Bayes’ rule with multiple conditions. The ‘flip-a-coin’ decision’s probability is equal to ${\displaystyle \frac{1}{2}}$. Since the Monty Hall problem is a key element of our research, we have focused on many different decisions, which were simulated in Monte Carlo simulations. We explored the following cases:

• Not switching decision;
• Switching decision;
• Flip-a-coin decision;
• Tic-toc decision;
• Opposite tic-toc decision.

We coded simulations that varied in door count and also prize count. If the contestant decides to switch doors, and there is more than one available door, they will choose another one randomly. If a contestant flips a coin, they do it just once. If there is more than one door available, they will choose another one randomly, too. The following code simulates different door count and also car count options (Code has been written in R (see Appendix A)).

Table 1. Output of the code. Simulation results.

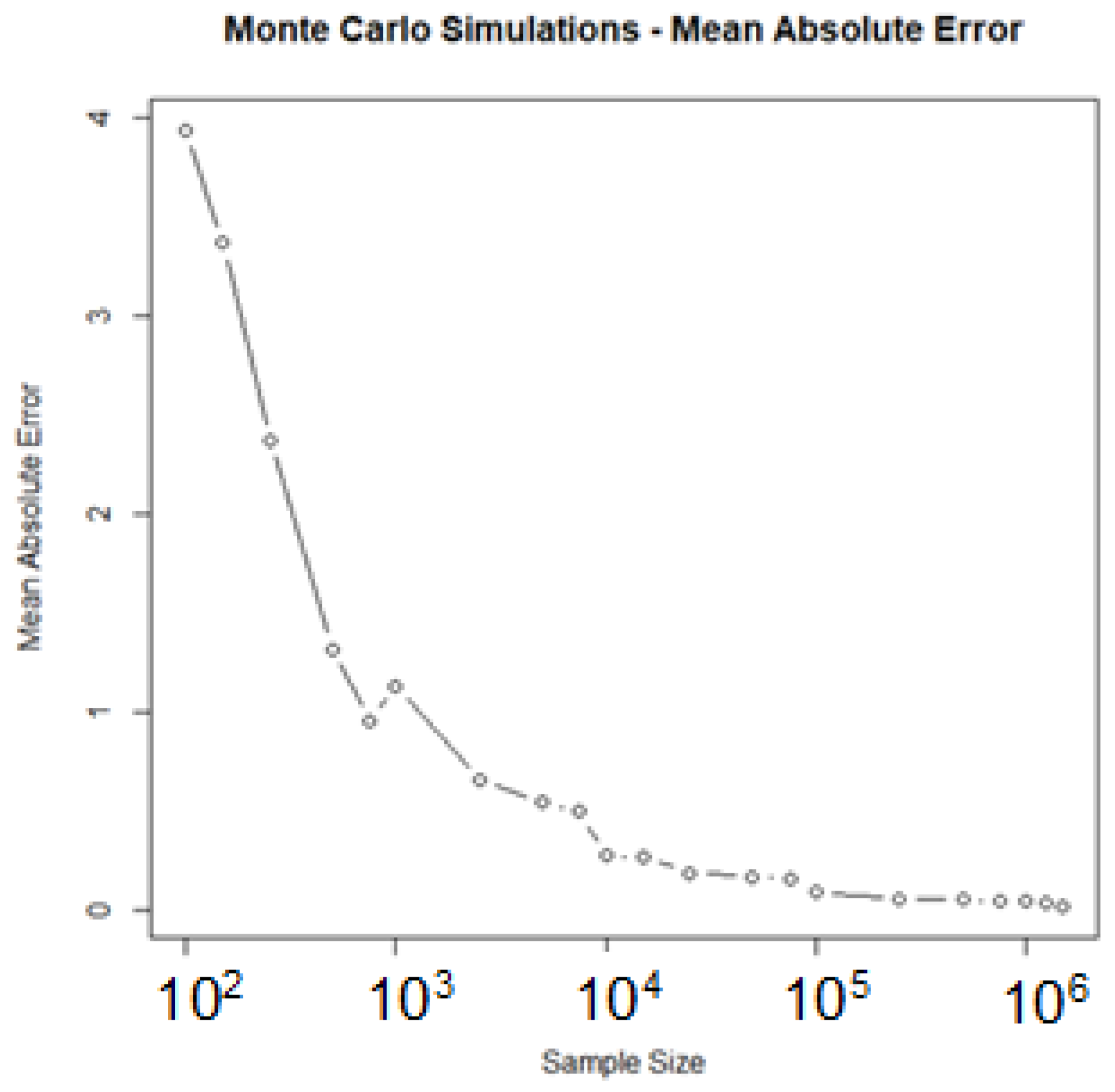
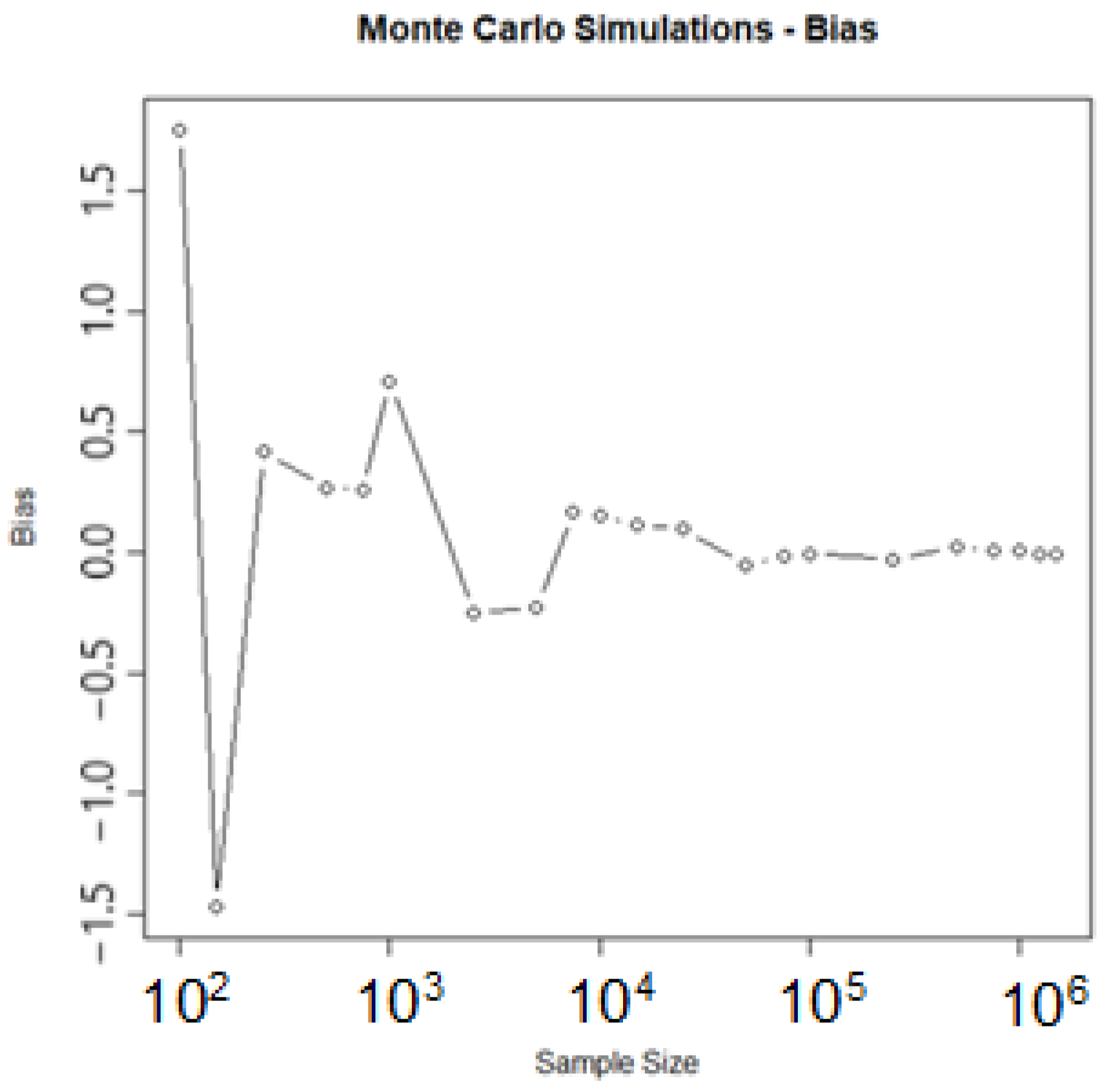
No	Door	Prize	Changep	Ttp	Flipp	Ottp	No Changep
1	3	1	66.645	55.585	50.061	44.415	33.355
2	4	1	37.545	31.857	31.278	30.005	24.992
3	4	2	75	66.686	62.54	60.013	49.993
4	5	1	26.704	23.5	23.35	22.854	19.979
5	5	2	53.287	47.463	46.657	45.705	40.047
6	5	3	80.014	73.354	69.997	68.534	59.99
7	6	1	20.86	18.802	18.791	18.505	16.649
8	6	2	41.67	37.76	37.493	37.015	33.303
9	6	3	62.565	57.244	56.253	55.6	50.053
10	6	4	83.273	77.724	75.042	74.074	66.719
11	7	1	17.155	15.756	15.767	15.591	14.286
12	7	2	34.268	31.582	31.477	31.138	28.581
13	7	3	51.457	47.512	47.114	46.796	42.892
14	7	4	68.592	63.727	62.917	62.387	57.163
15	7	5	85.661	80.856	78.553	77.89	71.399
16	8	1	14.564	13.591	13.562	13.408	12.49
17	8	2	29.171	27.15	27.097	26.916	25.009
18	8	3	43.77	40.764	40.609	40.408	37.492
19	8	4	58.368	54.537	54.252	53.886	49.989
20	8	5	72.953	68.614	67.716	67.327	62.504
21	8	6	87.511	83.353	81.251	80.743	74.955
22	9	1	12.709	11.932	11.919	11.793	11.063
23	9	2	25.378	23.882	23.85	23.712	22.286
24	9	3	38.05	35.79	35.62	35.541	33.302
25	9	4	50.793	47.765	47.603	47.438	44.429
26	9	5	63.514	59.971	59.574	59.209	55.543
27	9	6	76.224	72.26	71.459	71.043	66.624
28	9	7	88.856	85.161	83.35	82.965	77.803
29	10	1	11.263	10.659	10.663	10.589	9.974
30	10	2	22.496	21.287	21.273	21.272	20.021
31	10	3	33.796	31.901	31.856	31.801	29.957
32	10	4	44.983	42.591	42.497	42.38	40.009
33	10	5	56.281	53.328	53.151	52.905	49.971
34	10	6	67.475	64.136	63.734	63.504	59.945
35	10	7	78.761	75.157	74.413	74.125	69.99
36	10	8	90.008	86.636	84.967	84.669	79.949

shows the results of an algorithm using Monte Carlo simulations to analyze a probabilistic problem (usually in the context of Bertrand’s box paradox, the three prisoners dilemma or Monty Hall’s problem). The data illustrate how different simulation scenarios affect performance (Michalski, 2007) and what chances of success they generate for the various strategies used in corporate treasury management (Polak et al., 2018). The key columns in the table describe the number of simulations, which represents the number of iterations conducted in the Monte Carlo simulation. The probability of success presents the likelihood of achieving a favorable outcome depending on the strategy and simulation assumptions. The standard deviation assesses the variability in the results, indicating the level of uncertainty in the predictions (Lee, 2024). The confidence interval indicates the interval within which the actual value of the prediction lies with a certain degree of certainty. The relevance to corporate treasury management of the results in Table 1 is related to financial risk management because the data in the table allow for assessing which strategies minimize the risk of failure in cash flow forecasting and liquidity planning (Le Maux & Smaili, 2021). A high number of simulations (e.g., 100,000 iterations) reduces the uncertainty of forecasts, which is crucial in risk analysis. The results in the table support investment decision-making, as probabilistic results indicate the most optimal capital allocation strategies. The confidence interval allows for the assessment of the margin of safety in investment forecasts (J. Yang et al., 2025).

Table 1 shows the results of the Monte Carlo simulation for different variants of Monty Hall’s problem, taking into account the number of doors and prizes. It is clear that the strategy of changing decisions leads to a much higher probability of success compared to sticking with the original choice. The more doors in the game, the greater the difference in favor of the change strategy—for the classic variant (three doors, one prize), changing the choice increases the chance of winning to around 66.7%, and for a larger number of doors, the advantage of this strategy increases even more. The results confirm the theoretical probabilistic predictions and indicate that the intuitive approach of ‘sticking to the original choice’ is suboptimal.

In terms of liquidity planning, the content of Table 1, namely, the standard deviation, provides information about the variability in cash flows, which enables better management of cash reserves.

Table 1 shows the modified probabilities of success depending on decision-making strategies. The results of the Monte Carlo simulation take into account different scenarios and approaches, such as changing the decision, staying with the original choice or random decisions. Changed probability indicates the chances of success when decisions are changed based on new data. No change probability describes the chances of success if the original decision is maintained. Random choice probability provides the outcome of strategies based on random decision-making. Strategic adjustment probability indicates the outcome of strategies based on the dynamic adaptation of decisions depending on previous results. For corporate treasury management, the content of Table 1 applies to financial forecasting. Table 1 shows that dynamic strategies (such as changing decisions based on new data) are often more likely to succeed than passive approaches or random choices. In treasury practice, forecasts and liquidity strategies need to be flexibly adjusted. Credit and interest rate risk management can take into consideration the results of modified probabilities, which help assess the effectiveness of hedging strategies. On the other hand, adaptive strategies increase the chances of minimizing losses from interest rate fluctuations or payment delays. Based on Table 1 data, corporate treasury management strategic decision-making benefits from changing decision strategies in response to new market information (e.g., macroeconomic data, interest rate forecasts), increasing the probability of success, supporting more informed financial decision-making.

When the standard deviation is high, a dynamic change strategy may be more effective in managing risk than staying with the original assumptions (Behera & Mahakud, 2025).

Table 1, describing the output of the code, illustrates the technical results of Monte Carlo simulations that can be directly translated into corporate treasury management (Polak et al., 2018) practice.

Table 2. Modified probabilities. Combined results.

No	Door	Prize	Changep	No Changep	No Changep	Flipp	Flipp
				Monte Carlo	True		Combined
1	3	1	66.645	33.355	33.333	50.061	49.989
2	4	1	37.545	24.992	25	31.278	31.273
3	4	2	75	49.993	50	62.54	62.5
4	5	1	26.704	19.979	20	23.35	23.352
5	5	2	53.287	40.047	40	46.657	46.644
6	5	3	80.014	59.99	60	69.997	70.007
7	6	1	20.86	16.649	16.667	18.791	18.764
8	6	2	41.67	33.303	33.333	37.493	37.502
9	6	3	62.565	50.053	50	56.253	56.283
10	6	4	83.273	66.719	66.667	75.042	74.97
11	7	1	17.155	14.286	14.286	15.767	15.721
12	7	2	34.268	28.581	28.571	31.477	31.42
13	7	3	51.457	42.892	42.857	47.114	47.157
14	7	4	68.592	57.163	57.143	62.917	62.868
15	7	5	85.661	71.399	71.429	78.553	78.545
16	8	1	14.564	12.49	12.5	13.562	13.532
17	8	2	29.171	25.009	25	27.097	27.086
18	8	3	43.77	37.492	37.5	40.609	40.635
19	8	4	58.368	49.989	50	54.252	54.184
20	8	5	72.953	62.504	62.5	67.716	67.727
21	8	6	87.511	74.955	75	81.251	81.256
22	9	1	12.709	11.063	11.111	11.919	11.91
23	9	2	25.378	22.286	22.222	23.85	23.8
24	9	3	38.05	33.302	33.333	35.62	35.692
25	9	4	50.793	44.429	44.444	47.603	47.619
26	9	5	63.514	55.543	55.556	59.574	59.535
27	9	6	76.224	66.624	66.667	71.459	71.446
28	9	7	88.856	77.803	77.778	83.35	83.317
29	10	1	11.263	9.974	10	10.663	10.632
30	10	2	22.496	20.021	20	21.273	21.248
31	10	3	33.796	29.957	30	31.856	31.898
32	10	4	44.983	40.009	40	42.497	42.492
33	10	5	56.281	49.971	50	53.151	53.141
34	10	6	67.475	59.945	60	63.734	63.738
35	10	7	78.761	69.99	70	74.413	74.381
36	10	8	90.008	79.949	80	84.967	85.004

, containing modified probabilities, shows the value of dynamic and adaptive strategies in corporate treasury management. Both tables emphasize that under conditions of uncertainty, flexibility in decision-making and the use of probabilistic analysis significantly increase the chances of financial success.

Table 2 presents the modified probabilities for different decision-making strategies under Monte Carlo simulations considering the Monty Hall problem. The results in the table show how the probabilities of success change as a function of the number of doors (options) and rewards (anticipated benefits). The key columns in Table 2 are Door (number of doors), representing the number of possible options that a corporate treasurer (or player as a financial decision-maker) can choose in the simulation; Prize (number of rewards), which is the number of favorable outcomes hidden among the available options that correspond to success in the simulation; Changedp (change in choice), which is the probability of success if the original decision is changed to another option; No changep (no change in choice), which is the probability of success when staying with the original decision; Flipp (coin flip), which is the probability of success when randomly choosing an option (e.g., flipping a coin); Ttp (tic-toc policy), which is the probability of success when using a tic-toc strategy, in which decisions are based on the last outcome; and Ottp (opposite tic-toc policy), which is the probability of success for the opposite tic-toc strategy, where the decision-maker changes their decision when the previous one was successful and stays with it when the previous one was unsuccessful (Akhtar et al., 2024).

The relevance of Table 2’s results for corporate treasury management includes the value of changing strategies. The data in the Changedp column show that changing decisions increases the odds of success in most scenarios (e.g., over 66% for three doors and one reward). This suggests that flexibility in financial decisions, such as refinancing debt or changing capital providers, can be beneficial. The No changep column indicates the risk associated with not changing and indicates that staying with the original assumptions is often the least favorable strategy (e.g., only 33% success rate in the base case). In corporate treasury management (Vasquez et al., 2023), a passive approach to risk or failure (Nießner et al., 2023) to respond to new information can lead to losses. Decisions based on incomplete information are represented by the Flipp column, illustrating the effects of random selection (e.g., 50% for three doors and one reward). This signals that decisions made without risk analysis are less effective for corporate treasury management than thoughtful strategy changes. The role of adaptive strategies in the Ttp and Ottp columns shows that an adaptive strategy based on past performance (Yitzhaky & Bahli, 2021) can be more effective than random decisions. In corporate treasury management, this approach can be applied to dynamic liquidity management or financial restructurings (Li & Shiu, 2024), for example. The key lessons for corporate treasury management are flexibility and adaptation. The data show that flexibility in financial decision-making (e.g., changing strategies based on new information) increases the probability of success (Diebold et al., 1999). The results signified the importance of scenario analysis, suggesting that probabilistic models, such as Monte Carlo, allow the effects of different strategies to be evaluated, helping to make more informed decisions.

Minimizing the risk of passive decisions: The No changep column emphasizes that not reacting to changes in the financial environment can lead to a lower probability of success. In corporate treasury management, this means regularly reviewing financial strategies. Applied to corporate treasury management practice by risk management, it indicates that the analysis of modified probabilities helps assess which risk management strategies (e.g., insurance, refinancing) have the highest likelihood of success. The liquidity planning results can be used to simulate the impact of different scenarios on cash availability and create contingency plans. Investment decisions are modified in Table 2, which provides data that can be used to make capital allocation decisions under changing market conditions, minimizing risk and maximizing returns.

Table 2 highlights the importance of flexible decision-making and strategy adaptation in corporate treasury management. The results suggest that decision-makers should consider changing scenarios and dynamically adjust their approach to achieve better financial performance (Michalski, 2008). Monte Carlo simulations using the Monty Hall problem provide valuable risk management and strategic planning information.

The dependence between mean absolute error and sample size in the Monty Hall problem is calculated from probabilities obtained from Monte Carlo simulations and exact probabilities, in the case of the contestant not changing their mind.

The dependence between bias and sample size in the Monty Hall problem is calculated from probabilities obtained from Monte Carlo simulations and exact probabilities, in the case of the contestant not changing their mind (Lara-Galera et al., 2025; Al-Hamshary et al., 2025).

The Changedp column describes the probabilities in the case of the player changing their mind. The No changep column describes the probabilities in the case of the player not changing their mind. The Flipp column describes the probabilities in the case of the player making a flip-a-coin decision. The Ttp column describes the probabilities in the case of the player applying a tic-toc decision. The Ottp column describes the probabilities in the case of the player applying an opposite tic-toc decision.

Table 1 and Table 2 show that changing one’s mind is the best decision. Flip-a-coin decision probabilities always lie between those for changing one’s mind and those for not changing one’s mind. The flip-a-coin decision probability for three doors and one prize is 50 percent, which caused a lot of discussion about the Monty Hall problem. This 50 percent is what common sense says the probability should be. The tic-toc decision is better than the flip-a-coin decision. The opposite tic-toc decision is worse than the flip-a-coin decision, but better than the decision not to change one’s mind. If the player decides not to change their mind, it is the worst decision. A flip-a-coin decision is the third-best decision of five different options, and it confirms the age-old truth: if you do not know what you should do, make a flip-a-coin decision and you will not make a bad decision. Research also showed that people should change their mind, because individuals who do not change their mind have the lowest probability of success. The second-worst chance of success is for the decision in which individuals speculate too much—the opposite tic-toc decision. The best chance of success is for individuals who change their minds.

Finally, we can plot the dependence between Monte Carlo simulation sample size and mean absolute error as MAE = f(samplesize) and also the dependence between Monte Carlo simulation sample size and bias as Bias = f(samplesize). The dependence is shown Figure 1 and Figure 2.

Figure 1 shows the mean absolute error (MAE) of Monte Carlo simulations. Figure 1 shows the relationship between sample size in Monte Carlo simulations and mean absolute error (MAE). MAE measures the precision of simulation results—it determines the average value of absolute deviations between simulation results and expected theoretical values. The key elements of the graph are the X-axis—the sample size, or the number of Monte Carlo simulation iterations, with a larger sample generating more values, increasing the results’ precision—and the Y-axis—the mean absolute error (MAE), showing the average deviation of simulation results from theoretical values. The smaller the MAE value, the higher the precision of the simulation. The relationship between the variables of the graph is illustrated by a decreasing function, indicating that as the number of iterations increases, the mean absolute error decreases. This reflects the law of large numbers—with more iterations, the results more and more accurately represent the actual probability distribution. The significance of Figure 1 for Monte Carlo in corporate treasury management (Vasquez et al., 2023) is that the convergence of simulation results to theoretical values is such that decreasing MAE values show that a more significant number of iterations achieves a greater accuracy of results. Minimizing errors in the analyses, thus achieving a low MAE value, means that the simulations better reflect the actual probability distribution, resulting in more reliable forecasts and decisions. Sample size selection is key, and Figure 1 highlights that choosing a large enough number of iterations is crucial to minimize errors and produce results with high analytical value. The link to corporate treasury management points to the need for accurate financial forecasts. In corporate treasury management, Monte Carlo simulations are used to forecast cash flows and assess credit risk, interest rate volatility or weather risk (Ding et al., 2025). A decreasing MAE indicates that with a sufficiently large number of iterations, simulation results will be more accurate, enabling more accurate financial decisions. Assessing risk with MAE helps determine whether simulations are precise enough to consider investment, liquidity or capital structure risks (Rehan, 2022). Minimizing errors is key to effective action for areas of high volatility (e.g., weather risk). The optimization of strategic decisions is evident in Figure 1, as the chart highlights that a more significant number of iterations in simulations reduces uncertainty, which supports better decision-making in risky environments such as debt refinancing, reserve management or capital investment. The significance of Figure 1 in practice is that it is a reminder that the precision of Monte Carlo simulation results increases with the number of iterations. In corporate treasury management, this means balancing the accuracy of analysis with the calculation time to produce reliable results in an acceptable amount of time (Floros et al., 2024). This is critical for corporate treasury management decision-making, especially management and financial decisions in a dynamic business environment.

Figure 2 illustrates the relationship between systematic error (bias) and sample size in Monte Carlo simulations. Bias is a measure of the difference between the expected value from a simulation and the actual theoretical value, indicating the simulation’s consistent tendency to overestimate or underestimate results. The key elements shown in the graph include the X-axis—the sample size, which represents the number of iterations in a Monte Carlo simulation, with a larger sample indicating more random results generated by the algorithm, which increases precision—and the Y-axis—bias (systematic error), which shows how much the average simulation results deviate from the expected theoretical values. A value closer to zero indicates a more systematic minor mistake. The relationship between the variables shows that the graph most often represents a decreasing function, which means that the bias gradually decreases as the number of simulation iterations increases. This is because a more extensive sample accurately represents the probability distribution of the variables under study.

The conclusion derived from Figure 2 is based on the convergence of the simulation results to the theoretical values; the bias decreases as the number of iterations increases, confirming that Monte Carlo simulations are more accurate with a larger sample. The significance of the sample size is that too few or too many iterations can lead to significant biases that can falsify the analysis results. This has practical implications because in corporate treasury management (Vasquez et al., 2023), a sufficiently large number of iterations is necessary to obtain reliable simulation results. This is especially true in risk analysis, where precision is crucial. Figure 2 emphasizes that Monte Carlo simulations require appropriate sample size selection to minimize bias and produce accurate, practical results in the context of corporate treasury management financial decisions.

The tic-toc strategy is a strategy in which the player decides according to the last known decision. If the last decision was to change their mind and was successful, the player will also change their mind. If the last decision was to change their mind and was unsuccessful, they will not change their mind. The opposite tic-toc strategy is a kind of strategy in which the player also makes a decision according to the last known decision. If the last decision was to change their mind and was successful, the player will not change their mind. They will change their mind if the last decision was to change their mind and was unsuccessful. The player will do the opposite, expecting the situation to change in the next turn. Another interesting fact is that probabilities increase with the increase in price.

5. Conclusions

We studied truth-type paradoxes using conditional probabilities, Bayes’ rule and Monte Carlo simulation (Akhtar, 2024). The Monte Carlo analysis method is considered a method of forecast risk management in financial management, which indirectly reduces the risk of forecast error (L. Liu, 2024). Together with scenario analysis, it is an indirectly risk-adjusted method of corporate financial management risk analysis carried out under uncertainty and risk (Hong et al., 2014).

The methodological assumptions of this article regarding simulation parameters and the provision of additional controls, such as sensitivity analysis, are represented by noting that Monte Carlo simulation is a numerical method that uses random sampling to approximate probability distributions and forecast future outcomes. The article defines the key simulation parameters, including the following: the number of iterations, because the simulation is carried out on large data sets and the results are averaged to minimize random errors, with a higher number of iterations leading to more stable results; probability distributions, because each random variable (e.g., cash flows, interest rate volatility) is modeled using an appropriate distribution (e.g., normal, log-normal); sample drawing, because the input data are generated using a pseudo-random method, which allows for the reproduction of realistic economic scenarios; correlations between variables, because mechanisms have been introduced that take into account the relationships between key financial variables, which increases the precision of modeling; and an objective function, because the valuation of the corporate treasury and the analysis of the risk are associated with cash flow forecasts and interest rate volatility.

To ensure the reliability and stability of the results, additional control techniques were applied, such as sensitivity analysis, which was used to assess the impact of individual variables on the final simulation results. This makes it possible to identify key risk factors and assess the stability of the model in different scenarios. Simulation errors resulting from the limited number of iterations were evaluated using the mean absolute error, which measures the average deviation of the simulation results from the theoretical values. Systematic error was also analyzed because it determines whether the simulation generates results with a tendency to overestimate or underestimate real values. A comparison of the Monte Carlo simulation results with analytical methods (conditional probability, Bayes’ rule) and the literature on the subject indicates that the validation of the results allows for an assessment of the reliability of the model and its application in financial management practice. The approach used in this article ensures the reliability of the results thanks to a combination of advanced probabilistic methods, error control and sensitivity analysis. Monte Carlo simulation allows for a comprehensive assessment of financial risk and provides valuable information for corporate treasury management in conditions of uncertainty.

We recommend that future research on the application of the three Monte Carlo paradoxes to corporate treasury management should focus on analyzing the extended use of paradoxes in predicting extreme financial scenarios (Z. Wang et al., 2024), as paradoxes can help manage risk in rare events such as economic crises or unexpected market changes. Integrating the three paradoxes with dynamic scenario models is essential because paradox-based Monte Carlo models can support the continuous adjustment of financial strategies in a dynamic economic environment (Luo & Liu, 2024). The use of paradoxes in evaluating the effectiveness of working capital management strategies (Hung & Dinh, 2022) is essential because risk analysis based on the three paradoxes improves the effectiveness of managing a company’s short-term financing (S. Chen et al., 2025). The use of the three paradoxes in weather risk (weather risk) modeling is recommended and encouraged because paradox-based Monte Carlo simulations can be used to assess the impact of extreme weather events on cash flows (Sabripoor & Ghousi, 2024).

Bertrand’s box paradox helps describe how conditional probabilities affect the prediction of financial stability for low-probability but high-impact events, and how risk analysis changes when uncertainty (Mamani et al., 2024) is included in weather risk inputs (M. M. Hasan et al., 2022).

The three prisoners dilemma allows us to describe how additional information about weather risk affects financial hedging decisions and whether information asymmetry (Elroukh, 2025) between counterparties in financial transactions can be effectively managed using this paradox (Adamolekun, 2024).

The Monty Hall problem helps describe whether changing financial strategy based on new weather data increases the chances of maintaining cash flow stability and what risk protection decisions (such as weather insurance) are optimal in light of this paradox (Demiraj et al., 2024).

The Bertrand box paradox in a Monte Carlo simulation will identify the most critical points of influence of conditional probabilities on cash flows (Sabripoor & Ghousi, 2024), enabling more precise forecasting and planning of financial reserves. The three prisoners dilemma indicates that incorporating additional information will reduce the risk of erroneous decisions, especially in situations of high weather risk or information asymmetry in financial contracts (Elroukh, 2025). The Monty Hall problem demonstrates that changing strategies in response to new weather data will allow companies to better protect themselves from the effects of adverse weather events, such as by purchasing appropriate insurance in advance.

In terms of recommendations for future research, it is worth considering the applicability of the three weather risk paradoxes to corporate financial management. Bertrand’s box paradox can improve the forecasting of the risk of production downtime due to extreme weather events, taking into account the conditional probability of such events. It can also help optimize cash reserves (Elyasiani & Movaghari, 2024) for unforeseen weather-related losses. The three prisoners dilemma can enable the assessment of the impact of additional weather data on financial hedging decisions, such as energy futures, and the management of the risk of information asymmetry (Nusair et al., 2024) between insurers and companies (Behera & Mahakud, 2025). The Monty Hall problem will enable decisions to change insurance strategies based on current weather forecasts and allow the examination of the effectiveness of changing energy or resource providers in response to climate change (Alam et al., 2024).

In future research, we look forward to answering the research questions so that the Bertrand box paradox of Monte Carlo analysis with conditional probabilities can significantly improve the quality of forecasts and reduce the risk of financial shortfalls in the face of weather risk (Dsouza et al., 2024). Properly applied, the three prisoners dilemma will enable the collection of additional weather information to reduce the risk of erroneous financial decisions by 20–30% by better allocating resources to protect against the effects of extreme events (Kalash, 2024). The Monty Hall problem will diversify changes in financial strategy based on current weather forecasts and increase the probability of avoiding financial losses by up to 50%, as confirmed by Monte Carlo simulations.

Future research should focus on incorporating these paradoxes into early warning systems for financial management (Tobisova et al., 2022) and developing models that account for dynamic changes (Luo & Liu, 2024) in the financial and climatic environment (L. Zhang & Gao, 2024).

Recommendations for corporate financial management and policymakers, specifically, short-term (up to a year) recommendations for decision-makers, include implementing Monte Carlo simulations using the three paradoxes for ongoing financial risk analysis, with a focus on liquidity management (S. B. Hasan et al., 2022); considering conditional probabilities (Bertrand’s paradox) to optimize cash reserves; using the three prisoners dilemma to assess the impact of new financial and economic data on investment decisions; and conducting rapid simulations of decisions in a dynamically changing environment (Luo & Liu, 2024), based on the Monty Hall Problem, to avoid decision errors.

Recommendations for decision-makers in corporate financial management include introducing regulations requiring advanced simulation tools, such as Monte Carlo, in financial risk management and establishing reporting standards for using probabilistic data in corporate cash flow forecasts (Rehman et al., 2024).

Medium-term recommendations (up to three years) for decision-makers in corporate treasury management include encouraging the development of predictive models based on the three paradoxes, taking into account industry-specific and weather risks, integrating Monte Carlo simulations into ERP systems and treasury management platforms (Akhtar, 2022) to enable continuous risk monitoring and analysis, and using the three prisoners dilemma to improve decision-making processes in the context of long-term strategic investments while expanding strategic scenarios based on the Monty Hall problem to effectively respond to changes in capital structure and the market environment (Li & Shiu, 2024).

Medium-term recommendations (up to three years) for policymakers (Elroukh, 2025) include encouraging companies to invest in advanced data analytics technologies, offering tax breaks (Pang et al., 2024) or subsidies for implementing Monte Carlo simulations in financial management (L. Liu et al., 2025; Akhtar et al., 2018), and introducing regulations to support the use of probabilistic analysis in financial decisions (Akhtar et al., 2024), especially in sectors exposed to weather risk.

Longer-term recommendations (beyond three years) for policymakers point to the need to undertake building an organizational culture that supports decision-making based on probabilistic data and Monte Carlo scenarios, and to develop comprehensive risk management systems that incorporate Bertrand’s paradox into long-term financial forecast models and create long-term capital allocation strategies using the three prisoners dilemma to account for unexpected information, along with improving adaptation processes by using the Monty Hall problem to manage changes in the regulatory and market environment (Fan et al., 2024).

Longer-term recommendations (beyond three years) for policymakers include guidance on developing a regulatory framework to support the use of advanced probabilistic analysis in the management of corporate financial resources internationally, promoting collaboration between the public and private sectors (da Costa Moraes et al., 2025) in researching the application of the Monte Carlo method to risk management, including weather risk, and creating publicly available analytical platforms that support small- and medium-sized enterprises in implementing advanced risk simulations (Worku, 2021; Belas et al., 2024a).

Key steps for policymakers (Das et al., 2024) should include supporting education and training, introducing educational programs for treasury managers that teach advanced Monte Carlo methods and their application to risk management (Vega-Gutiérrez et al., 2025), and creating industry standards that include implementing uniform standards for the use of probabilistic analysis in financial reporting (Kumar & Symss, 2024).

Key steps for policymakers (Elroukh, 2025) should include supporting technology and funding the research and development of analytical tools that integrate Monte Carlo into corporate financial management (Tobisova et al., 2022). Recommendations must avoid overlooking future monitoring and evaluation by encouraging the creation of mechanisms to monitor the effectiveness of corporate Monte Carlo methods and their impact on financial stability (Park, 2022).

Bertrand’s paradox indicates that, pending results, conditional probabilities can reduce the risk of unforeseen financial events, improving forecast accuracy by 20–30%. The three prisoners dilemma allows additional information about risks, such as weather, to improve the efficiency of financial decisions by better managing information asymmetry (Nusair et al., 2024) and optimizing resource allocation. The Monty Hall problem shows that regularly adjusting financial strategies based on simulations increases the probability of economic success by 40–50%, especially in sectors exposed to market volatility (Kumar & Symss, 2024).

Recommendations are based on incorporating three Monte Carlo paradoxes into corporate financial management processes (L. Liu et al., 2025). Policies (Das et al., 2024) supporting education, technological development and regulations encouraging the use of these methods will improve the long-term performance and financial stability of companies (Carrick, 2023).

Similarly, in the Monte Carlo method, predictions are made for each financial management decision of factors affecting the value of treasury growth under various future scenarios (L. Liu et al., 2025). Monte Carlo analysis should show whether the treasury management action being evaluated should or should not be implemented by the company (Kayani et al., 2025), since the expected value of treasury growth is a key parameter in this procedure (Carrick, 2023).

Monte Carlo analysis is better in terms of information than sensitivity analysis. It is used to analyze the treasury management (Tobisova et al., 2022) of an enterprise under risk and uncertainty (Mamani et al., 2024) by examining the sensitivity of treasury protection, creation and accumulation to changes in single factors (Akgün & Memiş Karataş, 2024). Monte Carlo analysis is, in a sense, an extension of decision tree analysis, which is applicable when the treasury management process under analysis consists of a sequence of decisions and when decisions made at subsequent moments depend on the results of previous decisions (Farooq et al., 2024).

Monte Carlo simulation is a type of analysis linked to sensitivity analysis enriched with probability distributions of explanatory variables. It involves the use of pseudo-random number generators to mimic the time course of cash flows that will take place in a company (Yudaruddin et al., 2024). Like scenario analysis, it allows for the estimation of the expected value of creating, protecting or accumulating corporate treasure (Alban et al., 2017), measures of risk and other parameters, and is considered a more accurate method. Monte Carlo analysis uses a mathematical model to describe treasury management (Tobisova et al., 2022). The first step in its application to treasury management is to create a model containing the company’s free cash flow, FCF. After determining the probability distributions of each random variable, the simulation software makes a random selection of each variable (Banu et al., 2020). The selected value of each random variable, along with the specified values of certain variables, is then used to determine expected cash flows (Athari et al., 2024). Such a process is repeated several times, and each time, specific results are obtained, which are used to construct the probability distribution, its expected value and standard deviation. The final result of the Monte Carlo analysis is, as in the case of scenario analysis and decision tree analysis (L. Liu et al., 2025), the expected net present value (Fantazzini, 2009), based on which the company can decide to accept or reject the implementation of a treasury management project (Steffen, 2018), the risk effectiveness of which is analyzed based on this method.

In the process of evaluating corporate treasury management undertaken under conditions of risk (Jajuga, 2023), in addition to methods that take risk into account indirectly, Monte Carlo simulation is preferred to measures based on the coefficient of variation assessing the effectiveness of the activity that is the subject of treasury management decisions (Zvarikova et al., 2024), or those based on the modification of measures by adjustments due to the need to take risk into account (Park, 2022).

The coefficient of variation is a measure of risk, indicating what the level of risk is per unit of a financial parameter (Alban et al., 2017). In the use of the coefficient of variation, priority for implementation should be given to financial management measures whose performance has a lower coefficient of variation. Monte Carlo simulation avoids the simplistic generalizations implied by the coefficient of variation (Belas et al., 2024b).

We discovered why much of the discussion of the Monty Hall problem in the 1990s took place, and why so many researchers believed that the probability was 50 percent. This 50 percent represents the decision to flip a coin. We found that players should change their minds, which is the best decision of all those studied. The worst decision is the one in which players do not change their minds. The second-worst decision is the one in which players speculate too much—the reverse tic-toc decision. On the other hand, correct speculation is positive—the tic-tac decision is the second-best decision. This study revealed a lot about Monty Hall’s problem and life more broadly. The purpose of the study has been achieved.

This article thematically covers forecast risk management using Monte Carlo simulation to solve veridical-type paradoxes. The use of Monte Carlo simulation as an advanced tool for managing financial forecast risk in financial management is presented. This study analyzed three probabilistic paradoxes—the Bertrand box paradox, the three prisoners dilemma and the Monty Hall Problem—which were used to analyze and solve key problems in corporate financial management (Belas et al., 2023). The study aimed to see how Monte Carlo simulations can help resolve these paradoxes and provide tools for more accurate financial risk forecasting under uncertainty (L. Liu et al., 2025). The paper uses numerical (Monte Carlo simulations) and analytical (Bayes’ rule, conditional probabilities) methods. Simulations were carried out under different scenarios, considering different decision options and outcomes. In the discussion on Bertrand’s box paradox, it was shown how conditional probabilities affect the accuracy of cash flow forecasts, especially in liquidity risk analysis. In the context of the three prisoners dilemma, it was revealed that additional information allows for more precise investment decisions, such as allocating capital to projects with different risk profiles. Regarding the Monty Hall problem, it was proven that flexibility and changing strategies (e.g., debt refinancing) increase the probability of achieving favorable financial results. The importance of Monte Carlo simulation for corporate financial management is undeniable, and it can be used to forecast financial risks, improve the accuracy of cash flow forecasts and liquidity management and reduce cash flow volatility. It also enables the optimization of financial reserves based on probability distributions.

Future practical applications of paradoxes in financial management and investment decision-making involve the optimization of corporate treasury management strategies. Monty Hall’s paradox indicates that flexibility in financial decision-making leads to better results. In corporate treasury practice, this could mean changing the debt refinancing strategy after more favorable market conditions have been identified, thus dynamically managing liquidity by adjusting investment strategies to changing macroeconomic scenarios, and using Monte Carlo to forecast the future value of a corporate treasury and determine the optimal level of cash reserves.

Investment decisions under information asymmetry should help solve the three prisoners dilemma in the future, as it relates to decision-making under the influence of new information. It can be used to analyze the impact of additional market data on the selection of investment projects—e.g., the choice between a high-risk start-up and a stable company—and to model capital allocation decisions—changing original investment decisions after obtaining new economic forecasts can increase the chances of a higher rate of return.

The management of capital structure and credit risk may be better addressed in the future by unraveling the Bertrand paradox, which allows for the analysis of the impact of conditional probability on financial risk. It can be applied in credit risk management because Monte Carlo can simulate the probability of customer default and help determine the optimal credit policy, as well as optimize capital structure, because it assesses the risk associated with different sources of financing under conditions of random interest rate volatility. Predictive models for cash flow forecasting can also benefit from our proposal in the future, as Monte Carlo in combination with the Bertrand paradox can be used to more accurately forecast cash availability when accompanied by an analysis of the conditional probability of a financial deficit, and can also optimize hedging strategies and predict exchange rate risks based on random market fluctuations.

In the future, the application of our proposal may support the development of early warning systems for companies, as future research should focus on integrating probabilistic methods into early warning systems. The application of probabilistic paradoxes in financial management and investment management indicates the potential for increasing the accuracy of strategic decisions by dynamically incorporating newly emerging information. Monte Carlo in combination with these methods allows for more precise forecasting and risk minimization, which can lead to an increase in the financial stability of companies.

The results of Monte Carlo analysis in corporate treasury management are applicable to capital structure management in assessing the impact of different financing strategies on the financial stability of a company.

The results of this study indicate that Monte Carlo simulations, due to their probabilistic modeling capabilities, provide more precise and practical tools for risk management in corporate treasury management compared to traditional methods of sensitivity or coefficient-of-variation analysis. Integrating probabilistic paradox analysis enables more informed financial decisions, contributing to the long-term growth of a company’s value.

Research suggests that the practical application of these methods should include the development of early warning systems for corporate financial management. This should be complemented by the integration of Monte Carlo simulation with ERP tools and the use of advanced probabilistic analysis in strategic financial planning used in corporate financial management. This article contributes to the development of financial risk management tools by pointing out the potential of Monte Carlo simulation in resolving probabilistic paradoxes and improving the financial stability of enterprises.