Long-Range Behaviour and Correlation in DFA and DCCA Analysis of Cryptocurrencies
Abstract
:1. Introduction
2. Brief Literature Review
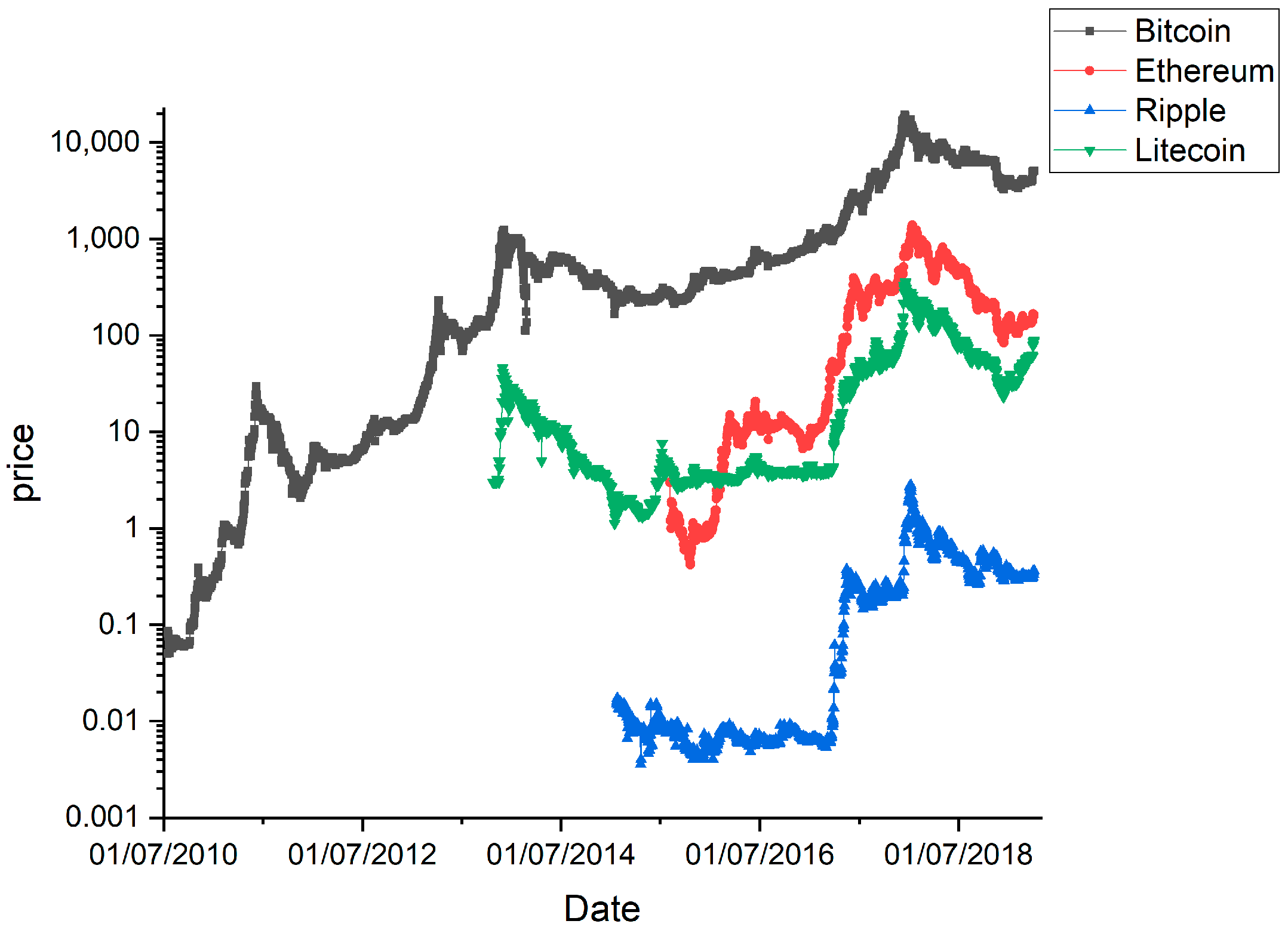
3. Methodology and Data
4. Results
5. Concluding Remarks
5.1. Main Conclusions
5.2. Potential Implications for Markets and Investors
5.3. Limitations and Future Research
Author Contributions
Funding
Conflicts of Interest
References
- Alvarez-Ramirez, José, Eduardo Rodriguez, and Carlos Ibarra-Valdez. 2018. Long-range correlations and asymmetry in the Bitcoin market. Physica A 492: 948–55. [Google Scholar] [CrossRef]
- Al-Yahyaee, Khamis, Walid Mensi, and Seong-Min Yoon. 2018. Efficiency, multifractality, and the long-memory property of the Bitcoin market: A comparative analysis with stock, currency, and gold markets. Finance Research Letters 27: 228–34. [Google Scholar] [CrossRef]
- Anagnostidis, Panagiotis, Christos Varsakelis, and Christos Emmanouilides. 2016. Has the 2008 financial crisis affected stock market efficiency? The case of Eurozone. Physica A 447: 116–28. [Google Scholar] [CrossRef]
- Andreou Elena, Nikitas Pittis, and Aris Spanos. 2001. On modelling speculative prices: The empirical literature. Journal of Economic Surveys 15: 187–220. [Google Scholar] [CrossRef]
- Antonakakis, Nikolaos, Ioannis Chatziantoniou, and David Gabauer. 2019. Cryptocurrency market contagion: Market uncertainty, market complexity, and dynamic portfolios. Journal of International Financial Markets, Institutions and Money 61: 37–51. [Google Scholar] [CrossRef] [Green Version]
- Bachelier, Louis. 1964. Theory of speculation. In The Random Character of Stock Prices. Edited by Paul Cootner. Cambridge: MIT Press. First published 1900. [Google Scholar]
- Bank for International Settlements. 2015. Digital Currencies. S.L.: Committee on Payments and Market Infrastructures. Basel: Bank for International Settlements. [Google Scholar]
- Bariviera, Aurelio. 2017. The inefficiency of Bitcoin revisited: A dynamic approach. Economics Letters 161: 1–4. [Google Scholar] [CrossRef] [Green Version]
- Bariviera, Aurelio, María José Basgall, Waldo Hasperué, and Marcelo Naiouf. 2017. Some stylized facts of the Bitcoin market. Physica A: Statistical Mechanics and Its Applications 484: 82–90. [Google Scholar] [CrossRef] [Green Version]
- Bartos, Jakub. 2015. Does Bitcoin follow the hypothesis of efficient market? International Journal of Economic Sciences IV: 10–23. [Google Scholar] [CrossRef]
- Cajueiro, Daniel, and Benjamin Tabak. 2004a. The Hurst exponent over time: Testing the assertion that emerging markets are becoming more efficient. Physica A 336: 521–37. [Google Scholar] [CrossRef]
- Cajueiro, Daniel, and Benjamin Tabak. 2004b. Evidence of long range dependence in Asian equity markets: The role of liquidity and market restrictions. Physica A 342: 656–64. [Google Scholar] [CrossRef]
- Cajueiro, Daniel, and Benjamin Tabak. 2006. Testing for predictability in equity returns for European transition markets. Economic Systems 30: 56–78. [Google Scholar] [CrossRef]
- Cajueiro, Daniel, and Benjamin Tabak. 2008a. Testing for long-range dependence in world stock markets. Chaos, Solitons & Fractals 37: 918–27. [Google Scholar]
- Cajueiro, Daniel, and Benjamin Tabak. 2008b. Testing for time-varying long-range dependence in real estate equity returns. Chaos, Solitons & Fractals 38: 293–307. [Google Scholar]
- Campbell-Verduyn, Malcolm. 2018. Bitcoin, crypto-coins, and global anti-money laundering governance. Crime, Law and Social Change 69: 283–305. [Google Scholar] [CrossRef]
- Cao, Guangxi, and Minjia Zhang. 2015. Extreme values in the Chinese and American stock markets based on detrended fluctuation analysis. Physica A 436: 25–35. [Google Scholar] [CrossRef]
- Carbone Anna, Giuliano Castelli, and Harry Stanley. 2004. Time dependent Hurst exponent in financial time series. Physica A 344: 267–71. [Google Scholar] [CrossRef]
- Chaffee, Eric. 2018. The Heavy Burden of Thin Regulation: Lessons Learned from the SEC’s Regulation of Cryptocurrencies. Mercer Law Review 70: 615. [Google Scholar]
- Chakrabarti, Bikas, Anirban Chakraborti, and Arnab Chatterjee. 2006. Econophysics and Sociophysics: Trends and Perspectives. Weinheim: Wiley-VCH Verlag. [Google Scholar]
- Corbet, Shaen, Brian Lucey, Andrew Urquhart, and Larisa Yarovaya. 2018. Cryptocurrencies as a financial asset: A systematic analysis. International Review of Financial Analysis 62: 182–99. [Google Scholar] [CrossRef]
- El Alaoui, Marwane, Elie Bouri, and David Roubaud. 2018. Bitcoin price–volume: A multifractal cross-correlation approach. Finance Research Letters. [Google Scholar] [CrossRef]
- Fama, Eugene. 1970. Efficient Capital Markets: A Review of Theory and Empirical Work. The Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Ferreira, Paulo. 2018. Dynamic long-range dependences in the Swiss stock market. Empirical Economics 2018: 1–33. [Google Scholar] [CrossRef]
- Ferreira, Paulo, and Andreia Dionísio. 2015. Revisiting covered interest parity in the European Union: The DCCA Approach. International Economic Journal 29: 597–615. [Google Scholar] [CrossRef]
- Ferreira, Paulo, Andreia Dionísio, and Gilney Zebende. 2016. Why does the Euro fail? The DCCA approach. Physica A 443: 543–54. [Google Scholar] [CrossRef]
- Ferreira, Paulo, Luís Loures, José Nunes, and Andreia Dionísio. 2017. The behaviour of share returns of football clubs: An econophysics approach. Physica A 472: 136–44. [Google Scholar] [CrossRef]
- Ferreira, Paulo, Éder Pereira, Marcus da Silva, and Hernane Pereira. 2019. Detrended correlation coefficients between oil and stock markets: The effect of the 2008 crisis. Physica A 517: 86–96. [Google Scholar] [CrossRef]
- Granger, Clive, and Oskar Morgenstern. 1963. Spectral analysis of New York stock market prices. Kyklos 16: 1–27. [Google Scholar] [CrossRef]
- Jiang, Yonghong, He Nie, and Weihua Ruan. 2018. Time-varying long-term memory in Bitcoin market. Finance Research Letters 25: 280–84. [Google Scholar] [CrossRef]
- Jovanovic, Franck, and Philippe Le Gall. 2001. Does God practice a random walk? The ‘financial physics’ of a nineteenth-century forerunner, Jules Regnault. European Journal of the History of Economic Thought 8: 332–62. [Google Scholar] [CrossRef]
- Khuntia, Sashikanta, and Jamini Pattanayak. 2018. Adaptive market hypothesis and evolving predictability of bitcoin. Economics Letters 167: 26–28. [Google Scholar] [CrossRef]
- Köchling, Gerrit, Janis Müller, and Peter N. Posch. 2018. Does the introduction of futures improve the efficiency of Bitcoin? Finance Research Letters 30: 367–70. [Google Scholar] [CrossRef]
- Kristoufek, Ladislav. 2014. Measuring correlations between non-stationary series with DCCA coefficient. Physica A 402: 291–98. [Google Scholar] [CrossRef]
- Kristoufek, Ladislav, and Miloslav Vosvrda. 2013. Measuring capital market efficiency: Global and local correlations structure. Physica A 392: 184–93. [Google Scholar] [CrossRef]
- Kyriazis, Nikolaos. 2019. A Survey on Efficiency and Profitable Trading Opportunities in Cryptocurrency Markets. Journal of Risk and Financial Management 12: 67. [Google Scholar] [CrossRef]
- Lahmiri, Selim, and Stelios Bekiros. 2018. Chaos, randomness and multi-fractality in Bitcoin market. Chaos, Solitons & Fractals 106: 28–34. [Google Scholar]
- Li, Yannan, Willy Susilo, Guomin Yang, Yong Yu, Xiaojiang Du, Dongxi Liu, and Nadra Guizani. 2019. Toward Privacy and Regulation in Blockchain-based Cryptocurrencies. IEEE Network, 1–70. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit. 1963. The variation of certain speculative prices. The Journal of Business 36: 394–419. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit, and James Wallis. 1969. Some long-run properties of geophysical records. Water Resources Research 5: 321–40. [Google Scholar] [CrossRef]
- McCauley, Joseph, Kevin Bassler, and Gemunu Gunaratne. 2008. Martingales, detrending data, and the efficient market hypothesis. Physica A 387: 202–16. [Google Scholar] [CrossRef]
- Nadarajah, Saralees, and Jeffrey Chu. 2017. On the inefficiency of Bitcoin. Economics Letters 150: 6–9. [Google Scholar] [CrossRef]
- Osborne, Martin. 1959. Brownian motion in the stock market. Operations Research 7: 145–73. [Google Scholar] [CrossRef]
- Osborne, Martin. 1962. Periodic structure in the Brownian motion of stock prices. Operations Research 10: 345–79. [Google Scholar] [CrossRef]
- Peng, Chung-Kang, Sergey Buldyrev, Shlomo Havlin, Michael Simons, Harry Eugene Stanley, and Ary Goldberger. 1994. Mosaic organization of DNA nucleotides. Physical Review 49: 1685. [Google Scholar] [CrossRef] [PubMed]
- Peng, Chung-Kang, Shlomo Havlin, Harry Stanley, and Ary Goldberger. 1995. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos: An Interdisciplinary Journal of Nonlinear Science 49: 82–87. [Google Scholar] [CrossRef] [PubMed]
- Pereira Éder, Marcus da Silva, Ivan da Cunha Lima, and Hernane Pereira H. 2018. Trump’s Effect on stock markets: A multiscale approach. Physica A 512: 241–47. [Google Scholar] [CrossRef]
- Podobnik, Boris, and Harry Stanley. 2008. Detrended cross-correlation analysis: A new method for analyzing two non-stationary time series. Physical Review Letters 100: 084102. [Google Scholar] [CrossRef] [PubMed]
- Podobnik, Boris, Zhi-Qiang Jiang, Wei-Xing Zhou, and Harry Eugene Stanley. 2011. Statistical tests for powerlaw cross-correlated processes. Physical Review E 84: 066118. [Google Scholar] [CrossRef] [PubMed]
- Van Wegberg, Rolf, Jan-Jaap Oerlemans, and Oskar van Deventer. 2018. Bitcoin money laundering: Mixed results?: An explorative study on money laundering of cybercrime proceeds using bitcoin. Journal of Financial Crime 25: 419–35. [Google Scholar] [CrossRef]
- Samuelson, Paul. 1965. Proof that properly anticipated prices fluctuate randomly. Industrial Management Review 6: 41–49. [Google Scholar]
- Silva, Paulo, Marcelo Klotzle, Antonio Pinto, and Leonardo Gomes. 2019. Herding behavior and contagion in the cryptocurrency market. Journal of Behavioral and Experimental Finance 22: 41–50. [Google Scholar] [CrossRef]
- Tiwari, Aviral, Rabin Jana, Debojyoti Das, and David Roubaud. 2018. Informational efficiency of Bitcoin—An extension. Economics Letters 163: 106–9. [Google Scholar] [CrossRef]
- Urquhart, Andrew. 2016. The inefficiency of Bitcoin. Economics Letters 148: 80–82. [Google Scholar] [CrossRef]
- Urquhart, Andrew. 2018. What causes the attention of Bitcoin? Economics Letters 166: 40–44. [Google Scholar] [CrossRef] [Green Version]
- Yen, Gili, and Cheng-Few Lee. 2008. Efficient market hypothesis (EMH): Past, present and future. Review of Pacific Basin Financial Markets and Policies 11: 305–29. [Google Scholar] [CrossRef]
- Zebende, Gilney. 2011. DCCA cross-correlation coefficient: Quantifying level of cross-correlation. Physica A 390: 614–18. [Google Scholar] [CrossRef]
- Zhang, Wei, Pengfei Wang, Xiao Li, and Dehua Shen. 2018a. The inefficiency of cryptocurrency and its cross-correlation with Dow Jones Industrial Average. Physica A 510: 658–70. [Google Scholar] [CrossRef]
- Zhang, Wei, Pengfei Wang, Xiao Li, and Dehua Shen. 2018b. Some stylized facts of the cryptocurrency market. Applied Economics 50: 5950–65. [Google Scholar] [CrossRef]
- Zhang, Yuanyuan, Stephen Chan, Jeffrey Chu, and Saralees Nadarajah. 2019. Stylised facts for high frequency cryptocurrency data. Physica A 513: 598–612. [Google Scholar] [CrossRef]
- Zhao, Xiaojun, Pengjian Shang, and Jongjong Huang. 2017. Several fundamental properties of DCCA cross-correlation coefficient. Fractals 25: 1750017. [Google Scholar] [CrossRef]



| Cryptocurrency | Period | Observations |
|---|---|---|
| Bitcoin (BTC) | 16 July 2010–5 April 2019 | 3185 |
| Ethereum (ETH) | 6 August 2015–5 April 2019 | 1338 |
| Ripple (XRP) | 21 January 2015–5 April 2019 | 1536 |
| Litecoin (LTC) | 23 October 2013–5 April 2019 | 1990 |
| Bitcoin | Ethereum | Ripple | Litecoin | |
|---|---|---|---|---|
| Mean | 0.0036 | 0.0030 | 0.0021 | 0.0017 |
| Std. Dev. | 0.0676 | 0.0757 | 0.1083 | 0.0765 |
| Minimum | −0.8488 | −0.9163 | −0.9973 | −0.9345 |
| Maximum | 1.4744 | 0.3830 | 1.0280 | 0.8904 |
| Skewness | 2.9622 | −1.1293 | 0.8260 | 0.6468 |
| Kurtosis | 93.1595 | 18.8855 | 23.2271 | 33.8733 |
| Cryptocurrency | DFA Exponent |
|---|---|
| Bitcoin (BTC) | 0.5166 ± 0.0076 |
| Ethereum (ETH) | 0.5347 ± 0.0111 |
| Ripple (XRP) | 0.4980 ± 0.0124 |
| Litecoin (LTC) | 0.4439 ± 0.0051 |
| Cryptocurrency | Efficiency Index (EI) |
|---|---|
| Bitcoin (BTC) | 0.0026 |
| Ethereum (ETH) | 0.0061 |
| Ripple (XRP) | 0.0027 |
| Litecoin (LTC) | 0.0089 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, N.; Silva, C.; Ferreira, P. Long-Range Behaviour and Correlation in DFA and DCCA Analysis of Cryptocurrencies. Int. J. Financial Stud. 2019, 7, 51. https://doi.org/10.3390/ijfs7030051
Costa N, Silva C, Ferreira P. Long-Range Behaviour and Correlation in DFA and DCCA Analysis of Cryptocurrencies. International Journal of Financial Studies. 2019; 7(3):51. https://doi.org/10.3390/ijfs7030051
Chicago/Turabian StyleCosta, Natália, César Silva, and Paulo Ferreira. 2019. "Long-Range Behaviour and Correlation in DFA and DCCA Analysis of Cryptocurrencies" International Journal of Financial Studies 7, no. 3: 51. https://doi.org/10.3390/ijfs7030051
APA StyleCosta, N., Silva, C., & Ferreira, P. (2019). Long-Range Behaviour and Correlation in DFA and DCCA Analysis of Cryptocurrencies. International Journal of Financial Studies, 7(3), 51. https://doi.org/10.3390/ijfs7030051






