Abstract
Internet-of-Things (IoT) devices are interconnected objects embedded with sensors and software, enabling data collection and exchange. These devices encompass a wide range of applications, from household appliances to industrial systems, designed to enhance connectivity and automation. In distributed IoT networks, achieving reliable decision-making necessitates robust consensus mechanisms that allow devices to agree on a shared state of truth without reliance on central authorities. Such mechanisms are critical for ensuring system resilience under diverse operational conditions. Recent research has identified three common limitations in existing consensus mechanisms for IoT environments: dependence on synchronised networks and clocks, reliance on centralised coordinators, and suboptimal performance. To address these challenges, this paper introduces a novel consensus mechanism called Randomised Asynchronous Consensus with Efficient Real-time Sampling (RACER). The RACER framework eliminates the need for synchronised networks and clocks by implementing the Sequenced Probabilistic Double Echo (SPDE) algorithm, which operates asynchronously without timing assumptions. Furthermore, to mitigate the reliance on centralised coordinators, RACER leverages the SPDE gossip protocol, which inherently requires no leaders, combined with a lightweight transaction ordering mechanism optimised for IoT sensor networks. Rather than using a blockchain for transaction ordering, we opted for an eventually consistent transaction ordering mechanism to specifically deal with high churn, asynchronous networks and to allow devices to independently and deterministically order transactions. To enhance the throughput of IoT networks, this paper also proposes a complementary algorithm, Peer-assisted Latency-Aware Traffic Optimisation (PLATO), designed to maximise efficiency within RACER-based systems. The combination of RACER and PLATO is able to maintain a throughput of above 600 mb/s on a 100-node network, significantly outperforming the compared consensus mechanisms in terms of network node size and performance.
1. Introduction
The proliferation of Internet of Things (IoT) devices has revolutionised various sectors, from smart homes [1] and cities [2] to industrial control systems [3] and health monitors [4], but has also introduced significant security risks such as hacking [5], data breaches [6], and physical tampering [7] due to their reliance on wireless connectivity and internet access. The decentralised nature of IoT systems complicates achieving consensus and maintaining transaction integrity among multiple interacting stakeholders and devices. In response, consensus mechanisms have emerged as crucial solutions, providing a framework for distributed systems to agree on network states or transaction outcomes, thereby preventing disputes, detecting anomalies, and ensuring seamless collaboration without relying on central authorities [8]. This decentralised approach enhances system resilience by mitigating single-point failures.
IoT-focused consensus mechanisms in the literature commonly make a number of assumptions that can affect the practicality of their algorithms in real-world scenarios. Some of these assumptions include a synchronous or semi-synchronous network [9,10], the use of a coordinator node, which introduces a central point of failure [11] or low performance which may limit the number of applications the consensus mechanism is usable in [12,13]. Cryptocurrency-focused consensus mechanisms often incorporate a monetary system, which may not be suitable for sensor-based IoT networks. Additionally, the inherent unreliability of IoT nodes due to intermittent wireless reception, power-saving states, or task-induced delays can cause validator- or leader-based consensus mechanisms to stall under synchronous or partially synchronous network assumptions. Moreover, many existing IoT-focused consensus mechanisms lack effective mechanisms to control network latency, leading to “runaway latency” during traffic surges and causing prolonged unresponsiveness. We identify centralisation, restrictive network assumptions, and poor performance as the primary challenges that our proposed IoT consensus mechanism aims to address. Subsequent sections will provide a detailed examination of these issues.
Synchronous Network Assumptions and Centralised Leaders
In synchronous IoT consensus networks, all devices must synchronise their actions precisely, providing strong integrity guarantees but introducing significant security vulnerabilities. Any device failure or compromise can halt the entire network due to its role as a choke point, making such systems susceptible to targeted attacks [14]. Additionally, centralised leader nodes in these networks serve as single points of control and failure, concentrating risks and attracting malicious actors aiming to disrupt operations by targeting the leader node. These centralised architectures not only limit adaptability but also introduce substantial security liabilities [15]. To address these challenges, RACER, an asynchronous consensus mechanism without a central leader, and PLATO, a traffic optimisation algorithm designed to minimise message latency, are introduced in subsequent sections to enhance both security and performance in IoT systems.
IoT Consensus and Traffic Optimisation
To address the identified challenges, we propose two algorithms: Randomised Asynchronous Consensus with Efficient Real-time Sampling (RACER) and Peer-assisted Latency-Aware Traffic Optimisation (PLATO). RACER, a variant of the Sequenced Probabilistic Double Echo (SPDE) protocol, operates asynchronously without a central leader, ensuring resilience against Byzantine behaviours through decentralised transaction ordering. PLATO is a distributed traffic optimisation algorithm that uses trend detection to assess real-time network capacity and adjusts consensus parameters based on RACER’s gossip protocol to mitigate latency issues. By functioning asynchronously and eliminating the need for centralised leadership, RACER ensures eventual consistency and independent device operations. PLATO enhances performance by dynamically adjusting message-sending rates based on detected latency trends, optimising network efficiency. Together, RACER and PLATO address synchronous assumptions, centralisation, and poor performance in IoT consensus mechanisms.
Research Contributions
The key advantages of our algorithm over other IoT-focused consensus algorithms can be summarised as follows:
- Robustness in asynchronous environments: RACER eliminates dependence on synchronous network assumptions or timing guarantees, enabling fault-tolerant transaction ordering in dynamically changing IoT environments. This allows RACER to operate reliably, even under unpredictable delays and intermittent connectivity.
- Decentralised consensus mechanism: by eliminating centralised leadership in consensus processes, RACER removes single points of failure and enhances resilience against targeted attacks or leader compromises, ensuring robustness in heterogeneous IoT deployments.
- Scalability under realistic workloads: Through simulations with 100 nodes processing large transactions, RACER demonstrates significantly higher throughput than existing IoT-focused consensus protocols in the literature. This highlights its ability to efficiently handle high-volume and complex transaction scenarios typical of modern IoT deployments.
- End to end system validation: RACER and PLATO are fully implemented in Python 3.10, enabling comprehensive experiments with the complete software stack rather than isolated components. This holistic implementation allows for more realistic evaluations of system performance under real-world conditions compared with fragmented testing approaches.
This paper is structured as follows: Section 2 covers recent consensus mechanisms from the literature. Section 3 details the IoT consensus mechanism and traffic optimisation algorithm. Section 4 explains our Python implementation of both the consensus mechanism and traffic optimisation algorithms. Section 5 presents the experimental results relating to traffic optimisation algorithm selection and impacts on consensus performance. Finally, Section 6 and Section 7 provide the discussion and concluding remarks, respectively.
2. Related Work
Consensus mechanisms are fundamental for enabling reliable operations and trustless interactions in IoT ecosystems. These mechanisms allow distributed nodes to agree on a shared network state, ensuring integrity, availability, and security in resource-constrained environments. They also support functionalities beyond transactions, such as authentication and authorisation. Various consensus types exist, including Proof of Work (PoW) [16], Proof of Stake (PoS) [17], and Practical Byzantine Fault Tolerance (PBFT) [18], each with trade-offs in security, efficiency, and scalability. PoW is computationally intensive, while PoS reduces energy costs but risks centralisation [19]. PBFT offers high throughput but requires pre-established node identities [20]. Recent research focuses on adapting these mechanisms for IoT, addressing challenges like device heterogeneity and connectivity variability [21], with hybrid models emerging to enhance resilience and scalability in complex IoT environments [22].
PoEWAL [12] modifies Bitcoin’s consensus mechanism for IoT devices by reducing computational load through shorter mining periods. Miners compete based on hash values with the most consecutive zeros. Ties are broken using “Proof of Luck”, selecting the node with the lowest hash value. PoEWAL requires synchronised clocks and uses dynamic difficulty adjustment but faces limitations in transaction throughput due to its reliance on time-synchronised operations.
Microchain [9] is a lightweight consensus mechanism for IoT inspired by Proof of Stake (PoS). It uses two key components: Proof of Credit (PoC), where validators are selected based on credit weight to produce blocks, and Voting-based Chain Finality (VCF), which resolves forks and ensures blockchain integrity. Microchain operates under synchronous network assumptions, providing persistence and liveness guarantees. However, it relies on synchronised clocks among devices for its operation.
PoSCS [13] is a consensus mechanism for the Perishable Food Supply Chain (PFSC), integrating IoT, blockchain, and databases to manage supply chain data. Unlike traditional currency-based PoS systems, PoSCS uses a reputation system with four factors—Influence, Interest, Devotion, and Satisfaction—to pseudorandomly select block producers. These producers also perform minimal PoW mining to regulate block creation time. The mechanism employs a hybrid architecture, storing supply chain data both on the blockchain and in a cloud database. Once an object completes its journey, it is archived from IoT devices to the cloud. However, PoSCS’ reliance on cloud storage and limited throughput may pose challenges for certain implementations.
Huang et al. [11] introduced Credit-Base Proof of Work (CBPoW) for IoT devices, where nodes earn positive scores by following consensus rules or receive negative scores for malicious actions like lazy tips and double-spending. Nodes with low PoW credit face penalties, making it harder for them to add transactions. CBPoW uses a tiered network with lite nodes collecting data and full nodes maintaining the tangle. While addressing specific attacks, the IoTA DAG implementation in CBPoW has a central point of failure [23].
Proof of Block and Trade (PoBT) [24] is a consensus mechanism tailored for business blockchain applications. It operates through two stages: trade verification, where source and destination nodes validate transactions before forwarding them to an orderer, and consensus formation, which uses an algorithm to select participating nodes based on their trade counts. Each session node receives a unique random number; the block is only committed if the sum of these numbers from responding nodes matches the expected value, ensuring contributions are valid and preventing malicious activity. PoBT demonstrates higher efficiency than Hyperledger Fabric but may lack generalisability for IoT applications.
Tree Chain [10] employs a tree-structured blockchain where a single randomly selected validator commits transactions to enhance efficiency. The consensus algorithm uses two randomisation levels at transaction and blockchain to identify validators responsible for specific consensus codes, with assignments based on a Key Weight Metric (KWM) derived from the hash of their public key. The setup involves validators expressing interest and the highest KWM validator generating a genesis block. Tree Chain enables near real-time processing without computational puzzles but requires a synchronous network.
Proof of Authentication (PoAh) [25] is a lightweight consensus mechanism designed for resource-constrained environments like IoT networks, aiming to create a sustainable blockchain. It integrates an authentication process during block validation, using ElGamal encryption for signing blocks with private keys and verifying via public keys, while trusted nodes initialised with a trust value of tr = 10 validate blocks through signature checks and MAC address verification in two rounds. Blocks are broadcast by users, who first share their public key. Trusted nodes authenticate these blocks, adjusting trust values. Successful authentication increases a node’s trust (+1), and failed attempts decrease it (−1). Untrusted nodes (tr = 0) gain partial trust (tr = 0.5) after validating blocks while detecting fake blocks grants tr = 1. Nodes with trust below a threshold (th = 5) are removed, allowing non-trusted nodes to participate. Validated blocks are broadcast with PoAh identifiers and linked via cryptographic hashes to form the blockchain, balancing security and efficiency for constrained devices. Depending on the network’s threat model, excessive centralisation may not be appropriate for some implementations.
The reviewed consensus mechanisms demonstrate innovative adaptations of existing protocols to suit specific domains such as IoT, supply chain management, and business applications. However, they collectively face challenges related to reliance on synchronised networks, limited transaction throughput, and dependencies on centralised components or cloud storage. A summary of all the consensus mechanisms reviewed in this section can be found in Table 1. In the following section, we will cover the materials and methods related to our consensus mechanism.

Table 1.
A comparison of the consensus mechanisms in the related work section compared against IoT-relevant metrics.
3. Materials and Methods
In the materials and methods section, we will give a general overview of our IoT consensus mechanism, and our traffic optimisation algorithm.
3.1. Proposed IoT Consensus Mechanism
RACER utilises a specialised Byzantine Broadcast (BB) mechanism combined with casual ordering via vector clocks to achieve consensus in the IoT. This approach is designed specifically to address the unique challenges faced by IoT devices, including dynamic environments and unstable network conditions. By focusing on lightweight algorithms that maintain Byzantine tolerance and minimise latency, RACER avoids the need for full State Machine Replication (SMR), which would be too resource intensive for many IoT applications.
The chosen consensus mechanism in RACER, Sequenced Probabilistic Double Echo (SPDE) [26], relies on probabilistic guarantees to ensure efficient message dissemination across the network. Unlike traditional mechanisms like Proof of Work (PoW) or Proof of Stake (PoS), which are energy-intensive and require significant node investment, respectively, SPDE uses a sampling-based approach for validation that reduces computational overhead while maintaining robust security properties. This makes RACER particularly suitable for IoT devices where energy efficiency and performance are critical.
In contrast to Byzantine Fault Tolerance (BFT) methods that necessitate pre-established identities and can become complex as node populations grow, the sampling-based consensus in RACER offers a balance between decentralisation and efficiency. It enhances scalability without compromising on security, making it an ideal solution for IoT devices constrained by limited computational power and energy availability. By avoiding full SMR, which would be impractical for many IoT scenarios due to high resource demands, RACER provides robust consensus through probabilistic validation that requires fewer resources from individual devices. This makes it a more viable option for large-scale, decentralised IoT applications where energy efficiency is a priority.
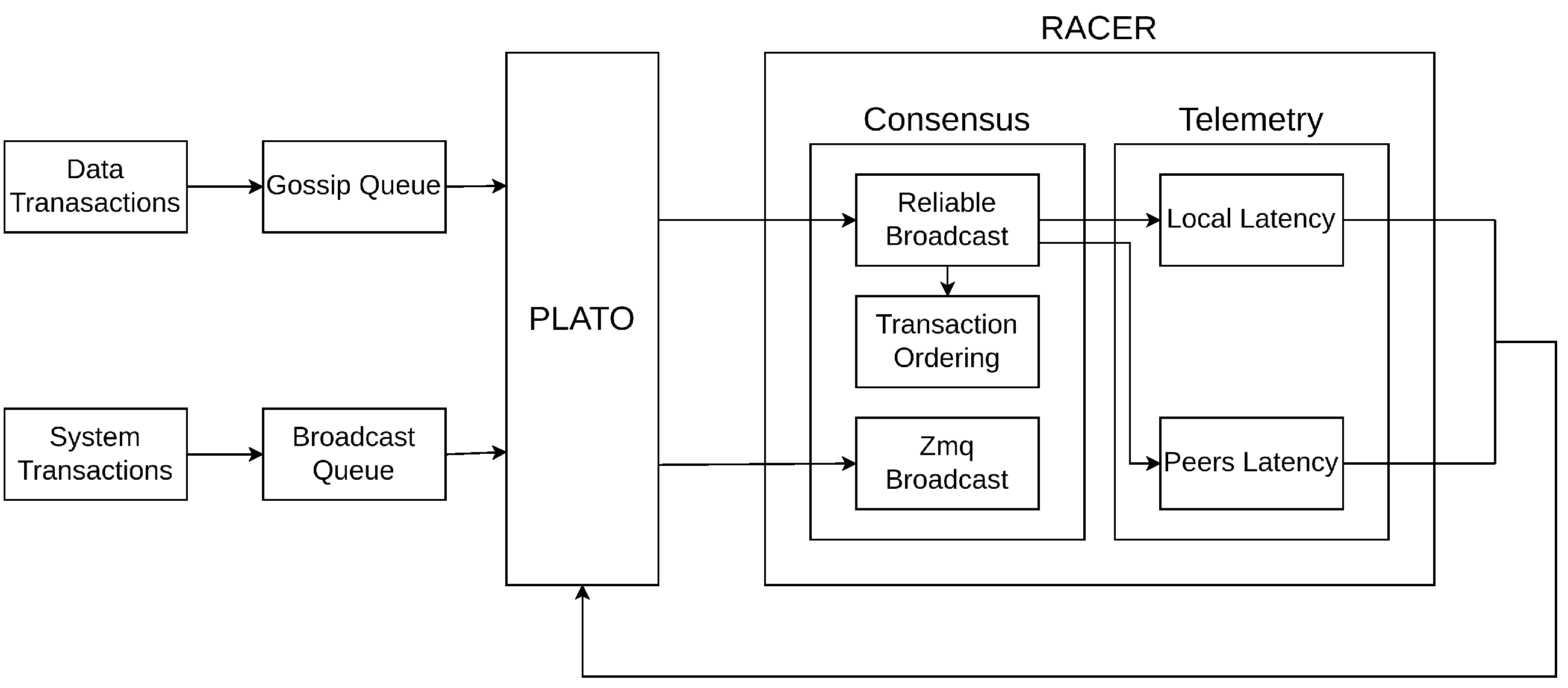
SPDE uses randomised network topologies as it converges towards consensus through random sampling of neighbouring nodes. In distributed networks, four primary types of network topologies are typically utilised for scalability: traditional clique-based designs that result in quadratic message complexity (O(n2)), star-based architectures like HotStuff [27] with linear message complexity (O(n)), tree-based communication structures that distribute vote aggregation across a hierarchical framework, as observed in ByzCoin [28] and Kauri [29], and gossip protocols that probabilistically disseminate messages through randomly selected nodes, shown by Algorand [30], Tendermint [31], and Gosig [32]. We opted for randomised gossip networks as our network topology due to their balance between communication complexity and fault tolerance. Randomised gossiping reduces the network complexity compared with clique-based designs, avoids the leader bottleneck associated with star-based topologies, and circumvents the need for reconfiguration seen in tree-based structures. Although gossip-based topologies are susceptible to duplicate message broadcasts (an issue mitigated through message aggregation), their inherent fault-tolerant nature due to the absence of a fixed network hierarchy or structure enables our chosen topology to achieve an optimal balance between efficiency and resilience, particularly suitable for IoT devices. A graphical overview of RACER and PLATO can be found in Figure 1.
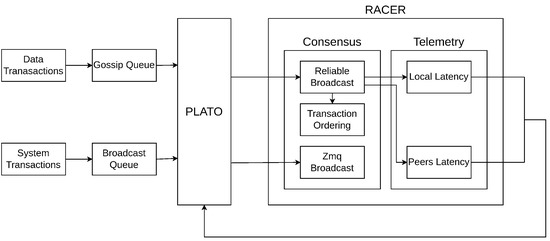
Figure 1.
The RACER consensus mechanism involves nodes continuously completing rounds of Reliable Broadcast (also called Sequenced Probabilistic Double Echo (SPDE) throughout the paper). Once nodes successfully broadcast transactions, transactions are deterministically sequenced. RACER provides PLATO telemetry on self-reported local latency and latency data from our peers.
We specifically selected and adapted the Sequenced Probabilistic Double Echo for our IoT consensus and gossiping algorithm as it provides the following security properties (note that ∈ [0, 1] and represents a failure probability of the system):
- Byzantine tolerance of up to f = (n−1)/3, where f is the number of malicious nodes and n is the total number of nodes on the network.
- No Creation: This condition ensures that if a correct process never broadcast more than n messages, then no other correct process will deliver more than these n messages.
- Integrity: It guarantees that any message delivered by a correct process was indeed broadcasted by another correct process .
- Validity: If a correct process initially broadcasts a sequence of messages, it should eventually deliver the same sequence with at least probability . This ensures that there is a high likelihood that what is broadcast will also be delivered by the sender.
- Totality: Once one correct process delivers n messages, every other correct process should also deliver these exact n messages eventually with probability of at least . It reflects a form of agreement across all correct processes regarding the delivery of messages.
- Consistency: This condition ensures that if multiple correct processes deliver sequences of n messages each, they will receive and deliver exactly the same sequence of messages with high probability of at least . It enforces uniformity in the message sequences delivered across all correct processes.
3.1.1. Transaction Ordering in RACER
To meet RACER’s need for lightweight transaction ordering without centralisation or reliance on external actors, we designed a mechanism that achieves eventual consistency through atomic messaging guarantees from SPDE and gossip algorithms. Each transaction incorporates a vector clock, a logical timestamp used to establish event order across distributed nodes [33,34]. This mechanism tracks causality and concurrency via node-specific timestamps, enabling event relationship identification without a global clock. To resolve conflicts when transactions share identical vector clock values, a tie-breaker based on transaction hashes is applied: transactions with smaller numerical hash values take precedence, leveraging cryptographic hash security to ensure consistent ordering. Vector clocks differ fundamentally from blockchain-based ordering systems, offering a lightweight solution. Blockchains depend on heavy metadata storage within blocks and consensus mechanisms such as Proof of Work (PoW) or Proof of Stake (PoS) to synchronise all nodes. In contrast, vector clocks use simple node-specific counters to record event sequences locally, avoiding the overhead of global agreement per transaction. This reduces storage demands and improves real-time performance by retaining only essential sequence data. Nodes synchronise through direct communication, ensuring eventual consistency where all nodes ultimately agree on transaction order. By combining vector clocks with tie-break algorithms and a gossip protocol, RACER achieves decentralised operation without centralised coordination or bottlenecks in dynamic networks. The implementation employs Python’s SortedSet from the SortedContainers library to efficiently handle transaction ordering and tie-breaking [35].
3.1.2. Message Batching in RACER
Message batching is critical to RACER’s performance in dynamic network environments. The system utilises a gossiping protocol with two distinct message types: sensor data transmitted via request/reply (REP/REQ) sockets to randomly selected peers and broadcasted protocol messages distributed network-wide. This approach optimises IoT efficiency by mitigating congestion and energy use through randomised peer-to-peer exchanges, avoiding synchronised transmissions that strain networks. It ensures robustness and scalability even when nodes fail or showcase intermittent connectivity, while rapid dissemination of protocol messages facilitates efficient consensus mechanisms.
To maintain scalability under varying network demands, RACER employs a message batching mechanism that combines both data and protocol messages. For sensor data messages, the BatchedMessage object allows multiple transactions to be aggregated into a single transmission, handling integrity (hashing) and authenticity (digital signatures) checks for each individual message. Protocol messages, which require broadcasting rather than gossiping, are managed through multi-topic broadcast messages. This feature enables broadcasters to bundle different protocol messages while ensuring that subscribers receive only the relevant topics they are listening to. The batching mechanism is further leveraged by PLATO’s traffic optimisation algorithm to dynamically adjust network latency.
When we discuss PLATO, the traffic optimisation algorithm, in the next section, we will see the message batching method exploited to dynamically adjust network latency.
3.1.3. P2P Network Telemetry in RACER
To optimise performance under fluctuating network conditions, RACER uses a distributed system for tracking network delays. This framework uses periodic checks to adapt to changes in the network’s operational state. Leveraging its gossip communication method, nodes randomly sample latency data across the network. Each node tracks two types of delay metrics: its own internal measurements and estimates gathered from neighbouring nodes. Combining local and peer-reported data provides nodes with a comprehensive understanding of overall network delays. This insight supports advanced decision-making within RACER’s subsystems, such as the PLATO algorithm.
PLATO integrates latency telemetry with message aggregation strategies to monitor network load (e.g., increasing congestion or stability). Based on this information, it dynamically adjusts how messages are grouped for transmission, increasing batch density during peak traffic to reduce strain and improve efficiency. This adaptive approach ensures RACER maintains reliability and responsiveness in heterogeneous environments.
All the core components of RACER have now been covered. In the following section, we will discuss RACER, a traffic optimisation algorithm and companion algorithm for RACER.
3.2. Proposed Traffic Optimisation Algorithm
Congestion control in distributed systems involves mechanisms to manage data flow, prevent network congestion, and optimise resource use [36]. Techniques such as traffic shaping, rate limiting, and congestion avoidance algorithms ensure stable performance by minimising packet loss and delays. PLATO employs a multi-stage approach to enable latency-aware operation in RACER nodes. This allows nodes to dynamically adjust message transmission rates and sizes, maximising network throughput while adapting to fluctuating network conditions. Figure 2 shows at a high level how PLATO functions, which we will summarise below:
- PLATO waits for sufficient latency data from peers and from its own latency data collection. Latency data are a list of floats that records the round trip time of messages.
- PLATO ingests local latency data (from the node running the algorithm itself), latency data from peers, and also creates a weighted latency value.
- All three latency values are smoothed using a trend-filtering algorithm to remove noise.
- A trend detection algorithm takes a window of latency data and identifies rising, lowering, or stable trends.
- A decision value is given to RACER, which augments the frequency and size of gossip messages and broadcast messages.
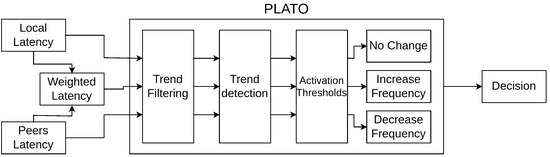
Figure 2.
PLATO is a traffic optimisation algorithm and a companion for RACER. PLATO takes latency data from RACER and then processes it to decide whether the latency is increasing in nature, decreasing in nature, or stable. RACER uses these insights to optimise the performance of the network.
Figure 2.
PLATO is a traffic optimisation algorithm and a companion for RACER. PLATO takes latency data from RACER and then processes it to decide whether the latency is increasing in nature, decreasing in nature, or stable. RACER uses these insights to optimise the performance of the network.
PLATO is an algorithm which allows nodes to independently estimate network latency and adjust their latency estimates dynamically. Raw RTT data alone are insufficient for meaningful analysis due to high noise. To refine RTT data for PLATO’s requirements, we employ trend filtering and detection techniques. The following sections detail these algorithms in detail.
3.2.1. Trend Filtering
Trend filtering focuses on removing the noise and inconsistencies of our RTT data and providing a more comprehensible stream to our trend detection algorithm. If the trend detection algorithm receives data with no clear trend, such as data with prominent peaks followed by substantial troughs, it will be very difficult to do any sort of trend detection. As the RTT data can fluctuate from fractions of a second all the way up to a number of minutes, the performance of the trend filtering algorithm is critical for a reliable traffic optimisation algorithm. we will briefly introduce the trend filtering algorithms we are considering for implementation into PLATO.
Moving Average
A moving average is a technique used to analyse data by calculating the average of a specific number of consecutive data points within a dataset. It involves sliding a window across the dataset, calculating the average for each window, and then moving the window forward to include the next set of data points while excluding the previous ones. This process helps to smooth out fluctuations and reveal underlying trends or patterns in the data. Moving averages are commonly used on time series data and are well known for use in economics, such as examining gross domestic product [37] and algorithmic trading [38]. In our PLATO experiments, we will consider the following moving averages:
- Simple moving average (SMA) [39].
- Exponential moving average (EMA) [40].
- Kaufman adaptive moving average (KAMA) [41].
- Zero lag exponential moving average (ZLEMA) [42].
Kalman Filter
The Kalman filter, created by Rudolf E. Kálmán [43] is a recursive Bayesian estimator that is commonly used in signal processing and time series analysis. It operates by extracting underlying trends from noisy observations through an iterative process of state estimation. At each time step, the Kalman filter integrates new measurements with the system’s dynamics, as modelled by a state transition model, to improve its estimate of the underlying state. This estimation process includes uncertainty estimations, allowing the filter to spot the difference between genuine trends and random fluctuations. By adaptively adjusting its estimates based on the differences between measurements and the dynamic system model, the Kalman filter provides smoothed data that identifies the underlying trend, commonly found in IoT sensor data [44,45].
Savitzky–Golay filter
The Savitzky–Golay filter, created by Abraham Savitzky and Marcel J.E. Golay [46], works by fitting a low-degree polynomial (typically linear or quadratic) to subsets of adjacent data points within a moving window. This polynomial fitting is performed via least squares regression, resulting in a smoothed estimate for each data point. Unlike other smoothing methods that simply average neighbouring points, the Savitzky–Golay filter provides a more sophisticated approach by considering the local polynomial approximation. This technique allows it to remove noise from the data while maintaining important features such as peaks, valleys, and fast changes in the signal. The filter’s ability to keep the structure of the underlying signal makes it useful in applications such as in biomedical signal processing [47], chromatography [48], and spectroscopy [49].
3.2.2. Trend Detection
Trend detection in time series data is a fundamental aspect of numerous fields ranging from economics [50] to environmental sciences [51]. It involves the analysis and identification of underlying patterns or trends within sequential data points over time. The primary goal is to discern meaningful directional changes, whether ascending, descending, or stationary, amidst the noise and variability present in the data. Various statistical and computational techniques are employed for trend detection, encompassing classical methods such as moving averages, exponential smoothing, and linear regression [52], as well as more sophisticated approaches including Fourier analysis [53], autoregressive integrated moving average (ARIMA) modelling [39], and machine learning algorithms. These methods facilitate the characterisation and understanding of data, which are used for forecasting future trends and informing decision-making processes in various domains.
For use in PLATO, we investigate two trend detection algorithms: the Relative Strength Index (RSI) and the True Strength Index (TSI). Commonly used in financial contexts, the incorporation of RSI and TSI into this analysis may appear unconventional. However, an analysis of the underlying algorithms and theoretical rationales for their selection will be provided in Section 5.
Relative Strength Index
RSI is a momentum oscillator developed by J. Welles Wilder [54], and is well known for usage in financial markets [55]. Fundamentally, the RSI algorithm gauges the momentum of data movements over a specified time frame, enabling identification of rising or lowering conditions. Its suitability for time series data on IoT devices lies in its capacity to identify patterns among dynamic data streams. The RSI calculation involves three variables, RS, Average Gain, and Average Loss. RSI is calculated as and RS is calculated as . The initial calculations for Average Gain and Average Loss are based on a 14-window average, while the next calculation uses previous averages to calculate the gain and loss. As shown by the simple operations in the equations, the RSI should be well suited to the low-powered IoT devices.
True Strength Index
TSI is a technical indicator designed to offer insights into both the direction and strength of a trend in financial markets. Developed by William Blau [56], the TSI combines multiple exponential moving averages of data changes over two different time periods, thereby smoothing out short-term fluctuations while capturing longer-term trends. By subtracting the longer-term moving average from the shorter-term one and then smoothing this difference, the TSI filters out noise and highlights significant data movements. Unlike other momentum oscillators (such as the previously mentioned RSI), the TSI accounts for both trend direction and momentum. The calculation of the TSI is slightly more involved than the RSI, and revolves around calculations of multiple exponential moving averages.
The RSI and TSI algorithms were specifically selected as they are both simple to calculate, easy to implement, have a low number of configurable parameters, and are both usable on non-monotonic data sets (data sets with values that do not consistently increase or decrease).
To summarise the last two sections, trend filtering focuses on removing noise from data, while trend detection focuses on the direction, or the trend that data are moving towards. Trend filtering and trend detection are the main parts of PLATO, which we will cover in more detail in the following section.
4. Implementation
In this section, we will cover the implementation of our IoT consensus mechanism, RACER, and our traffic optimisation algorithm, PLATO.
4.1. Consensus Mechanism Implementation
SPDE is a gossiping protocol that uses randomisation and sampling to probabilistically determine if a gossip has been accepted by the network rather than waiting for a confirmation from each individual node. This allows the network to achieve logarithmic latency and communication complexity. The SPDE gossiping protocol allows RACER to reliably propagate messages across nodes in the network, even when nodes fail or act unpredictably. This is an important primitive in distributed systems called reliable broadcast [57]. There are three main phases to SPDE:
- Setup Phase.
- Echo and Feedback Phase.
- Delivery Phase.
The SPDE (Sequenced Probabilistic Double Echo) gossip protocol operates in three phases: setup, echo/feedback, and delivery. During the setup phase, the network is prepared for message dissemination. The echo/feedback phase monitors message delivery across the network, while the delivery phase forwards the message to the application layer of each node once a predefined threshold of nodes confirms receipt.
In our Python implementation (The Github link for RACER can be found here: https://github.com/brite3001/RACER/, accessed on 2 April 2025), the command function plays a critical role as an asynchronous message bus, receiving objects and dispatching them to appropriate handler functions for processing. This allows nodes to run concurrently without being blocked by internal processes, ensuring timely reception of messages. For instance, during the setup phase, the command function handles subscription management by asynchronously passing SubscribeToPublisher objects to relevant handlers. Additionally, two key protocol messages are the EchoResponse and ReadyResponse. Nodes publish an EchoResponse upon receiving a gossiped message and a ReadyResponse once they have received a sufficient number of EchoResponses. This “double echo” mechanism ensures additional certainty that the message has been widely adopted by the IoT network.
Now that we have covered some preliminary information related to the gossip protocol, we will continue to describe the pseudocode based on the Python implementation.
4.1.1. Setup Phase
The setup phase prepares nodes (including our node) for incoming gossip messages. It begins by initialising common values and is detailed in Algorithm 1. In the code, the BatchedMessage object is abbreviated to , which holds one or more data message objects.
Lines 4–7 create an echo subscribe group, causing our node to subscribe to peers in this group, enabling feedback receipt from these peers. Lines 8–12 perform a similar subscription process but with a different subset of nodes from the network. Lines 13–20 notify subscribed peers that our node has joined their subscription list, prompting them to prepare for incoming BatchedMessage transmissions.
| Algorithm 1 Setup Phase |
|
4.1.2. Echo and Feedback Phase
In the echo and feedback phase, the network’s message reach is assessed. If the node is the original sender of a message not yet retransmitted, it broadcasts the message for the first time and waits for widespread acknowledgement. Algorithm 2 outlines this process.
| Algorithm 2 Echo and Feedback Phase |
|
Initially, the sender updates its vector clock to track outgoing messages. Lines 4–11, then check how many nodes have already received the message. If feedback from at least feedbackThreshold nodes confirms receipt, further propagation is unnecessary. Otherwise, the BatchedMessage is sent to nodes yet to receive it.
Lines 14–20 verify whether the node has received readyThreshold EchoReplies from its echoSubscribe group (established during setup). Finally, lines 21–29 reconfirm if the node meets or exceeds the readyThreshold for received echoes. Success triggers a ReadyResponse message. If not, non-responding nodes are logged, and the process is marked as failed.
4.1.3. Delivery Phase
The delivery phase (Algorithm 3) operates similarly to the echo and feedback phases. Like these stages, it waits for a threshold of network acceptance by sampling peer responses. Once a message is marked as delivered, we probabilistically assume it has propagated throughout the network.
Lines 2–10 of the delivery phase involve collecting ReadyResponses from peers. If at least deliveryThreshold responses are received from peers in the readySubscribe group, the process continues. If failures or timeouts occur before meeting this threshold, the node exits early. Lines 11–16 finalise the SPDE gossip process. Upon reaching the deliveryThreshold, the node confirms the message as delivered to the network. RACER then sequences the message using its associated vector clock. In cases where two messages share identical vector clock values, RACER applies a tie-break mechanism to resolve ordering.
| Algorithm 3 Delivery Phase |
|
4.1.4. Real World Deployments
In designing and developing RACER, we prioritised time-insensitive IoT applications, such as environmental monitoring, agricultural sensors, and asset tracking, while rigorously testing the protocol under harsh conditions to ensure robustness. Stress tests simulated adverse scenarios, including high transaction latency, large individual transactions, extensive block sizes, and randomised node selection for gossip protocol dissemination. To align with IEEE 802.15.4 [58], RACER can incorporate several optimisations: transaction compression limits block sizes to 127 bytes, transfer rates are constrained within the standard’s 100–250 kbit/s bandwidth, consensus network sampling is synchronised with device sleep states (e.g., CSMA/CA backoffs and superframe structures), and latency is optimised for sub-second response times to support time-sensitive use cases within IoT constraints. These adjustments enable RACER to operate efficiently in low-power, resource-constrained environments while maintaining reliability across diverse applications. The protocol’s peer-to-peer architecture and transaction ordering guarantees make it well suited for decentralised scenarios with unstable network coverage, such as agriculture monitoring, asset tracking, and disaster response.
In a low-power LoRaWAN-based agricultural sensor network, Raspberry Pi nodes monitor soil moisture, temperature, and pest activity across a large field. RACER ensures Byzantine resilience by reliably broadcasting critical sensor data (e.g., sudden pest outbreaks) even if a subset of nodes malfunctions or reports spoofed data. Vector clocks maintain eventual consistency across decentralised irrigation controllers, while PLATO dynamically adjusts LoRa transmission schedules based on fluctuating network latency (e.g., during heavy rain). This enables autonomous, consensus-driven decisions, such as triggering localised irrigation or pest control without relying on a centralised server.
A ZigBee mesh network of Odroid nodes tracks industrial equipment (e.g., forklifts, robots) in a factory with intermittent connectivity. RACER guarantees deterministic message ordering for real-time location updates, ensuring that even if a node is temporarily offline or spoofing data, consensus on asset positions remains intact. PLATO continuously monitors latency trends in the mesh to optimise ZigBee channel usage, reducing collisions during peak traffic. This allows decentralised decision-making, such as rerouting equipment automatically when a forklift’s battery is low or a zone becomes congested without a central coordinator.
In post-disaster scenarios, battery-constrained ZigBee nodes deployed on Raspberry Pi-based emergency sensors (e.g., gas leaks and structural damage) form a resilient mesh. RACER ensures critical alerts (e.g., “leak detected”) are broadcast reliably, even as nodes fail or adversaries inject false alarms. PLATO adapts message timeout parameters in real-time based on network instability, prioritising urgent updates over less critical telemetry. This enables autonomous, consensus-based triage of emergency response actions (e.g., deploying drones to a specific zone) without relying on fragile centralised infrastructure.
Each example leverages RACER’s fault tolerance and PLATO’s adaptive optimisation to address real-world constraints (limited power, unreliable connectivity) while focusing on decentralised, consensus-driven outcomes.
4.2. Traffic Optimisation Implementation
PLATO will be responsible for controlling the message latency across the network. PLATO does this by providing RACER with data related to network latency trends. Congestion monitoring consists of two Python functions: the increasing congestion monitoring algorithm and the decreasing congestion monitoring algorithm. we will start by explaining the increasing congestion algorithm, as shown in Algorithm 4, followed by the decreasing congestion algorithm, which will be shown in Section 4.2.2. Both these algorithms follow a similar core structure, which involves the following:
- Trend filtering—used to remove noise from data.
- Trend detection—used to detect a directional change in data trend.
- Latency adjustment—manages frequency at that messages are sent.
| Algorithm 4 Increase Congestion Monitoring Algorithm |
|
4.2.1. Increasing Congestion Monitoring Algorithm
We will now discuss the increasing congestion monitoring algorithm in detail.
First, nodes apply the same trend filtering algorithm to both their own latency data and that of their peers. They then compute a weighted average using the filtered results from both sources. Our implementation uses the Savitzky–Golay filter, and our rationale for this choice is detailed in Section 5.
The process is divided into two latency increase scenarios: lines 4–8 and lines 9–28.
Lines 4–8 identify latency estimates that lag significantly behind the weighted RTT. When network latency rises rapidly, nodes immediately double their latency estimate to reduce message transmission frequency, aiming to stabilise network latency.
Lines 9–28 address scenarios where latency does not escalate sharply. Lines 10–19 initialise variables for calculating trends using RSI (see Section 5), incorporating both local and peer latency data. Nodes then determine a theoretical latency increase value and verify if it stays within the maxGossipTime threshold. Subsequent variables for latency targets and RSI targets are also configured.
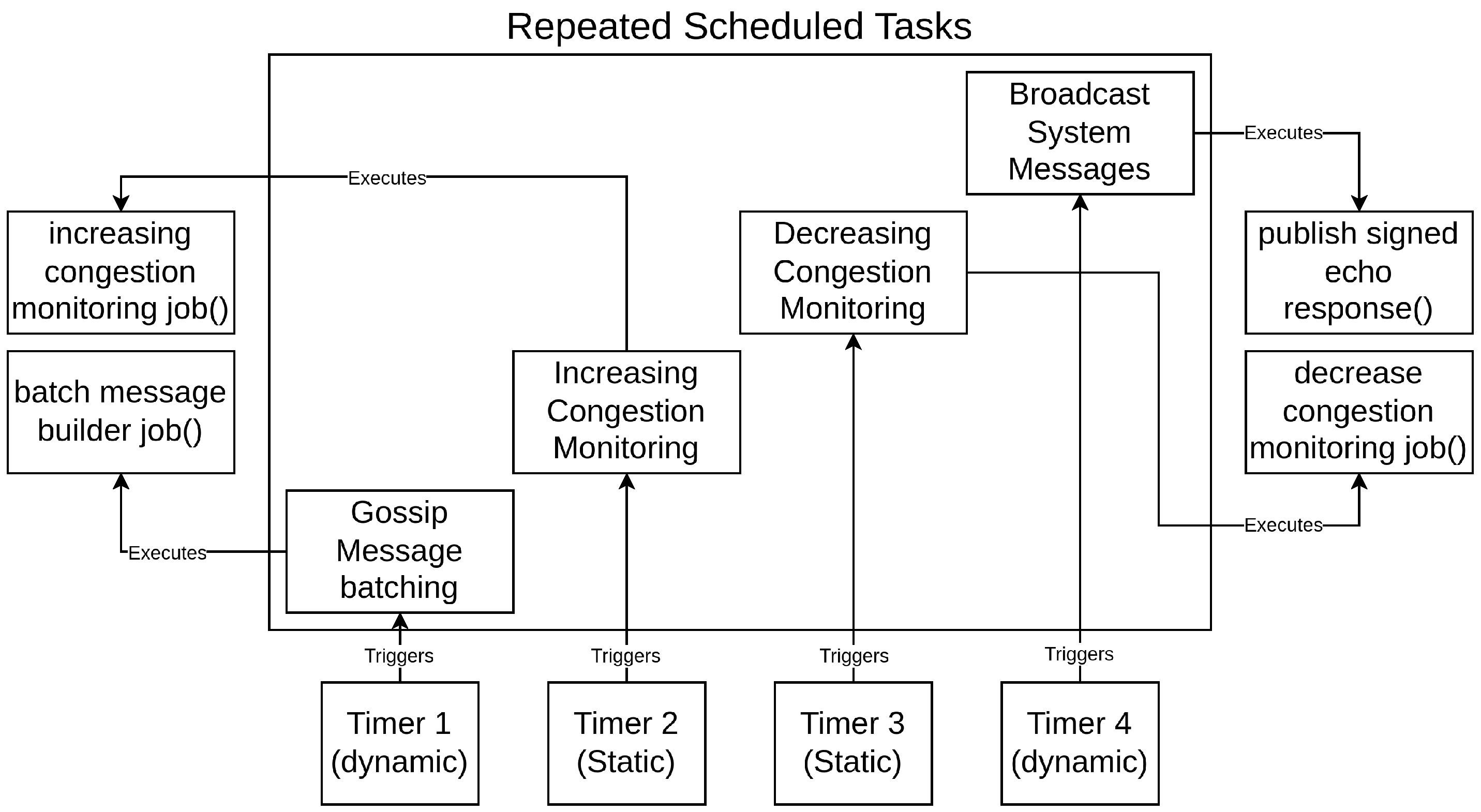
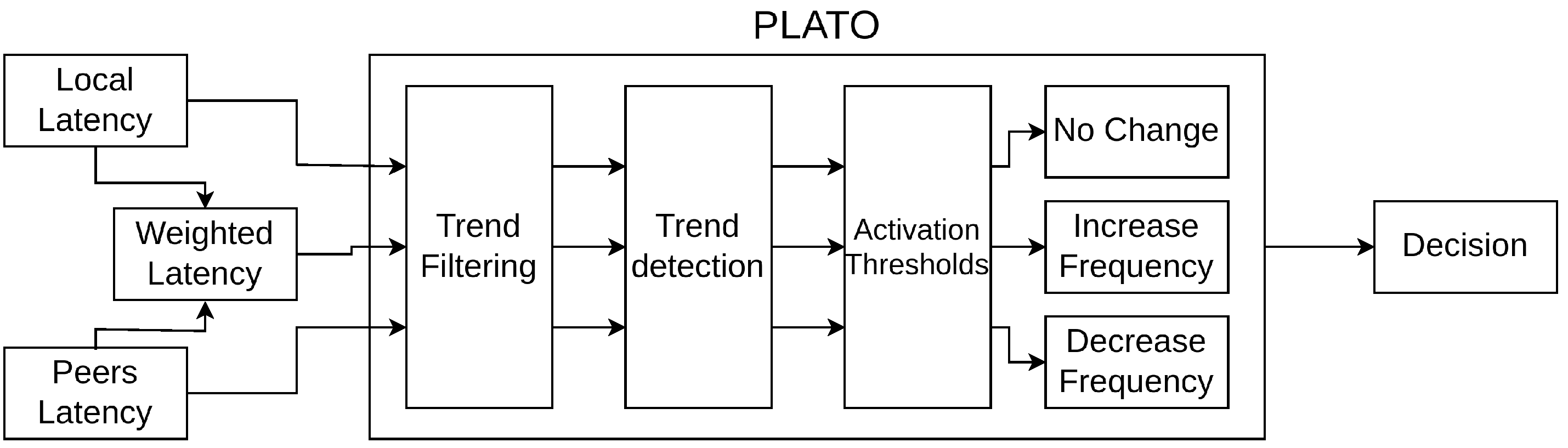
Lines 20–25 determine whether a node should increase its target latency (thereby reducing message-sending frequency). This requires the calculated RSI to exceed 70, the underMaxTarget flag to be active, and the targetLatency flag to be enabled. If all conditions are met, the node updates its latency estimate and pending frequency values. Flags are then set to notify the task scheduler to reduce the frequency of these operations. An overview of the scheduler function is shown in Figure 3.
Figure 3.
Shows the flow of scheduled tasks involving their triggers based on individual timers and the functions they call. Timers related to message sending are dynamically updated according to network conditions while monitoring jobs are static.
Nodes also need a mechanism to detect decreasing latency. In the following section, we will discuss the decreasing congestion monitoring algorithm, a scheduled job that allows nodes to detect decreasing latency.
4.2.2. Decreasing Congestion Monitoring
The decreasing congestion monitoring algorithm (see Algorithm 5) is a streamlined version of the increasing congestion algorithm designed to detect long term trends. It employs a longer sliding window to analyse data over extended periods, resulting in more conservative latency adjustments. This ensures the algorithm only reduces latency when a clear, sustained signal of improvement is detected. Below is an explanation of the algorithm’s pseudocode.
| Algorithm 5 Decrease Congestion Monitoring Algorithm |
|
The algorithm begins by initialising variables such as smoothed latency, weighted latency, RSI values for trend detection, and a theoretical latency reduction estimate (lines 1–7). Lines 8–9 then establish flags for minimumLatency and currentLatency values.
Lines 10–19 evaluate whether a node qualifies to reduce latency. Four criteria must be met:
- Both the node’s and its peer’s RSI values are below 30.
- The proposed latency exceeds the minimum latency threshold.
- The proposed latency is higher than the most recent recorded latency.
- The proposedLatencyAboveLatestLatency flag prevents adjustments if the proposed latency is too close to the current estimate.
If all conditions are satisfied, the node proceeds similarly to the increasing congestion algorithm: it updates latency estimates and schedules timing adjustments based on the new values.
In both the increasing and decreasing congestion monitoring algorithms, there is a notable change in the window size for both the Savitzky–Golay filter and the RSI algorithm. The increasing congestion algorithm starts with a window size of 14 for RSI (commonly used as a default parameter in financial applications); we found this value also performed well in our ad hoc tests. For the Savitzky–Golay filter, we could not find commonly used default parameters but found that a window size of 14, with a polynomial degree of 1, performed well.
In the decreasing congestion algorithm, we increase this window size from 14 to 21. This increase in window size allows the decreasing congestion algorithm to confirm the latency trend over a longer time frame before allowing RACER to increase its message-sending rate.
In this section, we discussed PLATO, a latency-aware traffic optimisation algorithm that dynamically adjusts message transmission rates to manage network latency. PLATO comprises two components: an increasing congestion monitor, which identifies rising latency and reduces message-sending frequency to mitigate congestion, and a decreasing congestion monitor, which detects falling latency and increases transmission rates to utilise available network capacity. The subsequent section presents the results of our consensus mechanism, RACER, alongside the performance of the PLATO algorithm.
5. Results
The section presents the experimental results to evaluate the performance of both RACER and PLATO. We start by covering the experimental design of our performance tests, then explore results related to trend detection performance, memory and runtime performance, and a number of other tests. We conclude the discussion section by ranking algorithm pairs based on their performance across a diverse set of tests, and we show the impacts of PLATO on our consensus mechanism, RACER.
5.1. Experimental Design
This section will focus on testing trend detection and trend filtering algorithms for use in PLATO, our traffic optimisation algorithm.
To test our trend filtering/trend detection pair, we will use a number of metrics to gain a balanced view of the algorithm pair across a number of metrics. These metrics include the following:
- Algorithm Performance—CPU time, execution time, and memory usage.
- Network Fault Tolerance—success rate of gossiped messages.
- Latency Estimate Accuracy—ability to adjust latency towards a predefined target.
Algorithm performance assesses computational demands such as CPU time (duration of active processing), total execution time (including input/output and memory operations), and memory usage. Gossip performance reflects how effectively a decentralised communication method delivers messages, requiring them to meet minimum delivery standards. Failures indicate network latency that hinders message distribution. Latency performance evaluates PLATO’s ability to keep average RTT within a 10-s target by tracking deviations using statistical metrics: the MAD and RMSE. These measures quantify differences between observed RTTs and the target, with lower values signalling stronger alignment with desired latency levels.
Our experiment also uses a number of parameters, which will be detailed below in Table 2, Table 3 and Table 4.

Table 2.
Node specific test parameters.

Table 3.
Gossip protocol test parameters.

Table 4.
PLATO test parameters.
5.2. Simulation
To identify the best combination of trend filtering and trend detection algorithms, a test was created to test the combinations of algorithms in different scenarios. These scenarios are outlined in Table 5:

Table 5.
Test Scenarios.
Each test is run one after the other, with a 60 s gap between each test. The fast test is used as a stress test to see if the combination of algorithms can adapt quickly enough to a large transactional load. PLATO configurations that manage to have the lowest number of delivery threshold failures tend to perform the best. The slow test checks PLATO’s ability to detect easing latency, and the mixed test simulates a chaotic peer-to-peer network with messages being sent and received at random intervals.
Each one of the algorithm combinations listed in Table 6 will go through this test scenario:

Table 6.
PLATO algorithm tests.
The computer used to conduct these tests was an Asus laptop with an Intel i7-5500U and 8 GB of DDR3 ram. The operating system was PopOS! (Ubuntu 22.04 LTS).
5.3. Trend Detection Performance
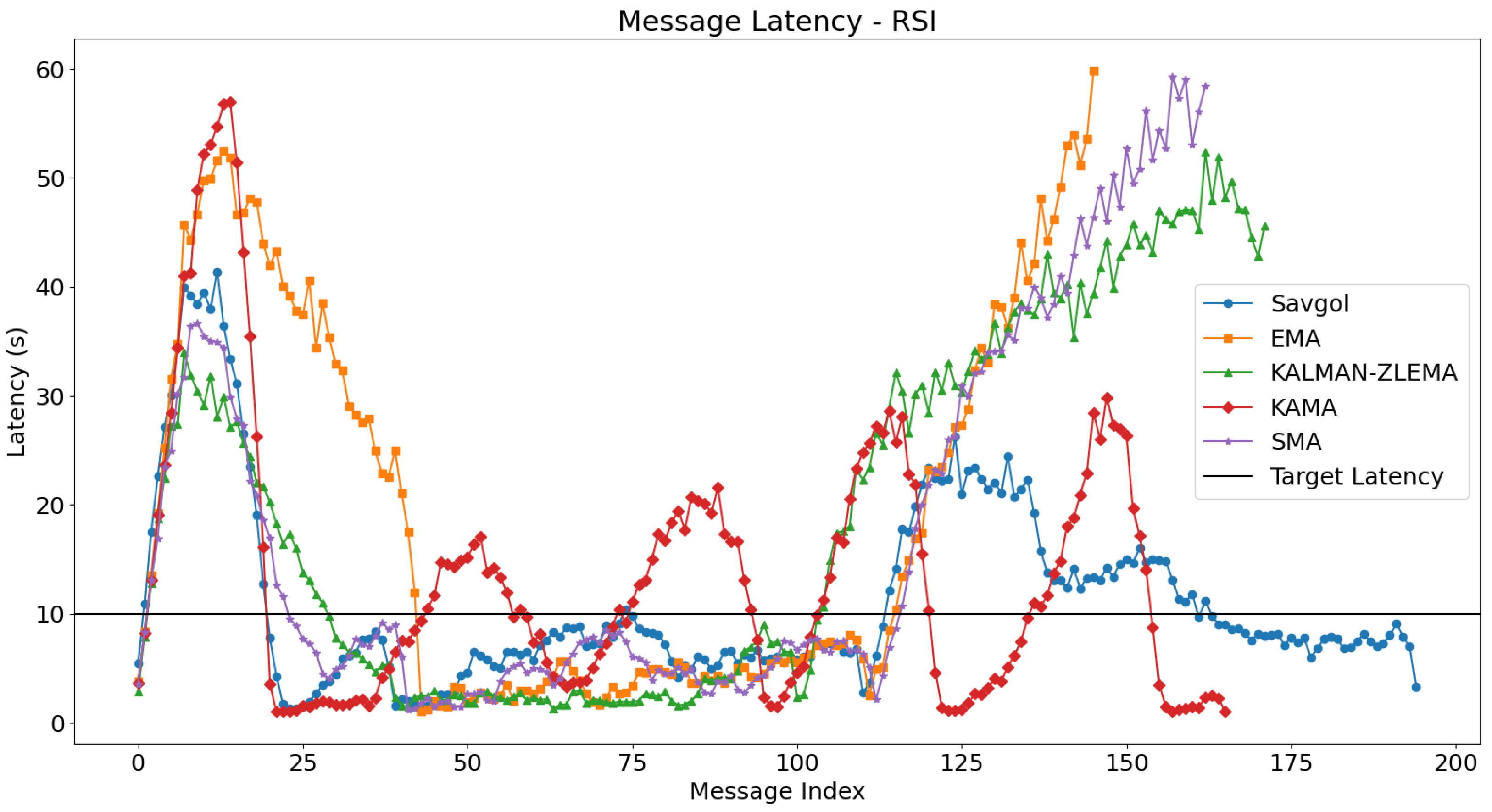
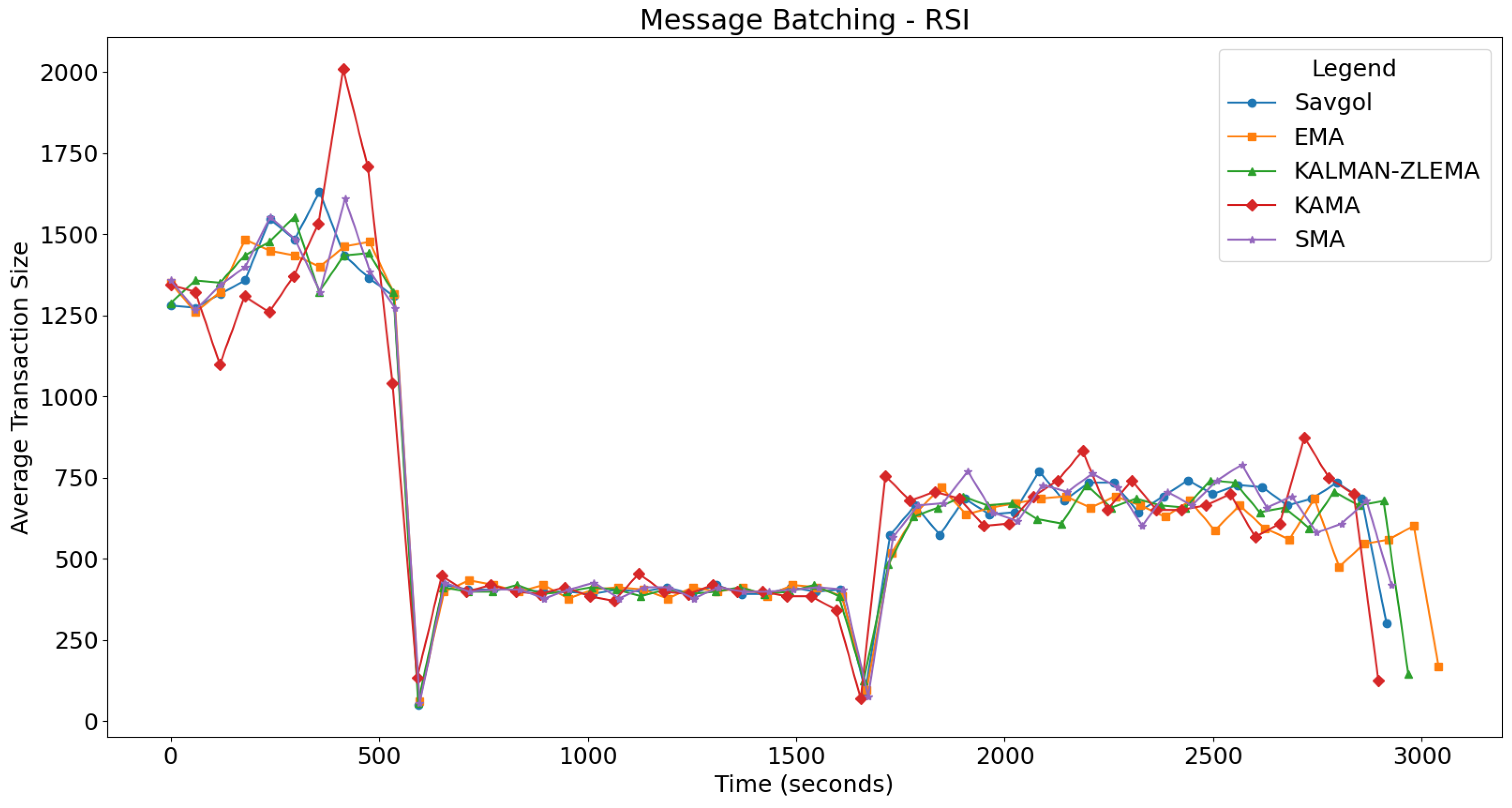
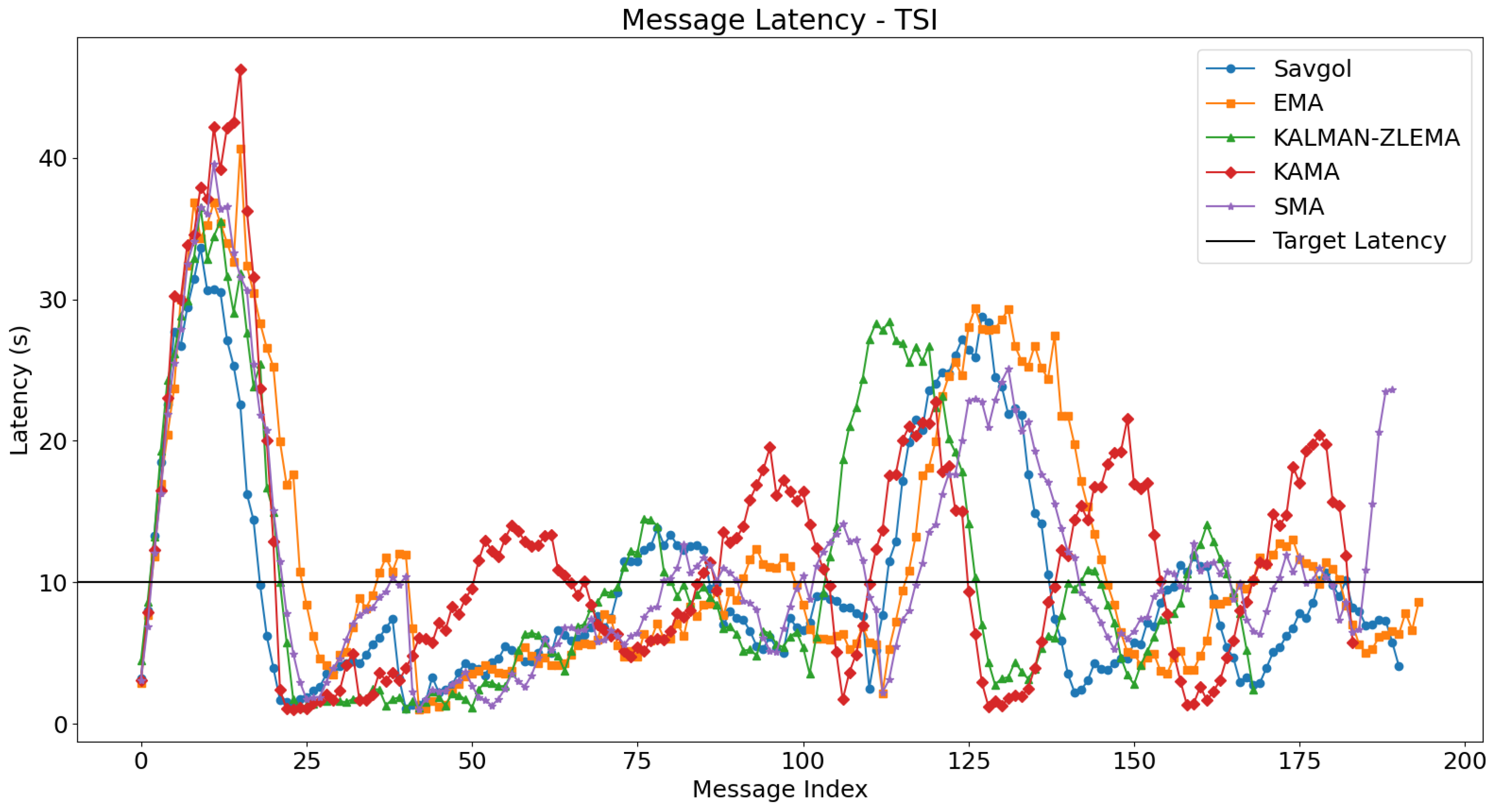
For each test, we will look at how algorithms performed in the fast, slow, and mixed portions of the test. The fast portion of the test occurs before 500 s, the slow portion of the test occurs between 500 and 1500 s, and the mixed part of the test occurs after 1500 s. For each test, we’ll refer to Figure 4 for message latency discussion, and Figure 5 for batching related discussion. The boundaries between these tests can be seen in Figure 5.
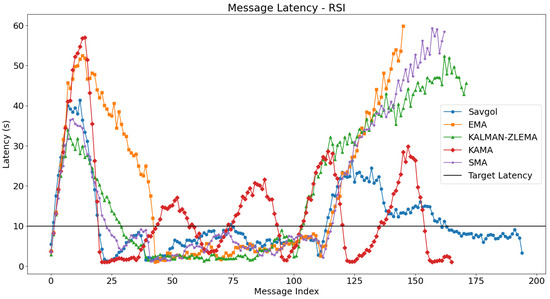
Figure 4.
Plots the average time taken for a gossip to be delivered network wide, using the RSI algorithm for trend detection. Algorithms target the black line at y = 10. Algorithms that follow this line closely perform better.
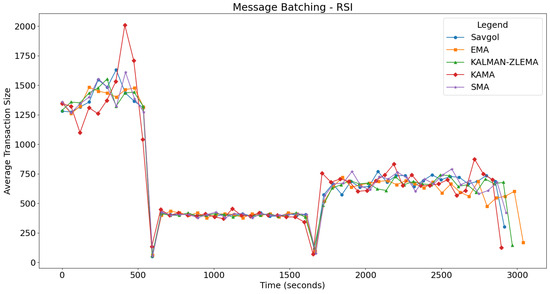
Figure 5.
Displays the average size of gossips when the RSI trend detection algorithm is used.
The first part of our trend detection tests involved combining RSI with each trend filtering algorithm. SMA displayed strong performance in the fast section by maintaining latency below 40 s and quickly reducing it during transitions to the slow section, although it failed to achieve the targeted 10-s latency. Conversely, EMA performed poorly throughout all sections, with high latencies exceeding 50 s in the fast section and unstable performance. KAMA presented outlier-like behaviour by topping out at nearly 60 s during the slow section and oscillating without runaway latency but failing to provide stable conditions. KALMAN-ZLEMA demonstrated low latency in the slow section yet faltered significantly with high latencies and instability in the mixed section. SAVGOL, however, emerged as a consistent performer across all sections, reaching only 40 s during the fast phase and effectively managing latency increases in the slow and mixed phases without runaway issues, indicating its effective trend filtering capabilities compared with others when paired with RSI.
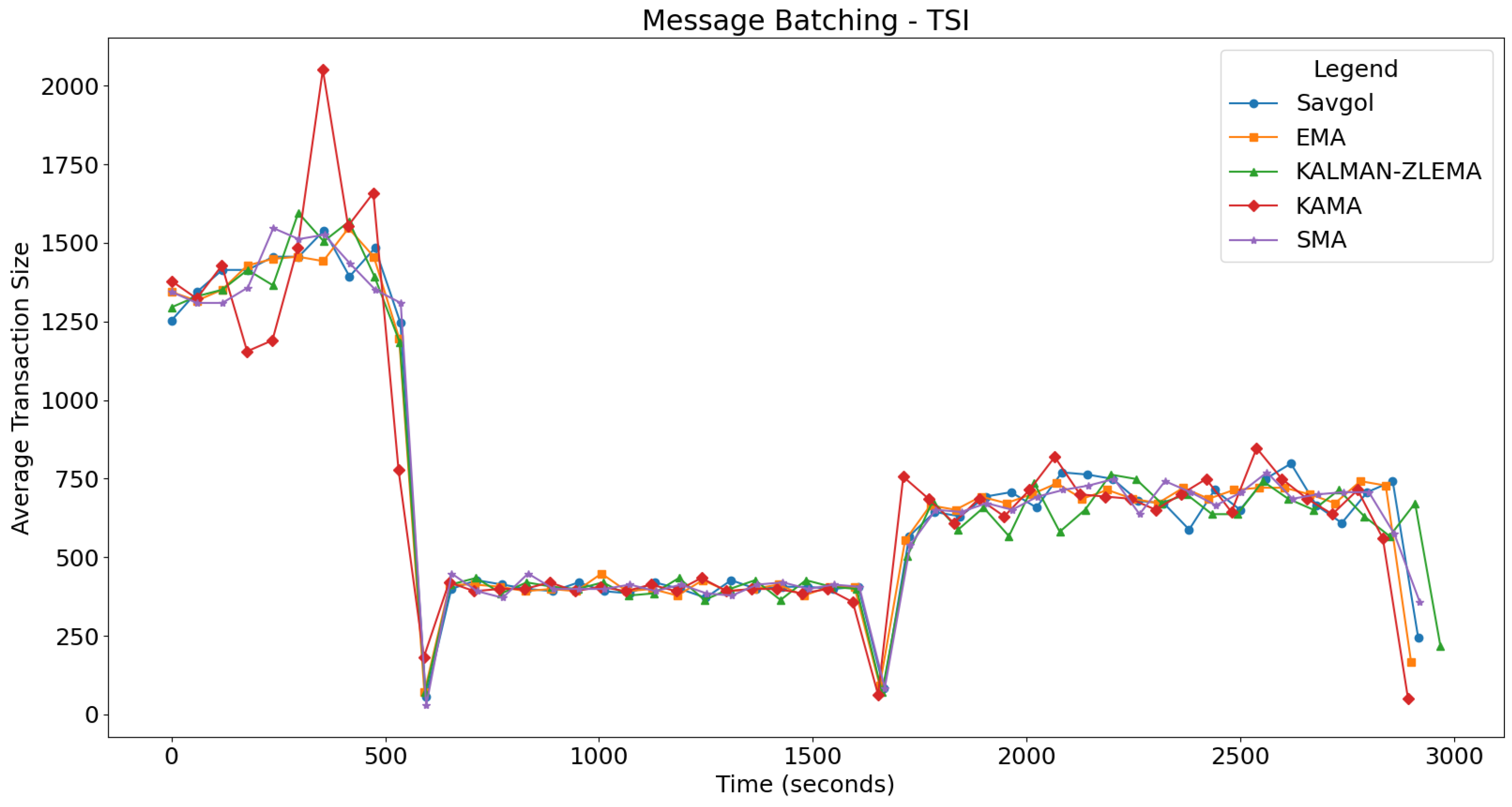
The integration of TSI as a trend detection algorithm generally led to performance improvements across various moving average algorithms in latency tests, as shown in Figure 6. Specifically, SMA and EMA presented reduced latency spikes by about 10 s in the fast test section, with SMA showing steady improvement in slow and mixed sections; EMA also managed to avoid runaway latency towards the end of the mixed section. KAMA demonstrated a similar reduction in maximum latency during the fast phase but remained unstable throughout other segments due to continuous oscillation. The KALMAN-ZLEMA algorithm mirrored these positive trends, effectively matching target latencies without experiencing runaway latency at the test’s conclusion. Notably, SAVGOL was an exception as it showed performance degradation, particularly through undesirable oscillations in the mixed section, despite satisfactory results in fast and slow sections. Overall, TSI facilitated better resource utilisation and more consistent latency control across most algorithm pairs, except for KAMA, which continued to show instability irrespective of the trend detection method employed. The message batching results for TSI are shown in Figure 7, showing similar results to RSI. In the following section, we will look at the resource utilisation of these algorithm pairs.
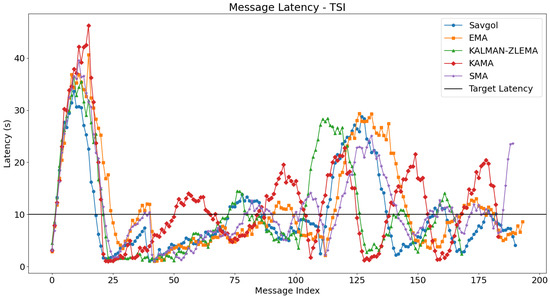
Figure 6.
Plots the average time taken for a gossip to be delivered network-wide, using the TSI algorithm for trend detection. Algorithms target the black line at y = 10. Algorithms that follow this line closely perform better.
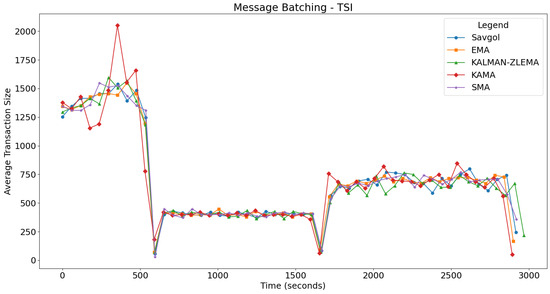
Figure 7.
Displays the average size of gossips when the TSI trend detection algorithm is used.
5.4. Runtime Performance
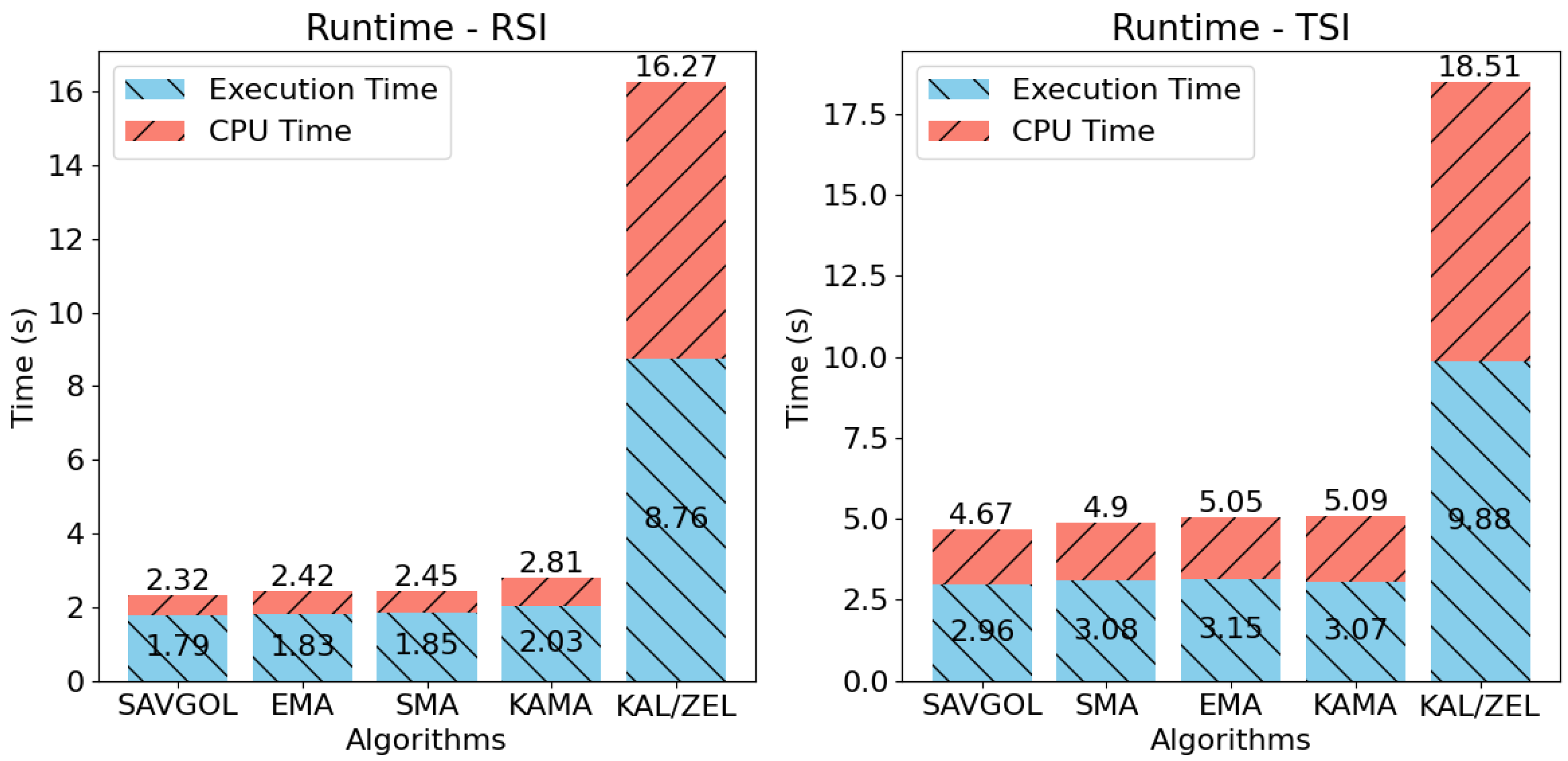
The runtime performance of the proposed algorithms is characterised by two key outcomes, as shown in Figure 8. Moving average-based methods demonstrate significantly faster execution times compared with the combination of Kalman Filter and ZLEMA. This difference is credited to two primary factors. First, the latter algorithmic approach integrates three components: RSI/TSI paired with Kalman Filter and ZLEMA, which increases computational complexity. Second, the implementation of the Kalman filter lacked runtime optimisations, resulting in prolonged execution times relative to simpler moving average-based algorithms.
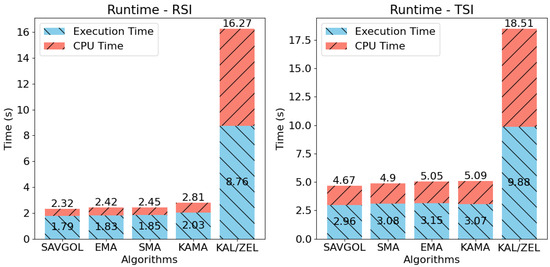
Figure 8.
Runtime tests for each trend filtering algorithm when combined with RSI and TSI. Lower is better.
The additional complexity of the TSI trend detection algorithm is also visible in this test. On average, the TSI algorithm added 1–3 s of runtime across all tests.
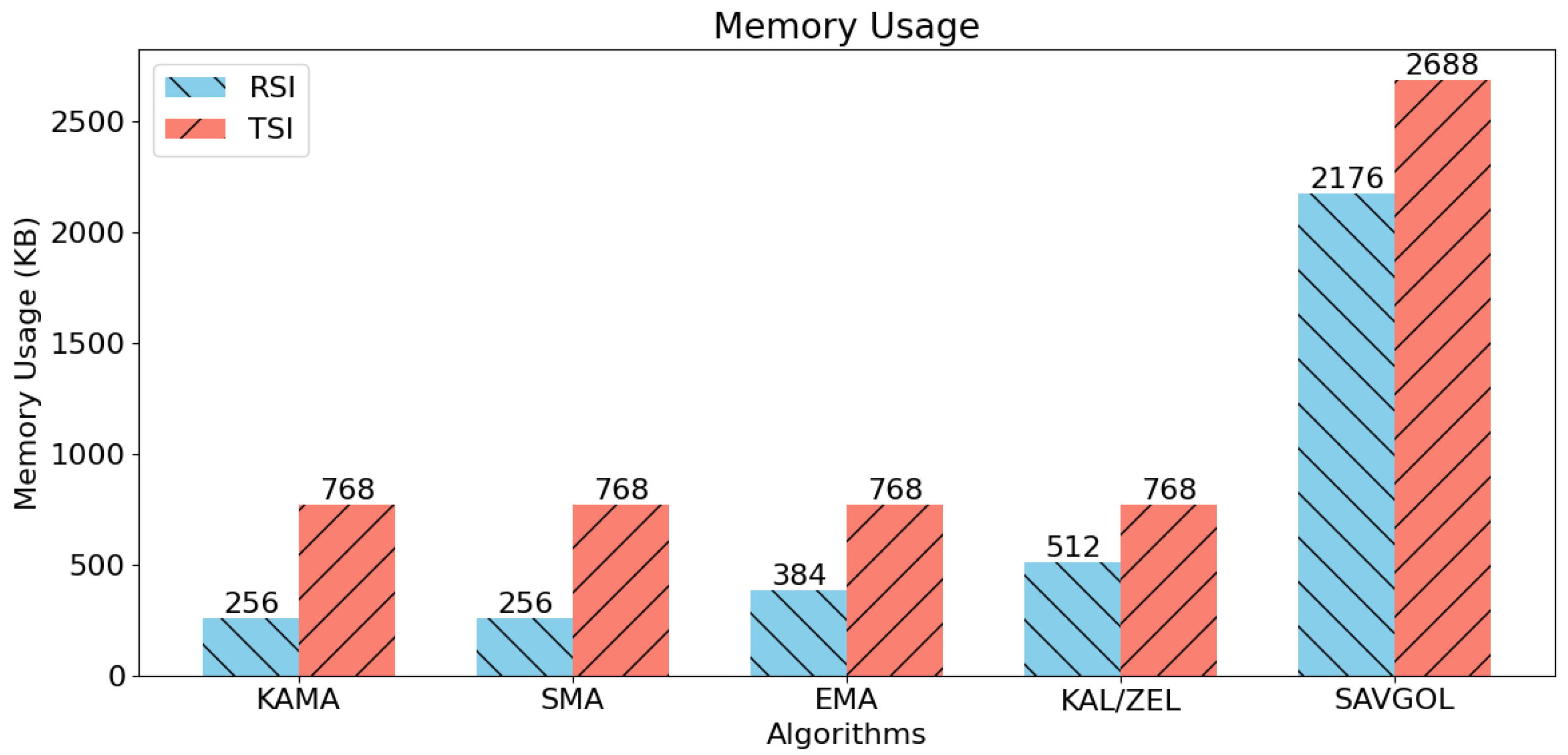
5.5. Memory Usage
Figure 9 shows the memory consumptions of the algorithm pairs during our tests. Notably, the Kalman Filter/ZLEMA pair has memory usage in line with the other moving average-based algorithms. However, the Savitzky–Golay filter was the outlier in this test, requiring 4–8 times more memory than other algorithm pairs.
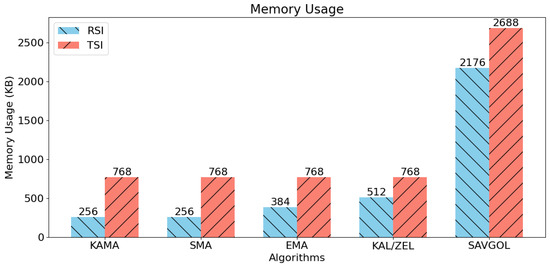
Figure 9.
Memory usage tests comparing each combination of trend filtering and trend detection algorithms. Lower is better.
Comparing RSI to TSI in the memory usage tests, we see TSI required an additional 500 kb of memory across all tests.
5.6. Communication Fault Tolerance
This test tracks the number of messages that fail to meet the contagion threshold for the SPDE gossip algorithm. Messages that fail to meet this threshold are classed as undelivered, meaning a node is not sure if the message has propagated to the entire network. Re-gossiping the message to the network to avoid this is a valid option, but at this stage, no re-gossiping is occurring; nodes attempt to gossip a message only once.
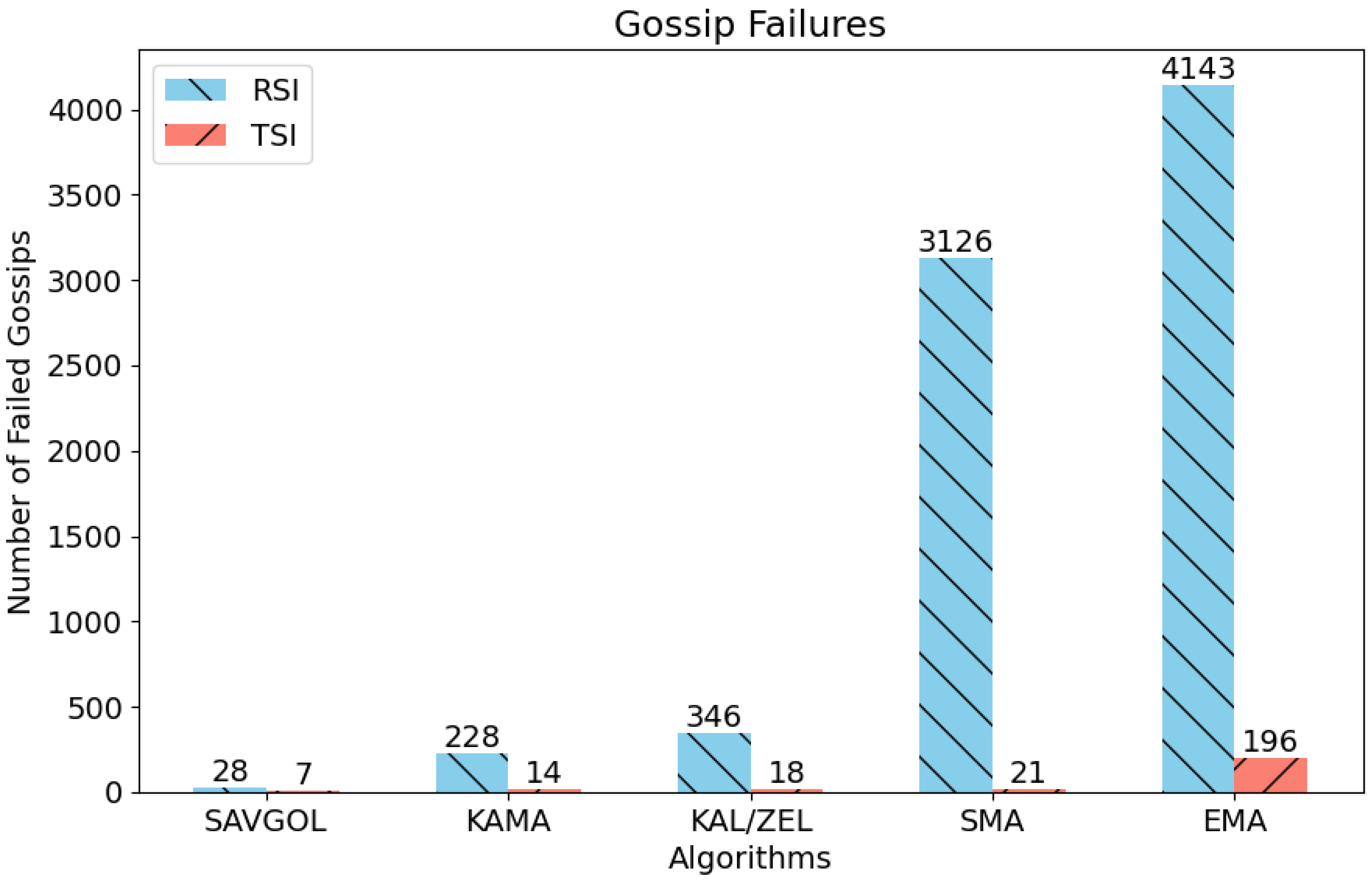
Figure 10 presents a noticeable difference between the performance metrics of algorithms paired with RSI and those paired with TSI. The results indicate that, except for the Savitzky–Golay filter, algorithm combinations paired with RSI exhibit subpar performance. Conversely, algorithm pairs associated with TSI demonstrate significantly lower rates of failed gossips.
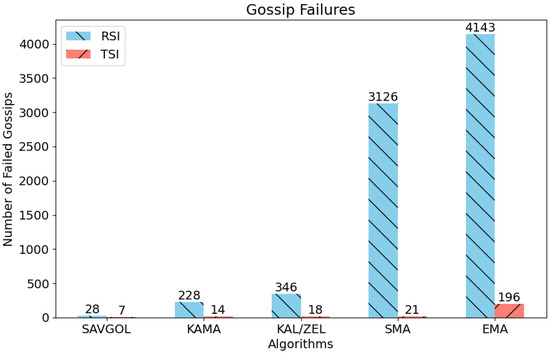
Figure 10.
Displays the number of network faults (failed gossips) generated by each algorithm pair. Fewer faults indicate a better-performing algorithm pair.
These findings are confirmed by the message latency tests depicted in Figure 4, showing the vast majority of algorithm pairs struggled to cope with fast and mixed sections of the test protocol, resulting in higher latency. The subsequent runaway latency was found to have a cascading effect, leading to hundreds or thousands of failed message gossips.
In comparison, TSI-based algorithm combinations have far fewer failed message gossips. This outcome is consistent with the improved performance observed in the associated message latency graph (Figure 6), where TSI-paired algorithms displayed lower and more stable latency values that closely tracked the latency target of 10 s.
5.7. Latency Performance Evaluation
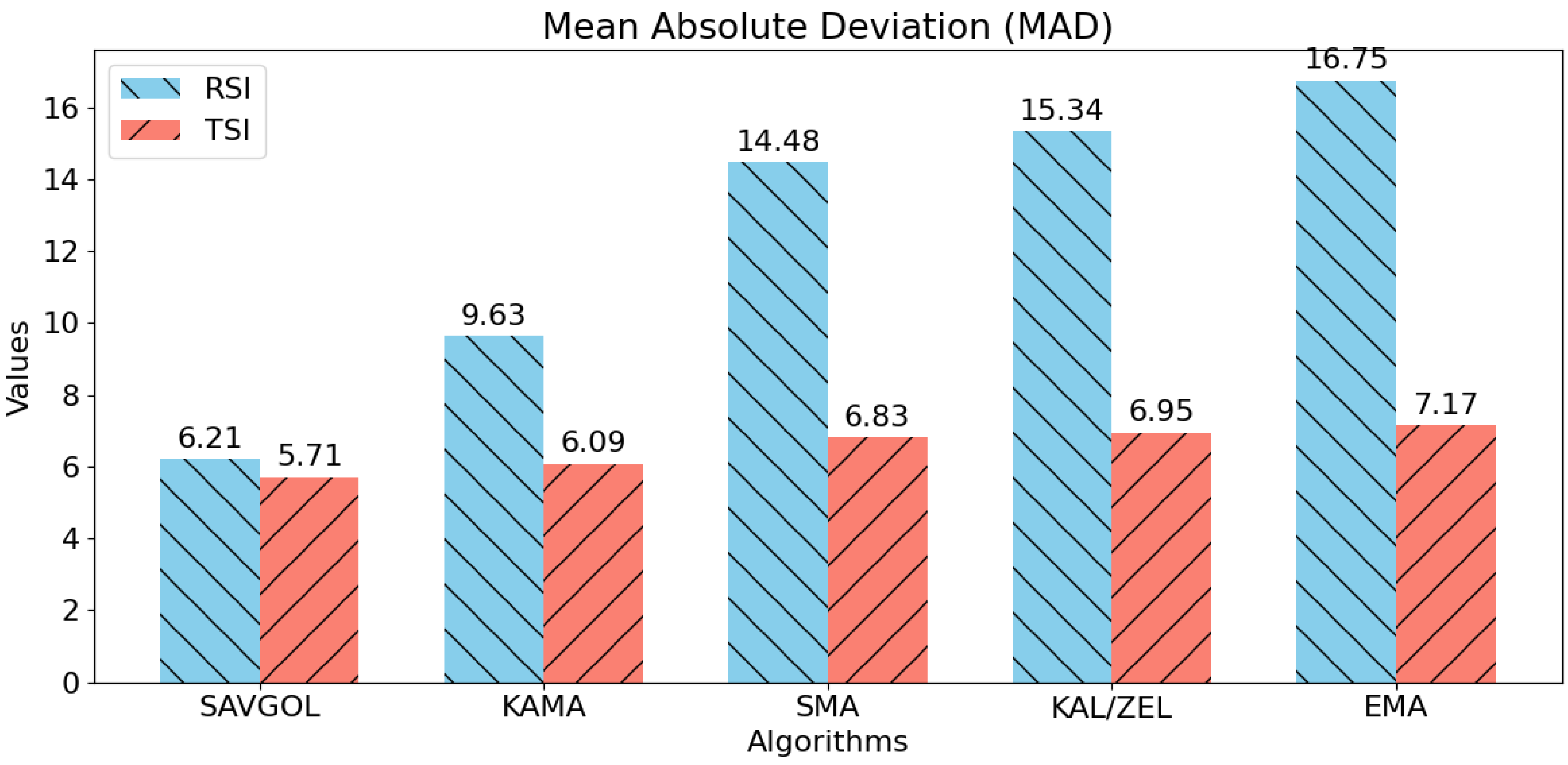
A comparative analysis of our confirmation timing graphs (Figure 4 and Figure 6) shows a horizontal line at y = 10, representing the latency target. We analysed statistical measures of deviation RMSE and MAD between this target and latency values for different trend filtering algorithms. Results indicate that methods closer to the target line generally have less variability and more stable network latency performance.
Notably, Figure 11 highlights differences between algorithm pairs using RSI versus TSI. RSI-based pairs performed significantly worse than TSI-based counterparts, which showed lower deviations overall. The Savitzky–Golay filter was an exception, as its performance with both RSI and TSI inputs remained comparable.
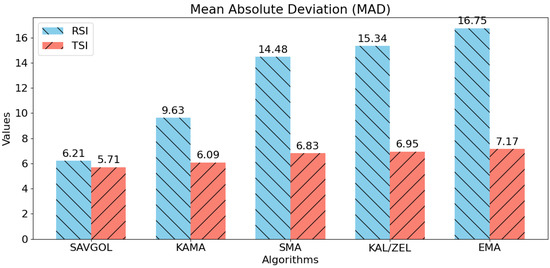
Figure 11.
MAD scores for each algorithm pair combination. A reduced MAD score represents lower volatility, which means more stable network latency. Lower is better.
Similarly, Figure 12 shows that algorithms paired with TSI outperformed those using RSI in terms of RMSE metrics. Again, the Savitzky–Golay filter was the sole exception, demonstrating consistent performance across both indicators.

Figure 12.
RMSE scores for each algorithm pair. Lower RMSE values indicate that an algorithm pair can more accurately track the 10-s latency target. Lower RMSE values are better.
We have covered all the tests used to compare our trend filtering/trend detection algorithm pairs. We will now highlight the final scores for each algorithm pair.
5.8. Algorithm Test Scores
A simple scoring system is used for each test. Algorithm pairs that perform the best in a particular category will receive 5 points, followed by the second-best scoring algorithm with 4 points. The algorithm pair performing the worst for a particular test will receive 1 point.
A preliminary look at both Table 7 and Table 8 shows that the SAVGOL algorithm performed well under both RSI and TSI; SMA also performed consistently well. An algorithm that faced challenges across the test suite was the KALMAN-ZLEMA combination. we have finished looking at all the results for our candidate algorithm combination for PLATO. In the following section, we will take our highest-performing algorithm pair, RSI-SAVGOL, and apply it to our RACER consensus mechanism using PLATO.

Table 7.
RSI algorithm pair scores.

Table 8.
TSI algorithm pair scores.
5.9. Applying Traffic Optimisation
This section examines performance gains for RACER when integrated with PLATO. The basic version of RACER sends messages immediately but does not account for varying network latencies. PLATO’s traffic optimisation provides IoT nodes with real time latency data, enabling decentralised adjustments to balance throughput and latency across the network. Table 9 summaries RACER performance tests both with and without PLATO enabled.

Table 9.
A summary of the different test which make up the lines on Figure 1. Nodes will have a chance to send a message according to the message interval. Nodes will roll a random number to determine if they have permission to gossip the message. Nodes also select a random message size. These configurations simulate a chaotic peer to peer network to test the performance benefits of using our proposed consensus mechanism with our proposed traffic optimisation algorithm.
The “Send Chance” column indicates the probability that a node generates a data message during each interval, while “Padding” specifies the payload size of messages. These parameters alongside the message generation interval are randomised using Python’s random.random() function to introduce variability between nodes during testing.
Simulations for 10 node configurations ran on an Asus Zenbook UX303 Laptop (purchased in Melbourne, Australia in 2014). The 100 node simulations used a custom built workstation with a AMD Ryzen 9 7950X equipped with 64GB DDR5 RAM, with parts sourced from Melbourne, Australia. Both systems utilised Docker containers to model individual nodes and used Linux distributions. The Asus Zenbook was running PopOS! 22.04 made by System76 in Denver, Colorado, while the workstation ran Arch Linux.
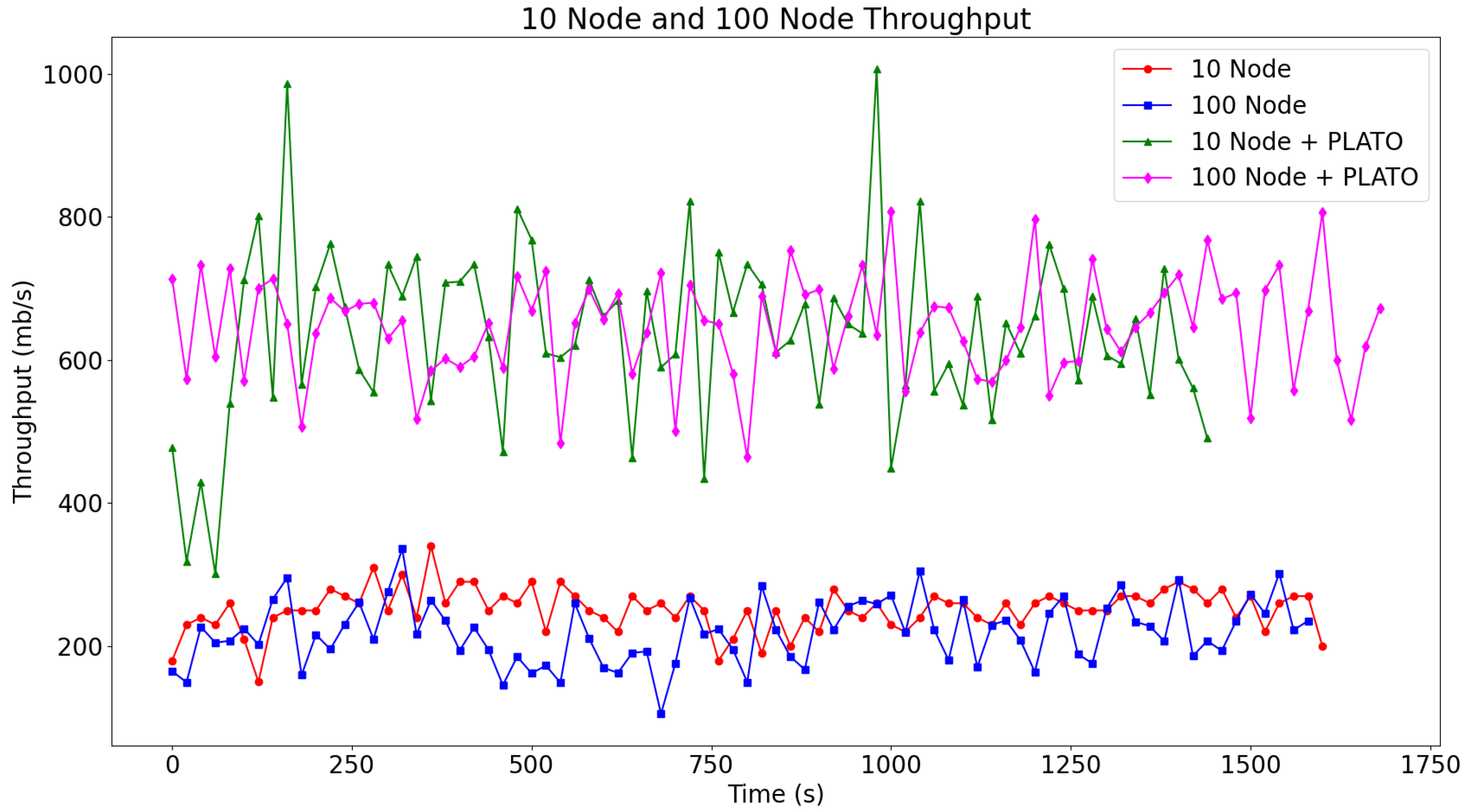
The throughput of these four tests is graphed as four lines on Figure 13. The two lower lines of the Figure 13 represent the throughput before the addition of PLATO, while the two upper lines represent the throughput after implementing PLATO. Implementing PLATO alongside RACER increases throughput of the network by about 2.5 times and scales to both the 10 node network and the 100 node network. In Table 10 we attempt to show comparable metrics from the IoT consensus mechanisms mentioned in the related work section. Unfortunately, it is difficult to directly compare our work against theirs, as most of the related works had insufficient performance information to calculate a throughput metric. Most of the related works focused on metrics specifically related to their domain or their novel consensus method, rather than overall performance of the network.
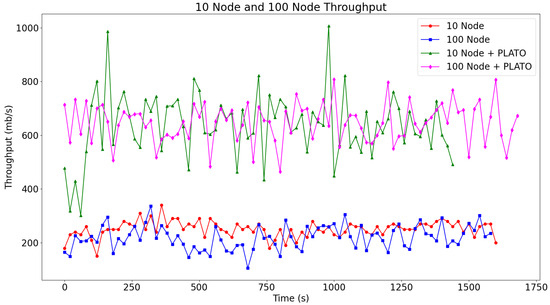
Figure 13.
The two bottom lines show the throughput of the proposed consensus mechanism without the traffic optimisation algorithm. The two lines above represent the throughput benefits after adding our proposed traffic optimisation algorithm to each node on the network.

Table 10.
IoT consensus from related work.
6. Discussion
The study evaluated combinations of different algorithms with RSI and TSI indices to assess their performance in terms of stability, computational resource efficiency, and error handling during communication. The RSI-SAVGOL and TSI-SAVGOL pairs demonstrated strong stability and consistent results across various test scenarios designed to measure fault tolerance:
- RSI-SAVGOL performed well with fast and mixed data segments, maintaining steady communication latency with minimal fluctuations.
- However, the Savitzky–Golay method required significantly more memory (4–8 times higher than other algorithms), which could limit its use in devices with constrained resources.
The following is in contrast with the above:
- RSI-KALMAN-ZLEMA and TSI-KALMAN-ZLEMA combinations underperformed due to inadequate parameter tuning of the Kalman filter component.
- These configurations struggled with fast/mixed data segments, requiring up to four times more CPU time than moving-average-based methods.
While RSI-SAVGOL generally outperformed other setups in latency performance, TSI-SAVGOL slightly reduced stability but still delivered acceptable results overall.
The research highlights the potential of Savitzky–Golay algorithms for applications demanding consistent performance across diverse conditions, though their high memory demands must be carefully considered in resource-constrained environments.
The integration of PLATO into the RACER consensus mechanism demonstrates a significant improvement in network throughput, achieving approximately 2.5 times higher performance across both 10 node and 100 node configurations (Figure 13). This enhancement underscores the efficacy of decentralised traffic optimisation for IoT networks, where latency variability is unpredictable. By enabling nodes to dynamically adjust message propagation based on real time latency data, PLATO mitigates bottlenecks while maintaining consensus integrity. Notably, this scalability across network sizes (10 vs. 100 nodes) suggests that RACER and PLATO can accommodate heterogeneous IoT deployments without proportional performance degradation, a critical feature for large scale industrial or urban IoT ecosystems.
The experimental results highlight the trade-offs between node count, message generation parameters, and latency tolerance. For instance, while the 10 node configuration with PLATO achieved lower latency (10 s) compared with its 100 node counterpart (15 s), throughput remained consistent relative to non-PLATO baselines. This indicates that PLATO’s adaptive mechanisms effectively balance load distribution even as network complexity increases. The hardware differences between testbeds (e.g., Intel i7 vs. AMD Ryzen 9) may have influenced absolute performance metrics, but the proportional improvement of PLATO (2.5× across both setups) suggests strong algorithmic robustness.
When bench marked against existing IoT consensus mechanisms in Table 10, RACER demonstrates competitive throughput and latency characteristics despite gaps in direct comparability. The following is an example:
- Throughput: At 100 nodes, RACER’s 600 MB/s throughput outperforms PoEWAL (unspecified but slower) and matches Tree-chain’s transactional capacity (250 tx/s), assuming similar data densities. Scalability: While CBPoW and PoBT operate at smaller scales, RACER’s ability to handle 100 nodes without compromising throughput positions it favourably for distributed IoT applications.
RACER was able to operate at a much higher throughput and network size compared with the consensus mechanisms reviewed in the literature. These disparities come down to some core differences in the consensus mechanisms:
- Byzantine Broadcast over state machine replication: Our consensus mechanism focused on a simpler problem in consensus, specifically Byzantine Broadcast, rather than doing full state machine replication (often achieved via blockchains). For our IoT domain (sensor data transfer) we targeted a simpler consensus problem to align with the reduced resources on IoT devices, and a tolerance to sensor data temporarily falling out of sync across devices.
- Gossiping, randomisation, and sampling: Through a combination of gossiping messages over subsets of nodes, randomising network topologies and sampling responses rather than collecting responses from all consensus participants. These three features assisted RACER by reducing bottle necks associated with star and hierarchical topologies, and avoiding additional protocol overhead by sampling, rather then gathering votes from all nodes.
However, limitations persist. The absence of direct latency/throughput trade off data in prior works complicates nuanced comparisons. For instance, PoSCS’s execution times (ranging from milliseconds to hours) highlight variability not fully captured by RACER’s static 15 s target. Additionally, simulations on Docker containers may underestimate real-world IoT constraints such as energy limitations or heterogeneous device capabilities.
7. Conclusions
RACER is a consensus mechanism focused for use on IoT devices. RACER had three goals in mind: no reliance on synchronous networks or synchronous clocks, no dependence on a central node for consensus, improving performance compared with other IoT focused consensus mechanisms. To meet goals one and two, we implemented a random gossiping algorithm (SPDE) and enhanced it with a lightweight IoT focused transaction ordering mechanism, message batching functionality for improved scalability, and decentralised network telemetry to detect changing network conditions. To meet goal three, performance, we implemented PLATO, a companion algorithm for RACER which optimises network traffic and manages rapidly changing network conditions. PLATO was designed to maximise throughput, while maintaining a preset latency.
To validate PLATO, we conducted an extensive set of experiments using a full implementation in Python. We tested a range of trend filtering and trend detection algorithm pairs for PLATO, and simulated them extensively under different network environments to find a suitable pair. RSI-SAVGOL was found to be the best performing trend filtering/trend detection pair.
We then validated both RACER and PLATO by simulating a 10 node network on a laptop, and a 100 node network on a server, both using docker for the deployment. We found that combining RACER and PLATO resulted in a 2.5 times throughput increase, validating its performance for dynamic, high traffic IoT environments. While a direct performance comparison between the other IoT mechanisms found in the related works section is not possible, we tested RACER on a larger simulated network, using very large transactions. Compared with the consensus mechanisms from the related work section, RACER was able to handle a much larger volume of transactions, even under constantly changing network environments.
To address RACER’s real-world applicability, its design choices directly align with the constraints of IoT deployments such as smart cities, industrial automation, and healthcare monitoring. For instance, in smart city infrastructure, RACER’s Byzantine Broadcast and vector clocks ensure fault-tolerant data synchronisation among distributed sensors (e.g., traffic cameras or environmental monitors), while PLATO reduces gossip overhead in dense node networks, mitigating bandwidth congestion on constrained IoT SBCs like Raspberry Pi. In industrial automation, the protocol’s minimal centralisation avoids single points of failure in critical systems (e.g., factory floors with thousands of sensors) and its adaptability to IEEE 802.15.4 standards ensures compatibility with existing low power wireless infrastructures, such as Zigbee based devices. For healthcare monitoring, RACER’s eventual consistency guarantees reliable aggregation of patient data from wearable or implanted sensors, while compressing transactions to fit into tiny payloads and preserving battery life through sleep-state alignment with IEEE 802.15.4’s superframe structures. However, deployment challenges remain: hardware feasibility requires optimising RACER’s consensus computations for energy constrained devices (e.g., using lightweight cryptographic primitives), addressing heterogeneous node capabilities in mixed IoT ecosystems, and ensuring seamless integration with legacy systems. Potential optimisations could include dynamic parameter tuning (e.g., adjusting block sizes based on real-time network load) or leveraging edge computing to offload heavy computations.
RACER is able to function without synchronised clocks, has no central point of failure or coordinator node, and has performance which is suitable for medium to large IoT networks.
In the future with the asynchronous consensus framework built for RACER already in place, we would analyse the fault tolerance of RACER more formally, investigate the power efficiency on real IoT SBCs, investigate scalability with larger networks (virtual and physical) and look into developing an intrinsic Sibyl defence mechanism compatible with IoT hardware.
Author Contributions
Conceptualisation, Z.A.; Methodology, Z.A.; Software, Z.A.; Supervision, H.M. and N.C.; Writing—original draft, Z.A.; Writing—review and editing, Z.A., H.M. and D.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the SmartSat C.R.C., whose activities are funded by the Australian Government’s C.R.C. Programme.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The implementation for RACER can be found at the following Github link: https://github.com/brite3001/RACER/ accessed on 2 April 2025.
Acknowledgments
The authors would like to thank SmartSat CRC for providing scholarship funding and BAE Systems Australia, our industry collaborator.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jauw, M.G.; Lisanti, Y.; Fang, A.J. Smart Living Revolution: Examining IoT Adoption for Homes. In Proceedings of the 2024 International Conference on IoT Based Control Networks and Intelligent Systems (ICICNIS), Bengaluru, India, 17–18 December 2024; pp. 469–474. [Google Scholar] [CrossRef]
- Nguyen, H.; Nawara, D.; Kashef, R. Connecting the indispensable roles of IoT and artificial intelligence in smart cities: A survey. J. Inf. Intell. 2024, 2, 261–285. [Google Scholar] [CrossRef]
- Serpanos, D. Industrial Internet of Things: Trends and Challenges. Computer 2024, 57, 124–128. [Google Scholar] [CrossRef]
- Nidhi; Rawat, B.S.; Srivastava, A.; Garg, N. Health Monitoring Transforming Using IoT: A Review. In Proceedings of the 2024 IEEE International Conference on Computing, Power and Communication Technologies (IC2PCT), Greater Noida, India, 9–10 February 2024; Volume 5, pp. 17–22. [Google Scholar] [CrossRef]
- Popoola, O.; Rodrigues, M.; Marchang, J.; Shenfield, A.; Ikpehai, A.; Popoola, J. A critical literature review of security and privacy in smart home healthcare schemes adopting IoT & blockchain: Problems, challenges and solutions. Blockchain Res. Appl. 2024, 5, 100178. [Google Scholar]
- Kolevski, D.; Michael, K. Edge Computing and IoT Data Breaches: Security, Privacy, Trust, and Regulation. IEEE Technol. Soc. Mag. 2024, 43, 22–32. [Google Scholar] [CrossRef]
- Yang, X.; Shu, L.; Liu, Y.; Hancke, G.P.; Ferrag, M.A.; Huang, K. Physical Security and Safety of IoT Equipment: A Survey of Recent Advances and Opportunities. IEEE Trans. Ind. Inform. 2022, 18, 4319–4330. [Google Scholar] [CrossRef]
- Antonopoulos, A.M.; Harding, D.A. Mastering Bitcoin: Programming the Open Blockchain; O’Reilly Media, Inc.: Newton, MA, USA, 2023. [Google Scholar]
- Xu, R.; Chen, Y.; Blasch, E. Microchain: A light hierarchical consensus protocol for iot systems. In Blockchain Applications in IoT Ecosystem; Springer: Berlin/Heidelberg, Germany, 2020; pp. 129–149. [Google Scholar]
- Dorri, A.; Jurdak, R. Tree-Chain: A Fast Lightweight Consensus Algorithm for IoT Applications. In Proceedings of the Conference on Local Computer Networks, LCN, Sydney, NSW, Australia, 16–19 November 2020; pp. 369–372. [Google Scholar] [CrossRef]
- Huang, J.; Kong, L.; Chen, G.; Wu, M.Y.; Liu, X.; Zeng, P. Towards secure industrial iot: Blockchain system with credit-based consensus mechanism. IEEE Trans. Ind. Inform. 2019, 15, 3680–3689. [Google Scholar] [CrossRef]
- Raghav; Andola, N.; Venkatesan, S.; Verma, S. PoEWAL: A lightweight consensus mechanism for blockchain in IoT. Pervasive Mob. Comput. 2020, 69, 101291. [Google Scholar] [CrossRef]
- Tsang, Y.P.; Choy, K.L.; Wu, C.H.; Ho, G.T.S.; Lam, H.Y. Blockchain-Driven IoT for Food Traceability with an Integrated Consensus Mechanism. IEEE Access 2019, 7, 129000–129017. [Google Scholar] [CrossRef]
- Stallings, W.; Brown, L. Computer Security: Principles and Practice; Pearson: London, UK, 2015. [Google Scholar]
- Coulouris, G.F.; Dollimore, J.; Kindberg, T. Distributed Systems: Concepts and Design; Pearson Education: London, UK, 2005. [Google Scholar]
- Nakamoto, S.; Bitcoin, A. A peer-to-peer electronic cash system. Bitcoin 2008, 4, 15. [Google Scholar]
- King, S.; Nadal, S. Ppcoin: Peer-to-Peer Crypto-Currency with Proof-of-Stake. Self-Published Paper. 19 August 2012. Available online: https://bitcoin.peryaudo.org/vendor/peercoin-paper.pdf (accessed on 2 April 2025).
- Castro, M.; Liskov, B. Practical byzantine fault tolerance. In Proceedings of the OsDI, New Orleans, LA, USA, 22–25 February 1999; Volume 99, pp. 173–186. [Google Scholar]
- Li, S.N.; Spychiger, F.; Tessone, C.J. Reward distribution in proof-of-stake protocols: A trade-off between inclusion and fairness. IEEE Access 2023, 11, 134136–134145. [Google Scholar] [CrossRef]
- Castro, M.; Liskov, B. Practical byzantine fault tolerance and proactive recovery. ACM Trans. Comput. Syst. 2002, 20, 398–461. [Google Scholar] [CrossRef]
- Trivedi, C.; Rao, U.P.; Parmar, K.; Bhattacharya, P.; Tanwar, S.; Sharma, R. A transformative shift toward blockchain-based IoT environments: Consensus, smart contracts, and future directions. Secur. Priv. 2023, 6, e308. [Google Scholar] [CrossRef]
- Venkatesan, K.; Rahayu, S.B. Blockchain security enhancement: An approach towards hybrid consensus algorithms and machine learning techniques. Sci. Rep. 2024, 14, 1149. [Google Scholar] [CrossRef]
- Silvano, W.F.; Marcelino, R. Iota Tangle: A cryptocurrency to communicate Internet-of-Things data. Future Gener. Comput. Syst. 2020, 112, 307–319. [Google Scholar] [CrossRef]
- Biswas, S.; Sharif, K.; Li, F.; Maharjan, S.; Mohanty, S.P.; Wang, Y. PoBT: A Lightweight Consensus Algorithm for Scalable IoT Business Blockchain. IEEE Internet Things J. 2020, 7, 2343–2355. [Google Scholar] [CrossRef]
- Puthal, D.; Mohanty, S.P.; Yanambaka, V.P.; Kougianos, E. PoAh: A Novel Consensus Algorithm for Fast Scalable Private Blockchain for Large-scale IoT Frameworks. arXiv 2020, arXiv:2001.07297. [Google Scholar]
- Guerraoui, R.; Kuznetsov, P.; Monti, M.; Pavlovic, M.; Seredinschi, D.A. AT2: Asynchronous Trustworthy Transfers. arXiv 2019, arXiv:1812.10844. [Google Scholar]
- Yin, M.; Malkhi, D.; Reiter, M.K.; Gueta, G.G.; Abraham, I. HotStuff: BFT consensus with linearity and responsiveness. In Proceedings of the 2019 ACM Symposium on Principles of Distributed Computing, Toronto, ON, Canada, 29 July–2 August 2019; pp. 347–356. [Google Scholar]
- Kogias, E.K.; Jovanovic, P.; Gailly, N.; Khoffi, I.; Gasser, L.; Ford, B. Enhancing bitcoin security and performance with strong consistency via collective signing. In Proceedings of the 25th Usenix Security Symposium (Usenix Security 16), Austin, TX, USA, 10–12 August 2016; pp. 279–296. [Google Scholar]
- Neiheiser, R.; Matos, M.; Rodrigues, L. Kauri: Scalable bft consensus with pipelined tree-based dissemination and aggregation. In Proceedings of the ACM SIGOPS 28th Symposium on Operating Systems Principles, Online, 26–29 October 2021; pp. 35–48. [Google Scholar]
- Chen, J.; Micali, S. Algorand. arXiv 2016, arXiv:1607.01341. [Google Scholar]
- Buchman, E. Tendermint: Byzantine Fault Tolerance in the Age of Blockchains. Ph.D. Thesis, University of Guelph, Guelph, ON, Canada, 2016. [Google Scholar]
- Li, P.; Wang, G.; Chen, X.; Long, F.; Xu, W. Gosig: A scalable and high-performance byzantine consensus for consortium blockchains. In Proceedings of the 11th ACM Symposium on Cloud Computing, Online, 19–21 October 2020; pp. 223–237. [Google Scholar]
- Mattern, F. Virtual Time and Global States of Distributed Systems; University Department of Computer Science: Kaiserslautern, Germany, 1988. [Google Scholar]
- Lamport, L. Time, clocks, and the ordering of events in a distributed system. Commun. ACM 1978, 21, 558–565. [Google Scholar] [CrossRef]
- Jenks, G. Python Sorted Containers. J. Open Source Softw. 2019, 4, 1330. [Google Scholar] [CrossRef]
- Kurose, J.; Ross, K. Computer Networks: A Top Down Approach Featuring the Internet; Pearson: London, UK, 2010. [Google Scholar]
- Perron, P.; Wada, T. Let’s take a break: Trends and cycles in US real GDP. J. Monet. Econ. 2009, 56, 749–765. [Google Scholar] [CrossRef]
- Salkar, T.; Shinde, A.; Tamhankar, N.; Bhagat, N. Algorithmic trading using technical indicators. In Proceedings of the 2021 International Conference on Communication information and Computing Technology (ICCICT), Mumbai, India, 25–27 June 2021; IEEE: Piscataway, NJ, USA; pp. 1–6. [Google Scholar]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hunter, J.S. The exponentially weighted moving average. J. Qual. Technol. 1986, 18, 203–210. [Google Scholar] [CrossRef]
- Kaufman, P.J. Trading Systems and Methods + Website; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 591. [Google Scholar]
- Ehlers, J.R.W. ZERO LAG (Well, Almost). Available online: https://www.mesasoftware.com/papers/ZeroLag.pdf (accessed on 28 January 2025).
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Lai, X.; Yang, T.; Wang, Z.; Chen, P. IoT implementation of Kalman filter to improve accuracy of air quality monitoring and prediction. Appl. Sci. 2019, 9, 1831. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, R.; Liu, S. A differentially private unscented Kalman filter for streaming data in IoT. IEEE Access 2018, 6, 6487–6495. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Acharya, D.; Rani, A.; Agarwal, S.; Singh, V. Application of adaptive Savitzky–Golay filter for EEG signal processing. Perspect. Sci. 2016, 8, 677–679. [Google Scholar] [CrossRef]
- Vivó-Truyols, G.; Schoenmakers, P.J. Automatic selection of optimal Savitzky- Golay smoothing. Anal. Chem. 2006, 78, 4598–4608. [Google Scholar] [CrossRef]
- Zimmermann, B.; Kohler, A. Optimizing Savitzky–Golay parameters for improving spectral resolution and quantification in infrared spectroscopy. Appl. Spectrosc. 2013, 67, 892–902. [Google Scholar] [CrossRef]
- Kahn, J.A.; Rich, R.W. Tracking the new economy: Using growth theory to detect changes in trend productivity. J. Monet. Econ. 2007, 54, 1670–1701. [Google Scholar] [CrossRef]
- Chandler, R.; Scott, M. Statistical Methods for Trend Detection and Analysis in the Environmental Sciences; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Grafakos, L. Classical Fourier Analysis; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Wilder, J.W. New Concepts in Technical Trading Systems; Trend Research: Greensboro, NC, USA, 1978. [Google Scholar]
- Bhargavi, R.; Gumparthi, S.; Anith, R. Relative strength index for developing effective trading strategies in constructing optimal portfolio. Int. J. Appl. Eng. Res. 2017, 12, 8926–8936. [Google Scholar]
- Blau, W. Momentum, Direction, and Divergence; John Wiley & Sons: Hoboken, NJ, USA, 1995; Volume 5. [Google Scholar]
- Bracha, G. Asynchronous Byzantine agreement protocols. Inf. Comput. 1987, 75, 130–143. [Google Scholar] [CrossRef]
- IEEE Std 802.15.4-2020 (Revision of IEEE Std 802.15.4-2015); IEEE Standard for Low-Rate Wireless Networks. IEEE: Piscataway, NJ, USA, 2020; pp. 1–800.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).