Convolution of Barker and Golay Codes for Low Voltage Ultrasonic Testing
Abstract
:1. Introduction
- We investigated the combined coded excitation technique for a low-voltage ultrasonic testing device, not like other existing works which focus on high-voltage situations.
- We provided extensive theoretical analysis and simulation results for all the possible combination of coded excitation for ultrasonic testing, not like other works on selected coding methods.
- Current combined coded excitation techniques are applied in ultrasonic imaging system only. This work opens the door for all ultrasonic testing devices for many other applications in a low-voltage situation.
2. Related Work
3. Materials and Methods
3.1. Matched Filter
3.2. Barker Code
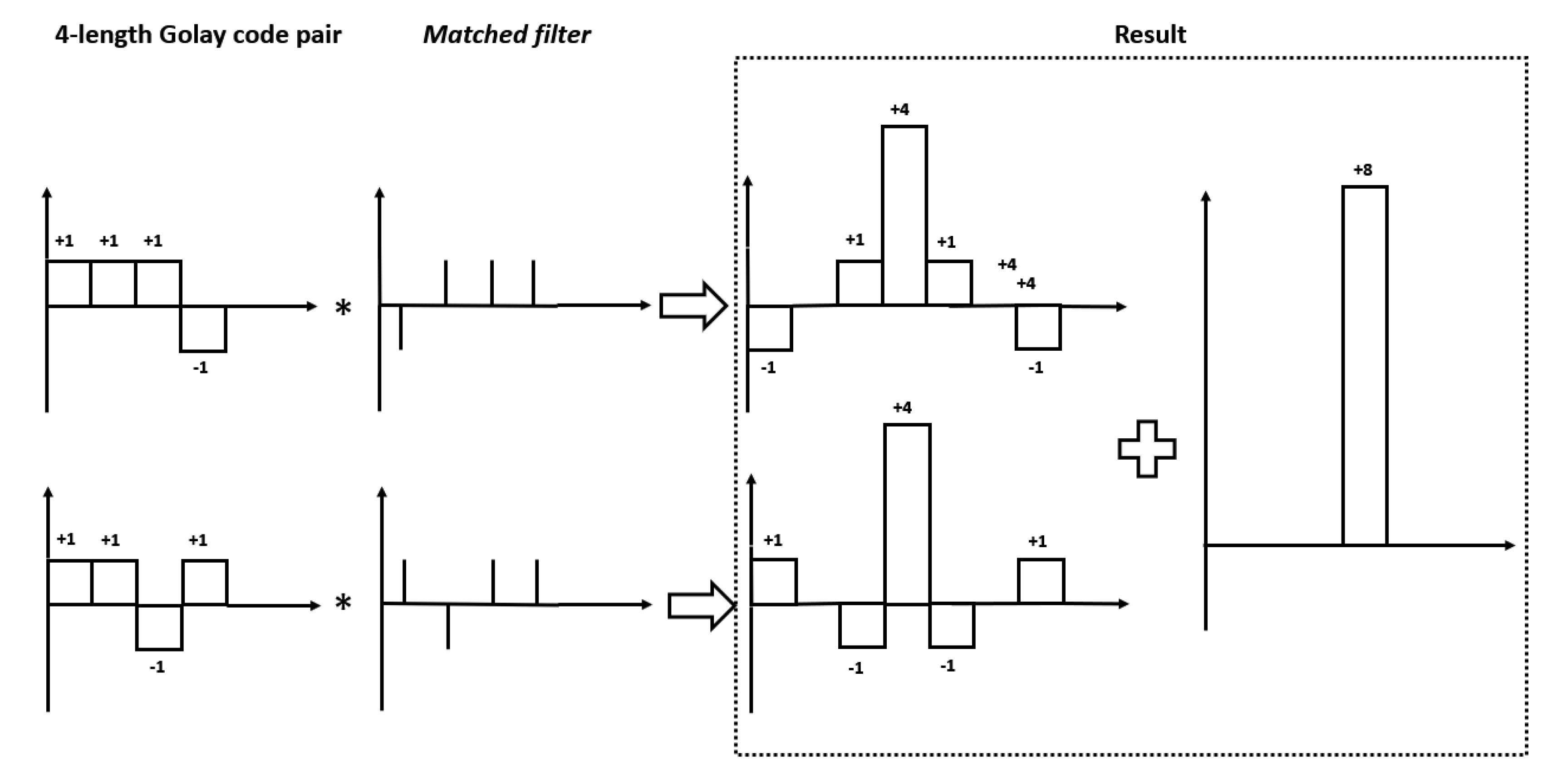
3.3. Golay Code
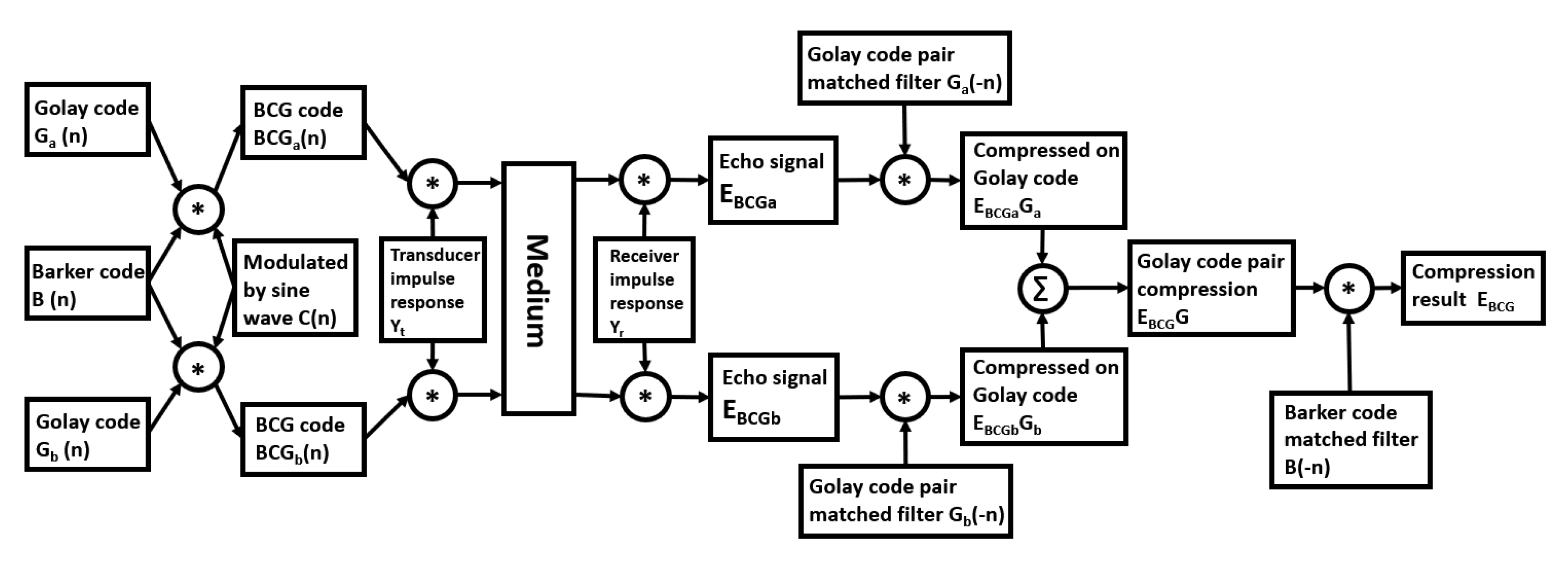
3.4. Convolution of Barker Code and Golay Code
4. Theoretical Analysis
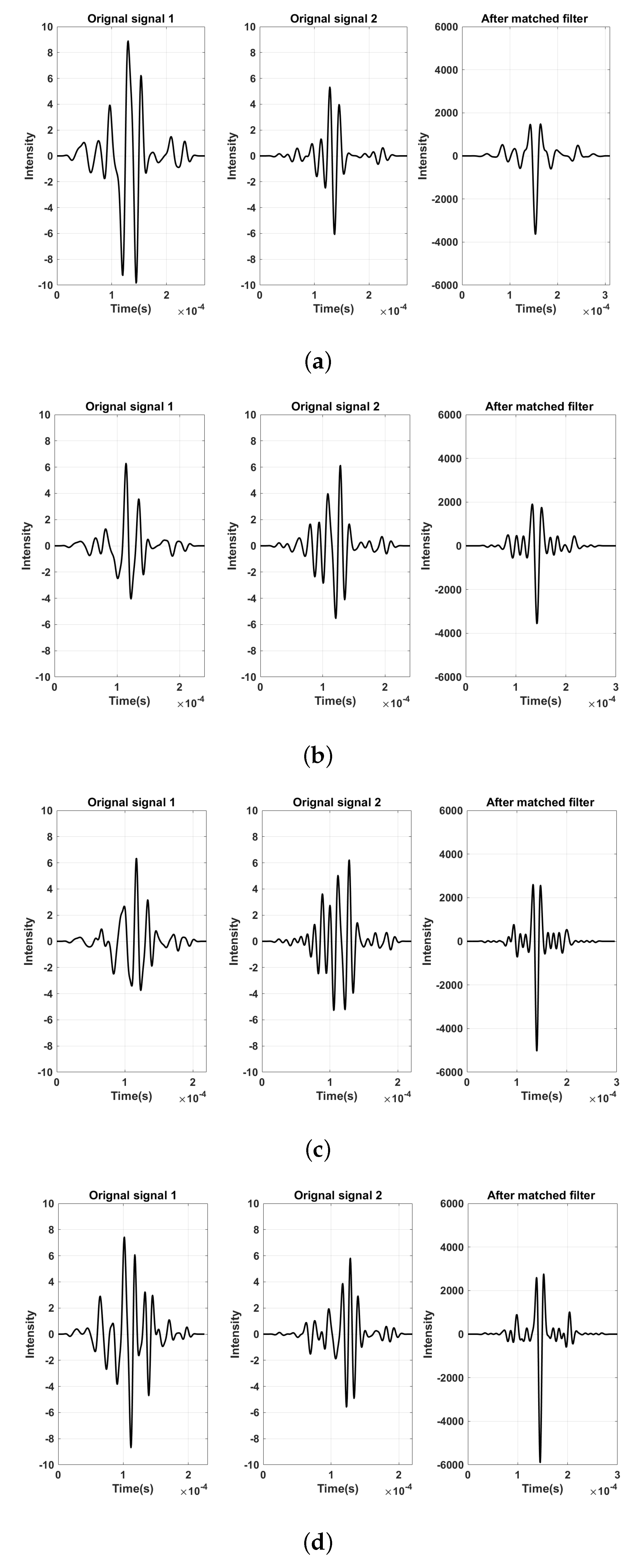
5. Simulation
5.1. Barker Code and Golay Code Simulation Result
5.2. Convolution of 3-Bit Barker Code and Various Length Golay Code
5.3. Convolution of 2-Bit Golay Code and Various Length Barker Code
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guyott, C.C.H.; Cawley, P.; Adams, R. The non-destructive testing of adhesively bonded structure: A review. J. Adhes. 1986, 20, 129–159. [Google Scholar] [CrossRef]
- Kim, P.; Jung, E.; Bae, S.; Kim, K.; Song, T.K. Barker-sequence-modulated golay coded excitation technique for ultrasound imaging. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016; pp. 1–4. [Google Scholar]
- Chiao, R.Y.; Hao, X. Coded excitation for diagnostic ultrasound: A system developer’s perspective. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 160–170. [Google Scholar] [CrossRef] [PubMed]
- Skolnik, M.I. Introduction to radar. Radar Handb. 1962, 2, 21. [Google Scholar]
- Kanzler, S.G.; Oelze, M.L. Improved scatterer size estimation using backscatter coefficient measurements with coded excitation and pulse compression. J. Acoust. Soc. Am. 2008, 123, 4599–4607. [Google Scholar] [CrossRef] [PubMed]
- Takeuchi, Y. An investigation of a spread energy method for medical ultrasound systems: Part one: Theory and investigation. Ultrasonics 1979, 17, 175–182. [Google Scholar] [CrossRef]
- O’Donnell, M. Coded excitation system for improving the penetration of real-time phased-array imaging systems. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 341–351. [Google Scholar] [CrossRef] [PubMed]
- Jedwab, J.; Parker, M.G. A construction of binary Golay sequence pairs from odd-length Barker sequences. J. Comb. Des. 2009, 17, 478–491. [Google Scholar] [CrossRef]
- Wang, M.; Cong, S.; Zhang, S. Pseudo Chirp-Barker-Golay coded excitation in ultrasound imaging. In Proceedings of the 2018 Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 4035–4039. [Google Scholar]
- Ricci, M.; Senni, L.; Burrascano, P. Exploiting pseudorandom sequences to enhance noise immunity for air-coupled ultrasonic nondestructive testing. IEEE Trans. Instrum. Meas. 2012, 61, 2905–2915. [Google Scholar] [CrossRef]
- Katz, N.; Nelson, M.; Goldbaum, M.; Chaudhuri, S.; Chatterjee, S. Detection of blood vessels in retinal images using two-dimensional matched filters. IEEE Trans. Med. Imaging 1989, 8, 263–269. [Google Scholar] [Green Version]
- Skolnik, M.I. Introduction to Radar Systems; McGraw Hill Book Co.: New York, NY, USA, 1980; 590p. [Google Scholar]
- Bancroft, J.C. Introduction to Matched Filters; CREWES Research: Calgary, AB, Canada, 2002. [Google Scholar]
- Barker, R. Group synchronizing of binary digital systems. In Communication Theory; Butterworth: London, UK, 1953; pp. 273–287. [Google Scholar]
- Turyn, R. On Barker codes of even length. Proc. IEEE 1963, 51, 1256. [Google Scholar] [CrossRef]
- Golay, M. Complementary series. IRE Trans. Inf. Theory 1961, 7, 82–87. [Google Scholar] [CrossRef]
- Török, I.; Seller, R. Pulse compression in search radar. Period. Polytech. Electr. Eng. 1998, 42, 391–408. [Google Scholar]








| CODE SYMBOL | LENGTH | CODE | SIDE-LOBE LEVEL (dB) |
|---|---|---|---|
| B2 | 2 | (+1, −1), (+1,+1) | −6 |
| B3 | 3 | +1, +1, −1 | −9.5 |
| B4 | 4 | (+1, −1, +1, +1), (+1, −1, −1, −1) | −12 |
| B5 | 5 | +1, +1, +1, −1, +1 | −14 |
| B7 | 7 | +1, +1, +1, −1, −1, +1, −1 | −16.9 |
| B11 | 11 | +1, +1, +1, −1, −1, −1, +1, − 1, −1, +1, −1 | −20.8 |
| B13 | 13 | +1, +1, +1, +1, −1, −1, −1, +1, +1, −1, +1, −1, +1 | −22.3 |
| CODE SYMBOL | CODE LENGTH | PSL (dB) | |
|---|---|---|---|
| Barker 3 | Golay 2 | 4 | −19 |
| Golay 4 | 6 | −23.4 | |
| Golay 8 | 10 | −28.6 | |
| Barker 5 | Golay 2 | 6 | −22 |
| Golay 4 | 8 | −24.8 | |
| Golay 8 | 12 | −28.8 | |
| Barker 7 | Golay 2 | 8 | −24.2 |
| Golay 4 | 10 | −26.4 | |
| Golay 8 | 14 | −29.6 | |
| Barker 11 | Golay 2 | 12 | −27.6 |
| Golay 4 | 14 | −29.2 | |
| Golay 8 | 18 | −31.4 | |
| Barker 13 | Golay 2 | 14 | −29.0 |
| Golay 4 | 16 | −30.2 | |
| Golay 8 | 20 | −32.2 | |
| CODE SYMBOL | CODE LENGTH | THEORETICAL RESULT | SIMULATION RESULT | ||
|---|---|---|---|---|---|
| SNR (dB) | PSL (dB) | SNR (dB) | PSL (dB) | ||
| Barker 7 | 7 | 16.9 | 18.5 | ||
| Golay 4 | 4 | 18.1 | - | 21.5 | - |
| B3G2 | 4 | 21.6 | 22.02 | ||
| B3G4 | 6 | 27.6 | 27.1 | ||
| B3G8 | 10 | 33.6 | 30.1 | ||
| B5G2 | 6 | 26.0 | 24 | ||
| B7G2 | 8 | 28.9 | 27.78 | ||
| B11G2 | 12 | 32.9 | 31.3 | ||
| B13G2 | 14 | 34.3 | 35.1 | ||
| M-sequence | 15 | 18.1 | 17.8 | ||
| Gold code | 15 | 18.1 | 17 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Z.; Rudlin, J.; Asfis, G.; Meng, H. Convolution of Barker and Golay Codes for Low Voltage Ultrasonic Testing. Technologies 2019, 7, 72. https://doi.org/10.3390/technologies7040072
Fan Z, Rudlin J, Asfis G, Meng H. Convolution of Barker and Golay Codes for Low Voltage Ultrasonic Testing. Technologies. 2019; 7(4):72. https://doi.org/10.3390/technologies7040072
Chicago/Turabian StyleFan, Zeng, John Rudlin, Giorgos Asfis, and Hongying Meng. 2019. "Convolution of Barker and Golay Codes for Low Voltage Ultrasonic Testing" Technologies 7, no. 4: 72. https://doi.org/10.3390/technologies7040072
APA StyleFan, Z., Rudlin, J., Asfis, G., & Meng, H. (2019). Convolution of Barker and Golay Codes for Low Voltage Ultrasonic Testing. Technologies, 7(4), 72. https://doi.org/10.3390/technologies7040072






