How Trade Dampens the Impact of Financial Frictions in the Presence of Large Firms
Abstract
1. Introduction
2. The Model Economy
2.1. Preferences and Demand
2.2. Production
2.3. Equilibrium
3. Open Economy Model
3.1. Symmetric Trade
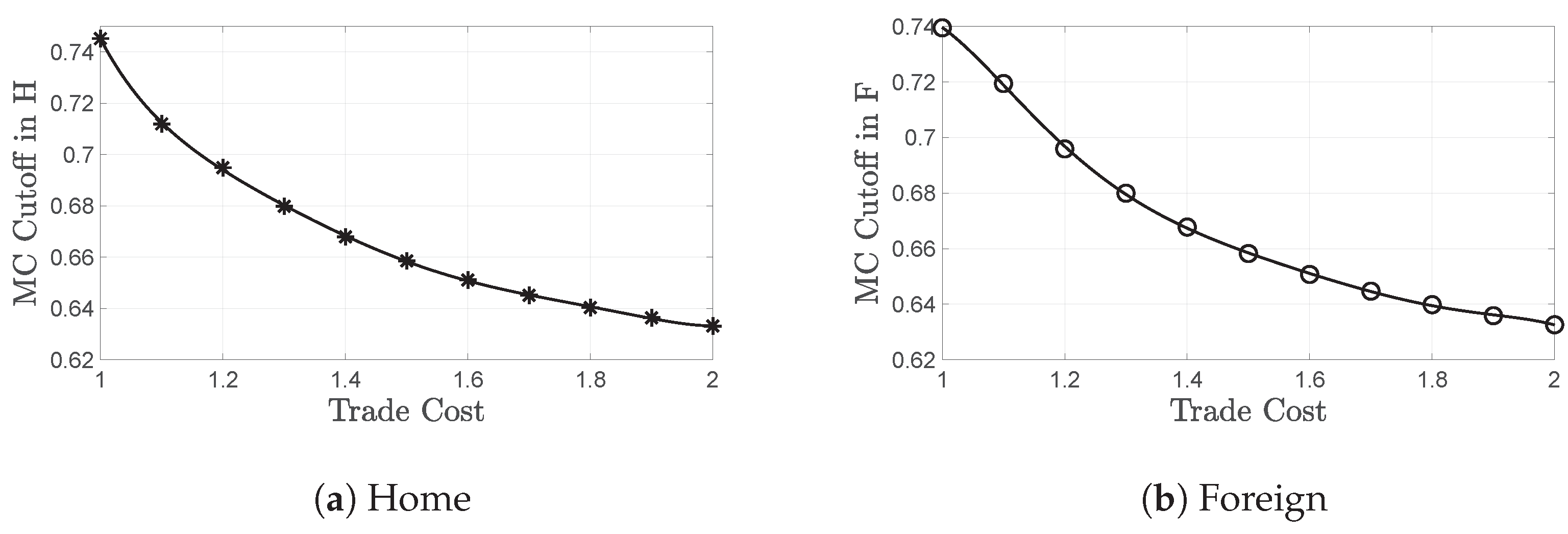
3.1.1. Selection Effect of Trade
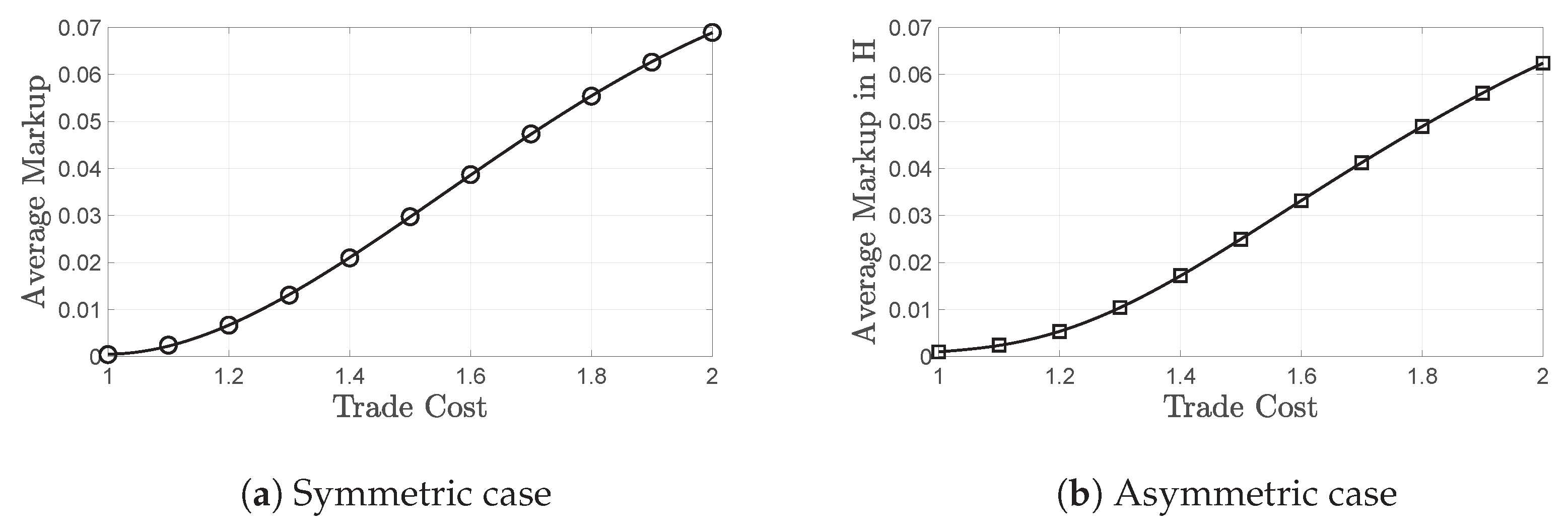
3.1.2. Pro-Competitive Effect of Trade
3.1.3. Selection Effect and Credit Constraints
3.1.4. Selection of Small versus Large Firms
3.2. Asymmetric Trade
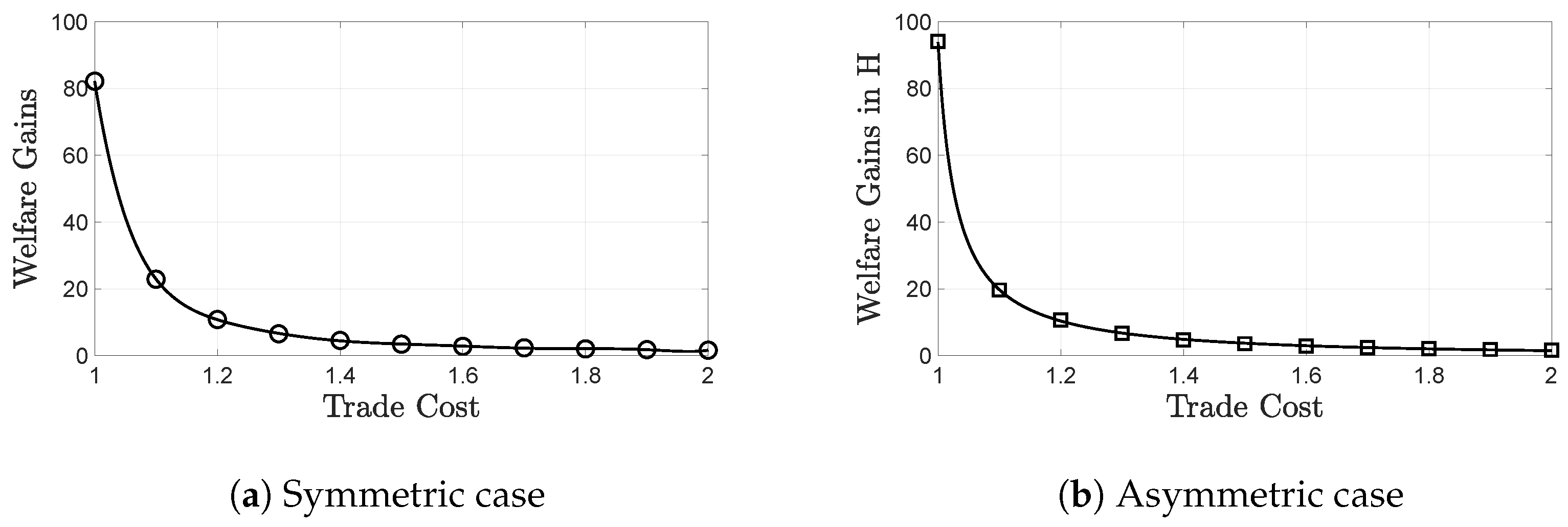
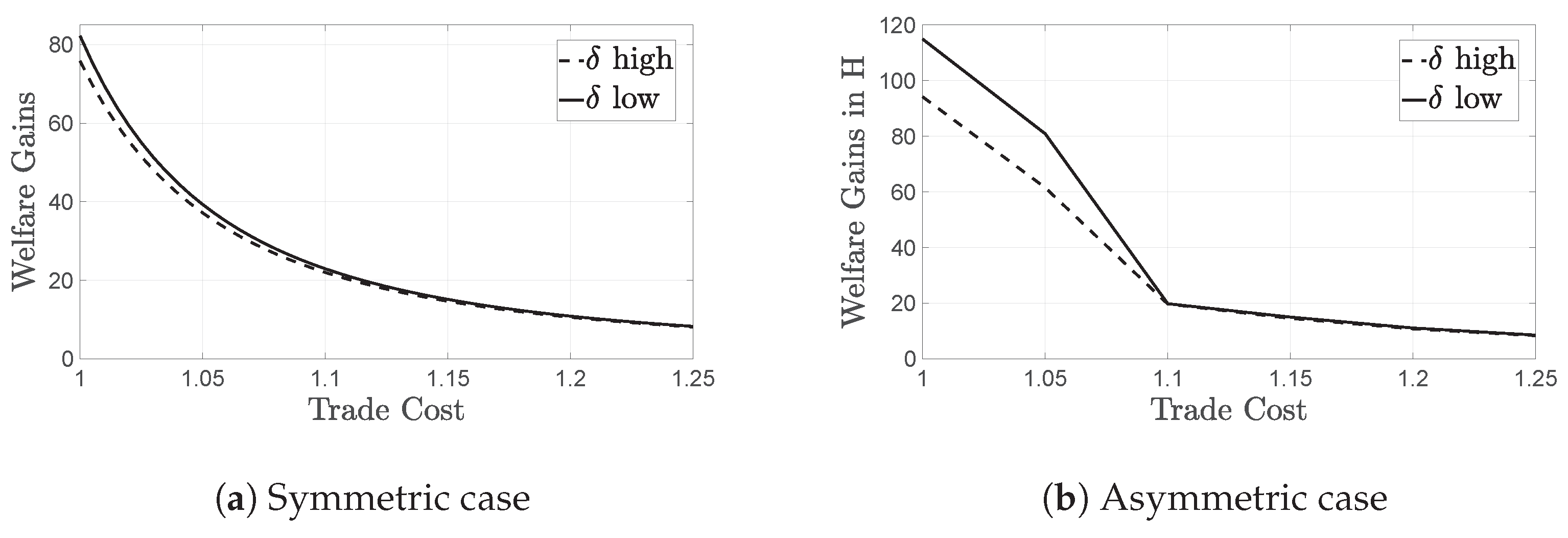
3.3. Welfare Gains from Trade
3.3.1. Welfare and the Oligopolistic Inefficiency
3.3.2. Welfare and Credit Constraints
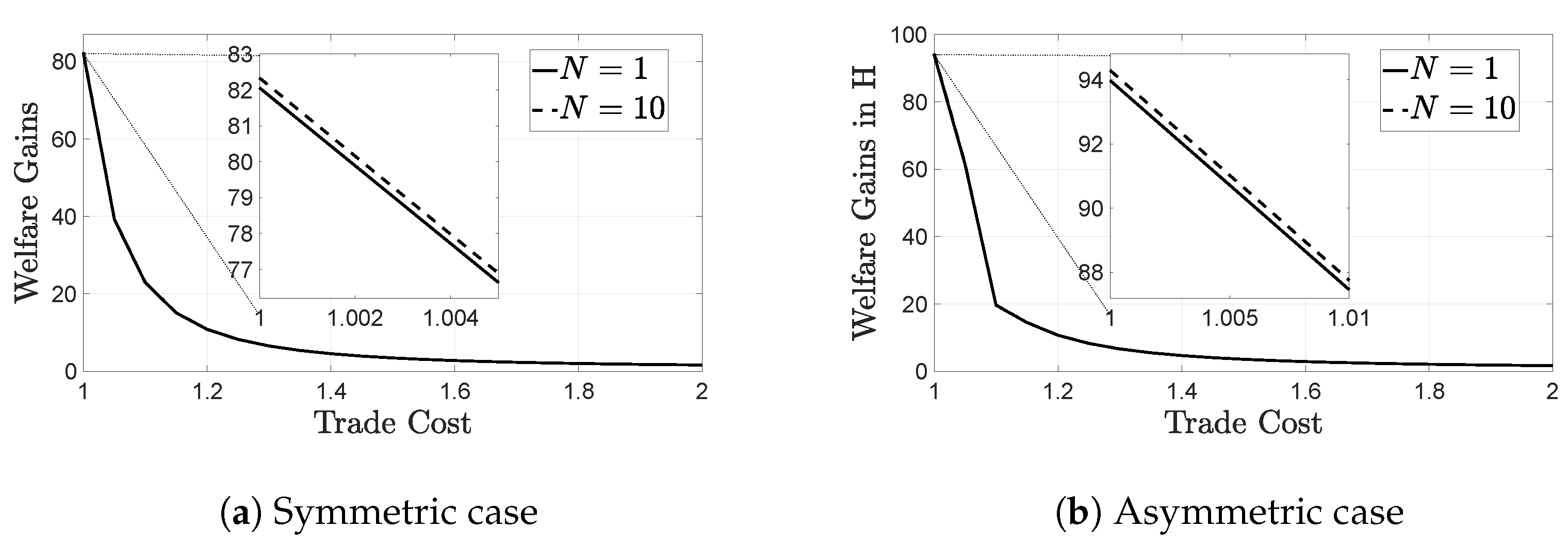
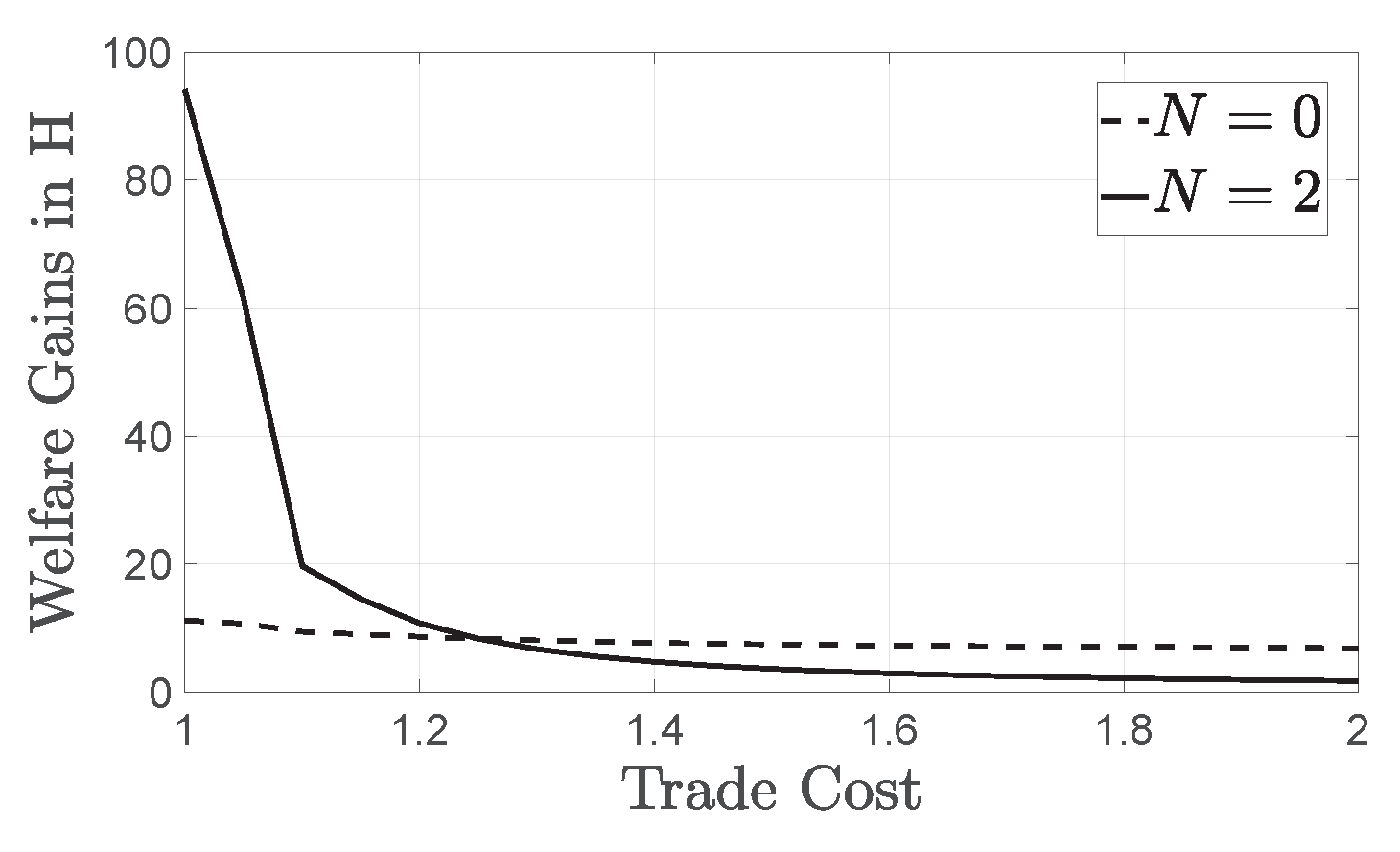
3.4. The Importance of Modeling Large Firms
4. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | |
| 2 | In equilibrium, MC firms make zero profit and hence I is equal to the wage income plus the profits of the CO firms. How these profits are distributed among consumers is irrelevant in models with quasi-linear preferences. |
| 3 | We go on to show that, even with homogenous productivities, CO firms charge higher markups. Therefore, assuming a productivity advantage for CO firms would only strengthen the results of our study. See for example Vavoura (2017) for a model where large firms are more productive than their smaller counterparts. |
| 4 | There is a growing literature documenting that large firms differ from their smaller counterparts also in their borrowing sources: large firms borrow from large digitalized banks, whereas small firms find it easier to obtain a loan from small banks (Lu et al. 2022; Mkhaiber and Werner 2021). As a result, although it remains beyond the scope of this paper, the number of operating small banks constitutes an important variable that should be considered separately from our measure of financial development. |
| 5 | As a result, credit constraints differences across firms are isomorphic to any differences in fixed operational costs regardless of whether they originate from credit market imperfections or not. |
| 6 | In fact, the cutoff relationship is preserved and Assumption 1 holds as long as the ratio of probabilities is higher than . |
| 7 | This assumption is common in oligopoly models. It implies that oligopoly rents are not eroded by entry (Neary 2016) and is supported by the empirical literature (see for example Barkai (2020) and Head and Spencer (2017)). CO firms can still choose to produce zero output in equilibrium, effectively exiting the market when they cannot make positive profits. Adding free entry for the CO firms is an interesting generalisation (see Section 3.1.4). |
| 8 | We compare the absolute markups. |
| 9 | The equilibrium condition giving the mass of MC firms M operating per product line follows:
|
| 10 | See Melitz and Redding (2014) for a review of the literature. |
| 11 | We use the following parameter values: , , , , , , , , , , , . Given that the same results can be shown analytically, our findings are not sensitive to changes in parameter values. |
| 12 | and hence since . |
| 13 | Analyzing trade between countries that are also asymmetric in their market size, is an interesting extension but we do not expect the results to differ from those of Melitz and Ottaviano (2008): in bigger markets, operate larger and more productive firms, both CO and MC in our case, product variety is larger and prices and markups are lower. |
| 14 | This generalized version of the model is not tractable enough to provide results analytically. To illustrate our findings, we use the same parameter values as in the symmetric case, with the additional parameters and . As shown below, our results are not sensitive to changes in parameter values of our key variables. |
| 15 | The exact same results hold in the symmetric case. |
References
- Antras, Pol, and Ricardo J. Caballero. 2009. Trade and capital flows: A financial frictions perspective. Journal of Political Economy 117: 701–44. [Google Scholar] [CrossRef]
- Atkin, David, and Amit K. Khandelwal. 2020. How distortions alter the impacts of international trade in developing countries. Annual Review of Economics 12: 213–38. [Google Scholar] [CrossRef]
- Autor, David, David Dorn, Lawrence F. Katz, Christina Patterson, and John Van Reenen. 2020. The fall of the labor share and the rise of superstar firms. The Quarterly Journal of Economics 135: 645–709. [Google Scholar] [CrossRef]
- Baccini, Leonardo, Giammario Impullitti, and Edmund J. Malesky. 2019. Globalization and state capitalism: Assessing vietnam’s accession to the wto. Journal of International Economics 119: 75–92. [Google Scholar] [CrossRef]
- Barkai, Simcha. 2020. Declining labor and capital shares. The Journal of Finance 75: 2421–463. [Google Scholar] [CrossRef]
- Bartik, Alexander W., Marianne Bertrand, Zoe Cullen, Edward L. Glaeser, Michael Luca, and Christopher Stanton. 2020. The impact of covid-19 on small business outcomes and expectations. Proceedings of the National Academy of Sciences USA 117: 17656–666. [Google Scholar] [CrossRef]
- Beck, Thorsten, and Asli Demirguc-Kunt. 2006. Small and medium-size enterprises: Access to finance as a growth constraint. Journal of Banking & Finance 30: 2931–943. [Google Scholar]
- Beck, Thorsten, Asli Demirgüç-Kunt, and Vojislav Maksimovic. 2005. Financial and legal constraints to growth: Does firm size matter? Journal of Finance 60: 137–77. [Google Scholar] [CrossRef]
- Bekaert, Geert, and Campbell R. Harvey. 1995. Time-varying world market integration. The Journal of Finance 50: 403–44. [Google Scholar] [CrossRef]
- Bekaert, Geert, Campbell R. Harvey, Christian T. Lundblad, and Stephan Siegel. 2011. What segments equity markets? The Review of Financial Studies 24: 3841–90. [Google Scholar] [CrossRef]
- Bernard, Andrew B., J. Bradford Jensen, Stephen J. Redding, and Peter K. Schott. 2007. Firms in international trade. The Journal of Economic Perspectives 21: 105–30. [Google Scholar] [CrossRef]
- Bernard, Andrew B., J. Bradford Jensen, Stephen J. Redding, and Peter K. Schott. 2018. Global firms. Journal of Economic Literature 56: 565–619. [Google Scholar]
- Bertoletti, Paolo, and Paolo Epifani. 2014. Monopolistic competition: Ces redux? Journal of International Economics 93: 227–38. [Google Scholar] [CrossRef]
- Bloom, Nicholas, Robert S. Fletcher, and Ethan Yeh. 2021. The Impact of COVID-19 on Us Firms. Technical Report. Cambridge, MA: National Bureau of Economic Research. [Google Scholar]
- Bloom, Nicholas, Aprajit Mahajan, David McKenzie, and John Roberts. 2010. Why do firms in developing countries have low productivity? American Economic Review 100: 619–23. [Google Scholar] [CrossRef]
- Ciani, Andrea, Marie Caitriona Hyland, Nona Karalashvili, Jennifer L. Keller, and Trang Thu Tran. 2020. Making It Big: Why Developing Countries Need More Large Firms. Washington, DC: World Bank Publications. [Google Scholar]
- Cirera, Xavier, Marcio Cruz, Arti Grover, Leonardo Iacovone, Denis Medvedev, Mariana Pereira-Lopez, and Santiago Reyes. 2021. Firm Recovery during COVID-19. Washington, DC: World Bank. [Google Scholar]
- Cleary, Sean. 2006. International corporate investment and the relationships between financial constraint measures. Journal of Banking & Finance 30: 1559–80. [Google Scholar]
- De Loecker, Jan, Pinelopi K. Goldberg, Amit K. Khandelwal, and Nina Pavcnik. 2016. Prices, markups, and trade reform. Econometrica 84: 445–510. [Google Scholar] [CrossRef]
- De Loecker, Jan, and Johannes Van Biesebroeck. 2018. Effect of international competition on firm productivity and market power. In The Oxford Handbook of Productivity Analysis. Oxford: Oxford University Press, p. 463. [Google Scholar] [CrossRef]
- De Loecker, Jan, and Frederic Warzynski. 2012. Markups and firm-level export status. The American Economic Review 102: 2437–71. [Google Scholar] [CrossRef]
- Edmond, Chris, Virgiliu Midrigan, and Daniel Yi Xu. 2015. Competition, markups, and the gains from international trade. The American Economic Review 105: 3183–221. [Google Scholar] [CrossRef]
- Fairlie, Robert. 2020. The impact of covid-19 on small business owners: Evidence from the first three months after widespread social-distancing restrictions. Journal of Economics & Management Strategy 29: 727–40. [Google Scholar]
- Foley, C. Fritz, and Kalina Manova. 2015. International trade, multinational activity, and corporate finance. Annual Review of Economics 7: 119–46. [Google Scholar] [CrossRef]
- Freund, Caroline, and Martha Denisse Pierola. 2015. Export superstars. Review of Economics and Statistics 97: 1023–32. [Google Scholar] [CrossRef]
- Greve, Hannes, Jann Lay, and Ana Negrete. 2022. How vulnerable are small firms to energy price increases? evidence from mexico. Environment and Development Economics, 1–21. [Google Scholar] [CrossRef]
- Head, Keith, and Barbara J. Spencer. 2017. Oligopoly in international trade: Rise, fall and resurgence. Canadian Journal of Economics/Revue Canadienne D’économique 50: 1414–44. [Google Scholar] [CrossRef]
- Henderson, Brian J., Narasimhan Jegadeesh, and Michael S. Weisbach. 2006. World markets for raising new capital. Journal of Financial Economics 82: 63–101. [Google Scholar] [CrossRef]
- Hottman, Colin, Stephen J. Redding, and David E. Weinstein. 2016. Quantifying the sources of firm heterogeneity. The Quarterly Journal of Economics 131: 1291–364. [Google Scholar] [CrossRef]
- Leibovici, Fernando. 2021. Financial development and international trade. Journal of Political Economy 129: 3405–46. [Google Scholar] [CrossRef]
- Lu, Zhiqiang, Junjie Wu, Hongyu Li, and Duc Khuong Nguyen. 2022. Local bank, digital financial inclusion and sme financing constraints: Empirical evidence from china. Emerging Markets Finance and Trade 58: 1712–25. [Google Scholar] [CrossRef]
- Manova, Kalina. 2013. Credit constraints, heterogeneous firms, and international trade. Review of Economic Studies 80: 711–44. [Google Scholar] [CrossRef]
- Mayer, Thierry, and Gianmarco I. P. Ottaviano. 2008. The happy few: The internationalisation of european firms. Intereconomics 43: 135–48. [Google Scholar] [CrossRef]
- Melitz, Marc J. 2003. The impact of trade on intra-industry reallocations and aggregate industry productivity. Econometrica 71: 1695–725. [Google Scholar] [CrossRef]
- Melitz, Marc J., and Gianmarco I. P. Ottaviano. 2008. Market size, trade, and productivity. The Review of Economic Studies 75: 295–316. [Google Scholar] [CrossRef]
- Melitz, Marc J., and Stephen J. Redding. 2014. Heterogeneous firms and trade. Handbook of International Economics 4: 1–54. [Google Scholar]
- Mkhaiber, Achraf, and Richard A. Werner. 2021. The relationship between bank size and the propensity to lend to small firms: New empirical evidence from a large sample. Journal of International Money and Finance 110: 102281. [Google Scholar] [CrossRef]
- Neary, J. Peter. 2003. Globalization and market structure. Journal of the European Economic Association 1: 245–71. [Google Scholar] [CrossRef]
- Neary, J. Peter. 2010. Two and a half theories of trade. The World Economy 33: 1–19. [Google Scholar] [CrossRef]
- Neary, J. Peter. 2016. International trade in general oligopolistic equilibrium. Review of International Economics 24: 669–98. [Google Scholar] [CrossRef]
- Nunn, Nathan, and Daniel Trefler. 2014. Domestic institutions as a source of comparative advantage. Handbook of International Economics 4: 263–315. [Google Scholar]
- Parenti, Mathieu. 2018. Large and small firms in a global market: David vs. goliath. Journal of International Economics 110: 103–18. [Google Scholar] [CrossRef]
- Pavcnik, Nina. 2002. Trade liberalization, exit, and productivity improvements: Evidence from chilean plants. The Review of Economic Studies 69: 245–76. [Google Scholar] [CrossRef]
- Pietrovito, Filomena, and Alberto Franco Pozzolo. 2021. Credit constraints and exports of smes in emerging and developing countries. Small Business Economics 56: 311–32. [Google Scholar] [CrossRef]
- Rodríguez-Pose, Andrés, Roberto Ganau, Kristina Maslauskaite, and Monica Brezzi. 2021. Credit constraints, labor productivity, and the role of regional institutions: Evidence from manufacturing firms in europe. Journal of Regional Science 61: 299–328. [Google Scholar] [CrossRef]
- Rosen, Sherwin. 1981. The economics of superstars. The American Economic Review 71: 845–58. [Google Scholar]
- Segarra, Agustí, and Mercedes Teruel Carrizosa. 2009. Small Firms, Growth and Financial Constraints. Technical Report. Xarxa de Referència en Economia Aplicada (XREAP). Barcelona: Universitat de Barcelona. Available online: https://www.urv.cat/media/upload/arxius/catedra-innovacio-empresarial/SmallFirmsGrowth.pdf (accessed on 2 August 2022).
- Shimomura, Ken-Ichi, and Jacques-François Thisse. 2012. Competition among the big and the small. The Rand Journal of Economics 43: 329–47. [Google Scholar] [CrossRef]
- Singh, Prakash, and Charanjit Kaur. 2021. Factors determining financial constraint of smes: A study of unorganized manufacturing enterprises in india. Journal of Small Business & Entrepreneurship 33: 269–87. [Google Scholar]
- Tito, Maria, and Ruoying Wang. 2017. Exporting and Frictions in Input Markets: Evidence from Chinese Data. Finance and Economics Discussion Series 2017-077. SSRN 3016790. Washington, DC: Board of Governors of the Federal Reserve System. [Google Scholar] [CrossRef]
- Trefler, Daniel. 2004. The long and short of the canada-us free trade agreement. American Economic Review 94: 870–95. [Google Scholar] [CrossRef]
- Vavoura, Chara. 2017. Liberalising Trade in the Shadow of Superstar Firms. Helsinki: Centre for research on Globalisation and Economic Policy (GEP), University of Nottingham, European Trade Study Group. Available online: http://www.etsg.org/ETSG2016/Papers/199.pdf (accessed on 2 August 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vavoura, C. How Trade Dampens the Impact of Financial Frictions in the Presence of Large Firms. Economies 2022, 10, 266. https://doi.org/10.3390/economies10110266
Vavoura C. How Trade Dampens the Impact of Financial Frictions in the Presence of Large Firms. Economies. 2022; 10(11):266. https://doi.org/10.3390/economies10110266
Chicago/Turabian StyleVavoura, Chara. 2022. "How Trade Dampens the Impact of Financial Frictions in the Presence of Large Firms" Economies 10, no. 11: 266. https://doi.org/10.3390/economies10110266
APA StyleVavoura, C. (2022). How Trade Dampens the Impact of Financial Frictions in the Presence of Large Firms. Economies, 10(11), 266. https://doi.org/10.3390/economies10110266




