Price Transmission Analysis of the International Soybean Market in a Trade War Context
Abstract
:1. Introduction
1.1. Critical Concept and Definitions
1.2. Previous Empirical Research
1.2.1. Law of One Price
1.2.2. Price Transmission
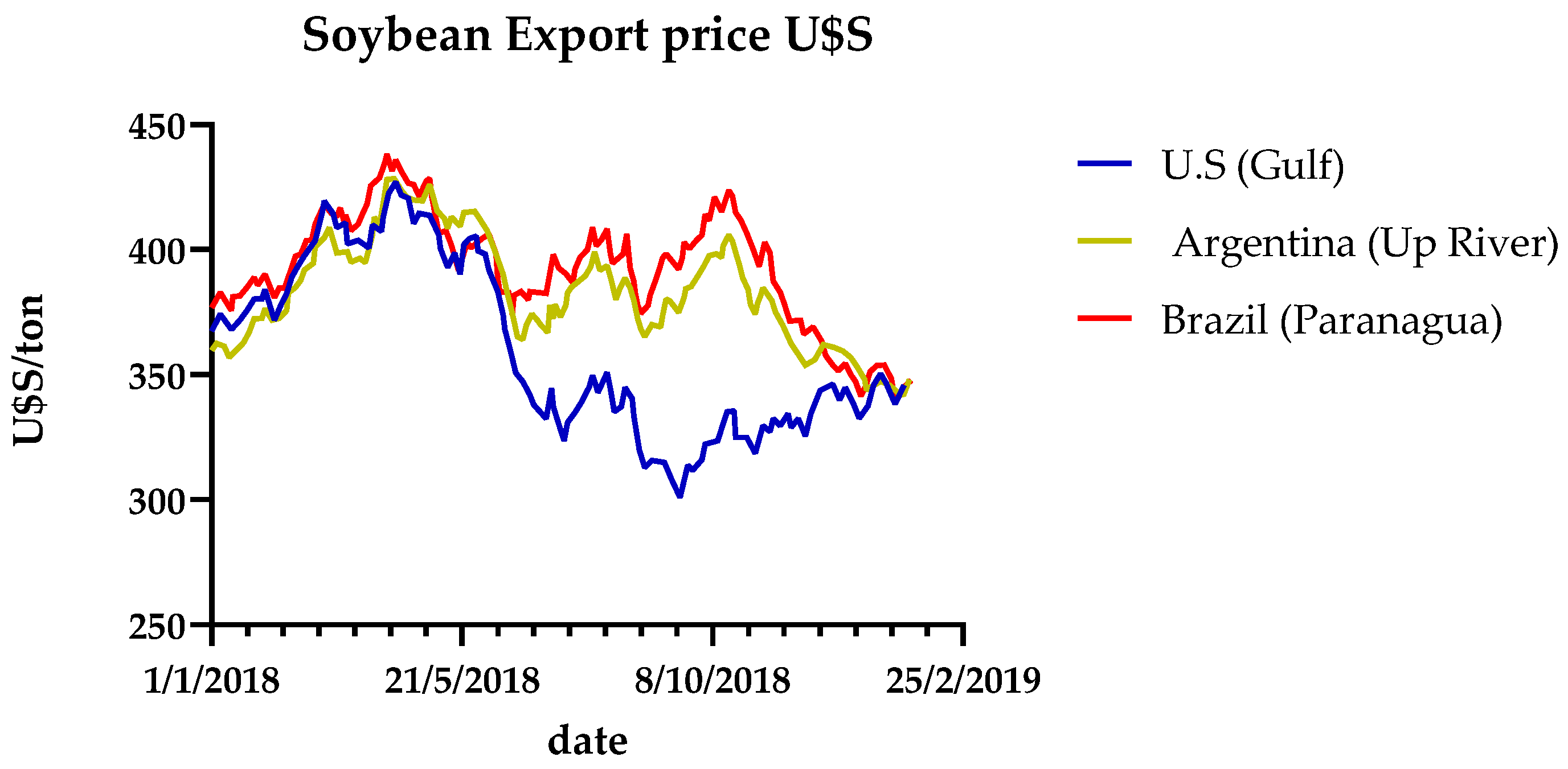
1.3. Policy Implications in the International Market of Soybean: Price Transmission and Cointegration
2. Methodology
2.1. Hypothesis
2.1.1. Market Cointegration and Structural Breaks Paradigm
- N0.1. The markets were not dislocated, i.e., there was cointegration between the markets.
- N0.2. The trade war did not introduce a break in the soybean market time series; therefore, the time series were stationary at first difference.
2.1.2. The Market Efficiency Affectation
- N0.1. The price transmission within the market was not affected.
- N0.2. The law of one price held in the USA–China trade war.
3. Results
3.1. Unit Root Test
3.2. Structural Breaks Test
3.3. Cointegration Test
3.4. Granger Causality Test
3.5. Vector Error Correction Model
3.5.1. VECM China Spot Market Pair Model
0.185∆LNCHINASPt−1 + 0.075∆LNCHIGFt−1
λ = −0.0546
← No short-term regressors from Dalian Futures
λ = −0.103251
← No short-term regressors from Paranguas
λ = −0.047338
← No short-term regressors from Rosario Futures
λ = −0.012727
← No short-term regressors from Rosario Spot
λ = −0.031843
3.5.2. VECM Dalian Futures
← No short-term regressors
λ = −0.138
← No short-term regressors
λ = −0.106
← No short-term regressors
λ = −0.135
← No short-term regressors
λ = −0.075
3.5.3. VECM Paranaguá
← No short-term regressors from Chicago
λ = −0.260808
← No short-term regressors from Rotterdam
λ = −0.273239
← No short-term regressors from Chicago Futures and Paranaguá Futures
3.5.4. VECM Rosario Spot
λ = −0.253019
← No short-term regressors from Rotterdam (alpha 10%)
λ = −0.213640
← No short-term regressors from Paranaguá Spot
λ = −0.318580
← No short-term regressors from Rosario Futures
λ = −0.203718
λ = −0.405295
4. Discussion
5. Conclusions
5.1. Policy Implications
5.2. Recommendation for Further Study
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Unrestricted Cointegration Rank Test (Trace) | ||||||
|---|---|---|---|---|---|---|
| PAIR TIME SERIES | No. of CE(s) | Eigenvalue | Statistic | Critical Value | Prob. | |
| Hypothesised | Trace | 0.05 | ||||
| LNROSFT LNROTTERDAM | Break 2014M8 | None | 0.128 | 24.75 | 15.49 | 0 |
| Trend assumption 3 | At most 1 | 0.066 | 8.19 | 3.84 | 0 | |
| LNROSFT LNROSSP | Break 2015M10 | None | 0.125 | 22.73 | 15.49 | 0 |
| Trend assumption 3 | At most 1 | 0.054 | 6.63 | 3.84 | 0.01 | |
| LNPARANAGUASP LNROSFT | Break 2014M09 | None | 0.15 | 28.67 | 15.49 | 0 |
| Trend assumption 3 | At most 1 | 0.073 | 9.11 | 3.84 | 0 | |
| LNDALIF LNROSSP | Break 2017M10 | None | 0.124 | 22.5 | 15.49 | 0 |
| Trend assumption 3 | At most 2 | 0.053 | 6.56 | 3.84 | 0.01 | |
| LNDALIF LNROSFT | Break 2010M10 | None | 0.156 | 30.35 | 25.87 | 0.01 |
| Trend assumption 4 | At most 1 | 0.079 | 9.91 | 12.51 | 0.13 | |
| LNCHINASP LNROTTERDAM | Break 2010M10 | None | 0.099 | 13.22 | 12.32 | 0.03 |
| Trend assumption 1 | At most 1 | 0.006 | 0.7 | 4.13 | 0.45 | |
| LNCHINASP LNROSSP | Break 2010M10 | None | 0.099 | 12.87 | 12.32 | 0.04 |
| Trend assumption 1 | At most 1 | 0.003 | 0.38 | 4.129 | 0.6 | |
| LNCHINASP LNROSFT | Break 2010M10 | None | 0.082 | 13.35 | 15.49 | 0.1 |
| Trend assumption 3 | At most 1 | 0.025 | 3.07 | 3.84 | 0.08 | |
| LNCHINASP LNPARANAGUASP | Break 2014M04 | None | 0.129 | 20.2 | 15.49 | 0.01 |
| Trend assumption 3 | At most 1 | 0.03 | 3.6 | 3.84 | 0.06 | |
| LNCHIGF LNROSFT | Break 2010M10 | None | 0.166 | 32.25 | 25.87 | 0.01 |
| Trend assumption 4 | At most 1 | 0.083 | 10.4 | 12.51 | 0.11 | |
| LNCHIGF LNCHINASP | Break 2010M11 | None | 0.159 | 29.3 | 25.87 | 0.02 |
| Trend assumption 3 | At most 1 | 0.068 | 8.51 | 12.51 | 0.21 | |
| LNROSSP LNROTTERDAM | Break 2010M11 | None | 0.129 | 19.57 | 15.49 | 0.01 |
| Trend assumption 3 | At most 1 | 0.024 | 2.95 | 3.84 | 0.09 | |
References
- Abdulai, Awudu. 2007. Spatial and Vertical price transmission in food staples market chains in Eastern and Southern Africa: What is the evidence? Paper presented at the FAO Trade and Markets Division Workshop on Staple Food Trade and Market Policy Options for Promoting Develop, Rome, Italy, March 1–2. [Google Scholar]
- Abdullahi, Kamal, and Joshep Phiri. 2018. The rise of china as a paralympic superpower. In The Palgrave Handbook of Paralympic Studies. London: Palgrave Macmillan, pp. 295–320. [Google Scholar] [CrossRef]
- Aguiar, Danilo R., and Geraldo Barros. 1991. Causality and asymetry in Brazilian soybean and derivatives prices transmission in 1980’s. Estudos Econômicos 53: 89–103. [Google Scholar] [CrossRef]
- Arnade, Carlos, Bryce Cooke, and Fred Gale. 2017. Agricultural price transmission: China relationships with world commodity markets. Journal of Commodity Markets 7: 28–40. [Google Scholar] [CrossRef]
- Baffes, John, and Mohamed I. Ajwad. 2001. Identifying price linkages: A review of the literature and an application to the world market of cotton. Applied Economics 33: 1927–41. [Google Scholar] [CrossRef]
- Barrett, Christopher B., and Jau Rong Li. 2002. Distinguishing between Equilibrium and Integration in Spatial Price Analysis. American Journal of Agricultural Economics 84: 292–307. Available online: http://www.jstor.org/stable/1244953 (accessed on 1 January 2021).
- Bown, Chad P., and Melina Kolb. 2020. Trump’s Trade War Timeline: An Up-to-Date Guide. Washington, DC: Peterson Institute for International Economics, pp. 1–21. Available online: https://www.piie.com/sites/default/files/documents/trump-trade-war-timeline.pdf (accessed on 4 July 2021).
- Correia das Neves, Leonidas. 1993. Margens de Comercializacao e Elasticidade de Transmissao de Precos na Industria de Esmagamento de Soja. Master’s disertation, da Universidade de São Paulo, USP ESALQ, Sao Paulo, Brazil. [Google Scholar]
- Cournot, Augustin. 1838. Research into the Mathematical Principles of the Theory of Wealth. London: The Macmillan Company. Available online: https://www3.nd.edu/~tgresik/IO/Cournot.pdf (accessed on 10 January 2021).
- Da Silva, Osvaldo Cândido, Bruno Ferreira, and Sinezio Fernandes. 2005. Transmissão de preços no mercado internacional da soja: Uma abordagem pelos modelos ARMAX e VAR. Encontro Nacional De Economia, xxxiii. Available online: https://www.researchgate.net/publication/4735886_Transmissao_de_precos_no_mercado_internacional_da_soja_uma_abordagem_pelos_modelos_ARMAX_e_VAR (accessed on 10 July 2021).
- de Moraes, Mauricio. 2002. Prêmio de exportação da soja brasileira. Master’s disertation, Universidade de São Paulo, para obtenção do título de Mestre em Ciências, Área de Concentração: Economia Aplicada, San Paulo, Brazil; p. 90. Available online: https://teses.usp.br/teses/disponiveis/11/11132/tde-26022003-141201/pt-br.php (accessed on 30 June 2021).
- de Sousa, Eliane, and Antônio Carvalho Campos. 2009. Transmissão Inter-Regional De Preços No Mercado Brasileiro De Soja. Análise Econômica 27. [Google Scholar] [CrossRef]
- Engle, Robert, and Clive W. J. Granger. 1987. Co-Integration and Error Correction: Representation, Estimation, and Testing. Econometrica 55: 251–76. [Google Scholar] [CrossRef]
- Gardner, Bruce L. 1975. The Farm-Retail Price Spread in a Competitive Food Industry. American Journal of Agricultural Economics 57: 399–409. [Google Scholar] [CrossRef]
- Giembinsky, Renata, and Marcio Holland. 2003. Resarch Gate Comportamento do Preço no Complexo Soja: Uma Análise de Cointegração e de Causalidade. Available online: https://www.researchgate.net/publication/4729910_Comportamento_do_Preco_no_Complexo_Soja_uma_Analise_de_Cointegracao_e_de_Causalidade (accessed on 20 August 2021).
- Jamet, Jean-Paul P., and Jean-Marc Chaumet. 2016. Soybean in China: Adaptating to the liberalization. OCL—Oilseeds and Fats, Crops and Lipids 23: D604. [Google Scholar] [CrossRef]
- Kerkelä, Leena, Heikki Lehtonen, and Jyrki Niemi. 2005. The Impacts of WTO Export Subsidy Abolition on the Agri-food Industry in the EU: A Preliminary Assessment, Discussion Papers. Helsinki: VATT, Valtion taloudellinen tutkimuskeskus, Government Institute for Economic Research. [Google Scholar]
- Lima, Samanta M. A., and Heloisa L. Burnquist. 1997. Lei do preço único no mercado internacional: Testes empiricos para exportações do complexo soja (grãos e farelo). In Congresso Brasileiro de Economia e Sociologia Rural. Natal: SOBER. [Google Scholar]
- Listorti, Giulia, and Roberto Esposti. 2012. Horizontal price transmission in agricultural markets: Fundamental concepts and open empirical issues. Bio-Based and Applied Economics 1: 81–108. [Google Scholar] [CrossRef]
- Machado, Eduardo Luiz, and Mario Antonio Margarido. 2000. Seasonal price transmission in soybean international market: The case of Brazil and Argentina. Pesquisa & Debate 12: 92–106. Available online: http://revistas.pucsp.br/index.php/rpe/article/viewFile/12010/8700 (accessed on 24 June 2021).
- Mafioletti, Robson Leandro. 2001. Formação de preços na cadeia agroindustrial da soja na década de 90. Revista de Economia e Sociologia Rural 39: 9–26. Available online: http://www.paranacooperativo.com.br/PPC/images/Biblioteca/DissertacaoRobsonMaffioletti.pdf (accessed on 22 April 2020).
- Margarido, Mario Antonio. 2012. Análise da transmissão espacial de preços no mercado internacional de soja. Revista de Economia e Administração 11: 281–303. [Google Scholar] [CrossRef]
- Margarido, Mario Antonio, and Eduardo Luis Leao Sousa. 1998. Formacao de precos da soja no brasil. Paper presented at the Congresso Brasileiro de Economia e Sociologia Rural (SOBER), Realizado em Poços de Caldas (MG), Sao Paulo, Brazil, August 10–14; Available online: http://www.iea.sp.gov.br/ftpiea/ie/1998/ASPII98-4.pdf (accessed on 26 April 2020).
- Margarido, Mario Antonio, Eduardo Leao Sousa, M. Z. Barbosa, and S. M. Freitas. 1999. Transmissão de preços no mercado internacional do grão de soja: Uma aplicação da metodologia de séries temporais. In Conference: Congresso Brasileiro de Economia E Sociologia Rural, 37., Foz do Iguaçu, 1999. Anais: SOBER. [Google Scholar]
- Margarido, Mario Antonio, Federico Turolla, and Carlos Bueno. 2007. The world market for soybeans: Price transmission into Brazil and effects from the timing of crop and trade. Nova Economia 17: 241–70. [Google Scholar] [CrossRef]
- Margarido, Mario Antonio, Federico Turolla, and Jocelynne Marie Fernandes. 2001. Análise da elasticidade de transmissão de preços no mercado internacional de soja. Pesquisa & Debate. Revista do Programa de Estudos Pós-Graduados em Economia Política 12: 5–40. [Google Scholar]
- Marshall, Alfred. 1890. Principles of Economics. New York: Macmillan and Company (Principles of Economics). Available online: https://books.google.co.uk/books?id=bykoAAAAYAAJ (accessed on 22 March 2022).
- Mundlak, Yair, and Donald F. Larson. 1992. On the Transmission of World Agricultural Prices. The World Bank Economic Review 6: 399–422. [Google Scholar] [CrossRef]
- Pino, Francisco, and Mariana Rocha. 1994. Soybean prices transmission in Brazil. Revista de Economia e Sociologia Rural 32: 345–61. [Google Scholar]
- Quiróz, Jorge, and Raimundo Soto. 1995. International Price Signals in Agricultural Markets: Do Governments Care? Washington, DC: The World Bank, Macroeconomics and Growth Division of the World Bank, October, Available online: https://www.researchgate.net/publication/5115465_International_Price_Signals_in_Agricultural_Markets_DoGovernments_Care (accessed on 6 July 2021).
- Rapsomanikis, George, David Hallam, and Piero Conforti. 2013. Produced by: Economic and Social More details Market Integration and Price Transmission in Selected Food and Cash Crop Markets of Developing Countries: Review and Applications. pp. 1–25. Available online: http://www.fao.org/3/y5117e/y5117e06.htm (accessed on 8 May 2021).
- Setser, Brad. 2019. Soybeans! Available online: https://www.cfr.org/blog/soybeans (accessed on 25 July 2021).
- Sharma, Ramesh. 2002. The Transmission of World Price Signals: Concepts, Issues and Some Evidence from Asian Cereal Markets. OECD Global Forum on Agriculture. Available online: https://books.google.co.uk/books?hl=en&lr=&id=p5XWAgAAQBAJ&oi=fnd&pg=PA141&dq=The+transmission+of+world+price+signals:+the+concept,+issues,+and+some+evidence+from+Asian+cereal+markets&ots=FNmsFbY78C&sig=cCZT1Ldb0UmwKSXF2KsJ2Ps-kfk#v=onepage&q=The_transmis&f=false (accessed on 1 December 2021).
- Smith, Adam. 1723. The Wealth of Nations/Adam Smith; Introduction by Robert Reich; Edited, with Notes, Marginal Summary, and Enlarged Index by Edwin Cannan. New York: Modern Library. Available online: https://search.library.wisc.edu/catalog/999905503902121 (accessed on 2 November 2021).
- Vassallo, Miguel, Miguel R. Carriquiry, Virginea Courdin, Veronica Durán, Federico García Suárez, Alfredo Hernández Gfeller, Norbeto Rodríguez, and Martha Tamosiunas. 2011. Dinámica y Competencia Intrasectorial en el agro Uruguay 2000–2010. Biblioteca Plural. Montevideo: Ediciones Universitarias. Available online: https://www.colibri.udelar.edu.uy/jspui/bitstream/20.500.12008/3870/1/Fagro_Vasallo_2012-03-13_webO.pdf (accessed on 17 August 2021).
- Vavra, Pavel, and Barry Goodwin. 2005. Analysis of Price Transmission along the Food Chain. OECD Food, Agriculture and Fisheries Papers, No. 3. Paris: OECD Publishing, November 1, pp. 1–58. ISSN 1815-6797. [Google Scholar] [CrossRef]
- Zhao, Yu, Miaomiao Yang, Yu Zhang, and Chunjie Qi. 2010. Impact on the Chinese soybean markets from international prices volatility: Empirical study based on VEC model. African Journal of Agricultural Research 5: 1943–50. [Google Scholar] [CrossRef]
| Price Series | Test Critical Value 5% | ADF Test Statistic | Prob. | Null Hypothesis | |
|---|---|---|---|---|---|
| LNCHIGF | −2.88 | < | −2.09 | 0.25 | Accepted |
| LNCHINASP | −2.88 | < | −1.47 | 0.55 | Accepted |
| LNDALIF | −2.88 | < | −1.83 | 0.36 | Accepted |
| LNPARANAGUASP | −2.88 | < | −2.25 | 0.19 | Accepted |
| LNROSFT | −2.88 | < | −2.55 | 0.11 | Accepted |
| LNROSSP | −2.88 | < | −2.37 | 0.15 | Accepted |
| LNROTTERDAM | −2.88 | < | −1.41 | 0.57 | Accepted |
| Price Series | Test Critical Value 5% | ADF Test Statistic | Prob. | Null Hypothesis | |
|---|---|---|---|---|---|
| LNCHIGF | −2.88 | > | −8.13 | 0.00 | Rejected |
| LNCHINASP | −2.88 | > | −8.06 | 0.00 | Rejected |
| LNDALIF | −2.88 | > | −10.26 | 0.00 | Rejected |
| LNPARANAGUASP | −2.88 | > | −7.42 | 0.00 | Rejected |
| LNROSFT | −2.88 | > | −7.44 | 0.00 | Rejected |
| LNROSSP | −2.88 | > | −7.99 | 0.00 | Rejected |
| LNROTTERDAM | −2.88 | > | −9.17 | 0.00 | Rejected |
| Price Series | Breaks | of Coefs. | Sum of Sq. Resids | Log-L | Schwarz Criterion | LWZ Criterion | Schwarz Breaks | LWZ Breaks |
|---|---|---|---|---|---|---|---|---|
| LNCHIGF | 2 | 5 | 0.728 | 140.92 | −4.93 | −4.75 | 2010M10 | 2010M11 |
| 3 | 7 | 0.630 | 149.84 | −5.00 | −4.75 | 2012M04 | 2014M09 | |
| 2014M09 | ||||||||
| LNCHINASP | 3 | 7 | 0.251 | 206.19 | −5.91 | −5.67 | 2010M11 | 2010M11 |
| 4 | 9 | 0.219 | 214.56 | −5.97 | −5.65 | 2012M08 | 2012M07 | |
| 5 | 11 | 0.198 | 221.00 | −6.00 | −5.61 | 2014M04 | 2015M10 | |
| 2015M10 | ||||||||
| 2017M10 | ||||||||
| LNDALIF | 3 | 7 | 0.429 | 173.41 | −5.38 | −5.13 | 2010M09 | 2010M09 |
| 4 | 9 | 0.385 | 180.11 | −5.41 | −5.09 | 2012M03 | 2012M03 | |
| 2015M09 | 2015M10 | |||||||
| 2017M10 | ||||||||
| LNPARANAGUASP | 3 | 7 | 0.806 | 134.63 | −4.75 | −4.50 | 2010M09 | 2010M09 |
| 2012M04 | 2012M04 | |||||||
| 2014M09 | 2014M09 | |||||||
| LNROSFT | 3 | 7 | 0.579 | 154.96 | −5.08 | −4.83 | 2010M10 | 2010M10 |
| 2014M09 | 2014M09 | |||||||
| 2016M05 | 2016M05 | |||||||
| LNROSSP | 2 | 5 | 1.00 | 120.91 | −4.60 | −4.37 | 2010M10 | 2010M10 |
| 3 | 7 | 0.916 | 126.75 | −4.62 | −4.28 | 2012M04 | 2014M08 | |
| 2014M07 | ||||||||
| LNROTTERDAM | 2 | 5 | 0.639 | 148.94 | −5.064 | −4.88 | 2010M10 | 2010M10 |
| 2014M08 | 2014M08 |
| Price Series | Test Critical Value 5% | ADF Test Statistic | Prob. | Break Date | |
|---|---|---|---|---|---|
| LNPARANAGUASP | −4.44 | > | −8.15 | <0.01 | 2012M07 |
| LNROTTERDAM | −4.44 | > | −9.74 | <0.01 | 2012M07 |
| LNCHIGF | −4.44 | > | −8.64 | <0.01 | 2014M09 |
| LNROSFT | −4.44 | > | −8.050 | <0.01 | 2016M05 |
| LNROSSP | −4.44 | > | −8.41 | <0.01 | 2016M05 |
| LNCHINASP | −4.44 | > | −8.83 | <0.01 | 2016M09 |
| LNDALIF | −4.44 | > | −11.50 | <0.01 | 2018M02 |
| Unrestricted Cointegration Rank Test (Trace) | |||||||
|---|---|---|---|---|---|---|---|
| LNCHIGF | LNCHINASP | LNDALIF | PARANAGUASP | LNROSFT | LNROSSP | ROTTERDAM | |
| LNCHIGF | X | 1 | 1 | 1 | 0 | 1 | 1 |
| LNCHINASP | 1 | X | 1 | 0 | 0 | 1 | 2 |
| LNDALIF | 1 | 1 | X | 1 | 0 | 1 | 1 |
| LNPARANAGUASP | 1 | 0 | 1 | X | 0 | 1 | 1 |
| LNROSFT | 0 | 0 | 0 | 0 | X | 1 | 0 |
| LNROSSP | 1 | 1 | 1 | 1 | 1 | X | 1 |
| LNROTTERDAM | 1 | 1 | 1 | 1 | 0 | 1 | X |
| Unrestricted Cointegration Rank Test (Trace) | |||||||
|---|---|---|---|---|---|---|---|
| LNCHIGF | LNCHINASP | LNDALIF | LNPARANAGUASP | LNROSFT | LNROSSP | LNROTTERDAM | |
| LNCHIGF | X | 1 | 1 | 1 | 1 | 1 | 1 |
| LNCHINASP | 1 | X | 1 | 1 | 1 | 1 | 2 |
| LNDALIF | 1 | 1 | X | 1 | 1 | 2 | 1 |
| LNPARANAGUASP | 1 | 1 | 1 | X | 1 | 1 | 1 |
| LNROSFT | 1 | 1 | 1 | 1 | X | 1 | 1 |
| LNROSSP | 1 | 1 | 2 | 1 | 1 | X | 1 |
| LNROTTERDAM | 1 | 2 | 1 | 1 | 1 | 1 | X |
| Granger Causality Test with One Lag | |||||||
|---|---|---|---|---|---|---|---|
| LNCHIGF | LNCHINASP | LNDALIF | LNPARANAGUASP | LNROSFT | LNROSSP | LNROTTERDAM | |
| LNCHIGF | X | ↑ | ↑ | ↑ | ∂ | ↑ | ∂ |
| LNCHINASP | ← | X | ← | ← | ← | ← | ← |
| LNDALIF | ← | ↑ | X | ← | ∂ | ← | ← |
| LNPARANAGUASP | ← | ↑ | ↑ | X | ∂ | ↑ | ← |
| LNROSFT | ∂ | ↑ | ∂ | ∂ | X | ↑ | ∂ |
| LNROSSP | ← | ↑ | ↑ | ← | ∂ | X | ← |
| LNROTTERDAM | ∂ | ↑ | ↑ | ↑ | ∂ | ↑ | X |
| Heteroskedasticity Tests | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Lag | D(LNCHINASP) | < | D(LNCHIGF) | Elasticity | Correlation LM Tests | Normality Test | Without Cross Term | With Cross Term | |
| CointEq1 | 1 | −5.46% | 7.51% | 1:0.95 | 0.9724 | 0.00000 | 0.9270 | 0.9662 | |
| D(LNCHINASP) | < | D(DALIF) | |||||||
| CointEq1 | 1 | −10.33% | −1.73% | 1:0.97 | 0.5821 | 0.00000 | 0.2897 | 0.2932 | |
| D(LNCHINASP) | < | D(PARANAGUASP) | |||||||
| CointEq1 | 1 | −4.73% | 5.04% | 1:1.03 | 0.9341 | 0.00000 | 0.6773 | 0.6915 | |
| D(LNCHINASP) | < | D(ROSFT) | |||||||
| CointEq1 | 1 | −1.27% | 6.48% | 1:2.43 | 0.9864 | 0.00000 | 0.4850 | 0.2489 | |
| D(LNCHINASP) | < | D(ROSSP) | |||||||
| CointEq1 | 1 | −3.18% | 1.45% | 1:1.26 | 0.9048 | 0.00000 | 0.3379 | 0.6308 | |
| D(LNCHINASP) | < | D(ROTTERDAM) | |||||||
| CointEq1 | 1 | −5.02% | 5.54% | 1:1.12 | 0.8665 | 0.00000 | 0.8224 | 0.8361 | |
| CointEq1 | Lag | ∆LNCHINASP | < | ∆LNCHIGF | ∆DALIF | ∆PARANAGUASP | ∆ROSFT | ∆ROSSP | ∆ROTTERDAM |
| λ | 1 | −1.40% | 15.64% | 0.10% | 0.50% | −4.81% | −3.74% | 3.56% | |
| Correlation LM | Normality Test | Without Cross Term | With Cross Term | ||||||
| 0.32740 | 0.00000 | 0.13050 | 0.05870 |
| Heteroskedasticity Tests | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Lag | ∆LNDALIF | < | ∆LNCHIGF | Elasticity | Correlation LM Tests | Normality Test | Without Cross Term | With Cross Term | |
| CointEq1 | 1 | −13.76% | −4.58% | 1:0.79 | 0.3891 | 0.00000 | 0.4118 | 0.3303 | |
| lag | ∆LNDALIF | < | ∆PARANAGUAS | ||||||
| CointEq1 | 1 | −10.60% | −3.36% | 1:0.89 | 0.2002 | 0.00000 | 0.2837 | 0.4106 | |
| lag | ∆LNDALIF | < | ∆ROSSP | ||||||
| CointEq1 | 1 | −7.53% | −3.07% | 1:1.06 | 0.3251 | 0.00000 | 0.3923 | 0.5137 | |
| lag | ∆LNDALIF | < | ∆ROTTERDAM | ||||||
| CointEq1 | 1 | −13.52% | −6.45% | 1:0.89 | 0.2351 | 0.00000 | 0.5950 | 0.8554 | |
| Lag | ∆PARANAGUA | < | ∆CHIGF | Elasticity | Correlation LM Tests | Normality Test | Without Cross Term | With Cross Term | |
|---|---|---|---|---|---|---|---|---|---|
| CointEq1 | 1 | −26.08% | −7.35% | 1:0.94 | 0.1305 | 0.00020 | 0.0015 | 0.0023 | |
| lag | ∆PARANAGUA | < | ∆ROTTERDAM | ||||||
| CointEq1 | 1 | −27.32% | −7.49% | 1:1.056 | 0.9821 | 0.00020 | 0.0002 | 0.0001 |
| Lag | ∆PARANAGUAS | < | ∆CHIGF | ∆ROTTERDAM | ||||
| 1 | −27.35% | −15.11% | 12.14% | |||||
| Correlation LM | Normality Test | Without Cross Term | With Cross Term | |||||
| 0.79050 | 0.00000 | 0.0132 | 0.0010 |
| Lag | ∆ROSSP | < | ∆CHIGF | Elasticity | Correlation LM Tests | Normality Test | Without Cross Term | With Cross Term | |
|---|---|---|---|---|---|---|---|---|---|
| CointEq1 | 3 | −25.30% | −4.95% | 1:0.798 | 0.4155 | 0.4298 | 0.0300 | 0.0591 | |
| lag | ∆ROSSP | < | ∆ROTTERDAM | ||||||
| CointEq1 | 1 | −21.36% | 16.91% | 1:0.848 | 0.3810 | 0.00220 | 0.1708 | 0.2306 | |
| lag | ∆ROSSP | < | ∆PARANAGUAS | ||||||
| CointEq1 | 3 | −31.86% | 5.63% | 1:0.858 | 0.3605 | 0.01930 | 0.4502 | 0.4405 | |
| lag | ∆ROSSP | < | ∆ROSFT | ||||||
| CointEq1 | 1 | −20.37% | 46.99% | 1:1.149 | 0.5674 | 0.0720 | 0.0005 | 0.0007 |
| Lag | ∆ROSSP | < | ∆CHIGF | ∆ROTTERDAM | ∆PARANAGUAS | ∆ROSFT | |
| 3 | −40.53% | −27.81% | 37.29% | −4.64% | 53.63% | ||
| Correlation LM | Normality Test | Without Cross Term | |||||
| 0.1255 | 0.00000 | 0.2217 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barboza Martignone, G.; Behrendt, K.; Paparas, D. Price Transmission Analysis of the International Soybean Market in a Trade War Context. Economies 2022, 10, 203. https://doi.org/10.3390/economies10080203
Barboza Martignone G, Behrendt K, Paparas D. Price Transmission Analysis of the International Soybean Market in a Trade War Context. Economies. 2022; 10(8):203. https://doi.org/10.3390/economies10080203
Chicago/Turabian StyleBarboza Martignone, Gustavo, Karl Behrendt, and Dimitrios Paparas. 2022. "Price Transmission Analysis of the International Soybean Market in a Trade War Context" Economies 10, no. 8: 203. https://doi.org/10.3390/economies10080203
APA StyleBarboza Martignone, G., Behrendt, K., & Paparas, D. (2022). Price Transmission Analysis of the International Soybean Market in a Trade War Context. Economies, 10(8), 203. https://doi.org/10.3390/economies10080203







