Quantifying Loss to the Economy Using Interrupted Time Series Models: An Application to the Wholesale and Retail Sales Industries in South Africa
Abstract
:1. Introduction
2. Materials and Methods
- Identify , the start of the intervention period;
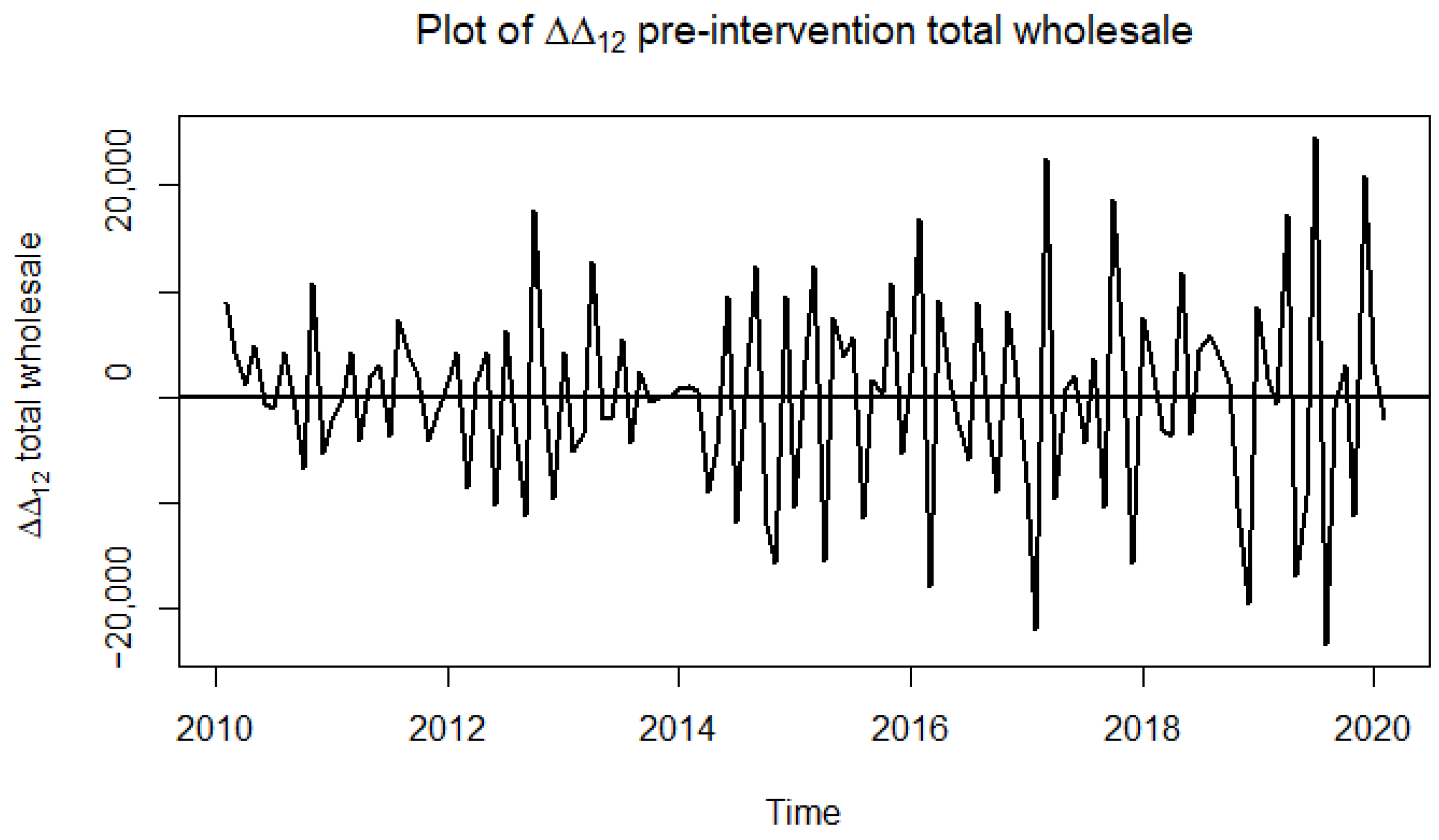
- Apply the Box–Jenkins methodology to fit an ARIMA model in the pre-intervention period;
- Use the pre-intervention model to forecast values in the intervention period (counterfactual);
- Obtain the differences between actual values in step (iii);
- Evaluate step (iv) to determine a model for the intervention effect;
- Use the results from step (v) to select the appropriate intervention variable;
- Use Equation (3) to estimate the intervention effects.
3. Results and Discussion
3.1. Pre-Intervention Models
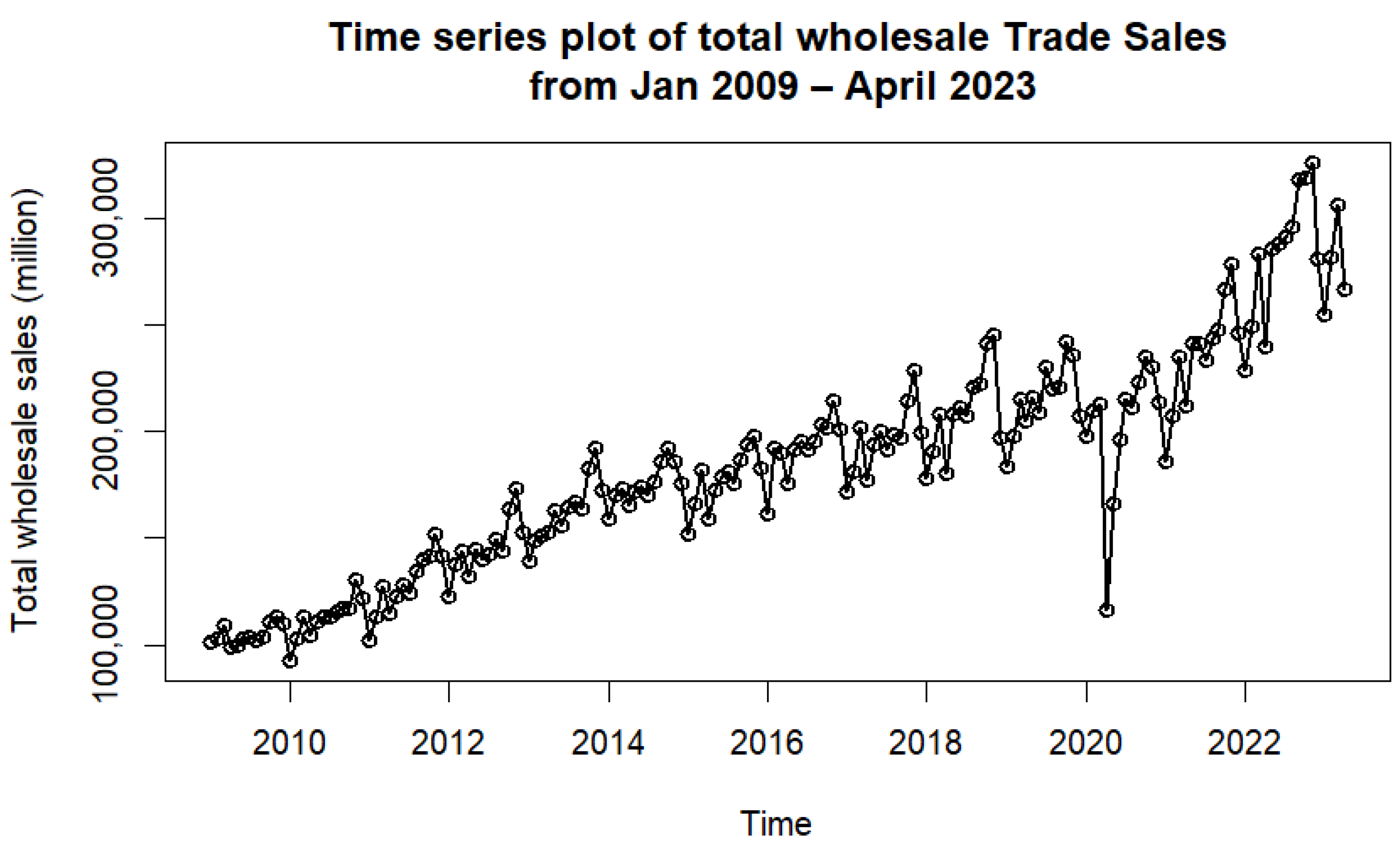
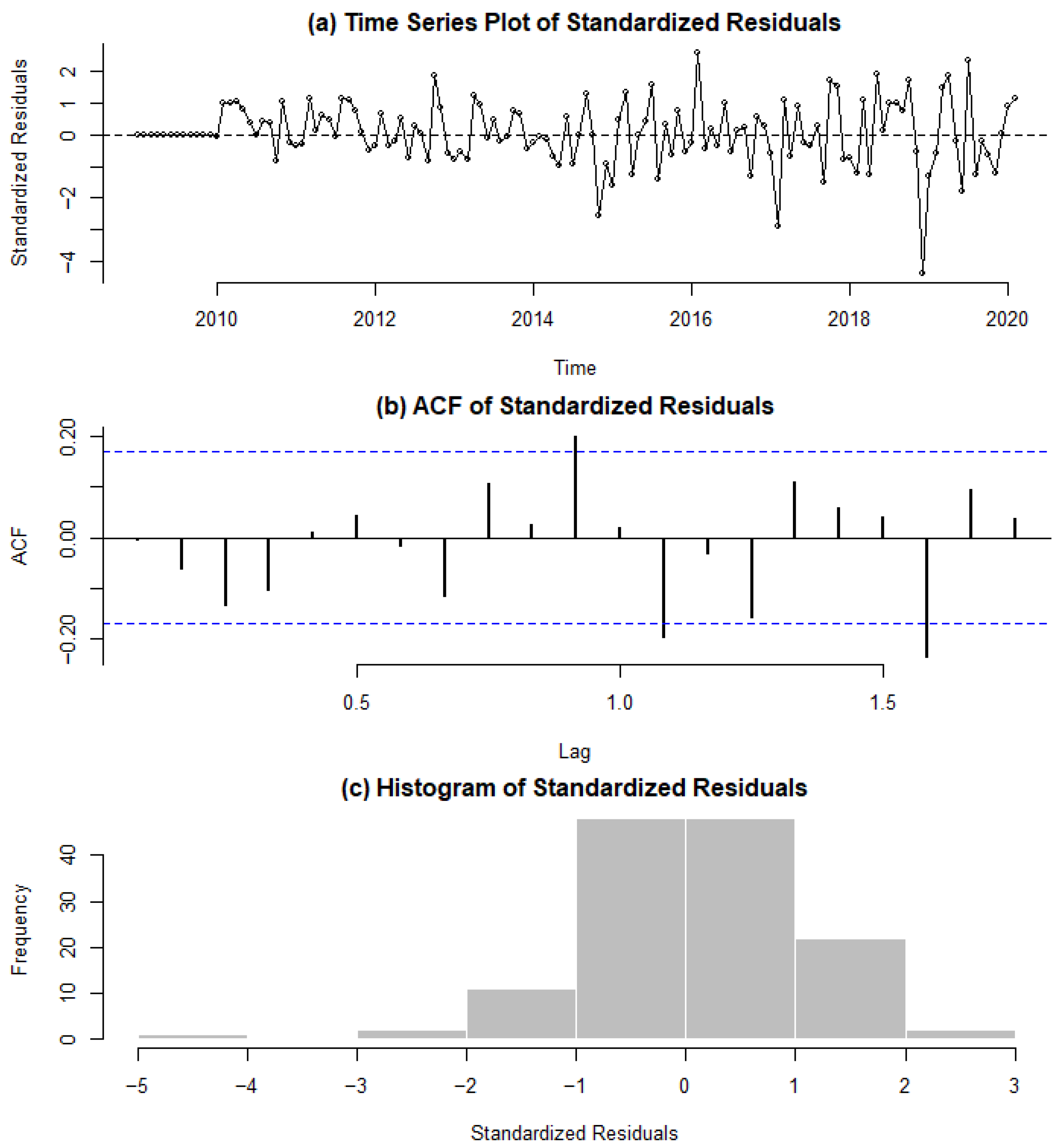
3.1.1. Wholesale
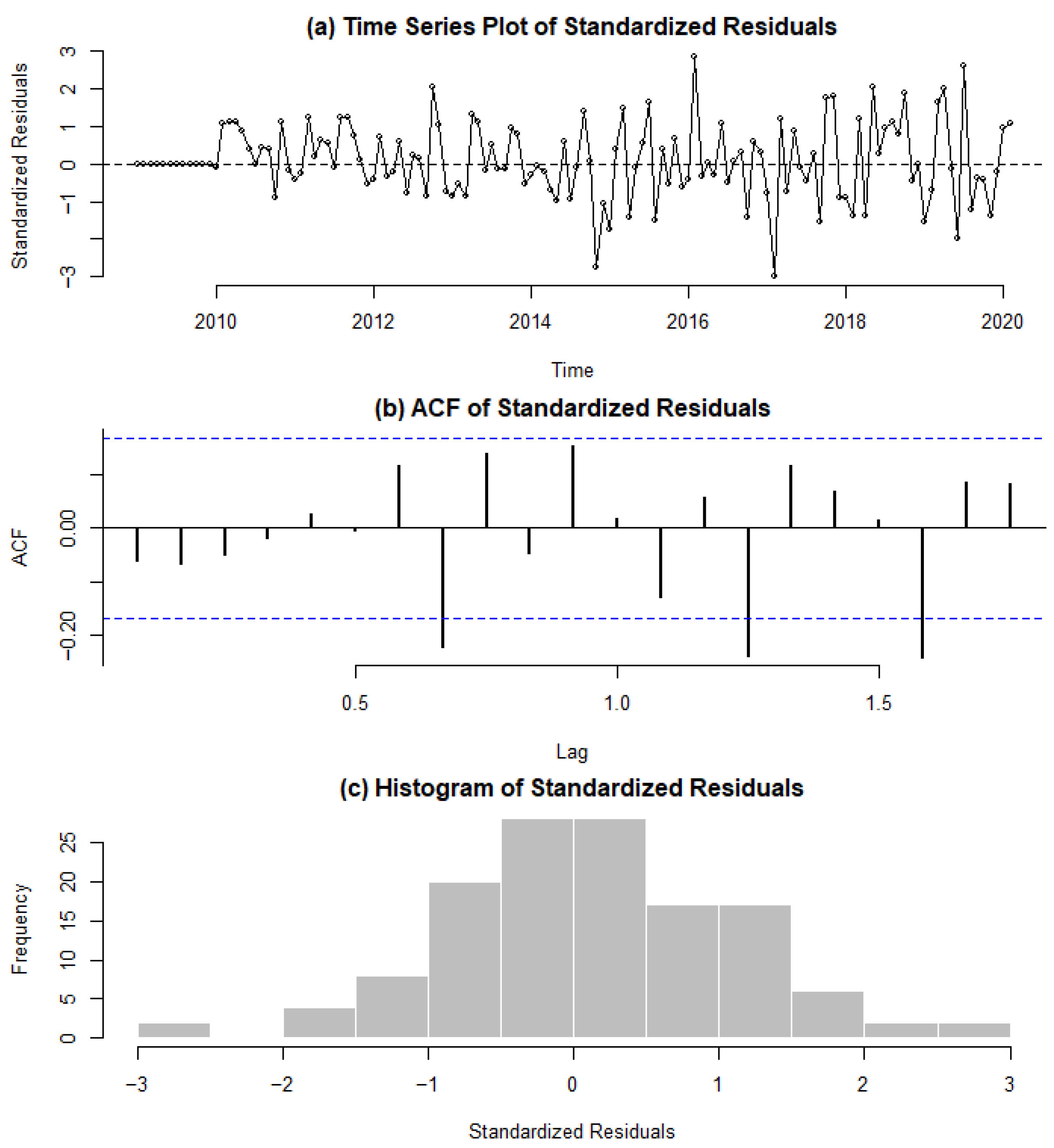
3.1.2. Retail
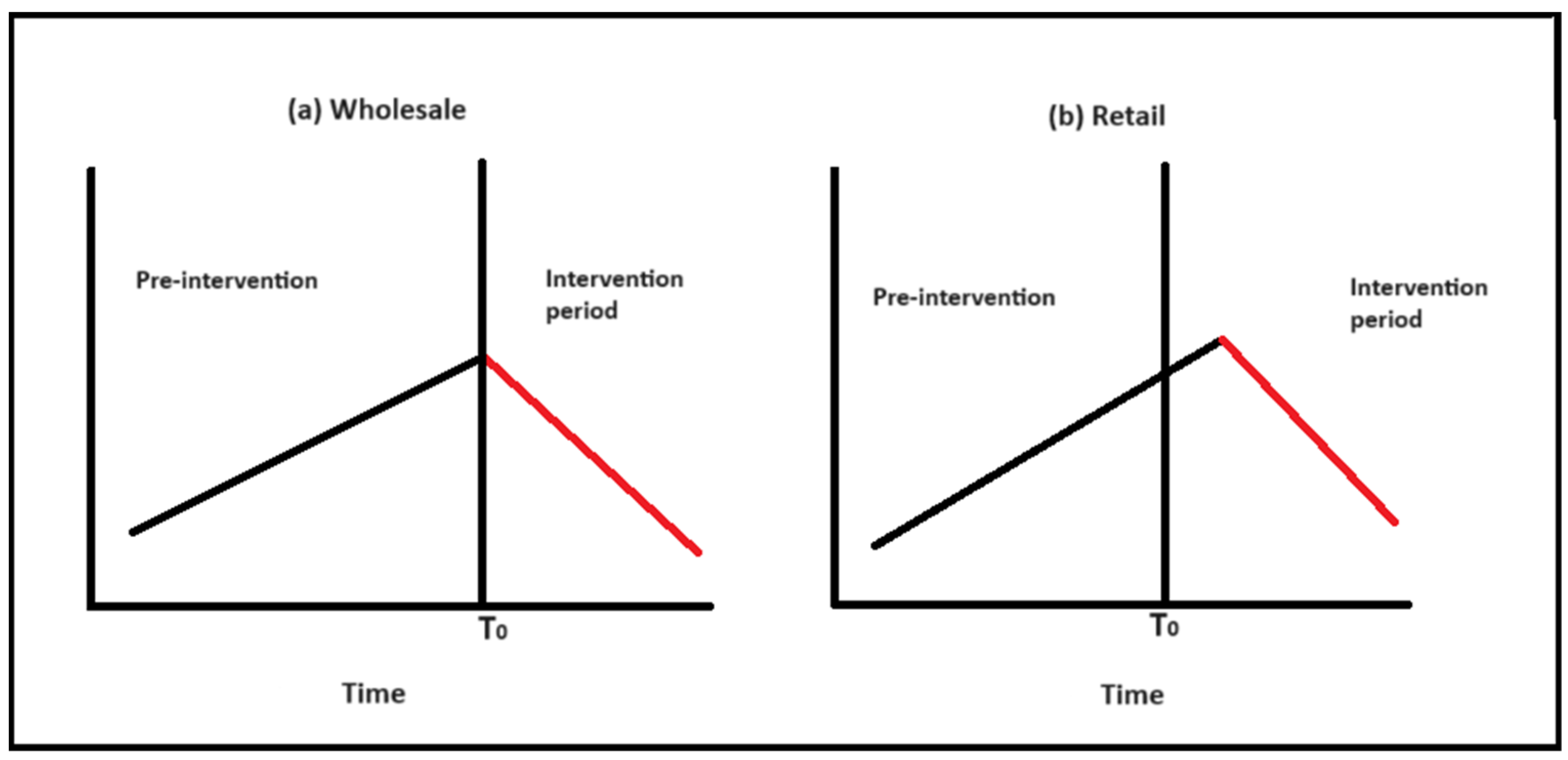
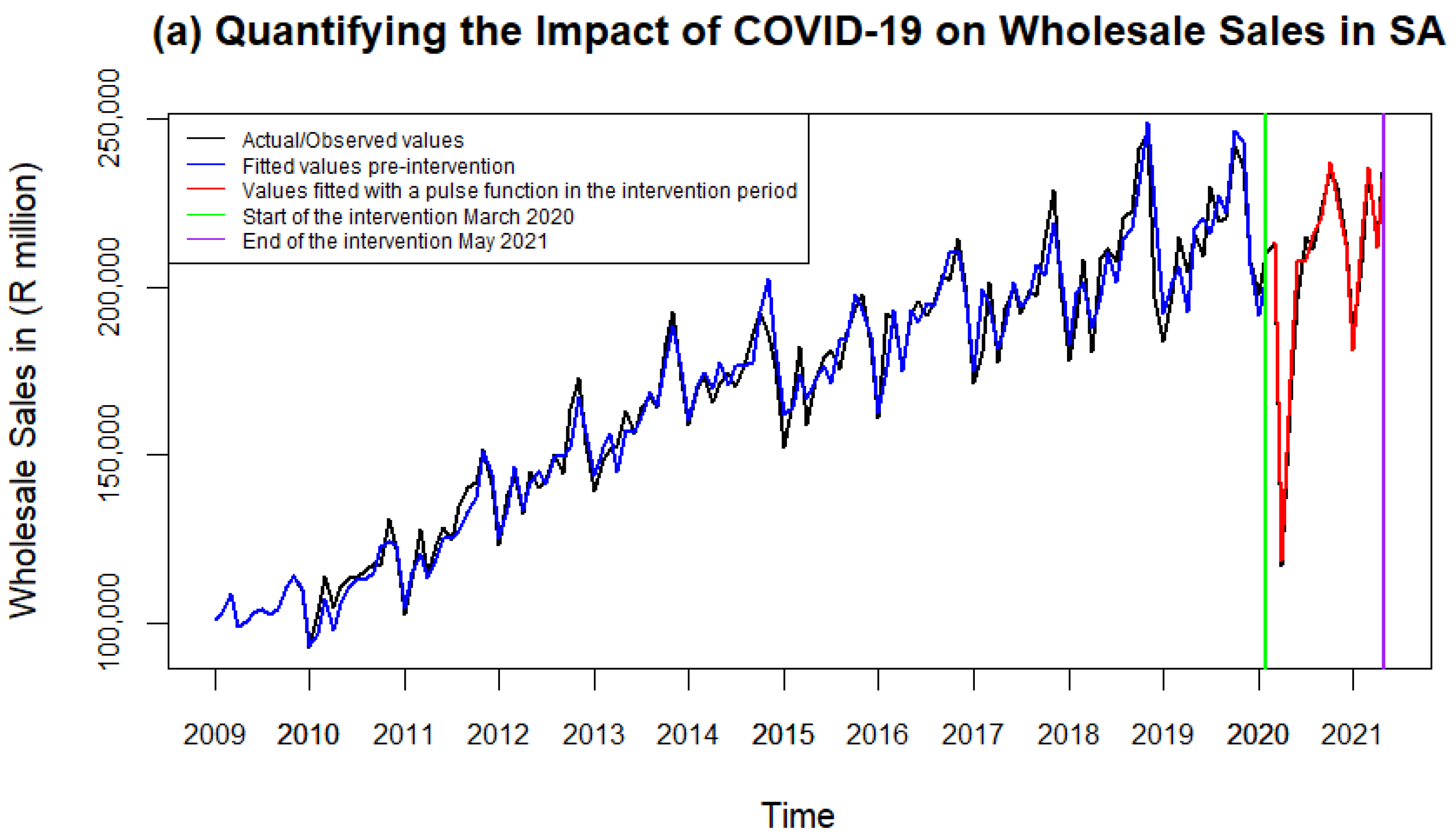
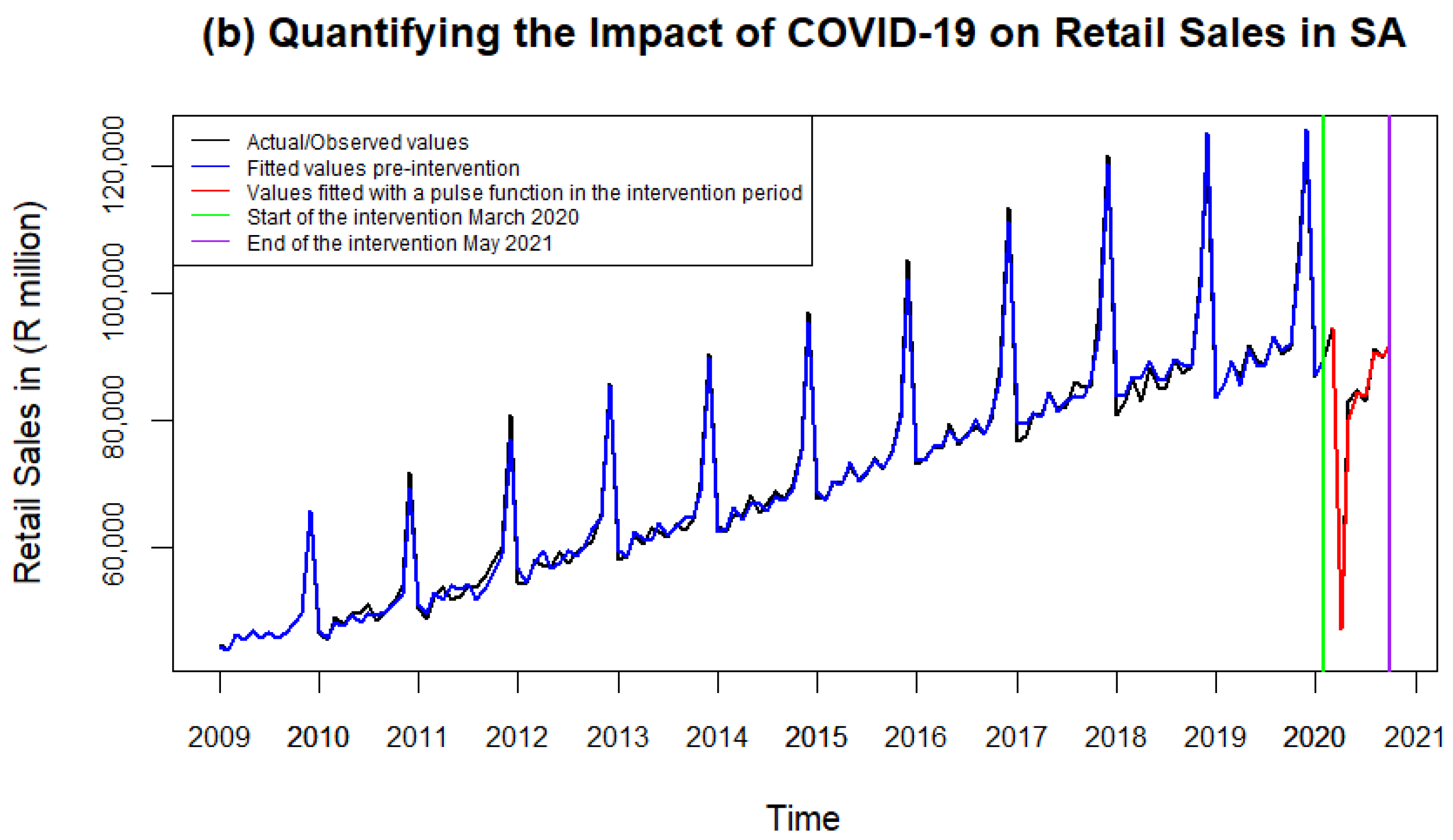
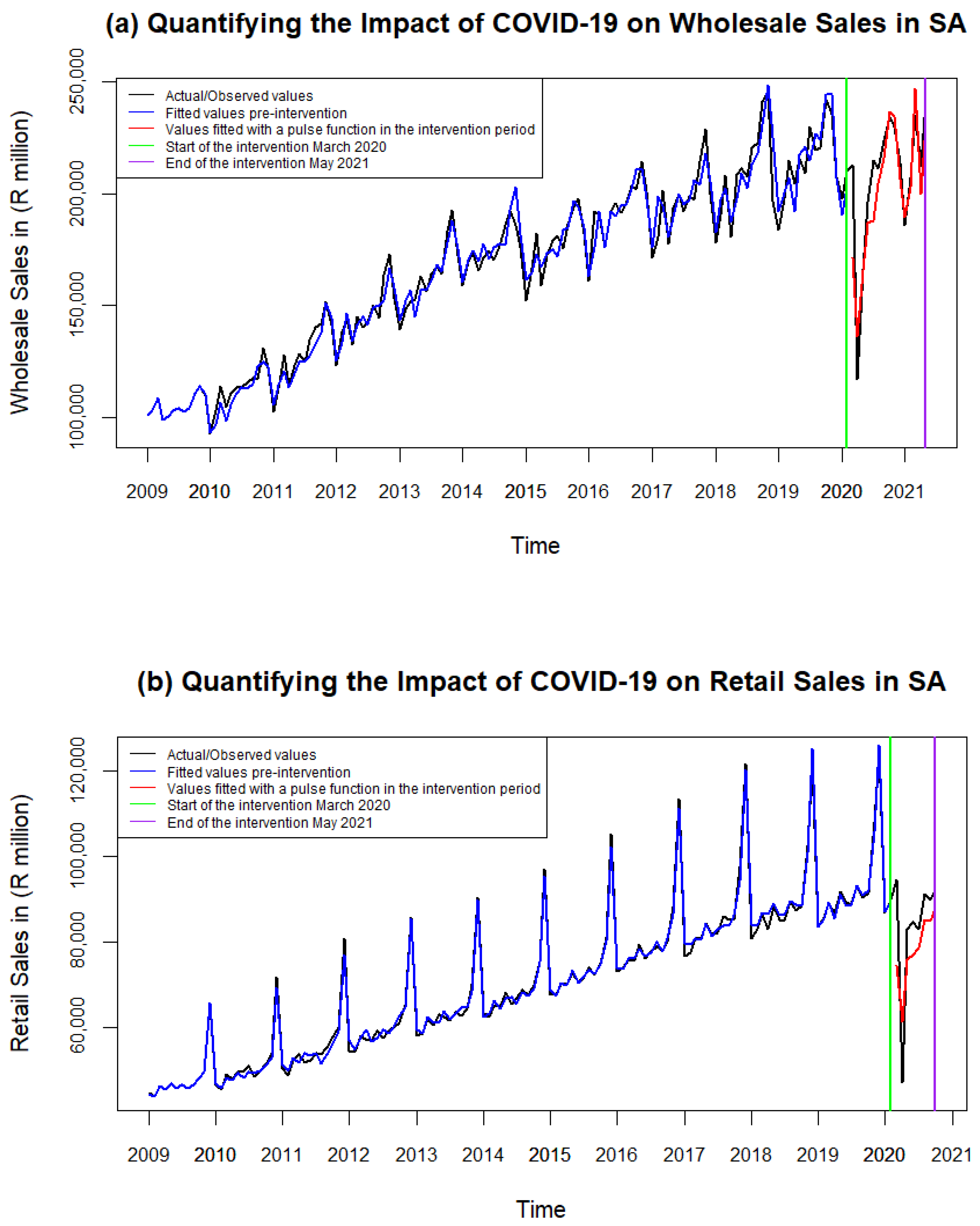
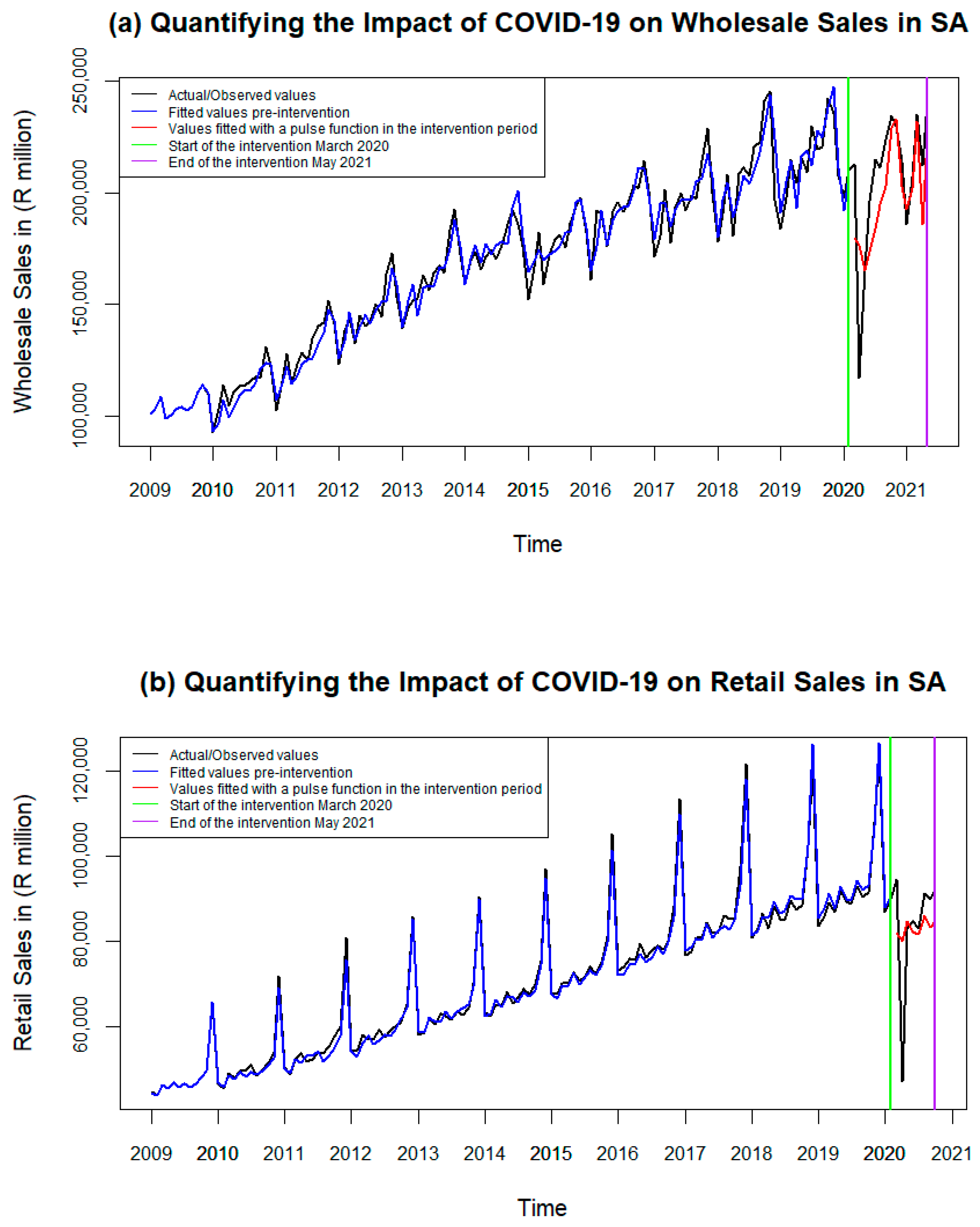
3.2. Intervention Analysis: Wholesale and Retail Sales
3.3. Three Approaches to Fitting a Pulse Function: Wholesale and Retail
3.3.1. Trial-and-Error Approach
3.3.2. Estimated Values/Actual Values (Quotient Approach)
3.3.3. , Where or Otherwise
3.4. Approach Selection: Wholesale
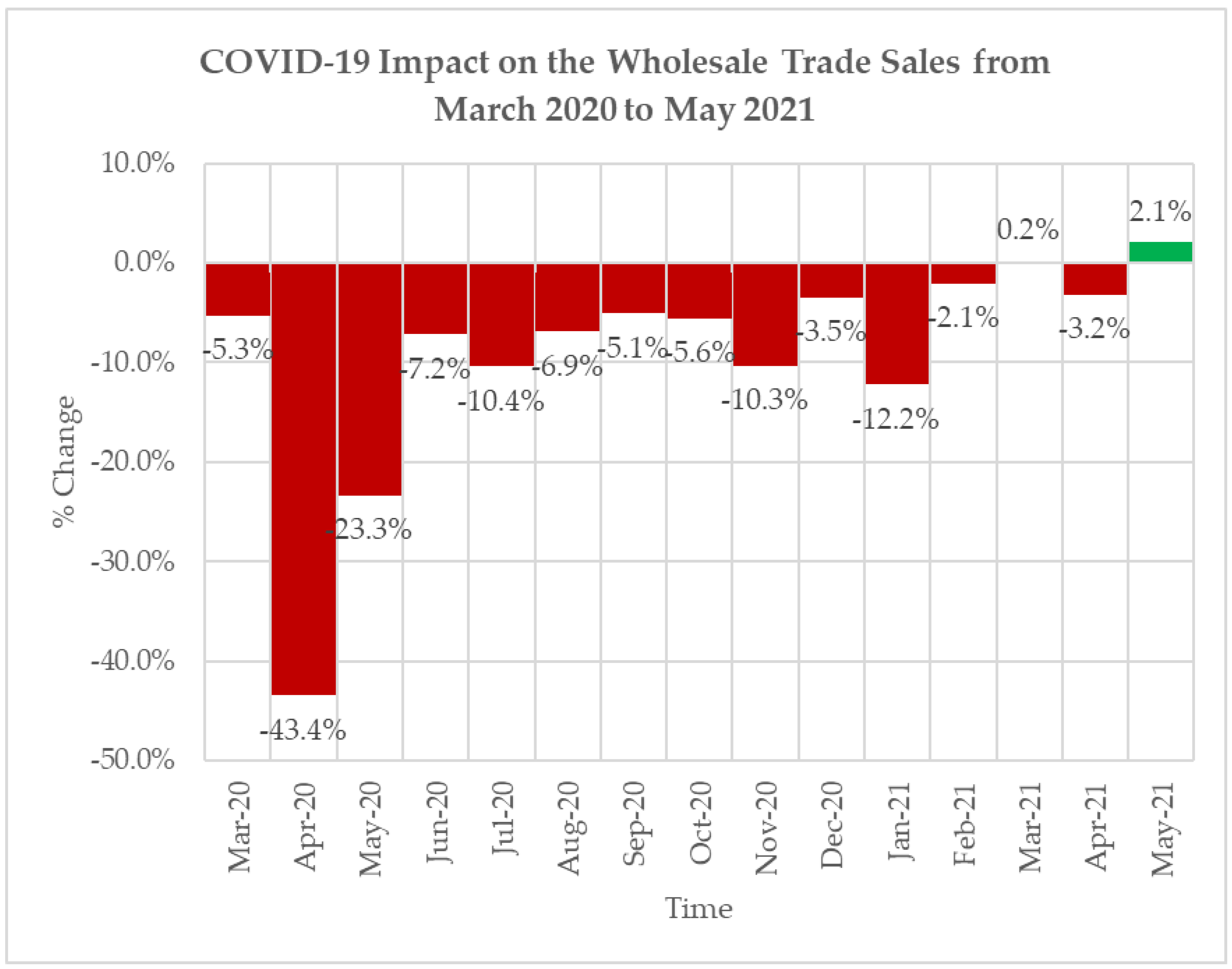
3.5. Intervention Effects: Wholesale
3.6. Approach Selection: Retail
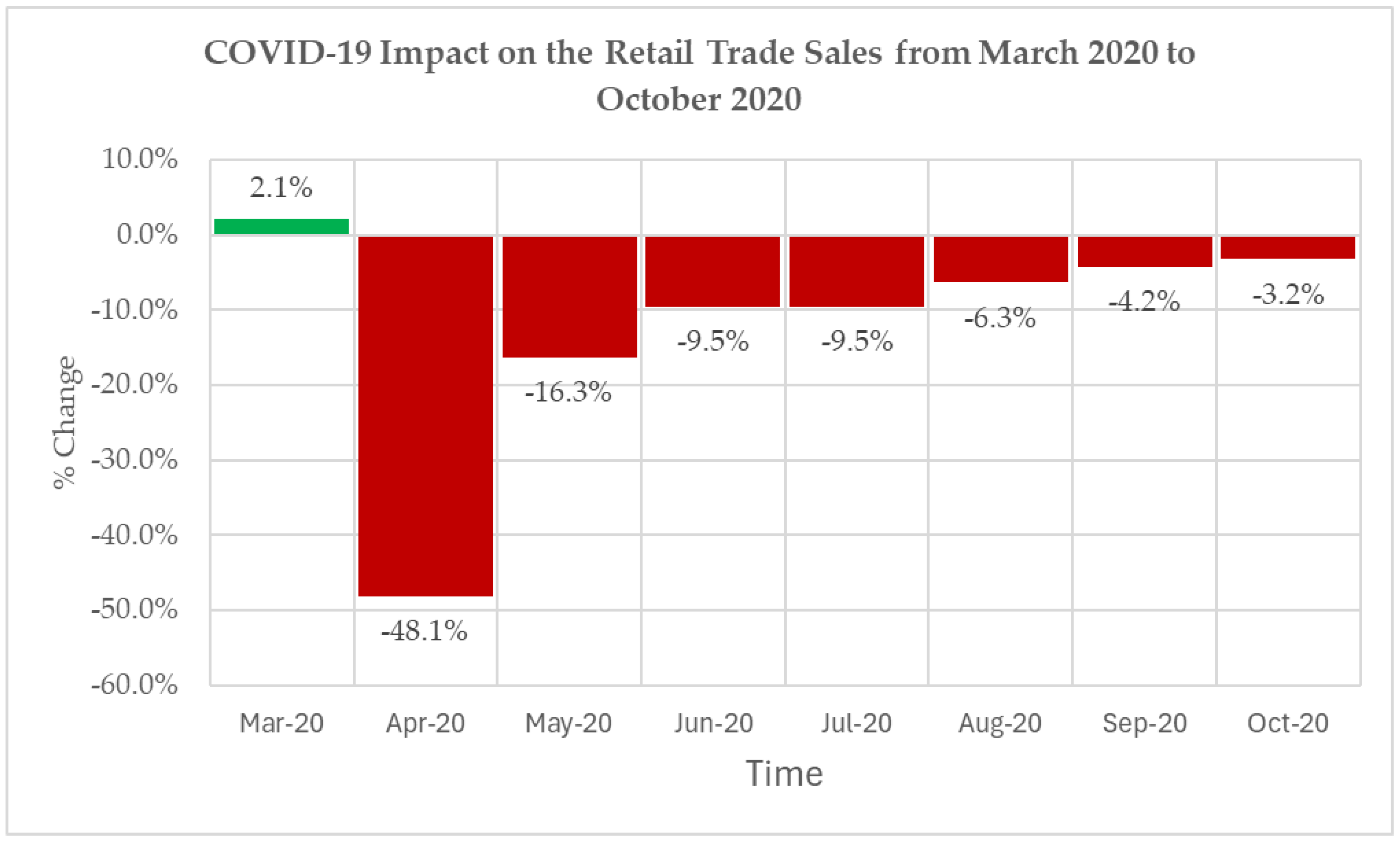
3.7. Intervention Effects: Retail
4. Conclusions
5. Study Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aliffia, Netha, Sediono Sediono, Suliyanto Suliyanto, Fariz Mardianto, and Dita Amelia. 2024. Modelling of world crude oil price based on pulse function intervention analysis approach. Media Statistika 16: 136–47. [Google Scholar] [CrossRef]
- Arndt, Channing, Rob Davies, Sherwin Gabriel, Laurence Harris, Konstantin Makrelov, Boipuso Modise, Sherman Robinson, Witness Simbanegavi, Dirk van Seventer, and Lillian Anderson. 2020. Impact of COVID-19 on the South African Economy-An Initial Analysis. SA-TIED Working Paper 111. Washington, DC: International Food Policy Research Institute. [Google Scholar]
- Bartholomew, Chekwube, Chrysogonus Nwaigwe, Ukamaka Orumie, and Godwin Nwafor. 2023. Intervention Analysis of COVID-19 Vaccination in Nigeria: The Naive Solution Versus Interrupted Time Series. Annals of Data Science 19: 1–26. [Google Scholar] [CrossRef]
- Bernal, Lopez, Stephen Soumerai, and Antonio Gasparrini. 2018. A methodological framework for model selection in interrupted time series studies. Journal of Clinical Epidemiology 103: 82–91. [Google Scholar] [CrossRef]
- Bernal, Lopez, Steven Cummins, and Antonio Gasparrini. 2017. Interrupted time series regression for the evaluation of public health interventions: A tutorial. International Journal of Epidemiology 46: 348–55. [Google Scholar] [CrossRef] [PubMed]
- Bogoch, Isaac, Alexander Watts, Andread Thomas-Bachli, Carmen Huber, Moritz Kraemer, and Kamran Khan. 2020. Pneumonia of Unknown Etiology in Wuhan, China: Potential for International Spread Via Commercial Air Travel. Journal of Travel Medicine 27: taaa008. [Google Scholar] [CrossRef]
- Bottomley, Christian, Anthony Scott, and Valerie Isham. 2019. Analysing Interrupted Time Series with a Control. Epidemiologic Methods 8: 1–10. [Google Scholar] [CrossRef]
- Box, George, and George Tiao. 1975. Intervention analysis with application to economic and environmental problems. Journal of the American Statistical Association 70: 70–79. [Google Scholar] [CrossRef]
- Box, George, Gwilym Jenkins, Gregory Reinsel, and Greta Ljung. 2015. Time Series Analysis: Forecasting and Control. Hoboken: John Wiley & Sons, pp. 428–77. [Google Scholar]
- Chamlin, Mitchell. 2017. An interrupted time series analysis of the differential impact of New Jersey’s BAC legislation on driver and passenger crash fatalities. Journal of Crime and Justice 40: 542–49. [Google Scholar] [CrossRef]
- Chikobvu, Delson, and Tendai Makoni. 2024. Modelling and Forecasting the Impact of the COVID-19 Pandemic on South Africa’s New Car Sales. Journal of Statistics Applications and Probability 13: 1127–40. [Google Scholar] [CrossRef]
- Chipumuro, Musara, Chikobvu Delson, and Makoni Tendai. 2024. Statistical Analysis of Overseas Tourist Arrivals to South Africa in Assessing the Impact of COVID-19 on Sustainable Development. Sustainability 16: 5756. [Google Scholar] [CrossRef]
- Chitiga-Mabugu, Margaret, Martin Henseler, Ramos Mabugu, and Hélène Maisonnave. 2021. Economic and distributional impact of COVID-19: Evidence from macro-micro modelling of the South African economy. South African Journal of Economics 89: 82–94. [Google Scholar] [CrossRef]
- Cryer, Jonathan, and Kung-Sik Chan. 2008. Time Series Analysis with Applications in R, 2nd ed. New York: Springer. [Google Scholar]
- Humphreys, David, Manuel Eisner, and Douglas Wiebe. 2013. Evaluating the Impact of Flexible Alcohol Trading Hours on Violence: An Interrupted Time Series Analysis. PLoS ONE 8: e55581. [Google Scholar] [CrossRef] [PubMed]
- Hyndman, Rob, and Yeasmin Khandakar. 2008. Automatic time series forecasting: The forecast package for R. Journal of Statistical Software 27: 1–22. [Google Scholar] [CrossRef]
- Inyang, Elisha, Edwin Nsien, Etebong Clement, and Dannjeh Agidi. 2023. Statistical Investigation of The Impact of Global Oil Politics: An Interrupted Time Series Approach. JP Journal of Mathematical Sciences 32: 1–13. [Google Scholar]
- Lam, Chiyung, Wai Ip, and Henry Lau. 2009. A business process activity model and performance measurement using a time series ARIMA intervention analysis. Expert Systems with Applications 36: 6986–94. [Google Scholar] [CrossRef]
- Makoni, Tendai, and Delson Chikobvu. 2023a. Assessing and Forecasting the Long-Term Impact of the Global Financial Crisis on Manufacturing Sales in South Africa. Economies 11: 158. [Google Scholar] [CrossRef]
- Makoni, Tendai, and Delson Chikobvu. 2023b. Evaluating and Predicting the Long-Term Impact of the COVID-19 Pandemic on Manufacturing Sales within South Africa. Sustainability 15: 9342. [Google Scholar] [CrossRef]
- Makoni, Tendai, and Delson Chikobvu. 2023c. Assessing and Forecasting the Long-Term Impact of the Global Financial Crisis on New Car Sales in South Africa. Data 8: 78. [Google Scholar] [CrossRef]
- Mamaro, Phulong, and Ndonwabile Mabandla. 2022. The influence of the COVID-19 pandemic on the financial performance of listed retail firms in South Africa. Acta Economica 20: 211–28. [Google Scholar] [CrossRef]
- Masena, Thabiso, and Sandile Shongwe. 2024a. Investigating the lingering effects of the pandemic on wholesale industry sales in South Africa. ITM Web of Conferences 67: 01021. [Google Scholar] [CrossRef]
- Masena, Thabiso, and Sandile Shongwe. 2024b. The impact of the pandemic on the retail industry sales in South Africa: A Box-Jenkins approach. ITM Web of Conferences 67: 01025. [Google Scholar] [CrossRef]
- McIntosh, Amy, Max Bachmann, Mark Siedner, Dickman Gareta, Janet Seeley, and Kobus Herbst. 2021. Effect of COVID-19 lockdown on hospital admissions and mortality in rural KwaZulu-Natal, South Africa: Interrupted time series analysis. BMJ Open 11: e047961. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, Douglas, Cheryl Jennings, and Murat Kulahci. 2015. Introduction to Time Series Analysis and Forecasting, 2nd ed. Hoboken: John Wiley & Sons. [Google Scholar]
- Pesaran, Hashem, and Ron Smith. 2016. Counterfactual analysis in macroeconometrics: An empirical investigation into the effects of quantitative easing. Research in Economics 70: 262–80. [Google Scholar] [CrossRef]
- Pridemore, Alex, Mitchell Chamlin, Maria Kaylen, and Evgeny Andreev. 2014. The Effects of the 2006 Russian Alcohol Policy on Alcohol-Related Mortality: An Interrupted Time Series Analysis. Alcoholism: Clinical and Experimental Research 38: 257–66. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. 2023. R. A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Schaffer, Andrea, Timothy Dobbins, and Sallie-Anne Pearson. 2021. Interrupted time series analysis using autoregressive integrated moving average (ARIMA) models: A guide for evaluating large-scale health interventions. BMC Medical Research Methodology 21: 58. [Google Scholar] [CrossRef]
- Sewell, William, Jacobus Steyn, Petrus Venter, and Roger Mason. 2016. Governance of strategically relevant research in the wholesale and retail sector. Risk Governance & Control: Financial Markets and Institutions 6: 60–68. [Google Scholar]
- Stats SA. 2024a. Statistical Release—Wholesale Trade Sales (Preliminary). Available online: https://www.statssa.gov.za/publications/P61412/P61412May2024.pdf (accessed on 25 August 2024).
- Stats SA. 2024b. Statistical Release—Retail Trade Sales (Preliminary). Available online: https://www.statssa.gov.za/publications/P62421/P62421May2024.pdf (accessed on 25 August 2024).
- Trapletti, Adrian, and Kurt Hornik. 2018. tseries: Time Series Analysis and Computational Finance. R Package version 0.10-43. Available online: https://CRAN.R-project.org/package=tseries (accessed on 8 June 2024).
- Venables, William, and Brian Ripley. 2002. Modern Applied Statistics with S, 4th ed. New York: Springer. [Google Scholar]
- Wu, Yi-Chi, Ching-Sung Chen, and Yu-Jiun Chan. 2020. The outbreak of COVID-19: An overview. Journal of Chinese Medical Association 83: 217–20. [Google Scholar] [CrossRef]
- Yoshioka, Eiji, Sharon Hanley, Yukihiro Sato, and Yasuaki Saijo. 2022. Impact of the COVID-19 pandemic on suicide rates in Japan through December 2021: An interrupted time series analysis. The Lancet Regional Health Western Pacific 24: 100480. [Google Scholar] [CrossRef]
- Zhong, Wenfang, Rong Yin, Yan Pan, Xiangliang Zhang, Andre Renzaho, Li Ling, Xingge Li, and Wen Chen. 2022. Long-Term Impact of COVID-19 on Hospital Visits of Rural Residents in Guangdong, China: A Controlled Interrupted Time Series Study. International Journal of Environmental Research and Public Health 19: 13259. [Google Scholar] [CrossRef]
- Zhou, Qin, Junxian Hu, Wensui Hu, Hailin Li, and Guo-Zhen Lin. 2023. Interrupted time series analysis using the ARIMA model of the impact of COVID-19 on the incidence rate of notifiable communicable diseases in China. BMC Infectious Diseases 23: 375. [Google Scholar] [CrossRef]
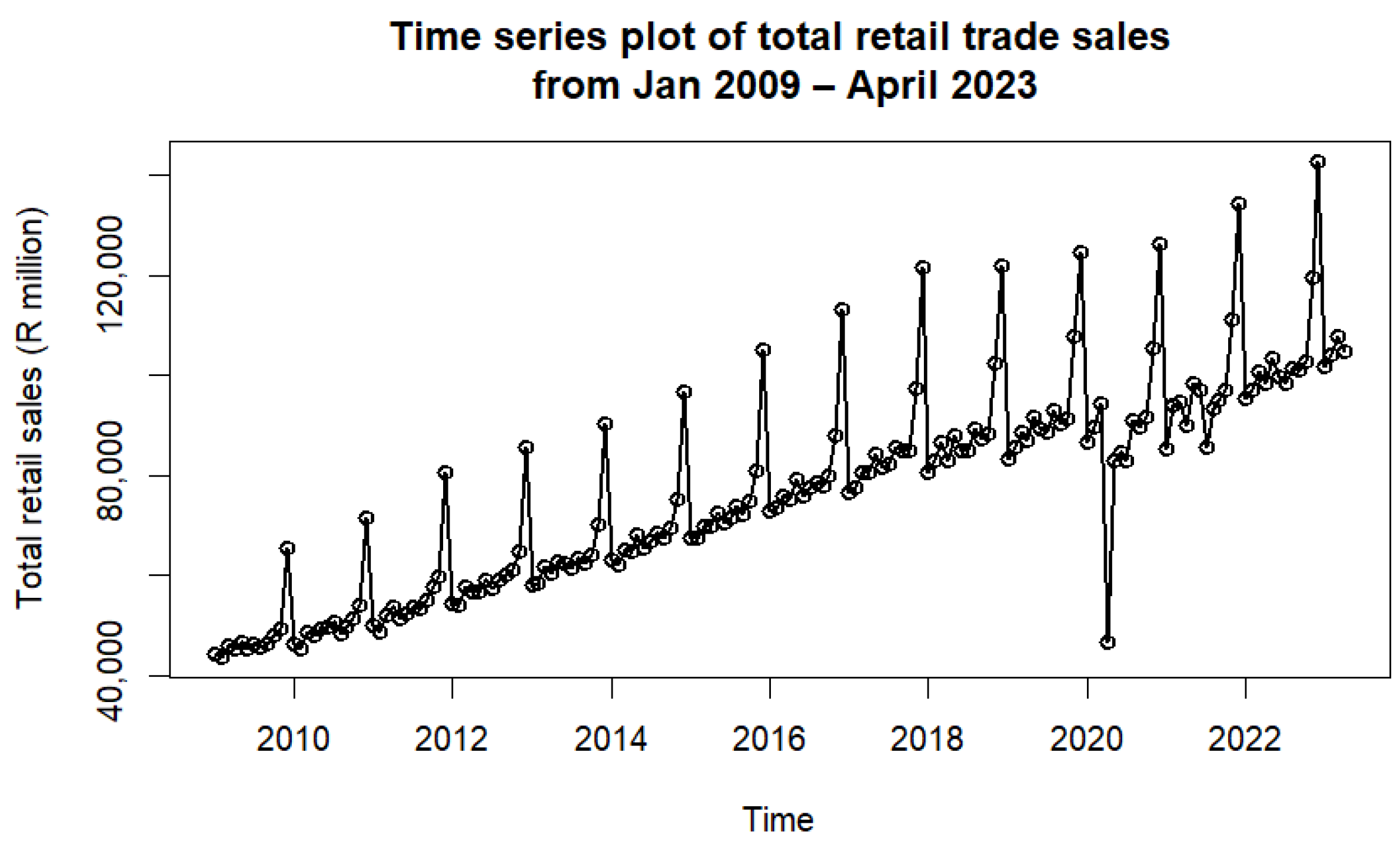
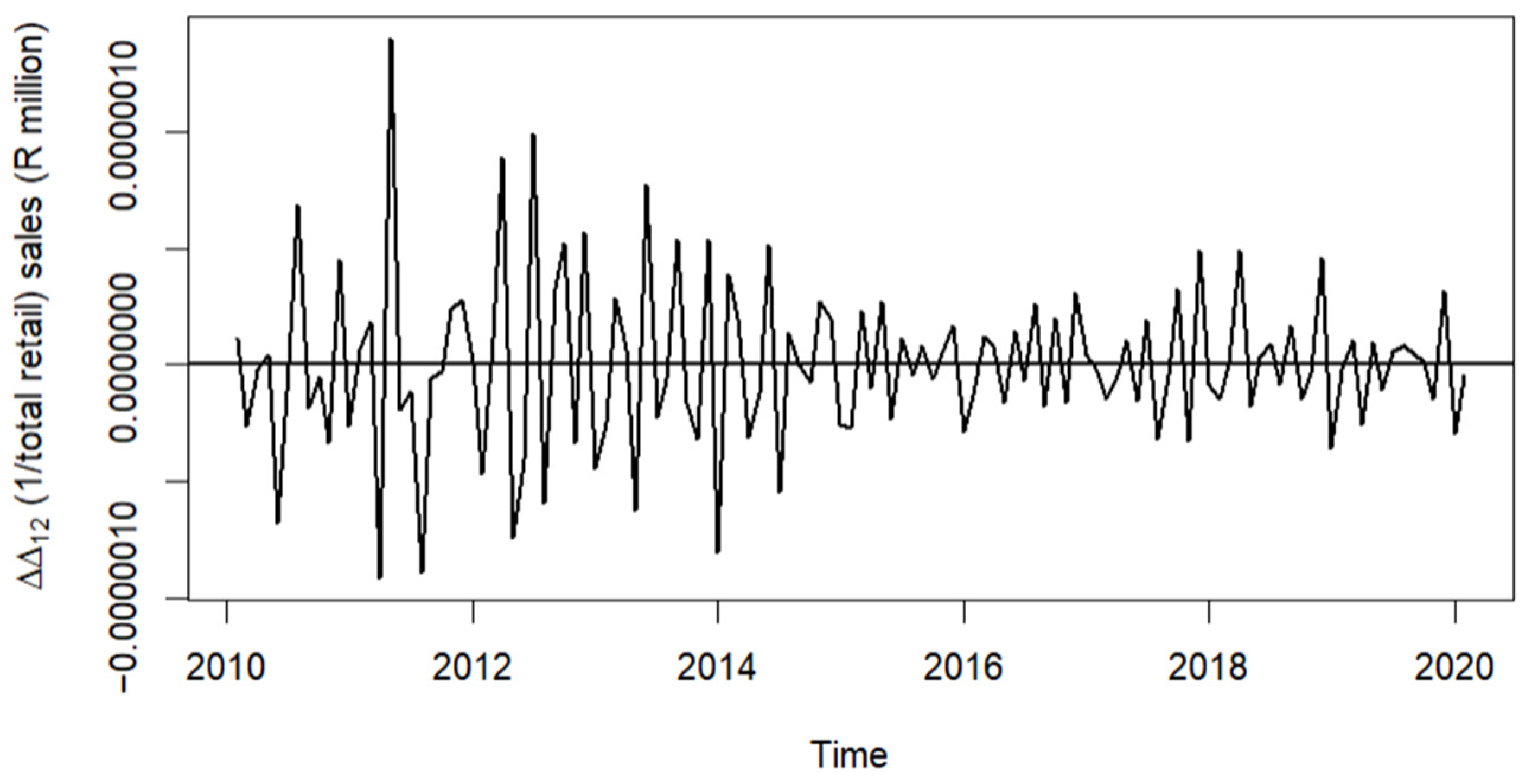
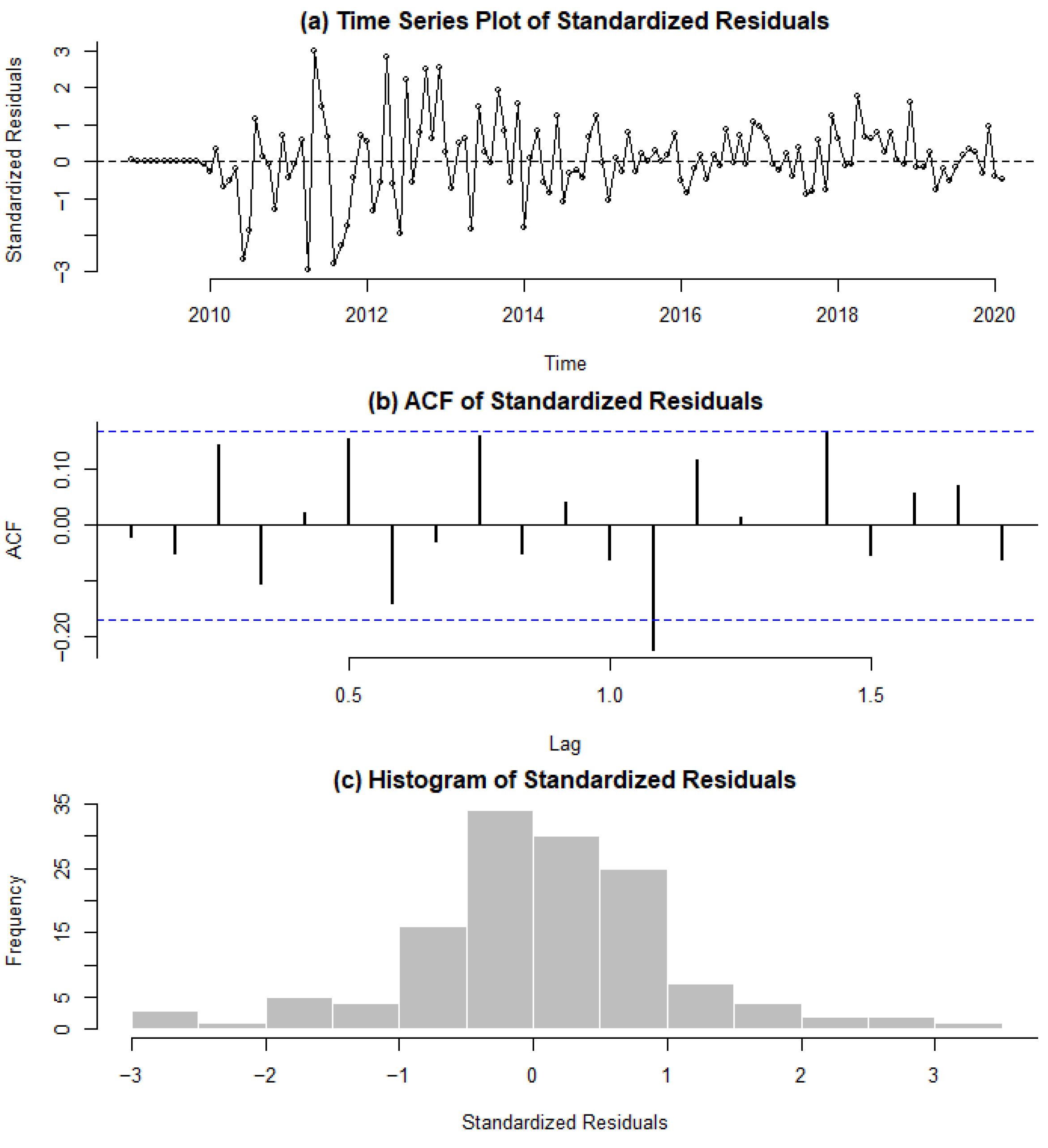
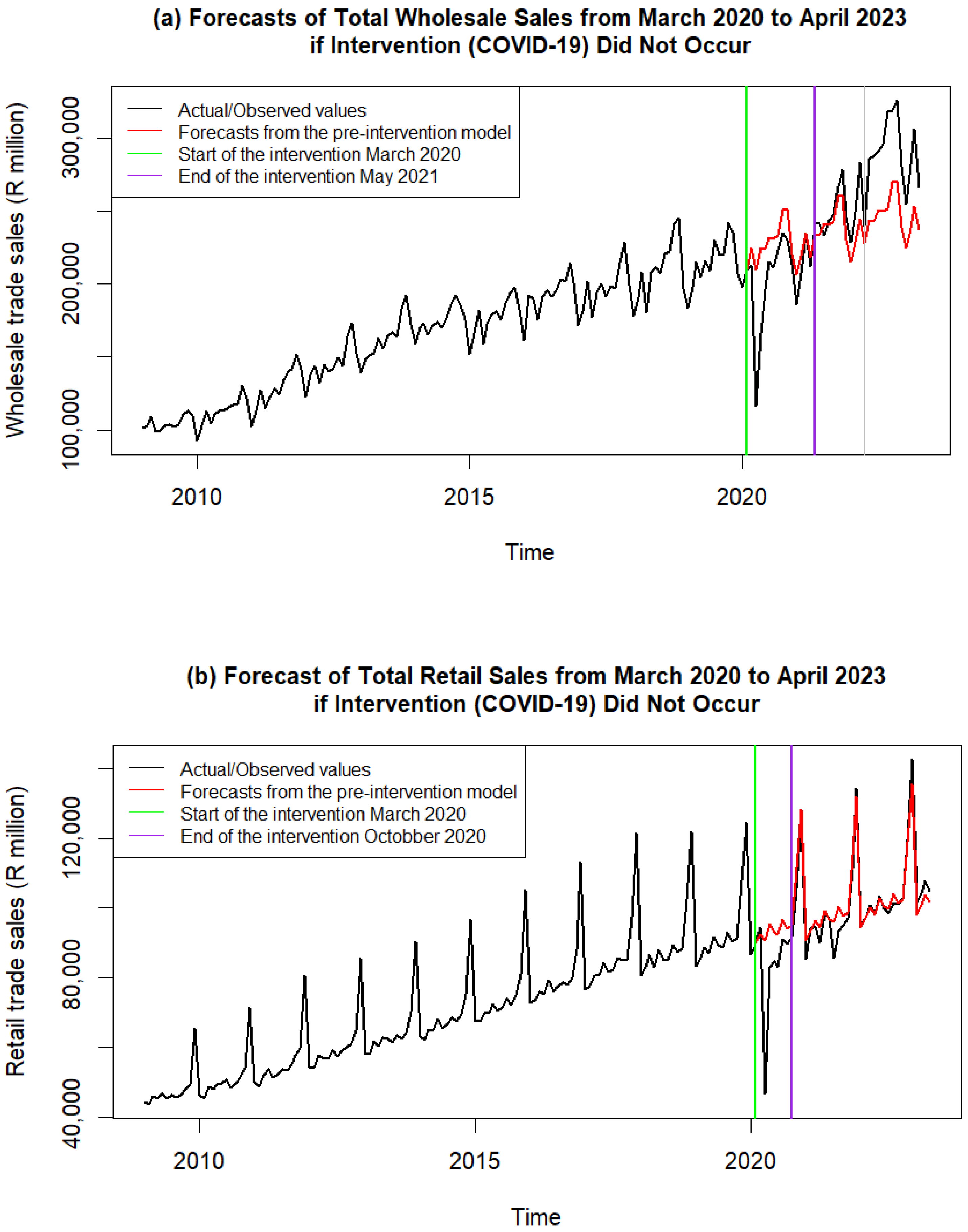
| Parameter | Estimate | Standard Error | Test Statistic | p-Value |
|---|---|---|---|---|
| −0.868733 | 0.144873 | −5.9965 | 2.02 | |
| −0.556278 | 0.081725 | −6.8068 | 9.98 | |
| 0.345427 | 0.172463 | 2.0029 | 0.04519 | |
| −0.530365 | 0.092548 | −5.7307 | 1.00 |
| Parameter | Estimate | Standard Error | Test Statistic | p-Value |
|---|---|---|---|---|
| −0.868733 | 0.144873 | −5.9965 | 2.02 |
| AIC | BIC | RMSE | MAPE | |
|---|---|---|---|---|
| Approach 1: Trial-and-Error | 2786.29 | 2803.77 | 4895.173 | 1.887742 |
| Approach 2: Fitted values/Observed values | 2848.31 | 2865.79 | 15,312.13 | 5.697709 |
| Approach 3: , if | 2909.66 | 2927.13 | 23,184.31 | 9.750518 |
| Date | Vector Covariates | % Change | Estimated COVID-19 Effect (Million) |
|---|---|---|---|
| Mar-2020 | −0.4 | −5.3% | –ZAR 12,022 |
| Apr-2020 | −3.0 | −43.4% | –ZAR 91,017 |
| May-2020 | −1.7 | −23.3% | –ZAR 52,399 |
| Jun-2020 | −0.4 | −7.2% | –ZAR 16,054 |
| Jul-2020 | −0.5 | −10.4% | –ZAR 24,100 |
| Aug-2020 | −0.3 | −6.9% | –ZAR 15,867 |
| Sep-2020 | 0.0 | −5.1% | –ZAR 11,943 |
| Oct-2020 | −0.3 | −5.6% | –ZAR 14,060 |
| Nov-2020 | −0.5 | −10.3% | –ZAR 25,798 |
| Dec-2020 | 0.0 | −3.5% | –ZAR 7657 |
| Jan-2021 | −0.6 | −12.2% | –ZAR 25,160 |
| Feb-2021 | 0.0 | −2.1% | –ZAR 4598 |
| Mar-2021 | 0.3 | 0.2% | ZAR 454 |
| Apr-2021 | 0.0 | −3.2% | –ZAR 7087 |
| May-2021 | 0.6 | 2.1% | ZAR 4970 |
| Total Effect | –ZAR 302,339 |
| AIC | BIC | RMSE | MAPE | |
|---|---|---|---|---|
| Approach 1: Trial-and-Error | 2225.67 | 2234.25 | 1106.46 | 0.8209 |
| Approach 2: Fitted values/Observed values | 2423.74 | 2432.32 | 10,141.92 | 11.4421 |
| Approach 3: , if | 2489.8 | 2498.38 | 13,167.4 | 13.9439 |
| Date | Vector Covariates | % Change | Estimated COVID-19 Effect (Million) |
|---|---|---|---|
| Mar-2020 | 0.2 | 2.1% | ZAR 1935 |
| Apr-2020 | −4.5 | −48.1% | −ZAR 43,534 |
| May-2020 | −1.6 | −16.3% | −ZAR 15,530 |
| Jun-2020 | −1.0 | −9.5% | −ZAR 8,866 |
| Jul-2020 | −1.0 | −9.5% | −ZAR 8744 |
| Aug-2020 | −0.7 | −6.3% | −ZAR 6073 |
| Sep-2020 | −0.5 | −4.2% | −ZAR 3966 |
| Oct-2020 | −0.4 | −3.2% | −ZAR 3058 |
| Total Effect | −ZAR 87,836 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masena, T.E.; Shongwe, S.C.; Yeganeh, A. Quantifying Loss to the Economy Using Interrupted Time Series Models: An Application to the Wholesale and Retail Sales Industries in South Africa. Economies 2024, 12, 249. https://doi.org/10.3390/economies12090249
Masena TE, Shongwe SC, Yeganeh A. Quantifying Loss to the Economy Using Interrupted Time Series Models: An Application to the Wholesale and Retail Sales Industries in South Africa. Economies. 2024; 12(9):249. https://doi.org/10.3390/economies12090249
Chicago/Turabian StyleMasena, Thabiso Ernest, Sandile Charles Shongwe, and Ali Yeganeh. 2024. "Quantifying Loss to the Economy Using Interrupted Time Series Models: An Application to the Wholesale and Retail Sales Industries in South Africa" Economies 12, no. 9: 249. https://doi.org/10.3390/economies12090249
APA StyleMasena, T. E., Shongwe, S. C., & Yeganeh, A. (2024). Quantifying Loss to the Economy Using Interrupted Time Series Models: An Application to the Wholesale and Retail Sales Industries in South Africa. Economies, 12(9), 249. https://doi.org/10.3390/economies12090249






