Abstract
The objective of this research is to study the Scratch programming language as a didactic tool to teach functions. The introduction of didactic tools allowing comprehension in simple and attractive ways is required. Given the traditional teaching/learning system, it is necessary to organize participatory and collaborative dynamic classrooms, which allow the interaction of students in activities where the educator modifies his or her traditional role as an advisor and the students take a more active role in learning through their own effort. In this sense, three activities using the Scratch programming language are proposed: the first one refers to the linear and affine functions, while the second one deals with the quadratic function and the third one is related to the exponential function. The participants in this study were 30 future teachers. The study considers the combination of magisterial lessons and active didactic methodologies as demonstration method, cooperative learning and gamification, also including the applied assessment. The activities, methodologies and assessment were evaluated by the participants with results higher than 4 in 5-point Likert scale for all cases, preferring the active methodologies than magisterial lessons.
1. Introduction
The recent study of 2016 conducted by the European Commission “Developing Computational Thinking in Compulsory Education, Implications for Policy and Practice” argues that in the past decade, computational thinking and its related concepts (for example, coding, programming or algorithmic thinking) are receiving increased attention in the educational field [1]. As a result, a lot of public and private implementation initiatives have arisen. Despite this widespread interest, the successful integration of computational thinking in compulsory education still faces unresolved issues and challenges [2]. Computational thinking as such was enunciated at the beginning of this decade. Jeannette Wing, Ph.D. in Computer Engineering from Massachusetts Institute of Technology (MIT), who is one of its greatest exponents, presented a definition focused on the use of computer concepts to carry out activities, from solving problems to understanding human behavior, going through systems’ design [3]. Computational thinking is based fundamentally on two learning theories: the constructivism of Jean Piaget, a Swiss psychologist and pedagogue who defended the endowment of tools for the student to solve problems [4], and the constructionism of Seymour Papert, a mathematician, computer scientist and American educator born in South Africa, who proposed the construction of mental models to understand the world around us [5]. Both learning theories focus on the construction of elements, following the maker philosophy to solve problems.
1.1. Scratch as a Computational Thinking Didactic Tool
Scratch is a visual programming language developed by a team from MIT Media Lab, led by Mitch Resnick. Scratch is used by students, teachers and parents to create simple animations and interactions, fostering computational thinking, thus putting into practice the theses of Piaget and Papert [6]. The main contribution of Scratch is that it is intended for early age users, which makes it directly applicable as a didactic tool devoted to teaching programming to elementary students. Increasingly, students are interested in programming as a creator of different utilities, applications and games. This interest appears more and more at early ages. Scratch offers a perspective advanced in knowledge but simple in management [7]. As a matter of fact, Scratch is used in education for a wide variety of applications, such as mathematics competences [8], interdisciplinary works [9], videogames [10], logical thinking [11] or robotics [12].
There are several studies that use Scratch as a tool to work in mathematical-based problems. In [13], Rodríguez Martínez et al. considered the use of Scratch in problems focusing on the divisibility concepts of the greatest common divisor and the least common multiple, achieving a statistically significant improvement in the participants who solved problems using Scratch. In [14], Shahbari et al. engaged 18 prospective teachers in a sequence of mathematical problems that utilized Scratch, concluding that the role of the sequence side-by-side with the guidelines of the instructor, had an important role in supporting the developments of learner’s meta-cognitive functions in mathematics problem-solving. Scratch has been also considered as a tool to teach geometry, using for instance a physical Scratch-based programmable artifact in order to design, implement and discuss geometry activities for primary school classes; results showed that it supposed a combination of mathematics learning opportunities for students and teachers [15].
In this paper, Scratch is used as a computational thinking didactic tool to teach functions. From the very beginning, since primary school courses, the acquisition of mathematical concepts through Scratch has been considered [13]. More specifically, the teaching of the Cartesian coordinate system, in accordance with the current educational curriculum, is a challenge for the teacher. The objective consists of students being able to describe positions and movements by means of coordinates, distances among points located in straight horizontal lines, parallelisms, perpendicularity, angles, turns, etc., using the geometric vocabulary [16].
This study considers the combination of magisterial lesson and active didactic methodologies, which are detailed in the following section, assessing the contents of the activities, the used methodologies and the applied assessment.
1.2. Active Didactic Methodologies and Scratch
The use of active didactic methodologies increases motivation and improves student learning autonomy in a significant way [17]. The motivation of the presented activities in this paper to show the teaching of the functions with Scratch is focused on proposing didactic alternatives. In this way, Scratch programming language is considered as a way to build the reality.
The challenge is to discern what strategies might be appropriate to be introduced in the curricula in order to achieve meaningful learning. Thus, given the traditional teaching/learning system, it is necessary to organize participatory and collaborative dynamic classrooms, which allows the interaction of students in activities where the educator modifies his or her traditional role as an advisor and the students take a more active role in learning through their own effort [18]. Therefore, a set of complementary active methodologies is sought, including the demonstration method, cooperative learning and gamification.
1.2.1. Demonstration Method
This method provides lessons by exhibiting and demonstrating. It demonstrates things, events, rules and sequences of activities, either directly or through using instructional media, which is relevant to the subject matter or material that will be presented. The purpose of teaching using the demonstration method is to show the process of occurrence of an event according to the teaching materials, how they are attained and the ease to be understood by the students in teaching learning process [19]. The demonstration method fits very well with the idea of computational thinking, since students share ideas and develop activities based on their own proposals, including new elements. Likewise, Scratch allows one to visualize in real time the programming of the performed task.
1.2.2. Cooperative Learning
As indicated by [20], “cooperative learning is promoted in the mid-twentieth century as a teaching strategy that favors school integration but it is proposed and supported by constructivist and sociocultural theorists as a promoter of cognitive and socio-affective development” [20]. Cooperative learning consists of the provision of small groups of students who work together in order to improve their learning. In this didactic methodology, there are three types, according to the stability or permanence of the group [21]:
- Informal groups: Teachers can use them during a specific didactic activity, so that they can last from a few minutes to an hour or the duration of a class. The final purpose is the improvement of attention and understanding of the considered task. Thus, the group organizes, analyses, explains and interprets the information appropriately;
- Formal groups: They are formed for a wide period of classes, for example, a trimester. Its purpose, as in the previous case, consists of participating and helping to organize, analyze and interpret the information, so that they cooperate for the achievement of individual and collective objectives;
- Cooperative base groups: These groups are formed for long periods of time, for example, a complete course. It is intended to establish long-lasting and helpful cooperative relationships. Thus, the group serves as a support so that students do not fall behind in their learning. Therefore, its objective is to motivate the students, while offering them permanent support through peers.
Taking into account that the activities outlined in this paper to reinforce concepts related to functions would be framed in a specific quarter, perhaps it would be appropriate to raise formal groups in class, which begin to work cooperatively with Scratch. These groups could be extended to the complete course, becoming cooperative base groups. This makes sense if this technological tool, or others related, are used throughout the rest of the course and it is desired to have a global vision of the development of the activity carried out by the working groups. In this case, it would be appropriate to monitor the work capacity of the groups at all times, in order to make changes when necessary. A suitable number for group size would be three students, and may even be two, if the computer resources of the educational center allow it.
1.2.3. Gamification
According to [22], the term gamification can be defined as “The process of game-thinking and game mechanics to engage users and solve problems”. The combination of the demonstration method and cooperative learning together with gamification manages to apply collaboratively dynamics and strategies of the game to the learning process. To accomplish this, a clear message should be defined intentionality, choosing the strategy to follow and finally evaluating and measuring progress. Games are traditionally used in early ages but stigmatized in more advanced ages, sometimes being considered a waste of time. However, in recent years, gamification has become a methodological trend with great presence in classrooms [23,24]. Consequently, a fast growth of the publications in the area of gamification in education has arisen over the past seven years. Moreover, the worldwide interest in the area is indicated by the number of countries in which the contributing authors are based and the number of institutions to which they are affiliated [25].
The approach carried out in the learning of functions through programming with Scratch is a game in itself. It allows the student to try different options until reaching the problem solution, without fear of making mistakes in the process. This is very interesting since the fact of not being able to reach the final solution may involve the student’s motivation to continue playing and improving; on the contrary, in the education system, usually the mistakes are penalized, which can lead to demotivation [26]
1.2.4. Combination of the Proposed Methodologies
The use of cooperative learning combined with the demonstration method and gamification would provide the following advantages:
- It promotes the cognitive and socio-affective development of group members, based on a work strategy that guides to solidarity through game as an additional motivational element;
- It involves the development of teamwork skills such as communication, interaction, cooperation, commitment, responsibility or leadership;
- It reorients the individual competitive effort towards positive uses of collaboration to the achievement of individual and collective objectives.
The objective of this paper is to study the Scratch programming language as a didactic tool to teach functions and analyze the suitability of different methodologies to teach functions. From this perspective, the following research questions are posed:
- Is Scratch a suitable teaching tool for teaching functions?
- How do future teachers value the activities, methodologies and evaluation used in a teaching experience to learn functions using Scratch?
2. Materials and Methods
2.1. Teaching of the Cartesian Coordinate System
2.1.1. Traditional Teaching Versus Didactic Proposal
The teaching of the Cartesian coordinate system is usually oriented to didactically explain the location in a map or graphic. It is also possible to play games such as the classic “Sea Battle”. Considering these possibilities, learning situations such as “El Cartesiano” have been proposed [27].
The didactic proposal which considers Scratch presented in this paper is focused on understanding the Cartesian coordinate system as an element integrated on the computer screen in which the student is working on. The idea is to show this proposal to future teachers who are learning mathematics didactics at the university, in order to propose an alternative to teach this topic. The Scratch scenario (the working window) is measured in pixels (px). The scenario dimensions are 480 px (width) by 360 px (height). Each pixel is a square which composes a digital image. Therefore, a high resolution image (1920 × 1200 px) is much bigger than the Scratch scenario, as shown in Figure 1.

Figure 1.
Scratch scenarios in a 1920 × 1200 px high resolution image.
2.1.2. The Cartesian Coordinate System in Scratch
Scratch allows one to select several scenarios as a template or to use new ones created by the user. There are predefined scenarios in the current version of Scratch (3.0), also available in the previous version (2.0), which show the Cartesian coordinate system as follows:
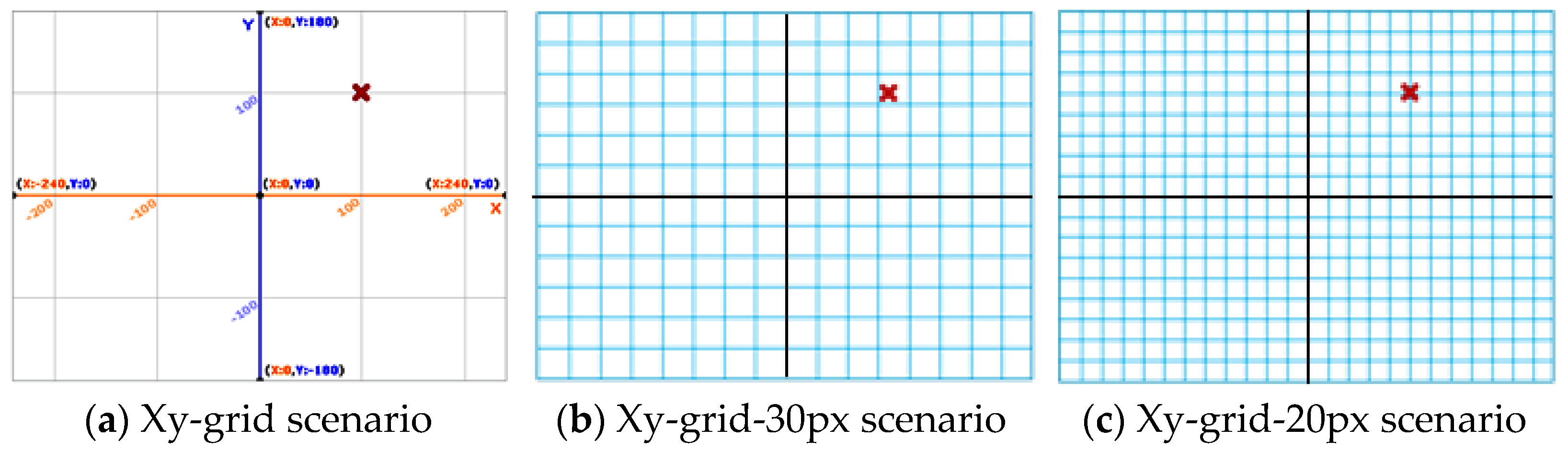
- Xy-grid scenario (Figure 2a): Cartesian coordinate system which origin is the center of the Scratch scenario. The limit points are presented in the axis of abscissas: (−240, 0) and (240, 0) and in the axis of ordinates: (0, 180) and (0, −180). It also includes a 100 × 100 square grid;
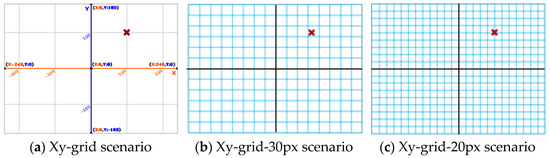 Figure 2. Scratch scenarios related to the Cartesian Coordinate System. As a reference a cross (object Button5) is located in coordinates (100, 100).
Figure 2. Scratch scenarios related to the Cartesian Coordinate System. As a reference a cross (object Button5) is located in coordinates (100, 100). - Xy-grid-30-px scenario (Figure 2b): 30 × 30 square grid. As the dimensions of the scenario are 480 × 360 px, there are 16 squares per row and 12 squares per column;
- Xy-grid-20-px scenario (Figure 2c): 20 × 20 square grid. In this case, for a 480 × 360 px scenario, there are 24 squares per row and 18 squares per column.
Scratch scenarios present a powerful didactic tool. On the one hand, the scenarios in Figure 2 are useful to work the area concept in flat figures, taking as a reference 100 × 100, 30 × 30 and 20 × 20 squares. On the other hand, to consider the position of an element in the screen, a Scratch object must be included. For instance, in the Figure 2 scenario, a cross (object Button5) is located at the coordinates (100, 100).
Once the Cartesian coordinate system is explained considering the Scratch scenarios, the didactic proposal of this paper is based on presenting and assessing three different activities based on linear, affine, quadratic and exponential functions considering the combination of the active didactic methodologies previously presented.
2.2. Proposed Activities
In this paper, three activities using the Scratch programming language are proposed: the first one refers to the linear and affine functions, while the second one deals with the quadratic function and the third one is related to the exponential function. The proposed activities were introduced to a group of 30 students of the Mathematics and its Didactics I subject of the Primary Education Degree of the Faculty of Education Sciences (FCEDU) of the University of Las Palmas de Gran Canaria (ULPGC). In the last didactic unit of this subject, dedicated to algebra, the linear, affine, quadratic and exponential functions are studied. The objective is to present these functions in a didactic way, so these activities were proposed as a reinforcement exercise.
2.2.1. Activity 1: Going to the Cinema with the Linear and Affine Functions
This section presents an activity applied to a linear function, which is then adapted to an affine function, based on a situation of daily life taking as a reference on a problem of multiplicative structure. This type of problems is identified with a rule of three in which there is direct proportionality. A suitable way of didactic resolution is the reduction to unity. Thus, the following problem is proposed:
“If the cost for 3 friends to go to the cinema is 18 €,
how much would it cost for 7 friends to go to the cinema?”
how much would it cost for 7 friends to go to the cinema?”
According to the technique which is usually explained for the direct rule of three, a cross-multiplication may be used as follows:
3 friends → 18 €
7 friends → x €
Therefore 3·x= 7·18 → x = 42 €
7 friends → x €
Therefore 3·x= 7·18 → x = 42 €
This way of resolution is far away from the practical form of calculation which is carried out in real life, which would happen to wonder how much a ticket costs and then multiplying the cost of a ticket by the number of friends who are going to the cinema, as follows:
“If the cost for 3 friends to go to the cinema is 18 €, then the ticket costs 18/3 = 6 €
Therefore, the cost for 7 friends is 7·6 = 42 €”
Therefore, the cost for 7 friends is 7·6 = 42 €”
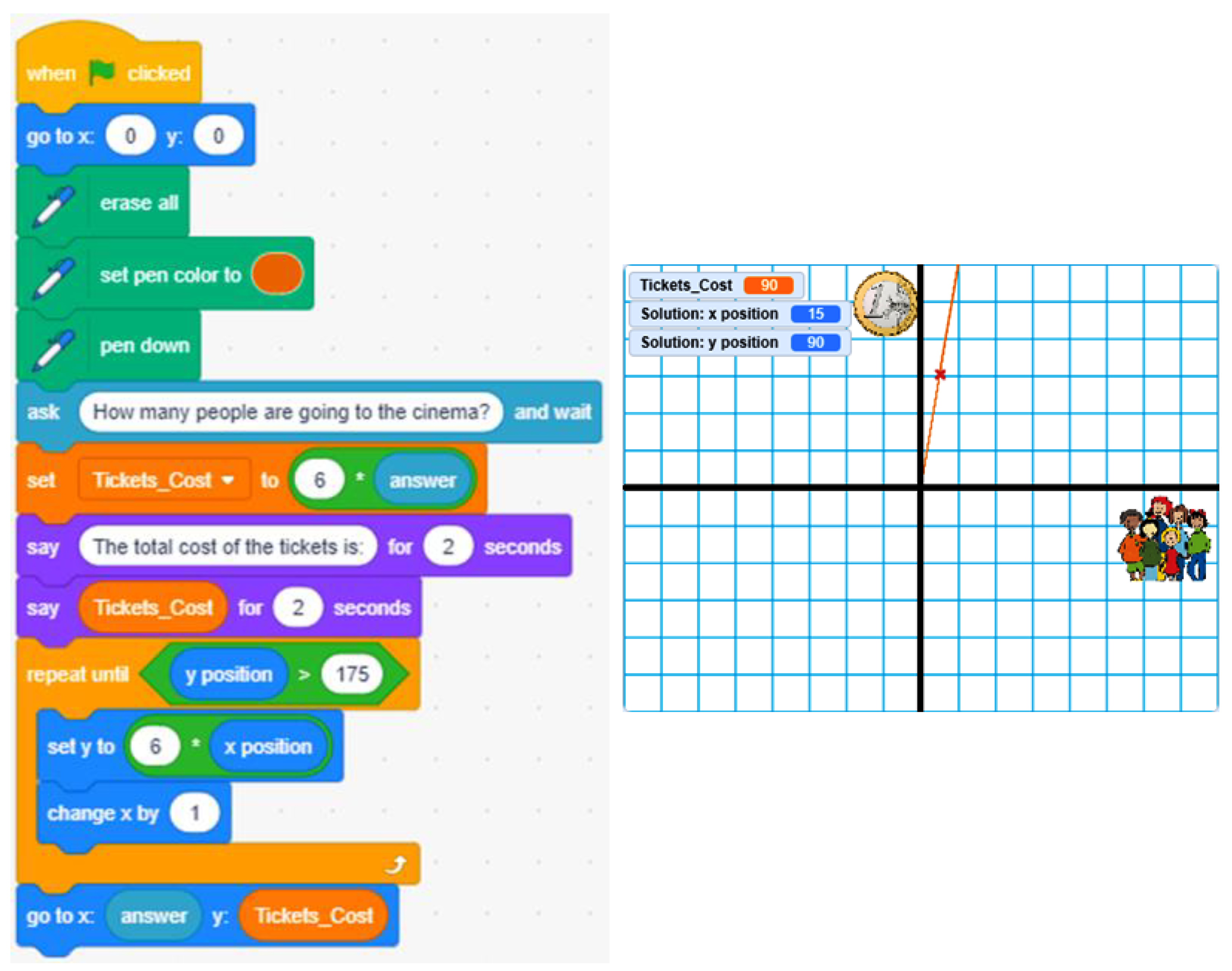
This problem applied to functions could then be understood as a linear function in which the slope (m in a linear function y = mx) would constitute the cost of the ticket (6 €), the independent variable x would be the number of friends, and the dependent variable y would be the total cost to go to the cinema. Based on this idea, a Scratch program could be proposed as follows:
- The previous example is presented considering 7 friends, so that students can see how practical the resolution by reduction to unity is.
- Students think in the framework in which the problem is represented (the Scratch screen), and following questions are proposed.
- In which quadrants of the coordinate system can the problem solution be found? Answer: First quadrant (linear function). The answer changes to the first and third quadrants if an affine function is considered.
- What would be the maximum number of friends we can consider taking into account that the result is within the Scratch screen? Answer: 30 friends (6·30 = 180: maximum ordinate in Scratch screen) for a linear function. Thus, the solution is x = 30 and y = 180. To show this result, the xy-grid-30px scenario could be used as a reference, as represented in Figure 3 (the cross marks the position for x = 15 and y = 90, just in the middle, and each square of the grid is 30 × 30). The answer changes depending on the ordinate of the origin if an affine function is considered.
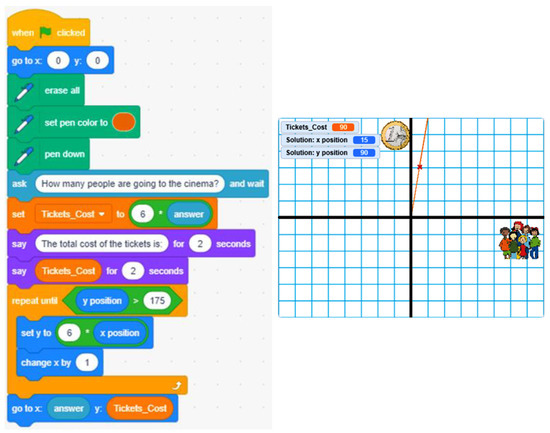 Figure 3. Linear function with the solution marked for 15 friends (cost = 90 €).
Figure 3. Linear function with the solution marked for 15 friends (cost = 90 €).
- A Scratch program is designed. In this program, the previously commented function is drawn and depending on the number of friends selected, the problem solution is marked on the function.
- The program is modified so that the user can also enter the cost of the ticket (using a variable instead of the value “6” in Figure 3).
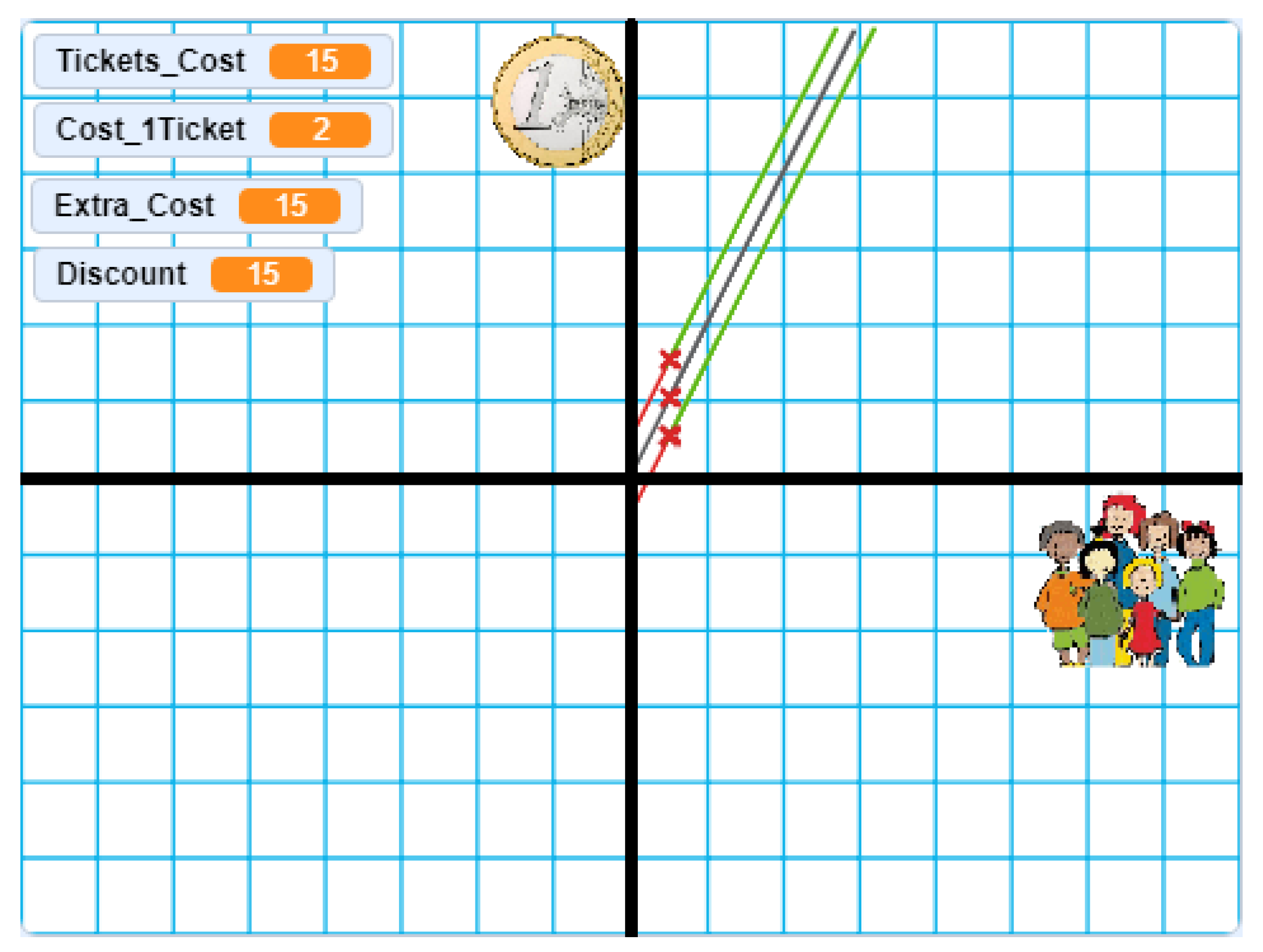
Once the linear function is studied, a variant can be considered to pass from the linear function y = mx to the affine function y = mx + n, giving meaning to the ordinate in origin n, proposing the following alternatives:
- On “movie day”, when tickets cost 2 €, and due to high demand, in order to avoid a massive purchase of online tickets, an extra cost has been placed on the purchase (over the total) of 15 €, when the number of purchased tickets is equal to or greater than 15.
- On “movie day”, when tickets cost 2 €, a cinema in crisis has decided a discount on the purchase (over the total) of 15 € to further promote the purchase, when the number of purchased tickets is equal to or greater than 15.
The affine functions corresponding to alternatives (1) and (2) are represented in Figure 4, which appear, respectively, above and below the linear function represented.
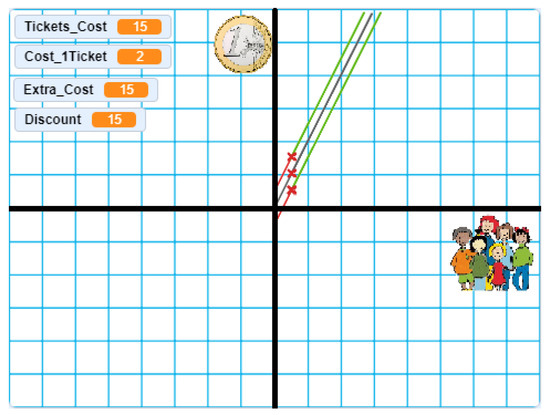
Figure 4.
Affine functions representation versus linear function.
2.2.2. Activity 2: Throwing the Ball into a Basket with Quadratic Functions
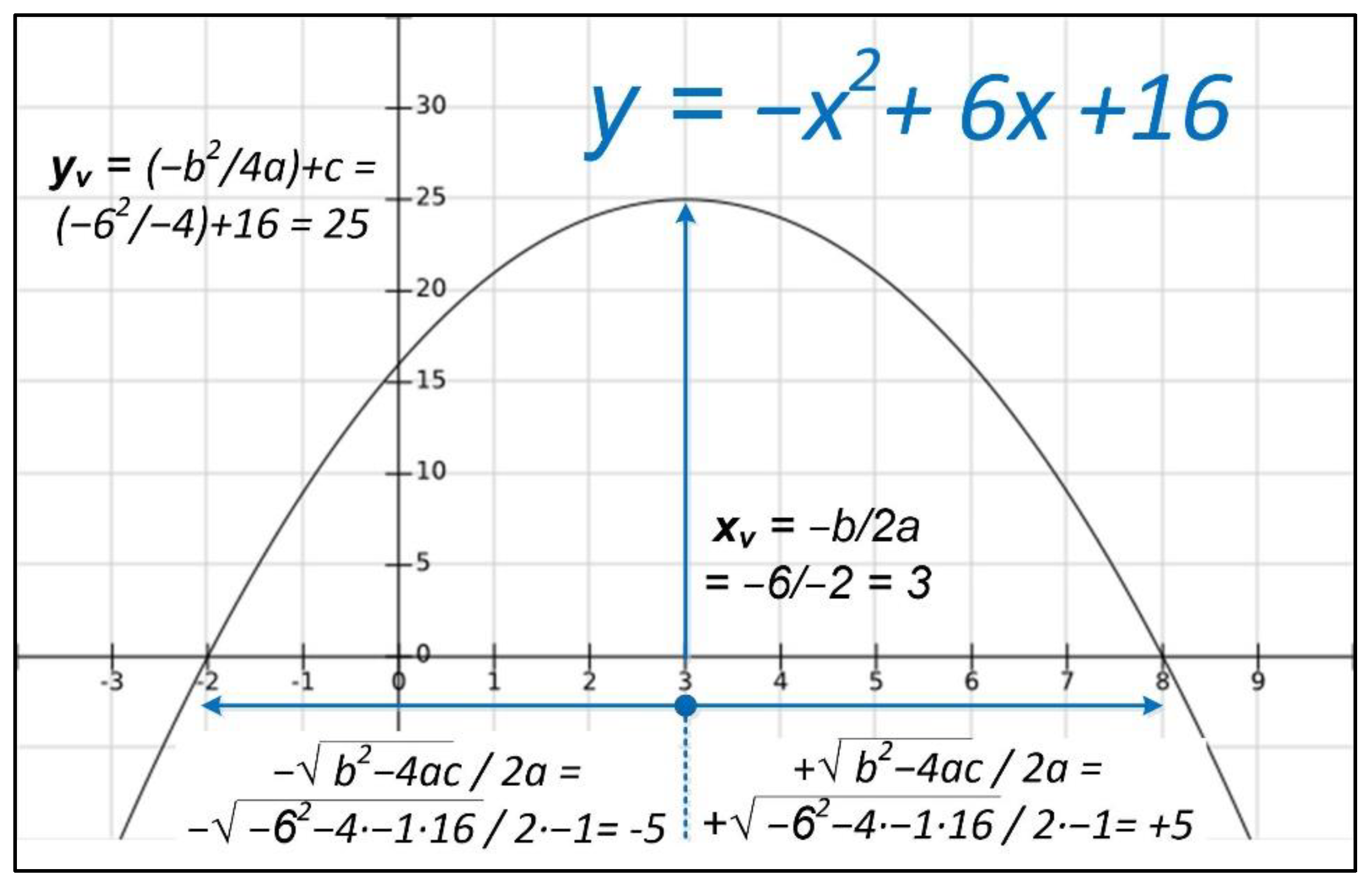
Many times, students face the resolution of second degree equations according to Equation (1):
y = ax2 + bx + c = 0
To proceed, they usually apply the formula expressed in Equation (2), which provides the possible solutions, without understanding its meaning graphically.
From this expression, it can be understood that when b2 − 4ac = 0, there will be a central point on the abscissa axis (x-axis) from which there will be an equal displacement to both left and right, which will determine the cut points with the x axis (y = 0) as long as b2 > 4ac (so that there are real solutions). This point is called THE vertex and its component on the x axis (xv) follows the expression presented in Equation (3).
Accordingly, the expression on the y-axis (yv) will be given by the expression presented in Equation (4):
An example of the discussed characteristics is shown in Figure 5 for the function y = −x2 + 6x + 16. This activity will attempt to discern the position of the vertex based on its expression by approximating the solution from a basic parabolic motion problem. Although students will not perform this kind of problem in physics until the first year of Baccalaureate, it will serve to acquire the basic knowledge of its operation.
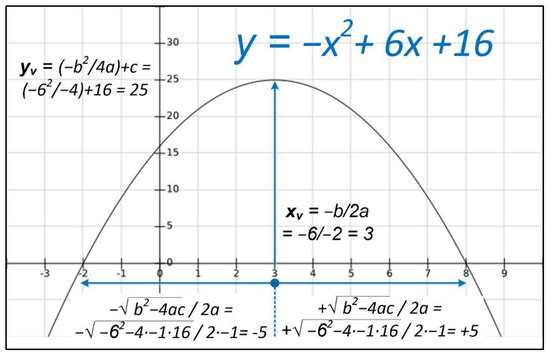
Figure 5.
Quadratic function with calculation of vertex and cut-off points with x axis.
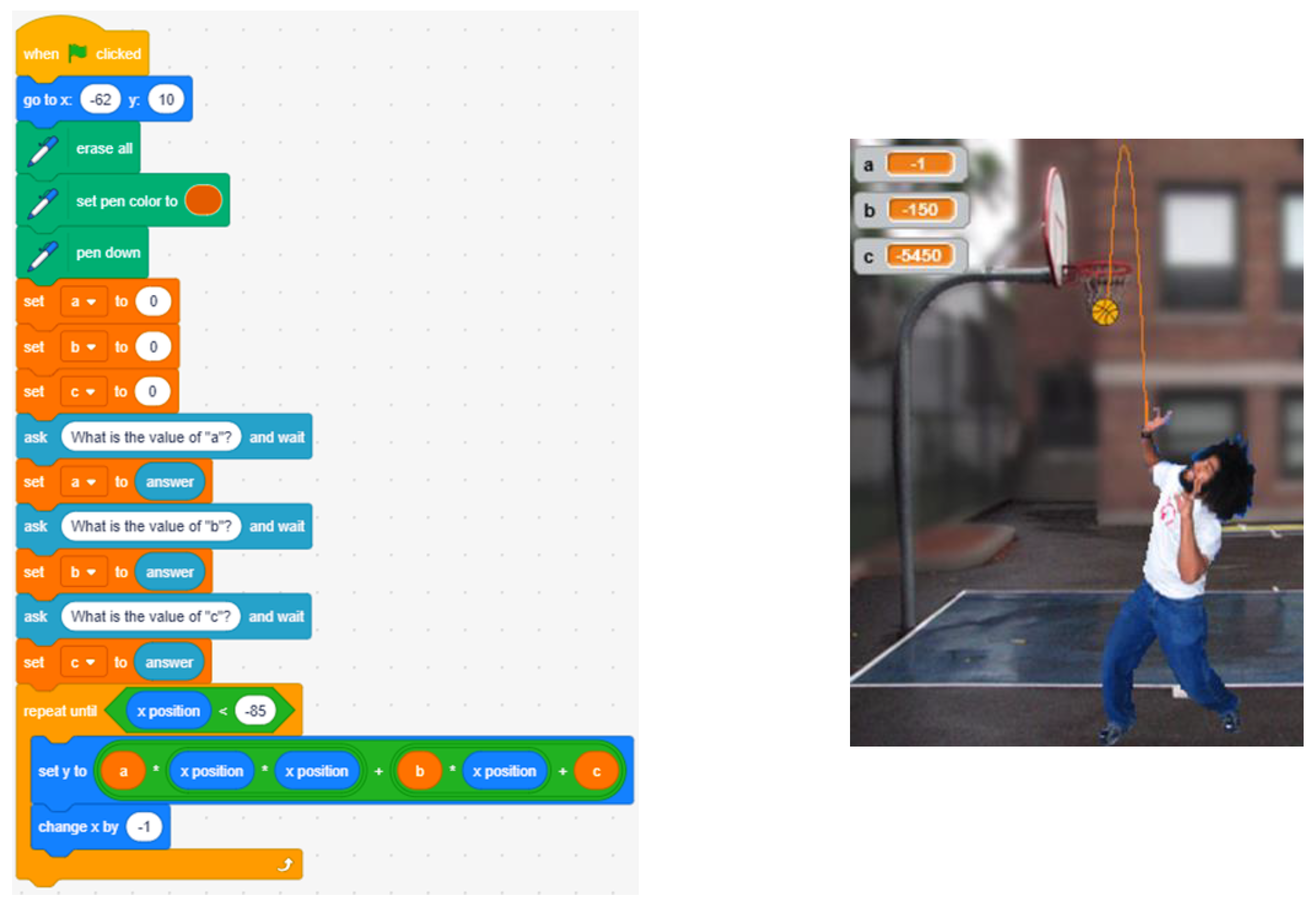
Starting from a simple Scratch program and a suitable scenario, the launching of a ball can be simulated by generating a parabola, as shown in Figure 6. The challenge would be to ask students to obtain adequate values for coefficients a, b and c after studying aforementioned aspects.
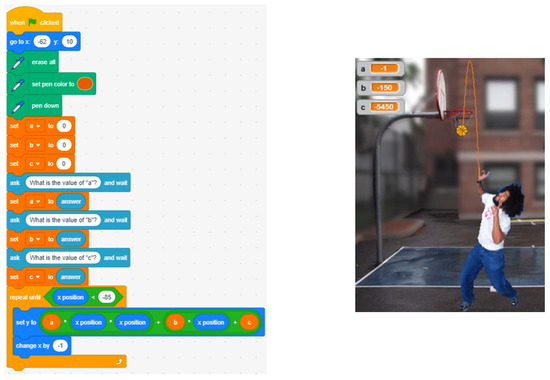
Figure 6.
Scratch program and parabola corresponding to coefficients a = −1, b = −150 and c = −5450.
2.2.3. Activity 3: Infecting with Exponential Functions
In this activity, students will understand how growth works in an exponential function, which is especially striking when the exponential function growth rate seems to be low, as is the case with this problem
“Suppose a virus with a daily infection rate of 5%, this means that each day there are an additional 5% of people infected by the virus. People will continue to infect at this rate until a vaccine is found. If we assume that the days constitute the independent variable ‘x’ of the problem, the number of infected people the dependent variable ’y’ of the problem, and that on day ’0’ there was only one infected person: estimate with a Scratch program on which day at most you could find the vaccine so that the solution of the problem is within the Scratch screen. Obtain also the exact solution’.
According to the proposed problem, it can be deduced that it can be expressed as presented in Equation (5).
Therefore, the number of infected people depending on the number of days for some values changes dramatically when the number of days increases, as presented in Table 1.

Table 1.
Infected people VS number of days.
- After 15 days, there are only 2 infected people;
- After 150 days, the situation could start to be alarming (1500 people infected);
- After 1500 days, “the power” of the exponential function is clearly shown: the resultant number represents 1021 times the world population.
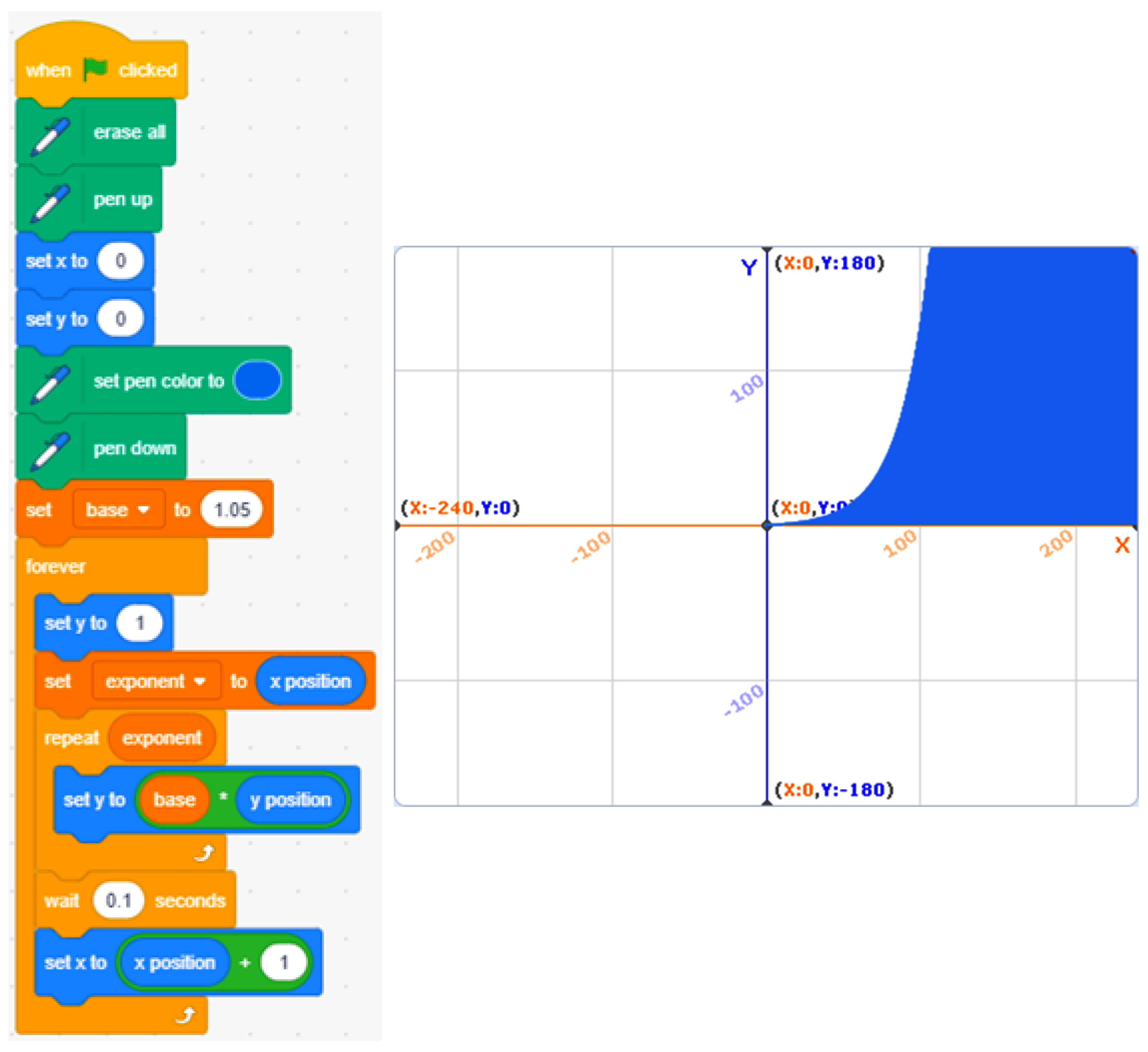
The related program in Scratch, which is provided to students, is based on a recursive program to multiply the base of the expression (1.05), the required times by the exponent (x). The program draws with the extension “Pen” the area below the exponential curve, which saturates the Scratch screen approximately for an x = 100, as shown in Figure 7. This value can be exactly calculated applying logarithms, as presented in (6).
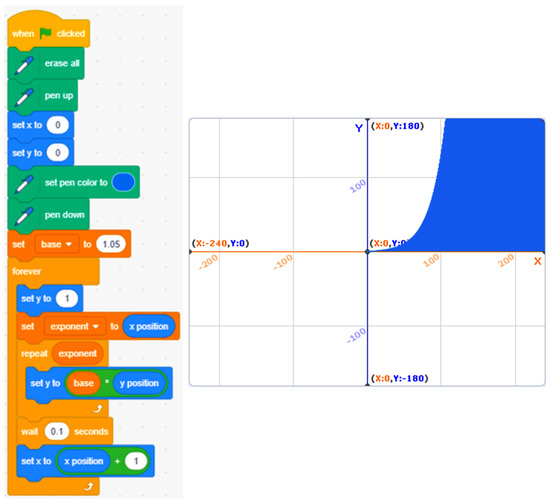
Figure 7.
Scratch exponential function program. The curve saturates for x = 107.
The result of expression (6) represents the maximum day at which the vaccine could be found, so the solution of the problem within the Scratch screen is day 106. For this number of days, the value of y is equal to 1.05106 = 176.22, which does not exceed the maximum value of the screen (ymax = 180). If an upper value is used (for example, 107), the maximum value would be exceeded (1.05107 = 185.03).
2.3. Data Collection
The data collection of the proposed activities is based on the evaluation of competences and therefore trying to identify the achievement of competencies in the student, so the objective will be to collect useful information in relation to student progress. This is key to define the assessment instruments and types.
2.3.1. Participants
The participants in this study were 30 future teachers. The participants are students of the Mathematics and its Didactics I subject of the first course of Primary Education Degree of the Faculty of Education Sciences (FCEDU) of the University of Las Palmas de Gran Canaria (ULPGC). From the 30 participants, 19 (63.33%) were women and 11 (36.67%) were men, all aged between 19 and 21 years old (19.2 years was the average).
Most of the participants (90%) did not know the Scratch programming language. All participants had no prior knowledge of teaching the functions considering the associated active methodologies.
2.3.2. Assessment Instruments
When defining the instruments for evaluating the activities carried out, the methodologies used in the teaching-learning process are also taken into account, so that they are adapted in a consistent manner. Thus, the considered instruments are the following:
- Observation: Starting from an adequate planning and systematization of evidence collection based on the work completed in a cooperative way. Students also act as observers, through a process of co-evaluation;
- Portfolio: Although the realization of the proposed activities is carried out in pairs or in trios, the portfolio is presented at two levels:
- −
- Group: Students would include Scratch programs of the activities carried out in a work folder, as well as a report indicating how they have developed it, highlighting the most relevant aspects;
- −
- Individual: Each student would also prepare for each activity a short report which includes comments and reflections on the work completed. A self-evaluation of the work completed is also included in a self-assessment report.
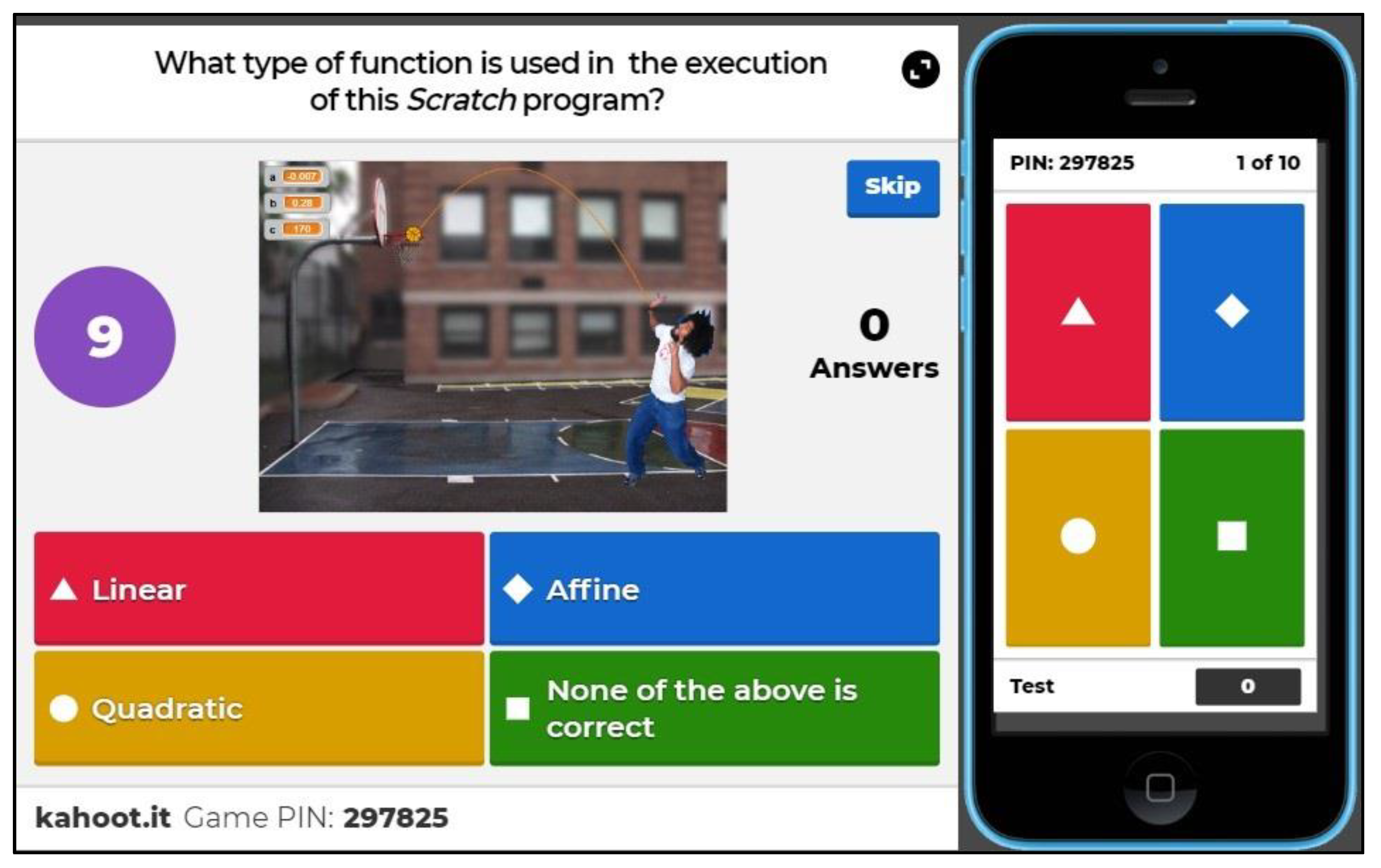
- Standardized test: At the end of the activities’ development, an individual standardized test will be proposed to the students, based on multiple choice reagents and a single closed response. It is intended to evaluate competences of understanding and application of terminology and methods and procedures, thus checking that the student has understood the activity both in its development and the related conclusions. Provided that the computer resources of the center are sufficient, a computer can be used by each student. Thus, for example, using the Kahoot! program (see example in Figure 8), reagents can be presented including images and videos if required, offering immediately the final result.
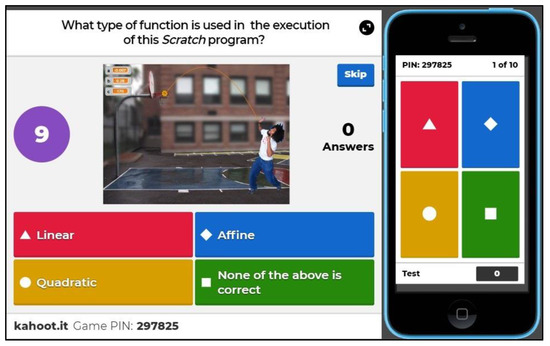 Figure 8. Question related to activities developed with Kahoot! software.
Figure 8. Question related to activities developed with Kahoot! software.
2.3.3. Assessment Types
The considered assessment types [28] are the following:
- Summative assessment: To make a decision on the qualification that the student deserves;
- Formative assessment: To determine the skills acquired by the student and help him to obtain mastery of competencies.
As a first step, an initial evaluation is proposed to determine the previous knowledge of the students. Likewise, during the development of the activities a continuous evaluation will be carried out based on the portfolio review, to conclude with a final evaluation. To sum up, a synthesis of the collection of evidence for the activities’ assessment is presented in Table 2.

Table 2.
Synthesis of evidence collection and weighted evaluation.
2.3.4. Considered Survey
After carrying out the considered activities and the assessment presented in Table 2, the survey shown in Figure 9, based on a 5-point Likert scale (1: strongly disagree; 2: disagree; 3: neither agree nor disagree; 4: agree; 5: strongly agree), was passed to the students.

Figure 9.
Proposed survey.
The survey was designed ad hoc by the authors for this research. Three key aspects related to the second research question were taken into account: the activities, the methodologies and the assessment. The questionnaire consisted of 12 questions, and since the three aspects were equally important, the same number of questions were assigned for each aspect—that is, four questions for each of the three aspects.
To validate the reliability of the survey as suitable data collecting instrument, Cronbach’s alpha method was considered, obtaining a value of 0.79. This score is assessed as adequate according to authors such as Nunnally [29], who states that a value of 0.5 or 0.6 would be sufficient for early stages of a research. Other authors, such as Huh et al. [30], consider that this reliability value should be equal or higher than 0.6 in exploratory research. Therefore, the survey used as an instrument in this paper counts on a high reliability rate.
3. Results
The survey results are presented in Table 3. The results show an average higher than 4 in all questions, highlighting the understanding of linear and affine functions (4.57) and quadratic functions (4.4) as well as the averages of activities (4.36) and assessment (4.35).

Table 3.
Survey results. Partial results for activities, methodologies and assessment together with the total are included.
The presented results show that students found the activities motivating. They understand that the combination of the proposed methodologies is an appropriate alternative to the magisterial lesson. Each theme is further analyzed in the Discussion section.
4. Discussion
In the following subsections, the results are discussed considering previous works and including the proposals for improvement commented by the students.
4.1. Activities
Students assessed activities by giving a maximum punctuation to activity 1 (average: 4.57), then activity 2 (average: 4.4) and finally activity 3 (average: 4.1). According to these results and students’ comments in the class, it seems that the first activity, based on linear and affine functions, was quite attractive to them since it was clear and simple. However, the understanding of the exponential function and the use of a recursive function to translate it into Scratch was more difficult to them and probably this is the reason of the survey result in this case. In fact, recursion and fractal thinking usually require more time and better tools, and scaffolds linking fractals and fractal thinking to the curriculum and the real world, as concluded by Lee and Jian in a recent study related to the assessment of computational thinking in Scratch fractal projects [31]. On the other hand, the modelling of the quadratic function in a context related to basketball has been also successful in the past in several scenarios, for instance, using a video of a trajectory as an initial step and concluding if it represents a parabola [32]. In our proposal, the originality of finding the required function coefficients in a Scratch environment motivated students to find not only one possible solution, but the optimum.
4.2. Methodologies
All considered methodologies were well assessed, especially highlighting gamification (average: 4.33). It is remarkable that students consider that the use of the considered methodologies is better than the magisterial lesson (average: 4.17) and that the use of Scratch is appropriate to model reality (average: 4.23). While students require the integration of active methodologies, it is important to note that there are still teachers who cling to their old magisterial lessons because they are afraid that if they abandon the teaching style that they know, they will lose control of the class. Consequently, it is key to orient the training of teachers on the positive pedagogical effects the new style would render: co-operative work and problem solving or research, among others, instead of only focusing towards the purely technical aspects [33]. Moreover, as perceived by students, Scratch is appropriate to model real-life scenarios. In fact, previous studies have shown that teachers feel that it is easy to connect programming to other teaching and learning activities in school, such as problem solving. However, sometimes there is a lack of directives for the integration, in terms of what type of programming should be implemented [34]. In this sense, it is important to know Scratch limitations and when another programming language, such as Python, should be used as an alternative.
4.3. Assessment
The different proposals included in the assessment were similarly accepted, with slight differences in the average results: 4.43 (portfolio), 4.4 (final objective assessment), 4.3 (initial objective assessment) and 4.27 (teaching observation). In this case, it is clear that the main motivation for the students is the realization of the Scratch activities which conform the portfolio. This Scratch portfolio approach was originally proposed as a possibility by Mitch Resnick and Karen Brennan. In this case, each member of the Scratch online community has a profile page. In this page, any member (scratcher) can display creations as well as other dimensions of participation, such as scratchers they follow. The teacher analyzes the portfolio of projects uploaded by a particular community member (student). This approach is specially focused on the development of computational thinking through Scratch programming activities [35]. In this sense, previous research of Permatasari et al. showed that more than 90% of learning outcomes were achieved following a portfolio assessment using a problem-based learning model with Scratch in the last cycle of the sequence. In this way, portfolio represented the main assessment tool with respect to pre-action testing and attitude observation [36].
4.4. Proposals for Improvement
The students indicated the following aspects as proposals for improvement:
- More time for its approach given the complexity of the program for some of them. It is observed that since they had not practiced before with Scratch, it was difficult to them to understand the program, which contrasts with the experience at an early age. From here, the importance of integrating programming at an early age is deduced, as with languages or any type of practical learning;
- Ask students to complete a program with Scratch, based on everything learned with these activities;
- The evaluation with Kahoot! was very well received, although it was indicated that the images shown should be highlighted to make their visualization easier.
4.5. Limitations and Future Research Lines
Although we have found interesting results, this study presents some limitations. On the one hand, the study sample is not very large. However, for a first exploratory study, it provides relevant information in the research context (Faculty of Education Sciences of the University of Las Palmas de Gran Canaria). On the other hand, the qualitative study may be enhanced considering additional instruments. Future works will extend the sample, also considering qualitative assessment instruments such as structured interviews.
Future research lines include the combination of the presented aspects with robotics, based on platforms such as Scratch for Arduino as well as the usage of other programming languages in different education levels.
5. Conclusions
The objective of this paper is to study the Scratch programming language as a didactic tool to teach functions and analyze the suitability of different methodologies to teach functions.
In this paper, we presented three innovative activities aimed at the block of functions of the subject of mathematics. The starting point was the use of Scratch software to didactically introduce the linear, affine, quadratic and exponential functions. The proposed activities were combined with active didactic methodologies in order to make the most of them, proposing at the same time a coherent assessment.
The proposed activities were introduced to a group of 30 students of the Mathematics and its Didactics I subject of the Primary Education Degree of the Faculty of Education Sciences (FCEDU) of the University of Las Palmas de Gran Canaria (ULPGC). The activities, methodologies and assessment were evaluated by these students with results higher than 4 in Likert scale for all cases, showing a preference for the proposed methods over the magisterial lesson. Students especially highlighted simple activities based on linear and affine functions as well as the use of gamification methodology and the assessment based on portfolios. Even though some students found the program complex, asking for more time to understand it, they also found it motivating, asking for additional activities on everything learned.
Author Contributions
Conceptualization, E.Q.G.; methodology, E.Q.G. and A.Z.L.; software, E.Q.G.; validation, E.Q.G. and A.Z.L.; formal analysis, E.Q.G. and A.Z.L.; investigation, E.Q.G.; resources, E.Q.G. and A.Z.L.; data curation, E.Q.G. and A.Z.L.; writing—original draft preparation, E.Q.G.; writing—review and editing, E.Q.G. and A.Z.L.; visualization, E.Q.G. and A.Z.L.; supervision, E.Q.G. and A.Z.L.; project administration, E.Q.G. and A.Z.L.; funding acquisition, E.Q.G. and A.Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available on request.
Acknowledgments
We would like to thank the group “Innovación Educativa en Diseño e Implementación de Sistemas Integrados (GIE-56)” of the University of Las Palmas de Gran Canaria and the educational innovation project “ROBOT-EDULPGC. Diseño, implementación y puesta en práctica de una plataforma modular de robótica educativa de bajo coste (PIE2020-56)” for their collaboration in this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Valovičová, L.; Ondruška, J.; Zelenický, L.; Chytrý, V.; Medová, J. Enhancing Computational Thinking through Interdisciplinary STEAM Activities Using Tablets. Mathematics 2020, 8, 2128. [Google Scholar] [CrossRef]
- Bocconi, S.; Chioccariello, A.; Dettori, G.; Ferrari, A.; Engelhardt, K. Developing Computational Thinking in Compulsory Education, Implications for Policy and Practice; Publications Office of the European Union: Luxembourg, 2016. [Google Scholar]
- Wing, J. Computational Thinking: What and Why? The Link, The magazine of Carnegie Mellon University’s School of Computer Science: Pittsburgh, PA, USA, 2010; pp. 1–6. [Google Scholar]
- Forman, G.; Pufall, P.B. Constructivism in the Computer Age; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1988. [Google Scholar]
- Papert, S.; Harel, I. Constructionism; Ablex Publishing Corporation: New York, NY, USA, 1991. [Google Scholar]
- Marji, M. Learn to Program with Scratch; No Starch Press: San Francisco, CA, USA, 2014. [Google Scholar]
- Corralero, N. Scratch. Programación fácil para educación primaria y secundaria [Easy programming for primary and secondary education]. Rev. Digit. Soc. Inf. 2011, 29, 1–10. [Google Scholar]
- Chiang, F.; Qin, L. A Pilot study to assess the impacts of game-based construction learning, using scratch, on students’ multi-step equation-solving performance. Interact. Learn. Environ. 2018, 26, 803–814. [Google Scholar] [CrossRef]
- Resnick, M.; Maloney, J.; Monroy-Hernández, A.; Rusk, N.; Eastmond, E.; Brennan, K.; Kafai, Y. Scratch: Programming for All. Commun. ACM 2009, 52, 60–67. [Google Scholar] [CrossRef]
- Vázquez-Cano, E.; Ferrer Delgado, D. La creación de videojuegos con Scratch en educación secundaria [Videogamescreation with Scratch in secondary school]. Commun. Pap. 2015, 4, 63–73. [Google Scholar] [CrossRef]
- Valle, J.E.M.; Salgado, V.C. Pensamiento lógico matemático con Scratch en nivel básico [Mathematical-logical thinking with Scratch at a basiclevel]. Vínculos 2013, 9, 87–95. [Google Scholar]
- Quevedo-Gutiérrez, E.G. Robot Position in the Cartesian Coordinate System: A Didactic Proposal. In Playing and Learning Using Robotics among University Students; Galstyan-Sargsyan, R., Belda-Torrijos, M., López-Jiménez, P.A., Pérez-Sánchez, M., Eds.; Nova Science Publishers Inc.: New York, NY, USA, 2019; pp. 61–74. [Google Scholar]
- Rodríguez-Martínez, J.A.; Rodríguez-Calero, J.A.; Saéz-López, J.M. Computational thinking and mathematics using Scratch: An experiment with 6th-grade students. Interact. Learn. Environ. 2019, 28, 316–327. [Google Scholar] [CrossRef]
- Shahbari, J.A.; Daher, W.; Baya’a, N.; Jaber, O. Prospective Teachers’ Development of Meta-Cognitive Functions in Solving Mathematical-Based Programming Problems with Scratch. Symmetry 2020, 12, 1569. [Google Scholar] [CrossRef]
- Baccaglini-Frank, A.E.; Santi, G.; Del Zozzo, A.; Frank, E. Teachers’ Perspectives on the Intertwining of Tangible and Digital Modes of Activity with a Drawing Robot for Geometry. Educ. Sci. 2020, 10, 387. [Google Scholar] [CrossRef]
- Quevedo-Gutiérrez, E.G.; Hernández, V.M.; Quevedo-Sarmiento, J.R.; Zapatera-Llinares, A. Lenguaje de Programación Scratch como Herramienta Didáctica para la Enseñanza del Sistema de Coordenadas Cartesianas en Educación Primaria [Scratch Programming Language as a Didactic Tool to Learnthe Cartesian Coordinate System in Primary School]. Form. Profr. Investig. Educ. Matemática 2017, 12, 187–202. [Google Scholar]
- Fuentes-Cabrera, A.; Parra-González, M.E.; López-Belmonte, J.; Segura-Robles, A. Learning Mathematics with Emerging Methodologies—The Escape Room as a Case Study. Mathematics 2020, 8, 1586. [Google Scholar] [CrossRef]
- Vega-Moreno, D.; Quevedo, E.; Llinás, O.; Hernández-Brito, J. Project—based learning using robots with open—source hardware and software. In Proceedings of the II Jornadas Iberoamericanas de Innovación Educativa En El Ámbito de Las TIC, Las Palmas de Gran Canaria, Spain, 12–13 November 2015; pp. 141–144. [Google Scholar]
- Ramadhan, N.; Surya, E. The Implementation of Demonstration Method to Increase Students’ Ability in Operating Multiple Numbers by using Concrete Object. Int. J. Sci. Basic Appl. Res. 2017, 34, 62–68. [Google Scholar]
- Salmerón, H.; Gutiérrez-Braojos, C.; Rodríguez, S.; Salmerón, P. Influencia del aprendizaje cooperativo en el desarrollo de la competencia para aprender a aprender en la infancia [Influence of cooperative learning in the development of the learning how to learn competence in childhood]. Rev. Esp. Orientac. Psicopedag. 2010, 21, 308–319. [Google Scholar] [CrossRef] [Green Version]
- Johnson, D.W.; Johnson, R.T. Cooperative Learning. School Improvement Programs. In A Handbook for Educational Leaders; Block, J.H., Everson, S.T., Guskey, H., Eds.; Scholastic Inc.: New York, NY, USA, 1995; pp. 25–26. [Google Scholar]
- Zichermann, G.; Cunningham, C. Gamification by Design: Implementing Game Mechanics in Web and Mobile Apps; O’Reilly Media: Cambridge, UK, 2011. [Google Scholar]
- Díez-Rioja, J.; Bañeres-Besora, D.; Serra-Vizern, M. Experiencia de gamificación en Secundaria en el Aprendizaje de Sistemas Digitales [Gamification experience in secondary school for digital systems learning]. Educ. Knowl. Soc. 2017, 18, 85–105. [Google Scholar] [CrossRef] [Green Version]
- Delgado-Gómez, D.; González-Landero, F.; Montes-Botella, C.; Sujar, A.; Bayona, S.; Martino, L. Improving the Teaching of Hypothesis Testing Using a Divide-and-Conquer Strategy and Content Exposure Control in a Gamified Environment. Mathematics 2020, 8, 2244. [Google Scholar] [CrossRef]
- Swacha, J. State of Research on Gamification in Education: A Bibliometric Survey. Educ. Sci. 2021, 11, 69. [Google Scholar] [CrossRef]
- Zamora, Á.; Ardura, D. ¿En qué medida utilizan los estudiantes de Física de Bachillerato sus propios errores para aprender? Una experiencia de autorregulación en el aula de secundaria [To what extent do high school physics students use their own mistakes to learn? An experience on self-regulation in a secondary school classroom]. Enseñanza Cienc. 2014, 32, 253–268. [Google Scholar]
- Santana, R. Situación de Aprendizaje: El Cartesiano. [Learning Situation: The Cartesian Coordinate System]. Consejería de Educación y Universidades, Gobierno de Canarias. Available online: https://www3.gobiernodecanarias.org/medusa/ecoescuela/sa/2014/09/02/el-cartesiano/ (accessed on 20 August 2021).
- Jornet-Meliá, J.M.; Martínez-Sánchez, A. Aprendizaje y Enseñanza: Aspectos Comunes a las Especialidades [Learning and Teaching: Common Aspects to Specialities]; Universidad Internacional de Valencia: Valencia, Spain, 2018. [Google Scholar]
- Nunnally, J.C. Psychometric Theory; McGraw-Hill: New York, NY, USA, 1967. [Google Scholar]
- Huh, J.; DeLorme, D.E.; Reid, L.N. Perceived third-person effects and consumer attitudes on prevetting and banning DTC advertising. J. Consum. Aff. 2006, 40, 90–116. [Google Scholar]
- Lee, C.S.; Jiang, B. Assessment of Computational Thinking (CT) in Scratch Fractal Projects: Towards CT-HCI Scaffolds for Analogical-fractal Thinking. In Proceedings of the 11th International Conference on Computer Supported Education (CSEDU), Heraklion, Crete, Greece, 2–4 May 2019; pp. 192–199. [Google Scholar]
- Schubert, M.; Ludwig, M. Modeling quadratic functions in the schoolyard. In Proceedings of the Research on Outdoor STEM Education in the digiTal Age (ROSETA), Porto, Portugal, 16–19 June 2020; pp. 155–162. [Google Scholar]
- Lara, S. Preparing Teachers and Schools for the 21st Century in the Integration of Information and Communication Technologies. Review of Recent Report in the U.S. Interact. Educ. Multimed. 2006, 12, 44–61. [Google Scholar]
- Humble, N.; Mozelius, P.; Sällvin, L. Remaking and reinforcing mathematics and technology with programming—Teacher perceptions of challenges, opportunities and tools in K-12 settings. Int. J. Inf. Learn. Technol. 2020, 37, 309–321. [Google Scholar] [CrossRef]
- Bilbao, J.; Olatz-García, C.R.; Bravo, E.; Varela, C. Different Types of Assessments for implementation of Computational Thinking. Int. J. Educ. Learn. Syst. 2018, 3, 27–31. [Google Scholar]
- Permatasari, L.; Yuana, R.A.; Maryono, D. Implementation of Scratch Application to Improve Learning Outcomes and Student Motivation on Basic Programming Subjects. J. Inform. Vocat. Educ. 2019, 2, 53–59. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).