Next Article in Journal
Introduction to Light Properties and Basic Principles of Spectroscopy at the High-School Level: A Pilot Study
Previous Article in Journal
From Hi-Tech to Hi-Touch: A Global Perspective of Design Education and Practice
Previous Article in Special Issue
In-Service and Pre-Service Science Teachers’ Enacted Pedagogical Content Knowledge about the Particulate Nature of Matter
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Education Sciences
Volume 13
Issue 3
10.3390/educsci13030315
education-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Analysis of the Relationship between Creativity in Fermi Problems Measured by Applying Information Theory, Creativity in Psychology, and Mathematical Creativity

by
Hidemichi Okamoto
1,*,
Mutfried Hartmann
1,* and
Tetsushi Kawasaki
2
1
Faculty of Natural and Social Sciences, Institute of Mathematics, University of Education Karlsruhe, 76133 Karlsruhe, Germany
2
Faculty of Education, Gifu University, Gifu 501-1112, Japan
*
Authors to whom correspondence should be addressed.
Educ. Sci. 2023, 13(3), 315; https://doi.org/10.3390/educsci13030315
Submission received: 6 February 2023 / Revised: 27 February 2023 / Accepted: 8 March 2023 / Published: 18 March 2023
(This article belongs to the Special Issue Fermi Problems in Mathematics and Science Education)
Browse Figures
Versions Notes

Abstract

:
Many educational institutions demand the development of creativity. However, it is still insufficient for encouraging creative work or thinking. One reason is the lack of simple tools to measure creativity in schools. This study focused on Fermi problems to solve the reason for this issue. Fermi problems have been suggested to be deeply related to creativity. However, few empirical studies have been conducted on their relationship. Therefore, this study conducted a survey and analyzed them by structural equation modeling. The results showed a moderate correlation between creativity in Fermi problems and creativity in psychology (r = 0.47, p < 0.01). Additionally, it was shown that there is a strong correlation between creativity in Fermi problems and mathematical creativity (r = 0.76, p < 0.01). Furthermore, regression analysis showed that creativity in Fermi problems is an important factor for measuring creativity in psychology and mathematical creativity.

1. Introduction

Creativity is considered central and essential to humans [1,2]. Therefore, it has been studied in various methods and contexts [3,4]. For example, there have been studies measuring creativity in psychology and others focusing on creativity in the specific domain of mathematics (i.e., mathematical creativity).
With the progress of such research, many educational institutions have begun to emphasize the development of creativity in schools [5,6]. Furthermore, it has been stated that creativity is an essential component in mathematical problem solving [7,8]. In addition, it has been suggested that mathematical creativity should be viewed as one sub-concept that constitutes and underlies mathematical competence [9]. In light of the above, it is reasonable to focus on the context of creativity in mathematics education as well. However, creativity is not sufficiently fostered in school mathematics education currently [10,11]. One reason for this is that schools and mathematics education tend to focus on the acquiring of mathematical knowledge and skills, and there are few simple ways to assess the abstract concept of creativity [12,13,14]. Furthermore, the lack of such evaluation tools makes it difficult to objectively assess how students’ creativity has developed. In studies measuring creativity, no consensus has been reached on the criteria for its evaluation [15,16,17]. In addition, there have been attempts to foster creativity through problem solving activities, such as mathematical modeling [8,10]. However, few empirical studies have been limited to making suggestions.
Therefore, the authors in this study focused on Fermi problems. These are real-world problems and are regarded as quick estimations that are made rationally, supplementing unclear assumptions with their own knowledge and experience [18,19,20,21,22]. Fermi problems have already been used as a practice for estimation and as a test for measuring modeling competence in schools [22,23]. Furthermore, the general Fermi problems have the advantage that they can be performed in a short time. Therefore, they could easily be used in school classes and can be considered cost-effective. Additionally, Fermi problems have consistently been shown to be deeply related to creativity in previous studies [10,24,25,26]. However, based on a few examples, most studies have been limited to assuming a strong relationship between Fermi problems and creativity. In other words, few empirical studies have analyzed the correlation between creativity in Fermi problems and other creativities.
Therefore, this study analyzed the correlations between three types of creativity: creativity in Fermi problems, creativity in psychology, and mathematical creativity. Furthermore, to solve the previously mentioned problem of the lack of consensus on evaluation criteria for measuring creativity, this study applied information theory, which has played an important role in the development of computer science [27,28,29]. Creativity in Fermi problems has been calculated, and correlation analysis has been conducted using the theory [29]. Moreover, this study analyzed whether Fermi problems can measure already established creativity (e.g., creativity in psychology) based on the results obtained from the analysis. It is critical to note that because this study focused on the relationships of creativities, mathematical ability was not considered in the survey subjects.

2. Literature Review

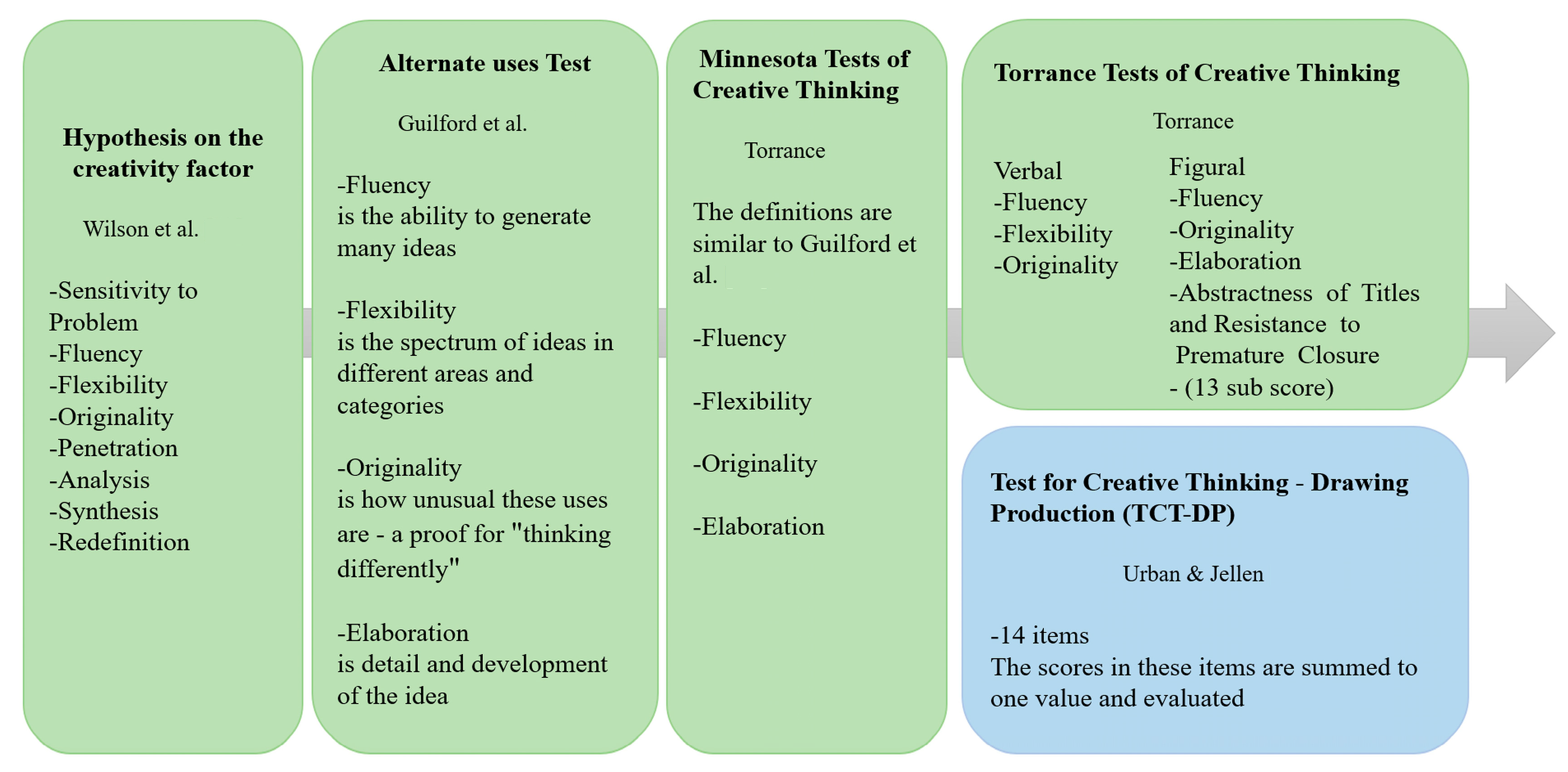
2.1. Creativity in Psychology

Creativity is diverse and does not have just one definition [30]. In support of this, Treffinger [31] collected and organized the literature on the definitions of creativity up to 2011 and found that there are more than 100 definitions. Therefore, even if the study were limited to creativity research in psychology, there are different ways of viewing and measuring creativity. The measurements of creativity continue to change and improve (see Figure 1).
For example, Wilson et al. [32] hypothesized that creativity could be divided into factors and was composed of those factors. Based on those hypotheses, Guilford et al. [33] created the Alternate Uses Test, which measures creativity by factor. This test was used to determine the following four factors: Fluency, which is the overall sum of generated uses; Originality, which is the statistical rarity of generated uses; Flexibility, which is the number of conceptual categories of generated uses; and Elaboration, which is the degree of detail [33,37]. An example of the content of this test is to think of uses for bricks (see Figure 2). Suppose the respondent considers three ideas: “building a house,” “building a wall,” and “it is used as a weapon to defeat enemies who attack suddenly.” In that case, Fluency would have 3 points. In addition, since two categories are created, build and use for weapons, Flexibility would have 2 points. Furthermore, points for Originality would be added for the idea that it is statistically rare on a relative basis. Moreover, points for Elaboration would be added for the highly detailed idea.
Torrance [34] developed the Minnesota Tests of Creative Thinking, in which four creativity factors, Fluency, Flexibility, Originality, and Elaboration, are also measured using the equally defined criteria of Guilford et al. [33]. Additionally, Torrance [35] extended these tests. The extended test is called the Torrance Test of Creative Thinking and introduced a figural and verbal test. It increased the number of creativity factors measured ([15], see Figure 1).
Several criticisms exist for the tests that attempt to measure creativity by factors [36,38,39,40]. In order to measure Originality, it has been pointed out that it is difficult to determine a cut-off point that would give a score with the occurrence rates of ideas, and a validity guarantee for the categorization of ideas. Moreover, it has been indicated that the creativity factors are related, making it challenging to view them as separate factors. For these reasons, Urban and Jellen [36,40] developed a creativity test called the Test for Creative Thinking-Drawing Production (hereinafter referred to as TCT-DP). Each of the 14 items is scored, and these scores are added to form a single value for creativity.
Additionally, several studies have criticized the factors defined by Guilford et al. [33] and Torrance [34,35]. For example, some researchers have pointed out the similarity between Fluency and Flexibility and have combined these factors into a single definition or have not considered Flexibility as a factor [8,41].
Many studies have used the occurrence rates of ideas to evaluate relative ratings [9,34,42]. However, the criteria for the cut-off points of the occurrence rates of ideas vary from study to study. Therefore, the kind of factors used in creativity tests and their definition and evaluation criteria are debatable because of their diversity.

2.2. Mathematical Creativity

There is also mathematical creativity, which focuses on the specific domain of mathematics. As with creativity in psychology, definitions of creativity vary widely. In addition, Nadjafikhah et al. [43] stated that it is difficult to define because of the complex nature of its structure and characteristics.
In light of this diversity of viewpoints, mathematical creativity has been studied from a wide range of perspectives. Sriraman [7], for example, conducted a qualitative study in which mathematicians were interviewed and their thought processes were analyzed. In contrast to such qualitative studies, there are quantitative studies that attempted to numerically measure individual mathematical creativity for students [42,44].
Some quantitative studies have analyzed the correlation between mathematical creativity and creativity in psychology, or even with mathematical competence [9,45]. These studies have revealed a link between mathematical ability and mathematical creativity, as well as between creativity in psychology and mathematical creativity. In many of those studies, creativity was viewed in terms of factors and evaluated with three creativity factors: Fluency, Flexibility, and Originality [16]. However, the measurement methods and criteria for those factors often vary from study to study. For instance, similar to the issues in creativity in psychology described above, the cut-off points for Originality are often different.

2.3. Fermi Problems

Fermi problems are named after the Italian nuclear physicist Enrico Fermi. Fermi problems are real-world problems and are regarded as quick estimations that are made rationally, supplementing unclear assumptions with their own knowledge and experience [18,19,20,21,22]. One of the most famous and typical Fermi problems is: How many piano tuners are in Chicago? [46,47] These problems have little information to solve them. Therefore, a solver has to break down a given problem into several thinkable questions to break through such unclear initial conditions [22,48].
This skill, breaking down a given problem into several thinkable questions, requires creativity [49]. Additionally, several studies stated the relationship between Fermi problems and creativity [10,24,25,26]. For example, Silver [10] suggested that solving Fermi problems promotes the development of Fluency since solvers pose problems and generate various solutions. In addition, Ärlebäck and Bergsten [25] visualized and analyzed the solution process of Fermi problems performed by high school students. They reported observing the students perform situations in the solution process in which they made estimates in a creative way based on their past experiences. Additionally, there is research on the relationship between Fermi problems and a particular creativity factor. Ferrando and Segura [50] investigated the connection between Fermi problems and Flexibility, one of the creativity factors, and found that solvers flexibly use multiple strategies for related Fermi problems and switch to another strategy depending on some contextual feature. Moreover, Author [29] analyzed the correlation between creativity in Fermi problems measured by the formula applying information theory and creativity in psychology. That study showed a moderate positive correlation between them.
However, some studies on the relationship between Fermi problems and creativity have involved only a small number of cases and not a large sample. In other words, the number of empirical studies in which the relationship between creativity in Fermi problems and other creativities has been analyzed using statistical analysis is small.

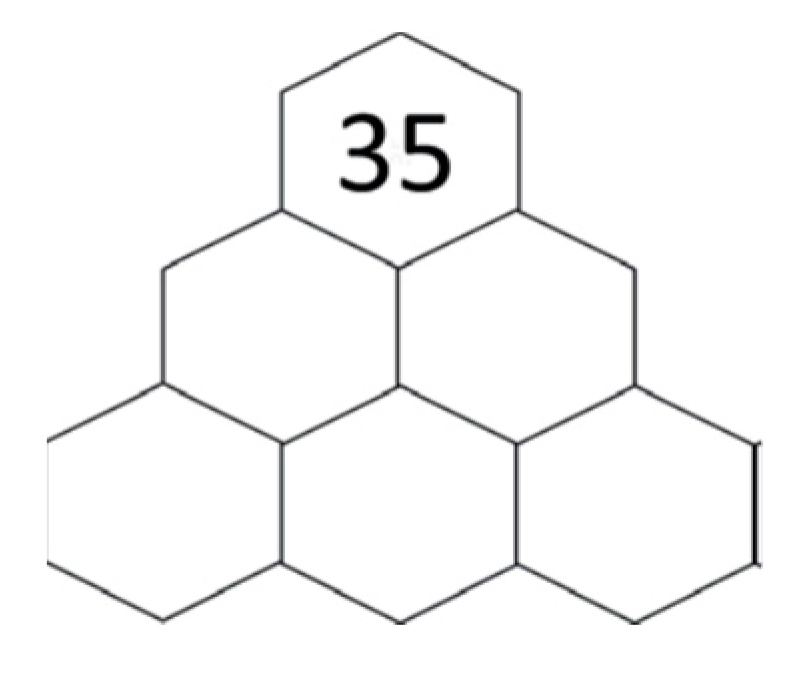
2.4. Information Theory

Information theory was proposed by Shannon [27] and Weaver [28] and has played an essential role in developing computer science and other fields. In information theory, all the different kinds of data (e.g., audio, text) are considered as information [27]. Therefore, it considers all such different kinds of data with a single measurement scale. The amount of information that one piece of information has is called self-information and is defined as follows [27,28,51]:
Let S be a system for events E1, E2, …, En, in which P(Ek) = pk with 0 ≤ pk  ≤ 1 and p₁ + p₂ + … + pn = 1.
The self-information for event Ek is written as I(Ek) and is defined as the following:
I(Ek) = −log2 pk
Several studies used this theory to measure creativity [29,52]. In particular, Author [29] applied this theory to measure creativity in Fermi problems. That study analyzed the relationship between creativity in Fermi problems and creativity in psychology measured by TCT-DP. That study proposed the following formula:
log21/P(x1) + log21/P(x2) +…+ log21/P(xn)
Each idea for solving the Fermi problem is defined as x1, x2, …, xn.
The incidence of ideas for solving the Fermi problem is defined as P(x1), P(x2), …, P(xn).
An example is considered with a Fermi problem: If you collected all the smartphones in the world, how many would there be? A subject considered where the smartphones were located. The subject thought of it as “company,” “smartphone store,” and “factory.” The incidence of “company” is 80%, the incidence of “smartphone store” is 70%, and the incidence of “factory” is 20%. The result for the subject is calculated as follows: x1 is “company.” x2 is “smartphone store.” x3 is “factory.”
log21/0.8 + log21/0.7 + log21/0.2
=0.32… + 0.51… + 2.32…
≈3.14
Hence, the subject’s creativity is 3.14 with Formula (2). As can be observed from the calculation, the lower the rate of occurrence of an idea, the higher the value. In information theory, information that is less likely to occur probabilistically is defined as having higher value, similar to the concept of Originality (see Figure 1 and Figure 2). Additionally, there is no need to set a cut-off point for evaluating Originality. Furthermore, this theory is applied because ideas for solving Fermi problems might also be considered as one type of information. In other words, the number of xn could be considered as Fluency in Fermi problems. P(xn) could be considered as Originality in Fermi problems. Thus, Formula (2) integrates Fluency in Fermi problems, which is evaluated based on the number of ideas to solve it, and Originality in Fermi problems, which is evaluated based on the probabilistic rarity of the ideas, evaluated as a single value.
However, Author’s [29] study was limited to a sample of one school. Therefore, this study used a more diverse sample to examine whether Formula (2) works. Furthermore, by conducting a regression analysis, which was not done in that study, this study explored whether it is possible to measure already established creativity (e.g., mathematical creativity) using Fermi problems.

3. Research Questions

1. Can we construct a good model among creativity in Fermi problems, evaluated using the formula applying information theory, creativity in psychology, and mathematical creativity?
2. Is it possible to measure creativity in psychology and mathematical creativity by Fermi problems?

4. Methodology

4.1. Participants

Table 1 shows the students who participated in this survey. They were from four schools.
This survey had 457 participants. Most of the students had no experience with Fermi problems because they were hardly used in the classroom. It was determined that the impact of having little experience with Fermi problems should not be considered, because the number of students with little experience was relatively small. In this study, the models considered in the analysis using structural equation modeling are five latent and thirteen observed variables. An a-priori sample size calculator for structural equation modeling indicated that the analysis required a sample size of at least 268 [53].

4.2. Implement

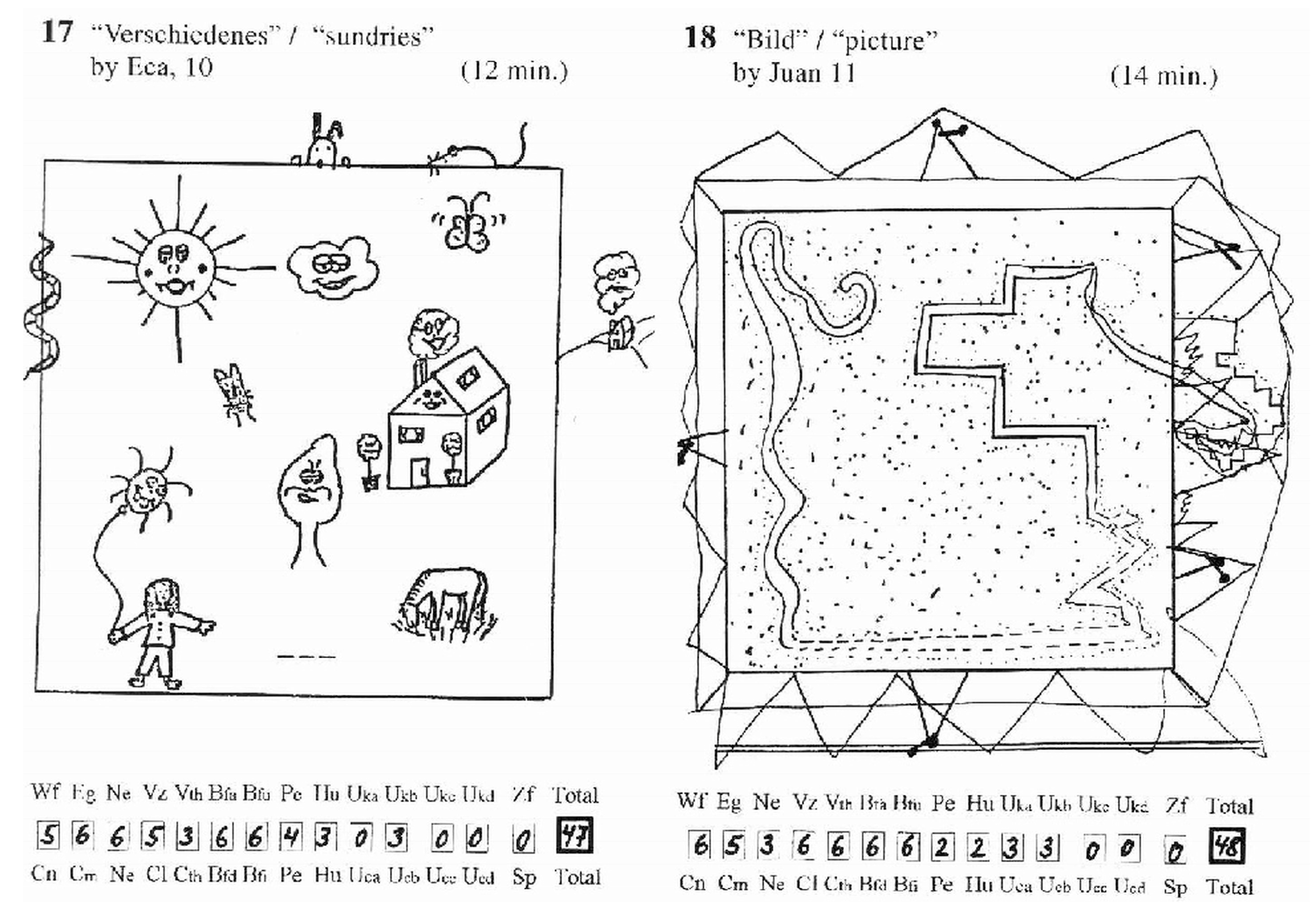
4.2.1. Test for Creative Thinking-Drawing Production (TCT-DP)

TCT-DP was created by Urban and Jellen [36] to measure creativity. In this test, the subject adds more figures to an incomplete picture and titles it (see Figure 3). First, the picture is evaluated on 14 items. The total of these scores is then used as the creativity score. TCT-DP is appropriate inter-rater reliability, with α = 0.81–0.99 for the total score and α ≥ 0.89 for the test criteria [36]. This study used this test for measuring creativity in psychology. In this test, subjects are evaluated on the number of new diagrams they add and how they draw, as well as other factors. This survey was evaluated based on the manual by Urban and Jellen [40].

4.2.2. Mathematical Creativity Test

This study adopted the mathematical creativity tests that were used in previous studies [9,42,54]. The evaluation methods in this study were directly adapted from those in the respective literature. Those tests have three creativity factors: Fluency (number of correct solutions), Flexibility (number of different categories of correct solutions), and Originality (the cut-off point is set, and the rarer the answer, the higher the score). The following tests were included in this survey:
  • Mathematical Creativity Test 1 [42]:
Subjects were presented with Figure 4, which showed polygons and diagonal lines drawn within it. Afterward, they were asked to predict and answer what happens when the number of sides of the polygon increases.
  • Mathematical Creativity Test 2 [9]:
The numbers are placed one by one in the hexagons of the pyramid. Each number in the pyramid can be calculated by always performing the same operation on the two numbers displayed below it. Subjects were asked to place a number in the pyramid in Figure 5 and answer as many as possible.
  • Mathematical Creativity Test 3 [54]:
Subjects were given a 5 cm × 5 cm square figure. They were asked to divide the square into five parts and to draw lines so that they all have the same area (5 cm2). Subjects were required to answer as many as possible ways to draw the line.

4.2.3. Fermi Problems Test

The following three Fermi problems were used in this survey [17,29]:
  • Fermi problem 1: How many liters of water does one person use in a year?
  • Fermi problem 2: If you collected all the smartphones in the world, how many would there be?
  • Fermi problem 3: If you collected all the cars in your country, how many would there be? Think of as many ways as you can to find out how many cars there are. Write down as many ways as you can to find out how many cars there are, and write them down in as much detail as you can, using sentences, formulas, and diagrams. You do not have to calculate how many cars there are in your country.
Creativity in Fermi problems in this study is calculated in the same way as was done by Author [29] (see Information Theory of the section in Literature Review).

4.3. Procedure of Survey

All tests were given in classrooms during regular class times. Students first took the Fermi problem test. Afterward, they conducted the Mathematical Creativity Test. Students subsequently performed TCT-DP. The explanation that the results would not influence their school grades allowed the participants to take the tests without stress. This survey was supervised by two teachers in the classroom. The subjects answered all survey problems individually.

4.4. Hypothesis Model for the Analysis

This study analyzed the following three hypothetical models with structural equation modeling. These hypothetical models were proposed based on previous studies [17,29,45,55]. Hypothetical Model 1 is a model that represents the correlation between creativity in Fermi problems, creativity in psychology measured by TCT-DP, and mathematical creativity (see Figure 6). Hypothetical Model 1 was designed to examine research question 1. Hypothetical Model 2 is a model of regression analysis with creativity in psychology as measured by the TCT-DP as the dependent variable and creativity in Fermi problems and mathematical creativity as independent variables. Hypothetical Model 3 is a model of regression analysis with mathematical creativity as the dependent variable and creativity in Fermi problems and creativity in psychology measured by TCT-DP as independent variables. Hypothetical Models 2 and 3 were designed to examine research question 2.

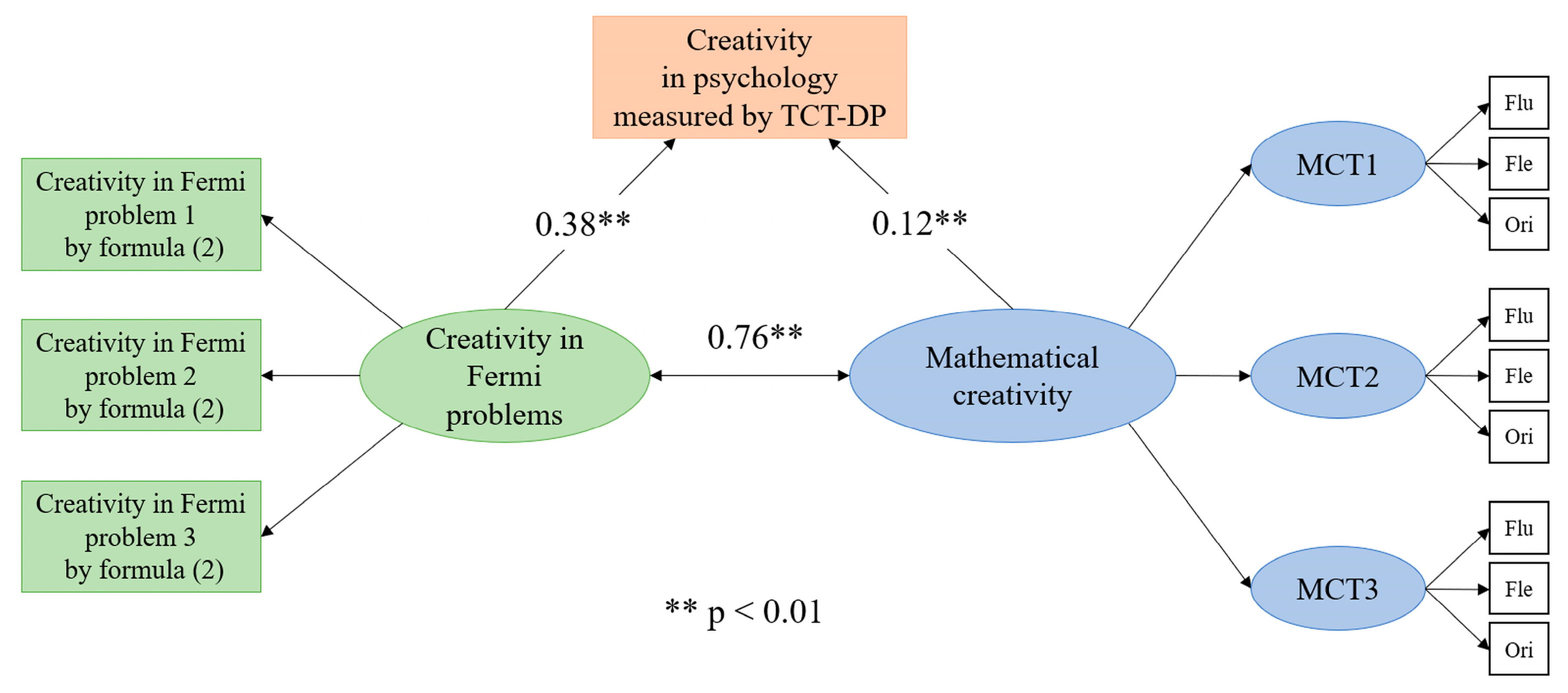
5. Results

The structural equation modeling analysis results determined that the three hypothetical models were acceptable (see Table 2). Below are the results for each index.
The chi-square test showed a significant difference in the models. The null hypothesis is frequently rejected in the chi-square test of exact fit, especially for large samples. Normally, it is preferred that the null hypothesis is not rejected; however, it was rejected in all models, probably because of the sample size [56]. All indicators were found to be good except the chi-square test [57,58,59].
Subsequently, the correlation and regression coefficients in each model are shown using Figure 7, Figure 8 and Figure 9. The cut-off point for determining the strength of the correlation coefficient in this study was the one used by Döring and Bortz [60].
There was a strong positive correlation between creativity in Fermi problems and mathematical creativity (r = 0.76, p < 0.01). Moderate correlations were also found between creativity in Fermi problems and creativity in psychology and between mathematical creativity and creativity in psychology (r = 0.47, p < 0.01; r = 0.41, p < 0.01).
Furthermore, using creativity in psychology as the dependent variable, creativity in Fermi problems had a larger regression coefficient than that of mathematical creativity (see Figure 8). Similarly, using mathematical creativity as the dependent variable, creativity in Fermi problems had a larger regression coefficient than that of creativity in psychology (see Figure 9).

6. Discussion

Firstly, research question 1 was considered. This study’s analysis allows us to say that creativity in Fermi problems, evaluated using the formula that applies information theory, could construct a relevant model that is good for creativity in psychology and mathematical creativity. Formula (2) does not need a cut-off point because it uses relative probabilities. Therefore, it potentially solves the cut-off point issue in creativity research. This study used a more diverse and larger sample than the one used by Author [29]. This may have increased the validity of Formula (2) based on the application of information theory. Furthermore, this study was able to construct models that included mathematical creativity, which was not addressed by Author [29]. In other words, we were able to extend the relevant model.
Subsequently, research question 2 was considered. Creativity in Fermi problems was found to be a relatively strong factor in predicting established creativities (i.e., creativity in psychology and mathematical creativity). Furthermore, when creativity in psychology and mathematical creativity were treated as independent variables, their impact on the dependent variable was not shown to be significant. For example, when mathematical creativity was treated as the dependent variable, the regression coefficient for creativity in psychology was 0.07. Therefore, it had little impact. A similar situation was the case with creativity in psychology as the dependent variable. Hence, using Fermi problems to measure creativity in psychology and mathematical creativity seems to be more effective.
In addition, when the results of the three hypothetical models are viewed comprehensively, it is suggested that creativity in Fermi problems is a kind of intermediary between the other two types of creativity. In the regression analysis results, when creativity in psychology and mathematical creativity were treated as independent variables, they were weak factors to each other. However, the correlation coefficients between creativity in psychology and mathematical creativity were moderately positive. This result suggests that creativity in Fermi problems may have influenced the correlation between those two creativities. It is possible to consider that the characteristics of Fermi problems caused this influence. Fermi problems require the transformation or decomposition of an initial problem into a solvable problem. The solvers need to consider various possibilities and generate ideas. This activity is seen as an essential process in creativity. Furthermore, Fermi problems are used as estimation and modeling problems in mathematics education. In other words, the characteristics of Fermi problems could be considered connected to both creativity in psychology and mathematical creativity.
Furthermore, the results of the analysis are discussed from an educational perspective. As mentioned earlier, one of the reasons why creativity is not sufficiently fostered in mathematics education is that there are few simple ways to measure established creativities (e.g., creativity in psychology). This study showed that Fermi problems could be used to measure creativity. Therefore, Fermi problems, which are already used in educational settings and can be performed in a short time, could be one of the tools used to measure creativity in schools in a simplified way.
In summary, while there are few empirical studies on the relationship between Fermi problems and creativity, this study provided several insights. However, this study had limitations. As noted in the literature review, there are various ways to measure creativity in psychology. Therefore, analyses using creativity tests not used in this study may lead to different results. For example, there are creativity tests in psychology that focus on linguistic ability, such as finding commonalities among several words. If the results of such creativity tests are used, it is conceivable that the results would differ from the results of this study because of the influence of language ability. Additionally, when measuring creativity in Fermi problems, our analysis did not include in its evaluation perspectives that are likely to be influenced by mathematical ability, such as the correctness of mathematical processing or what formulas were used. Therefore, this study did not consider influences related to mathematical ability. Previous studies have shown a correlation between mathematical creativity and mathematical ability [9,42]. Furthermore, since Fermi problems are treated as mathematical estimation problems, it is impossible to say that mathematical ability is not influenced completely. Therefore, the following formula, which also considers mathematical abilities, needs to be considered:
log21/P(x1) + log21/P(x2) +…+ log21/P(xn) × (Mathematical ability: 0.5/1.0/2.0)
Each idea for solving the Fermi problem is defined as x1, x2, …, xn.
The incidence of ideas for solving the Fermi problem is defined as P(x1), P(x2), …, P(xn). Mathematical ability is evaluated on a three-level scale (e.g., low, medium, and high). The numbers correspond, for example, to 0.5 for the low level, 1.0 for the medium level, and 2.0 for the high level.
One possible approach would be to evaluate this mathematical ability based on the correctness of the calculations and the level of the formula used, and to multiply it by Formula (2) as used in this study. In addition, Segura and Ferrando [61] identified and classified the types of errors that appear when solving Fermi problems. Establishing the level of correctness of the solution through the analysis of errors, such as their study, would improve the quality and validity of the formulas presented above.
As a future perspective, it will be examined whether similar results can be obtained when different creativity tests are used. This is because, as noted above, the tests measuring creativity used in this study are only one part of several tests. In addition, an analysis of related models that also include mathematical ability will be conducted and examined using the new extended formula, considering the correctness of the calculations and the mathematical skills used. Furthermore, the potential impact of creativity in Fermi problems on established creativity shown by this study makes it worthwhile to conduct further research on the use of Fermi problems to foster creativity. For example, a possible research design could divide the group into two groups, one with and one without Fermi problem activities, and conduct a longitudinal analysis using a growth curve model. We expect that the above research could contribute to the cultivation of creativity in students.

Author Contributions

Conceptualization, H.O.; Methodology, H.O.; Formal analysis, H.O.; Investigation, H.O.; Resources, M.H.; Data curation, H.O.; Writing—original draft, H.O.; Writing—review & editing, M.H. and T.K.; Visualization, H.O.; Supervision, M.H.; Funding acquisition, M.H. All authors have read and agreed to the published version of the manuscript.

Funding

The article processing charge was funded by the Baden-Württemberg Ministry of Science, Research and Culture and the University of Education Karlsruhe in the funding programme Open Access Publishing.

Institutional Review Board Statement

Participation was anonymous, i.e., all data were collected and analyzed anonymously. All study participants were informed about the scientific purpose of the study and informed consent was obtained from all participants. Verbal permission was obtained from all school directors of participants. Ethical review and approval were waived for this study due to all the above measures in the implementation.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Runco, M.A. Creativity: Theories and Themes: Research, Development, and Practice; Elsevier Academic Press: Burlington, MA, USA; London, UK, 2007. [Google Scholar]
  2. Picciuto, E.; Carruthers, P. The Origins of Creativity. Philos. Creat. 2014, 199, 199–223. [Google Scholar] [CrossRef] [Green Version]
  3. Rhodes, M. An Analysis of Creativity. Phi Delta Kappan 1961, 42, 305–310. [Google Scholar]
  4. Shimizu, D. Introduction of Review Articles about Approaches and Measurements in Studying Creativity. Cogn. Stud. 2019, 26, 283–290. [Google Scholar] [CrossRef]
  5. Piirto, J. Creativity for 21st Century Skills; SensePublishers: Rotterdam, The Netherlands, 2011; pp. 1–12. [Google Scholar] [CrossRef]
  6. Publications Office of the European Union. Key Competences for Lifelong Learning. Available online: https://op.europa.eu/en/publication-detail/-/publication/297a33c8-a1f3-11e9-9d01-01aa75ed71a1/language-en (accessed on 15 December 2022).
  7. Sriraman, B. The Characteristics of Mathematical Creativity. Math. Educ. 2004, 14, 19–34. [Google Scholar] [CrossRef] [Green Version]
  8. Lu, X.; Kaiser, G. Creativity in Students’ Modelling Competencies: Conceptualisation and Measurement. Educ. Stud. Math. 2022, 109, 287–311. [Google Scholar] [CrossRef]
  9. Kattou, M.; Kontoyianni, K.; Pitta-Pantazi, D.; Christou, C. Connecting Mathematical Creativity to Mathematical Ability. ZDM 2013, 45, 167–181. [Google Scholar] [CrossRef]
  10. Silver, E.A. Fostering Creativity through Instruction Rich in Mathematical Problem Solving and Problem Posing. ZDM 1997, 29, 75–80. [Google Scholar] [CrossRef]
  11. Thohari, C.A.F.; Budiyono; Pratiwi, H. Students’ Creativity Level on Solving Mathematics Problem. J. Phys. Conf. Ser. 2020, 1613, 012051. [Google Scholar] [CrossRef]
  12. Chamberlin, S.A.; Moon, S.M. Model-Eliciting Activities as a Tool to Develop and Identify Creatively Gifted Mathematicians. J. Second. Gift. Educ. 2005, 17, 37–47. [Google Scholar] [CrossRef]
  13. Shriki, A. Working like Real Mathematicians: Developing Prospective Teachers’ Awareness of Mathematical Creativity through Generating New Concepts. Educ. Stud. Math. 2010, 73, 159–179. [Google Scholar] [CrossRef]
  14. Shriki, A. A Model for Assessing the Development of Students’ Creativity in the Context of Problem Posing. Creat. Educ. 2013, 4, 430–439. [Google Scholar] [CrossRef] [Green Version]
  15. Kim, K.H. Can We Trust Creativity Tests? A Review of the Torrance Tests of Creative Thinking (TTCT). Creat. Res. J. 2006, 18, 3–14. [Google Scholar] [CrossRef]
  16. Pitta-Pantazi, D.; Kattou, M.; Christou, C. Mathematical Creativity: Product, Person, Process and Press. In Mathematical Creativity and Mathematical Giftedness: Enhancing Creative Capacities in Mathematically Promising Students; Singer, F.M., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 27–53. [Google Scholar] [CrossRef]
  17. Okamoto, H. Analysis of the Model Relating Creativity in Fermi Problems and General Creativity in Psychology and Mathematical Creativity. Int. J. Educ. Res. 2022, 10, 8. [Google Scholar]
  18. Morrison, P. Fermi Questions. Am. J. Phys. 1963, 31, 626–627. [Google Scholar] [CrossRef]
  19. Carlson, J.E. Fermi Problems on Gasoline Consumption. Phys. Teach. 1997, 35, 308–309. [Google Scholar] [CrossRef]
  20. Ärlebäck, J.B. On the use of realistic Fermi problems for introducing mathematical modelling in school. Math. Enthus. 2009, 6, 331–364. [Google Scholar] [CrossRef]
  21. Ärlebäck, J.B.; Albarracín, L. The Use and Potential of Fermi Problems in the STEM Disciplines to Support the Development of Twenty-First Century Competencies. ZDM 2019, 51, 979–990. [Google Scholar] [CrossRef] [Green Version]
  22. Greefrath, G.; Frenken, L. Fermi Problems in Standardized Assessment in Grade 8. Quadrante 2021, 30, 52–73. [Google Scholar] [CrossRef]
  23. Baum, M.; Bellstedt, M.; Buck, H.; Dürr, R.; Freudigmann, H.; Haug, F.; Hußmann, S.; Jürgensen, T.; Leuders, T.; Richter, K.; et al. Lambacher Schweizer 5 Mathematik für Gymnasien; Ernst Klett Verlag GmbH: Stuttgart, Germany, 2007. [Google Scholar]
  24. Goel, P.S.; Singh, N. Creativity and Innovation in Durable Product Development. Comput. Ind. Eng. 1998, 35, 5–8. [Google Scholar] [CrossRef]
  25. Ärlebäck, J.B.; Bergsten, C. On the Use of Realistic Fermi Problems in Introducing Mathematical Modelling in Upper Secondary Mathematics. In Modeling Students’ Mathematical Modeling Competencies: ICTMA 13; Lesh, R., Galbraith, P.L., Haines, C.R., Hurford, A., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 597–609. [Google Scholar] [CrossRef]
  26. Hartmann, M.; Borys, T.; Kawasaki, T.; Okamoto, H. Observing Creative Characteristics in Solving Fermi-Tasks by the Modelling and Creating Activity Diagram. In Proceedings of the 2019 International Joint Conference on Information, Media and Engineering, Osaka, Japan, 17–19 December 2019; pp. 97–100. [Google Scholar]
  27. Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
  28. Weaver, W. Recent Contributions to the Mathematical Theory of Communication. 1949. Available online: http://waste.informatik.hu-berlin.de/Lehre/ss11/SE_Kybernetik/reader/weaver.pdf (accessed on 10 November 2022).
  29. Okamoto, H. Measuring Creativity in the Fermi Problem, a Type of Mathematical Modelling, Applying Information Theory. J. Educ. Technol. Dev. Exch. 2022, 15, 1. [Google Scholar] [CrossRef]
  30. Runco, M.A. Creativity: Theories and Themes: Research, Development, and Practice, 2nd ed.; Academic Press: San Diego, CA, USA, 2014. [Google Scholar]
  31. Treffinger, D.J. Creativity, Creative Thinking, and Critical Thinking: In Search of Definitions; Center for Creative Learning Inc.: Sarasota, FL, USA, 2011. [Google Scholar]
  32. Wilson, R.C.; Guilford, J.P.; Christensen, P.R.; Lewis, D.J. A Factor-Analytic Study of Creative-Thinking Abilities. Psychometrika 1954, 19, 297–311. [Google Scholar] [CrossRef]
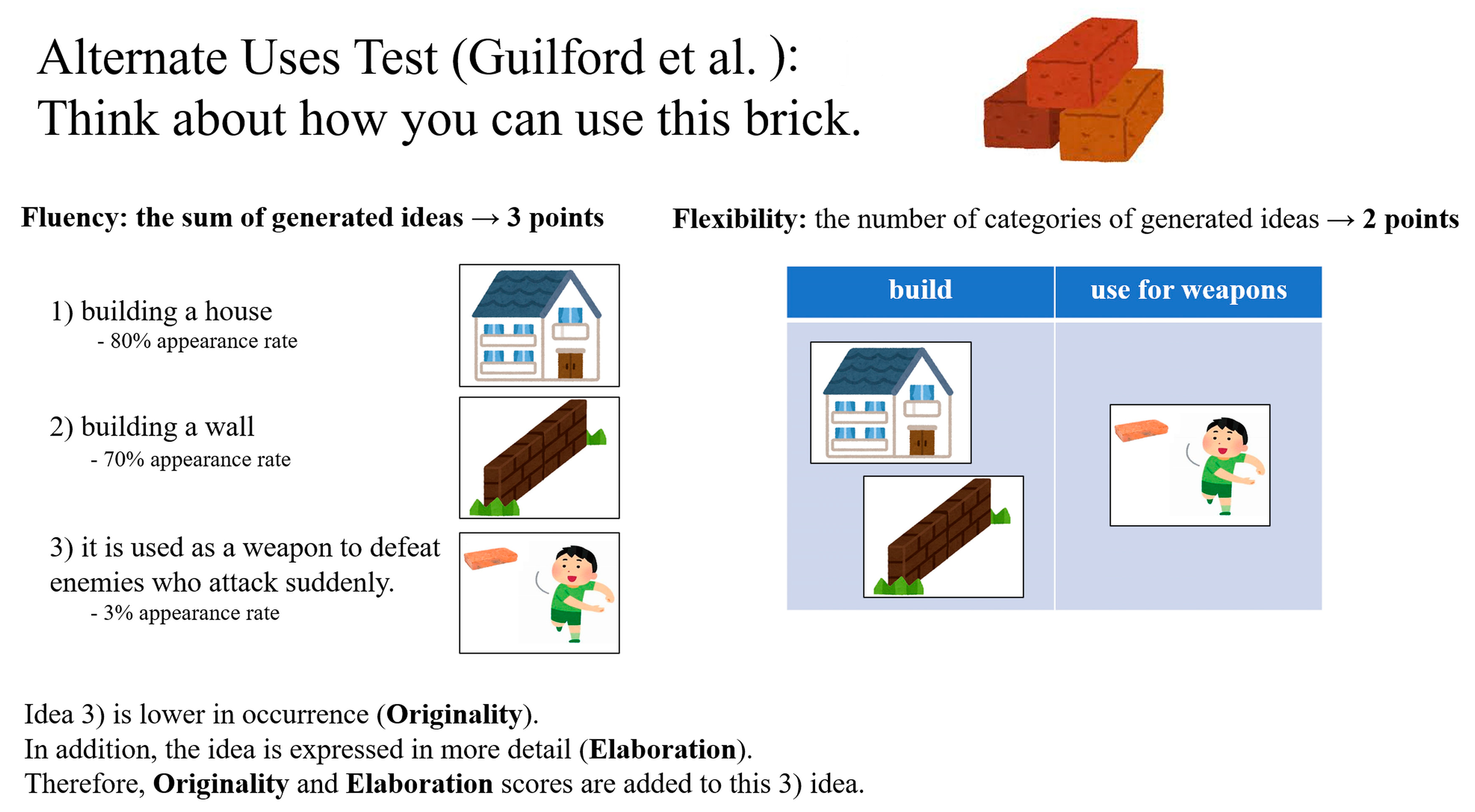
  33. Guilford, J.P.; Christensen, P.R.; Merrifield, P.R.; Wilson, R.C. Alternate Uses: Manual of Instructions and Interpretation; Sheridan Psychological Services: Orange, CA, USA, 1960. [Google Scholar]
  34. Torrance, E.P. Administration and Scoring Manual for Abbreviated form Ⅶ Minnesota Tests of Creative Thinking; University of Minnesota: Minneapolis, MI, USA, 1963. [Google Scholar]
  35. Torrance, E.P. The Torrance Tests of Creative Thinking–Norms: Technical Manual Research Edition—Verbal Tests, Forms A and B—Figural Tests, Forms A and B; Personnel Press: Princeton, NJ, USA, 1966. [Google Scholar]
  36. Urban, K.K.; Jellen, H.G. Test for Creative Thinking—Drawing Production; Swets Test Services: Frankfurt, Germany, 1996. [Google Scholar]
  37. Vartanian, O.; Smith, I.; Lam, T.K.; King, K.; Lam, Q.; Beatty, E.L. The Relationship between Methods of Scoring the Alternate Uses Task and the Neural Correlates of Divergent Thinking: Evidence from Voxel-Based Morphometry. NeuroImage 2020, 223, 117325. [Google Scholar] [CrossRef] [PubMed]
  38. Kratzmeier, H. Heidelberger Intelligenztest. HIT 1–2; Beltz: Weinheim, Germany, 1977. [Google Scholar]
  39. Urban, K.K. Assessing creativity: The test for creative thinking-drawing production (TCT-DP) the concept, application, evaluation, and international studies. Psychol. Sci. 2004, 46, 387–397. [Google Scholar]
  40. Urban, K.K.; Jellen, H.G. Test for Creative Thinking—Drawing Production, 2nd ed.; Pearson Assessment & Information GmbH: Frankfurt, Germany, 2010. [Google Scholar]
  41. Hébert, T.P.; Cramond, B.; Spiers Neumeister, K.L.; Millar, G.; Silvian, A.F.E. Paul Torrance: His Life, Accomplishments, and Legacy; University of Connecticut: Storrs, CT, USA, 2002. [Google Scholar]
  42. Mann, E.L. Mathematical Creativity and School Mathematics: Indicators of Mathematical Creativity in Middle School Students. Ph.D. Thesis, University of Connecticut, Storrs, CT, USA, 2005. [Google Scholar]
  43. Nadjafikhah, M.; Yaftian, N.; Bakhshalizadeh, S. Mathematical Creativity: Some Definitions and Characteristics. Procedia-Soc. Behav. Sci. 2012, 31, 285–291. [Google Scholar] [CrossRef] [Green Version]
  44. Balka, D.S. Using Research in Teaching: Creative Ability in Mathematics. Arith. Teach. 1974, 21, 633–636. [Google Scholar] [CrossRef]
  45. Kattou, M.; Christou, C.; Pitta-Pantazi, D. Mathematical creativity or general creativity? In Proceedings of the 9th Congress of European Research in Mathematics Education, Prague, Czech Republic, 4–8 February 2015; Krainer, K., Vondrová, N., Eds.; Charles University in Prague: Prague, Czech Republic, 2015; pp. 1016–1023. [Google Scholar]
  46. Peter-Koop, A. Fermi problems in primary mathematics classrooms: Pupils’ Interactive modelling processes. In Proceedings of the 27th annual conference of the Mathematics Education Research Group of Australasia (MERGA), Townsville, Sydney, 27–30 June 2004; Putt, I., Faragher, R., McLean, M., Mathematics Education Research Group of Australasia, Eds.; Melbourne University: Melbourne, Australia, 2004; pp. 454–461. [Google Scholar]
  47. Ärlebäck, J.B.; Albarracín, L. Developing a Classification Scheme of Definitions of Fermi Problems in Education from a Modelling Perspective. In Proceedings of the Tenth Congress of European Research in Mathematics Education, Dublin, Ireland, 1–5 February 2017; Dooley, T., Gueudet., G., Eds.; DCU Institute of Education and ERME: Dublin, Ireland, 2017; pp. 884–891. [Google Scholar]
  48. Albarracín, L.; Gorgorió, N. Devising a Plan to Solve Fermi Problems Involving Large Numbers. Educ. Stud. Math. 2014, 86, 79–96. [Google Scholar] [CrossRef]
  49. Helps, C.R.; Lunt, B. Problem Solving in Engineering: Creativity, Estimation and Critical Thinking are Essential Skills. In Proceedings of the 2001 Annual Conference Proceedings, Albuquerque, New Mexico, 24–27 June 2001; ASEE Conferences: Albuquerque, NM, USA, 2001; pp. 6.808.1–6.808.8. [Google Scholar] [CrossRef]
  50. Ferrando, I.; Segura, C. Fomento de La Flexibilidad Matemática a Través de Una Secuencia de Tareas de Modelización. Av. De Investig. En Educ. Matemática 2020, 17, 84–97. [Google Scholar] [CrossRef]
  51. Jones, D.S. Elementary Information Theory; Oxford University Press: New York, NY, USA, 1979. [Google Scholar]
  52. Snyder, A.; Mitchell, J.; Bossomaier, T.; Pallier, G. The Creativity Quotient: An Objective Scoring of Ideational Fluency. Creat. Res. J. 2004, 16, 415–419. [Google Scholar] [CrossRef]
  53. Sloper, D.S. A-Priori Sample Size Calculator for Structural Equation Models. Available online: http://www.danielsoper.com/statcalc (accessed on 10 November 2022).
  54. Pitta-Pantazi, D.; Sophocleous, P.; Christou, C. Spatial Visualizers, Object Visualizers and Verbalizers: Their Mathematical Creative Abilities. ZDM 2013, 45, 199–213. [Google Scholar] [CrossRef]
  55. Schoevers, E.M.; Kroesbergen, E.H.; Kattou, M. Mathematical Creativity: A Combination of Domain-General Creative and Domain-Specific Mathematical Skills. J. Creat. Behav. 2020, 54, 242–252. [Google Scholar] [CrossRef] [Green Version]
  56. Shi, D.; Lee, T.; Maydeu-Olivares, A. Understanding the Model Size Effect on SEM Fit Indices. Educ. Psychol. Meas. 2019, 79, 310–334. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  57. West, R.F.; Meserve, R.J.; Stanovich, K.E. Cognitive Sophistication Does Not Attenuate the Bias Blind Spot. J. Personal. Soc. Psychol. 2012, 103, 506–519. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  58. MacCallum, R.C.; Browne, M.W.; Sugawara, H.M. Power Analysis and Determination of Sample Size for Covariance Structure Modeling. Psychol. Methods 1996, 1, 130–149. [Google Scholar] [CrossRef]
  59. Hu, L.; Bentler, P.M. Cutoff Criteria for Fit Indexes in Covariance Structure Analysis: Conventional Criteria versus New Alternatives. Struct. Equ. Model. A Multidiscip. J. 1999, 6, 1–55. [Google Scholar] [CrossRef]
  60. Döring, N.; Bortz, J. Forschungsmethoden und Evaluation in Den Sozial- und Humanwissenschaften; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
  61. Segura, C.; Ferrando, I. Classification and Analysis of Pre-Service Teachers’ Errors in Solving Fermi Problems. Educ. Sci. 2021, 11, 451. [Google Scholar] [CrossRef]
Education 13 00315 g001 550
Figure 1. Overview of the transition of the test of creativity [32,33,34,35,36].
Figure 1. Overview of the transition of the test of creativity [32,33,34,35,36].
Education 13 00315 g001
Education 13 00315 g002 550
Figure 2. Example of the Alternate Uses Test [33].
Figure 2. Example of the Alternate Uses Test [33].
Education 13 00315 g002
Education 13 00315 g003 550
Figure 3. Some examples of answers for TCT-DP [39].
Figure 3. Some examples of answers for TCT-DP [39].
Education 13 00315 g003
Education 13 00315 g004 550
Figure 4. Figure for Mathematical Creativity Test 1.
Figure 4. Figure for Mathematical Creativity Test 1.
Education 13 00315 g004
Education 13 00315 g005 550
Figure 5. Figure for Mathematical Creativity Test 2.
Figure 5. Figure for Mathematical Creativity Test 2.
Education 13 00315 g005
Education 13 00315 g006 550
Figure 6. Hypothetical Model 1. Note: MCT1 represents the creativity of mathematical creativity test 1, Flu represents Fluency, Fle represents Flexibility, and Ori represents Originality.
Figure 6. Hypothetical Model 1. Note: MCT1 represents the creativity of mathematical creativity test 1, Flu represents Fluency, Fle represents Flexibility, and Ori represents Originality.
Education 13 00315 g006
Education 13 00315 g007 550
Figure 7. Analysis result of the Hypothetical Model 1.
Figure 7. Analysis result of the Hypothetical Model 1.
Education 13 00315 g007
Education 13 00315 g008 550
Figure 8. Analysis result of the Hypothetical Model 2.
Figure 8. Analysis result of the Hypothetical Model 2.
Education 13 00315 g008
Education 13 00315 g009 550
Figure 9. Analysis result of the Hypothetical Model 3.
Figure 9. Analysis result of the Hypothetical Model 3.
Education 13 00315 g009
Table
Table 1. Table of information about schools that participated in this survey.
Table 1. Table of information about schools that participated in this survey.
Country, AreaRange of AgesThe Number of Participants
School AJapan, Gifu12–14N = 149
School BJapan, Gifu13–14N = 223
School CGermany,
Baden-Württemberg		12–13N = 45
School DGermany,
Baden-Württemberg		13–14N = 40
Table
Table 2. Results for the model fitness index of hypothetical models.
Table 2. Results for the model fitness index of hypothetical models.
IndexHypothetical Models 1, 2, and 3
p0.00
χ2189.36
df62.00
CFI0.97
RMSEA0.06
SRMR0.05
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Okamoto, H.; Hartmann, M.; Kawasaki, T. Analysis of the Relationship between Creativity in Fermi Problems Measured by Applying Information Theory, Creativity in Psychology, and Mathematical Creativity. Educ. Sci. 2023, 13, 315. https://doi.org/10.3390/educsci13030315

AMA Style

Okamoto H, Hartmann M, Kawasaki T. Analysis of the Relationship between Creativity in Fermi Problems Measured by Applying Information Theory, Creativity in Psychology, and Mathematical Creativity. Education Sciences. 2023; 13(3):315. https://doi.org/10.3390/educsci13030315

Chicago/Turabian Style

Okamoto, Hidemichi, Mutfried Hartmann, and Tetsushi Kawasaki. 2023. "Analysis of the Relationship between Creativity in Fermi Problems Measured by Applying Information Theory, Creativity in Psychology, and Mathematical Creativity" Education Sciences 13, no. 3: 315. https://doi.org/10.3390/educsci13030315

APA Style

Okamoto, H., Hartmann, M., & Kawasaki, T. (2023). Analysis of the Relationship between Creativity in Fermi Problems Measured by Applying Information Theory, Creativity in Psychology, and Mathematical Creativity. Education Sciences, 13(3), 315. https://doi.org/10.3390/educsci13030315

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop