Game On: A Journey into Computational Thinking with Modern Board Games in Portuguese Primary Education
Abstract
1. Introduction
1.1. Computational Thinking and Unplugged Activities
1.2. Modern Board Games
1.3. National Educational Context and Relevant Curriculum
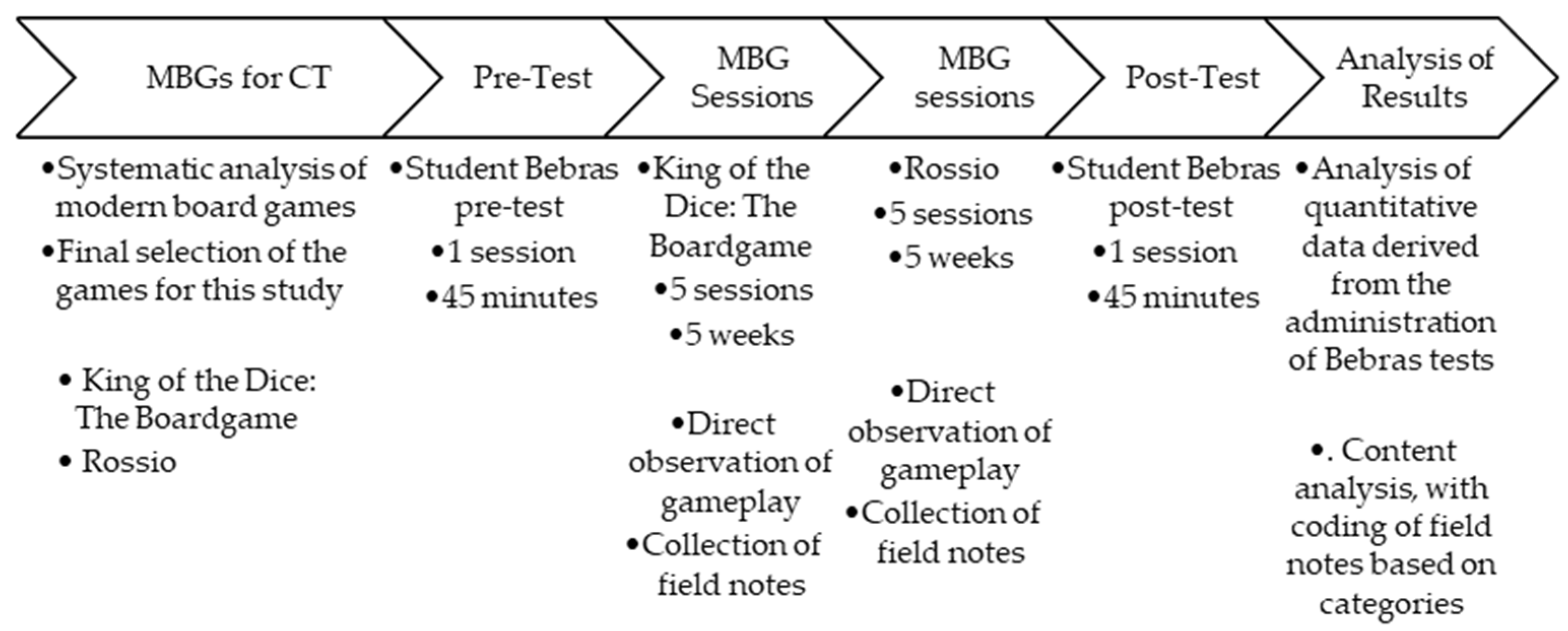
2. Materials and Methods
2.1. Selection of Modern Board Games
2.1.1. Systematic Analysis of Modern Board Games
2.1.2. Selection of the Modern Board Games for This Study
- King of the Dice: The Board Game.
- Rossio.
2.2. Participants and Data Collection
2.2.1. Statistical Analysis
2.2.2. Content Analysis
3. Results
3.1. Student Learning as a Result of Sessions with MBGs (RQ1)
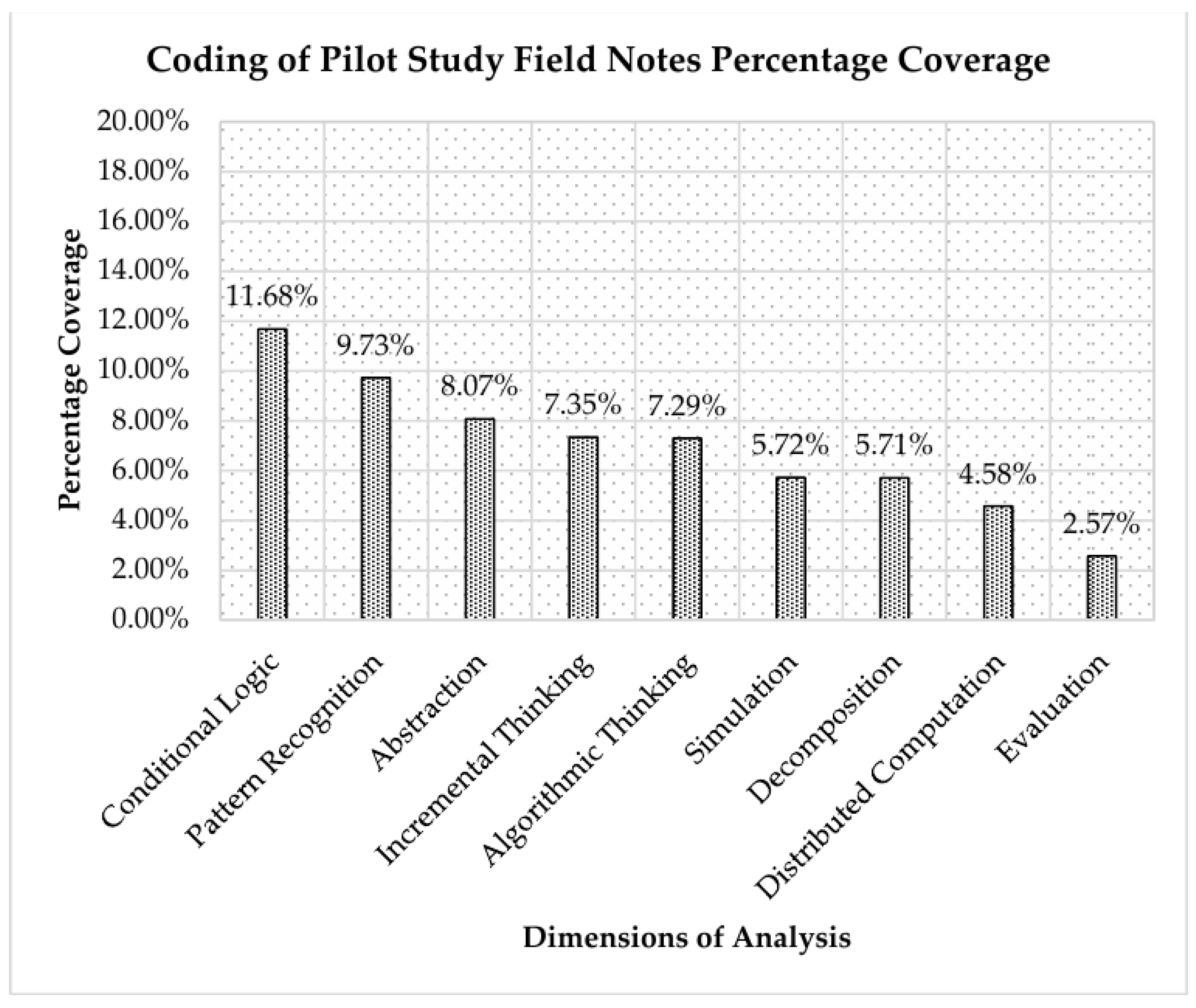
3.2. Content Analysis as a Result of Coding Field Notes (RQ2)
3.2.1. Example of Conditional Logic (Related to CT2)
Sierra.VG: ‘(…) I’m going to take two fours and two fives to try to make this sequence and take the merchant…no… I’d rather go and get the dragon…it’s almost impossible on the last turn to take a four and a five and then I can’t go and get anything (the merchant card required three fours and three fives).’
3.2.2. Example of Abstraction (Related to CT1)
November.LA: ‘My intention is to get this thief card, making the condition red > blue > green and being able to get two castles with it. Since I got it, I can take two (terrain tiles) and put them into play. I think I’ll choose this one. It’s the flower field, so I’m going to put it here (it has a diamond). I score more points here.’
3.2.3. Example of Decomposition (Related to CT3)
Romeo.SC: ‘I place this active card now (card with 4 yellow tiles worth 4 points), paying 3 coins. By my reckoning, I’ll score twelve points… because when I look at the tile area, I’ll be able to place enough tiles to make the card pattern at least once more (they were already visible twice). So that’s three times…3 × 4, that’s 12 points’.
3.2.4. Example of Generalisation (Related to CT5)
India.FM: ‘I’m not going to play this card; I’m going to throw it away…because I have less chance of getting it…I’d rather activate it downwards and get a coin. Now here (in the tile zone), I’m going to place this one here (placing her tile in the playing area) because I have a pattern like it in my yard… Now I’m going to play again (the tile placed was adjacent to another one like it), and I’m going to block someone because you can make this pattern here (a pattern of two yellows, one of the most common and most easily reached).’
3.2.5. Example of Evaluation (Related to CT4)
Lima.IB: ‘I think I’ll go for this one with 7 coins (The card had 3 yellow tiles worth 4 points).’
Quebec.SH: ‘You can’t go for the 7-coin one. You only have 6. I mean, you can, but you’ll be wasting a turn at this stage because if you want to activate it next round, you won’t be able to.’
Lima.IB: ‘Then I don’t know…’
Quebec.SH: ‘Get the one that costs 5 coins… you already have 6… so you can activate it on your next turn…’
Lima.IB: ‘But the pattern is the same, and I’m winning by one point less.’
Quebec.SH: ‘Yes… but you’re also spending two coins less and making the move now’.
4. Discussion and Implications
4.1. Discussion
4.2. Implications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wing, J. Computational Thinking. Commun. ACM 2006, 49, 140–158. [Google Scholar] [CrossRef]
- Yadav, A.; Stephenson, C.; Hong, H. Computational Thinking for Teacher Education. Commun. ACM 2017, 60, 55–62. [Google Scholar] [CrossRef]
- Angeli, C.; Voogt, J.; Fluck, A.; Webb, M.; Cox, M.; Malyn-Smith, J.; Zagami, J. A K-6 Computational Thinking Curriculum Framework: Implications for Teacher Knowledge. Educ. Technol. Soc. 2016, 19, 47–57. Available online: https://www.jstor.org/stable/jeductechsoci.19.3.47 (accessed on 25 July 2024).
- Caeli, E.N.; Yadav, A. Unplugged Approaches to Computational Thinking: A Historical Perspective. TechTrends 2020, 64, 29–36. [Google Scholar] [CrossRef]
- Aho, A.V. Computation and Computational Thinking. Comput. J. 2012, 55, 833–835. [Google Scholar] [CrossRef]
- Martins, A.R.Q.; Miranda, G.L.; Eloy, A.d.S. Uma Revisão Sistemática de Literatura Sobre Autoavaliação de Pensamento Computacional de Jovens. Renote 2020, 18, 2. [Google Scholar] [CrossRef]
- Bayeck, R.Y. Understanding Computational Thinking in the Gameplay of the African Songo Board Game. Br. J. Educ. Technol. 2024, 55, 259–276. [Google Scholar] [CrossRef]
- Yasar, O. Viewpoint a New Perspective on Computational Thinking: Addressing Its Cognitive Essence, Universal Value, and Curricular Practices. Commun. ACM 2018, 61, 33–39. [Google Scholar] [CrossRef]
- Bell, T.; Witten, I.; Fellows, M. Off-line activities and games for all ages. Comput. Sci. Unplug. 1998, 1, p. 1. Available online: https://classic.csunplugged.org/documents/books/english/unplugged-book-v1.pdf (accessed on 25 July 2024).
- Bell, T.; Vahrenhold, J. CS Unplugged—How Is It Used, and Does It Work? Springer International Publishing: Berlin/Heidelberg, Germany, 2018; Volume 11011, ISBN 9783319983554. [Google Scholar] [CrossRef]
- Nishida, T.; Kanemune, S.; Idosaka, Y.; Namiki, M.; Bell, T.; Kuno, Y. A CS Unplugged Design Pattern. SIGCSE Bull. Inroads 2009, 41, 231–235. [Google Scholar] [CrossRef]
- Berland, M.; Lee, V.R. Collaborative Strategic Board Games as a Site for Distributed Computational Thinking. Int. J. Game-Based Learn. 2011, 1, 65–81. [Google Scholar] [CrossRef]
- Berland, M.; Duncan, S. Computational Thinking in the Wild: Uncovering Complex Collaborative Thinking Through Gameplay. Educ. Technol. 2016, 56, 29–35. Available online: https://www.jstor.org/stable/44430490 (accessed on 2 June 2024).
- Scirea, M.; Valente, A. Boardgames and Computational Thinking: How to Identify Games with Potential to Support CT in the Classroom. In Proceedings of the FDG ’20: Proceedings of the 15th International Conference on the Foundations of Digital Games, Bugibba, Malta, 15–18 September 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Morais, A.; Sousa, H.; Joaquim, A.; Aires, A.; Catarino, P. Desenvolver o Pensamento Computacional Através Do Jogo de Mesa Tichu. 2023. Available online: https://www.researchgate.net/publication/377500165 (accessed on 25 June 2024).
- Chiazzese, G.; Fulantelli, G.; Pipitone, V.; Taibi, D. Engaging Primary School Children in Computational Thinking: Designing and Developing Videogames. Educ. Knowl. Soc. 2018, 19, 63–81. [Google Scholar] [CrossRef]
- Zhao, W.; Shute, V.J. Can Playing a Video Game Foster Computational Thinking Skills? Comput. Educ. 2019, 141, 103633. [Google Scholar] [CrossRef]
- Clarke, D.; Roche, A. The Power of a Single Game to Address a Range of Important Ideas in Fraction Learning. Aust. Prim. Math. Classr. 2010, 15, 18–24. Available online: https://files.eric.ed.gov/fulltext/EJ898705.pdf (accessed on 2 October 2024).
- Russo, J.A.; Roche, A.; Russo, T.; Kalogeropoulos, P. Examining Primary School Educators’ Preferences for Using Digital versus Non-Digital Games to Support Mathematics Instruction. Int. J. Math. Educ. Sci. Technol. 2024, 1–26. [Google Scholar] [CrossRef]
- Sousa, C.; Rye, S.; Sousa, M.; Torres, P.J.; Perim, C.; Mansuklal, S.A.; Ennami, F. Playing at the School Table: Systematic Literature Review of Board, Tabletop, and Other Analog Game-Based Learning Approaches. Front. Psychol. 2023, 14, 1160591. [Google Scholar] [CrossRef]
- Rosa, M.; Gordo, S.; Sousa, M.; Pocinho, R. Critical Thinking, Empathy and Problem Solving Using a Modern Board Game. In Proceedings of the Ninth International Conference on Technological Ecosystems for Enhancing Multiculturality, Barcelona, Spain, 27–29 October 2021; pp. 624–628. [Google Scholar] [CrossRef]
- Martinho, C.; Sousa, M. CSSII: A Player Motivation Model for Tabletop Games. In Proceedings of the Foundations of Digital Games 2023 (FDG 2023), Lisbon, Portugal, 12–14 April 2023; Volume 1. [Google Scholar] [CrossRef]
- Castronova, E.; Knowles, I. Modding Board Games into Serious Games: The Case of Climate Policy. Int. J. Serious Games 2015, 2, 63–75. [Google Scholar]
- Olympio, P.C.d.A.P.; Alvim, N.A.T. Board Games: Gerotechnology in Nursing Care Practice. Rev. Bras. Enferm. 2018, 71, 818–826. [Google Scholar] [CrossRef]
- Moya-Higueras, J.; Solé-Puiggené, M.; Vita-Barrull, N.; Estrada-Plana, V.; Guzmán, N.; Arias, S.; Garcia, X.; Ayesa-Arriola, R.; March-Llanes, J. Just Play Cognitive Modern Board and Card Games, It’s Going to Be Good for Your Executive Functions: A Randomized Controlled Trial with Children at Risk of Social Exclusion. Children 2023, 10, 1492. [Google Scholar] [CrossRef]
- Sousa, M.; Dias, J. From Learning Mechanics to Tabletop Mechanisms: Modding Steam Board Game to Be a Serious Game. In Proceedings of the 21st International Conference on Intelligent Games and Simulation, GAME-ON 2020, Aveiro, Portugal, 23–25 September 2020; pp. 41–48. [Google Scholar]
- Machuqueiro, F.; Piedade, J. Development of Computational Thinking Using Board Games: A Systematic Literature Review Based On Empirical Studies. Rev. Prism. Soc. 2022, 38, 5–36. Available online: https://revistaprismasocial.es/article/view/4766 (accessed on 25 September 2023).
- Rao, T.S.S.; Bhagat, K.K. Computational Thinking for the Digital Age: A Systematic Review of Tools, Pedagogical Strategies, and Assessment Practices; Springer: New York, NY, USA, 2024; Volume 72, ISBN 0123456789. Available online: https://link.springer.com/article/10.1007/s11423-024-10364-y (accessed on 25 July 2024).
- Su, J.; Weipeng, Y. A Systematic Review of Integrating Computational Thinking in Early Childhood Education. Comput. Educ. 2023, 4, 100122. [Google Scholar] [CrossRef]
- Bocconi, S.; Chioccariello, A.; Kampylis, P.; Wastiau, P.; Engelhardt, K.; Earp, J.; Horvath, M.; Malagoli, C.; Cachia, R.; Giannoutsou, N.; et al. Reviewing Computational Thinking; Office of the European Union: Luxembourg, 2022; ISBN 9789276472087. [Google Scholar] [CrossRef]
- Papert, S. The Children’s Machine; BasicBooks: New York, NY, USA, 1993. [Google Scholar]
- Sousa, M.; Zagalo, N.; Oliveira, P. Mechanics or Mechanisms: Defining Differences in Analog Games to Support Game Design. In Proceedings of the 2021 IEEE Conference on Games (CoG) 2021, Copenhagen, Denmark, 17–20 August 2021. [Google Scholar] [CrossRef]
- Booth, P. Game Play: Paratextuality in Contemporary Board Games; Bloomsbury Publishing (USA): New York, NY, USA, 2015; ISBN 9781628927443. [Google Scholar]
- Sousa, M.; Bernardo, E. Back in the Game Modern Board Games. Commun. Comput. Inf. Sci. 2019, 1164, 72–85. [Google Scholar] [CrossRef]
- Salen, K.; Zimmerman, E. Rules of Play—Game Design Fundamentals; The MIT Press: London, UK, 2004; ISBN 0-262-24045-9. [Google Scholar]
- Engelstein, G.; Shalev, I. Building Blocks of Tabletop Game Design; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Abingdon, UK, 2022; ISBN 9781138365490. [Google Scholar]
- Sousa, M. Mastering Modern Board Game Design to Build New Learning Experiences: The MBGTOTEACH Framework. Int. J. Games Soc. Impact 2013, 1, 68–93. [Google Scholar] [CrossRef]
- Machuqueiro, F.; Piedade, J. Exploring the Potencial of Modern Board Games to Support Computational Thinking. In Proceedings of the XXV Simpósio Internacional de Informática Educativa, Setúbal, Portugal, 16–18 November 2023. [Google Scholar] [CrossRef]
- Somma, R. Coding in the Classroom: Why You Should Care About Teaching Computer Science; No Starch Press, Inc.: San Francisco, CA, USA, 2020; ISBN 13-9781-7-185-0035-8. [Google Scholar]
- European Commission Eurydice. Available online: https://eurydice.eacea.ec.europa.eu/national-education-systems (accessed on 26 March 2024).
- Bocconi, S.; Chioccariello, A.; Dettori, G.; Ferrari, A.; Engelhardt, K.; Kampylis, P.; Punie, Y. Developing Computational Thinking: Approaches and Orientations in K-12 Education. In Proceedings of the EdMedia+ Innovate Learning, Association for the Advancement of Computing in Education (AACE), Vancouver, QC, Canada, 28–30 June 2016; pp. 1–7. Available online: https://publications.jrc.ec.europa.eu/repository/handle/JRC102384 (accessed on 26 March 2024).
- Matos, J.F.; Pedro, A.; Piedade, J. Integrating Digital Technology in the School Curriculum. Int. J. Emerg. Technol. Learn. 2019, 14, 4–15. [Google Scholar] [CrossRef]
- Coutinho, C.P. Metodologia de Investigação Em Ciências Sociais e Humanas; Edições Almedina SA: Coimbra, Portugal, 2015. [Google Scholar]
- Creswell, J. Research Design—Qualitative, Quantitative, and Mixed Methods Approache, 3rd ed.; Sage Publications: New York, NY, USA, 2009; ISBN 9781412965569. [Google Scholar]
- Dagiene, V.; Sentance, S.; Stupuriene, G. Developing a Two-Dimensional Categorization System for Educational Tasks in Informatics. Informatica 2017, 28, 23–44. [Google Scholar] [CrossRef]
- Cartelli, A.; Dagiene, V.; Futschek, G. Bebras Contest and Digital Competence Assessment. Int. J. Digit. Lit. Digit. Competence 2010, 1, 24–39. [Google Scholar] [CrossRef]
- Dagiene, V.; Stupuriene, G. Bebras—A Sustainable Community Building Model for the Concept Based Learning of Informatics and Computational Thinking. Inform. Educ. 2016, 15, 25–44. [Google Scholar] [CrossRef]
- Musaeus, L.H.; Musaeus, P. Computational Thinking and Modeling: A Quasi-Experimental Study of Learning Transfer. Educ. Sci. 2024, 14, 980. [Google Scholar] [CrossRef]
- Izu, C.; Mirolo, C.; Settle, A.; Mannila, L.; Stupuriene, G. Exploring Bebras Tasks Content and Performance: A Multinational Study. Inform. Educ. 2017, 16, 39–59. [Google Scholar] [CrossRef]
- Bardin, L. Análise de Conteúdo; Edições 70: São Paulo, Brazil, 2016. [Google Scholar]
- Machuqueiro, F.; Piedade, J. Modern Board Games and Computational Thinking: Results of a Systematic Analysis Process. EMI Educ. Media Int. 2024, 61, 161–183. [Google Scholar] [CrossRef]
- Mónico, L.; Alferes, V.; Castro, P.; Parreira, P. A Observação Participante Enquanto Técnica de Investigação Qualitativa. Pensar Enferm. 2017, 13, 30–36. [Google Scholar]
- NDTAC. A Brief Guide to Selecting and Using PrePost Assessments; Americans Institutes for Research: Arlington, VA, USA, 2006. [Google Scholar]
- Australian Maths Trust Bebras Solutions Guides. Available online: https://www.amt.edu.au/bebras-solutions-guides (accessed on 15 July 2024).
- Marôco, J. Analise Estatística Com o SPSS Statistics, 8th ed.; ReportNumber: Lisboa, Portugal, 2021. [Google Scholar]
- Jamovi Jamovi, Version 2.5; Software for Statistical Analysis; The Jamovi Project: Sydney, Australia. 2023; Available online: https://www.jamovi.org/ (accessed on 15 July 2024).
- Bogdan, R.; Biklen, S. Investigação Qualitativa em Educação: Uma Introdução à Teoria e Aos Métodos; Porto Editora: Porto, Portugal, 1994; ISBN 0205132669. [Google Scholar]
- Shin, N.; Bowers, J.; Roderick, S.; McIntyre, C.; Stephens, A.L.; Eidin, E.; Krajcik, J.; Damelin, D. A Framework for Supporting Systems Thinking and Computational Thinking through Constructing Models. Instr. Sci. 2022, 50, 933–960. [Google Scholar] [CrossRef]
- Grover, S.; Pea, R. Computational Thinking: A Competency Whose Time Has Come. Comput. Sci. Educ. 2017, 19, 1997–2004. [Google Scholar] [CrossRef]
- Brennan, K.; Resnick, M. New Frameworks for Studying and Assessing the Development of Computational Thinking. In Proceedings of the Annual Meeting of the American Educational Research Association, Vancouver, BC, Canada, 13–17 April 2012; Available online: http://scratched.gse.harvard.edu/ct/files/AERA2012.pdf (accessed on 15 July 2024).
- Rich, P.J.; Egan, G.; Ellsworth, J. A Framework for Decomposition in Computational Thinking. In Proceedings of the 2019 ACM Conference on Innovation and Technology in Computer Science Education, ITiCSE 2019, Aberdeen, UK, 5–8 July 2019; pp. 416–421. [Google Scholar] [CrossRef]
- Grover, S.; Pea, R. Computational Thinking in K-12: A Review of the State of the Field. Educ. Res. 2013, 42, 38–43. [Google Scholar] [CrossRef]
- Lee, T.Y.; Mauriello, M.L.; Ahn, J.; Bederson, B.B. CTArcade: Computational Thinking with Games in School Age Children. Int. J. Child. Comput. Interact. 2014, 2, 26–33. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates, Publishers: Mahwah, NJ, USA, 1988; ISBN 0805802835. [Google Scholar]
- Brackmann, C. Desenvolvimento Do Pensamento Computacional Através de Atividades Desplugadas Na Educação Básica. Ph.D. Thesis, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil, 2017. Available online: https://lume.ufrgs.br/handle/10183/172208 (accessed on 15 July 2024).
- Aguiar, A. O Impacto do Jogo de Regras na Aprendizagem e na Motivação do 1.º CEB, 2019. Master’s Thesis, Escola Superior de Educação Paula Frassinetti, Porto, Portugal, 2019; pp. 12–15. Available online: http://repositorio.esepf.pt/bitstream/ (accessed on 15 July 2024).
- Constantinou, V.; Ioannou, A. Development of Computational Thinking Skills through Educational Robotics. In Proceedings of the European Conference on Technology Enhanced Learning, Leeds, UK, 3–6 September 2018; Volume 2193, pp. 1–11. [Google Scholar]
- Boom, K.D.; Bower, M.; Siemon, J.; Arguel, A. Relationships between Computational Thinking and the Quality of Computer Programs. Educ. Inf. Technol. 2022, 27, 8289–8310. [Google Scholar] [CrossRef]
- Rodriguez, B.; Kennicutt, S.; Rader, C.; Camp, T. Assessing Computational Thinking in CS Unplugged Activities. In Proceedings of the 2017 ACM SIGCSE Technical Symposium on Computer Science Education, ITiCSE 2017, Bologna, Italy, 3–5 July 2017; pp. 501–506. [Google Scholar] [CrossRef]
- Zapata-Cáceres, M.; Marcelino, P.; El-Hamamsy, L.; Martín-Barroso, E. A Bebras Computational Thinking (ABC-Thinking) Program for Primary School: Evaluation Using the Competent Computational Thinking Test. Educ. Inf. Technol. 2024, 29, 14969–14998. [Google Scholar] [CrossRef]
- Leong, S.C. On Varying the Difficulty of Test Items. In Proceedings of the International Association for Educational Assessment 32nd Annual Conference, Sinagapore, 21–26 May 2006; pp. 1–6. [Google Scholar]
- Lonati, V.; Monga, M.; Malchiodi, D.; Morpurgo, A. How Presentation Affects the Difficulty of Computational Thinking Tasks: An IRT Analysis. In Proceedings of the 17th Koli Calling International Conference on Computing Education Research, Koli, Finland, 16–19 November 2017; pp. 60–69. [Google Scholar] [CrossRef]
- Zapata-Ros, M. Computational Thinking Unplugged. Educ. Knowl. Soc. 2019, 20, 1–29. [Google Scholar] [CrossRef]
- Dagiene, V. Information Technology Contests—Introduction to Computer Science in an Attractive Way. Inform. Educ. 2006, 5, 37–46. [Google Scholar] [CrossRef]



| Bebras Pre-Test | |||||||
| Questions | Name | Level | CT1 | CT2 | CT3 | CT4 | CT5 |
| 1 | Pearls | Easy | ~ | + | + | + | + |
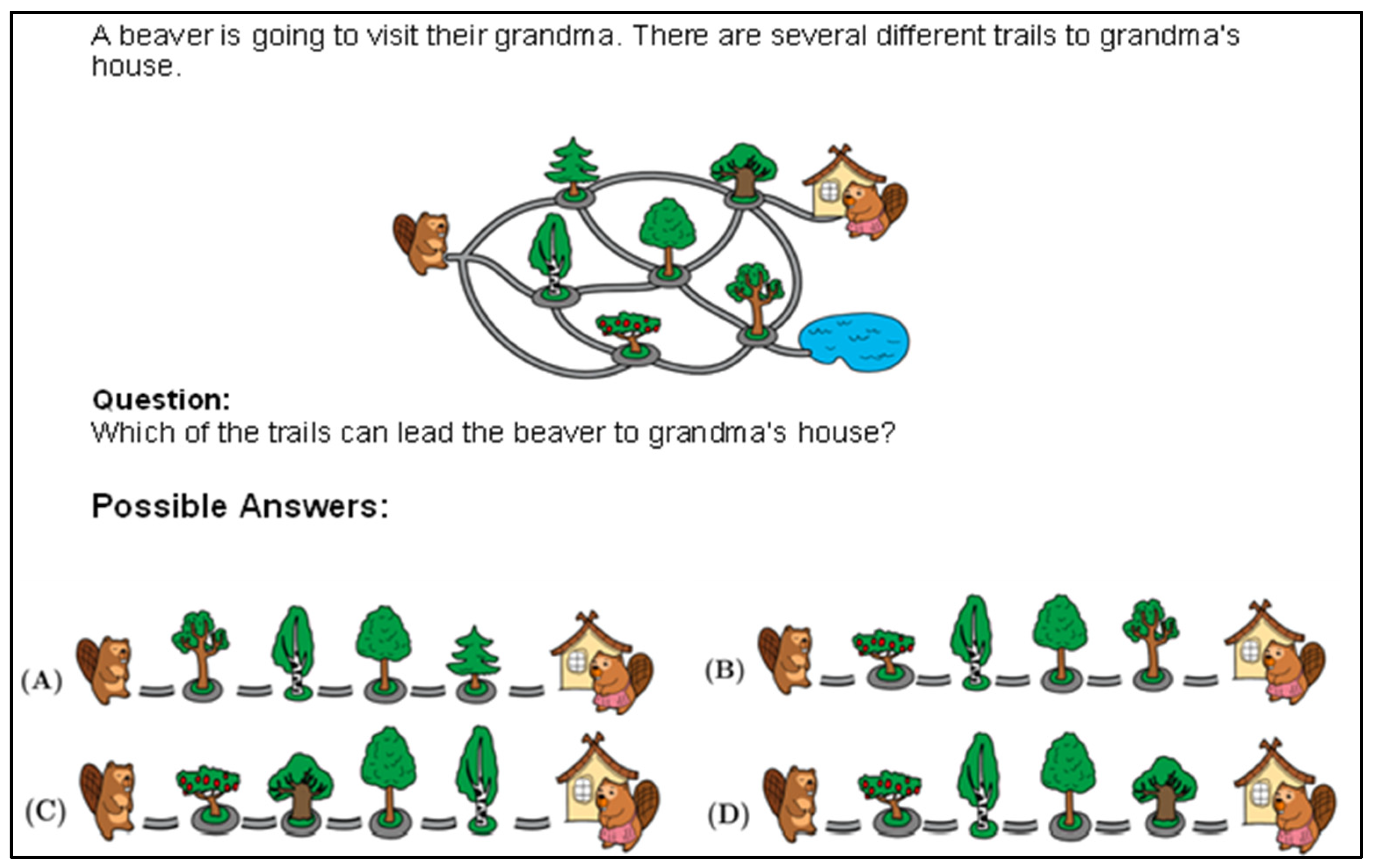
| 2 | Trail to Grandma | Easy | + | + | + | + | ~ |
| 3 | Building instruction | Easy | ~ | + | + | + | + |
| 4 | Beaver world cup ball | Easy | + | + | + | + | + |
| 5 | Birthday party | Medium | + | + | + | + | ~ |
| 6 | Strange payment | Medium | + | + | + | + | ~ |
| 7 | Tortoise and the Hare | Medium | ~ | + | + | + | + |
| 8 | Pick up sticks | Medium | ~ | + | + | + | + |
| 9 | Sailor’s necklace | Hard | ~ | + | + | + | + |
| 10 | Heart graphics | Hard | + | + | + | + | + |
| 11 | Mary’s neighbours | Hard | + | + | + | + | ~ |
| 12 | Colourful tower | Hard | ~ | + | + | + | + |
| Bebras Post-Test | |||||||
| Questions | Name | Level | CT1 | CT2 | CT3 | CT4 | CT5 |
| 1 | Lolly Shop | Easy | + | ~ | + | ~ | ~ |
| 2 | Cleaning the Lawn | Easy | + | + | + | ~ | ~ |
| 3 | Crossroads | Easy | + | + | + | + | ~ |
| 4 | Laughing Beavers | Easy | ~ | + | + | + | ~ |
| 5 | Space Travel | Medium | + | + | + | + | ~ |
| 6 | Stamps | Medium | ~ | ~ | + | + | + |
| 7 | Plates | Medium | + | + | + | + | + |
| 8 | Classifier | Medium | + | + | + | ~ | + |
| 9 | Double Parked | Hard | + | + | + | + | ~ |
| 10 | In Danger | Hard | + | + | ~ | + | ~ |
| 11 | Bridges and Islands | Hard | + | + | + | ~ | ~ |
| 12 | Wood Allergies | Hard | + | + | + | + | ~ |
| Easy Level = 6 Points | Easy Level = 9 Points | Easy Level = 12 Points |
|---|---|---|
| Question 1 | Question 5 | Question 9 |
| Question 2 | Question 6 | Question 10 |
| Question 3 | Question 7 | Question 11 |
| Question 4 | Question 8 | Question 12 |
| 24 Points | 36 Points | 48 Points |
| Bebras test maximum score = 108 points | ||
| CAT | DIM | DES | RAT |
|---|---|---|---|
| CT1—ABSTRACTION | Abstraction | The student describes a situation that demonstrates the expansion of a decision, plan, or logic to the entire game or future matches. | A high-level process of CT, used to capture essential properties of a problem, relegating irrelevant data in the design of efficient algorithms [1]. |
| CT2—ALGORITHMIC THINKING | Algorithmic Building | The student should plan their actions for ongoing game events or for events that have not yet occurred. This requires data manipulation and the development of a set of instructions. | A unique property of CT that refers to the creation of precise, step-by-step procedures with the aim of generating solutions to a problem by manipulating variables [58]. Algorithms are directly related to conditional logic [12]. |
| Simulation | The student tests a solution model for the algorithm previously created by defining the simulation as the enactment of the planned events. | It is a solution model for something that will eventually have a final version [12], enabling new ways of exploring, understanding, and representing the interconnections between elements of the system [58]. | |
| Conditional Logic | The student should globally reflect on the consequences of the truth value of their action/statement or choose possible alternatives. This requires the construction of a control structure based on ‘if–then–else’. | This is a fundamental part of CT, which requires the activation of logical and analytical thinking through puzzles and problem-solving scenarios. Overall, it is based on Boolean logic, meaning that whenever conditions and variables are used, spaces are opened up for the development of CT [1,59]. | |
| Incremental Thinking | The student gradually develops their action, relying on continuous process verification, thereby refining their moves. | According to Brennan and Resnick [60], learners must learn to ‘develop a little, experiment, then develop more’, repeatedly expanding their thinking until the goal is achieved. | |
| CT3—DECOMPOSITION | Decomposition | The student expresses their intentions regarding an objective move, executing it through small gameplay actions. | It consists of dividing a problem into sub-parts and solving each of them separately. This process can be identified as follows: (1) functional decomposition; (2) sequential decomposition; and (3) dependency decomposition [61]. |
| Distributed Computation | The student associates their plan with ideas from other classmates, distributing their knowledge across multiple considerations that will formalize a combined strategy. | It relates to the contribution of different participants to a common goal in a short space of time during various phases of the process of creating an algorithm, debugging, or simulation [12]. | |
| CT4— EVALUATION | Debugging | The student identifies issues in the actions initially planned or detects inaccuracies in their moves compared to the game instructions provided in the rule manual. | It refers to evaluating or verifying solutions, correcting behaviour, and solving problems by trial and error [58]. It requires comparing a solution with real-world data or expected results, improving it so that it behaves as expected [59,62]. |
| CT5—GENERALISATION | Pattern Recognitions | The student creates specific patterns from global patterns, generalising solutions for similar gameplay processes. | Participants relate objects, data, actions, and events to other similar phenomena. There is a prediction and generalisation of correct solutions and results [63]. |
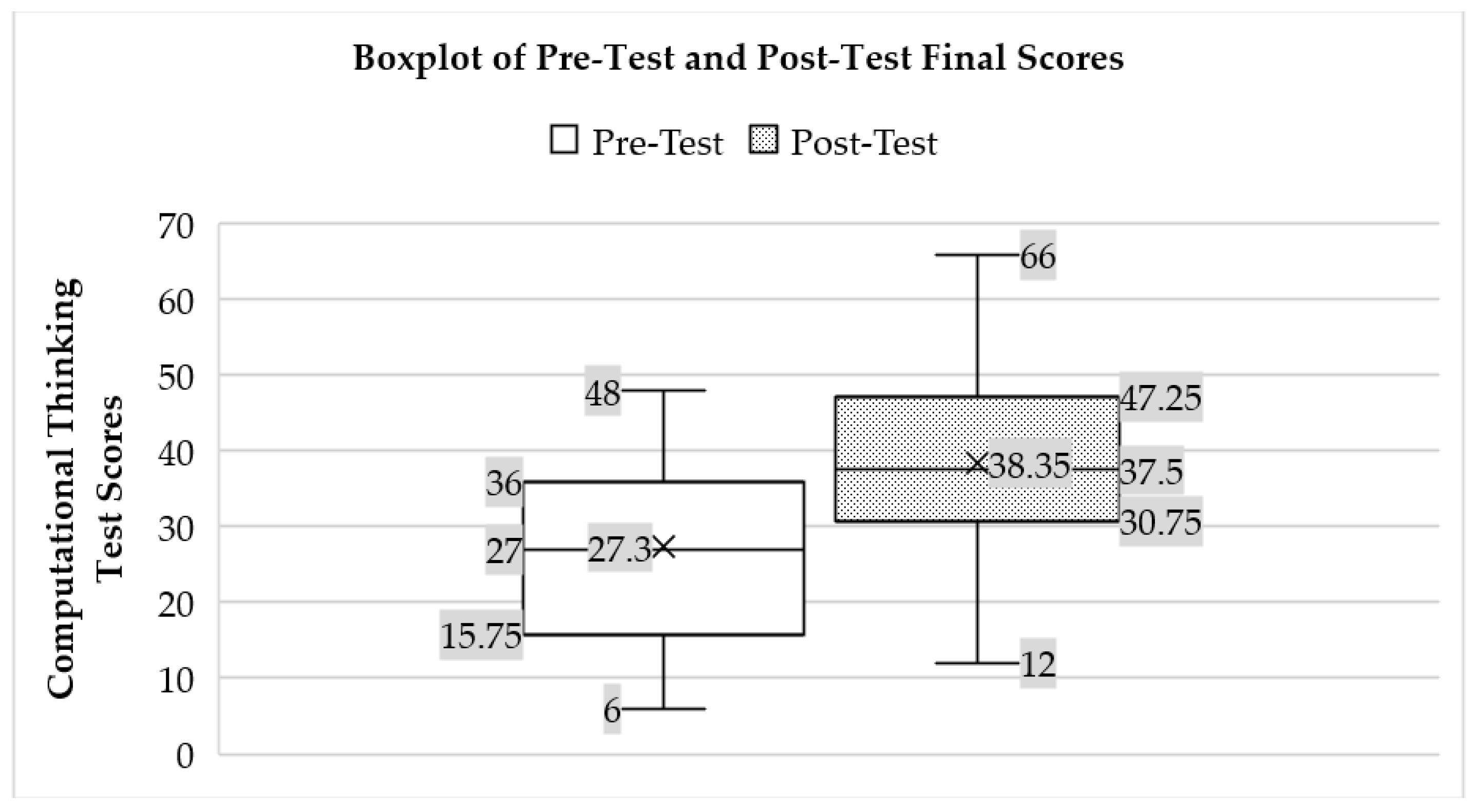
| Results | ||
|---|---|---|
| Descriptive Statistics | Pre-Test | Post-Test |
| N | 20 | 20 |
| Mean | 27.3 | 38.4 |
| Median | 27.0 | 37.5 |
| Mode | 36.0 | 51.0 |
| Standard deviation | 11.7 | 13.0 |
| Variance | 137 | 170 |
| Minimum | 6 | 12 |
| Maximum | 48 | 66 |
| Skewness | −0.0952 | 0.0296 |
| Std. error skewness | 0.512 | 0.512 |
| Kurtosis | −1.10 | 0.204 |
| Std. error kurtosis | 0.992 | 0.992 |
| Shapiro–Wilk W | 0.950 | 0.992 |
| Shapiro–Wilk p | 0.360 | 1.000 |
| 25th percentile | 17.3 | 32.3 |
| 50th percentile | 27.0 | 37.5 |
| 75th percentile | 36.0 | 45.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Machuqueiro, F.; Piedade, J. Game On: A Journey into Computational Thinking with Modern Board Games in Portuguese Primary Education. Educ. Sci. 2024, 14, 1182. https://doi.org/10.3390/educsci14111182
Machuqueiro F, Piedade J. Game On: A Journey into Computational Thinking with Modern Board Games in Portuguese Primary Education. Education Sciences. 2024; 14(11):1182. https://doi.org/10.3390/educsci14111182
Chicago/Turabian StyleMachuqueiro, Fábio, and João Piedade. 2024. "Game On: A Journey into Computational Thinking with Modern Board Games in Portuguese Primary Education" Education Sciences 14, no. 11: 1182. https://doi.org/10.3390/educsci14111182
APA StyleMachuqueiro, F., & Piedade, J. (2024). Game On: A Journey into Computational Thinking with Modern Board Games in Portuguese Primary Education. Education Sciences, 14(11), 1182. https://doi.org/10.3390/educsci14111182








