Can Correct and Incorrect Worked Examples Supersede Worked Examples and Problem-Solving on Learning Linear Equations? An Examination from Cognitive Load and Motivation Perspectives

Abstract

Research has advocated for the use of incorrect worked examples targeting specific conceptual barriers to enhance learning. From the perspective of cognitive load theory, we examined the relationship between instructional efficiency (correct and incorrect worked examples [CICWEs] vs. worked examples [WEs] vs. problem-solving [PS]), levels of expertise (low vs. high), and belief in achievement best (realistic vs. optimal) in learning linear equations across two experiments (N = 43 vs. N = 68). In the CICWE group, students compared an incorrect step in the incorrect worked example with the parallel correct step in the correct worked example and justified why the step was wrong. The WE group completed multiple worked example–equation pairs, while the PS group solved equivalent linear equations independently. As hypothesized, the WE group outperformed the PS group for low prior knowledge students, while the reverse occurred for high prior knowledge students, demonstrating the expertise reversal effect. In contrast, the CICWE group did not outperform either the PS or WE group. A student’s indication of optimal best, reflecting what is known as the ‘realistic–optimal achievement bests dichotomy’, aligns with his or her belief in their ability to perform tasks of varying complexity (simple task vs. complex task). Regarding the belief in achieving optimal best as an outcome of instructional manipulation, for low prior knowledge students, there were no significant differences across groups on either the realistic best or optimal best subscales. However, for high prior knowledge students, the groups differed significantly on the optimal best subscale, but not on the realistic best subscale. Importantly, the mental effort invested during learning was unrelated to students’ belief in achieving their optimal best.

1. Introduction

Linear equations are a key component of junior mathematics curricula worldwide (Schmidt et al., 2001). Mathematics educators and researchers consider students’ ability to solve linear equations a fundamental skill (Ballheim, 1999). According to Mayer (1992), solving linear equations is an essential part of the algebraic problem-solving process. Proficiency in solving these equations is critical, as it encourages students to apply algebra effectively in problem-solving. There is broad consensus among mathematics education researchers regarding the importance of algebra in problem-solving (Humberstone & Reeve, 2008; Kieran, 1992; Stacey & MacGregor, 1999).

Regrettably, research has shown that students often perform poorly when solving linear equations, particularly those involving negative pronumerals and/or negative numbers (e.g., 6x + 2(3 − x) = 34) (Ngu & Phan, 2022; Vicki et al., 2022). This poor performance limits students’ ability to use algebra for problem-solving purposes. For instance, a study by Stacey and MacGregor (1999) found that only about one-third of 900 middle school students were able to successfully use algebra to set up equations and then solve the problems. Improving students’ performance in solving linear equations is therefore a crucial educational goal. We believe that strengthening students’ ability to solve linear equations will provide a solid foundation for pursuing careers in science, technology, engineering, and mathematics (STEM), where algebraic problem-solving plays a pivotal role.

Research into effective instructional designs to enhance academic learning, particularly in mathematics, closely aligns with cognitive load theory (Sweller et al., 2011, 2019). The focus of the present study is on designing instructional strategies that reduce cognitive load while also enhancing students’ motivation to learn and master how to solve linear equations. Theorizing the concept of ‘optimal best practice’ or optimal functioning (Fraillon, 2004; Mascolo et al., 2010; Phan et al., 2016), Phan et al. (2017) argue that appropriate instructional design not only reduces cognitive load but also influences a student’s belief in their ability to achieve their optimal best. Building on this perspective, our previous empirical research (Ngu et al., 2023; Phan & Ngu, 2021) and the study presented in this article aimed to explore the relationships among cognitive load, instructional design, material complexity, and students’ belief in achieving their optimal best.

The present study builds on existing research regarding cognitive load and instructional design by comparing the effectiveness of three instructional approaches for learning linear equations with varying levels of complexity: correct and incorrect worked examples (CICWEs), worked examples (WEs), and problem-solving (PS). Two distinct cohorts were examined: elementary school students in China (N = 43) with low prior knowledge (Experiment 1) and secondary school students in Malaysia (N = 68) with high prior knowledge (Experiment 2). Our conceptualization suggests that an instructional design grounded in cognitive load theory (e.g., worked examples) can serve as a ‘motivational agent’, influencing students’ belief in their ability to achieve optimal best in solving linear equations.

2. Cognitive Load and Element Interactivity

Element interactivity is a measure of the complexity of learning material, a key concept in cognitive load theory (Sweller, 2012; Sweller et al., 2011, 1998). An element is defined as anything that requires learning, such as a number or a concept (Chen et al., 2017). The term ‘element interactivity’ describes the interaction between elements that must be simultaneously processed in working memory to enable understanding. Materials with high element interactivity place a higher demand on cognitive resources, resulting in high cognitive load, while materials with low element interactivity place a lower demand, resulting in lower cognitive load. Sweller et al. (2011) identify three types of cognitive load that influence learning:

• Intrinsic cognitive load is the cognitive load imposed by the inherent complexity of learning materials (Chen et al., 2023), which is influenced by the level of element interactivity and varies with the learner’s expertise in a given domain (Sweller, 2024). Experts in a specific domain can treat multiple interactive elements as a single unit of element, or schema, reducing the cognitive load. For instance, consider the linear equation 5x + 2(3 − x) = 12 (Appendix A). The first step in solving the equation involves expanding the bracket, resulting in 5x + 6 − 2x = 12. A learner with prior knowledge of bracket expansion can process 2(3 − x) as a single unit, thus reducing the element interactivity involved and lowering the cognitive load required to solve the equation.
• Germane cognitive load arises from the investment of cognitive resources to actively process and learn the essential aspects of the materials, which are intrinsic to the learning process (Sweller, 2010). For example, variable practice tasks can increase germane cognitive load by requiring learners to distinguish between different tasks that share a similar problem structure (Likourezos et al., 2019). As task variability increases, so does the element interactivity, and consequently, germane cognitive load. Thus, germane cognitive load does not act as an independent source of cognitive load; rather, it is considered a component of intrinsic cognitive load.
• Extraneous cognitive load is the cognitive load that does not contribute to learning and is typically caused by ineffective instructional design. It can be minimized by re-designing the instruction. For example, a problem-solving approach that requires learners to search for a solution path without guidance imposes a high level of element interactivity, which contributes to extraneous cognitive load. Replacing the problem-solving approach with worked examples can reduce extraneous cognitive load by providing learners with a clear solution path to understanding.

In line with our previous research (Ngu & Phan, 2022; Ngu et al., 2023), we applied the concept of element interactivity to assess the complexity of linear equations and to evaluate the relative efficiency of different instructional approaches.

3. Worked Example Effect and Expertise Reversal Effect

A worked example (WE) is an instructional tool that typically includes a problem, its solution procedure, and the answer (Atkinson et al., 2000; Sweller et al., 2011; Renkl, 2017; van Gog et al., 2019). The WE approach is particularly effective for novice learners during the initial stages of skill acquisition (e.g., van Gog et al., 2019). The solution procedure in a WE provides both the principles and their application, helping to scaffold the development of a schema. The worked example effect refers to the phenomenon where studying WEs not only reduces cognitive load but also leads to better performance outcomes compared to solving equivalent problems independently (van Gog et al., 2011). By focusing on the explicit solution steps, WE helps learners acquire schemas more efficiently, as it imposes a low level of element interactivity and, consequently, a low cognitive load. In contrast, problem-solving (PS) without guidance requires learners to independently search for a solution pathway, which can increase element interactivity and result in high extraneous cognitive load. This high cognitive load can interfere with schema acquisition, hindering the learning process.

Research in cognitive load has identified the expertise reversal effect (Kalyuga et al., 2003), which highlights the relationship between instructional methods and a learner’s level of expertise. Interestingly, an instructional approach that benefits novice learners may have a detrimental effect on expert learners. This effect has been consistently supported by research (Kalyuga et al., 2003). For example, in an earlier study, Kalyuga et al. (2001) found that the advantage of the worked example (WE) approach over the problem-solving (PS) approach diminished as learners became more knowledgeable in the subject matter. What was initially essential for novice learners became redundant and ineffective as their understanding deepened. This finding underscores a key theoretical insight: processing redundant information requires additional cognitive resources, which imposes extraneous cognitive load due to the limitations of working memory (Miller, 1956).

4. Correct and Incorrect Worked Examples (CICWEs)

While the use of worked examples (WEs) to support novice learning is well-established (e.g., Sweller et al., 2011), the use of correct and incorrect worked examples (CICWEs) is less commonly explored. An incorrect worked example typically contains one or more steps that differ from the correct solution. The key idea behind using incorrect examples is to prompt learners to analyze why a specific step is wrong (Barbieri & Booth, 2020; Yap & Wong, 2024). This process becomes especially valuable when the incorrect step or steps represent a conceptual barrier for the learner.

For instance, in the research by Große and Renkl (2007), the inclusion of an incorrect step aimed to help learners distinguish between critical concepts in the domain of probability, specifically the difference between relevant order and irrelevant order. Failing to differentiate between relevant order (which refers to the specific sequence of events) and irrelevant order (which pertains to a non-specific sequence) can hinder a learner’s ability to solve probability problems. By engaging with an incorrect example, learners are encouraged to refine their understanding of these key distinctions, which is crucial for successfully solving such problems.

According to Siegler (2002), exposing students to both correct and incorrect solution procedures can help them distinguish the differences and similarities between them, ultimately reducing the likelihood of selecting incorrect solution procedures in the future. Building on Siegler’s work, Booth et al. (2013) also examined the comparative effects of three types of worked examples for learning linear equations: correct only, incorrect only, and correct + incorrect. Using a cognitive tutor, students in each condition were asked to select a specific self-explanation (e.g., Equality is not preserved) related to a corresponding solution step (e.g., Why is that a wrong step for Ben to take?), choosing from a drop-down menu. The study found that a sequential presentation of a correct worked example followed by an incorrect worked example, or an incorrect worked example alone, was more effective than the correct worked example alone in helping students acquire conceptual knowledge of linear equations. This suggests that incorrect worked examples encourage deeper cognitive engagement by prompting students to justify why a particular step is incorrect, thus fostering a more thorough understanding of the material.

Comparing a correct worked example (WE) with an incorrect one side-by-side can help students acquire both conceptual and procedural knowledge (Durkin & Rittle-Johnson, 2012). This approach may include the use of prompts, such as “How is Matt’s way different from Justin’s way?” (p. 208), to encourage deeper learning, which has been shown to be more effective than simply pairing two correct worked examples. In their study, Durkin and Rittle-Johnson (2012) found that this comparison strategy is particularly beneficial because it directs students’ attention to the key misconceptions in the incorrect worked example, resulting in the acquisition of conceptual knowledge and procedure knowledge.

Research on learning algebra has shown that middle school students with low prior knowledge benefit from reflecting on errors in incorrect worked examples (WEs) (Barbieri & Booth, 2016). These students outperform those in the problem-solving condition when prompted to study and explain the errors in the incorrect WE. However, in the context of fractions, Heemsoth and Heinze (2014) found that reflecting on errors in incorrect WEs only benefited elementary school students with high prior knowledge. Additionally, Huang (2017) discovered that erroneous WEs are less effective than other types of examples, such as expert modeling examples, for learning statistical tasks. Huang suggests that identifying errors in incorrect WEs may require students to possess relevant prior knowledge in order to fully benefit from the experience.

Overall, the effectiveness of incorrect worked examples (WEs) across varying levels of prior knowledge remains somewhat inconclusive. Similarly, the simultaneous exposure of students to both correct and incorrect WEs is not guaranteed to be effective. For instance, Große and Renkl (2007) observed that, with complex mathematical topics such as probability problems, only students with high prior knowledge benefited from the use of correct and incorrect worked examples (CICWEs). This inconsistency suggests that the ability to identify errors in a WE may require students to draw on their prior knowledge (Huang, 2017).

What is unique about comparing a correct worked example (WE) with an incorrect WE from the perspective of cognitive load? According to Große and Renkl (2007), students exposed to the correct and incorrect worked example (CICWE) condition invest more germane cognitive load than those in other conditions, such as the correct WE only. As mentioned earlier, germane cognitive load is considered part of intrinsic cognitive load. When comparing a correct WE with an incorrect WE, students engage in learning the relevant aspects of the material, which is intrinsic in nature. As a result, germane cognitive load increases when students actively compare the two examples.

It is important to note that both the correct and incorrect WEs share the same linear equation, and therefore the same number of solution steps (Appendix B). From the perspective of element interactivity, comparing a pair of CICWEs concurrently—identifying errors and justifying why a solution step is wrong—may impose approximately twice the level of element interactivity compared to studying WEs sequentially. This increased element interactivity can place a higher demand on working memory, potentially disadvantaging students with low prior knowledge of linear equations. On the other hand, students with sufficient prior knowledge may not experience twice the level of element interactivity when comparing a pair of CICWEs concurrently. In summary, we have outlined the three types of cognitive load corresponding to the three instructional approaches (

Table 1. Instructional approach and type of cognitive load.

Instructional Approach	Type of Cognitive Load
Correct and incorrect worked examples (CICWEs).   The incorrect example typically has one or more steps differ from the correct example.   The incorrect example encourages a learner to examine why a particular solution step of the incorrect example is wrong.	Comparing a pair of CICWEs simultaneously requires learners to invest germane cognitive load.   Studying a pair CICWEs simultaneously imposes about twice the level of element interactivity (i.e., intrinsic cognitive load) compared to studying worked examples sequentially.
Worked examples (WEs).   The solution procedure of a WE encompasses principle knowledge and its application and thus scaffolding the development of schema.	Studying WEs imposes a low level of element interactivity and thus low cognitive load because it directs learners’ attention to explicit solution steps, helping them to develop solution schemas.
Problem-solving (PS).	Searching for a solution path to solve practice problems imposes a high level of element interactivity, which contributes to extraneous cognitive load and thus interferes with schema acquisition.

).

5. Motivation: Achieving Optimal Best

An important question addressed in the present study is whether and how an instructional approach may influence a student’s motivation to learn linear equations (Evans et al., 2024; Grund et al., 2024). Interestingly, research has introduced a positive psychological concept known as optimal best practice or optimal functioning (Fraillon, 2004; Mascolo et al., 2010; Phan et al., 2016), which reflects an individual’s state of motivation, inner strength, and personal resolve.

The study of self-efficacy (e.g., Bandura, 1997; Fast et al., 2010; Phan et al., 2016) from the social cognitive theory (Bandura, 1997, 2002) has one main point of reference, targeting a person’s belief in their perceived capacity to execute a specific course of action (Bandura, 1997). In contrast to self-efficacy, the concept of optimal best practice—as outlined in the Framework of Achievement Bests (Ngu et al., 2023; Phan et al., 2017)—addresses two levels of best practice:

• Optimal best (L₂)—This refers to a person’s belief in their maximum capability to master a complex task, shaped by their learning experiences. For example, successful learning to solve complex linear equations would influence a learner’s belief in their optimal best or notional best functioning.
• Realistic best (L₁)—This refers to a person’s belief in their ability to master a simpler task based on their learning experiences. For instance, successful learning to solve simpler linear equations would influence a learner’s belief in their actual best or realistic best.

The relationship between these two levels of best practice—L₁ and L₂—is termed the realistic–optimal achievement best dichotomy (Phan et al., 2017, 2019). This dichotomy may serve as a proxy or index of motivation, reflecting a person’s motivational state. Moreover, from our theoretical perspective (Ngu et al., 2023; Phan et al., 2017), the realistic–optimal achievement best dichotomy can function as a measure of the effectiveness of an instructional design.

According to Phan et al. (2017), the belief in achieving optimal best in a specific domain of functioning (e.g., optimal best in algebra problem-solving) requires some form of optimization (Phan et al., 2019). This optimization is facilitated by an optimizing agent, which helps promote belief in optimal best practice. In this context, an appropriate instructional design can serve as the optimizing agent, initiating and promoting motivational processes (e.g., effort expenditure) that, in turn, enhance a person’s belief in their ability to achieve optimal best outcomes.

Furthermore, our theoretical framework suggests that a belief in optimal best practice reflects a heightened state of motivation (Ngu et al., 2023; Phan et al., 2017, 2019). In contrast, a personal testament of sub-optimal best practice would indicate a low level of motivation, signaling disengagement or a lack of effort in the learning process. Facilitating a student’s belief in optimal best practice is a central goal of the educational system (Phan et al., 2019). A student’s belief in their optimal best may emerge from exposure to an appropriate instructional approach (Phan et al., 2017). Moreover, aside from enhancing optimal best belief, an appropriate instructional approach may help facilitate effective learning of a complex task (Ngu et al., 2023; Phan et al., 2017).

In contrast, an indication of realistic best or actual best (Fraillon, 2004; Mascolo et al., 2010; Phan et al., 2016) would reflect a student’s ability to master a simple task, independent of the instructional approach used (Ngu et al., 2023; Phan et al., 2017). Our empirical studies (Ngu et al., 2023; Phan & Ngu, 2021) have provided evidence to support the significance of our theoretical framework on optimal best practice, including the realistic–optimal achievement best dichotomy. For example, in a recent study involving university students, we used cluster analysis (Aldenderfer & Blashfield, 1985; Speece, 1994) to identify specific best practice profiles or distinct patterns of motivation for learning (Phan & Ngu, 2021). This pioneering research allowed us to conclude that realistic best (or actual best) tends to align with a low-to-moderate level of motivation for learning, while optimal best is associated with a high level of motivation.

6. The Target Domain: Linear Equations

This study examines three distinct types of linear equations, each requiring the manipulation of algebraic expressions on the left-hand side (see Appendix A). Linear equation containing negative numbers or pronumerals are considered more complex than their positive counterparts (Caglayan & Olive, 2010; Ngu & Phan, 2022). The linear equations, as presented in Appendix A, can be classified as follows:

• Type 1 equations: these involve only positive numbers and positive pronumerals (e.g., 2x + 3(1 + x) = 13).
• Type 2 equations: these involve positive numbers, a positive pronumeral, and a negative pronumeral (e.g., x + 2(3 − x) = 12).
• Type 3 equations: these include positive and negative numbers, as well as both positive and negative pronumerals (e.g., 4x − 2(1 − 2x) = 14 (Vlassis, 2002).

Given that Type 3 equations contain two negative components (a negative number and a negative pronumeral), and Type 2 equations contain only one negative (a negative pronumeral), Type 3 equations are considered more complex than Type 2 equations. Therefore, we categorize the equations by complexity level: Type 1 equations are the simplest, followed by Type 2 equations, and Type 3 equations are the most complex.

7. The Present Study

This study investigates the effectiveness of three instructional designs for learning linear equations. Additionally, it explores the relevance of the ‘realistic–optimal achievement best dichotomy’ (Phan et al., 2017, 2019) to advance the study of best practices in education (Fraillon, 2004; Mascolo et al., 2010; Phan et al., 2016). Our aim is to assess the suitability of the CICWE, WE, and PS approaches for teaching linear equations with varying levels of complexity, while considering differences in students’ prior knowledge. Specifically, we hypothesize the following:

According to cognitive load theory, the effectiveness of an instructional approach is typically more apparent in complex learning tasks than in simpler ones (Sweller et al., 2011). Therefore, the performance outcomes for Type 1 equations are expected to show no significant differences across the three instructional approaches, regardless of students’ prior knowledge (Hypothesis 1).

Consistent with the worked examples effect, the WE approach is expected to outperform the PS approach (Sweller et al., 2011). As previously discussed, studying a pair of CICWEs concurrently imposes roughly double the level of element interactivity compared to studying WE sequentially, as in the case of the WE approach. Research has produced mixed results on the benefits of exposing learners with low prior knowledge to both correct and incorrect worked examples (Barbieri & Booth, 2016; Große & Renkl, 2007). In the present study, students with low prior knowledge in the CICWE approach may not fully benefit from the additional instructional support. These students may lack the necessary prior knowledge to identify and correct errors in one of the solution steps in the incorrect worked example, even though they were cued to view the corresponding correct solution step in the correct worked example. As a result, the CICWE approach could overwhelm low prior knowledge students (Große & Renkl, 2007). In contrast, the PS approach may involve a similarly high level of element interactivity, given the need for students to actively search for a solution path. Therefore, for low prior knowledge students, performance outcomes for Type 2 and/or Type 3 equations are expected to follow this order: WE > PS > CICWE (Hypothesis 2a).

The PS approach is expected to be more effective than the WE approach for high prior knowledge students, in line with the expertise reversal effect (Kalyuga et al., 2003). In the present study, students with high prior knowledge are likely to treat multiple elements as a single element, enabling them to process the CICWE with a lower level of element interactivity compared to students with low prior knowledge. Furthermore, the CICWE approach offers high prior knowledge students the opportunity to allocate cognitive resources toward deep learning of the critical features of the solution steps. Specifically, the CICWE approach addresses conceptual barriers such as the manipulation of negative numbers and pronumerals when learning to solve linear equations. As Ericsson (2006) emphasizes, the development of expertise requires deliberate practice focused on improving specific areas of weakness within a domain (Pachman et al., 2013). In this context, deliberate practice targets the student’s weak points in understanding specific concepts related to solving linear equations. Consequently, the additional instructional support provided by the CICWE approach—targeting a particular conceptual barrier—would enable high prior knowledge students to perform better than those using the PS approach. Therefore, for high prior knowledge students, the performance outcomes for Type 2 and/or Type 3 equations are expected to follow this order: CICWE > PS > WE (Hypothesis 2b).

It is important to advance the study of the realistic–optimal achievement best dichotomy (Fraillon, 2004; Mascolo et al., 2010; Phan et al., 2016) by exploring a key question: to what extent do the findings of the present study support our earlier claim that there is a relationship between appropriate instructional approach and the belief in achieving optimal best? A novel aspect of our conceptualization is the suggestion that the belief in achieving an optimal best (Ngu et al., 2023; Phan & Ngu, 2021; Phan et al., 2017) may serve as a ‘proxy index’ of motivation for academic learning.

As previously noted, the relationship between cognitive load effects and instructional design typically emerges more clearly in the context of complex tasks rather than simple ones (Sweller et al., 2011). In other words, we expect learning outcomes to vary across the three instructional approaches for complex linear equations (Type 2 or Type 3), but not necessarily for simple linear equations (Type 1). Based on this reasoning, we propose two contrasting positions:

• Realistic best (i.e., realistic best subscale) would reflect a student’s belief in their ability to solve simple linear equations, which would not be a function of different instructional approaches.
• Optimal best (i.e., optimal best subscale) would reflect a student’s belief in their ability to solve complex linear equations, and this belief would be a function of different instructional approaches.

From this, we hypothesize that the three instructional approaches would differ on the optimal best subscale, but not on the realistic best subscale, regardless of a student’s level of prior knowledge (Hypothesis 3).

According to Paas et al. (2003), participants (e.g., students) are able to retrospectively assess the amount of mental effort they invested in cognitive tasks. Based on their rationale and empirical findings, we argue that a student’s subjective rating of mental effort can serve as a measure of cognitive load imposition (Krell et al., 2022). After completing the acquisition phase, students across the three instructional approaches rated their invested mental effort on a Likert scale ranging from 1 (extremely low) to 9 (extremely high) (Paas, 1992).

Building on our recent research (Ngu et al., 2023), we propose that a student’s indication of optimal best practice reflects their level of motivation. Additionally, we hypothesize an inverse relationship between mental effort and the belief in achieving optimal best, regardless of a student’s level of prior knowledge (Hypothesis 4).

The present research is novel and innovative for its advancement of cognitive load theory (Sweller, 2012; Sweller et al., 2011, 1998), which explores both the cognitive dimension and the motivational dimension of academic learning. Our study, which includes students from diverse learning and sociocultural contexts, builds upon existing research, including our recent studies (Granero-Gallegos et al., 2023; Ngu et al., 2023; Phan & Ngu, 2021). In summary, our research addresses the following questions:

(i)

Does an appropriate instructional approach influence a student’s belief in achieving optimal achievement best?

(ii)

Does a sub-optimal instructional approach influence a student’s belief in achieving realistic achievement best? Additionally, our inquiry examines the impact of learner expertise and instructional efficiency on learning linear equations of varying complexity.

Prior research has used a pre-test (Blayney et al., 2016) or compared students in different grade levels (Bokosmaty et al., 2015) to assess varying levels of prior knowledge (i.e., novice vs. expert learners). In the present study, we similarly used a pre-test as a baseline measure to determine students’ levels of prior knowledge in both Experiment 1 (i.e., Chinese students) and Experiment 2 (i.e., Malaysian students).

Table 2. Characteristics of the China sample and the Malaysia sample.

	China Sample	Malaysia Sample
Mean age	10.00 (SD = 0.26)	14.07 (SD = 0.21)
Grade level	Year 4	Form 1 students (equivalent to Year 8 students in Australia)
Gender	24 girls, 23 boys	38 girls, 30 boys
Ethnicity	Hokkian	Chinese (35%), Malay (45%), Indigenous Malaysian (30%)
Language of instruction	Mandarin	English for mathematics and science subjects
Mathematics curriculum	Mathematics curriculum standards	National curriculum for mathematics education
The topic of linear equations	Covered in elementary mathematics curriculum	Covered in junior secondary mathematics curriculum
Location of the school	Urban area	Rural area
Type of school	Public school	Public school
Prior knowledge	Basic knowledge of solving two-step linear equations	Basic knowledge of solving multi-step linear equations

summarizes the characteristics of the two samples (China vs. Malaysia). Notably, the samples differ in grade level, introduction to the topic of linear equations (elementary vs. secondary), and prior knowledge of linear equations (two-step vs. multi-step). These differences make this cross-cultural study particularly valuable for examining the roles of prior knowledge, instructional approach, cognitive load, and beliefs in achieving optimal performance in learning to solve linear equations.

8. Experiment 1

The dependent variables in this experiment included the mean scores for practice equations, mental effort, the post-test, and the Optimal Outcomes Questionnaire (realistic best subscale vs. optimal best subscale). To analyze the mean scores for practice equations and the post-test, we used mixed 3 × 3 ANOVAs, with the instructional approach (CICWE vs. WE vs. PS) as a between-subjects factor and equation type (Type 1 vs. Type 2 vs. Type 3) as a within-subjects factor. We used pairwise comparisons with Bonferroni correction to determine which groups differed from each other.

To examine the differences between the three instructional approaches (CICWE vs. WE vs. PS) for the pre-test, realistic best subscale, and optimal best subscale scores, we conducted a one-way ANOVA. If the one-way ANOVA indicated a significant effect, we performed a Tukey post hoc test to identify which groups differed from each other. The significance level was set at α = 0.05. We reported partial eta values, where η_p² = 0.01, η_p² = 0.06, η_p² = 0.14 correspond to small, medium, and large effect sizes, respectively (Cohen, 1988).

9. Methods

9.1. Participants

Forty-seven Year 4 elementary students from China (24 girls, 23 boys) consented to participate in the study. The mean age of the students was 10.00 years (SD = 0.26), and their ethnic background was Hokkian. The data were collected from two classes in an elementary school located in an urban area of Chengdu, China. The students followed the mathematics curriculum standards, and Mandarin was the language of instruction. One of the authors, who is proficient in both English and Mandarin, translated the test materials into Mandarin. The students had a basic knowledge of linear equations (e.g., 2x + 3 = 5, solve for x); however, they were considered novices with respect to the specific linear equations targeted in this study. Students were randomly assigned to one of three groups: the CICWE group (N = 16), the WE group (N = 16), and the PS group (N = 15). Four students did not complete all of the tasks and were excluded from the final analyses.

Due to incomplete data, we did not analyze the mental effort ratings, as many students failed to provide them. It is possible that the translation of ‘mental effort’ into Mandarin did not fully convey the intended meaning, which may have discouraged elementary students from rating their mental effort. As an alternative, we suggest that future research use subjective measures to assess perceived difficulty (Ayres, 2006). For example, a Likert scale question such as, ‘How difficult was the task?’, with responses ranging from 1 (extremely easy) to 9 (extremely hard), could be more appropriate. Previous research has demonstrated the effective use of this perceived difficulty scale to measure cognitive load in elementary school students (Agostinho et al., 2015).

Given the 3 × 3 mixed ANOVA experimental design, we used the ANOVA repeated measures, within-between interaction option in G*Power (Version 3.1.9.7) to calculate the minimum sample size required for both Experiment 1 and Experiment 2 (Faul et al., 2007). We acknowledge that the sample size may have been adequately powered for some analyses but not for others. For Experiment 1, the final sample size of 43 students exceeded the minimum requirement of 36 participants. This calculation was based on a priori power calculation for an effect size f = 0.25 for power = 80% and Type I error rate = 5%. We used the effect size f = 0.25, which is equivalent to a medium effect size of η_p² = 0.06 (Cohen, 1988).

Finally, ethics clearance for data collection was obtained from the Human Research Ethics Committee (HREC) at the University of New England (Approval Number: HE 11/057). Students in both Experiment 1 and Experiment 2 consented to participate in the study.

9.2. Materials

The materials for this study included the following: (1) a pre-test and a post-test, (2) an instruction sheet, (3) learning materials, and (4) the Optimal Outcomes Questionnaire.

Pre-Test and Post-Test. Both the pre-test and post-test consisted of 15 equations each, similar to the practice equations in terms of problem structure (Reed, 1987). The tests included an equal distribution of Type 1, Type 2, and Type 3 equations, with five equations from each type.

Instruction Sheet. The instruction sheet provided a definition of an equation, along with three worked examples demonstrating how to solve Type 1, Type 2, and Type 3 equations (see Appendix A). Prompts were included to help students understand the solution procedure (e.g., ‘Collect like terms’) (Rittle-Johnson & Star, 2007). This instruction sheet was used uniformly across all three groups.

Learning materials. Three sets of learning materials were designed to correspond to the three instructional approaches (see Appendix B). For the CICWE approach, we used six pairs of worked examples, where each pair shared the same linear equation. These six equations were identical to the six worked examples in the WE approach. For each pair, a correct worked example was presented first, followed by an incorrect worked example containing a wrong step. Next to the incorrect step, students were asked, ‘Can you explain why this step is incorrect?’ A hint was provided to prompt students to compare the incorrect step with the corresponding correct step in the parallel worked example. Students were then required to justify why the step was wrong. In line with previous research (Große & Renkl, 2007), the aim was to direct students’ attention to the critical features of the problem, particularly those related to manipulating algebraic expressions, such as the multiplication of negative numbers and pronumerals (e.g., −3 × −x = +3x and NOT −3x).

Manipulating algebraic expressions is a common challenge for students (Ayres, 2001). In the present study, we specifically drew students’ attention to errors related to the manipulation of algebraic expressions, rather than focusing on other concepts (e.g., the inverse operation), with the goal of supporting their learning. Furthermore, in line with prior research (Atkinson et al., 2000; Sweller et al., 2011), we varied the design of the algebraic expressions in the linear equations (e.g., by using different combinations of positive numbers, negative pronumerals, etc.) to engage students and encourage learning through the CICWE approach.

We argue that mastering the accurate manipulation of algebraic expressions is crucial for students’ success in solving linear equations. For instance, as illustrated in Appendix B, an incorrect solution step, such as 2x − 3 − x = 2 for the linear equation $2x-3\left(1-x\right)=2$ results from an error in manipulating the algebraic expression $-3\left(1-x\right)$. This error leads to subsequent incorrect steps and ultimately an incorrect solution. By actively comparing the correct and incorrect worked examples, we expected students to recognize the consequences of such errors, particularly how they contribute to incorrect solution steps. Therefore, we propose that exposure to CICWEs will help students identify misconceptions and learn the correct procedure for solving linear equations.

In line with prior research on worked examples (Sweller et al., 2011), the WE approach involved six worked example–equation pairs (see Appendix B). Students were required to study a worked example and then solve a practice linear equation that shared a similar problem structure (Reed, 1987). In the PS approach, students were asked to solve 12 linear equations, which were identical to the 12 equations used in the WE approach (see Appendix B). These 12 equations were equally distributed across Type 1, Type 2, and Type 3 equations, with four equations of each type. After completing the learning phase, students rated their perceived mental effort on a nine-point Likert scale ranging from 1 (extremely low) to 9 (extremely high) to indicate how much effort they had invested in learning (Paas, 1992).

The Optimal Outcomes Questionnaire. The Optimal Outcomes Questionnaire consists of two subscales: the realistic best subscale and the optimal best subscale. Each subscale contains 12 items rated on a five-point Likert scale, ranging from 1 (always false) to 5 (always true). These two subscales assess two key aspects: (i) personal attributes related to the realistic–optimal achievement best dichotomy, and (ii) the impact of instructional approaches on a student’s understanding of linear equations.

Example items from the realistic best subscale:

• I am content with what I have accomplished so far for the topic of solving equations.
• The practice exercise is not very effective in helping me learn how to solve equations.

In contrast, example items from the optimal best subscale:

• I can achieve much more for the topic of solving equations than I have indicated through my work so far.
• The practice exercise is very effective in helping me learn how to solve equations.

The Optimal Outcomes Questionnaire was originally designed with two subscales, each containing eight items: the realistic best subscale and the optimal best subscale. Together, these subscales enable researchers to assess the realistic–optimal achievement best dichotomy, which influences a student’s motivation. In this study, the same test materials (e.g., instructional design) were used across both sociocultural and academic contexts (i.e., China and Malaysia). Unlike prior research (e.g., Feldon et al., 2018), we argue that the realistic–optimal achievement best dichotomy, which reflects a student’s motivational state, could be linked to their perception of the instructional design. As such, we included four items for each subscale to measure students’ perceptions of the instructional design.

In a previous study, the reliability estimates for the two subscales, excluding the four items related to instructional design, were 0.81 for the realistic best subscale and 0.79 for the optimal best subscale (Phan et al., 2018). The Optimal Outcomes Questionnaire has been implemented and validated across various languages and sociocultural contexts, including English with secondary school students (Ngu et al., 2023), Mandarin with Taiwanese university students (Phan & Ngu, 2021), and Spanish with Spanish university students (Granero-Gallegos et al., 2023).

9.3. Procedure

Group testing was conducted under supervision in a regular classroom setting. At the outset, students were informed that they would complete four written tasks individually: (i) a pre-test (10 min), (ii) an acquisition phase that included an instruction sheet (5 min), practice equations, and a mental effort Likert scale (15 min), (iii) a post-test (10 min), and (iv) the Optimal Outcomes Questionnaire (5 min). Students were instructed to read the instructions on the first page of each task before beginning.

While completing the practice equations, students could refer to the instruction sheet and ask for help if needed. However, they were not permitted to seek assistance for other tasks (e.g., pre-test, post-test). Materials for each phase were distributed accordingly, and students’ responses were collected once the allocated time had expired. The exception was during the acquisition phase, where the instruction sheet was collected separately at the end of the phase.

In total, students across the three experimental groups were given the same amount of time to complete the pre-test, acquisition phase, post-test, and Optimal Outcomes Questionnaire. The primary difference between the groups was the design of the learning materials used during the acquisition phase.

9.4. Scoring

The dependent variables were the mean scores for the practice problems and the post-test. Each linear equation consisted of four steps (see Appendix B), and one mark was allocated for each correct step, yielding a total of four marks for a correct solution. No marks were awarded if an error occurred in the first step, even if subsequent steps were correct. We scored six and twelve practice equations for the WE group and the PS group, respectively.

In their study, Große and Renkl (2007) assigned numerical scores to self-explanation and examined the correlation between the quality of explanations and learning outcomes across different experimental conditions. Similarly, van Peppen et al. (2021) used numerical scores for practice activities where participants demonstrated their understanding of critical reasoning skills. In line with these studies, for each pair of CICWE, one mark was assigned for providing a correct explanation. Accepted explanations included responses like, “−3 multiplied by −x becomes 3x because negative times negative is positive; for example, 3(−2x) = −6x.” However, marks were not awarded for incomplete or unclear explanations (e.g., “x must be added”). As shown in Figure 1, the student’s justification highlights their ability to analyze the error, reinforcing the benefits of CICWE. Accordingly, while an accurate explanation is not the same as solving a linear equation correctly, we reasoned that if a student could provide a correct explanation for an error, they would understand the correct sequence of solution steps and the consequences of the error, including how it leads to subsequent incorrect steps. Thus, the ability to explain the error demonstrated the student’s grasp of the solution process, warranting the award of marks.

Due to the unequal number of practice problems in the WE and PS approaches, and the fact that there were only six explanations in the CICWE approach, we used mean proportion scores (or percentage scores) rather than raw scores for the pre-test, practice equations, and post-test in the final analysis. The marking was performed by both a researcher and the class teacher, who independently coded 20% of the sample for the pre-test, practice equations, and post-test. The inter-scorer reliability was found to be above 0.90. Additionally, the Cronbach’s alpha values for the pre-test, practice equations, and post-test were 0.88, 0.95, and 0.91, respectively, indicating high internal consistency across these measures.

10. Results and Discussion

Table 3. Means and standard deviations of scores on pre-test, practice equations, post-test, mental effort and realistic best subscale and optimal best subscale.

	CICWE		WE		PS
	M	(SD)	M	(SD)	M	(SD)
Experiment 1	n = 14		n = 15		n = 14
Pre-test (proportion)	0.18	0.15	0.21	0.17	0.20	0.25
Practice equations (proportion)
Type 1	0.82	0.37	0.90	0.28	0.63	0.42
Type 2	0.50	0.48	0.83	0.31	0.35	0.45
Type 3	0.23	0.29	0.42	0.46	0.18	0.37
Post-test (proportion)
Type 1	0.64	0.45	0.85	0.31	0.71	0.44
Type 2	0.06	0.12	0.09	0.17	0.10	0.16
Type 3	0.00	0.00	0.20	0.41	0.21	0.38
Realistic best subscale	2.53	0.51	2.34	0.51	2.72	0.44
Optimal best subscale	3.34	0.68	3.62	0.62	3.65	0.44
Experiment 2	n = 23		n = 23		n = 22
Pre-test (proportion)	0.31	0.27	0.26	0.31	0.37	0.33
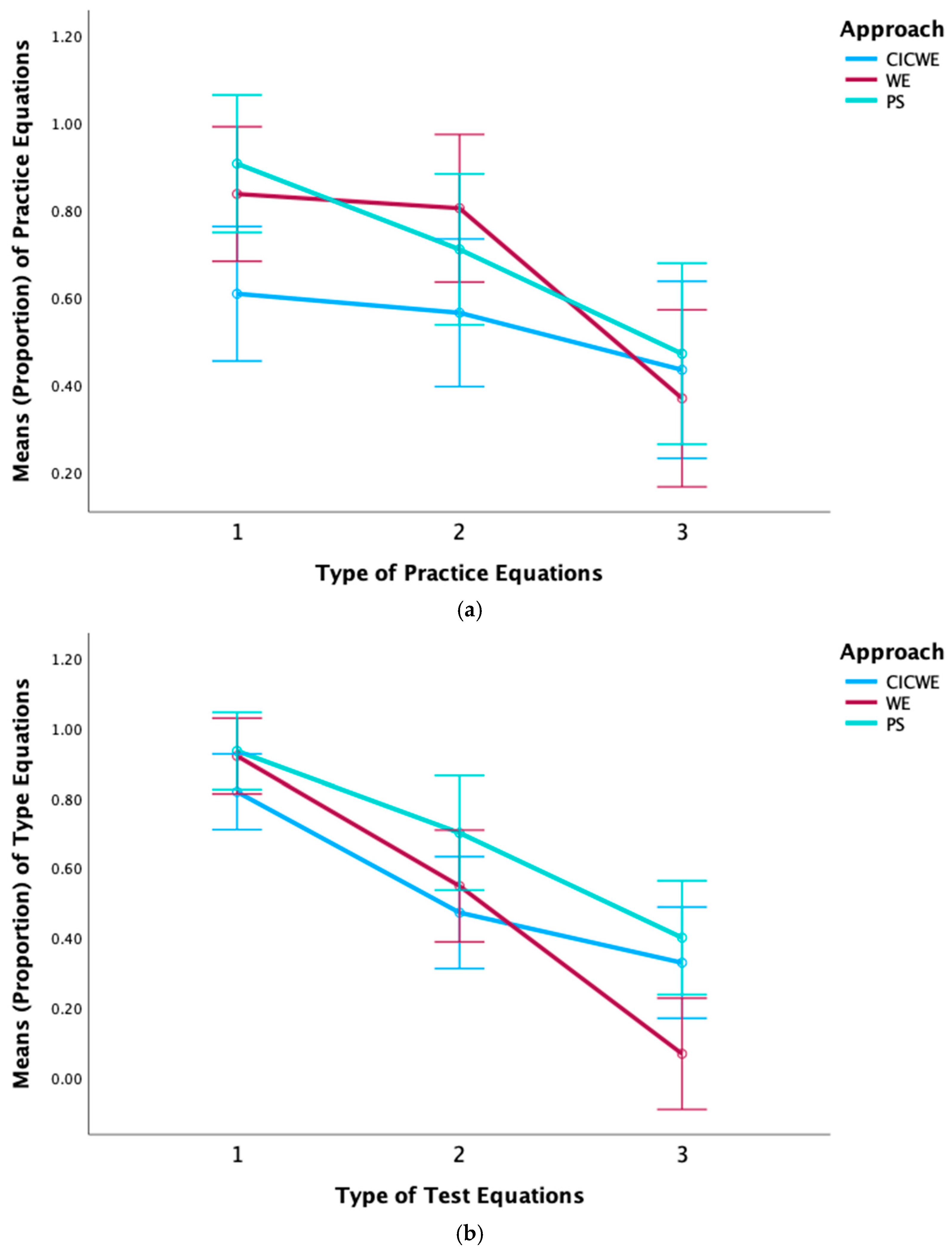
Practice equations (proportion)
Type 1	0.61	0.45	0.84	0.37	0.91	0.25
Type 2	0.57	0.46	0.80	0.35	0.71	0.40
Type 3	0.43	0.48	0.37	0.48	0.47	0.49
Post-test (proportion)
Type 1	0.82	0.31	0.92	0.24	0.93	0.22
Type 2	0.47	0.39	0.55	0.38	0.70	0.38
Type 3	0.33	0.41	0.07	0.22	0.40	0.48
Mental effort	5.17	1.61	4.52	1.86	4.86	2.19
Realistic best subscale	3.22	0.49	3.19	0.49	3.26	0.33
Optimal best subscale	3.54	0.45	3.79	0.55	3.90	0.40

Note: The number of practice equations for the CICWE, WE, and PS approaches was 6, 6, and 12, respectively. The pre-test and post-test had the same number (15) and type of equations. The complexity of the equation followed the order: Type 1 < Type 2 < Type 3. The realistic best subscale and optimal best subscale had 12 items each.

presents the means and standard deviations for the pre-test, practice equations, justification (regarding the wrong step in the incorrect WE), post-test, and Optimal Outcomes Questionnaire. We summarized the key variables analyzed in Experiment 1, including their classification and descriptive statistics, to guide the interpretation of results and the use of appropriate statistical methods (

Table 4. (a) A summary of the instructional approaches, pre-test, practice equations, post-test, realistic best subscale and optimal best subscale, including their descriptive statistics, in Experiment 1. (b) A summary of the instructional approaches, pre-test, practice equations, post-test, mental effort, realistic best subscale and optimal best subscale, including their descriptive statistics, in Experiment 2.

(a)
Instructional Approach		Mean	Median	Minimum	Maximum
CICW	Pre-test	0.18	0.17	0.00	0.38
	Practice equations
	Type 1	0.82	1.00	0.00	1.00
	Type 2	0.50	0.50	0.00	1.00
	Type 3	0.23	0.00	0.00	0.75
	Post-test
	Type 1	0.64	1.00	0.00	1.00
	Type 2	0.06	0.00	0.00	0.35
	Type 3	0.00	0.00	0.00	0.00
	Realistic best subscale	2.53	2.50	1.58	3.67
	Optimal best subscale	3.34	3.17	2.33	4.67
WE	Pre-test	0.21	0.22	0.00	0.43
	Practice equations
	Type 1	0.90	1.00	0.00	1.00
	Type 2	0.83	1.00	0.00	1.00
	Type 3	0.42	0.25	0.00	1.00
	Post-test
	Type 1	0.85	1.00	0.00	1.00
	Type 2	0.09	0.05	0.00	0.65
	Type 3	0.20	0.00	0.00	1.00
	Realistic best subscale	2.34	2.17	1.42	3.17
	Optimal best subscale	3.62	3.67	2.42	4.92
PS	Pre-test	0.20	0.06	0.00	0.75
	Practice equations
	Type 1	0.63	0.81	0.00	1.00
	Type 2	0.35	0.09	0.00	1.00
	Type 3	0.18	0.00	0.00	1.00
	Post-test
	Type 1	0.71	1.00	0.00	1.00
	Type 2	0.10	0.00	0.00	0.50
	Type 3	0.21	0.00	0.00	1.00
	Realistic best subscale	2.72	2.71	2.33	3.92
	Optimal best subscale	3.65	3.63	3.00	4.25
(b)
Instructional Approach		Minimum	Maximum	Mean	Mean
CICW	Pre-test	0.31	0.33	0.00	0.78
	Practice equations
	Type 1	0.61	1.00	0.00	1.00
	Type 2	0.57	0.50	0.00	1.00
	Type 3	0.43	0.00	0.00	1.00
	Post-test
	Type 1	0.82	1.00	0.00	1.00
	Type 2	0.47	0.25	0.00	1.00
	Type 3	0.33	0.20	0.00	1.00
	Mental effort	5.17	5.00	3.00	9.00
	Realistic best subscale	3.22	3.08	2.42	5.00
	Optimal best subscale	3.54	3.42	3.00	5.00
WE	Pre-test	0.26	0.10	0.00	1.00
	Practice equations
	Type 1	0.84	1.00	0.00	1.00
	Type 2	0.80	1.00	0.00	1.00
	Type 3	0.37	0.00	0.00	1.00
	Post-test
	Type 1	0.92	1.00	0.00	1.00
	Type 2	0.55	0.55	0.00	1.00
	Type 3	0.07	0.00	0.00	1.00
	Mental effort	4.52	5.00	1.00	9.00
	Realistic best subscale	3.19	3.33	2.33	4.25
	Optimal best subscale	3.80	3.83	2.58	4.67
PS	Pre-test	0.37	0.35	0.00	1.00
	Practice equations
	Type 1	0.91	1.00	0.00	1.00
	Type 2	0.71	1.00	0.00	1.00
	Type 3	0.47	0.22	0.00	1.00
	Post-test
	Type 1	0.93	1.00	0.00	1.00
	Type 2	0.70	0.93	0.00	1.00
	Type 3	0.40	0.00	0.00	1.00
	Mental effort	4.86	4.50	1.00	9.00
	Realistic best subscale	3.26	3.25	2.58	3.92
	Optimal best subscale	3.90	3.92	3.25	4.50

Note. Instructional approaches are independent variables (CICW, WE, PS) and the practice equations (Type 1, Type 2, Type 3), post-test (Type 1, Type 2, Type 3), mental effort, realistic best subscale and optimal best subscale are dependent variables.

a).

One-way ANOVA showed no significant differences among the three groups on the pre-test, F(2, 40) = 0.11, p = 0.90, confirming that students had equivalent prior knowledge of linear equations before the intervention.

For the practice equations, Levene’s test confirmed homogeneity of variances for Type 1 (p = 0.08) and Type 2 (p = 0.23) but was borderline for Type 3 (p = 0.05). Furthermore, Mauchly’s test for sphericity was met (p = 0.09). Mixed 3 (approach) × 3 (equation) ANOVA revealed a significant main effect for equation type, F(2, 80) = 36.22, p < 0.001, partial η² = 0.48, indicating that performance varied across the three types of equations (i.e., Type 1 > Type 2 > Type 3; see Figure 2a). However, as shown in Figure 2a, none of the lines intersect, with each line representing a different approach. This indicates that the interaction between approach and equation type was not significant (<1.00, n.s.). The main effect for instructional approach was significant, F(2, 40) = 4.07, p = 0.03, partial η² = 0.17.

Supporting our hypothesis, pairwise comparisons revealed no significant differences among the three groups for Type 1 equations. For Type 2 equations, where we expected differential performance based on prior knowledge, the WE group outperformed the PS group (Ms = 0.83 vs. 0.35), SE = 0.16, p = 0.01, in line with our hypothesis. As illustrated in Figure 2a, the difference in mean scores was most pronounced between the WE and PS groups for Type 2 equations. However, the other pairwise comparisons for Type 2 equations were not significant. Contrary to our hypothesis, pairwise comparisons did not indicate significant differences between the groups for Type 3 equations. As shown in Figure 2a, the mean scores across the three groups were relatively similar for both Type 1 and Type 3 equations.

For the post-test, Levene’s test confirmed homogeneity of variances for Type 1 (p = 0.098) and Type 2 (p = 0.19) but not for Type 3 (p = 0.03). However, Mauchly’s test for sphericity was violated (p < 0.001). As a result, we conducted a mixed 3 (approach) × 3 (equation) ANOVA on mean proportion scores, applying the Huynh–Feldt correction. The main effect for equation type was significant, F(1.67, 66.73) = 80.02, p < 0.001, η² = 0.67, indicating significantly different mean proportion scores across the three types of equations (i.e., Type 1 > Type 2 > Type 3). As shown in Figure 2b, mean scores were highest for Type 1 equations, followed by Type 3, and lowest for Type 2 across the three groups. The interaction between approach and equation type was not significant, nor was there a significant main effect for instructional approach (for both, F < 1.00, n.s.) Consistent with the practice equation results, Figure 2b shows that none of the lines intersect, with each line representing a different instructional approach. Furthermore, the mean scores for each equation type remained relatively consistent across the three groups.

Unexpectedly, both the WE and PS groups scored lower on Type 2 equations compared to Type 3 equations (see Figure 2b). One possible explanation is that students struggled with manipulating the negative pronumerals in the Type 2 equations. For example, in the equation x + 2(3 − x) = 12, the first solution step is x + 6 − 2x = 12. This implies that the subsequent solutions steps would involve the manipulation of a negative pronumeral, which could be particularly challenging to students (Ngu & Phan, 2022; Vlassis, 2002). There are two possibilities for Type 3 equations. Consider the equation x − 4(2 − x) = 7, where the first solution step is x − 8 + 4x = 7, which implies that the subsequent solution steps would involve a positive pronumeral. Also, consider x + 4(−2 − x) = 7, where the first solution step is x − 8 − 4x = 7, which means that the subsequent solution steps would involve a negative pronumeral and a negative number (Ngu & Phan, 2022).

The reliability estimates for the realistic best subscale and optimal best subscale were 0.66 and 0.73, respectively. Split-half reliability testing was conducted across both experiments, comparing the odd-numbered and even-numbered items. The reliability score remained consistent across both sets of items. One-way ANOVA revealed no significant differences between the three groups on either the realistic best subscale, F(2, 40) = 2.12, p = 0.13, or the optimal best subscale, F(2, 40) = 1.19, p = 0.31. These results provided partial support for the hypothesis. Although the WE group had a higher mean score than the PS group on Type 2 practice equations (see Figure 2a), they did not exhibit greater optimism regarding their future aspirations to learn mathematics.

In summary, the increasing complexity of the equations—ranging from Type 1 < Type 2 < Type 3—was reflected in the mean proportion scores for the practice equations and, to a lesser extent, the post-test across the three instructional approaches. The WE group outperformed the PS group on Type 2 practice equations; however, there were no significant differences between the groups on the post-test. Contrary to our hypothesis, the performance of the CICWE group did not align with past research, suggesting beneficial effects of incorrect examples for low prior knowledge students (Barbieri & Booth, 2016, 2020).

Interestingly, analysis of the realistic best subscale and optimal best subscale revealed that neither belief in realistic achievement best nor belief in optimal achievement best was a function of the instructional approach. This suggests that the three groups shared similar perceptions regarding their future potential for learning both simple tasks (e.g., Type 1 equations) and more complex tasks (e.g., Types 2 and 3 equations).

11. Experiment 2

According to the literature, the effectiveness of an instructional approach depends on a student’s level of expertise (Kalyuga et al., 2003). In Experiment 2, we invited Form 1 students (equivalent to Year 8 students in Australia), who had greater prior knowledge of linear equations than the Year 4 students in Experiment 1. These Year 8 students had studied multi-step linear equations (e.g., 5x − 3 = 2x + 7) four months before the start of Experiment 2. Therefore, the key difference between Experiment 1 and Experiment 2 was the students’ level of prior knowledge in linear equations.

One might question whether the cognitive development level of the two samples (i.e., China vs. Malaysia) differed. In examining the relationship between instructional approach and learning outcomes (e.g., academic performance), we argue that the development of domain-specific prior knowledge is a crucial factor that can profoundly influence learning (Kalyuga et al., 2003). For example, Cai et al. (2005) investigated elementary mathematics curricula across five countries (the US, South Korea, Russia, Singapore, and China) with respect to the development of algebraic concepts in earlier grades. In China, the elementary mathematics curriculum introduces formal algebraic thinking through the topic of solving linear equations, while in the US this topic is not typically taught in elementary school.

This contrast suggests that, unlike US mathematics educators, Chinese educators may have a different perspective: they believe that elementary school children’s cognitive development reaches a level that allows them to engage in logical reasoning when learning how to solve linear equations (e.g., multi-step equations). This viewpoint is essential, as it emphasizes the importance of cognitive growth in learning complex concepts like algebra (Grammer et al., 2013; Ojose, 2008; Yu-Kang & Law, 2009).

The importance of cognitive development (e.g., the cognitive development of a 7-year-old child versus that of a 12-year-old child) is emphasized in various theoretical accounts. For instance, despite valid and logical criticisms, Piaget’s (1963, 1990) theory of individual cognition asserts that children between the ages of 7 and 8, who are in the concrete operational stage of cognitive development, are capable of engaging in logical reasoning. According to Piaget, this cognitive ability further advances when a child reaches the formal operational stage. Reflecting Piaget’s (1963, 1990) theory, Markovits et al. (1989) found that children between the ages of 6 and 11 were able to distinguish between logical and illogical syllogisms.

Based on Piaget’s theoretical framework and existing research (e.g., Cai et al., 2005; Markovits et al., 1989; Ojose, 2008), we anticipated that students in Experiment 1 (mean age = 10) and Experiment 2 (mean age = 14) would be able to engage in logical reasoning as they worked through the solution steps of linear equations.

12. Method

12.1. Participants

The participants were 68 Form 1 students (38 girls, 30 boys) with a mean age of 14.07 years (SD = 0.21). They were recruited from two classes at a rural school in Malaysia and provided informed consent to participate in the study. The students came from diverse ethnic backgrounds: Malay (35%), Chinese (35%), and Indigenous (30%). Random assignment allocated 23 students to the CICWE group, 23 to the WE group, and 22 to the PS group.

These students followed the national curriculum for mathematics education, with Malay as the primary language of instruction. However, both mathematics and science were taught in English. According to the mathematics teacher, the students were expected to understand the test material, which was presented in English.

We used a repeated-measures ANOVA with a within-between interaction in G*Power to calculate the minimum sample size required for Experiment 2. The final sample size of 68 students exceeded the minimum requirement of 36 participants, based on a priori power calculations for an effect size, f = 0.25, for power = 80% and Type I error rate = 5% (Cohen, 1988).

12.2. Materials, Procedure, and Scoring

The test materials, procedure, and scoring were identical to those used in Experiment 1 and, therefore, are not described here. The Cronbach’s alpha values for the pre-test, practice equations, and post-test were 0.94, 0.90, and 0.93, respectively.

13. Results and Discussion

The means and standard deviations for the pre-test, practice equations, justification (i.e., regarding the wrong solution step in the incorrect WE), post-test, mental effort, and Optimal Outcomes Questionnaire are presented in Table 3. We provided a summary of key variables analyzed, including their classification and descriptive statistics, to guide interpretation of the results and the selection of appropriate statistical methods (Table 4b).

There were no significant differences among the three groups on the pre-test, F(2, 65) = 0.84, p = 0.44, suggesting that the groups had similar levels of prior knowledge of linear equations before the intervention. As expected, the mean proportion pre-test score of the Malaysian students was higher than that of the Chinese students.

To analyze the mean scores for the practice equations and post-test, we conducted a mixed 3 × 3 ANOVA, with instructional approach (CICWE, WE, PS) as the between-subjects factor and equation type (Type 1, Type 2, Type 3) as the within-subjects factor. For the practice equations, Levene’s test confirmed homogeneity of variances for Type 1 (p = 0.08) and Type 2 (p = 0.21) but not for Type 3 (p = 0.04). Mauchly’s test for sphericity was violated (p < 0.001). Using the Huynh–Feldt correction, we found a significant main effect for equation type, F(1.61, 104.43) = 27.21, p < 0.001, partial η² = 0.30, indicating differential mean scores within the three types of equations (i.e., Type 1 > Type 2 > Type 3) across the three instructional approaches. These results were consistent with the findings from Experiment 1. However, neither the interaction between instructional approach and equation type nor the main effect for instructional approach was significant (for both, F < 1, n.s.). In summary, as shown in Figure 3a, mean scores for both Type 1 and Type 2 equations were higher than those for Type 3 across all three groups. Additionally, none of the lines intersect, with each line representing a different instructional approach, and the mean scores for each equation type remained relatively consistent across the three groups.

For the post-test, similar to the practice equations, Levene’s test confirmed homogeneity of variances for Type 1 (p = 0.10) and Type 2 (p = 0.18), but not for Type 3, equations (p = 0.10). Mauchly’s test for sphericity was satisfied (p = 0.32). Mixed 3 (approach) × 3 (equation) ANOVA conducted on the post-test scores revealed a significant main effect for equation type, F(2, 130) = 95.01, p < 0.001, partial η² = 0.59. Similar to the results obtained for the practice equations, there were significant differences in mean scores across the three types of equations (i.e., Type 1 > Type 2 > Type 3, see Figure 3b). Additionally, the interaction between instructional approach and equation type was significant F(2, 65) = 5.62, p < 0.001, partial η² = 0.15, while the main effect for instructional approach was not significant (F < 1, n.s.) In summary, as illustrated in Figure 3b, mean scores for Type 3 equations were lower than those for Type 1 and Type 2 across all three groups, similar to the results obtained for the practice equations. Moreover, the mean scores for each equation type remained relatively consistent across groups. In contrast, the lines representing the PS and WE groups intersected, indicating that the PS group outperformed the WE group.

We hypothesized that performance on Type 1 equations would be independent of instructional approach. For high prior knowledge students, we also hypothesized that the order of instructional efficiency for Type 2 and/or Type 3 equations would be: CICWE > PS > WE. Pairwise comparisons revealed no significant differences among the groups for either Type 1 or Type 2 equations. However, for Type 3 equations, the PS group outperformed the WE group (Ms = 0.07 vs. 0.40), SE = 0.11, p = 0.02, demonstrating an expertise reversal effect (Figure 3b). There were no significant differences between CICWE and the other groups for Type 3 equations. Overall, the results supported Hypothesis 1 and partially supported Hypothesis 2b.

The reliability estimates for the realistic best subscale and optimal best subscale were 0.62 and 0.79, respectively. As hypothesized, the three groups did not differ on the realistic best subscale, F(2, 65) = 0.14, p = 0.87, but they did show significant differences on the optimal best subscale, F(2, 65) = 3.43, p = 0.04. A follow-up Tukey post hoc test revealed that the PS group scored higher than the CICWE group (group mean difference = 0.36, p = 0.04). No significant differences were found between the other group pairs (p > 0.05). These results suggest that the CICWE approach did not lead to greater motivation compared to either the PS or WE approach. Instead, exposure to the PS approach appeared to enhance high prior knowledge students’ optimistic perceptions of their ability to excel in solving complex linear equations.

Although the three groups did not differ in terms of mental effort, F(2, 65) = 0.68, p = 0.51, the results followed the predicted trend: CICWE > PS > WE (see Table 3). In support of Hypothesis 4, no significant correlations were found between mental effort and the optimal best subscale for the CICWE group, r(23) = 0.29, p = 0.17, the WE group, r(23) = 0.10, p = 0.64, or the PS group, r(22) = 0.30, p = 0.18. These findings suggest that cognitive load, as indicated by a student’s perceived mental effort, was not associated with belief in achieving optimal success.

In summary, a mixed 3 (approach) × 3 (equation) ANOVA conducted on both the practice equations and post-test revealed a significant main effect for equation type. This finding affirmed the three levels of complexity in Types 1, 2, and 3 equations. No statistically significant differences were observed among the three groups for the practice equations. However, consistent with prior research on the expertise reversal effect (Kalyuga et al., 2003), the PS group outperformed the WE group on the post-test as the complexity of the equations increased. The hypothesis that the CICWE approach would be more effective than both the PS and WE approaches for high prior knowledge students was not supported.

As hypothesized, regarding the realistic–optimal achievement best dichotomy (Phan et al., 2017) as an outcome of instructional manipulation, the three groups differed on the optimal best subscale but not on the realistic best subscale. The lack of significant correlations between mental effort and the optimal best subscale across all three groups provided partial validation of the hypothesis that cognitive load negatively impacts students’ belief in achieving optimal success. In other words, these results suggest that cognitive load, as reflected by students’ perceived mental effort, was not associated with subsequent belief in achieving their optimal best.

14. General Discussion

14.1. Theoretical and Practical Contributions for Consideration

The aim of this study was to investigate the relationship between instructional designs, material complexity, cognitive load imposition, and belief in achieving optimal success. We hypothesized that the relative effectiveness of the CICWE, WE, and PS approaches would depend on students’ prior knowledge and the complexity of the linear equations. As reported, performance on Type 1 equations did not differ across the three instructional approaches, regardless of a student’s prior knowledge level.

Consistent with previous research (Sweller et al., 2011), for low prior knowledge students, the WE group outperformed the PS group on Type 2 equations on the practice problems. However, contrary to our hypothesis, the performance of the CICWE group did not align with past research (Barbieri & Booth, 2016, 2020), which found a positive effect for providing incorrect examples to low prior knowledge students. The CICWE group seemed to lack the essential knowledge to identify and/or rectify the errors in the incorrect WEs, despite being prompted to view the parallel correct step in the correct WEs. Moreover, simultaneously examining both the correct and incorrect WEs, coupled with the task of justifying the error, may have imposed a high level of element interactivity, which likely disadvantaged low prior knowledge students due to excessive cognitive load.

Interestingly, the expertise reversal effect was observed in Experiment 2. An advantage of the PS approach over the WE approach was evident for Type 3 equations for students with high prior knowledge. Contrary to the findings of Große and Renkl (2007), students with high prior knowledge in the CICWE group did not outperform those in the PS or WE group. Overall, the findings of both experiments support the principles of cognitive load theory (Sweller et al., 2011). The suitability of an instructional approach would be more evident for complex rather than simple linear equations based on a student’s prior knowledge. Consistent with the results obtained by van Peppen et al. (2021), the CICWE group did not perform better than either the WE group or the PS group, regardless of prior knowledge.

As hypothesized, regardless of a student’s prior knowledge level, their indication of ‘realistic achievement best’ for simple linear equations was independent of the instructional approach used. In contrast, the instructional design did influence a student’s indication of ‘optimal achievement best’ for complex linear equations, particularly for students with higher prior knowledge. We speculate that students with higher prior knowledge may have perceived the appropriate instructional approach as a source of motivation, enhancing their self-confidence and determination (i.e., a student’s resolve and sustained concentration) to persist in learning (Phan et al., 2017).

Previous research (e.g., Feldon et al., 2018; Likourezos & Kalyuga, 2017) has suggested that cognitive load can influence a student’s motivation. For example, a high level of extraneous cognitive load might overwhelm a student’s comprehension, leading to a decline in their interest, persistence, and personal resolve. Conversely, germane cognitive load tends to facilitate student engagement, persistence, and motivation (Huk & Ludwigs, 2009; Rey & Buchwald, 2011). However, our study took a slightly different perspective by focusing on the concept of ‘optimal achievement best’ (Fraillon, 2004; Mascolo et al., 2010; Phan et al., 2016).

As outlined earlier, the aim of our research was to explore the relationship between the varying efficiencies of instructional approaches (considering both material complexity and cognitive load) and differing levels of motivation, as reflected in the ‘realistic–optimal achievement best dichotomy’. Research using structural equation modeling (SEM) (Kline, 2011; Schumacker & Lomax, 2004) found that optimal achievement best practices positively influenced intrinsic motivation for learning (β = 0.43, p < 0.001) (Phan et al., 2018). This suggests that a belief in achieving optimal best practice may, in part, serve as a proxy for a student’s intrinsic motivation for academic learning.

We propose, for future research, that belief in optimal achievement best could vary depending on instructional designs and the complexity of learning tasks. This idea aligns with our earlier work (Phan et al., 2017), which introduced the Framework of Achievement Bests, reflecting the philosophical underpinnings of our approach.

14.2. Limitations and Future Directions

While the present study makes valuable empirical contributions, several limitations should be considered. One challenge we faced was collecting data in regular classrooms across two cultural contexts. Several schools in both countries declined to participate in Experiment 1 and Experiment 2, a common issue in social science research, which many researchers, educators, and students encounter. As a result, the sample sizes in both cohorts were relatively small. Additionally, the assumption for variances, as tested by Levene’s test, was not met for all types of equations in both experiments. To address this issue, future research could aim to collect data from multiple schools to enhance statistical analyses.

Differential prior knowledge of linear equations was evident between Chinese students and Malaysian students due to differences in grade levels, which was confirmed by the pre-test scores. While we acknowledge the impact of prior knowledge upon learning, other factors could also have influenced students’ learning outcomes. These include ethnic composition (e.g., homogeneous vs. diverse groups), language (Mandarin vs. Malay), and differences in mathematics curricula (e.g., China vs. Malaysia). It is well established that China places a strong emphasis on mathematics education (Stevenson et al., 1990). Linear equations, for example, are introduced earlier in elementary school mathematics in China (Cai et al., 2005), whereas in Malaysia, this topic is typically covered later, in junior secondary education. This earlier introduction to algebra in China might provide students with an advantage. However, our results suggest otherwise, as the PS group did not outperform the WE group among Chinese students. Therefore, while cultural differences may have some impact, the findings primarily reflect the cognitive processes involved in learning linear equations, which seem to be more influential than cultural background.

While we accounted for prior knowledge through a pre-test, incorporating a mathematical ability measure (e.g., DPV) in future studies would allow for a more precise correlation between ability and performance to be established. Furthermore, socio-economic status (SES) data were not collected, which limited our ability to explore the relationship between performance and students’ SES. Given that SES can influence access to educational resources and learning outcomes (Tan, 2024), future research should consider including SES variables to provide a more comprehensive understanding of the factors affecting students’ learning of linear equations.

Additionally, similar to previous research (Große & Renkl, 2007; van Peppen et al., 2021), we assigned one mark (i.e., a numerical value) when a student provided a correct explanation for the error in the incorrect WE. We reasoned that students would have understood the correct sequence of solution steps if they could accurately explain the error. Future research could expand upon this by conducting interviews, either individually or in focus groups, to determine whether students truly understand the correct solution steps once they have provided an accurate explanation of the error in the solution.

In the present study, students in the CICWE group were exposed to six pairs of linear equations, each consisting of a correct worked example (WE) and an incorrect WE (with an error in Line 2, Appendix B) that shared the same linear equation. We hypothesized that the additional instructional support provided by the CICWE approach, which targeted conceptual barriers such as manipulating negative numbers and negative pronumerals, would help high prior knowledge students engage in deeper learning of the solution steps, particularly as they were required to justify incorrect solution step. Our results for the CICWE group, in fact, were consistent with those that Pillai et al. (2020) obtained. We expected that once the CICWE group could identify and justify the error in the incorrect WE, they would be able to understand the correct solution procedure for linear equations. However, we speculated that the lack of practice in solving equations might have disadvantaged the CICWE group. Studies by Barbieri and Booth (2016, 2020), in contrast, required students to solve practice problems after studying incorrect examples. Loibl et al. (2020) also highlighted that practice exercises facilitate the acquisition of procedural fluency. We therefore propose that future studies should incorporate practice problems after comparing the correct and incorrect WE. This design would target both the conceptual barriers (e.g., manipulation of negative numbers) and the procedural fluency needed to correctly execute solution steps.

Prior research has advocated side-by-side comparison instead of sequential comparison of two worked examples to decrease cognitive load by reducing the effort required to retrieving one of the worked examples (Richland & McDonough, 2010). In our study, although the CICWE pairs were presented sequentially, both the correct and incorrect WEs were visible to students at the same time. Thus, this presentation format likely reduced cognitive load. Nonetheless, we acknowledge that sequential presentation might limit the effectiveness of the CICWE approach, and we recommend that future research explore presenting CICWE examples side by side to maximize learning outcomes.

Although the CICWE approach did not outperform the PS and WE approaches for high prior knowledge students in this study, it remains worth exploring for other mathematical topics. For instance, future studies could examine the use of CICWE for teaching percentage problems, where students often struggle with interpreting contextual problem situations. A typical example might be: ‘After a 12% markup, the shoes now cost $34. How much did they originally cost?’ (Parker & Leinhardt, 1995). Students might mistakenly use intuition or faulty logical reasoning to calculate $34 × 12% and subtract the result from $34, resulting in a wrong answer. As an instructional approach, we could ask students to compare and justify the difference between the correct solution procedure generated by the correct format of an equation (e.g., $34 = x + x × 12%, where x represents the original price) and the incorrect solution procedure generated by the incorrect format of equation (e.g., x = $34 − $34 × 12%, where x represents the original price). This comparison could demonstrate how the CICWE approach might assist students in comprehending and solving percentage problems.

The expertise reversal effect (Kalyuga et al., 2003), which was observed in this study, highlights the importance of considering a student’s level of prior knowledge when designing instructional approaches. One possible future direction is to design worked examples that emphasize the ‘fading out’ of solution steps as students gain expertise (Renkl et al., 2002). This raises an interesting question: will a student’s motivation remain high as the teacher gradually removes scaffolding (i.e., the solution steps)? Exploring this question could provide insight into how instructional approaches influence motivation as students progress toward greater expertise. It would also be valuable to explore how a student’s increasing knowledge of the subject matter impacts their motivational beliefs, such as personal resolve—the internal state of decisiveness and concentration that helps a student stay on task despite obstacles (Phan et al., 2017, 2019). This concept of personal resolve aligns with the notion of ‘grit’ (Neroni et al., 2022; Rimfeld et al., 2016), and future research could investigate whether this internal motivation varies as students gain expertise.

15. Conclusions

In conclusion, the results of this study offer valuable insights with practical implications for international mathematics curriculum design. Across the two experiments involving Chinese and Malaysian students, we observed that the presence of complex elements (e.g., negative pronumerals) in linear equations significantly affects their overall complexity. These findings provide empirical evidence supporting cognitive load effects, consistent with prior research (Sweller et al., 2011). Instructional efficiency was more pronounced when students learned complex linear equations, regardless of students’ levels of expertise.

Additionally, this study contributes to the broader discourse on best practices in mathematics education (Ngu et al., 2023; Mascolo et al., 2010; Granero-Gallegos et al., 2023; Phan et al., 2016). It highlights that the cognitive load experienced during learning may adversely affect a student’s belief in their ability to achieve their optimal best in mathematics, reinforcing the need for designing instructional approaches that carefully manage cognitive load to support student motivation and achievement.