Nonsingular Integral-Type Dynamic Finite-Time Synchronization for Hyper-Chaotic Systems
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.3. Contribution
- N nonsingular integral-type controller design for the category of N-dimensional hyper-chaotic systems;
- The design of a new nonsingular integral-type controller for fast synchronization;
- The design of finite-time synchronization of a new six-dimensional master-slave systems;
- A plan that ensures finite-time stability and eliminates the effects of the chatting phenomenon.
1.4. Paper Organization
2. System Definition and Preliminaries
- (I)
- It should be stable asymptotically in subset ;
- (II)
- It should be finite-time convergent in subset . A convergence time exists with as and stays equal to zero thereafter. In addition, if , then the equilibrium is considered to be globally finite-time stable.
3. Main Results
3.1. Integral Terminal Sliding Surface
3.2. Finite-Time Integral-Type Hyper-Chaotic Synchronization
3.3. Finite Time Tracker Design
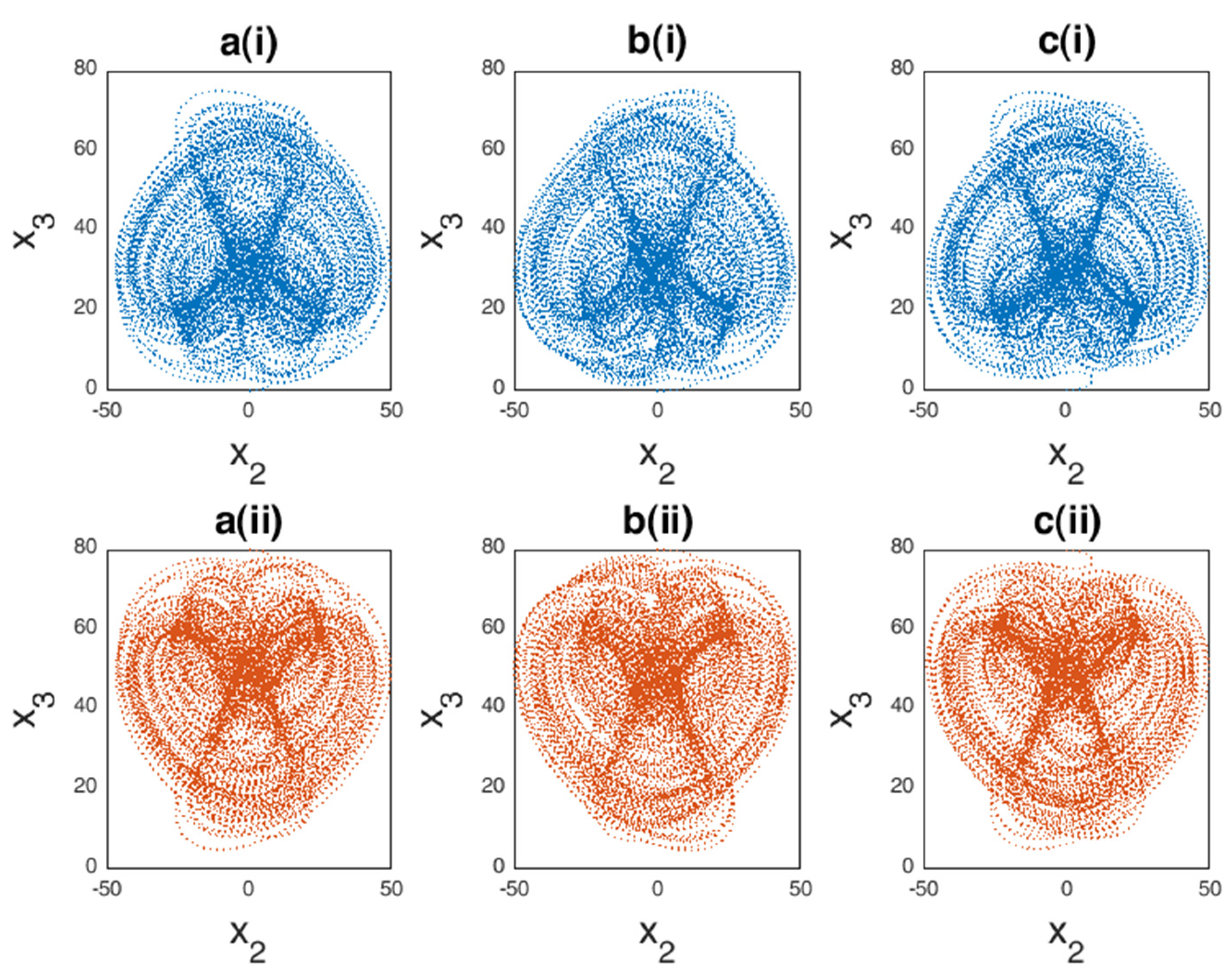
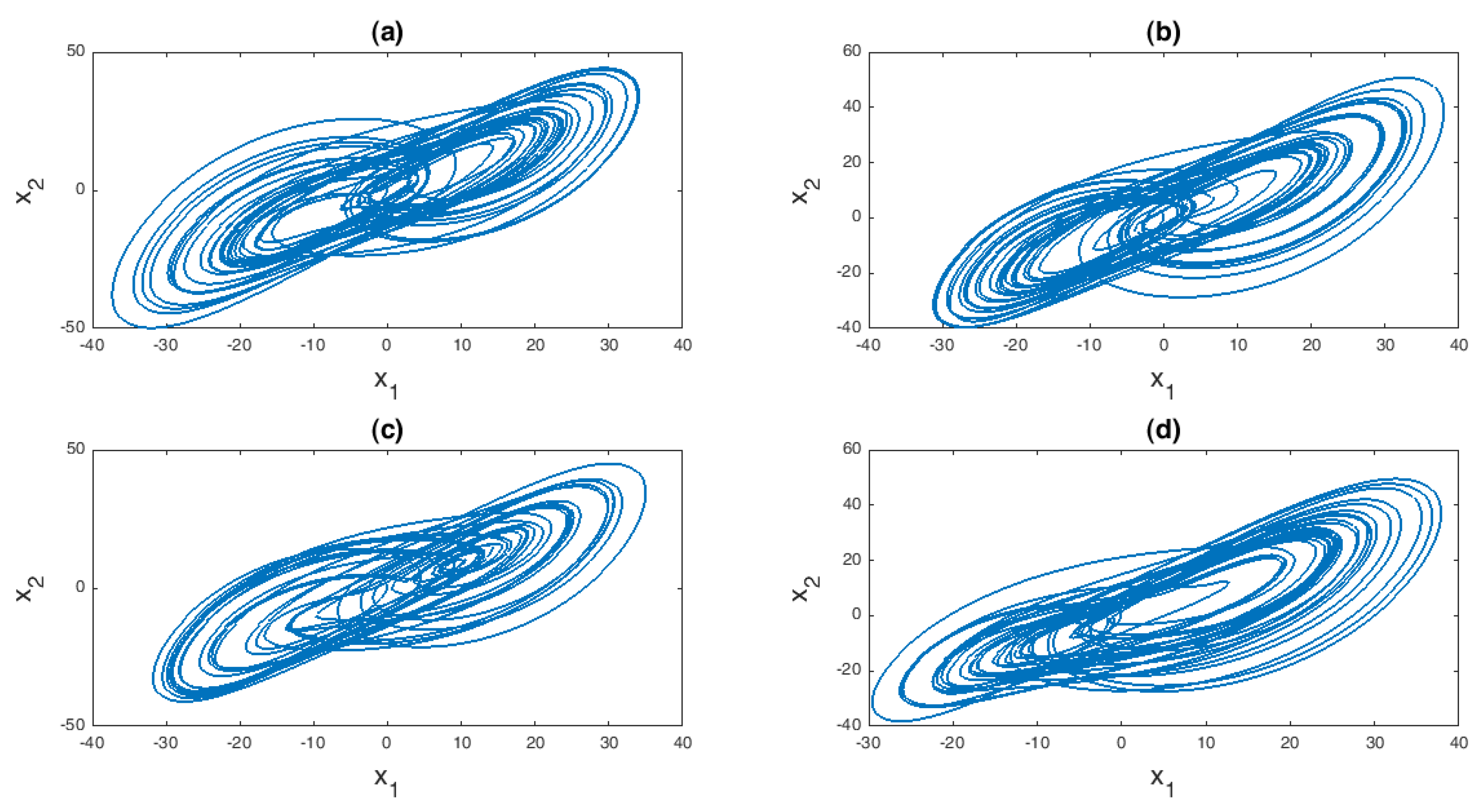
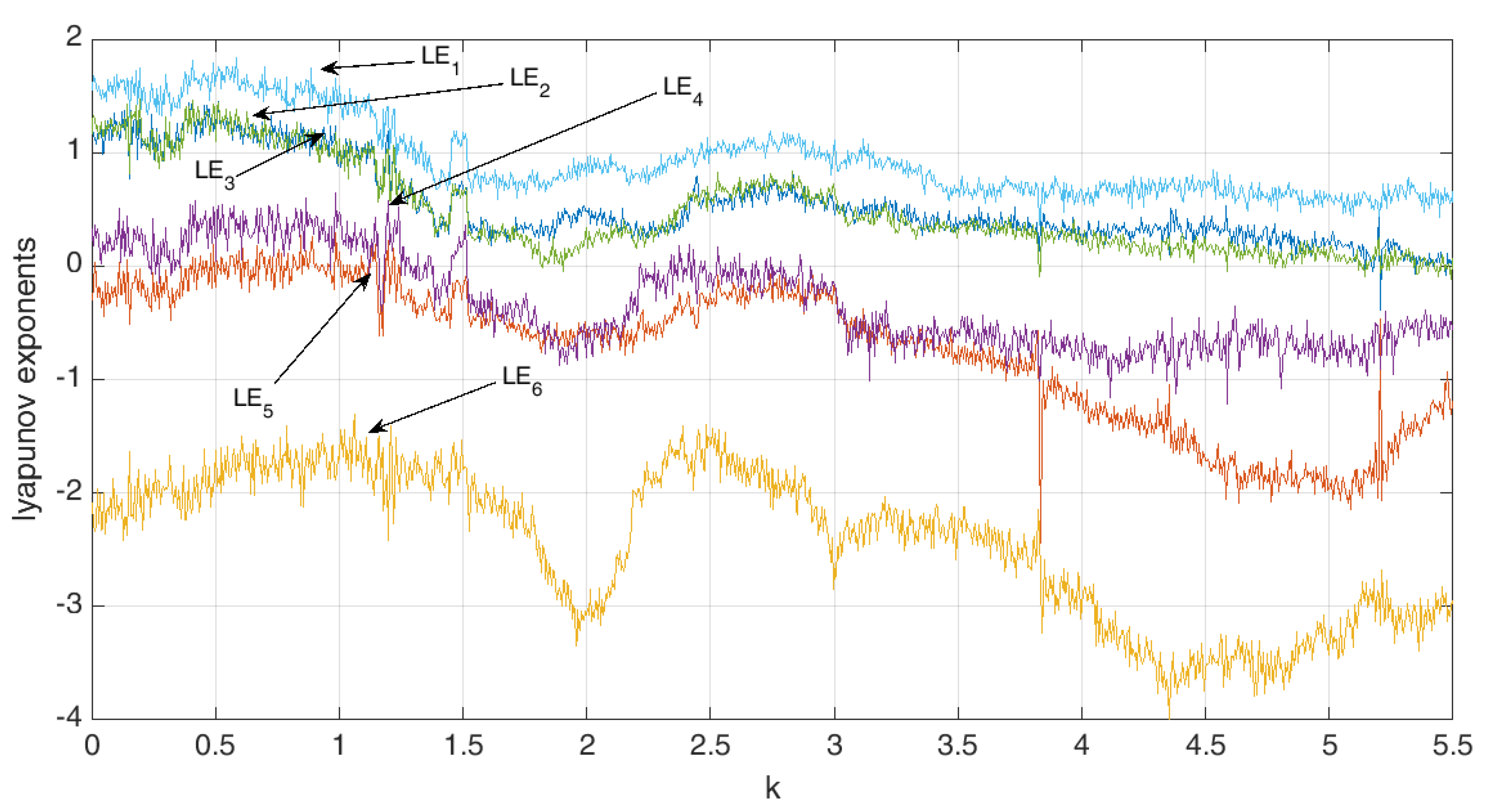
4. Simulation Results
4.1. Introduction and Formulation
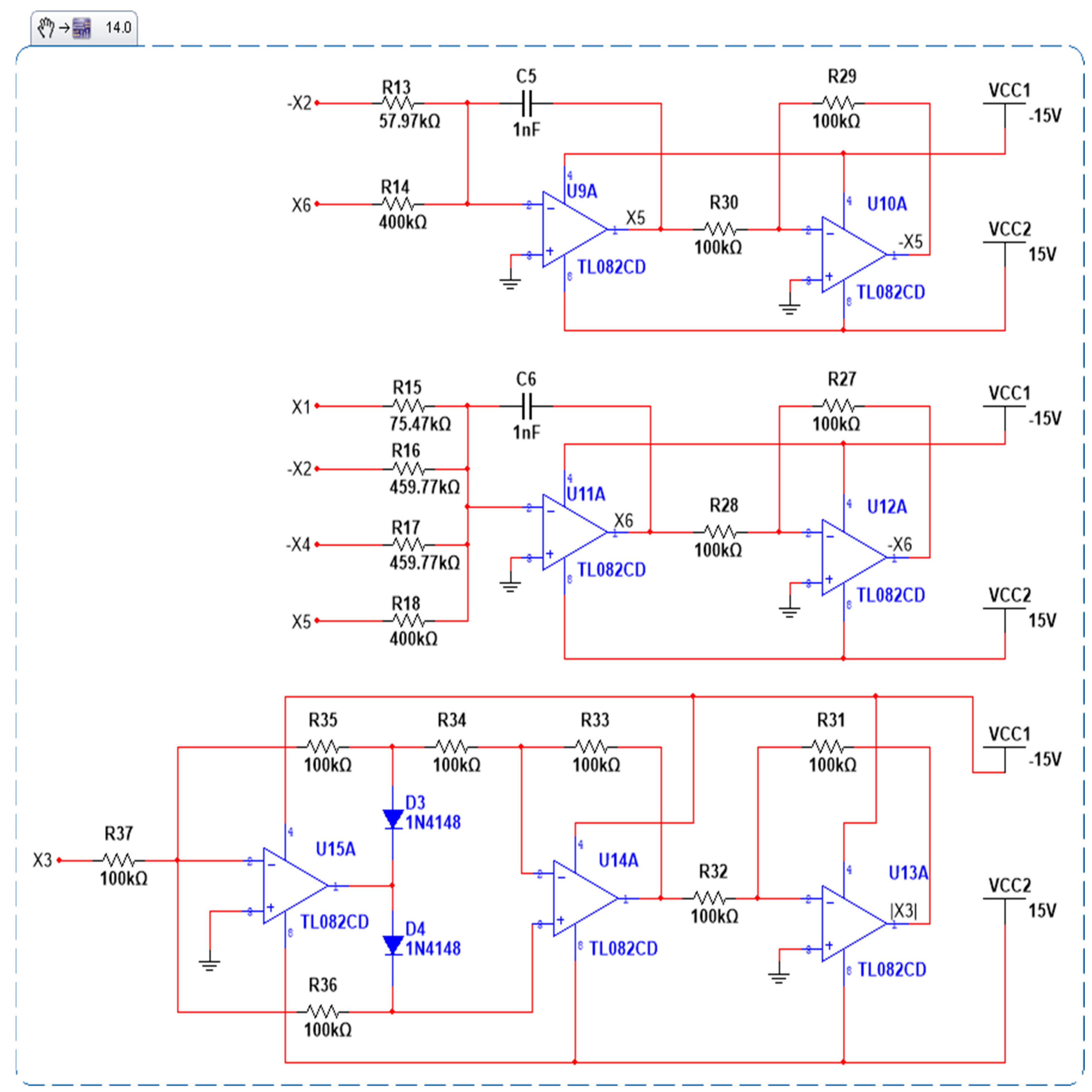
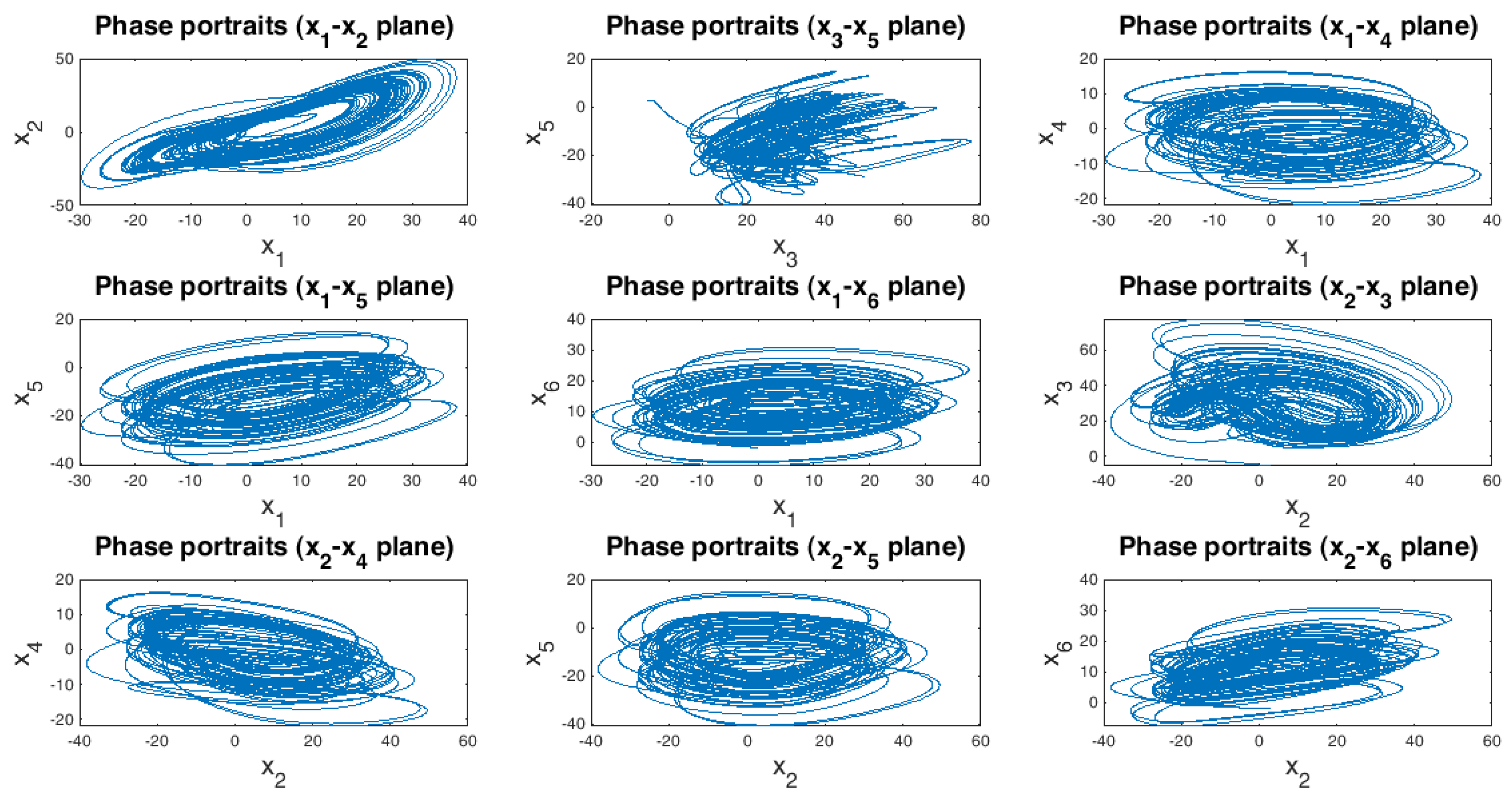
4.2. Circuit Realization of the New Hyperchaotic System
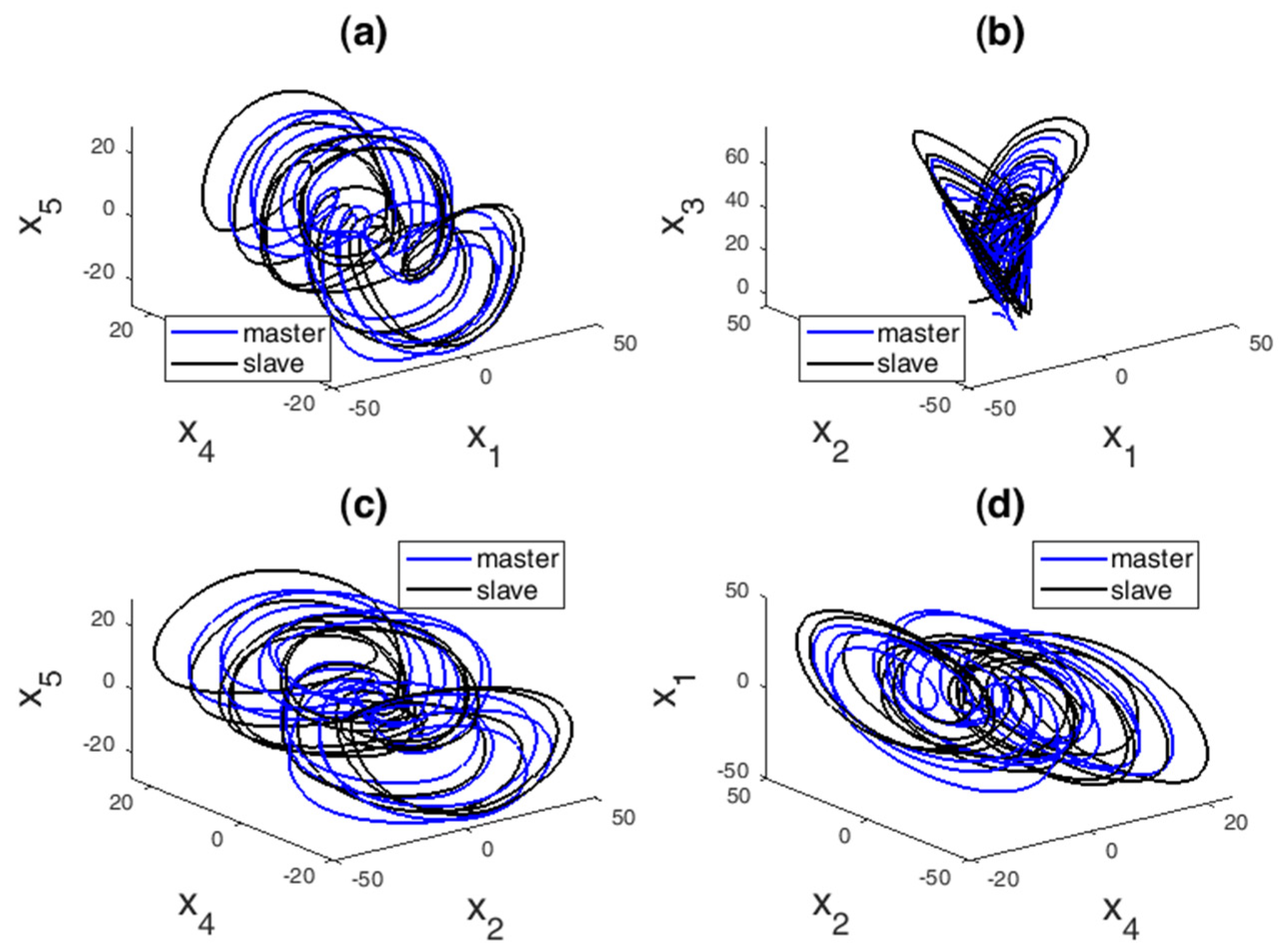
4.3. Hyper-Chaotic Synchronization
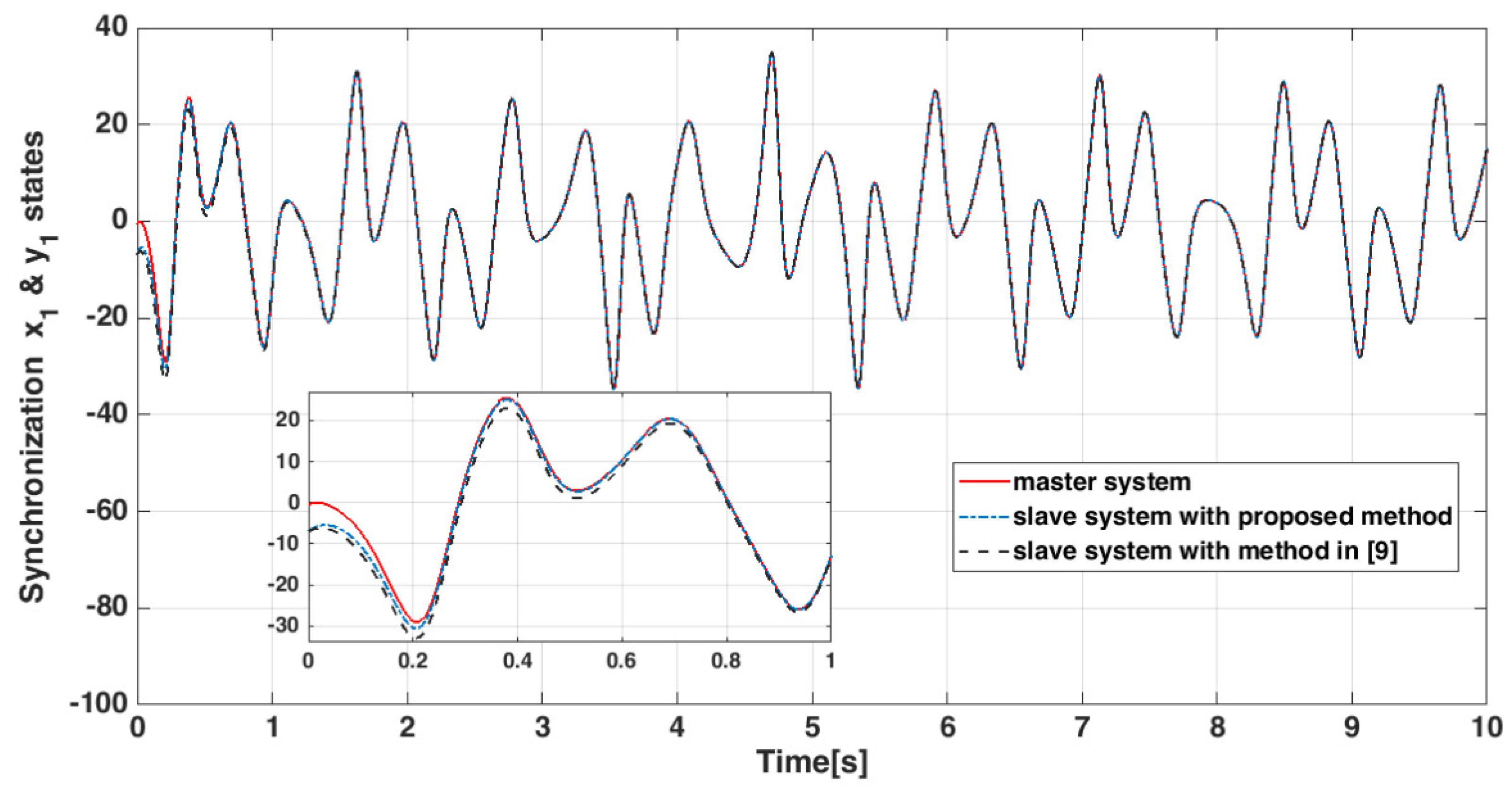
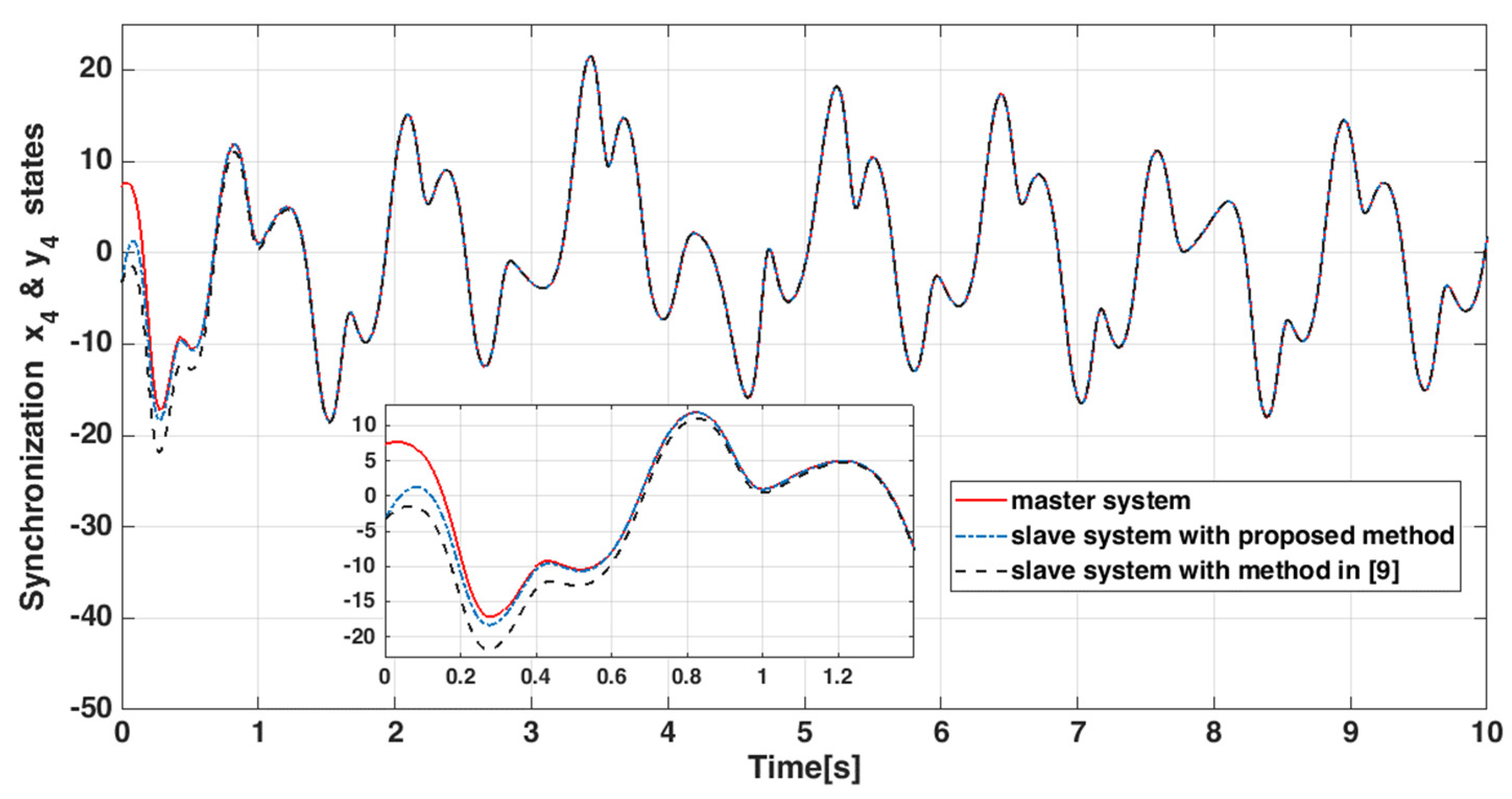
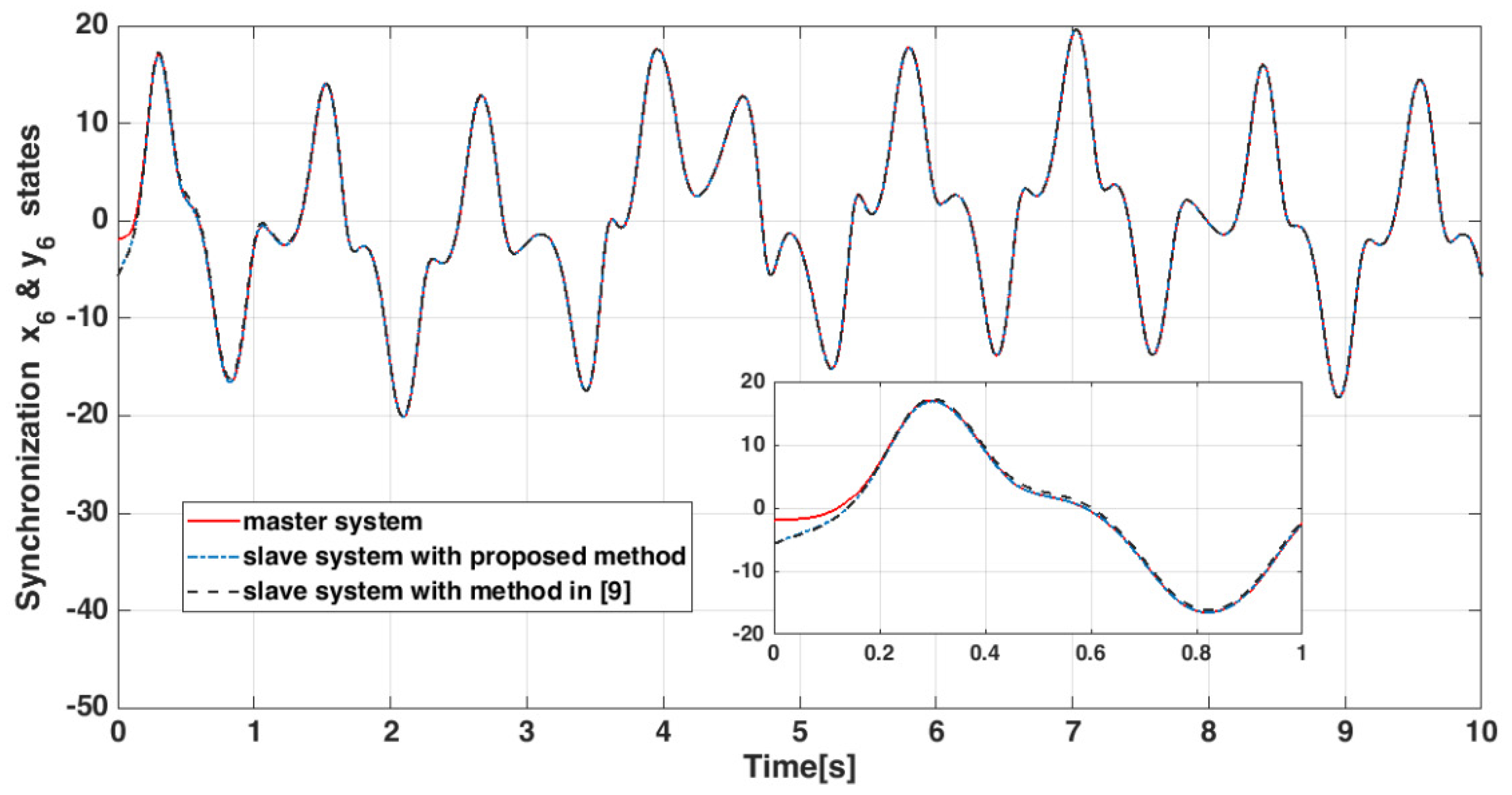
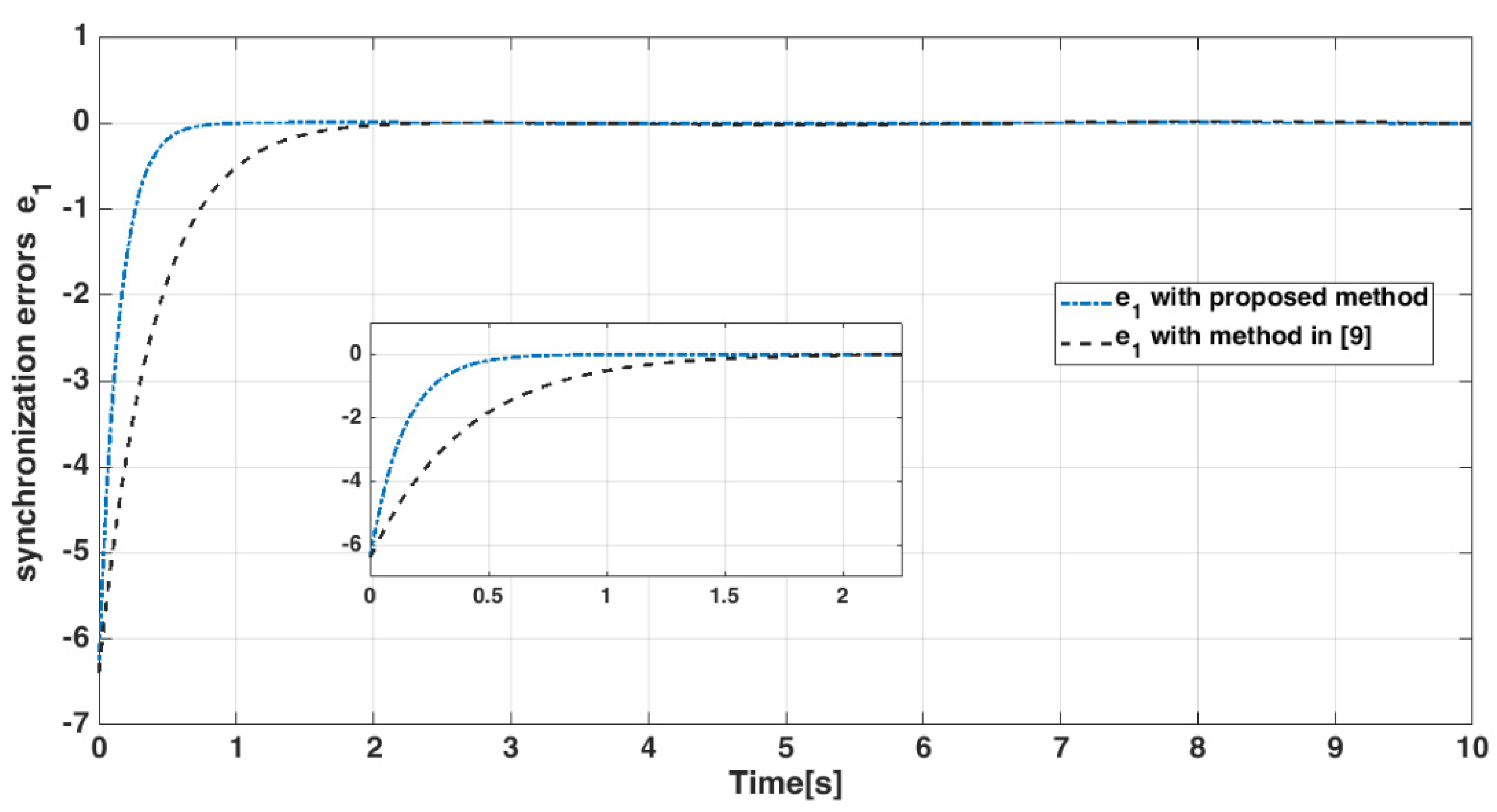
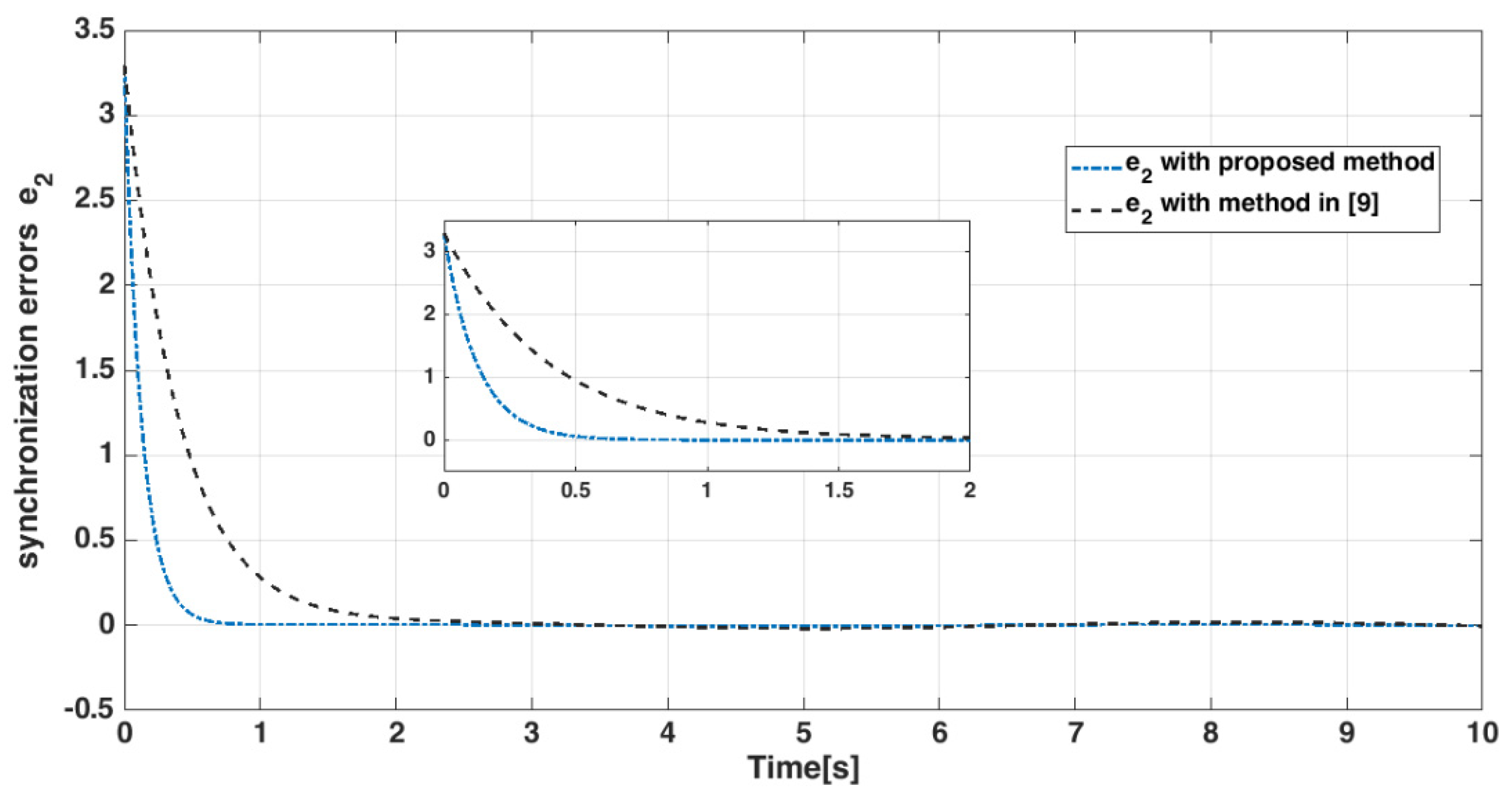
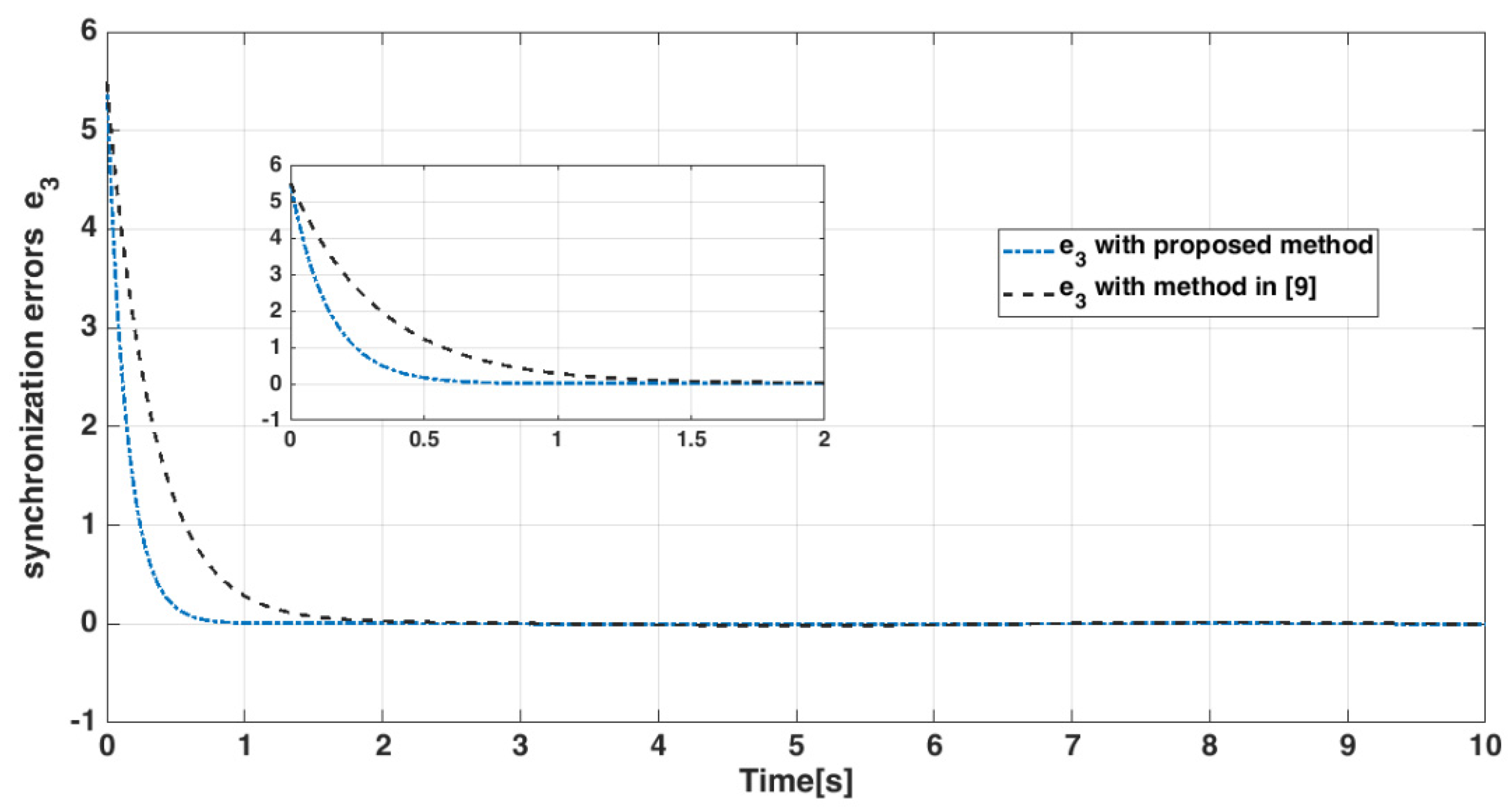
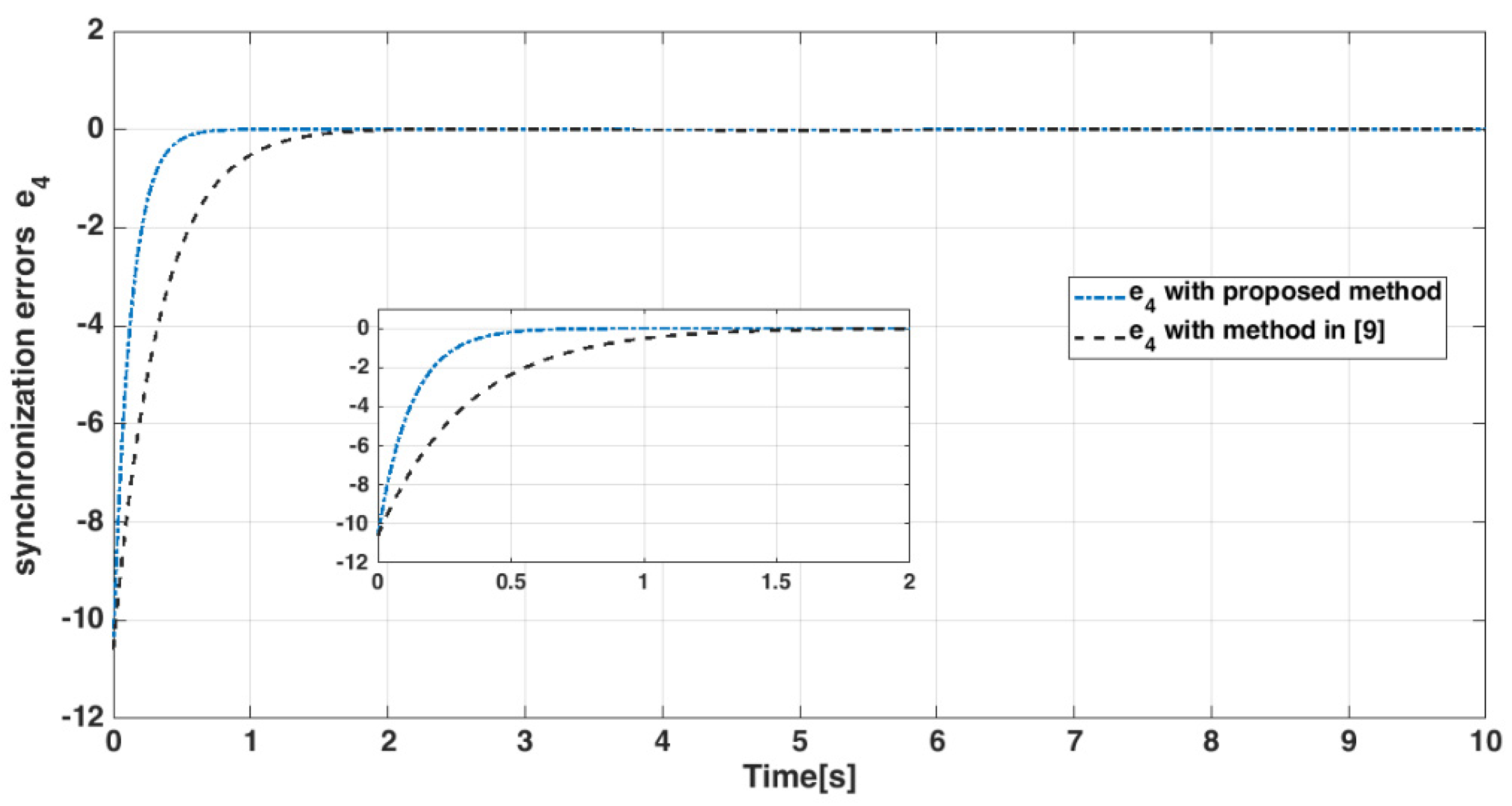
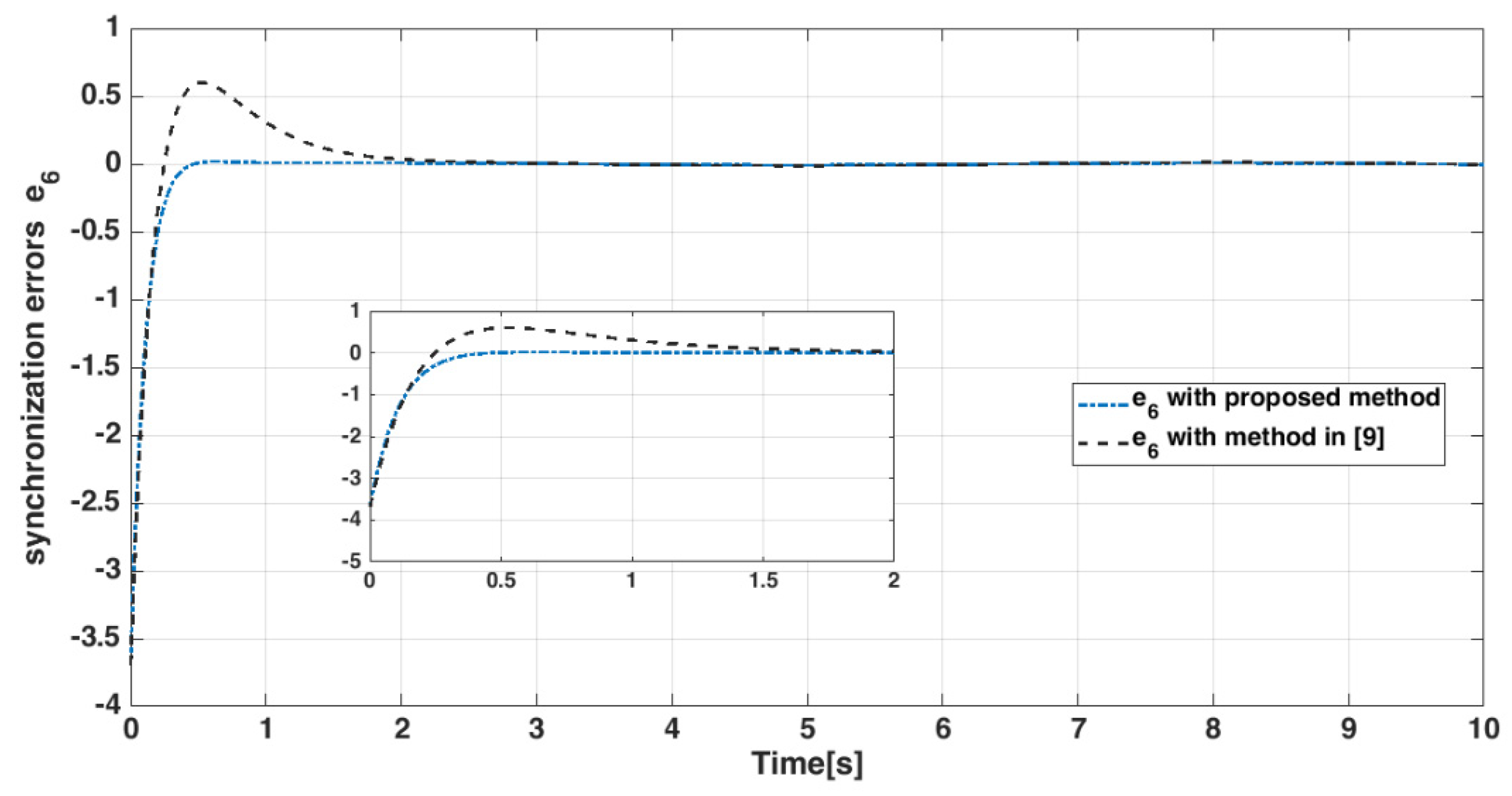
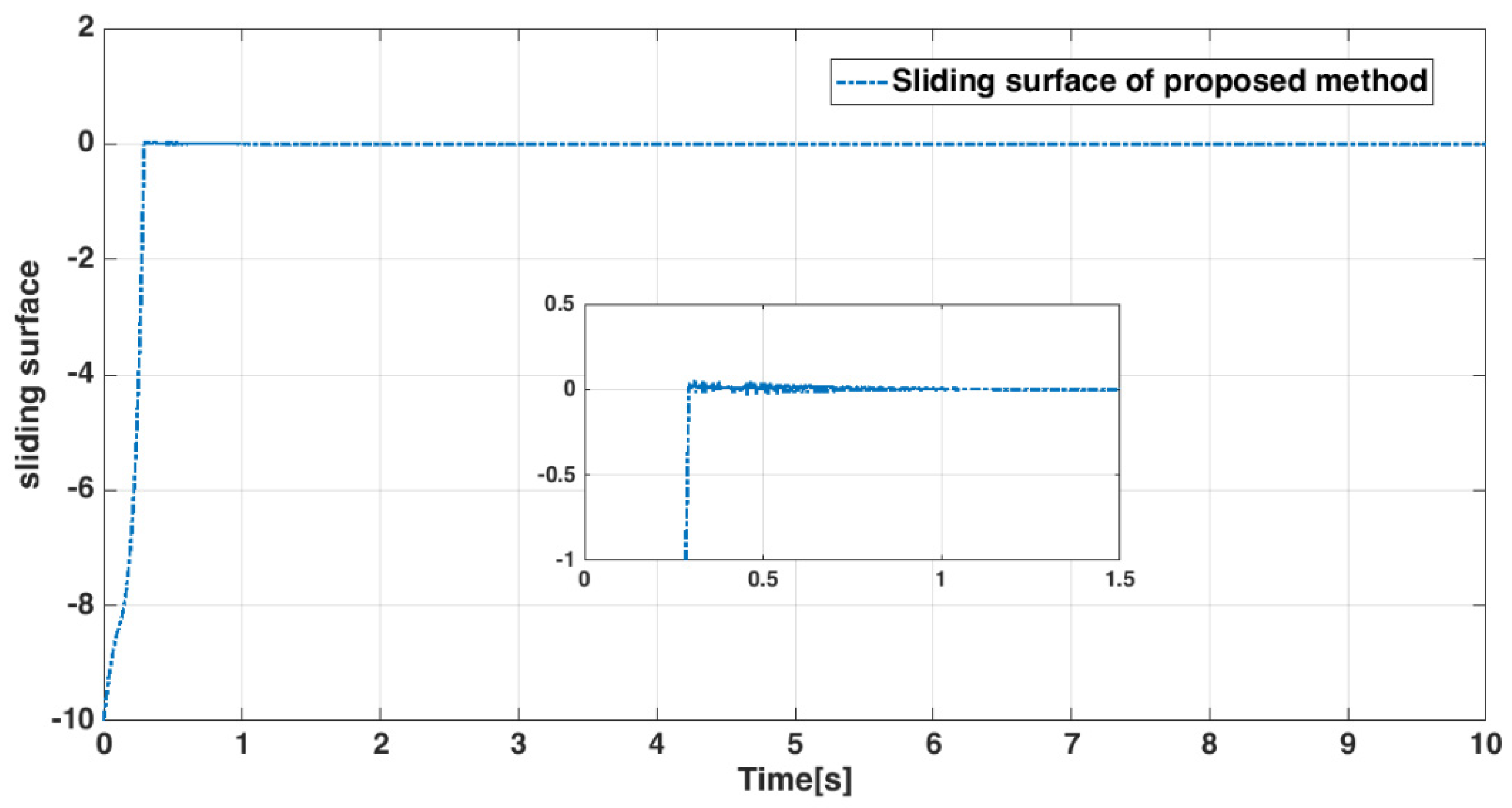
4.4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mahmoud, E.E.; Jahanzaib, L.S.; Trikha, P.; Abualnaja, K.M. Analysis and control of a fractional chaotic tumour growth and decay model. Results Phys. 2021, 20, 103677. [Google Scholar] [CrossRef]
- Iqbal, S.A.; Hafez, M.; Karim, S.A.A. Bifurcation analysis with chaotic motion of oblique plane wave for describing a discrete nonlinear electrical transmission line with conformable derivative. Results Phys. 2020, 18, 103309. [Google Scholar] [CrossRef]
- Guo, R.; Zhang, Y.; Jiang, C. Synchronization of Fractional-Order Chaotic Systems with Model Uncertainty and External Disturbance. Mathematics 2021, 9, 877. [Google Scholar] [CrossRef]
- Lin, C.-H.; Ho, C.-W.; Hu, G.-H.; Sreeramaneni, B.; Yan, J.-J. Secure Data Transmission Based on Adaptive Chattering-Free Sliding Mode Synchronization of Unified Chaotic Systems. Mathematics 2021, 9, 2658. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Ma, M.; Wang, M. Generation of grid multi-wing chaotic attractors and its application in video secure communication system. Multimed. Tools Appl. 2020, 79, 29161–29177. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, F.; Yu, J. A Chaotic Encryption Scheme in DMT for IM/DD Intra-Datacenter Interconnects. IEEE Photon. Technol. Lett. 2021, 33, 383–386. [Google Scholar] [CrossRef]
- Simhanath, Y. Religious Nationalism as Solution in the Chaotic Social, Economics and the Business Reality. Int. J. Relig. Cult. Stud. 2020, 2, 25–29. [Google Scholar] [CrossRef]
- Weinmeister, J.; Xie, N.; Gao, X.; Prasad, A.K.; Roy, S. Analysis of a Polynomial Chaos-Kriging Metamodel for Uncertainty Quantification in Aerospace Applications. In Proceedings of the AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.-X.; Yang, G.-H. Adaptive integral sliding mode control fault tolerant control for a class of uncertain nonlinear systems. IET Control Theory Appl. 2018, 12, 1864–1872. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Al-Harthi, B.H. A phenomenal form of complex synchronization and chaotic masking communication between two identical chaotic complex nonlinear structures with unknown parameters. Results Phys. 2019, 14, 102452. [Google Scholar] [CrossRef]
- Sha, D.; Ozbay, K.; Bian, Z.; Wang, D. A Polynomial Chaos Expansion Based Approach for Efficient and Robust Calibration of Stochastic Transportation Simulation Models. In Proceedings of the Transportation Research Board 100th Annual Meeting, Washington, DC, USA, 5–29 January 2021. [Google Scholar]
- Avanço, R.H.; Tusset, A.M.; Balthazar, J.M.; Nabarrete, A.; Navarro, H.A. On nonlinear dynamics behavior of an electro-mechanical pendulum excited by a nonideal motor and a chaos control taking into account parametric errors. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 23. [Google Scholar] [CrossRef]
- Lu, S.; Wang, X.; Wang, L. Finite-time adaptive neural network control for fractional-order chaotic PMSM via command filtered backstepping. Adv. Differ. Equ. 2020, 2020, 121. [Google Scholar] [CrossRef] [Green Version]
- Gunasekaran, N.; Joo, Y.H. Stochastic sampled-data controller for T–S fuzzy chaotic systems and its applications. IET Control Theory Appl. 2019, 13, 1834–1843. [Google Scholar] [CrossRef]
- Gunasekaran, N.; Srinivasan, S.; Zhai, G.; Yu, Q. Dynamical Analysis and Sampled-Data Stabilization of Memristor-Based Chua’s Circuits. IEEE Access 2021, 9, 25648–25658. [Google Scholar] [CrossRef]
- Morales, G.B.; Muñoz, M.A. Optimal Input Representation in Neural Systems at the Edge of Chaos. Biology 2021, 10, 702. [Google Scholar] [CrossRef]
- Abanin, D.A.; Bardarson, J.H.; De Tomasi, G.; Gopalakrishnan, S.; Khemani, V.; Parameswaran, S.A.; Pollmann, F.; Potter, A.C.; Serbyn, M.; Vasseur, R. Distinguishing localization from chaos: Challenges in finite-size systems. Ann. Phys. 2021, 427, 168415. [Google Scholar] [CrossRef]
- Taylor, L. The taming of chaos: Optimal cities and the state of the art in urban systems research. Urban Stud. 2021, 58, 3196–3202. [Google Scholar] [CrossRef]
- Kos, P.; Bertini, B.; Prosen, T. Chaos and Ergodicity in Extended Quantum Systems with Noisy Driving. Phys. Rev. Lett. 2021, 126, 190601. [Google Scholar] [CrossRef]
- Gunasekaran, N.; Joo, Y.H. Robust Sampled-data Fuzzy Control for Nonlinear Systems and Its Applications: Free-Weight Matrix Method. IEEE Trans. Fuzzy Syst. 2019, 27, 2130–2139. [Google Scholar] [CrossRef]
- Gunasekaran, N.; Saravanakumar, R.; Ali, M.S.; Zhu, Q. Exponential sampled-data control for T–S fuzzy systems: Application to Chua’s circuit. Int. J. Syst. Sci. 2019, 50, 2979–2992. [Google Scholar] [CrossRef]
- Xian, Y.-J.; Xia, C.; Guo, T.-T.; Fu, K.-R.; Xu, C.-B. Dynamical analysis and FPGA implementation of a large range chaotic system with coexisting attractors. Results Phys. 2018, 11, 368–376. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef]
- Rahman, Z.-A.S.A.; Jasim, B.H.; Al-Yasir, Y.I.A.; Hu, Y.-F.; Abd-Alhameed, R.A.; Alhasnawi, B.N. A New Fractional-Order Chaotic System with Its Analysis, Synchronization, and Circuit Realization for Secure Communication Applications. Mathematics 2021, 9, 2593. [Google Scholar] [CrossRef]
- Akinlar, M.A.; Tchier, F.; Inc, M. Chaos control and solutions of fractional-order Malkus waterwheel model. Chaos Solitons Fractals 2020, 135, 109746. [Google Scholar] [CrossRef]
- Yan, L.; Liu, J.; Xu, F.; Teo, K.L.; Lai, M. Control and synchronization of hyperchaos in digital manufacturing supply chain. Appl. Math. Comput. 2021, 391, 125646. [Google Scholar] [CrossRef]
- Batmani, Y. Chaos control and chaos synchronization using the state-dependent Riccati equation techniques. Trans. Inst. Meas. Control. 2018, 41, 311–320. [Google Scholar] [CrossRef]
- Bartolini, G.; Ferrara, A.; Levant, A.; Usai, E. On second order sliding mode controllers. In Variable Structure Systems, Sliding Mode and Nonlinear Control; Young, K., Özgüner, Ü., Eds.; Springer: London, UK, 1999; Volume 247, pp. 329–350. Available online: https://link.springer.com/chapter/10.1007/BFb0109984#citeas (accessed on 20 November 2021).
- Boiko, I.; Fridman, L. Analysis of chattering in continuous sliding-mode controllers. IEEE Trans. Autom. Control. 2005, 50, 1442–1446. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Wang, X. Advanced Sliding Mode Control for Mechanical Systems; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: New York, NY, USA, 2014; Volume 10. [Google Scholar]
- Yang, J.; Su, J.; Li, S.; Yu, X. High-Order Mismatched Disturbance Compensation for Motion Control Systems Via a Continuous Dynamic Sliding-Mode Approach. IEEE Trans. Ind. Inform. 2013, 10, 604–614. [Google Scholar] [CrossRef] [Green Version]
- Qiao, L.; Zhang, W. Adaptive non-singular integral terminal sliding mode tracking control for autonomous underwater vehicles. IET Control. Theory Appl. 2017, 11, 1293–1306. [Google Scholar] [CrossRef]
- Mobayen, S.; Karami, H.; Fekih, A. Adaptive Nonsingular Integral-type Second Order Terminal Sliding Mode Tracking Controller for Uncertain Nonlinear Systems. Int. J. Control Autom. Syst. 2021, 19, 1539–1549. [Google Scholar] [CrossRef]
- Rashidnejad, Z.; Karimaghaee, P. Synchronization of a class of uncertain chaotic systems utilizing a new finite-time fractional adaptive sliding mode control. Chaos Solitons Fractals X 2020, 5, 100042. [Google Scholar] [CrossRef]
- Tong, D.; Xu, C.; Chen, Q.; Zhou, W. Sliding mode control of a class of nonlinear systems. J. Frankl. Inst. 2020, 357, 1560–1581. [Google Scholar] [CrossRef]
- Shukla, M.K.; Sharma, B.B. Control and Synchronization of a Class of Uncertain Fractional Order Chaotic Systems via Adaptive Backstepping Control. Asian J. Control 2017, 20, 707–720. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Q.; Li, S. Adaptive Integral-Type Terminal Sliding Mode Fault Tolerant Control for Spacecraft Attitude Tracking. IEEE Access 2019, 7, 35195–35207. [Google Scholar] [CrossRef]
- Yang, Y. A time-specified nonsingular terminal sliding mode control approach for trajectory tracking of robotic airships. Nonlinear Dyn. 2018, 92, 1359–1367. [Google Scholar] [CrossRef]
- Dinga, S.; Park, J.H.; Chenc, C.C. Second-order sliding mode controller design with output constraint. Automatica 2020, 112, 108704. [Google Scholar] [CrossRef]
- Zhang, X. Robust integral sliding mode control for uncertain switched systems under arbitrary switching rules. Nonlinear Anal. Hybrid Syst. 2020, 37, 100900. [Google Scholar] [CrossRef]
- Abdurahman, A.; Jiang, H.; Teng, Z. Finite-time synchronization for memristor-based neural networks with time-varying delays. Neural Netw. 2015, 69, 20–28. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alattas, K.A.; Mostafaee, J.; Sambas, A.; Alanazi, A.K.; Mobayen, S.; Vu, M.T.; Zhilenkov, A. Nonsingular Integral-Type Dynamic Finite-Time Synchronization for Hyper-Chaotic Systems. Mathematics 2022, 10, 115. https://doi.org/10.3390/math10010115
Alattas KA, Mostafaee J, Sambas A, Alanazi AK, Mobayen S, Vu MT, Zhilenkov A. Nonsingular Integral-Type Dynamic Finite-Time Synchronization for Hyper-Chaotic Systems. Mathematics. 2022; 10(1):115. https://doi.org/10.3390/math10010115
Chicago/Turabian StyleAlattas, Khalid A., Javad Mostafaee, Aceng Sambas, Abdullah K. Alanazi, Saleh Mobayen, Mai The Vu, and Anton Zhilenkov. 2022. "Nonsingular Integral-Type Dynamic Finite-Time Synchronization for Hyper-Chaotic Systems" Mathematics 10, no. 1: 115. https://doi.org/10.3390/math10010115





