Abstract
The improved element-free Galerkin (IEFG) method is proposed in this paper for solving 3D Helmholtz equations. The improved moving least-squares (IMLS) approximation is used to establish the trial function, and the penalty technique is used to enforce the essential boundary conditions. Thus, the final discretized equations of the IEFG method for 3D Helmholtz equations can be derived by using the corresponding Galerkin weak form. The influences of the node distribution, the weight functions, the scale parameters of the influence domain, and the penalty factors on the computational accuracy of the solutions are analyzed, and the numerical results of three examples show that the proposed method in this paper can not only enhance the computational speed of the element-free Galerkin (EFG) method but also eliminate the phenomenon of the singular matrix.
1. Introduction
As an important elliptic differential equation, the Helmholtz equation has been widely applied in many different fields, such as mechanics, acoustics, physics, electromagnetics, engineering, and so on. It is well known that how to achieve the numerical solutions of Helmholtz equations effectively and accurately is one of the important directions in the scientific research.
Currently, many meshless methods have been used for researching Helmholtz equations, such as the element-free Galerkin (EFG) method [1], meshless Galerkin least-square method [2], meshless hybrid boundary-node method [3], boundary element-free method [4], and complex variable boundary element-free method [5,6]. Compared to the traditional finite difference method [7,8,9,10] and the finite element method, meshless methods [11,12,13,14,15] are based on scattered point approximation, which can avoid the mesh reconstruction, and thus a higher accuracy of the numerical solutions can be obtained.
As an important meshless method, the EFG method [16] was studied by Belytschko et al. In this method, a trial function is established by using the moving least-squares (MLS) approximation. Cheng et al. analyzed the error estimates of EFG method for potential problems [17]. Because the MLS approximation is based on the least-squares method [18,19,20,21,22], the disadvantages of the least-squares method also exist in the MLS approximation, in which sometimes ill-conditional or singular matrices occur.
In order to eliminate the singular matrices, the improved moving least-squares (IMLS) approximation [23] was proposed by Cheng et al., in which the orthogonal function system with a weight function is used as basis function, and thus can make up for the deficiency of the MLS approximation and has greater computational efficiency, using the IMLS approximation to establish the trial function. Thus, the improved element-free Galerkin (IEFG) method was applied for potential [24], transient heat conduction problems [25], the wave equation [26], the Schrödinger equation [27], advection–diffusion [28], elastodynamics [29], elastoplasticity [30], viscoelasticity [31], and diffusional drug release [32] problems. From these studies, we can see that under similar computational accuracy, the IEFG method has higher computational speed than the EFG method. As we know, meshless methods are based on node approximation without mesh reconstruction. When solving large deformation problems and dynamic propagation of cracks, the meshless method can obtain greater precision than the finite element method. In order to take advantage of the IEFG method further, Zhang et al. [33] developed the enriched IEFG method to solve 2D fracture problems. In this method, the enriched basis function is used at the tip of the crack. As a result, the singularity of the stresses at the tip of the crack can be shown better than in the IEFG method. Cai et al. [34] used the IEFG method for solving large elastoplasticity deformation problems. Three numerical examples are given to show that the numerical solutions are in good agreement with the solutions of finite element method software ANASYS and can enhance the computational efficiency of the EFG method.
By introducing the singular weight function into the MLS approximation, Lancaster et al. presented an interpolating MLS method [35]. The boundary conditions could be enforced directly in the corresponding meshless method. Based on the concept of an inner production, Ren et al. improved the interpolating MLS method [36] by using the singular weight function in interpolating points and orthogonalizing some of the base functions. Thus, the corresponding interpolating EFG method was presented for potential [37], transient heat conduction [38], and some mechanics [39,40,41] problems. Compared with the traditional EFG method, the interpolating EFG method has higher computational efficiency. Additionally, the interpolating smoothed particle method was developed by Qin et al. [42].
Using the nonsingular weight function, Wang et al. developed the improved interpolating MLS method [43], which can overcome the difficulties caused by the singular weight function in the interpolating MLS method, and used this method to construct the trial function. The improved interpolating EFG method was presented for potential [43] and several large deformation problems [44,45,46].
Based on the approximation of the vector function, the complex variable moving least-squares (CVMLS) approximation was presented by Cheng et al. [47]. Based on the CVMLS approximation and Galerkin weak form, the complex variable element-free Galerkin (CVEFG) method [48] was presented. Moreover, based on the conjugate basis function, Bai et al. proposed the improved CVMLS approximation to construct the shape function, and the improved CVEFG method was presented for elasticity problems [49]. The improved CVEFG method has higher computational accuracy and efficiency than the EFG method, but it cannot be applied to 3D problems directly because the complex theory is used. Chen et al. [50,51] proposed the complex variable reproducing kernel particle method.
By combining meshless methods and the finite difference method, the hybrid CVEFG method [52,53,54,55,56], dimension-splitting EFG method [57,58,59,60], dimension-splitting reproducing kernel particle method [61,62,63,64], interpolating dimension-splitting EFG method [65] and hybrid generalized interpolated EFG method [66] were proposed. These methods can greatly improve the computational efficiency of the traditional meshless method for solving multi-dimensional problems.
The IEFG method has some advantages over the traditional EFG method, such as higher computational efficiency, avoiding matrix inversion, and eliminating singular matrix. Therefore, it has been applied to many science and engineering problems. However, 3D Helmholtz equations have not been studied by the IEFG method yet, and the corresponding parameters cannot be discussed; thus, the computational accuracy and efficiency of the IEFG method for 3D Helmholtz equations are also uncertain. In order to overcome the disadvantage of the lower efficiency of the EFG method, this paper presents the IEFG method for solving 3D Helmholtz equations. The trial function was established by using the IMLS approximation, using the penalty technique to enforce the essential boundary conditions. The final discretized equations could be derived by using the corresponding weak form. Thus, we obtained the final formulate of the IEFG method for 3D Helmholtz equations.
In Section 4, the influences of the node distribution, the weight functions, the scale parameters, and the penalty factors on the computational accuracy of the solutions are analyzed by giving examples. It is shown that the IEFG method for Helmholtz equations is convergent. Compared with the EFG method, the IEFG method has greater computational speed. Moreover, the singular matrix can be eliminated.
2. The IMLS Approximation
The approximation of a function is
where is the basis function vector, is the basis function number, and
is the coefficient vector of .
In general,
The local approximation is
Define
where is a weighting function, and () are the nodes with influence domains covering point .
Equation (6) can be written as
where
and
From
we have
where
Equation (12) sometimes forms a singular or ill-conditional matrix. In order to make up for this deficiency, for basis functions
using the Gram–Schmidt process, we can obtain
and
Then, from Equation (12), can be obtained as
where
Substituting Equation (18) into Equation (5), we have
where
is the shape function.
This is the IMLS approximation [23], in which the shape function can be obtained more easily than the MLS approximation. Moreover, the IMLS approximation can also avoid the singular matrix. Thus, it can enhance the computational efficiency of the MLS approximation.
3. The IEFG Method for 3D Helmholtz Equations
The governing equation is
and the boundary conditions are
where is the wave number, is the given function, and are the given values, and , , () is the unit outward normal to the boundary in direction .
For 3D Helmholtz equations, the equivalent functional is
By introducing the penalty technique to apply the boundary conditions, we can obtain the modified functional
where is the penalty factor.
Let
We can obtain the following equivalent integral weak form
where
In the cubic domain , we employ nodes (). Thus, we have
From the IMLS approximation, we can obtain
where
From Equations (29) and (31), we have
where
Substituting Equations (31) and (33) into Equation (28), we have
In Equation (36), the form of is the same as Equation (32), and .
All integral terms in Equation (36) are analyzed as follows:
Let
Substituting Equations (37)–(42) into Equation (36), we can obtain
The is arbitrary; thus we can obtain
where
This is the IEFG method for 3D Helmholtz equations.
4. Numerical Examples
The formula of the relative error is
where
In order to illustrate the advantages of the IFFG method, we chose three examples from other literature. The nodes distributed in the problem domains of these numerical examples were regular, the linear basis function was selected, and 3 × 3 × 3 Gaussian points were selected in each integral cell. The IEFG and the EFG methods are used to solve these examples.
The following equation is considered in the first example:
The boundary conditions are
The problem domain is , and
is the analytical solution.
In order to study the convergence of the EFG and the IEFG methods for Helmholtz equations, all parameters of both methods were kept the same. The cubic spline weight functions were used, dmax = 1.35, . Table 1 shows the relationship between relative errors and node distribution. It is shown that, with the increase in nodes, the precision of numerical solutions improves as well, but the computational efficiency is reduced gradually. Therefore, the two methods in this paper are convergent. Both the computational accuracy and efficiency are considered, and 15 × 15 × 15 regularly distributed nodes are selected.

Table 1.
Relative errors and CPU times of the improved element-free Galerkin (IEFG) and element-free Galerkin (EFG) methods with the increase in node distribution.
The effects of the weight function, the scale parameter of the influence domain, and the penalty factor on solution of the IEFG method will be discussed.
- (1)
- Weight function
When the cubic spline function is used, 15 × 15 × 15 regularly distributed nodes and 14 × 14 × 14 background integral cells are selected, , dmax = 1.35. Thus, the smaller relative error is 0.6296%. When the quartic spline function is used, and the same regularly distributed nodes and background integral grids are used, , dmax = 1.28, the smaller relative error is 0.6274%. It is shown that the similar relative errors can be obtained when using two weight functions.
In addition, the singular matrix can be avoided in the IEFG method when using the cubic spline function. If dmax = 1.0, the quartic spline function is selected. Unfortunately, the singular matrix occurs and the final result cannot be obtained. When the cubic spline function is used, the relative error is 0.6451%.
Thus, the cubic spline function is selected.
- (2)
- Scale parameter
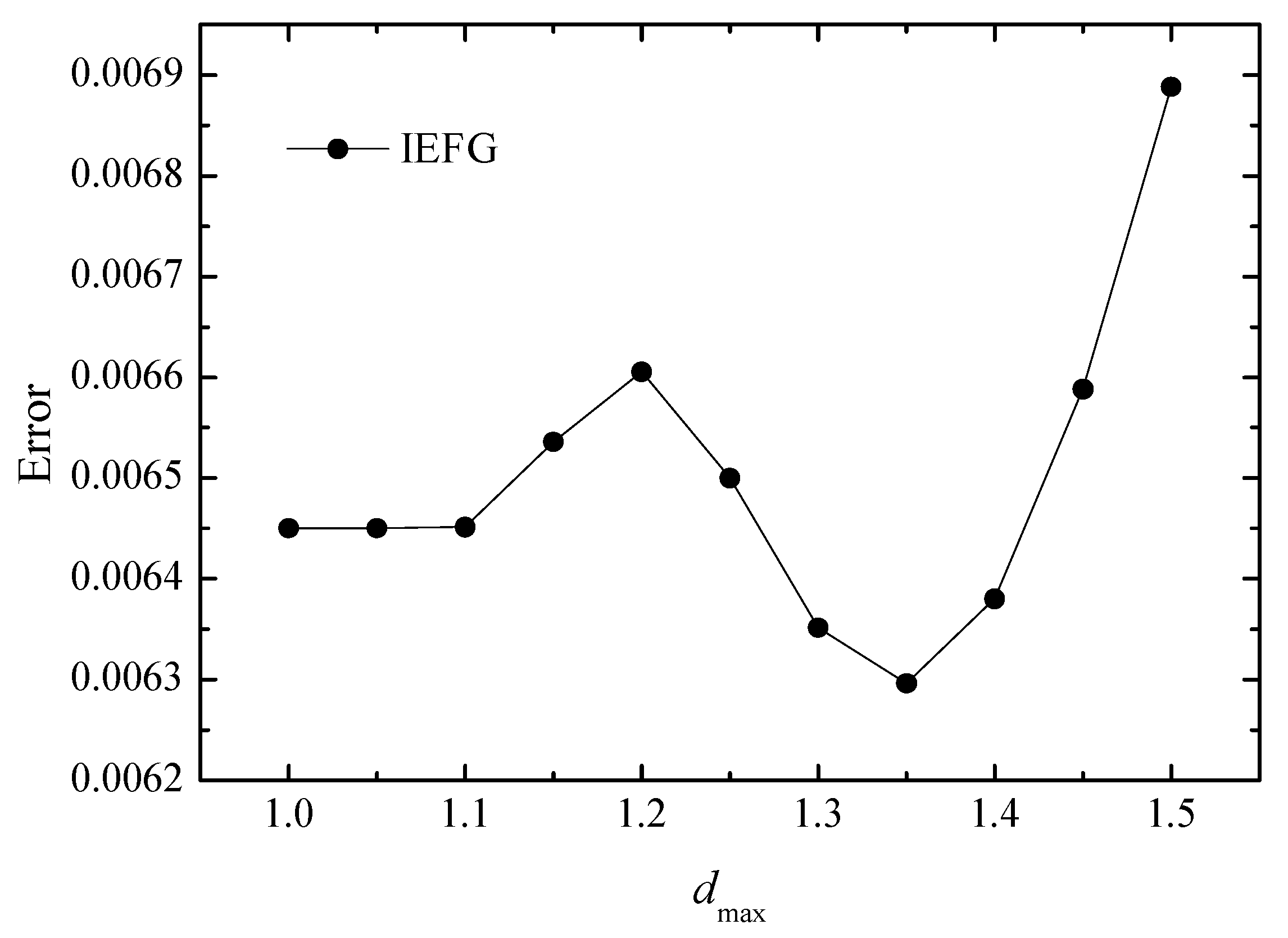
The same node distribution and background integral grids are selected, , and the cubic spline function is used. Figure 1 shows the relationship between dmax and relative errors. Because of the error of computer itself, the relative error become larger when dmax = 1.2. It is shown that when dmax = 1.35, the relative error is smaller.
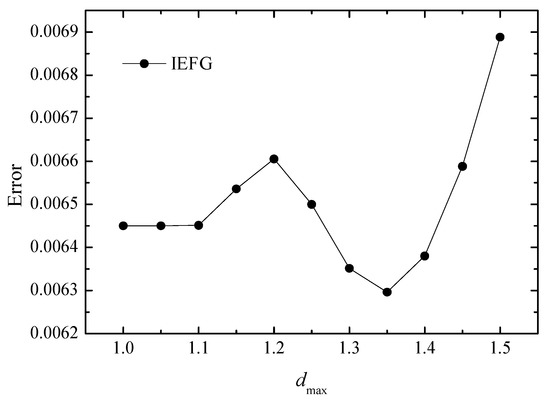
Figure 1.
The error of the numerical solutions of the IEFG method with the increase in dmax.
- (3)
- Penalty factor
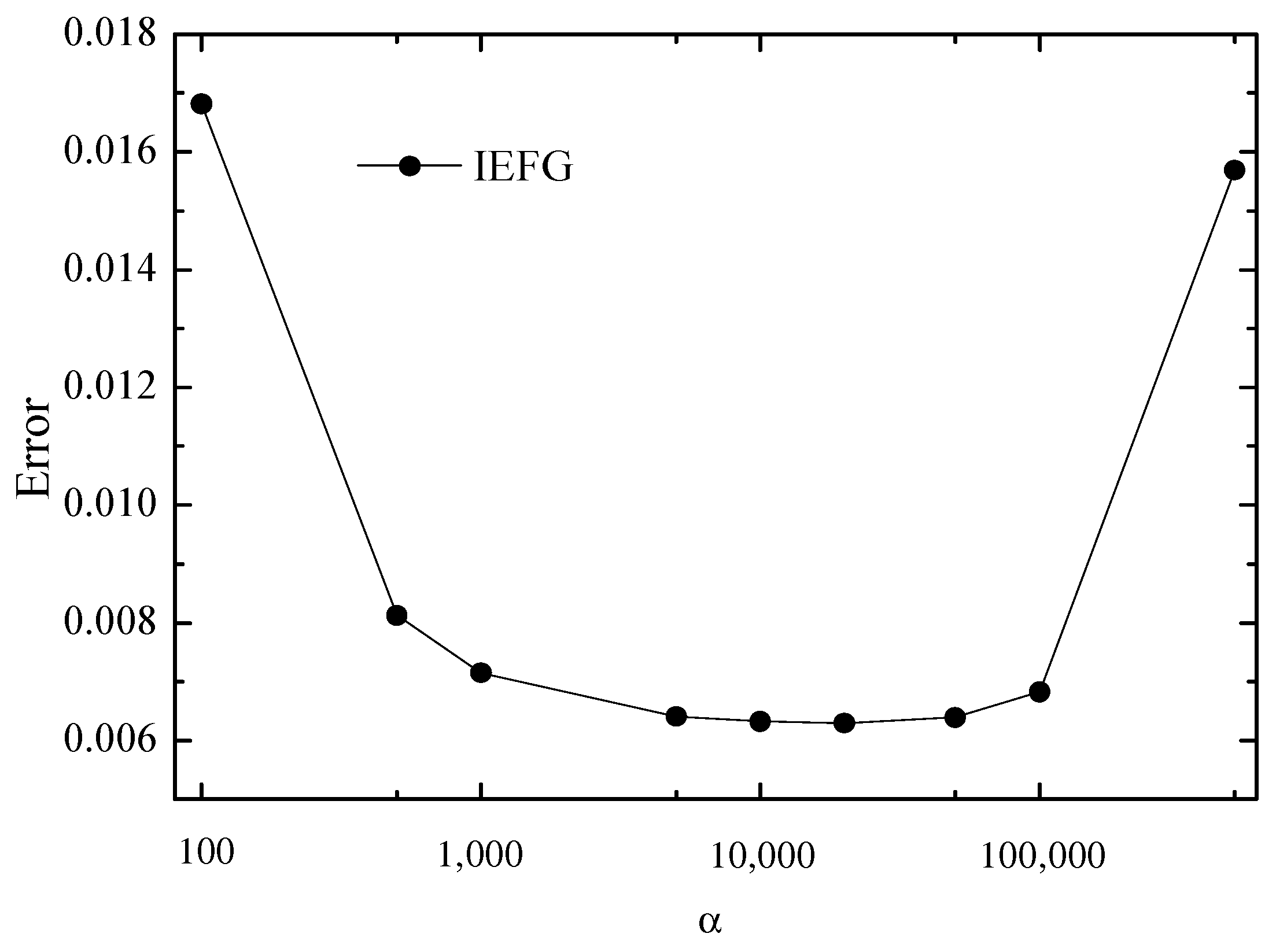
The same node distribution, background integral grids, and weight function are selected, dmax = 1.35. Figure 2 shows the relationship between and relative errors. It is shown that when , the relative error is smaller.
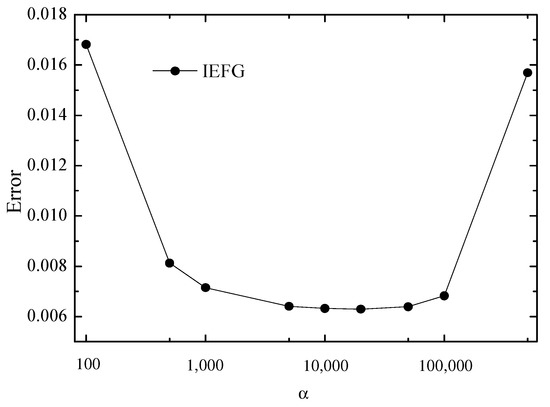
Figure 2.
The error of the numerical solutions of the IEFG method with the increase in α.
The IEFG method is selected to solve it, 15 × 15 × 15 regularly distributed nodes and 14 × 14 × 14 background integral cells are selected, and the cubic spline function is used, , dmax = 1.35. When using the EFG method to solve it, the same parameters are selected, and thus the relative errors of two methods are equal to 0.6296%.
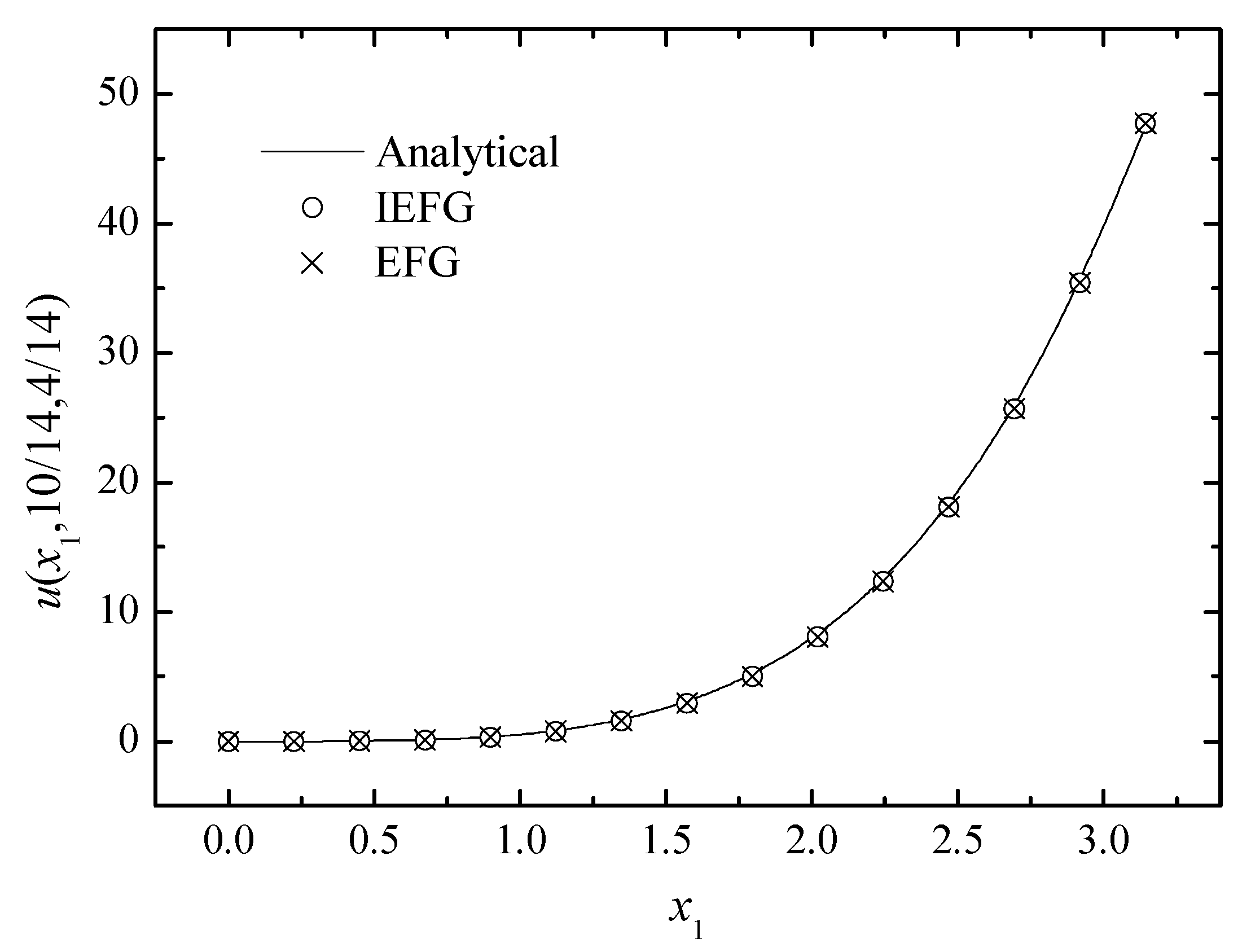
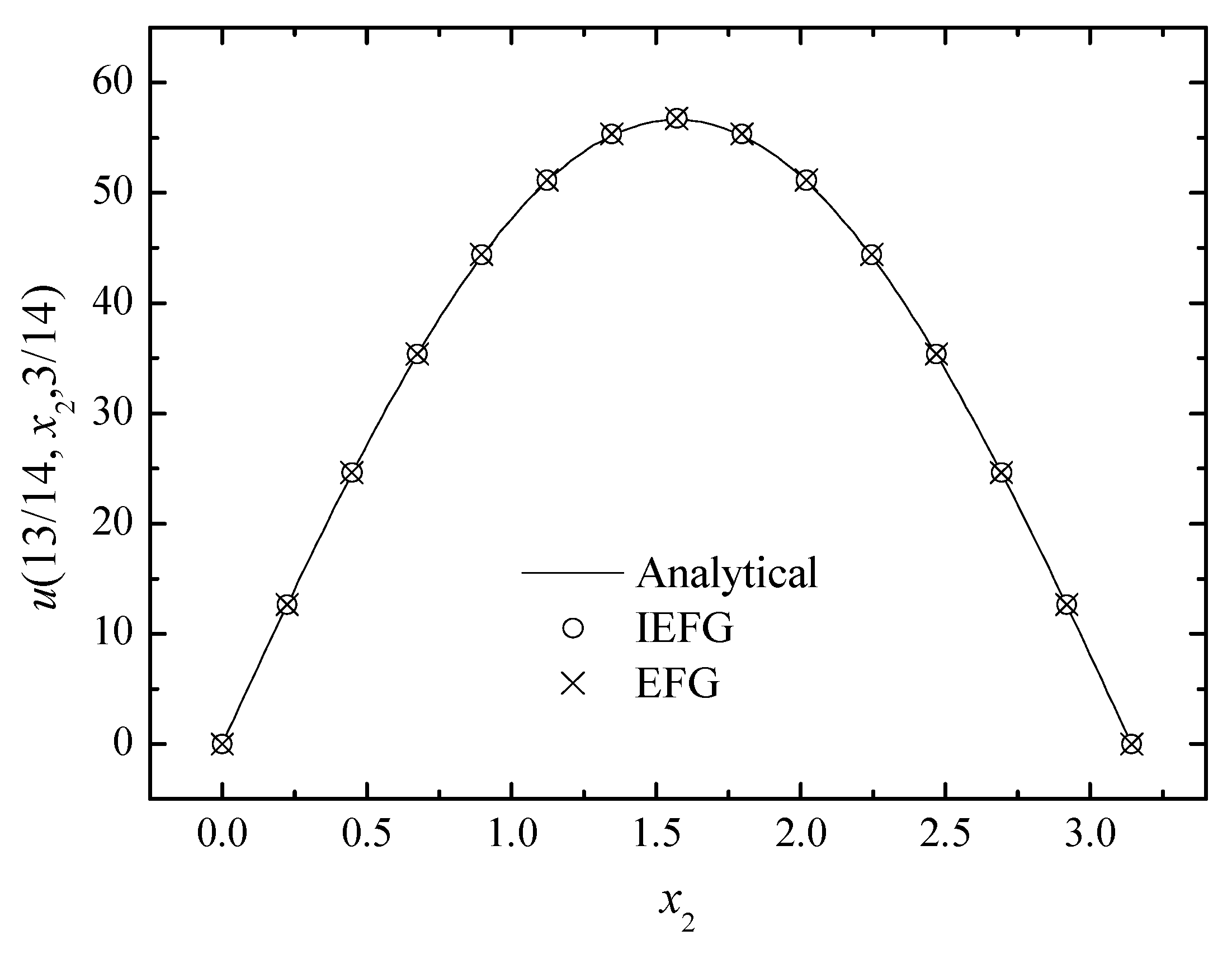
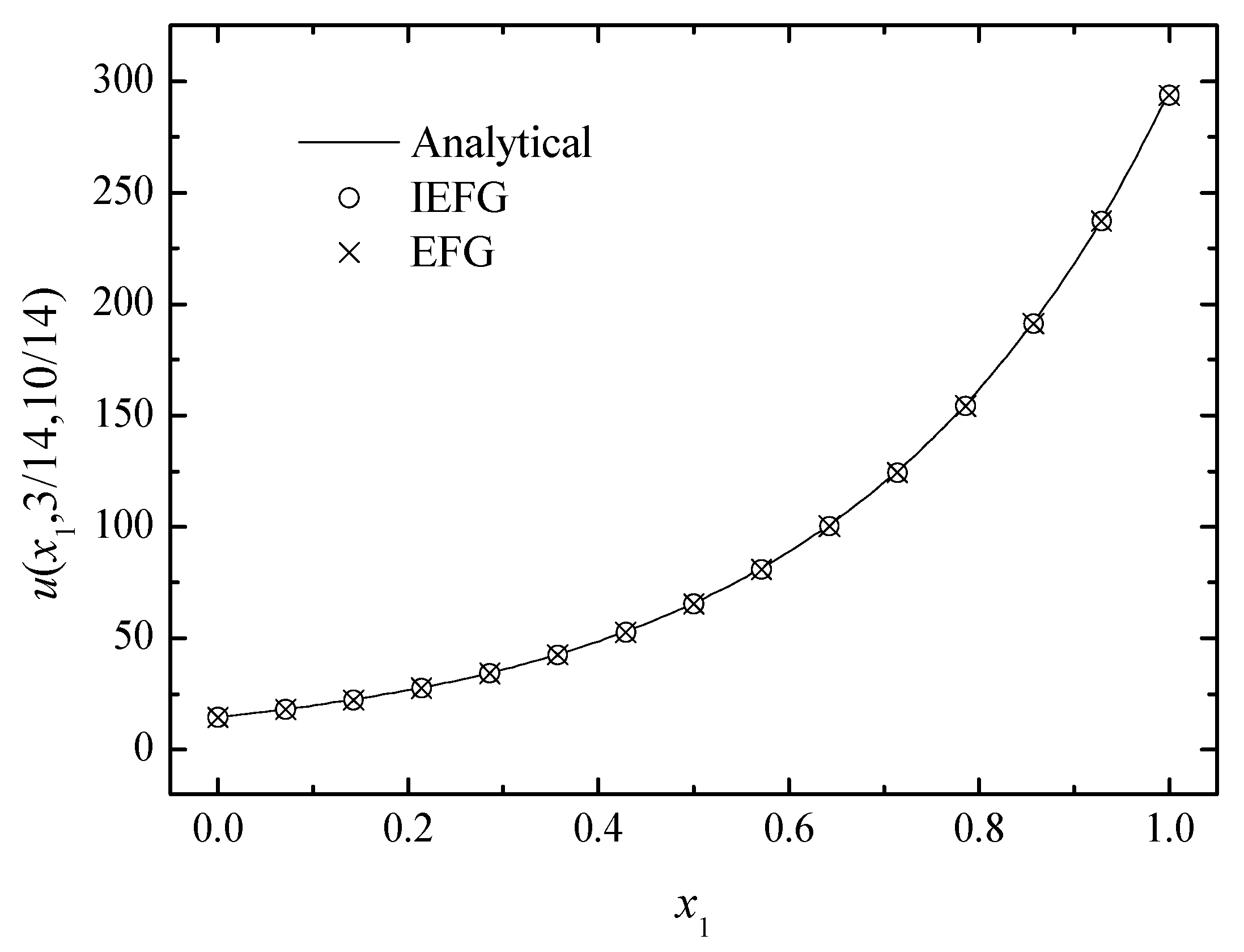
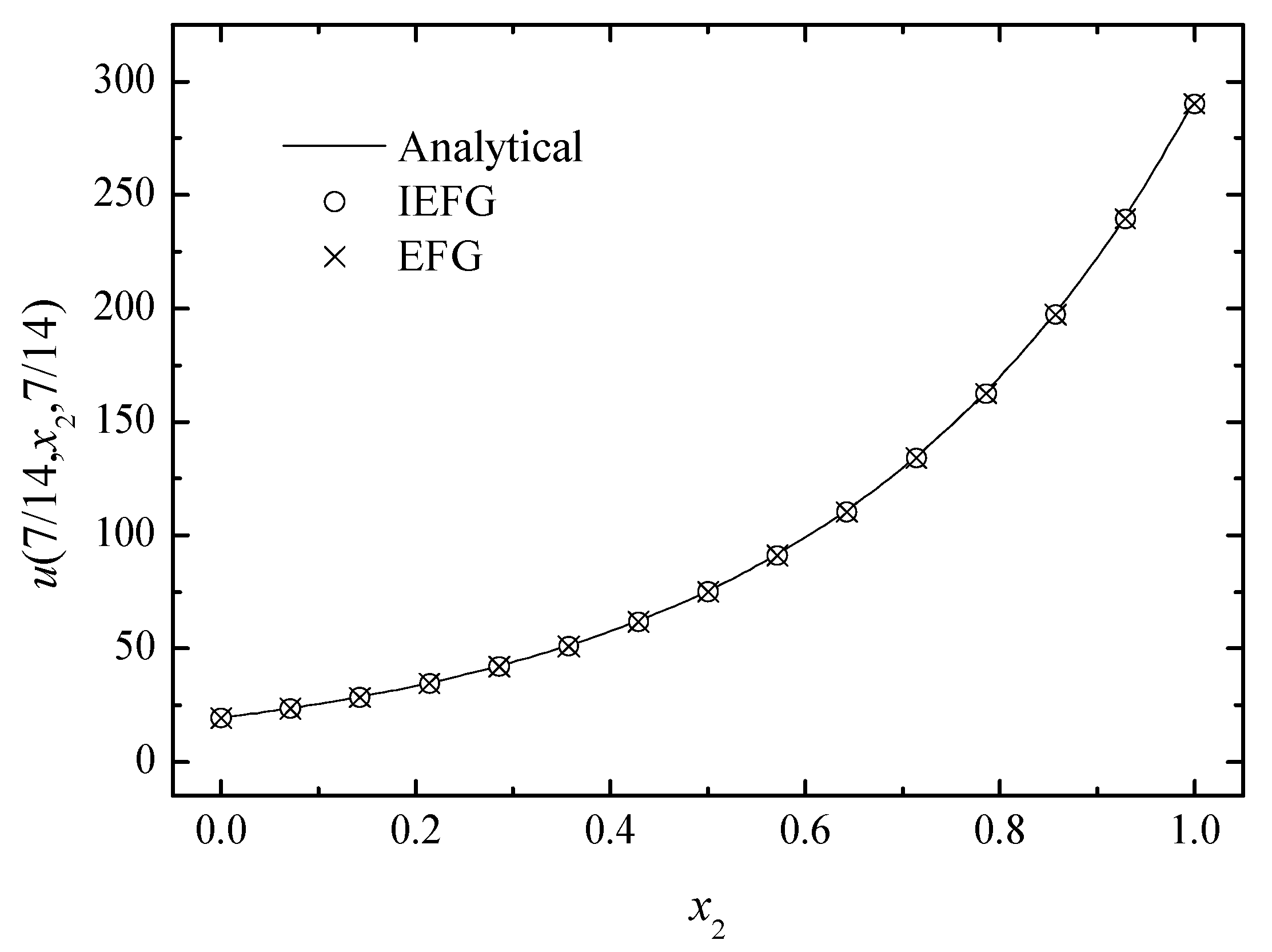
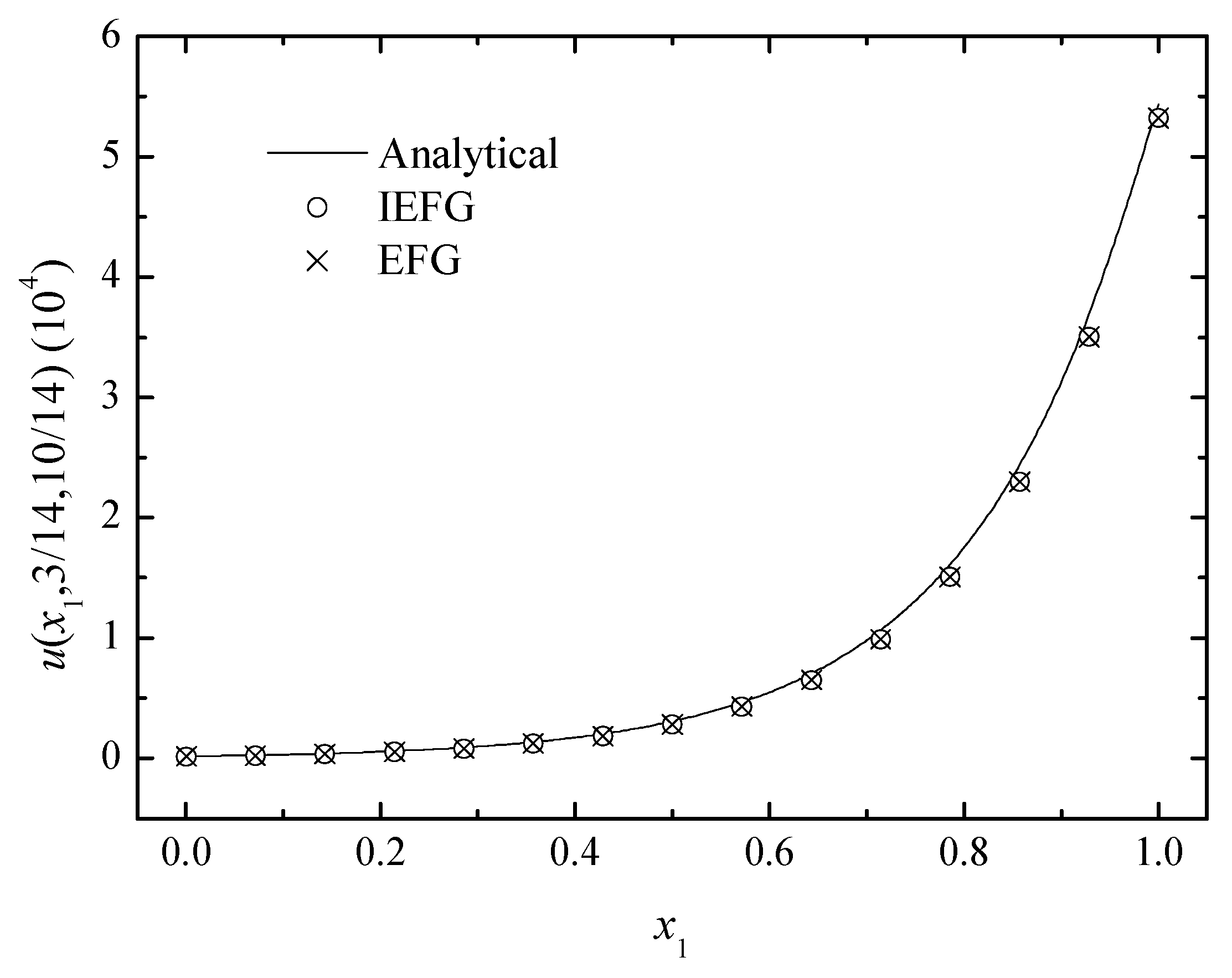
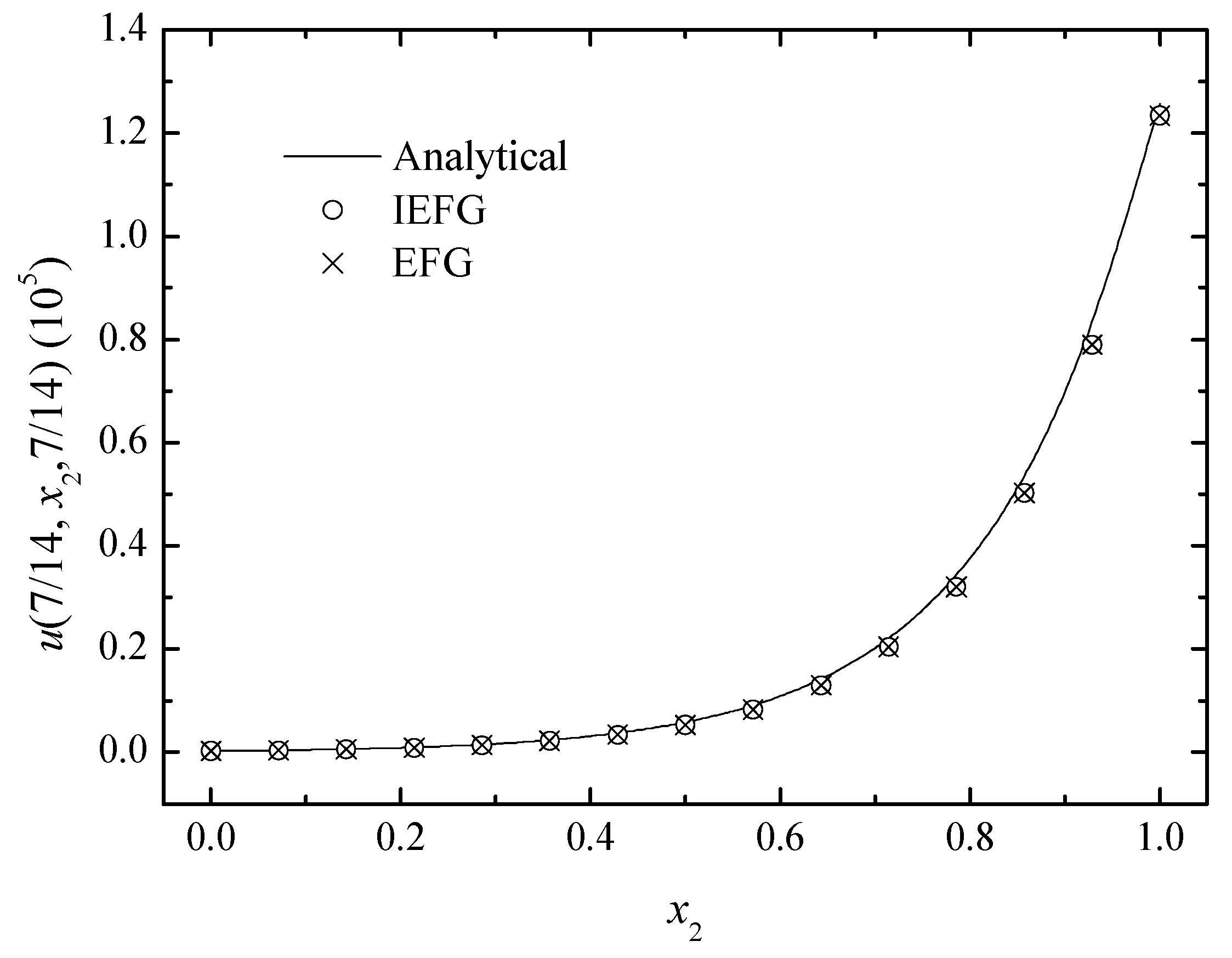
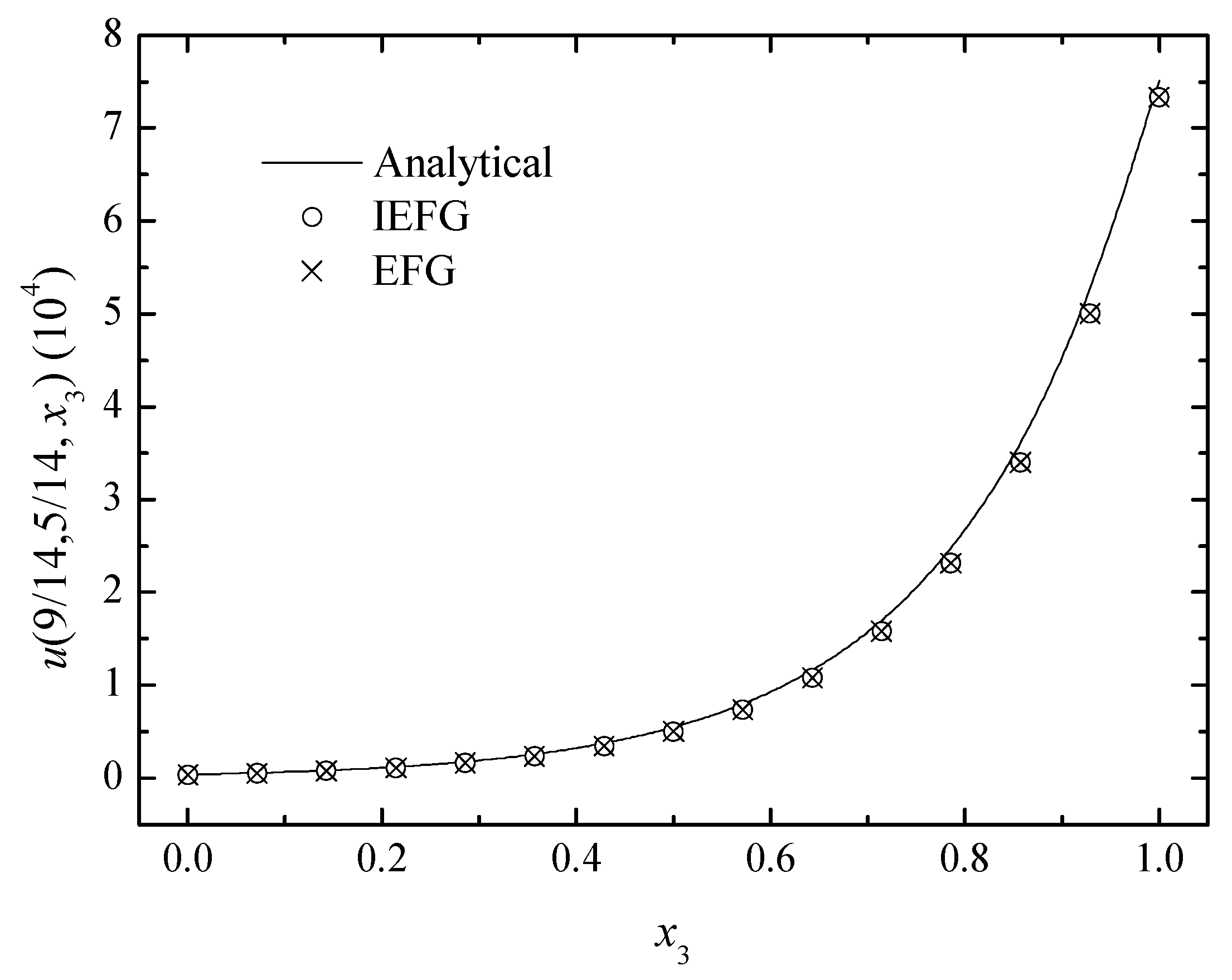
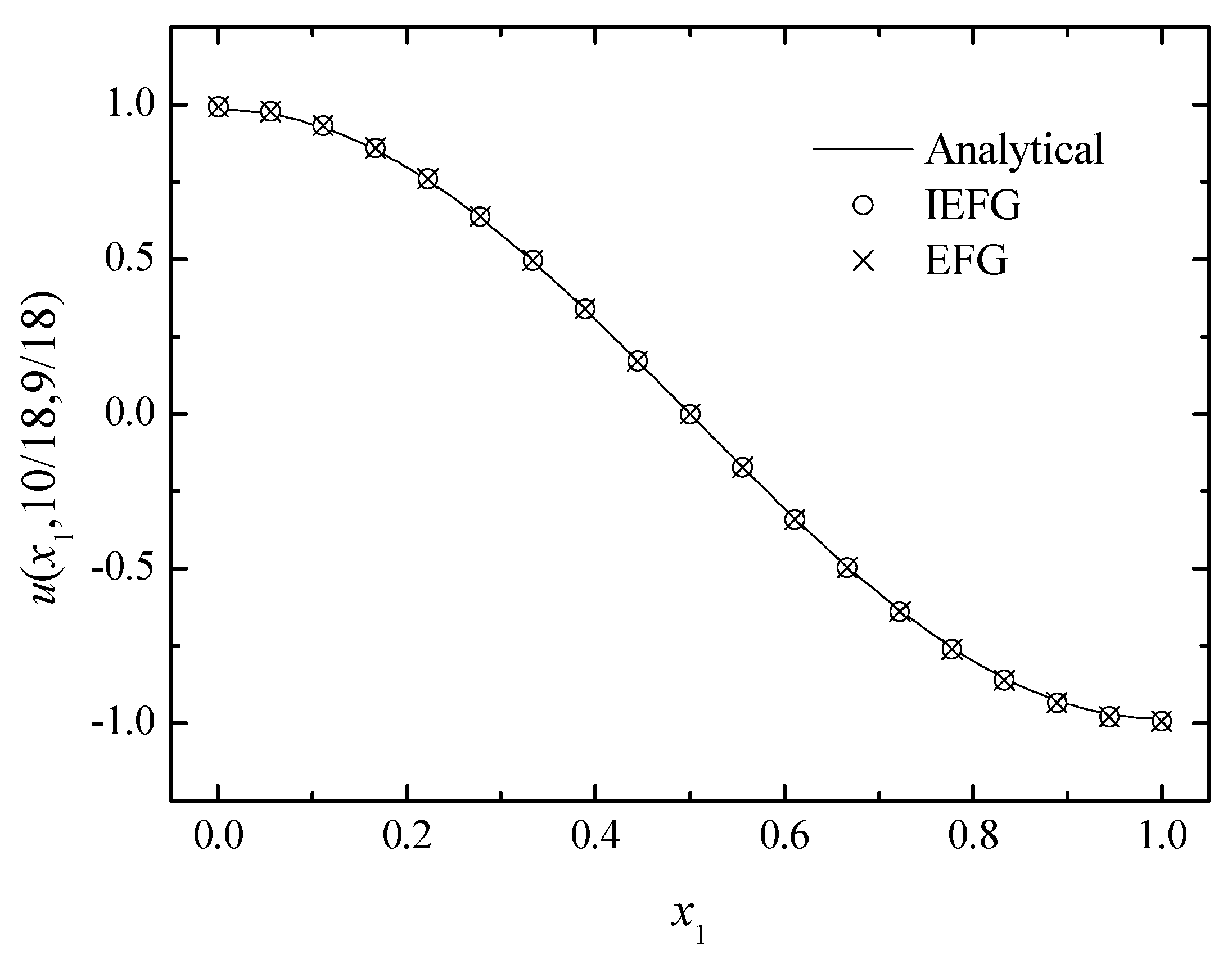
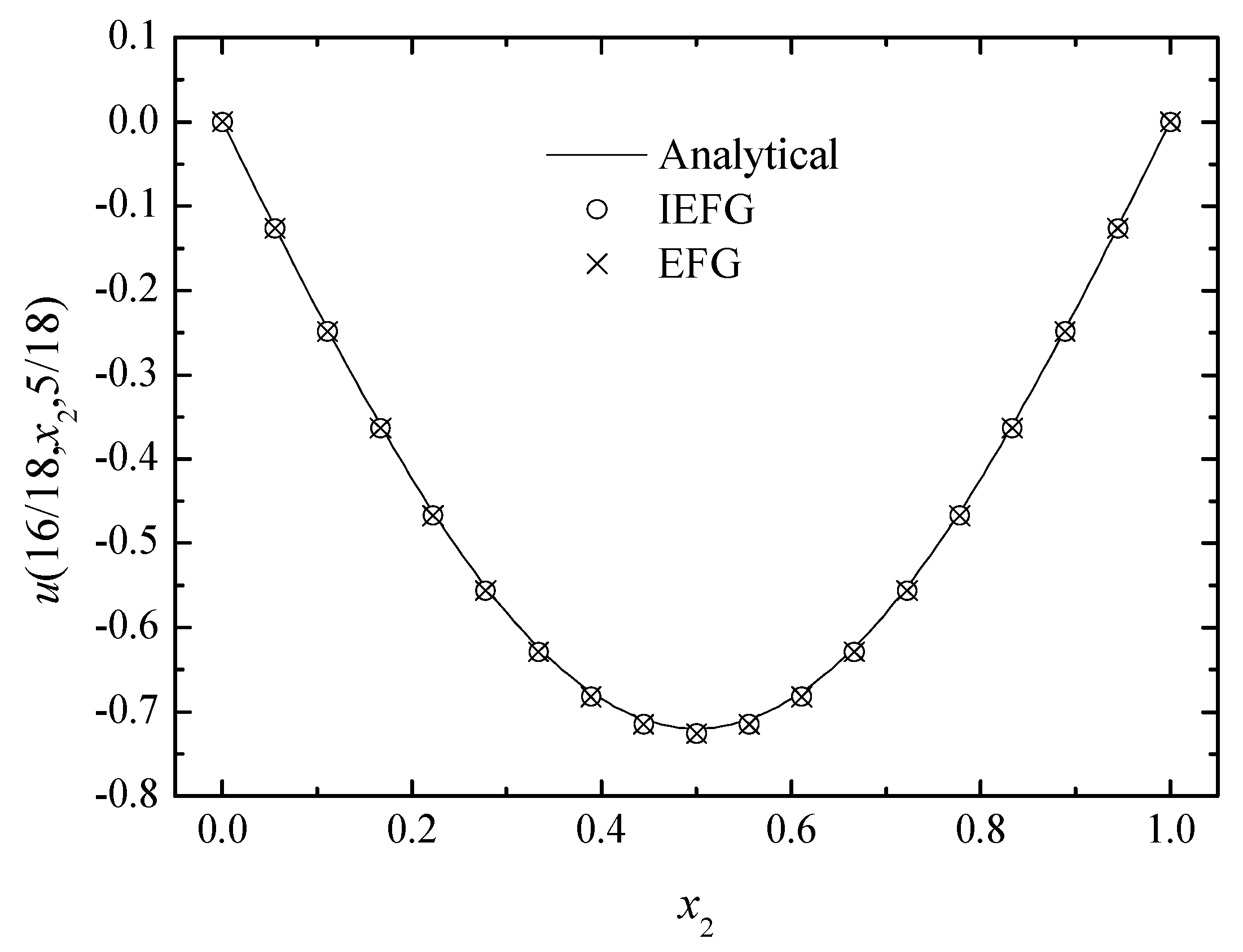
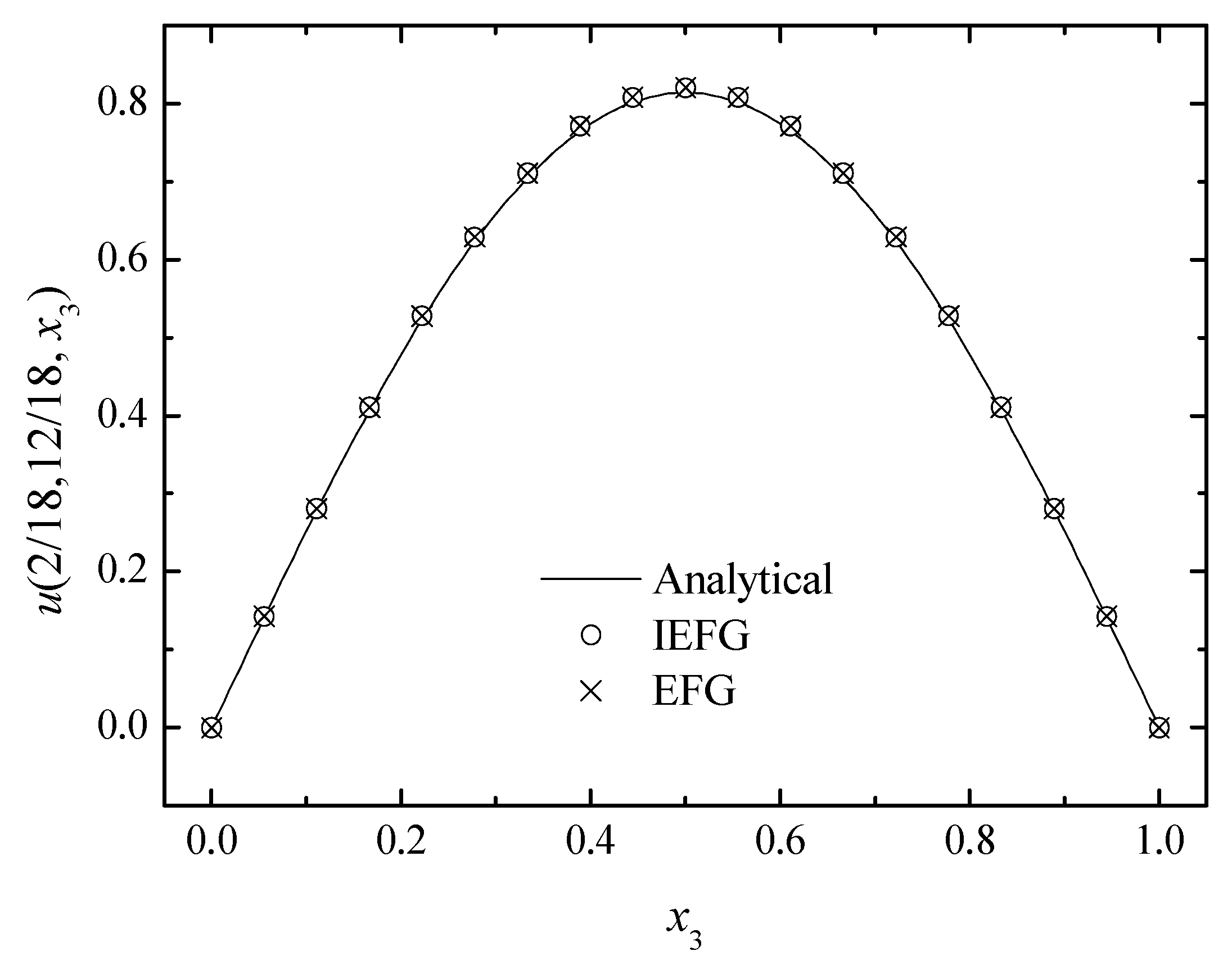
Figure 3, Figure 4 and Figure 5 show the comparison between numerical solutions and analytical ones, and the CPU times of the IEFG method and the EFG method are 92.1 s and 98.0 s, respectively. Obviously, higher computational efficiency can be obtained when using the IEFG method.
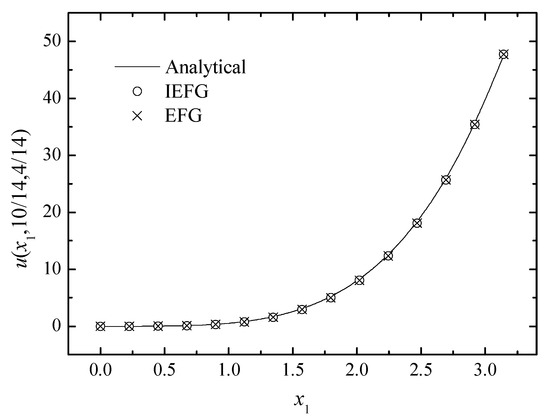
Figure 3.
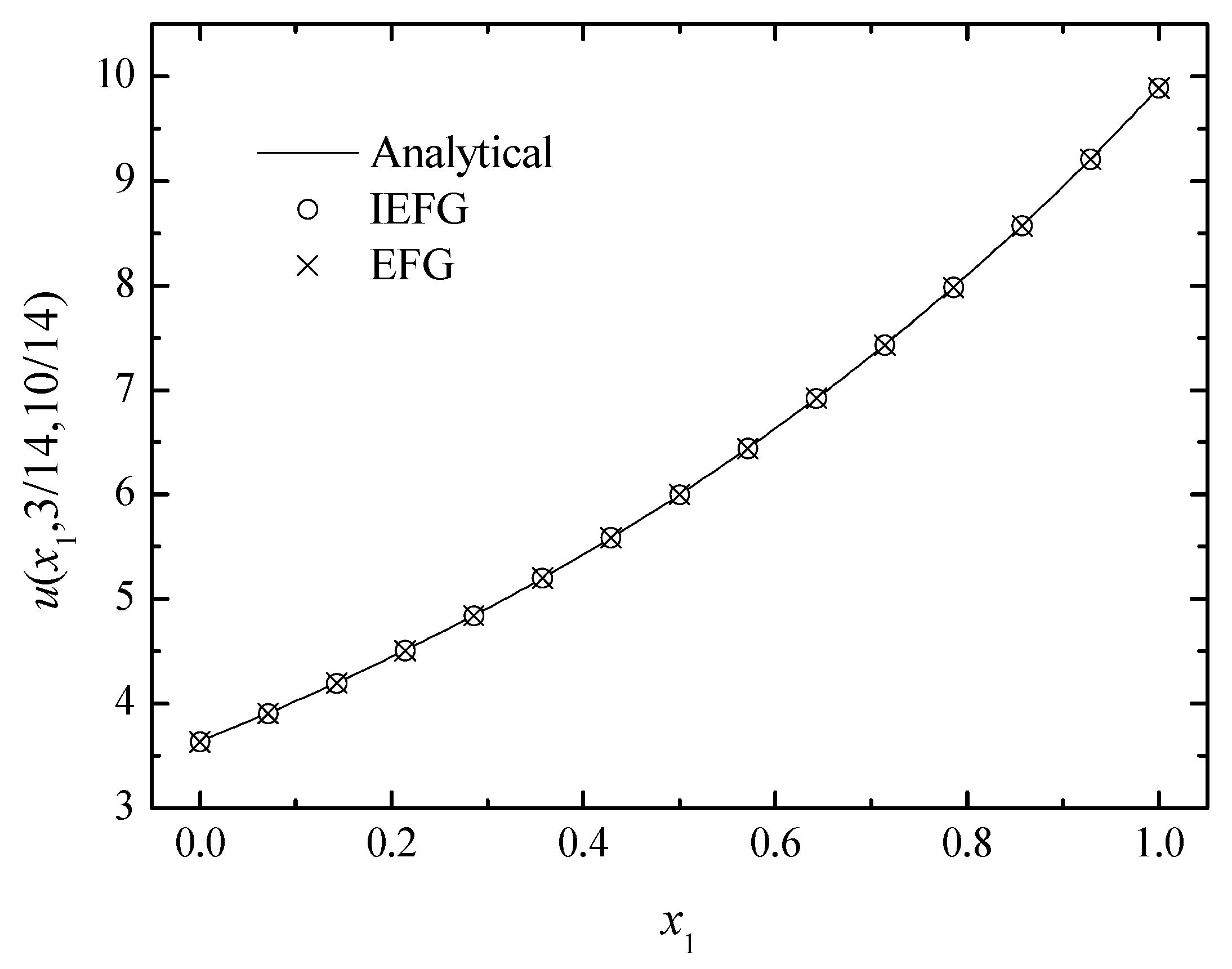
The comparison of the numerical and analytical solutions of the two methods along the x1-axis.
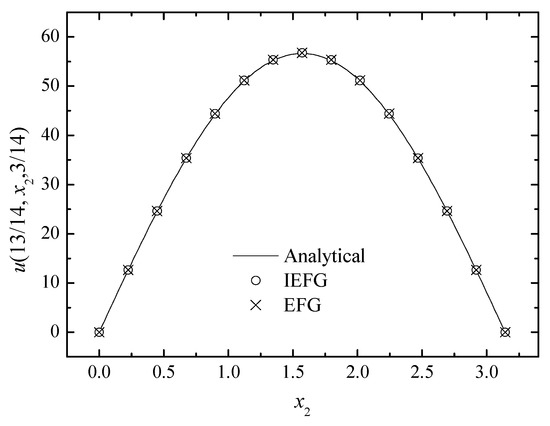
Figure 4.
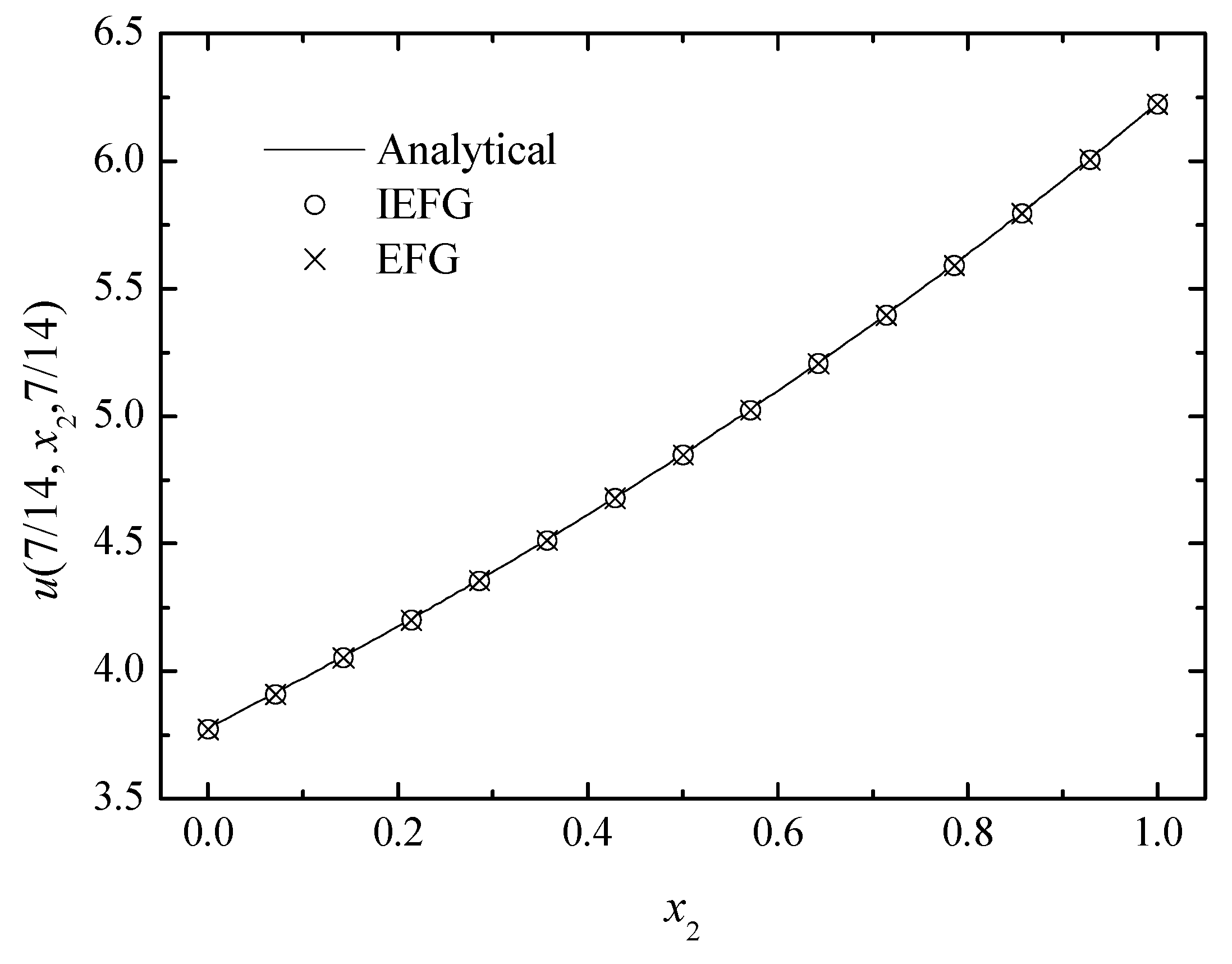
The comparison of the numerical and analytical solutions of the two methods along the x2-axis.
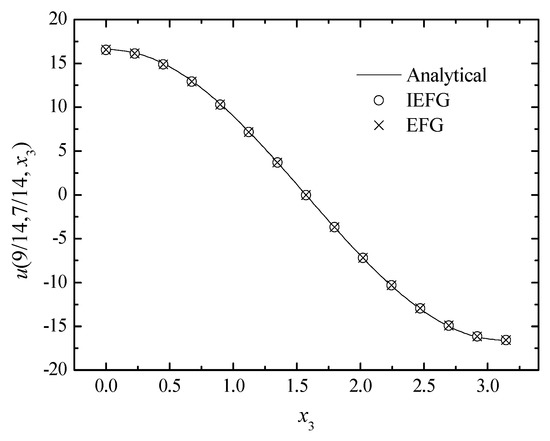
Figure 5.
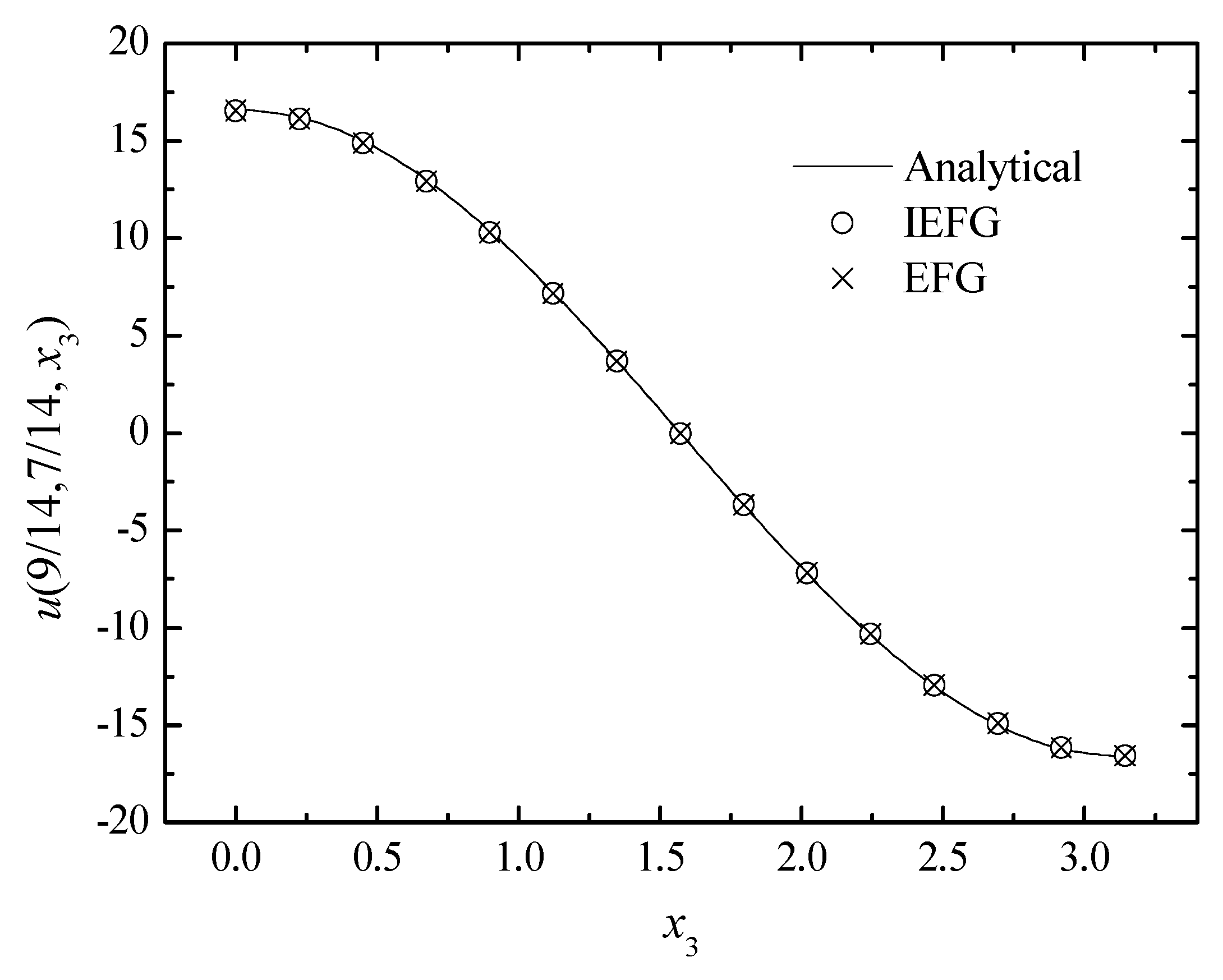
The comparison of the numerical and analytical solutions of the two methods along the x3-axis.
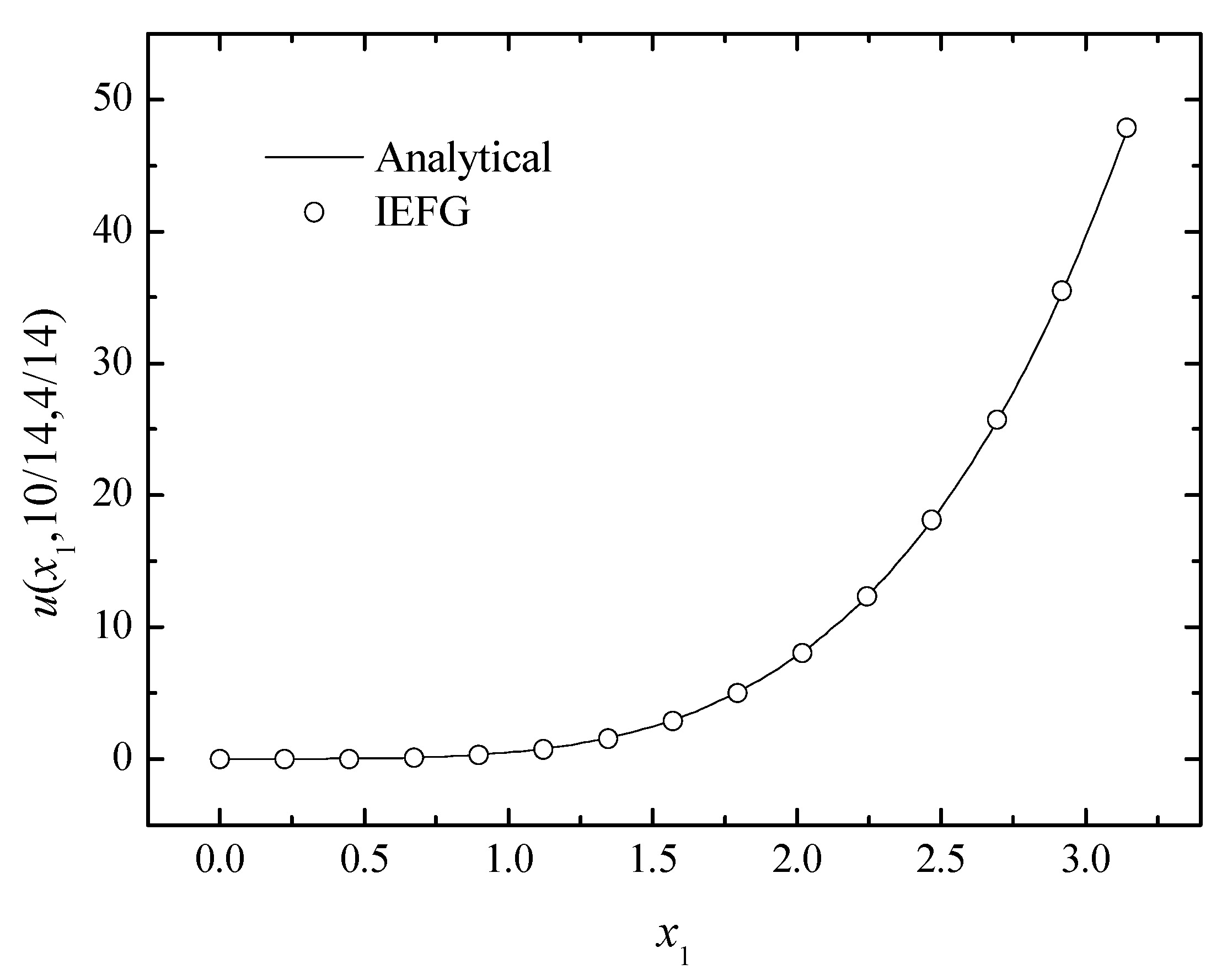
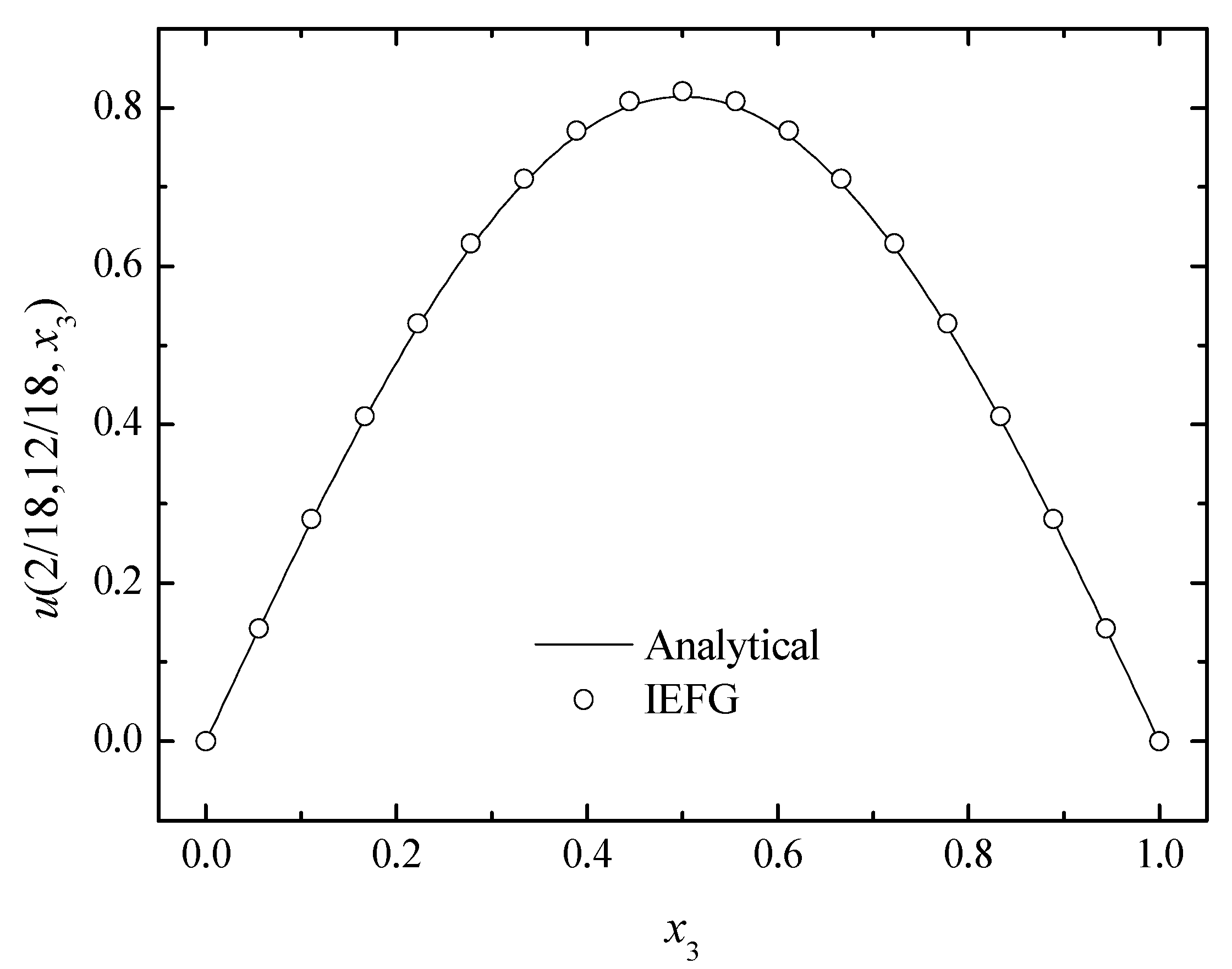
Additionally, the singular matrix can be avoided when constructing the shape functions when the IEFG is used. If dmax = 1.0 and other parameters are the same, two methods are used to solve it, and two different results are obtained. When the EFG method is used, the singular matrix occurs and the final result cannot be obtained. However, using the IEFG method to solve it, the relative error of the numerical solutions is 0.6451%. The numerical and analytical results are compared in Figure 6; it is shown that the numerical results are in good agreement with the analytical ones.
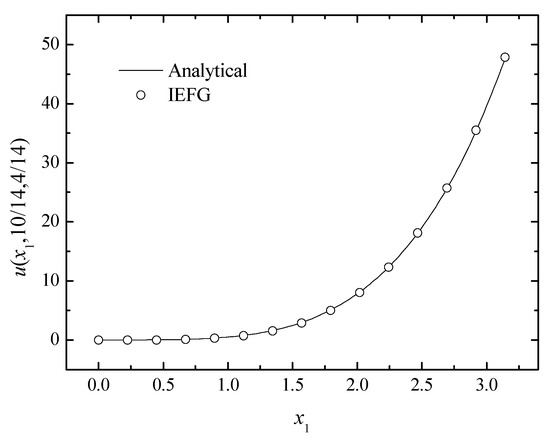
Figure 6.
The numerical and analytical solutions of the IEFG method along the x1-axis.
The second example [67] is
The boundary conditions are
The problem domain is , and
is the analytical solution.
We set k = 2, = 1, and = 0.5. The IEFG method is used to solve it, , dmax = 1.21. The 15 × 15 × 15 regularly distributed nodes and 14 × 14 × 14 background integral grids are used. When using the EFG method to solve it, the same parameters are selected, and thus the same computational accuracy can be obtained. The relative errors of both methods are equal to 0.0844%. Figure 7, Figure 8 and Figure 9 show the comparison of the numerical solutions of the two methods and the analytical ones. The CPU times of the IEFG method and the EFG method are 92.1 s and 98.0 s, respectively. We can see that the computational results of both methods are in very good agreement with the analytical ones.
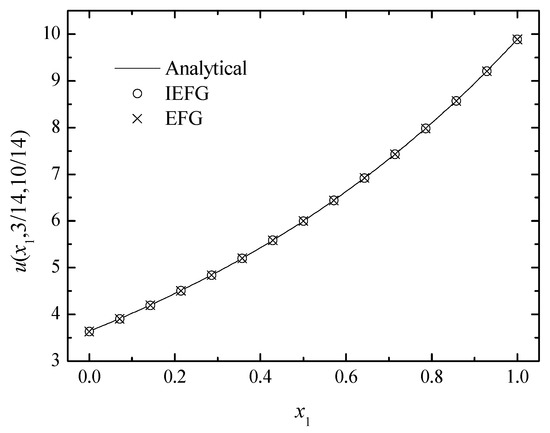
Figure 7.
The comparison of the numerical and analytical solutions of the two methods along the x1-axis.
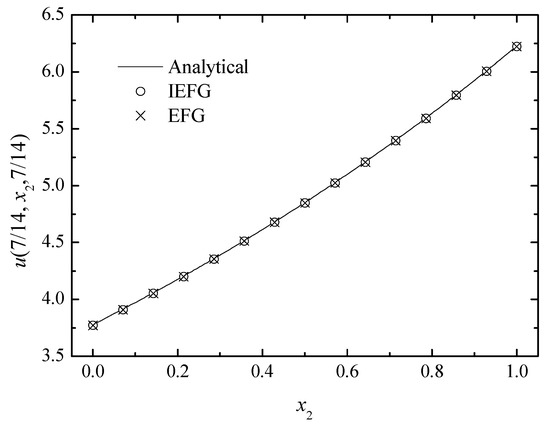
Figure 8.
The comparison of the numerical and analytical solutions of the two methods along the x2-axis.
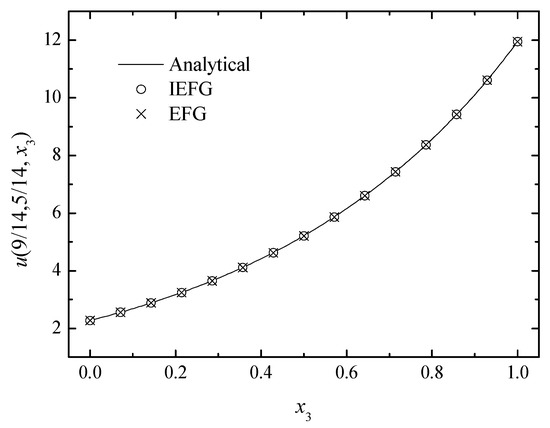
Figure 9.
The comparison of the numerical and analytical solutions of the two methods along the x3-axis.
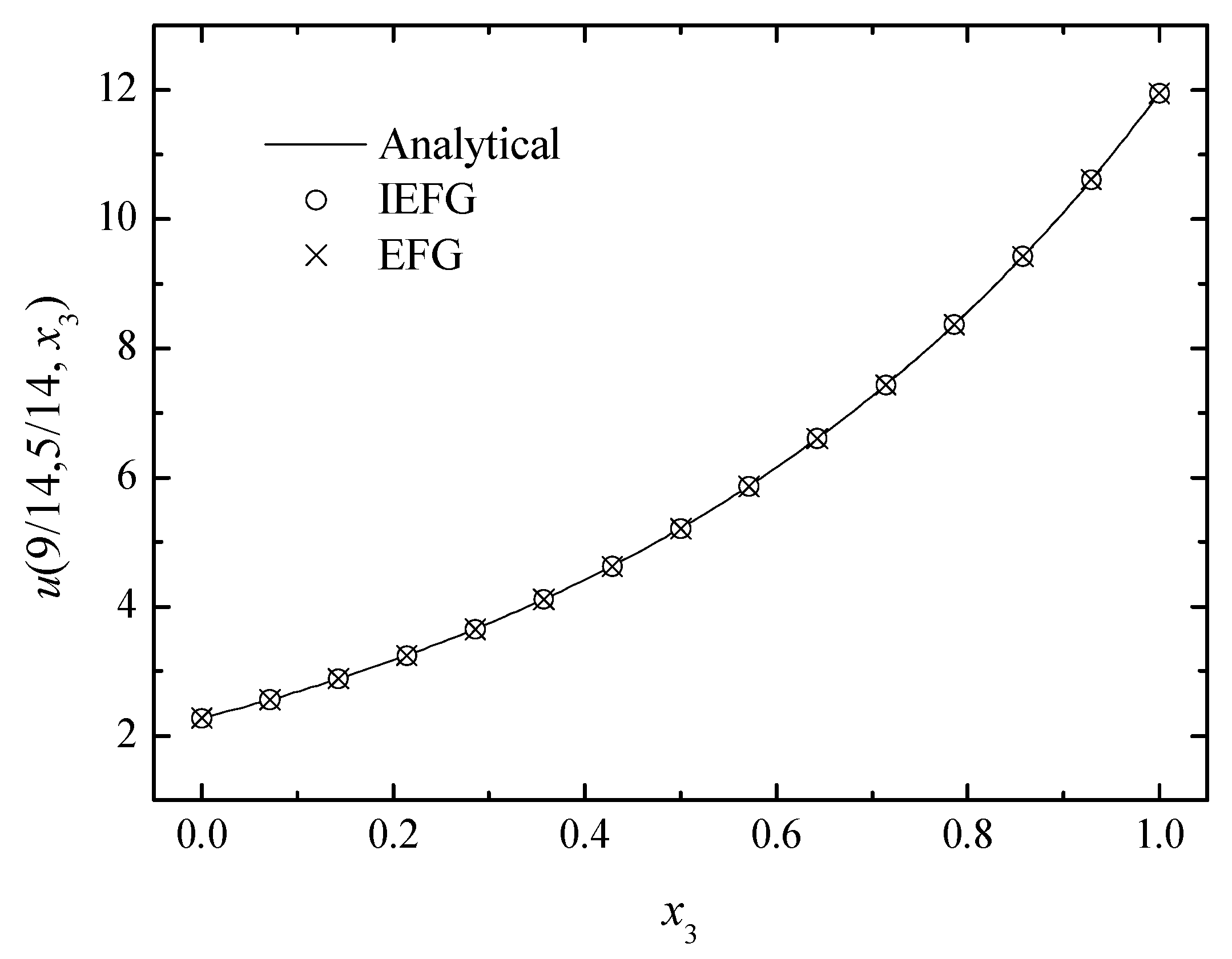
When different parameters are selected, k = 5, = 3, and = 2.7. Using two methods to solve it, the same parameters are used. Thus, the relative errors of both methods are equal to 0.5295%. Figure 10, Figure 11 and Figure 12 show the comparison of the numerical solutions of the two methods and the analytical ones, and the CPU times of the IEFG method and the EFG method are 92.1 s and 98.0 s, respectively. We can see that the computational results of both methods are in good agreement with the analytical ones.
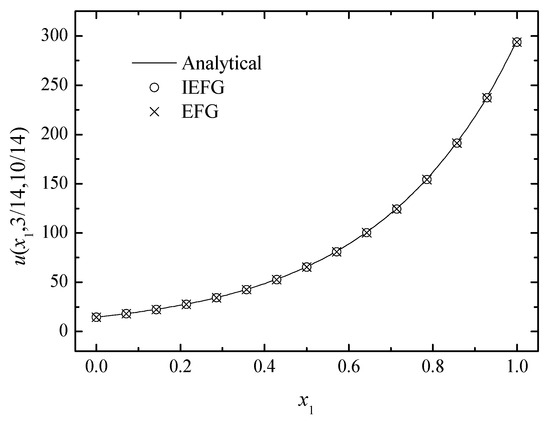
Figure 10.
The comparison of the numerical and analytical solutions of the two methods along the x1-axis.
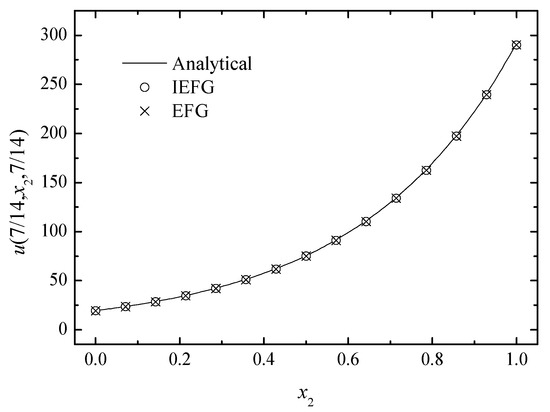
Figure 11.
The comparison of the numerical and analytical solutions of the two methods along the x2-axis.
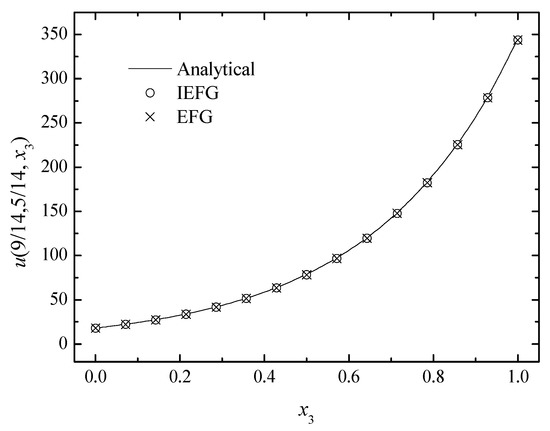
Figure 12.
The comparison of the numerical and analytical solutions of the two methods along the x3-axis.
We can select k = 10, = 5.8, and = 6.2. Using the two methods to solve it, the same parameters are used, and the relative errors of both methods are equal to 2.3884%. Figure 13, Figure 14 and Figure 15 show the comparison of the numerical solutions of the two methods and the analytical ones. The computational results of both methods are in good agreement with the analytical ones.
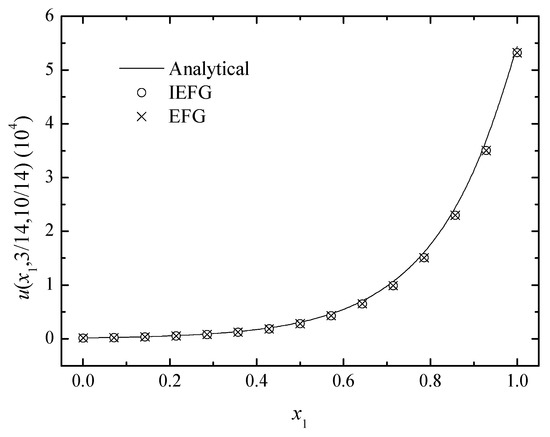
Figure 13.
The comparison of the numerical and analytical solutions of the two methods along the x1-axis.
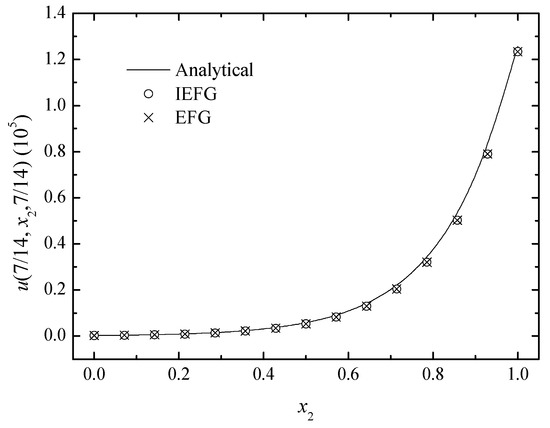
Figure 14.
The comparison of the numerical and analytical solutions of the two methods along the x2-axis.
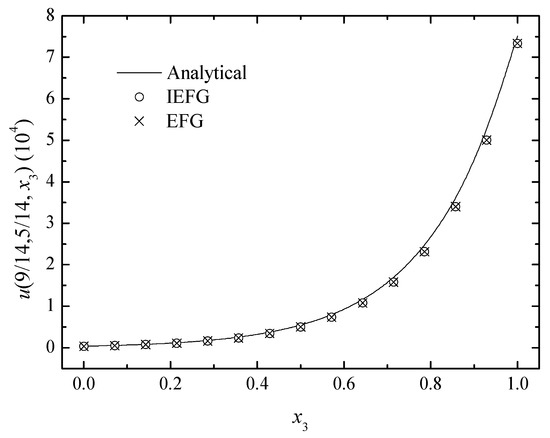
Figure 15.
The comparison of the numerical and analytical solutions of the two methods along the x3-axis.
From this example, we can draw two conclusions: On the one hand, the IEFG method has greater computational efficiency; on the other hand, the bigger the wave numbers are, the lower the computational accuracy.
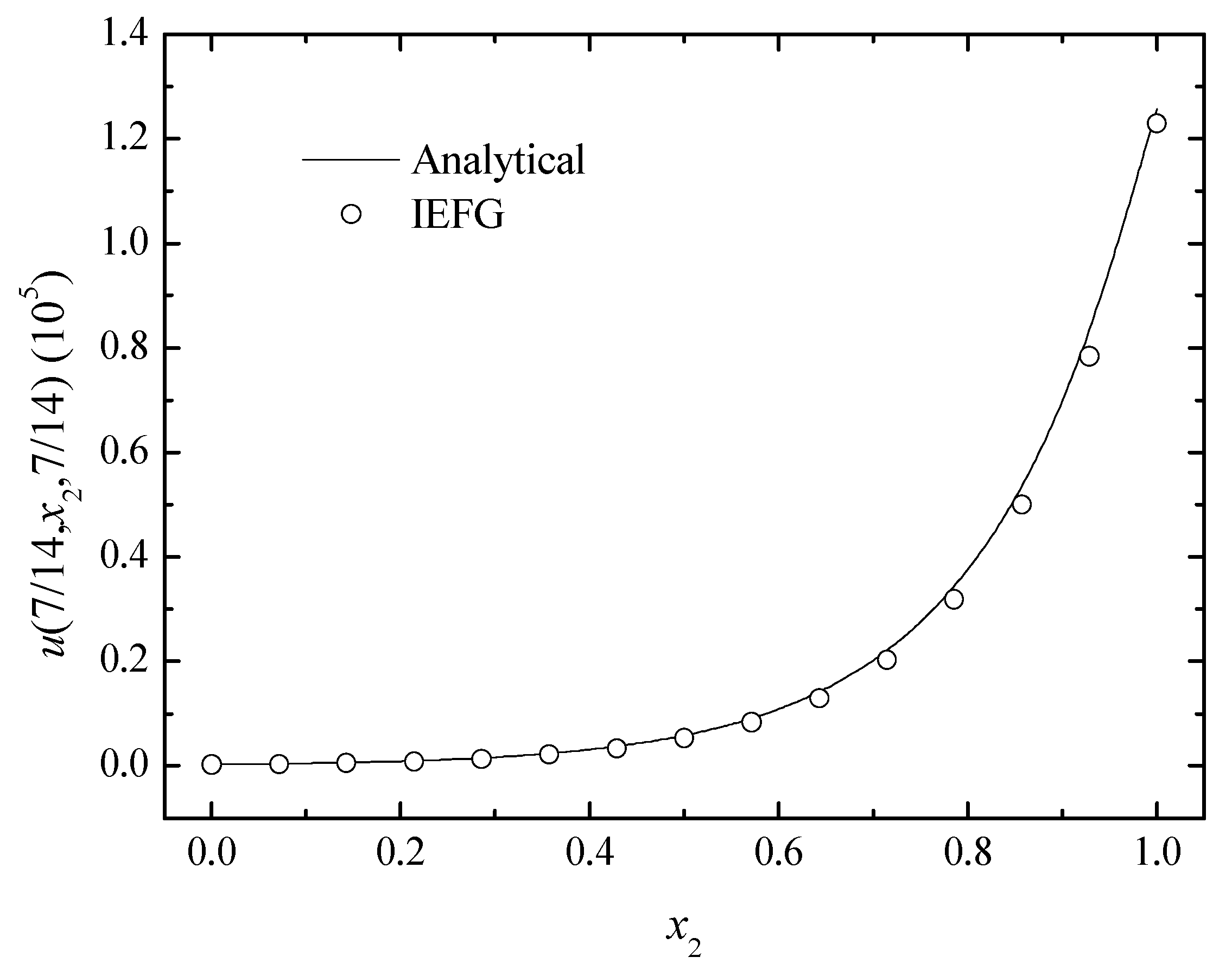
Similarly, if dmax = 1.0, we select k = 10, = 5.8, and = 6.2. When the EFG method is used, unfortunately, the singular matrix occurs. When the IEFG method is used, the relative error is 2.4229%. The numerical solutions and analytical ones are compared in Figure 16. It is shown that the numerical results are in good agreement with the analytical ones.
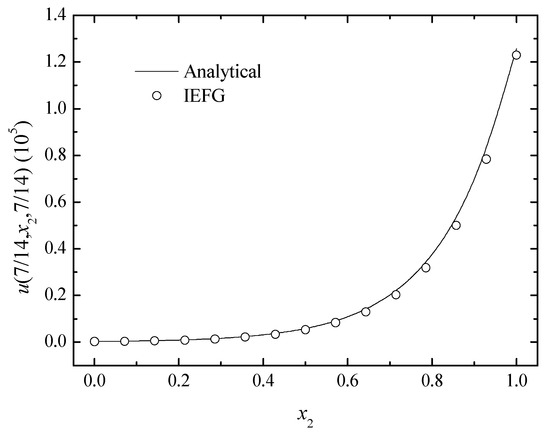
Figure 16.
The numerical and analytical solutions of the IEFG method along the x2-axis.
The third example [68] is
The boundary conditions are
The problem domain is , and
is the analytical solution.
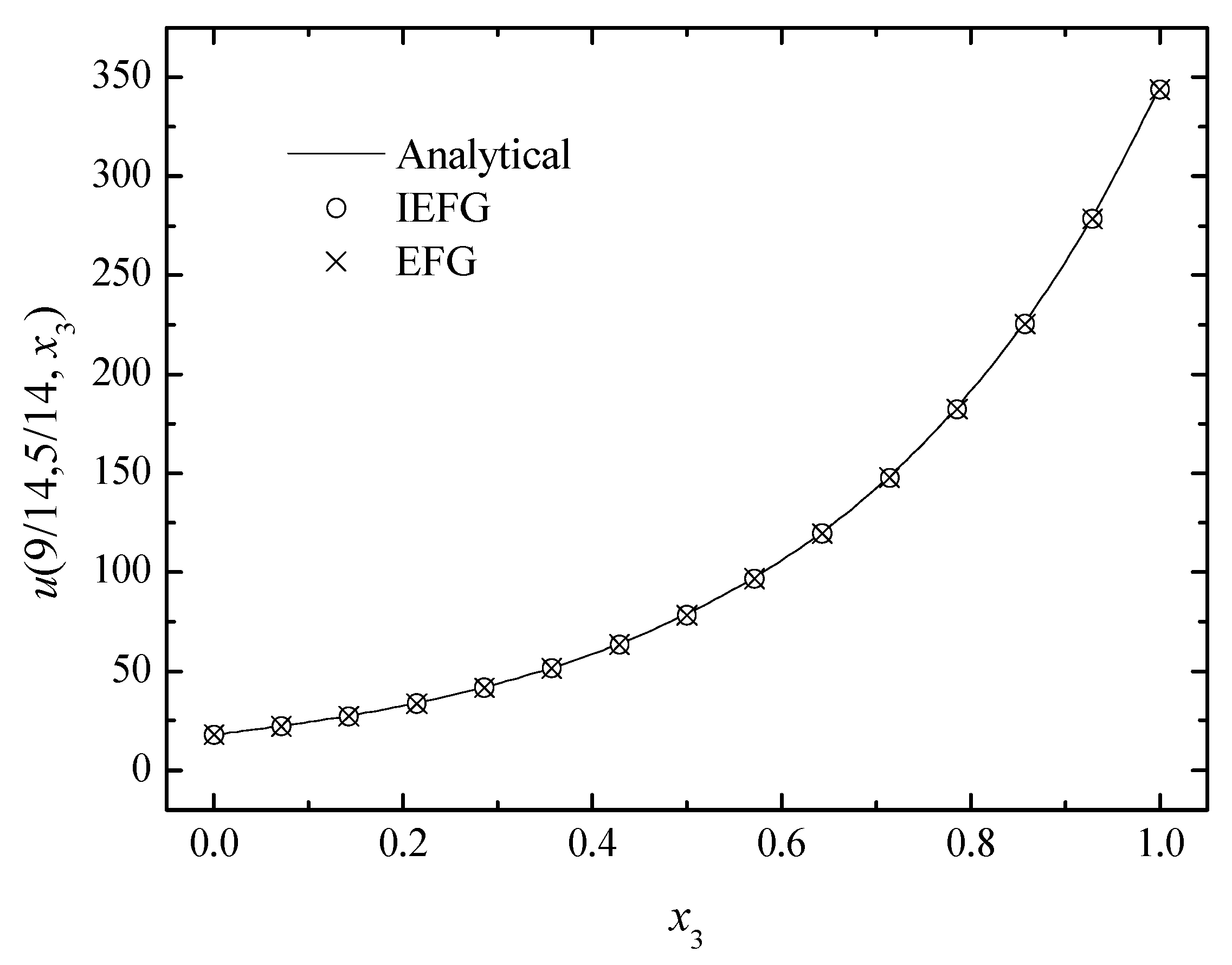
The IEFG method is used to solved it. The wave number is selected as 100, and 19 × 19 × 19 regularly distributed nodes and 18 × 18 × 18 background integral cells are used, , dmax = 1.1. When using the EFG method to solve it, the same parameters are selected, and the relative errors of both methods are equal to 0.8646%. Figure 17, Figure 18 and Figure 19 show the comparison of the numerical solutions and the analytical ones. We can see that numerical solutions are in good agreement with the analytical ones. The CPU times of the IEFG method and the EFG method are 200.6 s and 208.1 s, respectively.
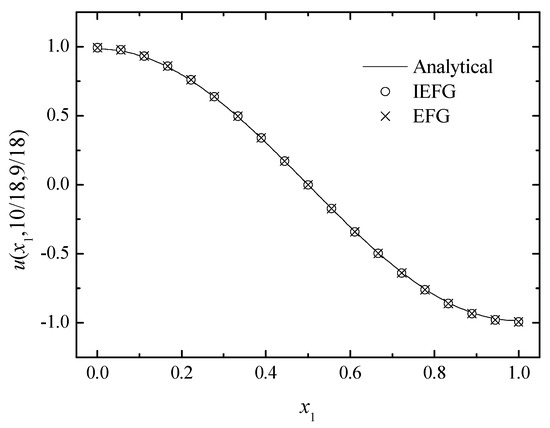
Figure 17.
The comparison of the numerical and analytical solutions of the two methods along the x1-axis.
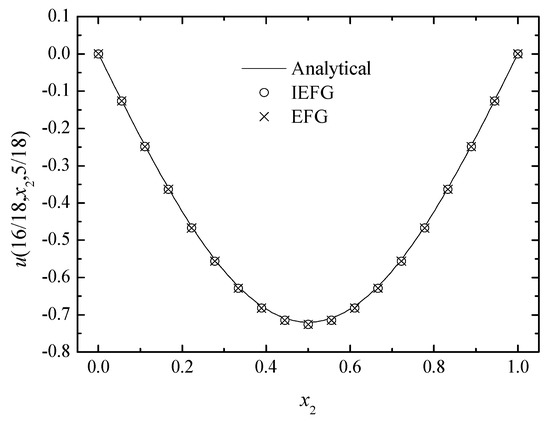
Figure 18.
The comparison of the numerical and analytical solutions of the two methods along the x2-axis.
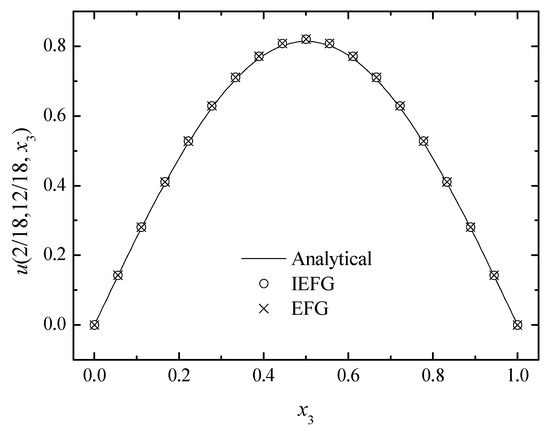
Figure 19.
The comparison of the numerical and analytical solutions of the two methods along the x3-axis.
A similar computational accuracy can be obtained when using the two methods, but the higher computational speed can be obtained when using the IEFG method.
Similarly, if dmax = 1.0, when the EFG method is used, the singular matrix occurs and the final result cannot be obtained. However, when the IEFG method is selected, the relative error is 0.8648%. The numerical solutions and the analytical one are compared in Figure 20, where it is shown that the numerical results are in good agreement with the analytical ones.
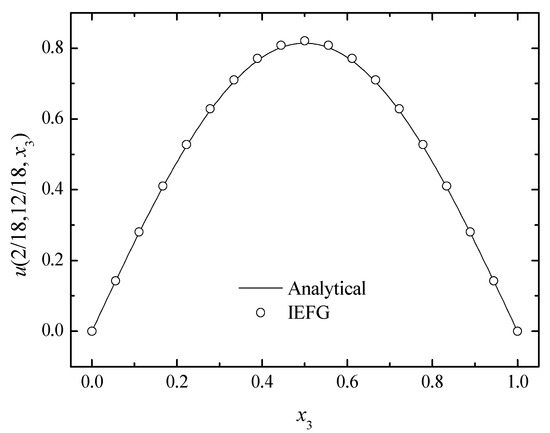
Figure 20.
The numerical and analytical solutions of the IEFG method along the x3-axis.
5. Conclusions
In order to solve 3D Helmholtz equations efficiently, the IEFG method is proposed in this paper.
Some numerical examples are given in Section 4, and the convergence of the IEFG method is proven numerically. From these examples, we can see that the IEFG method in this paper can not only enhance the computational speed of the traditional EFG method, but also eliminate the phenomenon of the singular matrix.
Author Contributions
Conceptualization, M.P.; methodology, M.P.; software, H.C.; writing—original draft preparation, H.C.; writing—review and editing, M.P.; visualization, H.C.; supervision, M.P.; funding acquisition, H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Innovation Project of Shanxi Colleges and Universities (grant number 2020L0344) and the Scientific Research Foundation of Taiyuan University of Science and Technology (grant number 20202065).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bouillarda, P.H.; Suleaub, S. Element-Free Galerkin solutions for Helmholtz problems: Formulation and numerical assessment of the pollution effect. Comput. Methods Appl. Mech. Eng. 1998, 162, 317–335. [Google Scholar] [CrossRef]
- Zeng, H.; Peng, L.; Zhao, G.; Han, C. A meshless Galerkin least-square method for the Helmholtz equation. Eng. Anal. Bound. Elem. 2011, 35, 868–878. [Google Scholar]
- Miao, Y.; Wang, Y.; Wang, Y.H. A meshless hybrid boundary-node method for Helmholtz problems. Eng. Anal. Bound. Elem. 2009, 33, 120–127. [Google Scholar] [CrossRef]
- Chen, L.C.; Liu, X.; Li, X.L. The boundary element-free method for 2D interior and exterior Helmholtz problems. Comput. Math. Appl. 2019, 77, 846–864. [Google Scholar]
- Li, X.L.; Zhang, S.G.; Wang, Y.; Chen, H. A complex variable boundary element-free method for potential and Helmholtz problems in three dimensions. Int. J. Comput. Methods 2020, 17, 1850129. [Google Scholar] [CrossRef]
- Chen, L.C.; Li, X.L. A complex variable boundary element-free method for the Helmholtz equation using regularized combined field integral equations. Appl. Math. Lett. 2020, 101, 106067. [Google Scholar] [CrossRef]
- Savovic, S.; Djordjevich, A. Numerical solution of diffusion equation describing the flow of radon through concrete. Appl. Radiat. Isot. 2008, 66, 552–555. [Google Scholar] [CrossRef] [PubMed]
- Ashyralyev, A.; Aggez, N. Finite Difference Method for Hyperbolic Equations with the Nonlocal Integral Condition. Discret. Dyn. Nat. Soc. 2011, 2011, 562385. [Google Scholar] [CrossRef] [Green Version]
- Ivanovic, M.; Svicevic, M.; Savovic, S. Numerical solution of Stefan problem with variable space grid method based on mixed finite element/finite difference approach. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 2682–2695. [Google Scholar] [CrossRef]
- Sowmiya, G.K.; Revathi, M. Numerical Method of Linear Hyperbolic Partial Differential Equation by Finite Difference Method with Conservation Law. Int. J. Adv. Sci. Technol. 2020, 29, 14–23. [Google Scholar]
- Thounthong, P.; Khan, M.N.; Hussain, I.; Ahmad, I.; Kumam, P. Symmetric radial basis function method for simulation of elliptic partial differential equations. Mathematics 2018, 6, 327. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, I.; Ahsan, M.; Din, Z.U.; Ahmad, M.; Kumam, P. An efficient local formulation for time-dependent PDEs. Mathematics 2019, 7, 216. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, I.; Ahmad, H.; Thounthong, P.; Chu, Y.M.; Cesarano, C. Solution of multi-term time-fractional PDE models arising in mathematical biology and physics by local meshless method. Symmetry 2020, 12, 1195. [Google Scholar] [CrossRef]
- Wang, F.Z.; Zheng, K.H.; Ahmad, I.; Ahmad, H. Gaussian radial basis functions method for linear and nonlinear convection-diffusion models in physical phenomen. Open Phys. 2021, 19, 69–76. [Google Scholar] [CrossRef]
- Dai, B.D.; Cheng, Y.M. Local boundary integral equation method based on radial basis functions for potential problems. Acta Phys. Sin. 2007, 56, 597–603. [Google Scholar]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin Methods. Int. J. Numer. Methods Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Cheng, R.J.; Cheng, Y.M. Error estimates of element-free Galerkin method for potential problems. Acta Phys. Sin. 2008, 57, 6037–6046. [Google Scholar]
- Cheng, J. Residential land leasing and price under public land ownership. J. Urban Plan. Dev. 2021, 147, 05021009. [Google Scholar] [CrossRef]
- Cheng, J. Analysis of commercial land leasing of the district governments of Beijing in China. Land Use Policy 2021, 100, 104881. [Google Scholar] [CrossRef]
- Cheng, J. Analyzing the factors influencing the choice of the government on leasing different types of land uses: Evidence from Shanghai of China. Land Use Policy 2020, 90, 104303. [Google Scholar] [CrossRef]
- Cheng, J. Data analysis of the factors influencing the industrial land leasing in Shanghai based on mathematical models. Math. Probl. Eng. 2020, 2020, 9346863. [Google Scholar] [CrossRef] [Green Version]
- Cheng, J. Mathematical models and data analysis of residential land leasing behavior of district governments of Beijing in China. Mathematics 2021, 9, 2314. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Chen, M.J. A boundary element-free method for linear elasticity. Acta Mech. Sin. 2003, 35, 181–186. [Google Scholar]
- Zhang, Z.; Zhao, P.; Liew, K.M. Analyzing three-dimensional potential problems with the improved element-free Galerkin method. Comput. Mech. 2009, 44, 273–284. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.F.; Cheng, Y.M.; Liew, K.M. The improved element-free Galerkin method for three-dimensional transient heat conduction problems. Sci. China Phys. Mech. Astron. 2013, 56, 1568–1580. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, D.M.; Cheng, Y.M.; Liew, K.M. The improved element-free Galerkin method for three-dimensional wave equation. Acta Mech. Sin. 2012, 28, 808–818. [Google Scholar] [CrossRef]
- Cheng, R.J.; Cheng, Y.M. Solving unsteady Schrödinger equation using the improved element-free Galerkin method. Chin. Phys. B 2016, 25, 020203. [Google Scholar] [CrossRef]
- Cheng, H.; Zheng, G.D. Analyzing 3D advection-diffusion problems by using the improved element-free Galerkin method. Math. Probl. Eng. 2020, 2020, 4317538. [Google Scholar] [CrossRef]
- Zhang, Z.; Hao, S.Y.; Liew, K.M.; Cheng, Y.M. The improved element-free Galerkin method for two-dimensional elastodynamics problems. Eng. Anal. Bound. Elem. 2013, 37, 1576–1584. [Google Scholar] [CrossRef]
- Yu, S.Y.; Peng, M.J.; Cheng, H.; Cheng, Y.M. The improved element-free Galerkin method for three-dimensional elastoplasticity problems. Eng. Anal. Bound. Elem. 2019, 104, 215–224. [Google Scholar] [CrossRef]
- Peng, M.J.; Li, R.X.; Cheng, Y.M. Analyzing three-dimensional viscoelasticity problems via the improved element-free Galerkin (IEFG) method. Eng. Anal. Bound. Elem. 2014, 40, 104–113. [Google Scholar] [CrossRef]
- Zheng, G.D.; Cheng, Y.M. The improved element-free Galerkin method for diffusional drug release problems. Int. J. Appl. Mech. 2020, 12, 2050096. [Google Scholar] [CrossRef]
- Zhang, Z.; Liew, K.M.; Cheng, Y.M.; Lee, Y.Y. Analyzing 2D fracture problems with the improved element-free Galerkin method. Eng. Anal. Bound. Elem. 2008, 32, 241–250. [Google Scholar] [CrossRef]
- Cai, X.J.; Peng, M.J.; Cheng, Y.M. The improved element-free Galerkin method for elastoplasticity large deformation problems. Sci. Sin. Phys. Mech. Astron. 2018, 48, 024701. [Google Scholar] [CrossRef]
- Lancaster, P.; Salkauskas, K. Surfaces generated by moving least squares methods. Math. Comput. 1981, 37, 141–158. [Google Scholar] [CrossRef]
- Ren, H.P.; Cheng, Y.M.; Zhang, W. Researches on the improved interpolating moving least-squares method. Chin. J. Eng. Math. 2010, 27, 1021–1029. [Google Scholar]
- Ren, H.P.; Cheng, Y.M. The interpolating element-free Galerkin (IEFG) method for two-dimensional potential problems. Eng. Anal. Bound. Elem. 2012, 36, 873–880. [Google Scholar] [CrossRef]
- Liu, D.; Cheng, Y.M. The interpolating element-free Galerkin method for three-dimensional transient heat conduction problems. Results Phys. 2020, 19, 103477. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, F.B.; Cheng, Y.M. The interpolating element-free Galerkin method for three-dimensional elastoplasticity problems. Eng. Anal. Bound. Elem. 2020, 115, 156–167. [Google Scholar] [CrossRef]
- Wu, Q.; Peng, P.P.; Cheng, Y.M. The interpolating element-free Galerkin method for elastic large deformation problems. Sci. China Technol. Sci. 2021, 64, 364–374. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Bai, F.N.; Liu, C.; Peng, M.J. Analyzing nonlinear large deformation with an improved element-free Galerkin method via the interpolating moving least-squares method. Int. J. Comput. Mater. Sci. Eng. 2016, 5, 1650023. [Google Scholar]
- Qin, Y.X.; Li, Q.Y.; Du, H.X. Interpolating smoothed particle method for elastic axisymmetrical problem. Int. J. Appl. Mech. 2017, 9, 1750022. [Google Scholar] [CrossRef]
- Wang, J.F.; Sun, F.X.; Cheng, Y.M. An improved interpolating element-free Galerkin method with nonsingular weight function for two-dimensional potential problems. Chin. Phys. B 2012, 21, 090204. [Google Scholar] [CrossRef]
- Liu, F.B.; Cheng, Y.M. The improved element-free Galerkin method based on the nonsingular weight functions for elastic large deformation problems. Int. J. Comput. Mater. Sci. Eng. 2018, 7, 1850023. [Google Scholar] [CrossRef]
- Liu, F.B.; Wu, Q.; Cheng, Y.M. A meshless method based on the nonsingular weight functions for elastoplastic large deformation problems. Int. J. Appl. Mech. 2019, 11, 1950006. [Google Scholar] [CrossRef]
- Liu, F.B.; Cheng, Y.M. The improved element-free Galerkin method based on the nonsingular weight functions for inhomogeneous swelling of polymer gels. Int. J. Appl. Mech. 2018, 10, 1850047. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Peng, M.J.; Li, J.H. The complex variable moving least-square approximation and its application. Acta Mech. Sin. 2005, 37, 719–723. [Google Scholar]
- Peng, M.J.; Liu, P.; Cheng, Y.M. The complex variable element-free Galerkin (CVEFG) method for two-dimensional elasticity problems. Int. J. Appl. Mech. 2009, 1, 367–385. [Google Scholar] [CrossRef]
- Bai, F.N.; Li, D.M.; Wang, J.F.; Cheng, Y.M. An improved complex variable element-free Galerkin method for two-dimensional elasticity problems. Chin. Phys. B 2012, 21, 020204. [Google Scholar] [CrossRef]
- Chen, L.; Cheng, Y.M. Reproducing kernel particle method with complex variables for elasticity. Acta Phys. Sin. 2008, 57, 1–10. [Google Scholar] [CrossRef]
- Chen, L.; Cheng, Y.M. The complex variable reproducing kernel particle method for elasto-plasticity problems. Sci. China Phys. Mech. Astron. 2010, 53, 954–965. [Google Scholar] [CrossRef]
- Cheng, H.; Peng, M.J.; Cheng, Y.M. The dimension splitting and improved complex variable element-free Galerkin method for 3-dimensional transient heat conduction problems. Int. J. Numer. Methods Eng. 2018, 114, 321–345. [Google Scholar] [CrossRef]
- Cheng, H.; Peng, M.J.; Cheng, Y.M. A hybrid improved complex variable element-free Galerkin method for three-dimensional potential problems. Eng. Anal. Bound. Elem. 2017, 84, 52–62. [Google Scholar] [CrossRef]
- Cheng, H.; Peng, M.J.; Cheng, Y.M. A fast complex variable element-free Galerkin method for three-dimensional wave propagation problems. Int. J. Appl. Mech. 2017, 9, 1750090. [Google Scholar] [CrossRef]
- Cheng, H.; Peng, M.J.; Cheng, Y.M. A hybrid improved complex variable element-free Galerkin method for three-dimensional advection-diffusion problems. Eng. Anal. Bound. Elem. 2018, 97, 39–54. [Google Scholar] [CrossRef]
- Cheng, H.; Peng, M.J.; Cheng, Y.M.; Meng, Z.J. The hybrid complex variable element-free Galerkin method for 3D elasticity problems. Eng. Struct. 2020, 219, 110835. [Google Scholar] [CrossRef]
- Meng, Z.J.; Cheng, H.; Ma, L.D.; Cheng, Y.M. The dimension split element-free Galerkin method for three-dimensional potential problems. Acta Mech. Sin. 2018, 34, 462–474. [Google Scholar] [CrossRef]
- Meng, Z.J.; Cheng, H.; Ma, L.D.; Cheng, Y.M. The dimension splitting element-free Galerkin method for 3D transient heat conduction problems. Sci. China Phys. Mech. Astron. 2019, 62, 040711. [Google Scholar] [CrossRef]
- Meng, Z.J.; Cheng, H.; Ma, L.D.; Cheng, Y.M. The hybrid element-free Galerkin method for three-dimensional wave propagation problems. Int. J. Numer. Methods Eng. 2019, 117, 15–37. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.D.; Meng, Z.J.; Chai, J.F.; Cheng, Y.M. Analyzing 3D advection-diffusion problems by using the dimension splitting element-free Galerkin method. Eng. Anal. Bound. Elem. 2020, 111, 167–177. [Google Scholar] [CrossRef]
- Peng, P.P.; Wu, Q.; Cheng, Y.M. The dimension splitting reproducing kernel particle method for three-dimensional potential problems. Int. J. Numer. Methods Eng. 2020, 121, 146–164. [Google Scholar] [CrossRef]
- Peng, P.P.; Cheng, Y.M. Analyzing three-dimensional transient heat conduction problems with the dimension splitting reproducing kernel particle method. Eng. Anal. Bound. Elem. 2020, 121, 180–191. [Google Scholar] [CrossRef]
- Peng, P.P.; Cheng, Y.M. Analyzing three-dimensional wave propagation with the hybrid reproducing kernel particle method based on the dimension splitting method. Eng. Comput. 2021, 1–17. [Google Scholar] [CrossRef]
- Peng, P.P.; Cheng, Y.M. A hybrid reproducing kernel particle method for three-dimensional advection-diffusion problems. Int. J. Appl. Mech. 2021, 13, 2150085. [Google Scholar] [CrossRef]
- Wu, Q.; Peng, M.J.; Cheng, Y.M. The interpolating dimension splitting element-free Galerkin method for 3D potential problems. Eng. Comput. 2021, 1–15. [Google Scholar] [CrossRef]
- Wang, J.F.; Sun, F.X. A hybrid generalized interpolated element-free Galerkin method for Stokes problems. Eng. Anal. Bound. Elem. 2020, 111, 88–100. [Google Scholar] [CrossRef]
- Marin, L. A meshless method for the numerical solution of the Cauchy problem associated with three-dimensional Helmholtz-type equations. Appl. Math. Comput. 2005, 165, 274–355. [Google Scholar] [CrossRef]
- Cheng, D.S.; Chen, B.W.; Chen, X.L. A robust optimal finite difference scheme for the three-dimensional Helmholtz equation. Math. Probl. Eng. 2019, 2019, 8532408. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).