An Attention-Preserving Network-Based Method for Assisted Segmentation of Osteosarcoma MRI Images
Abstract
:1. Introduction
- (1)
- A new MRI image segmentation method for osteosarcoma is proposed. Based on the attention mechanism, it solves the problem of recognizing multi-scale tumors, especially fine tumor regions, and effectively improves the processing accuracy of the segmentation network.
- (2)
- The use of a parallel partial decoder avoids the inability to balance local features with global features. Axial attention also solves the redundant computation problem of CNN-based methods and reduces the waste of resources. The CaPaN achieves a good trade-off between segmentation performance and inference speed, and the model has better performance than alternatives while requiring fewer parameters.
- (3)
- Accurate segmentation of small tumor regions is achieved by using CFP as a contextual module to obtain multi-scale information about tumors. The results of model segmentation are used as a reference basis for doctors’ clinical diagnoses in order to reduce the occurrence of missed and misdiagnoses, thus reducing the time and personnel cost associated with doctors’ repeated verifications when manually segmenting tumor regions.
- (4)
- In this experiment, an independent non-public dataset from the Second Xiangya Hospital of Central South University was used for a validation analysis. The results demonstrate that the CaPaN has a better performance in MRI image segmentation of osteosarcomas, especially for small target objects.
2. Related Work
3. System Model Design
3.1. CFP Module
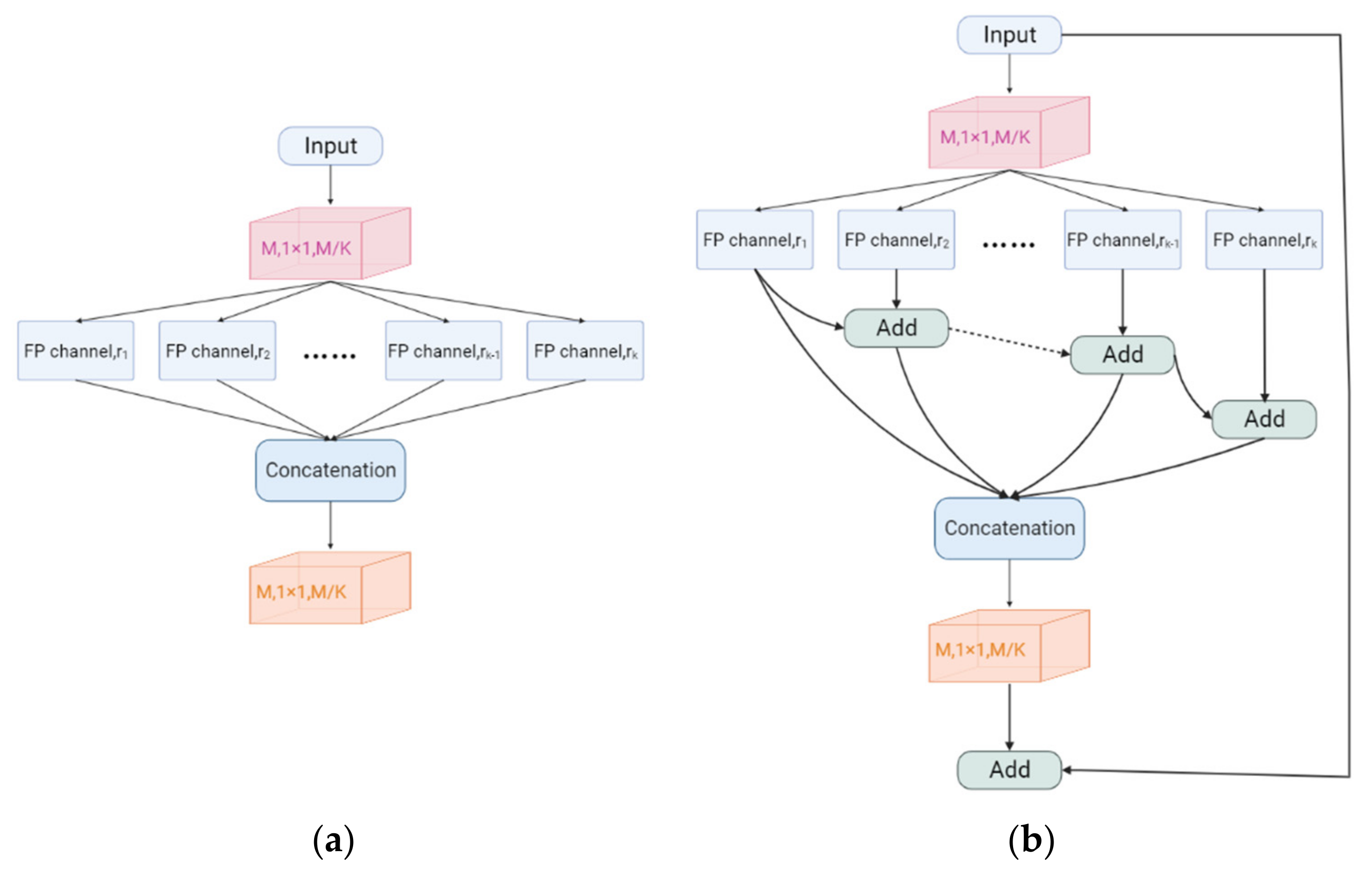
3.1.1. Feature Pyramid Channel



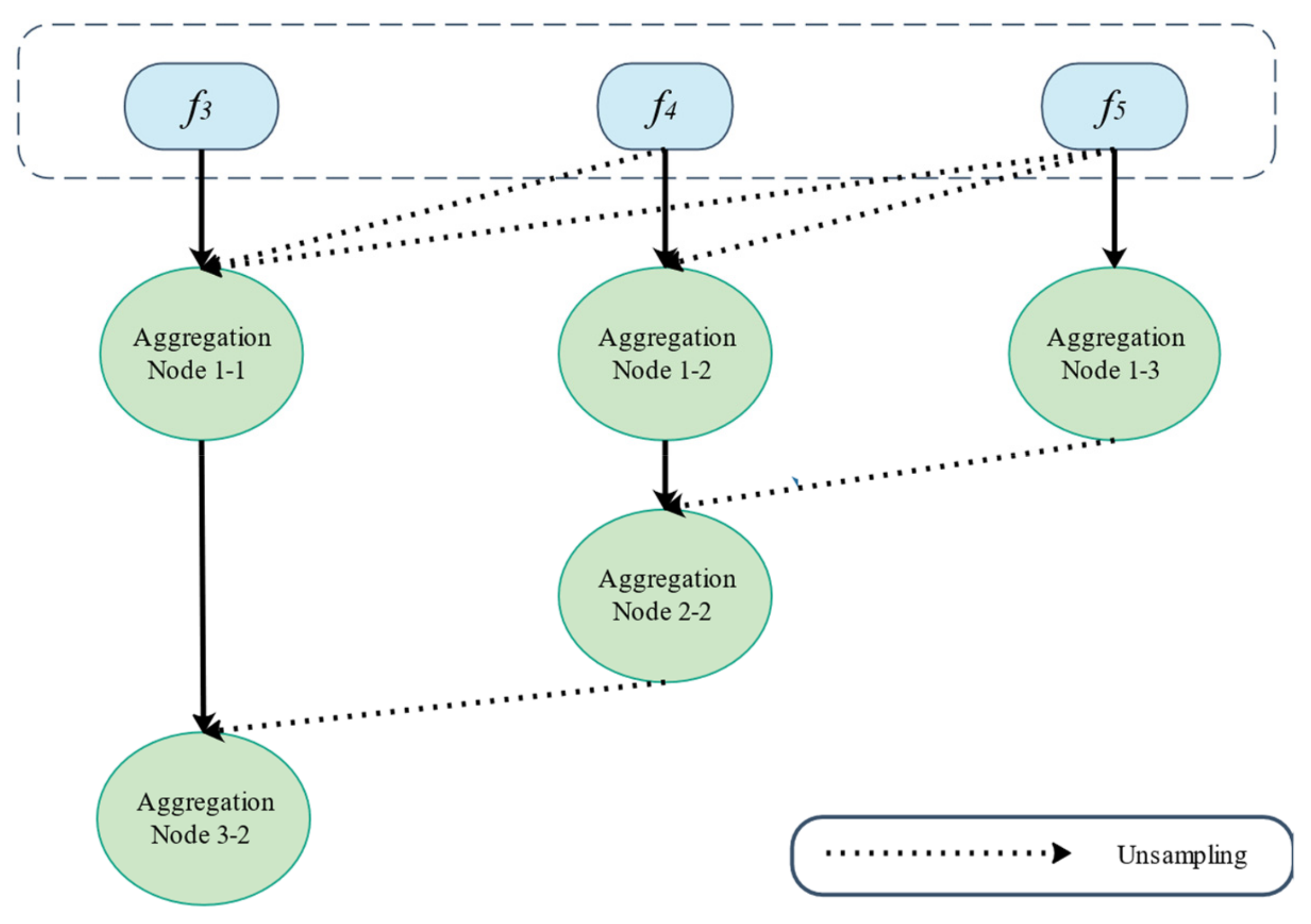
3.1.2. CFP Module Structure
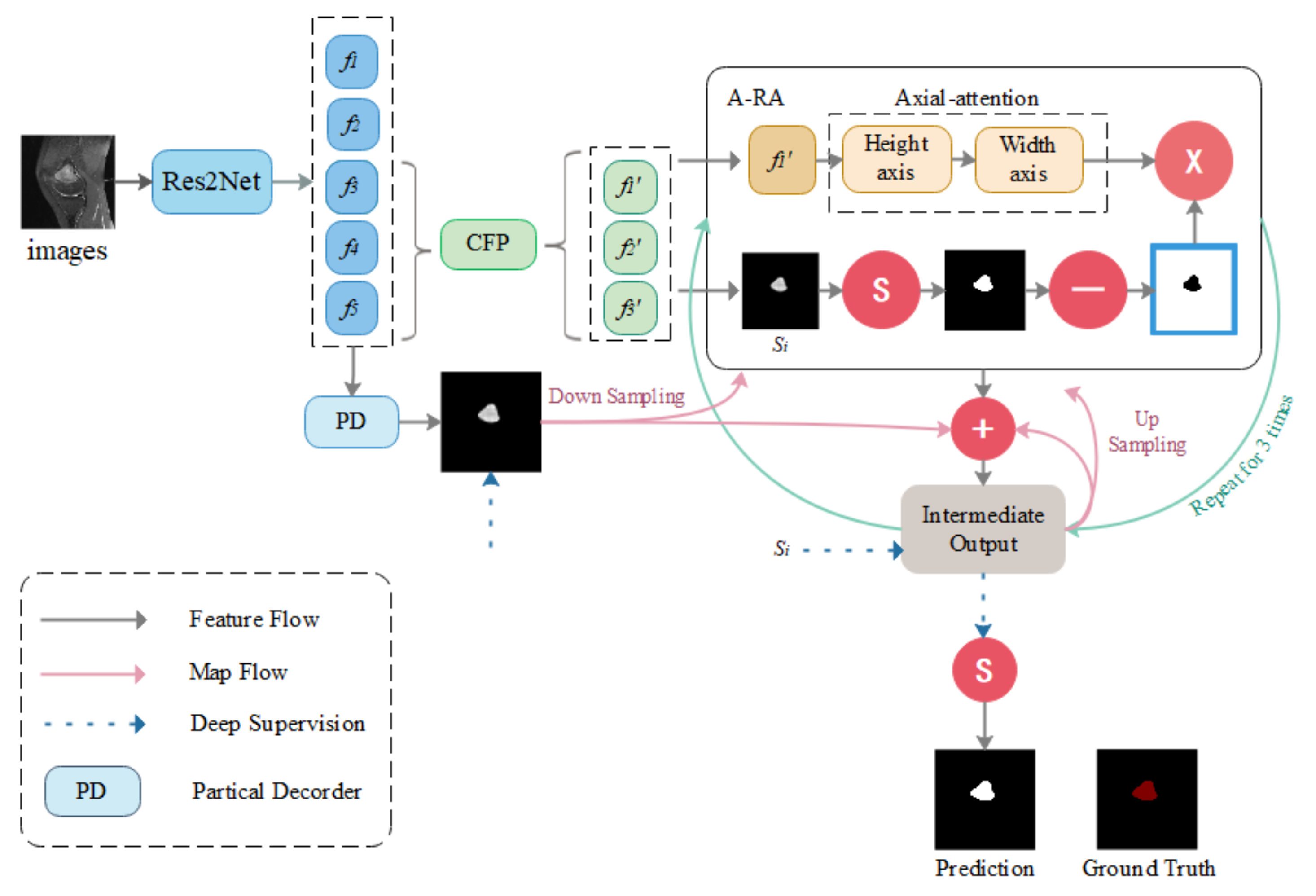
3.2. CaPaN Basic Structure
- Parallel Partial Decoder:
- Context Module:
- Axial Reverse Attention:
- Axial Reverse Attention:
- Small Object Segmentation Analysis:
4. Experimental Results
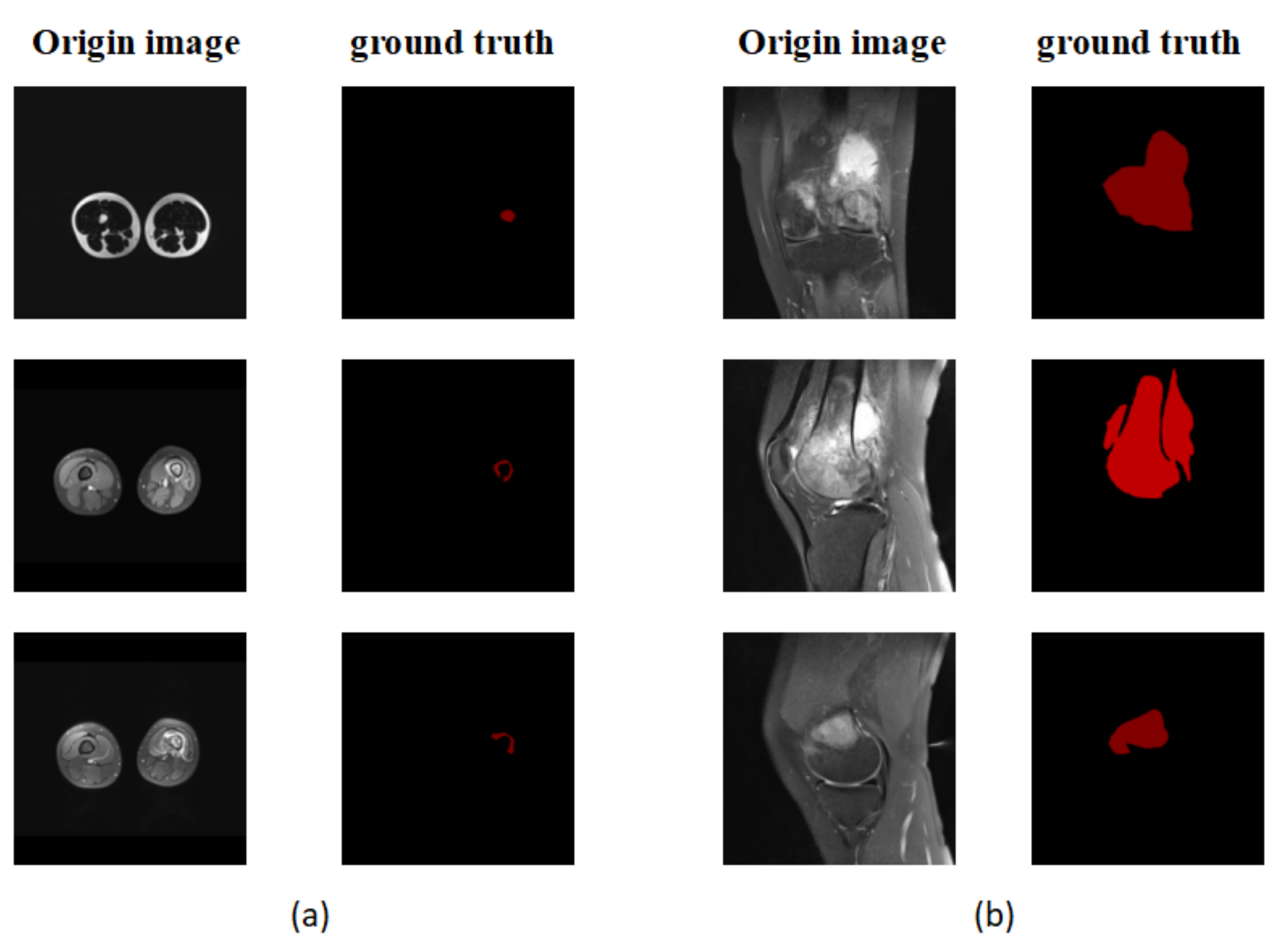
4.1. Datasets
4.2. Training Strategies
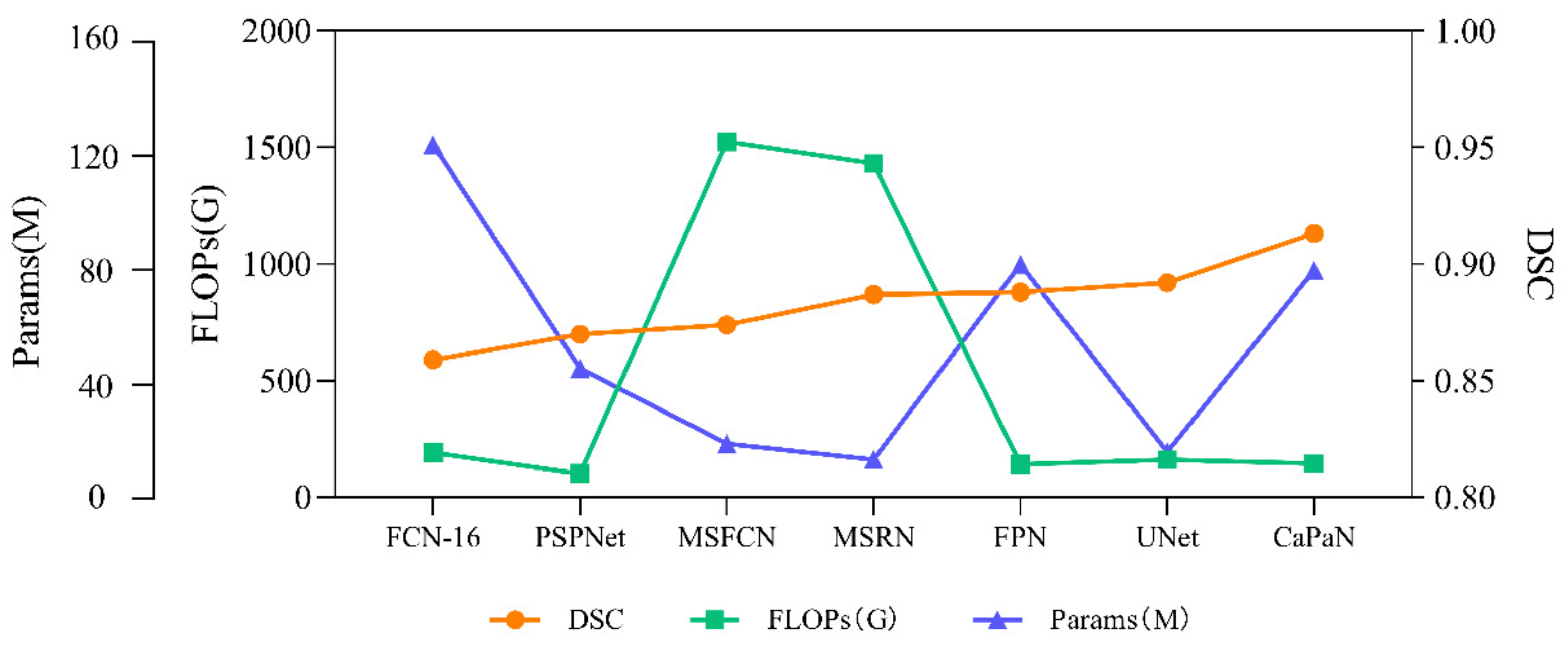
4.3. Algorithm Comparison
4.4. Evaluation Indicators
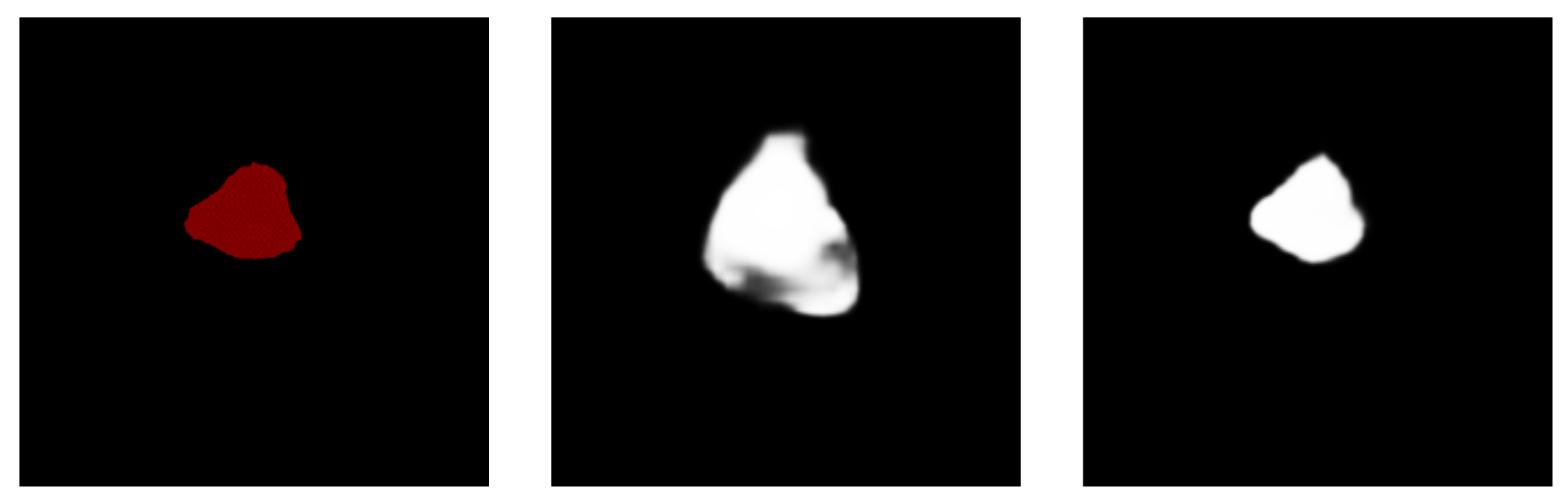
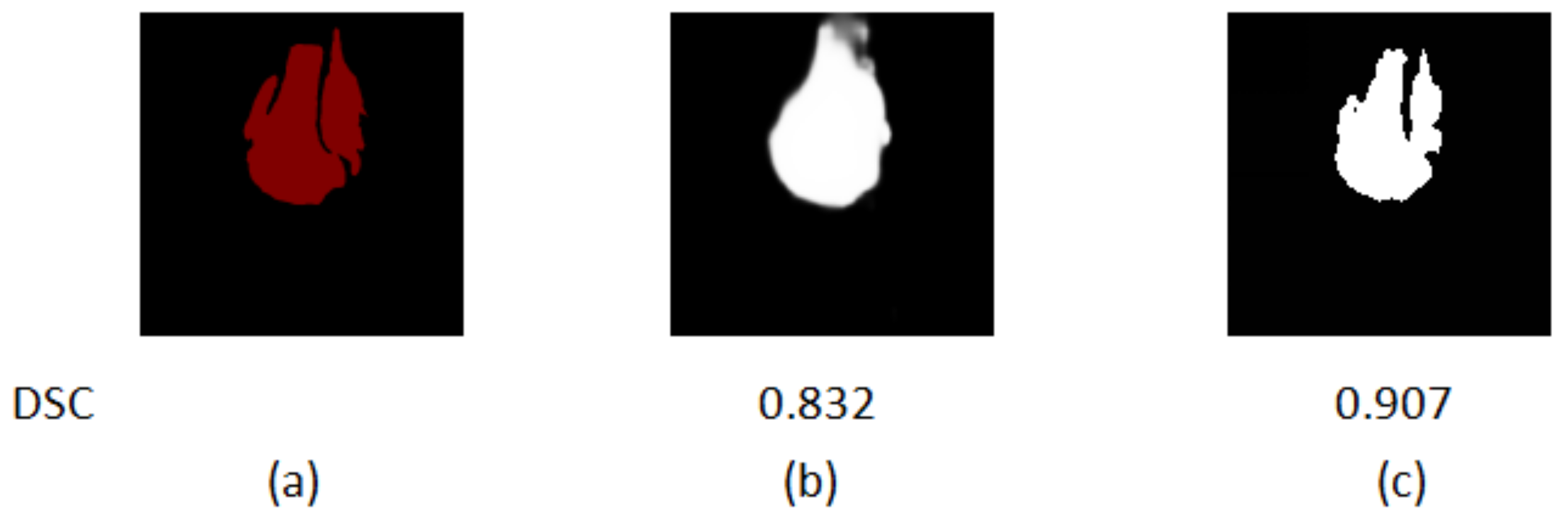
4.5. Results
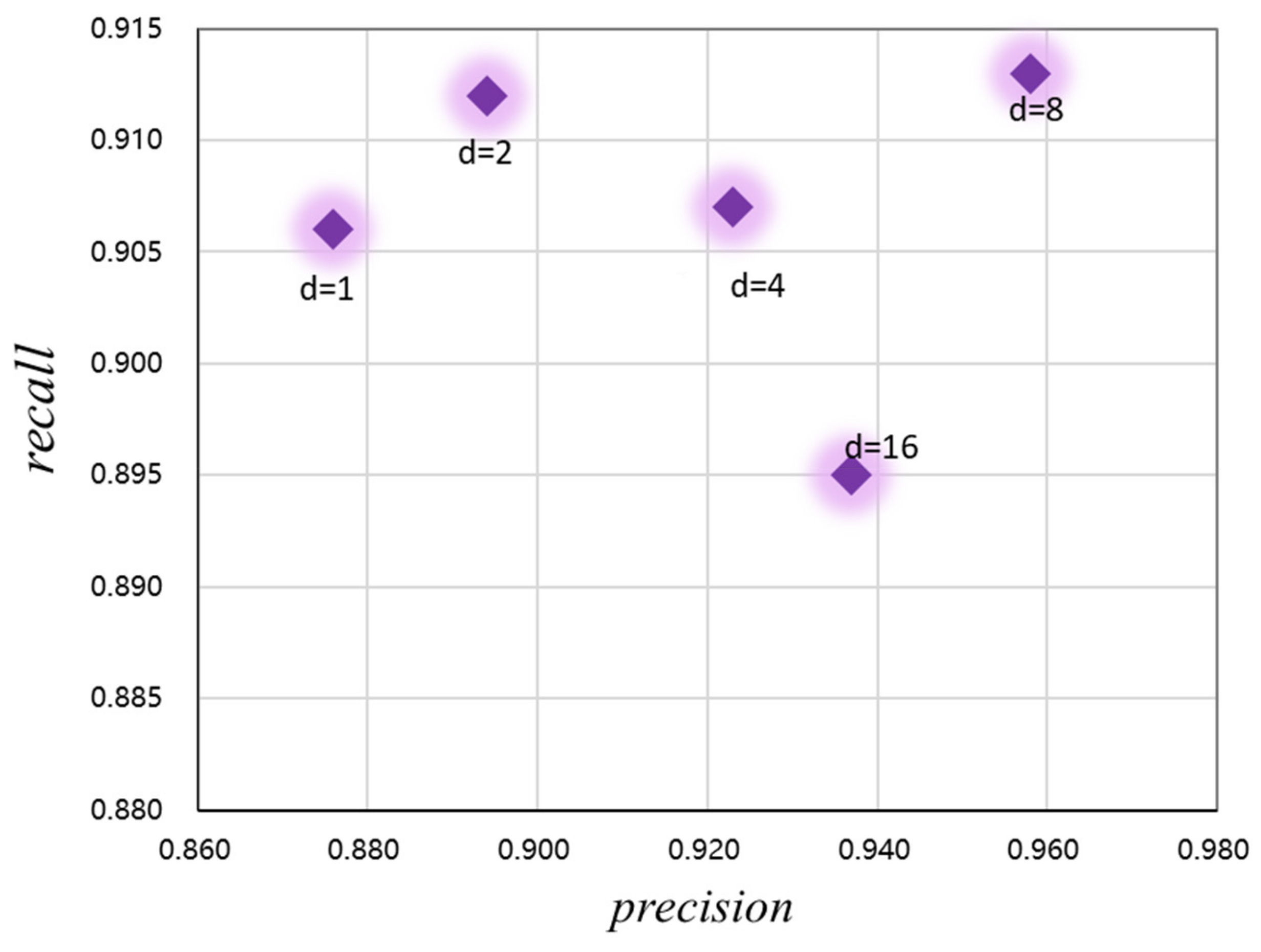
4.6. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Eaton, B.R.; Schwarz, R.; Vatner, R.; Yeh, B.; Claude, L.; Indelicato, D.J.; Laack, N. Osteosarcoma. Pediatr. Blood Cancer 2021, 68, e28352. [Google Scholar] [CrossRef] [PubMed]
- Mahore, S.; Bhole, K.; Rathod, S. Comparative analysis of machine learning algorithm for classification of different osteosarcoma types. In Proceedings of the 2021 12th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kharagpur, India, 6–8 July 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Kayal, E.B.; Kandasamy, D.; Yadav, R.; Bakhshi, S.; Sharma, R.; Mehndiratta, A. Automatic segmentation and RECIST score evaluation in osteosarcoma using diffusion MRI: A computer aided system process. Eur. J. Radiol. 2020, 133, 109359. [Google Scholar] [CrossRef] [PubMed]
- Sinha, A.; Dolz, J. Multi-scale self-guided attention for medical image segmentation. IEEE J. Biomed. Health Inform. 2021, 25, 121–130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Osadebey, M.; Pedersen, M.; Arnold, D.; Wendel-Mitoraj, K. Image quality evaluation in clinical research: A case study on brain and cardiac MRI images in multi-center clinical trials. IEEE J. Transl. Eng. Health Med. 2018, 6, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Yang, Y.; Yu, C.; Liu, J.; Duan, X.; Weng, Z.; Chen, D.; Liang, Q.; Fang, Q.; Zhou, J.; et al. Ensembled deep learning model outperforms human experts in diagnosing biliary atresia from sonographic gallbladder images. Images. Nat. Commun. 2021, 12, 1259. [Google Scholar] [CrossRef]
- Saraf, R.; Datta, A.; Sima, C.; Hua, J.; Lopes, R.; Bittner, M.L.; Miller, T.; Wilson-Robles, H.M. In silico modeling of the induction of apoptosis by Cryptotanshinone in osteosarcoma cell lines. IEEE ACM Trans. Comput. Biol. Bioinform. 2020. [Google Scholar] [CrossRef]
- Tian, X.; Tan, Y. Hospital evaluation mechanism based on mobile health for IoT system in social networks. Comput. Biol. Med. 2019, 109, 138–147. [Google Scholar]
- Cui, R.; Chen, Z.; Tan, Y.; Yu, G. A multiprocessing scheme for pet image pre-screening, noise reduction, segmentation and lesion partitioning. IEEE J. Biomed. Health Inform. 2021, 25, 1699–1711. [Google Scholar] [CrossRef]
- Yu, G.; Wu, J. Efficacy prediction based on attribute and multi-source data collaborative for auxiliary medical system in developing countries. Neural Comput. Applic. 2022, 34, 5497–5512. [Google Scholar] [CrossRef]
- Lou, A.; Guan, S.; Ko, H.; Loew, M. CaPaN: Context Axial reverse attention network for segmentation of small medical objects. arXiv 2021, arXiv:2108.07368. [Google Scholar]
- Chang, L.; Moustafa, N.; Bashir, A.K.; Yu, K. AI-driven synthetic biology for non-small cell lung cancer drug effectiveness-cost analysis in intelligent assisted medical systems. IEEE J. Biomed. Health Inf. 2021, 1–12. [Google Scholar] [CrossRef]
- Zhuang, Q.; Dai, Z. Deep active learning framework for lymph nodes metastases prediction in medical support system. Comput. Intell. Neurosci. 2022, 2022, 4601696. [Google Scholar] [CrossRef]
- Pang, S.; Pang, C.; Zhao, L.; Chen, Y.; Su, Z.; Zhou, Y.; Huang, M.; Yang, W.; Lu, H.; Feng, Q. SpineParseNet: Spine parsing for volumetric MR image by a two-stage segmentation framework with semantic image representation. IEEE Trans. Med. Imaging 2021, 40, 262–273. [Google Scholar] [CrossRef]
- Gou, F.; Wu, J. Triad link prediction method based on the evolutionary analysis with IoT in opportunistic social networks. Comput. Commun. 2022, 181, 143–155. [Google Scholar] [CrossRef]
- Li, L.; Gou, F.; Wu, J. Modified data delivery strategy based on stochastic block model and community detection with IoT in opportunistic social networks. Wirel. Commun. Mob. Comput. 2022, 2022, 5067849. [Google Scholar] [CrossRef]
- Oksuz, I.; Clough, J.R.; Ruijsink, B.; Anton, E.P.; Bustin, A.; Cruz, G.; Prieto, C.; King, A.P.; Schnabel, J.A. Deep learning-based detection and correction of cardiac MR motion artefacts during reconstruction for high-quality segmentation. IEEE Trans. Med. Imaging 2020, 39, 4001–4010. [Google Scholar] [CrossRef]
- Chen, L.; Bentley, P.; Mori, K.; Misawa, K.; Fujiwara, M.; Rueckert, D. DRINet for medical image segmentation. IEEE Trans. Med. Imaging 2018, 37, 2453–2462. [Google Scholar] [CrossRef]
- Gou, F.; Wu, J. Message transmission strategy based on recurrent neural network and attention mechanism in IoT system. J. Circuits Syst. Comput. 2022, 31, 2250126. [Google Scholar] [CrossRef]
- Wu, J.; Xia, J.; Gou, F. Information transmission mode and IoT community reconstruction based on user influence in opportunistic social networks. Peer to Peer Netw. Appl. 2022, 15, 1398–1416. [Google Scholar] [CrossRef]
- Tan, Y.; Wu, J.; Gou, F. A staging auxiliary diagnosis model for non-small cell lung cancer based the on intelligent medical system. Comput. Math. Methods Med. 2021, 2021, 6654946. [Google Scholar] [CrossRef]
- Zhan, X.; Long, H.; Duan, X.; Kong, G. A convolutional neural network-based intelligent medical system with sensors for assistive diagnosis and decision-making in non-small cell lung cancer. Sensors 2021, 21, 7996. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Zhou, Z.; Xie, P.; Xu, N.; Dai, Z. Intelligent segmentation medical assistance system for mri images of osteosarcoma in developing countries. Comput. Math. Methods Med. 2022, 2022, 6654946. [Google Scholar] [CrossRef]
- Deng, Y.; Gou, F.; Wu, J. Hybrid data transmission scheme based on source node centrality and community reconstruction in opportunistic social networks. Peer to Peer Netw. 2021, 14, 3460–3472. [Google Scholar] [CrossRef]
- Nasor, M.; Obaid, W. Segmentation of osteosarcoma in MRI images by K-means clustering, Chan-Vese segmentation, and iterative Gaussian filtering. IET Image Process. 2021, 15, 1310–1318. [Google Scholar] [CrossRef]
- Kayal, E.B.; Kandasamy, D.; Sharma, R.; Bakhshi, S.; Mehndiratta, A. Segmentation of osteosarcoma tumor using diffusion weighted MRI: A comparative study using nine segmentation algorithms. Signal Image Video Process. 2020, 14, 727–735. [Google Scholar] [CrossRef]
- Frangi, A.F.; Egmont-Petersen, M.; Niessen, W.J.; Reiber, J.H.C.; Viergever, M.A. Bone tumor segmentation from MR perfusion images with neural networks using multi-scale pharmacokinetic features. Image Vis. Comput. 2001, 19, 679–690. [Google Scholar] [CrossRef]
- Huang, W.-B.; Wen, D.; Yan, Y.; Yuan, M.; Wang, K. Multi-target osteosarcoma MRI recognition with texture context features based on CRF. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 3978–3983. [Google Scholar] [CrossRef]
- Mandava, R.; Alia, O.M.; Wei, B.C.; Ramachandram, D.; Aziz, M.E.; Shuaib, I.L. Osteosarcoma segmentation in MRI using dynamic Harmony Search based clustering. In Proceedings of the 2010 International Conference of Soft Computing and Pattern Recognition, Cergy-Pontoise, France, 7–10 December 2010; pp. 423–429. [Google Scholar] [CrossRef]
- Huang, W.B.; Wang, Y.J. A New Method for osteosarcoma recognition based on bayesian classifier. Appl. Mech. Mater. 2014, 543–547, 2901. [Google Scholar] [CrossRef]
- Nabid, R.A.; Rahman, M.L.; Hossain, M.F. Classification of osteosarcoma tumor from histological image using sequential RCNN. In Proceedings of the 2020 11th International Conference on Electrical and Computer Engineering (ICECE), Dhaka, Bangladesh, 17–19 December 2020; pp. 363–366. [Google Scholar]
- Hong, F.; Zhao, Y.; Sun, H.; Li, M.; Mei, J. Segmentation of osteosarcoma based on analysis of blood-perfusion EPI series. In Proceedings of the 2004 International Conference on Communications, Circuits and Systems (IEEE Cat. No.04EX914), Chengdu, China, 27–29 June 2004; Volume 2, pp. 955–959. [Google Scholar] [CrossRef]
- Michael, B.; Jaeger, P.F.; Isensee, F.; Maier-Hein, K.H. nnDetection: A self-configuring method for medical object detection. arXiv 2021, arXiv:2106.00817. [Google Scholar] [CrossRef]
- Luo, X.; Song, T.; Wang, G.; Chen, J.; Chen, Y.; Li, K.; Metaxas, D.N.; Zhang, S. SCPM-Net: An anchor-free 3D lung nodule detection network using sphere representation and center points matching. Med. Image Anal. 2022, 75, 102287. [Google Scholar] [CrossRef]
- Peng, H.; Sun, H.; Guo, Y. 3D multi-scale deep convolutional neural networks for pulmonary nodule detection. PLoS ONE 2021, 16, e0244406. [Google Scholar] [CrossRef]
- Gao, H.; Chen, Z.; Li, C. Hierarchical shrinkage multiscale network for hyperspectral image classification with hierarchical feature fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5760–5772. [Google Scholar] [CrossRef]
- Wu, J.; Gou, F.; Tian, X. Disease control and prevention in rare plants based on the dominant population selection method in opportunistic social networks. Comput. Intell. Neurosci. 2022, 2022, 1489988. [Google Scholar] [CrossRef]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support: DLMIA ML-CDS 2018 2018; Springer: Berlin/Heidelberg, Germany, 2018; Volume 11045. [Google Scholar] [CrossRef] [Green Version]
- Gao, S.-H.; Cheng, M.-M.; Zhao, K.; Zhang, X.-Y.; Yang, M.-H.; Torr, P. Res2Net: A New Multi-Scale Backbone Architecture. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 652–662. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Gou, F.; Xiong, W.; Zhou, X. A Reputation Value-Based Task-Sharing Strategy in Opportunistic Complex Social Networks. Complexity 2021, 2021, 8554351. [Google Scholar] [CrossRef]
- Shelhamer, E.; Long, J.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 936–944. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Xia, W.; Zhang, B.; Qiu, B.; Gao, X. MSFCN-multiple supervised fully convolutional networks for the osteosarcoma segmentation of CT images. Comput. Methods Progr. Biomed. 2017, 143, 67–74. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6230–6239. [Google Scholar] [CrossRef] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015. MICCAI 2015; Navab, N., Hornegger, J., Wells, W., Frangi, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9351. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Huang, L.; Xia, W.; Zhang, B.; Qiu, B.; Gao, X. Multiple supervised residual network for osteosarcoma segmentation in CT images. Comput. Med Imaging Graph. 2018, 63, 1–8. [Google Scholar] [CrossRef]
- Qadri, S.F.; Shen, L.; Ahmad, M.; Qadri, S.; Zareen, S.S.; Akbar, M.A. SVseg: Stacked sparse autoencoder-based patch classification modeling for vertebrae segmentation. Mathematics 2022, 10, 796. [Google Scholar] [CrossRef]
- Ahmad, M.; Qadri, S.F.; Qadri, S.; Saeed, I.A.; Zareen, S.S.; Iqbal, Z.; Alabrah, A.; Alaghbari, H.M.; Rahman, S.M.M. A lightweight convolutional neural network model for liver segmentation in medical diagnosis. Comput. Intell. Neurosci. 2022, 2022, 7954333. [Google Scholar] [CrossRef]
- Shen, Y.; Gou, F.; Dai, Z. Osteosarcoma MRI image-assisted segmentation system based on guided aggregated bilateral network. Mathematics 2022, 10, 1090. [Google Scholar] [CrossRef]
- Chang, L.; Yu, G. Effective data decision-making and transmission system based on mobile health for chronic disease management in the elderly. IEEE Syst. J. 2021, 15, 5537–5548. [Google Scholar] [CrossRef]
- Pang, S.; Feng, Q.; Lu, Z.; Jiang, J.; Zhao, L.; Lin, L.; Li, X.; Lian, T.; Huang, M.; Yang, W. Hippocampus segmentation based on iterative local linear mapping with representative and local structure-preserved feature embedding. IEEE Trans. Med. Imaging 2019, 38, 2271–2280. [Google Scholar] [CrossRef]
- Zhou, X.-Y.; Zheng, J.-Q.; Li, P.; Yang, G.-Z. ACNN: A full resolution dcnn for medical image segmentation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 31 May–31 August 2020; pp. 8455–8461. [Google Scholar] [CrossRef]
- Zhuang, Q.; Tan, Y. Auxiliary medical decision system for prostate cancer based on ensemble method. Comput. Math. Methods Med. 2020, 2020, 6509596. [Google Scholar] [CrossRef]
- Yang, W.; Luo, J.; Wu, J. Application of information transmission control strategy based on incremental community division in IoT platform. IEEE Sensors J. 2021, 21, 21968–21978. [Google Scholar] [CrossRef]





| Indicator Name | Description |
|---|---|
| Params | Number of participants |
| Pr | Precision [49], |
| FLOPs | The number of calculations required by the model |
| MAE | Average absolute error [50], |
| F1-score | A combination of precision and recall, |
| DSC | Average DSC value |
| IoU | Average IOU value |
| test_mean Specificity | Average specificity at test, |
| test_mean Sensitivity | Average sensitivity during testing, |
| Structure measure | Structural metrics [51] |
| Degree of Dataset Enhancement | Average DSC | F1 | MAE |
|---|---|---|---|
| No enhancement | 0.467 | 0.341 | 0.018 |
| Four kinds of enhancements | 0.871 | 0.843 | 0.010 |
| Six kinds of enhancements | 0.901 | 0.892 | 0.007 |
| MODEL | PR | F1 | DSC | FLOPS | PARAMS |
|---|---|---|---|---|---|
| FCN-16S | 0.922 ± 0.09 | 0.900 ± 0.08 | 0.859 ± 0.07 | 190.35 G | 134.3 M |
| PSPNET | 0.856 ± 0.09 | 0.872 ± 0.03 | 0.870 ± 0.06 | 101.55 G | 49.07 M |
| MSFCN | 0.881 ± 0.06 | 0.906 ± 0.05 | 0.874 ± 0.03 | 1524.34 G | 20.38 M |
| MSRN | 0.893 ± 0.03 | 0.918 ± 0.04 | 0.887 ± 0.03 | 1431.23 G | 14.27 M |
| FPN | 0.914 ± 0.11 | 0.919 ± 0.07 | 0.888 ± 0.08 | 141.14 G | 88.63 M |
| U-NET | 0.922 ± 0.09 | 0.923 ± 0.05 | 0.892 ± 0.04 | 160.16 G | 17.26 M |
| CAPAN | 0.936 ± 0.03 | 0.932 ± 0.02 | 0.913 ± 0.05 | 144.41 G | 86.38 M |
| Divided Objects | PR | F1 | DSC | IOU | Recall |
|---|---|---|---|---|---|
| Whole dataset | 0.913 | 0.897 | 0.901 | 0.842 | 0.905 |
| Small target objects | 0.936 | 0.932 | 0.913 | 0.865 | 0.927 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Gou, F.; Wu, J. An Attention-Preserving Network-Based Method for Assisted Segmentation of Osteosarcoma MRI Images. Mathematics 2022, 10, 1665. https://doi.org/10.3390/math10101665
Liu F, Gou F, Wu J. An Attention-Preserving Network-Based Method for Assisted Segmentation of Osteosarcoma MRI Images. Mathematics. 2022; 10(10):1665. https://doi.org/10.3390/math10101665
Chicago/Turabian StyleLiu, Feng, Fangfang Gou, and Jia Wu. 2022. "An Attention-Preserving Network-Based Method for Assisted Segmentation of Osteosarcoma MRI Images" Mathematics 10, no. 10: 1665. https://doi.org/10.3390/math10101665
APA StyleLiu, F., Gou, F., & Wu, J. (2022). An Attention-Preserving Network-Based Method for Assisted Segmentation of Osteosarcoma MRI Images. Mathematics, 10(10), 1665. https://doi.org/10.3390/math10101665







