Abstract
Resolution decrease and motion blur are two typical image degradation processes that are usually addressed by deep networks, specifically convolutional neural networks (CNNs). However, since real images are usually obtained through multiple degradations, the vast majority of current CNN methods that employ a single degradation process inevitably need to be improved to account for multiple degradation effects. In this work, motivated by degradation decoupling and multiple-order attention drop-out gating, we propose a joint deep recovery model to efficiently address motion blur and resolution reduction simultaneously. Our degradation decoupling style improves the continence and the efficiency of model construction and training. Moreover, the proposed multi-order attention mechanism comprehensively and hierarchically extracts multiple attention features and fuses them properly by drop-out gating. The proposed approach is evaluated using diverse benchmark datasets including natural and synthetic images. The experimental results show that our proposed method can efficiently complete joint motion blur and image super-resolution (SR).
Keywords:
motion deblurring; image super-resolution; multi-order attention; gated learning; decoupling MSC:
37M99
1. Introduction
Motion blur and resolution decrease are the two dominant forms of image quality degradation. The former is caused by the relative motion between the camera and the object, while the latter is generally originated by down-sampling. The inverse processes of these degradation forms are individual motion deblurring and image SR—recovering clear images from blurred ones or reconstructing high-resolution (HR) images from low resolution (LR) ones, respectively, which are the practical main means to deal with image quality degradation.
Assuming the original sharp image is , and the blurred image is ; if ignoring the effect of the non-linear camera response function (CRF), theoretically the motion blur degradation may be represented as:
where represents the motion blur kernel, denotes the convolution operation and usually indicates the random noise. According to Equation (1), obviously, the inverse motion deblurring process is a typical ill-conditioned problem because for one clear image there are possibly many blur images corresponding to it.
Actually, there are two different implementation methods for motion deblurring, namely, blind deblurring or the non-blind method. The usual non-blind method acquires the clear image based on the estimated blur kernel and the observation . However, the major difference in blind deblurring is that no kernel estimation is required. Due to the end-to-end mapping and the powerful approximation properties, CNNs are particularly well suited for blind motion deblurring. For example, some recent CNN-based works [,] are presented for blind deblurring duties.
Compared with motion blur degradation, in the process of resolution degeneration, in addition to the low pass blur filter and the noise , there is another degradation down-sampling operator at work. For an HR image x, a typical resolution degradation model to acquire the corresponding LR image is formulated as:
where denotes a low pass blur filter, denotes the convolution operation, indicates a down-sampling (decimating) operation, and represents the noise. Obviously, the inverse problem of Equation (2)—image SR—is also a typical ill-posed one as there is usually a non-unique solution.
Motion blur degradation is superficially seen to be a simpler problem than resolution degeneration due to there being no down-sampling operation. However, motion blur is most likely to be non-linear or non-uniform, which is usually more complex than resolution degradation (the blur kernel is generally linear and uniform). This makes it a difficult challenge to directly estimate the blur kernel used for non-blind deblurring.
In recent years, deep learning-based networks, especially CNN-based methods, have been the mainstream of image SR and motion deblurring research, such as [,,]. Although CNN-based image SR and deblurring methods have reported fairly good results, CNN-based image restoration is far from simple when the resolution and motion blur are reduced simultaneously. In this case, either image SR or motion deblurring does not work well due to degraded convolution or the blur kernels not being equivalent, and the two degradation processes are not complementary with each other when they occur simultaneously.
Recently, there have been some CNN works [,,] that have addressed simultaneous image SR and motion deblurring. All of these methods explicitly or implicitly adopt a global or local feature coupling structure—a deblurring part and an SR part are involved or intervene with each other, to recover the resolution and the motion details at the same time. Actually, these recovery methods only construct different comprehensive CNN mapping networks from the degraded images to the corresponding sharp and high-resolution ones, but do not fully utilize the characteristics of motion deblurring and image SR to achieve decoupling. Therefore, even if the results of these methods are good, they lack an explanation and have low efficiency.
On the other hand, typical deep image recovery models always use the residual connection to convey features. However, due to a lack of ability to mine the feature information across different layers, some complex residual variants are proposed, such as DRRN [] and RDN [], etc. Among them, RDN (Residual Dense Network) is representative, which uses not only local dense residual learning but also global residual learning, to extract and adaptively fuse the local and global features from all the observed layers. Since RDN makes full use of multiple hierarchical features, it is very beneficial to construct an image restoration model. In addition to the work on feature learning across different layers, recent attention mechanism-based methods, for example, RCAN [] and SAN [], select and enhance useful and important channel feature maps of the same layer through weighting for image or video restoration. In fact, these channel feature attention methods utilize the first- or second-order statistics of the channel maps of certain layers to calculate the dependence of channel features, and then select and weigh the important features. However, single first- or second-order feature statistics cannot make full use of the relationship between different channel feature maps.
In order to overcome the limitations of coupling recovery and single-order attention feature weighting, in this work, we first analyze the compound multiple degradation model of motion blur and resolution reduction and discuss the maximum likelihood (ML) solution of the degradation model. Then, based on the analysis, we discuss decoupling induction multi-task learning and the CNN model construction method for multiple degradation image restoration. In addition, we obtain the first-order and second-order attention features of the decoupled structures for motion deblurring and SR, respectively, and obtain the third-order attention features by combining local series and parallel features. On this basis, for the sake of improving the feature redundancy and generalization ability of multi-order attention fusion, we utilize the drop-out gating integration method, which enhances the robustness and stability of the proposed multi-order attention mechanism.
An example result of the proposed method to deal with compound degeneration (motion blur as well as 4× down-sampling) is shown in Figure 1, where the comparisons to those results of RCAN [] and SCGAN [] are also demonstrated. The dominant contributions of the work are summed up as follows:

Figure 1.
An example result of the presented decoupling induction and multi-order attention gating model for joint deblurring and 4× super-resolution. The details in the recovered image of our proposed method (d) are much clearer than those of RCAN [] (b) and SCGAN [] (c); the LR and blurred image is shown (a).
- We propose a novel joint motion deblurring and image SR model based on decoupling induction and multi-order attention drop-out gating. The proposed method can overcome the limitation of the single type degeneration assumption to achieve joint recovery with the aid of decoupling induction multi-task learning.
- We propose the use of decoupling dual-branch multi-order attention features for clear HR image reconstruction and select the drop-out gating learning method to enhance the robustness and the generalization of features’ fusion.
- We validate and compare the presented model, not only with the publicly available and widely used natural image datasets, but also with synthetic images completely different from the training images. We show that, through decoupling induction and multi-order attention drop-out gating learning, our method can produce visual results of a quality that competes with the most advanced motion deblurring and image SR methods for LR and blurred images.
2. Related Work
2.1. Joint Image Deblur and SR
Compared with the traditional image SR methods, the first CNN-based image SR method, SRCNN [,], proposed by Dong et al., can generate more accurate HR details owing to powerful non-linear mapping. To extend three convolutional layers of SRCNN to a deeper level, Kim et al. [] presented a true deep image SR model called VDSR via residual connection []. Recently, Liu et al. [] also proposed a multi-scale deep encoder–decoder network called MSDEPC to super resolve LR images with the edge maps’ prior information. In addition, Ledig et al. [] proposed the application of a generative adversarial network (GAN) [] for image SR, called SRGAN. SRGAN takes the perceptual loss and the adversarial loss to supervise the reconstruction of super-resolved images and can obtain more realistic SR results.
CNNs also play an effective role in motion deblurring. Xu et al. [] and Sun et al. [] developed some CNN-based methods to recover blurred images based on blur kernel estimation. Besides these non-blind deep methods, some deep blind deblurring methods [,] are also proposed. Nah et al. [] applied a multiple scales CNN to recover clear images directly. Motivated by the work, Tao et al. [] designed a simple structure motion deblurring network characterized by scale recursion. Moreover, inspired by the work of image translation [], Ramakrishnan et al. [] first applied GAN for motion deblurring. Then, Kupyn et al. [] proposed DeblurGAN for blind motion deblurring, which utilizes the WGAN [] with a gradient penalty to avoid the mode collapse issue in the classical GAN. Subsequently, Kupyn et al. [] presented a new and very efficient GAN-based model for single image motion deblurring, named DeblurGAN-v2, which is based on a relativistic conditional GAN with a double-scale discriminator. Furthermore, for meteorological prediction application, Manzo et al. [] adopted a pretrained deep network-based architecture for clouds’ image description and classification. Recently, in order to address the problem that blurred images suffer from other degradation such as down-scaling and compression, Xu et al. [] proposed the enhanced deep pyramid network (EDPN) model for blurry image restoration, by fully exploiting the self-scale and cross-scale similarities.
Few works can use CNNs for simultaneous motion deblurring and SISR. Xu et al. [] solve the problem of super-resolving blurred facial images by SCGAN. However, their method is restricted to facial images, and it is not easy to obtain a good performance in real scenarios. Zhang et al. [] proposed using a deep encoder–decoder model to perform joint motion deblurring and image SR. Zhang et al. [] once again proposed a gated fusion method for concurrent motion deblurring and image SR. Recently, Liang et al. [] utilized the dual supervised network to address this issue. However, they did not achieve satisfactory results. In addition, for plug-and-play image SR, Zhang et al. [] proposed a new blind SR framework to achieve the processing of arbitrary blur kernels. In addition, Zhang et al. [] proposed a dual supervised learning strategy to fully exploit the representation capacity of their deep model, which imposes constraints between LR and HR images.
2.2. Attention
In addition to feature transfer by residual connection, the attention mechanism is another widely used method for feature preservation and enhancement used in many image SR models [,,,]. Zhang et al. presented the RCAN [] (residual channel attention network) model that utilizes channel attention with residual blocks to adjust the task adaptability of channel features and to strengthen their expression ability. Since RCAN only uses the first-order statistical information of channel features, Dai et al. [] presented the so-called SAN (second-order attention network) model, which replaces the global average pooling with the global covariance pooling (second-order statistics) to obtain a better effect of channel features’ selection and enhancement. Very recently, Niu et al. [] designed a novel pixel-guided dual-branch attention network (PDAN) to jointly restore image details and the spatial scale.
In addition, Wang et al. [] proposed the extraction and fusion of temporal and spatial attention features for video restoration. Furthermore, Fu et al. [] introduced a dual attention network—containing one spatial branch and one channel branch for scene segmentation, which can adaptively extract and integrate the local and non-local features of spatial and channel attention.
3. Methodology
3.1. Multiple Degradation Decoupling Induction
For motion deblurring and image SR, we used the following equations to describe the corresponding degradation models, which are used to generate the LR and blur images for training.
where Equation (3) represents one typical motion degradation of a certain image sequence-averaging blur and Equation (4) denotes the process of image resolution reduction. Here, and in Equation (3) represent a sharp image of one clear HR image sequence (the image number of the sequence is N) and the corresponding blur image, respectively; and and in Equation (4) are the HR image and the corresponding LR image, respectively. in the equation denotes the additional noise (normally it is Gaussian white noise). is the down-sampling operator (can be bicubic sub-sampling).
Based on Equations (3) and (4), the motion blur and the resolution reduction compound degeneration may be formulated as
Obviously, averaging frame images lead to blurring degradation and the subsequent down-sampling operation also reduces the resolution of the generated blur image.
Theoretically, if the frame averaging blur kernel and the spatial down-sampling kernel are denoted as and , respectively, Equation (5) can be generalized as the following:
Here the kernel convolution is defined as a new kernel S. This equation means the comprehensive function of multi-degradation basically equals one blur operation. Moreover, according to Equation (6), the residual between the sharp HR image and the degraded observation is easily calculated. Assuming the image data obey the Gaussian distribution, a solution of maximum likelihood estimation (MLE) for Equation (6) can be obtained by . Naturally, if the residual is looked upon as the high-frequency details of , the observation y becomes its approximation component. Here, if assuming the details can be decoupled into the deblurring details and the SR details that is , the MLE solution is further expressed as
According to Equation (7), if we can obtain the deblurring and the SR details individually through deep decoupling induction learning, then the original clear and HR image can be recovered. Moreover, although changing the sequence between motion blur and resolution reduction will lead to the multiple degraded models being different from Equation (5), the MLE solution with decoupling details (Equation (7)) remains the same. This indicates that our proposed decoupling induction method is robust to different sequences of multiple degenerated images.
3.2. Multi-Order Attention Gating
The decoupled deblurring features and SR features were then exploited to calculate the first-order channel attention (FOCA) and the second-order channel attention (SOCA), respectively. Meanwhile, their SOCAs were concatenated to calculate the FOCA again, which acquires the so-called third-order channel attention (TOCA). Then, all the acquired multiple order attentions were fused with multi-routes gating. Closing a route means that the corresponding feature attention is blocked and cannot be used for subsequent reconstruction. In fact, we used the drop-out mechanism—a probability of 0.5 was used to turn off some feature attentions randomly. The above processes are called multi-order attention drop-out gating. We used a similar method to calculate the FOCA and the SOCA, as explored in RCAN [] and SAN []. Based on the principles of the SOCA and FOCA, we give the mathematical description of the third-order channel attention (TOCA) and multi-order attention drop-out gating learning in the following.
Given the deblurring feature maps and the SR feature maps , assume they are with C feature channels and size . Note that the channel size of and does not need to be equal and in the following we just take as an example. We reshape the feature map to a matrix with the size ; each element of which is C dimension. Here, if we treat the feature elements as samples, then the covariance matrix may be calculated and decomposed by the eigenvalue decomposition (EIG) as:
where , , and I and 1 are the identity matrix and the all-ones matrix, respectively. In addition, U is an orthogonal matrix and is a diagonal matrix with eigenvalues in decreasing order. Then, the normalized covariance matrix can be acquired as ; is a positive real number. Obviously, the normalized covariance contains the correlations of channel-wise features. Let ; the c-th channel-wise statistics can be obtained by global pooling as:
Based on the equation, the feature weighting coefficient can be obtained through a simple sigmoid gating function [] as:
where WD and WU are usually the convolution layers to adjust the number of feature channels to C/r and C, respectively. and are individually the sigmoid functions and RELU function. Thus, for deblurring feature the second-order channel attention (SOCA) weighting is represented as:
Based on the equation, the SOCA weighting for image SR features , can be similarly described as . Then, and are concatenated and passed through the FOCA to obtain the final TOCA. Let ; we calculate the global average pooling along each channel dimension and then transform the statistics with channel scaling convolution layers and proper activation functions to obtain the FOCA weighting, which can be described as:
where is the value at the position of the c-th concatenated SOCA features , and WS and WI are the channel up-scaling and down-scaling convolution layers, similar to WU and WD in Equation (10). Finally, the third-order channel attention (TOCA) weighting can be denoted as:
If the FOCA of the deblurring features and SR features are denoted as and , respectively, then all the multi-order attention features, ,, ,, and are sent to one five-routes gate for fusion. The gate works with the drop-out mechanism. Let the j-th route switch be a random variable rj and obey the Bernoulli distribution with the parameter p (which is set to 0.5 in our practice)—that is rj ~ Bernoulli(p)—and then, all the attention that can pass through will be fused by concatenation as:
3.3. Network Architecture
Based on Equation (7), we can design two CNN branches to learn the deblurring details and the SR details separately. This step is called decoupling induction learning. Moreover, we can individually calculate their multiple orders attention features, and utilize the drop-out gating method to fuse them. Here the step is named multi-order attention drop-out gating. The fused attention features concatenated with the LR and blur input images are then sent to the subsequent reconstruction module to obtain the final SR result.
The overall architecture of the proposed model is illustrated in Figure 2. Our model contains four dominant modules: the first one is the deblurring features extraction module, which can be used to predict the sharp LR image; the second one is the SR features extraction module, which can be utilized to obtain the super-resolved blur images; the third is the proposed multi-order attention drop-out gating module, which calculates different order attentions and fuses them with the drop-out gating mechanism; and the fourth one is the reconstruction module to recover the final clear and SR result. In the figure, the four modules mentioned are indicated by dashed boxes of different colors.
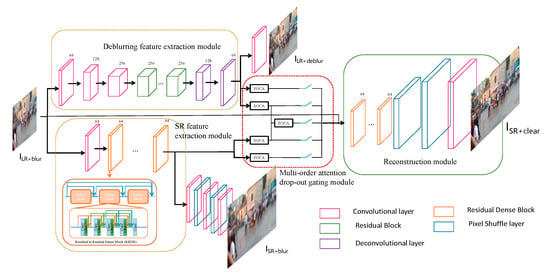
Figure 2.
The overall architecture of the proposed model. Our model mainly contains four modules—deblurring feature extraction, SR feature extraction, multi-order attention drop-out gating, and reconstruction. An LR and blur input image is first passed through the separate SR and deblurring branches to obtain the decoupled features; then, they go through a multi-order attention drop-out gating fusion, before being reconstructed to output a super-resolved and clear image.
3.3.1. Deblurring Feature Extraction
This module aims to acquire the decoupled deblurring features, and henceforth, sharp LR images from blurry LR images ILR+blur. Inspired by [], we adopted a residual encoder–decoder structure in this module. The encoder part is composed of several convolution layers which reduce the size of feature maps to a quarter of the input image size. We then added nine residual blocks between the encoder and decoder to refine the deblurring features. Then, the decoder exploits two deconvolutional upscaling layers to raise the resolution of the deblurring feature maps. Additionally, based on the deblurring features, we can use another two convolution operations to obtain a deblur LR image ILR+deblur (see Figure 2).
Here, we denote the output deblurring features of the decoder as xdb, which were later sent to the multi-order attention gating module. All the used activation layers are the leaky rectified linear units (LeakyReLU), and we used IN (instance normalization) operations in the residual blocks instead of the BN (batch normalization) ones, because the BN layer may reduce the flexibility of the network and undermine the scale information by normalizing the features and increasing computation. The mapping relationship learned from this module between the input ILR+blur and the output xdb can be described as:
where and are the down-scaling convolution layers of an encoder, and are the deconvolution layers of a decoder, RB represents the nine residual blocks, and Hc is the first convolution layer acting on the input ILR+blur. The activation and normalization operations are included in the layers by default.
3.3.2. SR Feature Extraction
The purpose of this module is to obtain decoupled SR image details. We utilized eight residual dense blocks [] (each block contains five convolution operations with four LeakyReLU layers; see Figure 2 for reference) and one convolution layer to construct the deep structure to extract the high-frequency spatial detail features. From this, the super-resolved blur image ILR+blur can also be acquired through two consecutive pixel shuffle layers and several convolution layers. To maintain the spatial information, neither the pooling layer nor stride operation is used in the module. At the same time, no normalization operations are applied. If denoting the extracted SR features as xsr, then the mapping relationship learned from the module between the input ILR+blur and the output xsr can be described as:
where represents the eight consecutive residual dense blocks.
3.3.3. Multi-Order Attention Drop-Out Gating
This module summarizes the multiple orders attention of the learned deblurring features xdb and the SR features xsr to obtain high-frequency image recovering details. xdb and xsr are the inputs of the module and their first-order, second-order, and common third-order feature attention maps are calculated, respectively. Then, all these attention features are concatenated and sent to the drop-out layer to obtain the final feature maps . The mapping relationship of this module and its processing details can be referred to in the previous Section 3.3.2 and Figure 2.
3.3.4. Reconstruction Module
In this module, the gated attention features and the blur LR image are sent into 16 residual dense blocks [] and the result is further fed to two-pixel shuffle layers to improve the spatial resolution to 4×. After that, two convolution layers are used to acquire the final SR and clear image ISR+clear. Since most operations of our model are performed in the LR low dimension functional space, the computation cost both in training and in the testing stages is quite low. The mapping relationship of the module is described as:
where RDB16 is the 16 consecutive residual dense blocks, P1 and P2 are the two-pixel shuffle layers, and H2c represents two convolution operations.
3.4. Loss Functions
Our proposed model has three outputs: the LR deblurring image ILR+db, the SR blur image ISR+blur, and the clear SR image ISR+clear. Then, the total loss of our model contains three parts: the LR but clear image loss, the HR but blur image loss, and the final HR and clear image loss. In our case, we usually calculate the difference between a certain output and its expectation with the norm and treat it as the loss. The three losses of our model can be described as:
where , , and are the expectations of the three outputs, respectively. N is the number of training samples. Thus, the total loss is the sum of the above three losses:
where is the loss balance factor, which is set to be 0.5 in our experiments.
In addition, sometimes in order to generate a more realistic image, we also consider introducing an SSIM [] measure into the loss . At this time, the loss can be modified as:
where the is used to balance these two terms, which is set to 0.84.
4. Experimental Results
4.1. Datasets and Training Details
Many experiments and performance comparisons are performed on the well-known public blur datasets: the GOPRO dataset [] and the dataset developed by Lai et al. []. Originated from some natural video sequences, the GOPRO [] dataset contains 2103 high-resolution training pairs (the sharp image and the blurry image) and 1111 test images. The size of every image in the dataset is 1280 × 720. The motion-blurred image is obtained by averaging several neighboring frame images and the LR image can be acquired by bicubic down-sampling on the corresponding HR image. In contrast to GOPRO, the dataset of Lai et al. [] is composed of many man-made generated blur images, in which each degenerated image is the convolution result of the sharp image with a blur kernel. Here, the size of the degraded kernel may range from 21 × 21 to 75 × 75. Note that Lai et al.’s dataset [] contains both uniform and non-uniform blurred images. The main characteristics of the two datasets are summarized in Table 1.

Table 1.
Basic dataset characteristics of GOPRO [] and Lai et al. [].
The training of the proposed model can be divided into two steps. In the first step, the model is trained by supervision with the LR blurry patches ILR+blur, the sharp LR patches ILR+clear, and the clear HR patches IHR+clear. During training, the loss of our model (Equation (22)) is minimized. In the second step, the trained model is finetuned by using Equation (23) to replace the original in Equation (22). The training procedure is implemented by the SGD solver from Pytorch [] and the learning rate decreases from 0.01 to 0.00001 and the decay is set to be 0.5. In addition, the moment of the used solver is 0.9 and the batch size of the training samples is 12. It takes about two days to train the proposed model if using an Nvidia Titan GTX1080ti GPU.
4.2. Experiments and Comparisons
Based on numerous LR and blurry input images on different test datasets, we performed lots of joint image deblurring and SR experiments and made comparisons with some recent SOTA (state-of-the-art) image SR models [,,], the deblurring method [], and the multiple degradations recovery approaches [,,,]. We also compared the combination method of the SR algorithm [] and the deblurring method []. For fair play, all the comparisons were made by using the public codes provided by these methods. For those ones which cannot be publicly acquired (such as ED-DSRN []), we used our dataset to retrain the original networks. The comparisons with these related methods using the datasets of GOPRO [] and Lai et al. [], in terms of the PSNR, the SSIM, the model parameters, and the test time, are demonstrated in Table 2 and Table 3. The visual results of these methods are also compared in Figure 3, Figure 4 and Figure 5.

Table 2.
The comparisons with SOTA methods of the quantitative performance on GOPRO dataset []. Best results are marked in bold.

Table 3.
The comparisons with SOTA methods of the quantitative performance on Lai et al. dataset []. Best results are marked in bold.

Figure 3.
The details in the deblurred and super-resolved (4×) images generated by the presented decoupled induction and multi-attention drop-out gating model on GOPRO [] and Lai et al. []; using our method, the image details are clearer than the ones acquired from RCAN [], SCGAN [], and GFN [].

Figure 4.
More visual comparison of our model with other methods on GOPRO [].

Figure 5.
More visual comparison of our model with other methods on Lai et al. [].
According to Table 2 and Table 3, it is clear that in most cases our model achieves the best multi-degradation recovery effects, and only in certain special scenarios, it is slightly inferior to GFN [] (see Figure 3d,e), which seems to be the best joint image SR and the deblurring algorithm available at present. In Figure 3d,e and Figure 4, although the PSNR is slightly lower, the image we recovered looks better than the image generated by GFN []. Such contradictions may stem from the fact that the calculation of PSNR or SSIM only requires the neighborhood operations of certain image pixels and cannot reflect the true perception of human vision. In light of the quantitative metrics in Table 2 and Table 3, it is easy to see that, compared to the other methods, even under multiple different blurs and LR datasets, the proposed method can achieve the best or the second best PSNR and SSIM performance.
According to Figure 5, we can easily see that on the Lai et al. [] dataset, our approach shows a significant improvement. Although adjustments have been made to RCAN by fine-tuning the dataset, it still cannot compete with our trained network (see Figure 5b,g). It is clear that Figure 5b,g contains less texture detail than Figure 5e,j. This performance gap is mainly due to the lack of an encoder–decoder structure, which is a key architecture when designing a blind deblurring network. Although the performance of the retrained SCGAN is better than its pre-trained model, because of its small model capacity, this method cannot handle complex non-uniform blurs well.
In general, compared with other methods, especially GFN, the superiority of our method lies in (1) our two branches (super-resolution and motion deblurring), which are fully disentangled, whereas GFN’s are not; and (2) we use multi-order attention to obtain the attention features of the two branches at different orders separately, and perform gated fusion through the drop-out mechanism, whereas GFN computes the correlation of different branches for fusion. Due to the simpler structure, the GFN method has fewer parameters and a faster computation speed than our approach. However, in practical applications, assuming no particular requirements for machine memory or computing speed, our method can be used in preference if the scene is rich in significant textures and the objects have multi-scale variations. Benefiting from joint attention learning, our method produces clearer and higher resolution images with good perceptual quality.
5. Ablation Study
For the sake of dissecting the role of the key components of the proposed decoupling induction and multi-order attention gating model, several variants were developed and tested: (1) deblurring alone, (2) SR alone, (3) without TOCA, and (4) no drop-out gating. These variants were trained with almost the same hyper-parameters as our original model. For the variants of deblurring alone and SR alone, the FOCA and SOCA features were concatenated and pushed to the reconstruction module. For the variant without TOCA, there were only four attention routes (,,,) for drop-out gating. The final variant used direct concatenating to replace drop-out gating. The results are shown in Table 4.

Table 4.
Ablation study on GOPRO [] dataset. The best results are indicated in bold.
From Table 4, it is clear that without drop-out gating, the performance of the proposed approach is much suppressed. At the same time, the high-order attention TOCA really can help to improve the reconstruction effects. In addition, it seems that the deblurring branch contributes more than the SR forking in multiple degradation decoupling reconstruction. Thus, we can conclude that the proposed mechanism of multi-order attention and drop-out gating is very effective for joint deblurring and super-resolution.
6. Conclusions
In this work, we proposed an effective end-to-end deep model which can deal with multiple degeneration problems for concurrent motion deblurring and image SR. Inspired by the idea of decoupled learning and multi-order attention features selection, our model firstly manages to construct the discrete network structures of motion deblurring and image SR respectively, and then realizes selective features’ enhancement and fusion through multi-order attention drop-out gating. Many experimental results and comparisons to other SOTA methods were carried out to demonstrate the superior performance of our method in compound degradation recovery and generalization power.
Future work will focus on two aspects. The first one is to investigate why the deblurring branch matters more than SR forking in the proposed multiple degradation reconstruction approaches. Secondly, based on blur and resolution reduction, if more degeneration action (such as noise interference) is also introduced, a way to obtain a good image recovery effect will be investigated.
Author Contributions
Conceptualization, Y.C. and H.L.; methodology, Y.C. and H.L.; software, Y.C. and X.Z.; writing—original draft preparation, Y.C.; writing—review and editing, H.L.; visualization, X.Z.; funding acquisition, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant No. 61971004, the Natural Science Foundation of Anhui Province, grant No. 2008085MF190, the Key Project of Natural Science of Anhui Provincial Department of Education, grant No. KJ2019A0083 and KJ2021A1289, and the Open Project Fund of the Key Laboratory of Computational Intelligence and Signal Processing of the Ministry of Education (Anhui University), grant No. 2020A002.
Data Availability Statement
The links to the public datasets used in the paper are as follows: GOPRO dataset: https://github.com/SeungjunNah/DeepDeblur_release (accessed on 1 December 2021), Lai’s dataset []: http://vllab.ucmerced.edu/wlai24/cvpr16_deblur_study/ (accessed on 1 December 2021).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sun, J.; Cao, W.; Xu, Z.; Ponce, J. Learning a convolutional neural network for non-uniform motion blur removal. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 769–777. [Google Scholar] [CrossRef] [Green Version]
- Nah, S.; Kim, T.H.; Lee, K.M. Deep multi-scale convolutional neural network for dynamic scene deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hawaii, HI, USA, 21–26 July 2017; pp. 3883–3891. [Google Scholar] [CrossRef] [Green Version]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar] [CrossRef]
- Xi, S.; Wei, J.; Zhang, W. Pixel-Guided Dual-Branch Attention Network for Joint Image Deblurring and Super-Resolution. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Nashville, TN, USA, 19–25 June 2021; pp. 532–540. [Google Scholar] [CrossRef]
- Tao, X.; Gao, H.; Shen, X.; Wang, J.; Jia, J. Scale-recurrent network for deep image deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 8174–8182. [Google Scholar] [CrossRef]
- Xu, X.; Sun, D.; Pan, J.; Zhang, Y.; Pfister, H.; Yang, M.-H. Learning to super-resolve blurry face and text images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hawaii, HI, USA, 21–26 July 2017; pp. 251–260. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, F.; Dong, H.; Guo, Y. A deep encoder-decoder networks for joint deblurring and super-resolution. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Alberta, AB, Canada, 15–20 April 2018; pp. 1448–1452. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, H.; Hu, Z.; Hu, Z.; Lai, W.-S.; Wang, F.; Yang, M.-H. Gated fusion network for joint image deblurring and super-resolution. In British Machine Vision Conference (BMVC); Springer: London, UK, 2018. [Google Scholar] [CrossRef] [Green Version]
- Ying, T.; Jian, Y.; Liu, X. Image super-resolution via deep recursive residual network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hawaii, HI, USA, 21–26 July 2017; pp. 3147–3155. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image super-resolution. In Proceedings of the IEEE conference on computer vision and pattern recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2472–2481. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 August 2018; pp. 286–301. [Google Scholar] [CrossRef] [Green Version]
- Dai, T.; Cai, J.; Zhang, Y.; Xia, S.-T.; Zhang, L. Second-order attention network for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, NY, USA, 15–20 June 2019; pp. 11065–11074. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Fu, Z.; Han, J.; Shao, L.; Hou, S.; Chu, Y. Single image super resolution using multi-scale deep encoder-decoder with phase congruency edge map guidance. Inf. Sci. 2019, 473, 44–58. [Google Scholar] [CrossRef] [Green Version]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar] [CrossRef] [Green Version]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Farley, W.D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar]
- Xu, L.; Ren, J.S.; Liu, C.; Jia, J. Deep convolutional neural network for image deconvolution. In Advances in Neural Information Processing Systems; Cornel University: Ithaca, NY, USA, 2014; pp. 1790–1798. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.709.7888&rep=rep1&type=pdf (accessed on 1 November 2021).
- Isola, P.; Zhu, J.-Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hawaii, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar] [CrossRef] [Green Version]
- Ramakrishnan, S.; Pachori, S.; Gangopadhyay, A.; Raman, S. Deep generative filter for motion deblurring. In Proceedings of the IEEE International Conference on Computer Vision, Honolulu, HI, USA, 21–26 July 2017; pp. 2993–3000. [Google Scholar] [CrossRef] [Green Version]
- Kupyn, O.; Budzan, V.; Mykhailych, M.; Mishkin, D.; Matas, J. DeblurGAN: Blind motion deblurring using conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8183–8192. [Google Scholar] [CrossRef] [Green Version]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein Gan. arXiv 2017. Available online: https://arxiv.org/abs/1701.07875 (accessed on 1 November 2021).
- Kupyn, O.; Martyniuk, T.; Wu, J.; Wang, Z. DeblurGAN-v2: Deblurring (Orders-of-Magnitude) Faster and Better. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 8878–8887. [Google Scholar] [CrossRef] [Green Version]
- Manzo, M.; Pellino, S. Voting in transfer learning system for ground-based cloud classification. In Machine Learning and Knowledge Extraction; Cornel University: Ithaca, NY, USA, 2021; Volume 3, pp. 542–553. [Google Scholar] [CrossRef]
- Xu, R.; Xiao, Z.; Huang, J.; Zhang, Y.; Xiong, Z. EDPN: Enhanced deep pyramid network for blurry image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 414–423. [Google Scholar] [CrossRef]
- Liang, Z.; Zhang, D.; Shao, J. Jointly solving deblurring and super-resolution problems with dual supervised network. In Proceedings of the 2019 IEEE International Conference on Multimedia and Expo (ICME), Shanghai, China, 8–12 July 2019; pp. 790–795. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Zhang, L. Deep plug-and-play super-resolution for arbitrary blur kernels. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 1671–1681. [Google Scholar] [CrossRef]
- Zhang, D.; Liang, Z.; Shao, J. Joint image deblurring and super-resolution with attention dual supervised network. Neurocomputing 2020, 412, 187–196. [Google Scholar] [CrossRef]
- Wang, X.; Chan, K.C.; Yu, K.; Dong, C.; Loy, C.C. Edvr: Video restoration with enhanced deformable convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019; pp. 1954–1963. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 18–20 June 2019; pp. 3146–3154. [Google Scholar] [CrossRef] [Green Version]
- Niu, W.; Zhang, K.; Luo, W.; Zhong, Y. Blind motion deblurring super-resolution: When dynamic spatio-temporal learning meets static image understanding. IEEE Trans. Image Process. 2021, 30, 7101–7111. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lai, W.-S.; Huang, J.-B.; Hu, Z.; Ahuja, N.; Yang, M.-H. A comparative study for single image blind deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1701–1709. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8024–8035. [Google Scholar]
- Zhang, K.; Zuo, W.; Zhang, L. Learning a single convolutional super resolution network for multiple degradations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3262–3271. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).