Full Hermite Interpolation and Approximation in Topological Fields

Abstract

By using generalized divided differences, we study the simultaneous interpolation of an m times continuously differentiable function and its derivatives up to a fixed order in a topological field K. If K is a valued field, then simultaneous Hermite interpolation and approximation are considered. Newton interpolating series are used in the case of an infinite number of conditions of interpolation. Applications to the numerical approximation of variational problems, the solution of a functional equation and, in the case of p-adic fields, the representation of solutions of a boundary value problem for an equation of the Fuchsian type illustrate the efficiency of the theoretical results.

1. Introduction

In 1885, Weierstrass [1] proved the theorem on the density of polynomials in the real Banach space $C\left(\right[a,b\left]\right)$ of real continuous functions defined on the interval $[a,b]$ endowed with the sup norm. Then, De la Vallée Poussin, Bernstein, Stone, and Whitney [2] obtained a series of important extensions of this result including the density of polynomials in the real space $C^m\left([a,b]\right)$ of the m times continuously differentiable real-valued functions. Combining the approximation with the interpolation at a finite number of points from $[a,b]$, a problem of simultaneous interpolation and approximation follows. Such approximations may be very useful in different problems. If the approximated function is m times continuously differentiable, that is, $f\in C^m\left([a,b]\right)$, then it is desirable to obtain also simultaneous approximation of the function and its derivatives up to a fixed order, as in the case of Bernstein polynomials.

A series of results established in the case of real functions were extended to the non-Archimedean valued fields (see [3,4,5]). Weierstrass theorem was also proved for non-Archimedean valued fields as the field of p-adic numbers (see, for instance, [6,7]).

In this paper, we consider K a complete topological field of zero characteristic and D an open subset of K such that $\overline{D}$ is a compact subset of K. Basic results on topological fields may be found in various books as [8,9]. If $f:\overline{D}\to K$, $f\in C^m\left(\overline{D}\right)$, for arbitrary elements ${\alpha }_0,\dots ,{\alpha }_n\in \overline{D}$, by extending the notion of divided difference to generalized divided difference (see [10,11], for the real case), a corresponding Newton interpolating polynomial $N_n\left(x\right)$ is defined. This polynomial is a solution of the Hermite interpolation problem (see Lemma 2). In the case of valued fields, where Weierstrass theorem holds, the proof of Theorem 1 presents a method to construct polynomials that simultaneously realize the Hermite interpolation and the approximation of a function $f\in C^m\left(\overline{D}\right)$.

Let ${\left\{{\alpha }_i\right\}}_{i\ge 0}$ be a sequence of elements from $\overline{D}$. The Newton interpolating series at ${\left\{{\alpha }_i\right\}}_{i\ge 0}$ is defined as a generalization of the Newton interpolating polynomials (see Section 4). In the case of real numbers, these series were used to approximate the solutions of boundary value problems for ordinary differential equations (see [12,13,14]). Theorem 2 shows that in the case of p-adic numbers, for D an open subset of the set ${\mathbb{Z}}_p$ (the set p-adic integers), every infinitely differentiable function $f:\overline{D}\to {\mathbb{Z}}_p$ and all its derivatives can be interpolated at a suitable purely periodic sequence ${\left\{{\alpha }_i\right\}}_{i\ge 0}$ of period p, by a uniformly convergent Newton interpolating series.

Section 5 contains applications of the theoretical results.

Variational problems arising in analysis, mechanics, geometry seek to determine the maxima and minima of functionals. There are many papers on numerical approximation of the solutions of variational problems, which use the differential transform method, Adomian decomposition method or Taylor series direct method (see, for example, refs. [15,16,17] and references therein). Usually, these methods are based on differential equations attached to the studied problems. 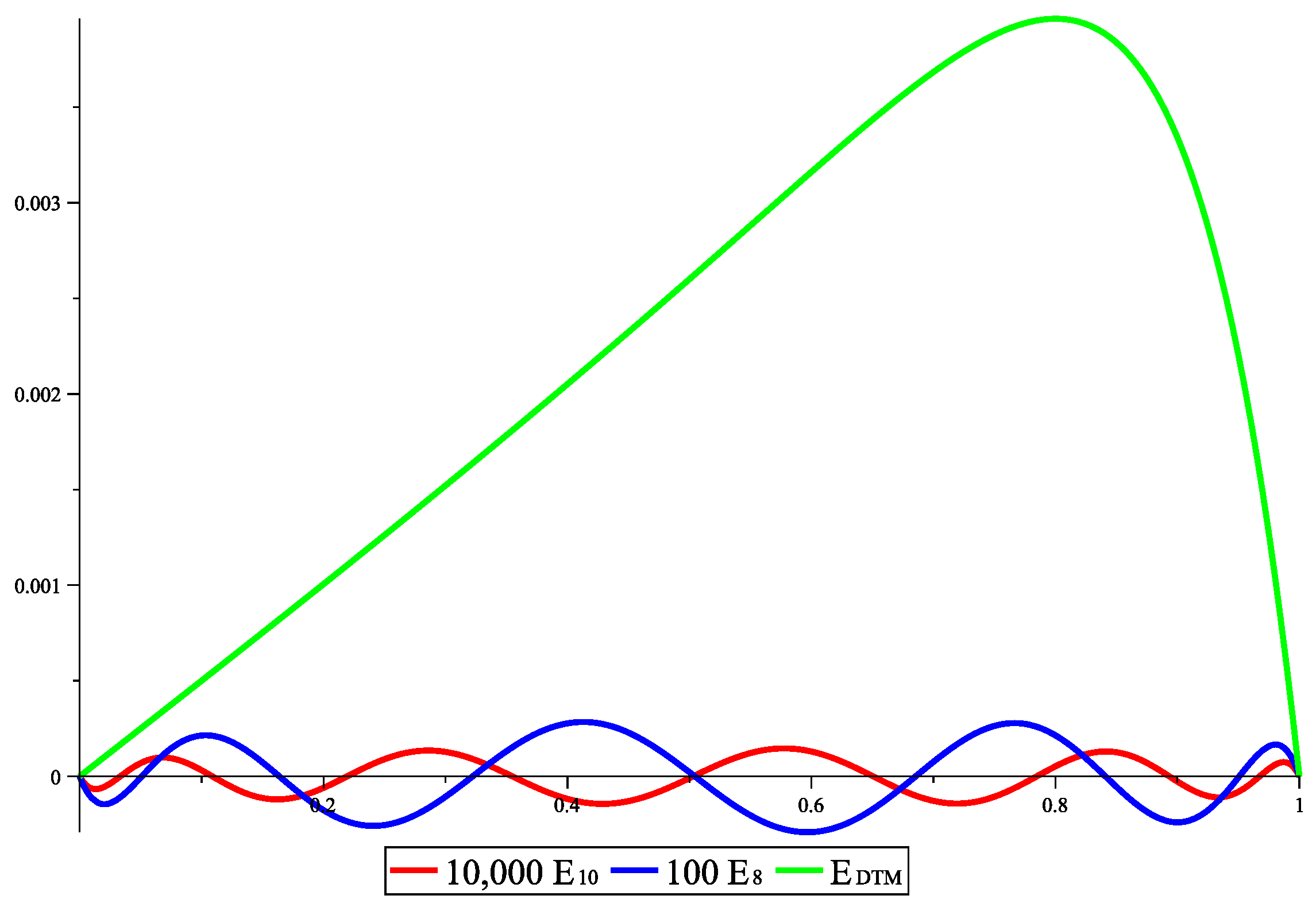Our method presented in Section 5.1 applies Theorem 1 to the initial functional. This method finds the solution of the problem without any discretization, and it provides a high accuracy. To show the efficiency of this method, we present, as a numerical example, a comparison with the differential transform method.

Functional equations are equations in which the unknowns are functions. A functional equation in two or more variables is formally equivalent to a family of simultaneous equations in one variable (see [18]). Conjugacy functional equations is a large class of functional equations including Schröder’s equation. In Section 5.2, we represent a solution of a Schröder’s equation as a Newton interpolating series. This representation improves the solutions found by Koenigs algorithm or power series representation presented in [18].

By considering ordinary differential equations in which the real numbers are replaced by the field of p-adic numbers, for a fixed prime number p, the p-adic ordinary differential equations are obtained (see [19,20]). In Section 5.3, we study the p-point boundary value problem for an equation of the Fuchsian type (see, for example, refs. [20,21]). The solutions we find are represented as Newton interpolating series.

2. On Generalized Divided Differences

Let K be a complete topological field of zero characteristic, let D be an open subset of K such that $\overline{D}$ is a compact subset of K, and let $f:\overline{D}\to K$ be a continuous function. If ${\left\{{\alpha }_i\right\}}_{i\ge 0}$ is a sequence of distinct elements from $\overline{D}$, then, as in the real case (see, for example, ref. [22]), one can define the divided difference of order n of f with respect to ${\alpha }_0,{\alpha }_1,\dots ,{\alpha }_n$, denoted by $f[{\alpha }_0,{\alpha }_1,\dots ,{\alpha }_n]$. Thus, $f\left[{\alpha }_0\right]:=f\left({\alpha }_0\right)$,

$$f[{\alpha }_0,{\alpha }_1]:=\frac{f\left({\alpha }_1\right)-f\left({\alpha }_0\right)}{{\alpha }_1-{\alpha }_0},$$

and by recurrence, for $i\ge 1$,

$$f[{\alpha }_0,\dots ,{\alpha }_i]:=\frac{f[{\alpha }_1,\dots ,{\alpha }_i]-f[{\alpha }_0,\dots ,{\alpha }_{i-1}]}{{\alpha }_i-{\alpha }_0}.$$

(1)

Since

$$f[{\alpha }_0,\dots ,{\alpha }_k]={\displaystyle \sum _{i=0}^k}\frac{f\left({\alpha }_i\right)}{{\displaystyle \prod _{\begin{array}{c}j=0,\\ j\ne i\end{array}}^k}({\alpha }_i-{\alpha }_j)},$$

(2)

the divided differences are symmetric functions of their arguments.

The derivatives of a function f from $\overline{D}$ to K are defined just as in the real or complex case. If m is a non-negative integer, as usually, we denote by $C^m\left(\overline{D}\right)$, the set of functions $f:\overline{D}\to K$ having continuous derivatives $f^{\left(k\right)}$, for all $k\le m$. Similarly, the partial derivatives of a multivariate function $f(x_1,\dots ,x_n)$ are defined by the formula

$$\frac{\partial f}{\partial x_k}(x_1,\dots ,x_n)=\underset{h\to 0}{lim}\frac{f(x_1,\dots ,x_k+h,\dots ,x_n)-f(x_1,\dots ,x_k,\dots ,x_n)}{h},$$

for every $k=1,\dots ,n$.

Example 1.

Consider the topological field $K=\mathbb{R}\left(T\right)$ (i.e., the field of rational functions with real coefficients) with the discrete topology and $f:K\to K$ a polynomial function defined as $f\left(x\right)={\displaystyle \sum _{i=0}^d}{a}_i{x}^i$, with $a_i\in K$, $i=0,1,\dots ,d.$ Since every $\alpha \in K$ has the neighborhood $\left\{\alpha \right\}$, it follows that every convergent or Cauchy sequence with elements from K is almost constant (i.e., it is constant for all but a finite number of indices). Hence, K is a complete topological field and f is a continuous function. Since

$$\frac{f\left(x\right)-f\left(\alpha \right)}{x-\alpha }={\displaystyle \sum _{i=0}^{d-1}}{a}_{i+1}{x}^{d-1-i}{\alpha }^i,$$

for $x\ne \alpha$, it follows that

$$\underset{x\to \alpha }{lim}\frac{f\left(x\right)-f\left(\alpha \right)}{x-\alpha }=Df\left(\alpha \right),$$

where $Df$ is the ordinary derivative of the polynomial f. Thus, $f\in C^m\left(K\right)$, for every m.

The notion of divided differences can be extended to the case of coincident elements to obtain the generalized divided differences (see [10], Ch. 6, Sec. 1 or [11], p. 14). Thus, if ${\alpha }_0,{\alpha }_1,\dots ,{\alpha }_n$ are distinct elements from $\overline{D}$, then the divided difference of order $n+1$$f[{\alpha }_0,\dots ,{\alpha }_n,{\alpha }_n]$ can be defined as

$$\begin{array}{cc}\hfill f[{\alpha }_0,\dots ,{\alpha }_n,{\alpha }_n]& =\underset{x\to {\alpha }_n}{lim}f[{\alpha }_0,\dots ,{\alpha }_n,x]\hfill \\ \hfill & =\underset{x\to {\alpha }_n}{lim}\frac{f[{\alpha }_0,\dots ,{\alpha }_{n-1},x]-f[{\alpha }_0,\dots ,{\alpha }_{n-1},{\alpha }_n]}{x-{\alpha }_n}\hfill \\ \hfill & =\frac{\partial }{\partial {\alpha }_n}f[{\alpha }_0,\dots ,{\alpha }_n].\hfill \end{array}$$

More generally, suppose that $x_0,x_1,\dots ,x_m$ are arbitrary elements in $\overline{D}$ such that ${\alpha }_0,\dots {\alpha }_r\in \overline{D}$ are distinct and, for $i=0,\dots ,r$, exactly $k_i$ elements $x_j$ are equal to ${\alpha }_i$, where $k_0+k_1+\dots +k_r=m+1$. Then, for $f\in C^m\left(\overline{D}\right)$, the generalized divided difference of order m, $f[x_0,x_1,\dots ,x_m]$, is defined by

$$f[x_0,x_1,\dots ,x_m]:=\frac{1}{(k_0-1)!\dots (k_r-1)!}·\frac{{\partial }^{k_0+\dots +k_r-r-1}}{\partial {\alpha }_0^{k_0-1}\dots \partial {\alpha }_r^{k_r-1}}f[{\alpha }_0,\dots ,{\alpha }_r].$$

(3)

Remark 1.

Notice that the usual formulas for differentiating the sum, difference, product and quotient of two functions as well as the Leibnitz formula hold for functions defined on open subsets of K. Moreover, by (2), for distinct elements ${\alpha }_0,{\alpha }_1,\dots {\alpha }_r$, the divided difference $f[{\alpha }_0,\dots ,{\alpha }_r]={\displaystyle \sum _{i=0}^r}f\left({\alpha }_i\right)R_i({\alpha }_0,\dots ,{\alpha }_r)$, where $R_i$ are rational functions of ${\alpha }_0,{\alpha }_1,\dots {\alpha }_r$. Then, as in the Example 1, the derivatives of $R_i$ are defined by ordinary derivatives of polynomials. Hence, we get that the partial derivatives of $f[{\alpha }_0,\dots ,{\alpha }_r]$ commute and the divided differences are well defined by (3). In this case, we denote

$$\begin{array}{cc}\hfill f[x_0,x_1,\dots ,x_m]& =f[{\left({\alpha }_0\right)}_{k_0},{\left({\alpha }_1\right)}_{k_1},\dots ,{\left({\alpha }_r\right)}_{k_r}]\hfill \\ \hfill & =f[\underset{k_{0}times}{\underbrace{{\alpha }_0,\dots ,{\alpha }_0}},\underset{k_{1}times}{\underbrace{{\alpha }_1,\dots ,{\alpha }_1}},\dots ,\underset{k_{r}times}{\underbrace{{\alpha }_r,\dots ,{\alpha }_r}}].\hfill \end{array}$$

3. Simultaneous Hermite Interpolation and Approximation

The following result extends (2) to generalized divided differences.

We assume in the following that K is a complete topological field of zero characteristic and D is an open subset of K such that $\overline{D}$ is a compact subset of K.

Lemma 1.

If ${\alpha }_0,{\alpha }_1,\dots {\alpha }_r$ are distinct points in $\overline{D}$, and $k_0,k_1,\dots ,k_r$ are positive integers, $\mathrm{k}=(k_0,k_1,\dots ,k_r)$, then there exist the elements $C_{i,j}^{\mathrm{k}}\in K$, $i=0,1,\dots ,r$, $j=0,1,\dots ,k_i-1$, such that, for any function $f\in C^m\left(\overline{D}\right)$, where $m=k_0+k_1+\dots +k_r$,

$$f[{\left({\alpha }_0\right)}_{k_0},{\left({\alpha }_1\right)}_{k_1},\dots ,{\left({\alpha }_r\right)}_{k_r}]={\displaystyle \sum _{i=0}^r}{\displaystyle \sum _{j=0}^{k_i-1}}{C}_{i,j}^{\mathrm{k}}{f}^{\left(j\right)}\left({\alpha }_i\right).$$

(4)

Moreover, the elements $C_{i,j}^{\mathrm{k}}$ are given by $C_{i,j}^{\mathrm{k}}=\frac{P_{i,j}^{\mathrm{k}}({\alpha }_0,\dots ,{\alpha }_r)}{Q_{i,j}^{\mathrm{k}}({\alpha }_0,\dots ,{\alpha }_r)}$, where $P_{i,j}^{\mathrm{k}}$ are polynomials with coefficients in $\mathbb{Z}$ such that $P_{i,k_i-1}^{\mathrm{k}}=\pm 1$, and $Q_{i,j}^{\mathrm{k}}({\alpha }_0,\dots ,{\alpha }_r)={\displaystyle \prod _{0\le s<t\le r}}{({\alpha }_t-{\alpha }_s)}^{n_{s,t}}$ with $n_{s,t}$ non-negative integers.

Proof. 

By (2) and (3), we get

$$f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_r\right)}_{k_r}]=\frac{1}{(k_0-1)!\dots (k_r-1)!}·\frac{{\partial }^{k_0+\dots +k_r-r-1}}{\partial {\alpha }_0^{k_0-1}\dots \partial {\alpha }_r^{k_r-1}}\left({\displaystyle \sum _{i=0}^r}f\left({\alpha }_i\right){\displaystyle \prod _{\begin{array}{c}j=0,\\ j\ne i\end{array}}^r}{({\alpha }_i-{\alpha }_j)}^{-1}\right).$$

Now, (4) follows from Leibnitz rule. □

The next lemma presents the Newton interpolating formula for arbitrary points of interpolation. In this case, the Newton interpolating polynomial $N_{\alpha ,\mathrm{k}}\left(x\right)$ is defined by using generalized divided differences, and it is a solution of a Hermite interpolation problem.

Lemma 2.

Let ${\alpha }_0,{\alpha }_1,\dots {\alpha }_r$ be distinct elements from $\overline{D}$ and $k_0,k_1,\dots ,k_r$ be positive integers. Denote $\alpha =({\alpha }_0,{\alpha }_1,\dots {\alpha }_r)$ and $\mathrm{k}=(k_0,k_1,\dots ,k_r)$. If $f\in C^m\left(\overline{D}\right)$, $m=k_0+k_1+\dots +k_r$, then

$$f\left(x\right)=N_{\alpha ,\mathrm{k}}\left(x\right)+f[{\left({\alpha }_0\right)}_{k_0},{\left({\alpha }_1\right)}_{k_1},\dots ,{\left({\alpha }_r\right)}_{k_r},x]u_{k_0{\alpha }_0,k_1{\alpha }_1,\dots ,k_r{\alpha }_r}\left(x\right),$$

(5)

where

$$N_{\alpha ,\mathrm{k}}\left(x\right)={\displaystyle \sum _{j=1}^{k_0}}f\left[{\left({\alpha }_0\right)}_j\right]u_{(j-1){\alpha }_0}\left(x\right)+{\displaystyle \sum _{j=1}^{k_1}}f[{\left({\alpha }_0\right)}_{k_0},{\left({\alpha }_1\right)}_j]u_{k_0{\alpha }_0,(j-1){\alpha }_1}\left(x\right)+\dots$$

$$+{\displaystyle \sum _{j=1}^{k_r}}f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-1}\right)}_{k_{r-1}},{\left({\alpha }_r\right)}_j]u_{k_0{\alpha }_0,\dots ,k_{r-1}{\alpha }_{r-1},(j-1){\alpha }_r}\left(x\right)$$

(6)

and

$$u_{k_0{\alpha }_0,k_1{\alpha }_1,\dots ,k_s{\alpha }_s}\left(x\right)={(x-{\alpha }_0)}^{i_0}{(x-{\alpha }_1)}^{i_1}\dots {(x-{\alpha }_s)}^{i_s},s=0,1,\dots ,r.$$

Moreover, $N_{\alpha ,\mathrm{k}}\left(x\right)$ is the unique polynomial of degree less than m that satisfies the following Hermite interpolating problem:

$$N_{\alpha ,\mathrm{k}}^{\left(j\right)}\left({\alpha }_i\right)=f^{\left(j\right)}\left({\alpha }_i\right),i=0,1,\dots ,r,j=0,1,\dots ,k_i-1.$$

(7)

Proof. 

Suppose, first, that $x\ne {\alpha }_i$, $i=0,1,\dots ,r$. By (1), (3) and using the Leibnitz formula, we get

$$\begin{array}{cc}\hfill f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_r\right)}_{k_r},x]& =\frac{1}{(k_0-1)!\dots (k_r-1)!}\frac{{\partial }^{k_r-1}}{\partial {\alpha }_r^{k_r-1}}\dots \frac{{\partial }^{k_0-1}}{\partial {\alpha }_0^{k_0-1}}\left(\frac{f[{\alpha }_0,\dots ,{\alpha }_{r-1},x]-f[{\alpha }_0,\dots ,{\alpha }_{r-1},{\alpha }_r]}{x-{\alpha }_r}\right)\hfill \\ \hfill & =\frac{1}{(k_0-1)!\dots (k_{r-1}-1)!}\frac{{\partial }^{k_{r-1}-1}}{\partial {\alpha }_{r-1}^{k_{r-1}-1}}\dots \frac{{\partial }^{k_0-1}}{\partial {\alpha }_0^{k_0-1}}\left(\frac{f[{\alpha }_0,\dots ,{\alpha }_{r-1},x]}{{(x-{\alpha }_r)}^{k_r}}\right)\hfill \\ \hfill & -\frac{1}{(k_r-1)!}\frac{{\partial }^{k_r-1}}{\partial {\alpha }_r^{k_r-1}}\left(\frac{f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-1}\right)}_{k_{r-1}},{\alpha }_r]}{x-{\alpha }_r}\right)\hfill \\ \hfill & =\frac{1}{{(x-{\alpha }_r)}^{k_r}}\frac{1}{(k_0-1)!\dots (k_{r-1}-1)!}\frac{{\partial }^{k_{r-1}-1}}{\partial {\alpha }_r^{k_{r-1}-1}}\dots \frac{{\partial }^{k_0-1}}{\partial {\alpha }_0^{k_0-1}}f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-1}\right)}_{k_{r-1}},x]\hfill \\ \hfill & -\frac{1}{(k_r-1)!}{\displaystyle \sum _{j=0}^{k_r-1}}\left(\genfrac{}{}{0pt}{}{k_r-1}{j}\right)\frac{(k_r-j-1)!j!f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-1}\right)}_{k_{r-1}},{\left({\alpha }_r\right)}_{k_r-j}]}{{(x-{\alpha }_r)}^{j+1}}\hfill \\ \hfill & =\frac{f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-1}\right)}_{k_{r-1}},x]}{{(x-{\alpha }_r)}^{k_r}}-{\displaystyle \sum _{j=0}^{k_r-1}}\frac{f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-1}\right)}_{k_{r-1}},{\left({\alpha }_r\right)}_{k_r-j}]}{{(x-{\alpha }_r)}^{j+1}}.\hfill \end{array}$$

Similarly,

$$f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-1}\right)}_{k_{r-1}},x]=\frac{f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-2}\right)}_{k_{r-2}},x]}{{(x-{\alpha }_{r-1})}^{k_{r-1}}}-{\displaystyle \sum _{j=0}^{k_{r-1}-1}}\frac{f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-2}\right)}_{k_{r-2}},{\left({\alpha }_{r-1}\right)}_{k_{r-1}-j}]}{{(x-{\alpha }_{r-1})}^{j+1}}.$$

Hence,

$$\begin{array}{cc}\hfill f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_r\right)}_{k_r},x]& =\frac{f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-2}\right)}_{k_{r-2}},x]}{{(x-{\alpha }_{r-1})}^{k_{r-1}}{(x-{\alpha }_r)}^{k_r}}-{\displaystyle \sum _{j=0}^{k_{r-1}-1}}\frac{f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-2}\right)}_{k_{r-2}},{\left({\alpha }_{r-1}\right)}_{k_{r-1}-j}]}{{(x-{\alpha }_r)}^{k_r}{(x-{\alpha }_{r-1})}^{j+1}}\hfill \\ \hfill & -{\displaystyle \sum _{j=0}^{k_r-1}}\frac{f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-1}\right)}_{k_{r-1}},{\left({\alpha }_r\right)}_{k_r-j}]}{{(x-{\alpha }_r)}^{j+1}}.\hfill \end{array}$$

Continuing in this way, we find

$$\begin{array}{cc}\hfill f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_r\right)}_{k_r},x]& =\frac{f[{\left({\alpha }_0\right)}_{k_0},x]}{{(x-{\alpha }_1)}^{k_1}\dots {(x-{\alpha }_r)}^{k_r}}-{\displaystyle \sum _{i=1}^r}{\displaystyle \sum _{j=0}^{k_i-1}}\frac{f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{i-1}\right)}_{k_{i-1}},{\left({\alpha }_i\right)}_{k_i-j}]}{{(x-{\alpha }_r)}^{k_r}\dots {(x-{\alpha }_{i+1})}^{k_{i+1}}{(x-{\alpha }_i)}^{j+1}}\hfill \\ \hfill & =\frac{f\left(x\right)}{{(x-{\alpha }_0)}^{k_0}\dots {(x-{\alpha }_r)}^{k_r}}-{\displaystyle \sum _{i=0}^r}{\displaystyle \sum _{j=0}^{k_i-1}}\frac{f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{i-1}\right)}_{k_{i-1}},{\left({\alpha }_i\right)}_{k_i-j}]}{{(x-{\alpha }_r)}^{k_r}\dots {(x-{\alpha }_{i+1})}^{k_{i+1}}{(x-{\alpha }_i)}^{j+1}}.\hfill \end{array}$$

Hence we get (5).

Suppose, secondly, that $x={\alpha }_i$. For $x={\alpha }_0$, the equality (5) is obvious. If $x={\alpha }_i$, for $i>0$, the statement follows from the previous case, for $r=i-1$ and $x={\alpha }_i$.

To prove (7), we write (5) for $N_{\alpha ,\mathrm{k}}\left(x\right).$ Since $deg{N}_{\alpha ,\mathrm{k}}\left(x\right)=m-1$, we get

$$N_{\alpha ,\mathrm{k}}\left(x\right)={\displaystyle \sum _{j=1}^{k_0}}{N}_{\alpha ,\mathrm{k}}\left[{\left({\alpha }_0\right)}_j\right]u_{(j-1){\alpha }_0}\left(x\right)+{\displaystyle \sum _{j=1}^{k_1}}{N}_{\alpha ,\mathrm{k}}[{\left({\alpha }_0\right)}_{k_0},{\left({\alpha }_1\right)}_j]u_{k_0{\alpha }_0,(j-1){\alpha }_1}\left(x\right)+\dots$$

$$+{\displaystyle \sum _{j=1}^{k_r}}{N}_{\alpha ,\mathrm{k}}[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-1}\right)}_{k_{r-1}},{\left({\alpha }_r\right)}_j]u_{k_0{\alpha }_0,\dots ,k_{r-1}{\alpha }_{r-1},(j-1){\alpha }_r}\left(x\right).$$

(8)

From (6) and (8), it follows that the corresponding generalized divided differences of f and $N_{\alpha ,\mathrm{k}}$ are equal. Thus, $N_{\alpha ,\mathrm{k}}\left[{\left({\alpha }_0\right)}_j\right]=f\left[{\left({\alpha }_0\right)}_j\right],$ $j=1,\dots ,k_0$, and by Lemma 1, we get (7) for $i=0.$ Similarly, by $N_{\alpha ,\mathrm{k}}[{\left({\alpha }_0\right)}_{k_0},{\left({\alpha }_1\right)}_j]=f[{\left({\alpha }_0\right)}_{k_0},{\left({\alpha }_0\right)}_j],$$j=1,\dots ,k_1$ and by Lemma 1, we get (7), for $i=1$ and so on. Hence, the lemma is proved. □

If K is a field, an absolute value or a valuation of rank one on K is a function $|·|:K\to \mathbb{R}$ such that:

(i) $\left|x\right|\ge 0$, for all $x\in K$ and $\left|x\right|=0$ if and only if $x=0$;

(ii) $\left|xy\right|=\left|x\right|\left|y\right|$, for all $x,y\in K$;

(iii) $|x+y|\le \left|x\right|+\left|y\right|$, for all $x,y\in K$.

In this case, $(K,|·\left|\right)$ is called a valued field.

If instead of the triangle inequality (iii), $|·|$ satisfies the stronger inequality,

(iii)${}^{\prime }$$|x+y|\le max\left\{\right|x|,|y\left|\right\}$, for all $x,y\in K$,

then the absolute value is called non-Archimedean and $(K,|·\left|\right)$ is called a non-Archimedean valued field.

If $(K,|·\left|\right)$ is a valued field, then for the topology defined by the metric $d(x,y)=|x-y|$, K is a topological field (see, for example, ref. [5]).

Remark 2.

If $K=\mathbb{R}$ and $|·|$ is the natural absolute value and, for a fixed m, $f\in C^m\left([a,b]\right)$, then by Weierstrass Approximation Theorem, for every $\epsilon >0$, there exists a polynomial P such that $\parallel f^{\left(k\right)}-P^{\left(k\right)}{\parallel }_{[a,b]}<\epsilon$, for $k=0,1,\dots ,m$, where ${\parallel ·\parallel }_{[a,b]}$ is the sup norm on $C\left(\right[a,b\left]\right)$ (see, for instance, [22], Ch. VI).

Consider p a prime number, $K={\mathbb{Q}}_p$ the field of p-adic numbers and ${|·|}_p$ the p-adic absolute value normed such that ${\left|p\right|}_p=\frac{1}{p}$ (see, for example, refs. [3,4,5]). The field $({\mathbb{Q}}_p,|·{|}_p)$ is a non-Archimedean valued field, and ${\mathbb{Z}}_p=\{x\in {\mathbb{Q}}_p{:\left|x\right|}_p\le 1\}$ is its valuation ring called the ring of p-adic integers. Note that ${\mathbb{Z}}_p$ is a compact set which is clopen set in $({\mathbb{Q}}_p,|·{|}_p)$ (i.e., an open and closed subset of $({\mathbb{Q}}_p,|·{|}_p)$. A p-adic integer is a formal series ${\displaystyle \sum _{i\ge 0}}{a}_i{p}^i$ with integral coefficients $a_i$ such that $0\le a_i\le p-1$. The set $M=\{x\in {\mathbb{Z}}_p:|x{|}_p<1\}$ is the unique maximal ideal of ${\mathbb{Z}}_p$ and the quotient ${\mathbb{Z}}_p/M$ is called the residue field of ${\mathbb{Q}}_p$. It is a finite field with p elements.

If $f:{\mathbb{Z}}_p\to K$, $f\in C\left({\mathbb{Z}}_p\right)$, then, for every $\epsilon >0$, there exists a polynomial P with coefficients in ${\mathbb{Q}}_p$ such that ${\parallel f-P\parallel }_{{\mathbb{Z}}_p}<\epsilon$, where ${\parallel ·\parallel }_{{\mathbb{Z}}_p}$ is the sup norm on $C\left({\mathbb{Z}}_p\right)$ (see [6,7]).

Now, we prove a theorem on simultaneous interpolation and approximation of functions and their derivatives.

Theorem 1.

Consider $(K,|·\left|\right)$ a complete valued field of zero characteristic and let $D\subset K$ be an open set such that $\overline{D}$ is a compact subset of K. Suppose that the Weierstrass Approximation Theorem holds for every $f\in C^m\left(\overline{D}\right)$, where m is a fixed positive integer. If ${\alpha }_0,{\alpha }_1,$$\dots ,$${\alpha }_r\in \overline{D}$ are distinct elements, $k_0,k_1,\dots ,k_r$ are positive integers with $m=k_0+k_1+\dots +k_r$, and $f\in C^m\left(\overline{D}\right)$; then, for every $\epsilon >0$, there exists a polynomial P, with coefficients in K, such that

$$\parallel f^{\left(k\right)}-P^{\left(k\right)}{\parallel }_{\overline{D}}<\epsilon ,k=0,1,\dots ,m,$$

(9)

and

$$f^{\left(j\right)}\left({\alpha }_i\right)=P^{\left(j\right)}\left({\alpha }_i\right),i=0,1,\dots ,r,j=0,1,\dots ,k_i-1,$$

(10)

where ${\parallel ·\parallel }_{\overline{D}}$ is the sup norm on $C\left(\overline{D}\right)$.

Proof. 

Let ${\epsilon }^{\prime }>0$. Then, by the Weierstrass Approximation Theorem, there exists a polynomial Q such that

$$\parallel f^{\left(k\right)}-Q^{\left(k\right)}{\parallel }_{\overline{D}}<{\epsilon }^{\prime },k=0,1,\dots ,m.$$

(11)

By Lemma 2, the equality (5) holds for Q, so we can write:

$$Q\left(x\right)={\displaystyle \sum _{j=1}^{k_0}}Q\left[{\left({\alpha }_0\right)}_j\right]u_{(j-1){\alpha }_0}\left(x\right)+{\displaystyle \sum _{j=1}^{k_1}}Q[{\left({\alpha }_0\right)}_{k_0},{\left({\alpha }_1\right)}_j]u_{k_0{\alpha }_0,(j-1){\alpha }_1}\left(x\right)+\dots$$

$$+{\displaystyle \sum _{j=1}^{k_r}}Q[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-1}\right)}_{k_{r-1}},{\left({\alpha }_r\right)}_j]u_{k_0{\alpha }_0,\dots ,k_{r-1}{\alpha }_{r-1},(j-1){\alpha }_r}\left(x\right)$$

$$+Q[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-1}\right)}_{k_{r-1}},{\left({\alpha }_r\right)}_{k_r},x]u_{k_0{\alpha }_0,\dots ,k_{r-1}{\alpha }_{r-1},k_r{\alpha }_r}\left(x\right).$$

(12)

Consider the polynomial

$$P\left(x\right)={\displaystyle \sum _{j=1}^{k_0}}f\left[{\left({\alpha }_0\right)}_j\right]u_{(j-1){\alpha }_0}\left(x\right)+{\displaystyle \sum _{j=1}^{k_1}}f[{\left({\alpha }_0\right)}_{k_0},{\left({\alpha }_1\right)}_j]u_{k_0{\alpha }_0,(j-1){\alpha }_1}\left(x\right)+\dots$$

$$+{\displaystyle \sum _{j=1}^{k_r}}f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-1}\right)}_{k_{r-1}},{\left({\alpha }_r\right)}_j]u_{k_0{\alpha }_0,\dots ,k_{r-1}{\alpha }_{r-1},(j-1){\alpha }_r}\left(x\right)$$

$$+Q[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-1}\right)}_{k_{r-1}},{\left({\alpha }_r\right)}_{k_r},x]u_{k_0{\alpha }_0,\dots ,k_{r-1}{\alpha }_{r-1},k_r{\alpha }_r}\left(x\right).$$

(13)

Under the notations from Lemma 1, we denote by C the positive constant

$$C=max\left\{\left|C_{i,j}^{\mathrm{s}}\right|:\mathrm{s}=(s_0,\dots ,s_r),0\le s_i\le k_i,i=0,\dots ,r,j=0,\dots ,k_i-1\right\}.$$

By (4), and (11), we can write:

$$\left|f[{\left({\alpha }_0\right)}_{s_0},{\left({\alpha }_1\right)}_{s_1},\dots ,{\left({\alpha }_t\right)}_{s_t}]-Q[{\left({\alpha }_0\right)}_{s_0},{\left({\alpha }_1\right)}_{s_1},\dots ,{\left({\alpha }_t\right)}_{s_t}]\right|$$

$$\le C{\displaystyle \sum _{i=0}^r}{\displaystyle \sum _{j=0}^{s_i-1}}|f^{\left(j\right)}\left({\alpha }_i\right)-Q^{\left(j\right)}\left({\alpha }_i\right)|\le C{\epsilon }^{\prime }\left(s_0+\dots +s_r\right)\le C{\epsilon }^{\prime }m,$$

for every $t\le r$, $s_t\le k_t$.

By (12) and (13), for any $k=0,1,\dots ,m$ we have:

$$\left|Q^{\left(k\right)}\left(x\right)-P^{\left(k\right)}\left(x\right)\right|\le {\displaystyle \sum _{j=1}^{k_0}}\left|Q\left[{\left({\alpha }_0\right)}_j\right]-f\left[{\left({\alpha }_0\right)}_j\right]\right|\left|u_{(j-1){\alpha }_0}^{\left(k\right)}\left(x\right)\right|+\dots$$

$$+{\displaystyle \sum _{j=1}^{k_r}}\left|Q[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-1}\right)}_{k_{r-1}},{\left({\alpha }_r\right)}_j]-f[{\left({\alpha }_0\right)}_{k_0},\dots ,{\left({\alpha }_{r-1}\right)}_{k_{r-1}},{\left({\alpha }_r\right)}_j]\right|\left|u_{k_0{\alpha }_0,\dots ,k_{r-1}{\alpha }_{r-1},(j-1){\alpha }_r}^{\left(k\right)}\left(x\right)\right|.$$

Therefore, if M denotes the positive constant

$$M=max\left\{{∥u_{i_0{\alpha }_0,i_1{\alpha }_1,\dots ,i_r{\alpha }_r}^{\left(k\right)}∥}_{\overline{D}}:0\le i_s\le k_s,0\le s\le r,0\le k\le m\right\},$$

then

$${∥Q^{\left(k\right)}-P^{\left(k\right)}∥}_{\overline{D}}\le C{\epsilon }^{\prime }mM\left(k_0+\dots +k_r\right)=C_1{\epsilon }^{\prime },$$

where $C_1=C{m}^{2}M$. Thus, for $k=0,1,\dots ,m$,

$$\parallel f^{\left(k\right)}-P^{\left(k\right)}{\parallel }_{\overline{D}}\le \parallel f^{\left(k\right)}-Q^{\left(k\right)}{\parallel }_{\overline{D}}+{\parallel Q^{\left(k\right)}-P^{\left(k\right)}\parallel }_{\overline{D}}<(1+C_1){\epsilon }^{\prime }.$$

Hence, by choosing ${\epsilon }^{\prime }=\frac{\epsilon }{1+C_1}$, it follows (9). Finally, by Lemma 2, we obtain (10) and the theorem follows. □

4. Infinite Interpolation by Newton Interpolating Series

Let $(K,|·\left|\right)$ be a complete valued field of zero characteristic and $D\subset K$ be an open set such that $\overline{D}$ is a compact subset of K. Let ${\left\{{\alpha }_i\right\}}_{i\ge 0}$ be a sequence of elements from $\overline{D}$. Consider the polynomials:

$$u_0=1,u_i={\displaystyle \prod _{j=0}^{i-1}}(X-{\alpha }_j),i\ge 1.$$

(14)

Then

$${\displaystyle \sum _{i=0}^{\infty }}{a}_i{u}_i,a_i\in K,$$

(15)

is called a Newton interpolating series in one variable with coefficients in K at${\left\{{\alpha }_i\right\}}_{i\ge 0}$. We say that a function $f:\overline{D}\to \mathbb{R}$ can be represented as Newton interpolating series at ${\left\{{\alpha }_i\right\}}_{i\ge 0}$, if there exists a series of the form (15) which converges absolutely and converges uniformly to f on $\overline{D}$. If a function f can be represented as a Newton interpolating series at ${\left\{{\alpha }_i\right\}}_{i\ge 0}$, then the partial sums $S_n\left(x\right)$ of the series (15) define a sequence of polynomial functions which approximate uniformly f and $S_n\left({\alpha }_i\right)=f\left({\alpha }_i\right)$, $i=0,1,\dots ,n$.

In the case of real numbers, for $D=(a,b)$, power series or even fractional power series can be used to approximate solutions of initial value problems for differential equations or fractional differential equations, respectively (see, for instance, [23]). As regarding the boundary value problems for differential equations, the Newton interpolating series is a suitable tool for approximating solutions. For example, the case of a purely periodic interpolating sequence ${\left\{{\alpha }_i\right\}}_{i\ge 0}$ of period m (i.e., for every $i,$${\alpha }_{i+m}={\alpha }_i$) is studied in [13], while applications in the case of an interpolating sequence with distinct terms can be found in [14] for ordinary differential equations and in [12] for systems of ordinary differential equations. Other methods based on simultaneous interpolation and approximation, which are used to approximate solutions of boundary value problems for differential equations, are presented in [24,25].

In this paper, we consider applications of Newton interpolating series at ${\left\{{\alpha }_i\right\}}_{i\ge 0}$, when the interpolating sequence is purely periodic of period m. Then

$$u_i=v^{q\left(i\right)}{\displaystyle \prod _{j=0}^{r\left(i\right)-1}}(X-{\alpha }_j),$$

where $v={\displaystyle \prod _{i=0}^{m-1}}(X-{\alpha }_i)$ and $i=q\left(i\right)m+r\left(i\right)$ is the Euclidean division written for any positive integer i. We denote by Y the formal series (15),

$$Y:={\displaystyle \sum _{i=0}^{\infty }}{a}_i{u}_i,a_i\in K$$

(16)

and

$$DY:={\displaystyle \sum _{i=0}^{\infty }}{a}_{i}D{u}_i={\displaystyle \sum _{i=0}^{\infty }}{a}_i^{\left(1\right)}{u}_i,a_i^{\left(1\right)}\in K,$$

its formal derivative series obtained by termwise differentiation of the series Y and by reordering the terms in a suitable form to obtain a Newton interpolating series at ${\left\{{\alpha }_k\right\}}_{k\ge 0}$. For example, if $m=2$, then

$$\begin{array}{cc}\hfill u_i& ={(X-{\alpha }_0)}^{q\left(i\right)+r\left(i\right)}{(X-{\alpha }_1)}^{q\left(i\right)},\hfill \\ \hfill D{u}_i& =i{u}_{i-1}+{(-1)}^{r\left(i\right)}q\left(i\right)({\alpha }_0-{\alpha }_1)u_{i-2},i=2,3,\dots ,\hfill \\ \hfill a_i^{\left(1\right)}& =(i+1)a_{i+1}+{(-1)}^i({\alpha }_0-{\alpha }_1)(q\left(i\right)+1)a_{i+2},i=0,1,\dots .\hfill \end{array}$$

Remark 3.

In the case of real numbers, for $D=(a,b)$, if $f:[a,b]\to \mathbb{R}$ is an infinitely differentiable function such that $\underset{n\to \infty }{lim}\frac{{(b-a)}^n{\parallel f^{\left(n\right)}\parallel }_{[a,b]}}{n!}=0$, it is known (see [13], Theorem 3.5) that f may be represented as a Newton interpolating series at ${\left\{{\alpha }_i\right\}}_{i\ge 0}$.

Notice that there are continuous functions $f:[a,b]\to \mathbb{R}$ which can be represented as Newton interpolating series at ${\left\{{\alpha }_i\right\}}_{i\ge 0}$, but they are not differentiable at some points of $[a,b]$. For example, we consider $a=-1,$ $b=1$, $m=2$, ${\alpha }_0=-1$, ${\alpha }_1=1$ and $f\left(x\right)=\left|x\right|$. Since

$$\left|x\right|=\sqrt{1-(1-x^2)}=1+{\displaystyle \sum _{i=1}^{\infty }}\frac{{(-1)}^{i-1}}{2^{2i-1}i}\left(\genfrac{}{}{0pt}{}{2i-2}{i-1}\right){(x-1)}^i{(x+1)}^i,$$

we can see that f is a sum of this Newton interpolating series at ${\left\{{\alpha }_i\right\}}_{i\ge 0}$ on $[a,b]$, but f is not differentiable at $x=0$.

It is known that Δ, the domain of convergence of the series from (16), has the form $\Delta ={\displaystyle \bigcup _{k=0}^{m-1}}{I}_k$, where for every $k=0,\dots ,m-1$, $I_k$ is an interval containing ${\alpha }_k$. These intervals depend on $\rho =\frac{1}{\underset{i\to \infty }{lim\; sup}|a_i{|}^{1/i}}$, the roots of the derivative $u_m^{\prime }\left(x\right)$ and the roots of the equation $|u_m\left(x\right)|={\rho }^m$ (see [13], Theorem 2.2). If there exists an interval $I_k$ and x is an interior point of this interval and $S\left(x\right)$ is the sum of the series, then there exists its derivative $S^{\prime }\left(x\right)$ which is the sum of the derivative series.

Now, consider the complete field of p-adic numbers, $K={\mathbb{Q}}_p$ and $D\subset {\mathbb{Z}}_p$ an open subset of K such that $\overline{D}$ is a compact subset. In order to interpolate a function $f\in C^{\infty }\left(\overline{D}\right)$ by a function which is representable into a Newton interpolating series, we need the following lemma.

Lemma 3.

Let $({\mathbb{Q}}_p,|·{|}_p)$ be the p-adic field and let $D\subset {\mathbb{Z}}_p$ be an open subset of K such that $\overline{D}$ is a compact subset of ${\mathbb{Q}}_p$. Assume that ${\left\{{\alpha }_i\right\}}_{i\ge 0}$ is a purely periodic interpolating sequence of period p from $\overline{D}$ such that ${\alpha }_0,\dots ,{\alpha }_{p-1}$ is a set of representatives of the residue field of ${\mathbb{Q}}_p$ (that is, for all $i,j\in \{0,1,\dots ,p-1\}$, $i\ne j$, ${\alpha }_i$ and ${\alpha }_j$ have distinct image in the residue fields of ${\mathbb{Q}}_p$). If there exists a positive constant C such that for every non-negative integer i, $|a_i{|}_p\le C$, then the series defined in (15) converges absolutely and converges uniformly on $\overline{D}$ to a continuous function $S\left(x\right)$. Moreover, there exists the derivative $S^{\prime }\left(x\right)$ of $S\left(x\right)$, for every $x\in \overline{D}$, and it is the sum of the derivative series of $S\left(x\right)$.

Proof. 

Since ${\alpha }_0,\dots ,{\alpha }_{p-1}$ is a set of representatives of the residue field of ${\mathbb{Q}}_p$, for every $x\in {\mathbb{Z}}_p$, there exists ${\alpha }_j$ such that $|x-{\alpha }_j{|}_p\le \frac{1}{p}$. Then, we get $|u_i{\left(x\right)|}_p\le \frac{1}{p^{q\left(i\right)}}$, $|a_i{u}_i{\left(x\right)|}_p\le \frac{C}{p^{q\left(i\right)}}$, and because ${|·|}_p$ is non-Archimedean, the series (15) converges absolutely and converges uniformly on $\overline{D}$ to a continuous function $S\left(x\right)$. Since, by induction on i, we get $u_i^{\prime }={\displaystyle \sum _{k=1}^p}{C}_{i-k}^{\left(i\right)}{u}_{i-k}$, where $C_{i-k}^{\left(i\right)}\in {\mathbb{Z}}_p$, $C_{i-1}^{\left(i\right)}=i$, $u_j=0$ if $j<0$, it follows that the coefficients $a_i^{\left(1\right)}$ of the derivative series are linear combinations of $a_{i+1},\dots ,a_{i+p},$ with coefficients in ${\mathbb{Z}}_p$. Thus, $a_i^{\left(1\right)}\in {\mathbb{Z}}_p$ and the derivative series converges absolutely and converges uniformly on $\overline{D}$ to a function $\tilde{S}\left(x\right)$. If $x_0\in \overline{D}$ is fixed, then, for any $x\ne x_0$,

$$\frac{S\left(x\right)-S\left(x_0\right)}{x-x_0}-\tilde{S}\left(x_0\right)={\displaystyle \sum _{i=0}^{\infty }}{a}_i\left(\frac{u_i\left(x\right)-u_i\left(x_0\right)}{x-x_0}-u_i^{\prime }\left(x_0\right)\right).$$

Then, by Taylor’s formula, which holds for polynomial functions,

$$\frac{u_i\left(x\right)-u_i\left(x_0\right)}{x-x_0}-u_i^{\prime }\left(x_0\right)=(x-x_0){\displaystyle \sum _{k=2}^i}\frac{u_i^{\left(k\right)}\left(x_0\right){(x-x_0)}^{k-2}}{k!}.$$

Since, by (14), $u_i={\displaystyle \prod _{j=0}^{p-1}}{(X-{\alpha }_j)}^{n_j}$, where $n_j=q\left(i\right)+1$ if $j\le r\left(i\right)-1$, and $n_j=q\left(i\right)$ otherwise, we get

$$u_i^{\left(k\right)}\left(x\right)=\sum _{k_0+\dots +k_{p-1}=k}\frac{k!}{k_0!\dots k_{p-1}!}{\left({(x-{\alpha }_0)}^{n_0}\right)}^{\left(k_0\right)}\dots {\left({(x-{\alpha }_{p-1})}^{n_{p-1}}\right)}^{\left(k_{p-1}\right)}$$

$$=k!\sum _{\begin{array}{c}{k}_0+\dots +k_{p-1}=k\\ k_0\le n_0,\dots ,k_{p-1}\le n_{p-1}\end{array}}\left(\genfrac{}{}{0pt}{}{n_0}{k_0}\right)\dots \left(\genfrac{}{}{0pt}{}{n_{p-1}}{k_{p-1}}\right){(x-{\alpha }_0)}^{n_0-k_0}\dots {(x-{\alpha }_{p-1})}^{n_{p-1}-k_{p-1}}.$$

Hence, $\frac{u_i^{\left(k\right)}\left(x_0\right)}{k!}\in {\mathbb{Z}}_p$ and

$${\left|\frac{S\left(x\right)-S\left(x_0\right)}{x-x_0}-\tilde{S}\left(x_0\right)\right|}_p\le C{|x-x_0|}_p,$$

which implies the lemma. □

Theorem 2.

Let $({\mathbb{Q}}_p,|·{|}_p)$ be the p-adic field and let $D\subset {\mathbb{Z}}_p$ be an open subset of ${\mathbb{Z}}_p$ such that $\overline{D}$ is a compact subset of ${\mathbb{Q}}_p$. Assume that ${\left\{{\alpha }_i\right\}}_{i\ge 0}\in \overline{D}$ is a purely periodic interpolating sequence of period p such that ${\alpha }_0,\dots ,{\alpha }_{p-1}$ is a set of representatives of the residue field of ${\mathbb{Q}}_p$. If $f:\overline{D}\to {\mathbb{Z}}_p$, $f\in C^{\infty }\left(\overline{D}\right)$ and there exists a positive constant C such that, for every non-negative integer j,

$$\underset{x\in \overline{D}}{sup}\left|f^{\left(j\right)}\left(x\right)\right|\le C,$$

then the series

$${\displaystyle \sum _{i=0}^{\infty }}{a}_i{u}_i\left(x\right),$$

(17)

where $a_i=f[{\left({\alpha }_0\right)}_{q\left(i\right)+1},\dots ,{\left({\alpha }_{r\left(i\right)-1}\right)}_{q\left(i\right)+1},{\left({\alpha }_{r\left(i\right)}\right)}_{q\left(i\right)},\dots ,{\left({\alpha }_{p-1}\right)}_{q\left(i\right)}],$ converges absolutely and converges uniformly on $\overline{D}$ to a function $S\left(x\right)$. Moreover, $S\in C^{\infty }\left(\overline{D}\right)$ and for every non-negative integer $i,j$,

$$S^{\left(i\right)}\left({\alpha }_j\right)=f^{\left(i\right)}\left({\alpha }_j\right).$$

(18)

Proof. 

Since ${\alpha }_i,i=0,1,\dots ,p-1$, is a set of representatives of the residue field of ${\mathbb{Q}}_p$, it follows that $|{\alpha }_i-{\alpha }_j{|}_p=1$, for every $i,j=0,1,\dots ,p-1$ with $i\ne j$. Then, by Lemma 1, we get ${\left|f[{\left({\alpha }_0\right)}_{k_0},{\left({\alpha }_1\right)}_{k_1},\dots ,{\left({\alpha }_r\right)}_{k_r}]\right|}_p\le C,$ for every non-negative integer $k_0,\dots ,k_r$. By Lemma 3, it follows that the series (17) converges absolutely and converges uniformly on $\overline{D}$ to a function $S\left(x\right)$ and $S\in C^{\infty }\left(\overline{D}\right)$. Then, by Lemma 1, we get (18) and so the theorem follows. □

5. Applications

5.1. Numerical Approximation of the Solutions of Variational Problems

Consider the variational problem

$$minI\left[y\right],I\left[y\right]={\displaystyle \underset{a}{\overset{b}{\int }}}F(x,y,y^{\prime },\dots ,y^{\left(r\right)})dx,$$

(19)

where F is a continuously differentiable function, with the boundary conditions

$$\begin{array}{c}y\left(a\right)=y_1,y^{\prime }\left(a\right)=y_1^{\prime },\dots ,y^{(r-1)}\left(a\right)=y_1^{(r-1)},\hfill \\ y\left(b\right)=y_2,y^{\prime }\left(b\right)=y_2^{\prime },\dots ,y^{(r-1)}\left(b\right)=y_2^{(r-1)}.\hfill \end{array}$$

(20)

Suppose that the variational problem (19), (20) has a unique solution $y\in$$C^r\left([a,b]\right)$. Then, by Theorem 1, for every $\epsilon >0$, there exists a polynomial P such that

$$\parallel y^{\left(k\right)}-P^{\left(k\right)}{\parallel }_{[a,b],\infty }<\epsilon ,k=0,1,\dots ,r,$$

(21)

and

$$y^{\left(j\right)}\left({\alpha }_i\right)=P^{\left(j\right)}\left({\alpha }_i\right),i=0,1,j=0,1,\dots ,r-1,{\alpha }_0=a,{\alpha }_1=b.$$

(22)

Example 2.

To illustrate the method we consider the variational problem [16]:

$$minI\left[y\right],I\left[y\right]={\displaystyle \underset{0}{\overset{1}{\int }}}{(y\left(x\right)+y^{\prime }\left(x\right)-4e^{3x})}^{2}dx;$$

(23)

subject to the boundary conditions

$$y\left(0\right)=1,y\left(1\right)=e^3.$$

(24)

From (21) and (22), it follows that the solution of the variational problem (23), (24) can be approximated by polynomials. This can be written as

$$P_n\left(x\right)=y\left(0\right)+y[0,1]x+x(x-1){\displaystyle \sum _{i=2}^n}{a}_i{x}^{i-2}.$$

The coefficients $a_k$, $k=2,\dots ,n$, are determined as solutions of the system of equations

$$\frac{\partial I\left[P_n\right]}{\partial a_k}=0.$$

Then, for $k=2,\dots ,n,$ we get

$${\displaystyle \underset{0}{\overset{1}{\int }}}2\left(\frac{\partial P_n\left(x\right)}{\partial a_k}+\frac{\partial P_n^{\prime }\left(x\right)}{\partial a_k}\right)(P_n\left(x\right)+P_n^{\prime }\left(x\right)-4e^{3x})dx=0.$$

Hence, it follows that

$${\displaystyle \underset{0}{\overset{1}{\int }}}\left(x^k+(k-1)x^{k-1}-(k-1)x^{k-2}\right)(P_n\left(x\right)+P_n^{\prime }\left(x\right)-4e^{3x})dx=0.$$

Thus

$${\displaystyle \sum _{i=2}^n}{c}_{ik}{a}_i=d_k,k=2,3,\dots ,$$

(25)

where

$$c_{ik}={\displaystyle \underset{0}{\overset{1}{\int }}}{x}^{k+i-4}(x^2+(k-1)x-k+1)(x^2+(i-1)x-i+1)dx,$$

$$d_k={\displaystyle \underset{0}{\overset{1}{\int }}}{x}^{k-2}(x^2+(k-1)x-k+1)(4e^{3x}-e^3-(e^3-1)x)dx.$$

By solving the linear system (25), we obtain the coefficients $a_i$ of the polynomial $P_n\left(x\right)$ which approximate the exact solution $y\left(x\right)=e^{3x}$. In

Table 1. Exact and approximate values of the solution of the boundary value problem (23)–(24).

x	Exact y	${\mathit{y}}_{\mathbf{DTM}}$ [16]	${\mathit{P}}_8$	${\mathit{P}}_{10}$
$0.1$	$1.34985880$	$1.35035927$	$1.34986095$	$1.34985881$
$0.2$	$1.82211880$	$1.82312475$	$1.82211703$	$1.82211879$
$0.3$	$2.45960311$	$2.46112459$	$2.45960204$	$2.45960312$
$0.4$	$3.32011692$	$3.32216898$	$3.32011969$	$3.32011691$
$0.5$	$4.48168907$	$4.48429018$	$4.48168928$	$4.48168906$
$0.6$	$6.04964746$	$6.05280952$	$6.04964454$	$6.04964747$
$0.7$	$8.16616991$	$8.16985405$	$8.16617067$	$8.16616989$
$0.8$	$11.02317638$	$11.02713929$	$11.02317852$	$11.02317638$
$0.9$	$14.87973172$	$14.88307423$	$14.87972932$	$14.87973172$
$1.0$	$20.08553692$	$20.08553692$	$20.08553692$	$20.08553692$

, we present the values of the exact solution $y\left(x\right)$, the approximate solution $y_{DTM}\left(x\right)$ obtained in [16] by using the differential transform method (DTM) and the approximate solutions $P_n\left(x\right)$ for $n=8$ and $n=10$ obtained by using the Hermite interpolation method.

We denote the errors of approximation by $E_{DTM}=y_{DTM}-y$ (for the differential transform method) and $E_n=P_n-y$ (for the Hermite interpolation method). Notice that $\underset{x\in [0,1]}{max}\left|E_{DTM}\left(x\right)\right|\approx 4\times {10}^{-3}$, while $\underset{x\in [0,1]}{max}\left|E_8\left(x\right)\right|\approx 3\times {10}^{-6}$ and $\underset{x\in [0,1]}{max}\left|E_{10}\left(x\right)\right|\approx 2\times {10}^{-8}$. We represent in Figure 1 the graph of the functions $E_{DTM}\left(x\right)$, $100·E_8\left(x\right)$ and 10,000$·E_{10}\left(x\right)$.

5.2. Solutions of Some Functional Equations with One Variable

A functional equation with one variable is an equation in which the unknown is a function.

Example 3.

The functional equation (see [18])

$$f\left[g\right(x\left)\right]=Af\left(x\right),$$

(26)

is called Schröder’s equation. For a given function g, we have to find one or more functions f and a real number $A\ne 1$ such that (26) holds. A Newton interpolating series can be used to solve some Schröder’s equations.

As an illustrative example, we consider the functional equation (see [18], p. 81)

$$f\left(\frac{x(x+1)}{2}\right)=\frac{f\left(x\right)}{2},x\in \mathbb{R}.$$

(27)

We search for a solution f of (27) as the sum of a convergent Newton interpolation series of the form

$$a_0+a_1{u}_1\left(x\right)+a_2{u}_2\left(x\right)+\dots ,$$

(28)

where

$$u_k\left(x\right)=\left\{\begin{array}{cc}xv{\left(x\right)}^{\lfloor \frac{k}{2}\rfloor },& \mathrm{if}k\mathrm{is}\mathrm{odd}\\ v{\left(x\right)}^{\lfloor \frac{k}{2}\rfloor },& \mathrm{if}k\mathrm{is}\mathrm{even}\end{array},v\left(x\right)=x(x+1),k\ge 1.\right.$$

Since $v(v\left(x\right)/2)=\frac{v\left(x\right)\left(v\right(x)+2)}{4}$, by (27) and (28), and supposing that the series (28) converges absolutely and converges uniformly to f on an interval $[a,b]$ such that $0,-1\in [a,b]$, we find $a_0=f\left(0\right)=0$ and

$$\frac{a_1}{2}v\left(x\right)+\frac{a_2}{4}v\left(x\right)(v\left(x\right)+2)+\frac{a_3}{2·4}v{\left(x\right)}^2(v\left(x\right)+2)+\frac{a_4}{4^2}v{\left(x\right)}^2{(v\left(x\right)+2)}^2$$

$$+\frac{a_5}{2·4^2}·v{\left(x\right)}^3{(v\left(x\right)+2)}^2+\frac{a_6}{4^3}v{\left(x\right)}^3{(v\left(x\right)+2)}^3+\dots$$

$$=\frac{1}{2}\left(a_{1}x+a_{2}v\left(x\right)+a_{3}xv\left(x\right)+a_4{v}^2\left(x\right)+a_{5}x{v}^2\left(x\right)+a_6{v}^3\left(x\right)+\dots \right).$$

Hence, we obtain $a_{2j+1}=0$, for every $j=0,1,\dots$, and, for $j\ge 1$,

$$\frac{a_{2j}}{2}={\displaystyle \sum _{i=\lfloor \frac{j+1}{2}\rfloor }^j}\frac{a_{2i}}{4^i}\left(\genfrac{}{}{0pt}{}{i}{2i-j}\right)2^{2i-j}$$

or, equivalently,

$$a_{2j}=\frac{1}{2^{j-1}-1}{\displaystyle \sum _{i=\lfloor \frac{j+1}{2}\rfloor }^{j-1}}\left(\genfrac{}{}{0pt}{}{i}{2i-j}\right)a_{2i}.$$

(29)

Thus, $a_4=a_2$, $a_6=\frac{2}{3}{a}_2$, $a_8=\frac{3}{7}{a}_2$, $a_{10}=\frac{26}{105}{a}_2$, $a_{12}=\frac{94}{651}{a}_2$, $a_{14}=\frac{3292}{41013}{a}_2$, ….

If f is a solution of (27), then for every constant γ, the function $\gamma f$ is also a solution of this functional equation. Hence, it follows that without loss of generality, we may choose $a_2=1$.

Denote $\delta =\sqrt{\frac{2}{3}}\approx .8165$. We prove by induction on $j\ge 2$ that

$$a_{2j}\le {\delta }^{j-2}.$$

(30)

It can be verified that (30) holds for $j\le 18$. Assume that (30) is true for $j\le n-1$, $n>18$. Then, from (29) and (30), and using the inequality

$$\left(\genfrac{}{}{0pt}{}{n-k}{k}\right)\le 2^k\left(\genfrac{}{}{0pt}{}{\lfloor \frac{n+1}{2}\rfloor }{k}\right),\mathrm{for}\mathrm{all}k\le \lfloor \frac{n+1}{2}\rfloor ,$$

we obtain

$$a_{2n}=\frac{1}{2^{n-1}-1}{\displaystyle \sum _{i=\lfloor \frac{n+1}{2}\rfloor }^{n-1}}\left(\genfrac{}{}{0pt}{}{i}{n-i}\right)a_{2i}=\frac{1}{2^{n-1}-1}{\displaystyle \sum _{k=1}^{n-\lfloor \frac{n+1}{2}\rfloor }}\left(\genfrac{}{}{0pt}{}{n-k}{k}\right)a_{2(n-k)}$$

$$\le \frac{1}{2^{n-1}-1}{\displaystyle \sum _{k=1}^{n-\lfloor \frac{n+1}{2}\rfloor }}{2}^k\left(\genfrac{}{}{0pt}{}{\lfloor \frac{n+1}{2}\rfloor }{k}\right){\delta }^{n-k-2}\le \frac{{\delta }^{n-2}}{2^{n-1}-1}\left({\left(1+\frac{2}{\delta }\right)}^{\lfloor \frac{n+1}{2}\rfloor }-1\right)<{\delta }^{n-2}.$$

Thus, if (30) is true for all $j<n$, it must be true for $j=n$, and the induction is complete.

By Weierstrass M-test, if $\delta \left|v\right(x\left)\right|<1$, it follows that the series (28) converges absolutely and uniformly on every interval $[c,d]\subset (\frac{-1-\sqrt{1+4{\delta }^{-1}}}{2},\frac{-1+\sqrt{1+4{\delta }^{-1}}}{2})$. Hence, if $[c,d]\subset (-1.7143,0.7143)$, the sum the series (28) is a solution of functional Equation (27).

We represent this solution in Figure 2. Notice that by using a power series, in [18], a solution of the equation is plotted on the interval $[0,0.5]$.

5.3. Boundary Value Problems for Differential Equations in the p-Adic Field

Example 4.

Let $({\mathbb{Q}}_p,|·{|}_p)$ be the non-Archimedean valued field of p-adic numbers.

Consider the following p-point boundary value problem for an equation of the Fuchsian type (see, for example, ref. [21])

$$v\left(x\right)y^{″}\left(x\right)+(ax+b)y^{\prime }\left(x\right)+{\nu }^{2}y\left(x\right)=0,x\in {\mathbb{Z}}_p,$$

(31)

with the boundary conditions

$$y\left({\alpha }_i\right)={\beta }_i,i=0,\dots ,p-1,$$

(32)

where $y:{\mathbb{Z}}_p\to {\mathbb{Q}}_p$, $y\in C^2\left({\mathbb{Z}}_p\right)$, $v\left(x\right)={\displaystyle \prod _{i=0}^p}(x-{\alpha }_i)$ and $a,b,\nu ,{\alpha }_i,{\beta }_i\in {\mathbb{Z}}_p$, $i=0,\dots ,p-1$ are constants. We study the solutions of this problems which can be represented as Newton interpolating series in one variable with p-adic coefficients at ${\left\{{\alpha }_i\right\}}_{i\ge 0}$, where the sequence ${\left\{{\alpha }_i\right\}}_{i\ge 0}$ is purely periodic of period p that is ${\alpha }_i={\alpha }_{r\left(i\right)}$ and $i=q\left(i\right)p+r\left(i\right)$ is the Euclidean division written for any integer i. Moreover, assume that $\{{\alpha }_i,i=0,1,\dots ,p-1\}$ is a set of representatives of the residue field of ${\mathbb{Q}}_p$. Hence, $|{\alpha }_i-{\alpha }_j{|}_p=1$, for every $i,j=0,1,\dots ,p-1$ with $i\ne j$ (see, for example, ref. [5]).

As in Section 4, we denote by Y the formal Newton interpolating series

$$Y={\displaystyle \sum _{i=0}^{\infty }}{a}_i{u}_i,$$

(33)

where

$$u_i=v^{q\left(i\right)}{\displaystyle \prod _{j=0}^{r\left(i\right)-1}}(X-{\alpha }_j).$$

Let $DY$, $D^{2}Y$ be the formal derivatives obtained by termwise differentiation of the series and by reordering the terms in a suitable form (see Section 4). Then, we get

$$DY:={\displaystyle \sum _{i=0}^{\infty }}{a}_{i}D{u}_i={\displaystyle \sum _{i=0}^{\infty }}{a}_i^{\left(1\right)}{u}_i,$$

$$D^{2}Y:={\displaystyle \sum _{i=0}^{\infty }}{a}_i^{\left(1\right)}D{u}_i={\displaystyle \sum _{i=0}^{\infty }}{a}_i^{\left(2\right)}{u}_i.$$

By replacing Y and its formal derivatives in (32) and computing, by a formal algebraic process, the coefficients of $u_i$, we get recursive formulas of the form

$$a_{k+p}=C_0{a}_k+C_1{a}_{k+1}+\dots +C_p{a}_{k+p-1},$$

where $a_0$, …, $a_{p-1}$ are parameters from ${\mathbb{Z}}_p$. Then, we choose a suitable open and compact subset D of ${\mathbb{Z}}_p$ such that the series (33) and its derivatives converge absolutely and uniformly on D. By (32), we find the parameters $a_0,\dots ,a_{p-1}$. Hence, the function defined by (33) is a solution of the problems (31) and (32).

We illustrate the method for the case $p=2$. In this case, we seek a solution of the differential equation

$$(x-{\alpha }_0)(x-{\alpha }_1)y^{″}\left(x\right)+(2x-{\alpha }_0-{\alpha }_1)y^{\prime }\left(x\right)+{\nu }^{2}y\left(x\right)=0,x\in {\mathbb{Z}}_2,$$

(34)

with the boundary conditions

$$y\left({\alpha }_i\right)={\beta }_i,i=0,1,$$

(35)

where $\nu ,{\alpha }_i,{\beta }_i\in {\mathbb{Z}}_2$, $i=0,1$ are constants. Since (see Section 4)

$$a_i^{\left(1\right)}=(i+1)a_{i+1}+{(-1)}^i({\alpha }_0-{\alpha }_1)(q\left(i\right)+1)a_{i+2},$$

(36)

we find

$$a_i^{\left(2\right)}=(i+1)a_{i+1}^{\left(1\right)}+{(-1)}^i({\alpha }_0-{\alpha }_1)(q\left(i\right)+1)a_{i+2}^{\left(1\right)}$$

$$=(i+1)(i+2)a_{i+2}+{(-1)}^{i+1}({\alpha }_0-{\alpha }_1)·((i+1)(q(i+1)+1)-(i+3)(q\left(i\right)+1))a_{i+3}$$

$$+{({\alpha }_0-{\alpha }_1)}^2(q\left(i\right)+1)(q\left(i\right)+2)a_{i+4}.$$

(37)

Since $(2x-{\alpha }_0-{\alpha }_1)u_i\left(x\right)=2u_{i+1}\left(x\right)+{(-1)}^i({\alpha }_0-{\alpha }_1)u_i\left(x\right)$, by replacing y and its formal derivatives in (34) and by computing the coefficients of $u_i$, we get

$$a_{i-2}^{\left(2\right)}+2a_{i-1}^{\left(1\right)}+{(-1)}^i({\alpha }_0-{\alpha }_1)a_i^{\left(1\right)}+{\nu }^2{a}_i=0.$$

Hence, from (36) and (37), it follows the recursive formula

$$a_{i+2}=-\frac{A\left(i\right)a_{i+1}+B\left(i\right)a_i}{{({\alpha }_0-{\alpha }_1)}^2{(q\left(i\right)+1)}^2},$$

(38)

where $A\left(i\right)={(-1)}^i({\alpha }_0-{\alpha }_1)(i+1)(q\left(i\right)-q(i-1))$ and $B\left(i\right)=i(i+1)+{\nu }^2$ are 2-adic integers.

Assume that $a_0,$$a_1$ are 2-adic integers. In order to estimate $|a_{i+2}{|}_2$, by (38), it is necessary to evaluate the maximum power $n_i$ of 2 that divides $\left(q\right(i)+1)!$ Since

$$n_i=⌊\frac{q\left(i\right)+1}{2}⌋+⌊\frac{q\left(i\right)+1}{2^2}⌋+⌊\frac{q\left(i\right)+1}{2^3}⌋+\dots \le \frac{q\left(i\right)+1}{2}\left(1+\frac{1}{2}+\dots \right)=q\left(i\right)+1,$$

we get

$$|a_{i+2}{|}_2\le 2^{2q\left(i\right)+2}.$$

For any $a\in {\mathbb{Z}}_2$ and $r>0$, we denote by $B(a,r)=\{x\in {\mathbb{Z}}_2:|x-a{|}_2\le r\}$. Consider the set $D=B\left({\alpha }_0,\frac{1}{2^3}\right)\bigcup B\left({\alpha }_1,\frac{1}{2^3}\right)$. Then, for every $x\in D$, we have: $|u_i{\left(x\right)|}_p\le \frac{1}{2^{3q\left(i\right)}}$. Hence, $|a_i{u}_i{\left(x\right)|}_p\le \frac{1}{2^{q\left(i\right)}}$. Since ${\mathbb{Q}}_2$ is a non-Archimedean valued field, it follows that the series (33) converges absolutely and uniformly on D, so $y\left(x\right)$ is well defined. Moreover, from (36) and (37), it follows that $y^{\prime }\left(x\right)$, $y^{″}\left(x\right)$ are continuous well-defined functions. By (35), we get

$$a_0={\beta }_0,a_1=\frac{{\beta }_1-{\beta }_0}{{\alpha }_1-{\alpha }_0}.$$

(39)

Thus, the function $y\in C^2\left(D\right)$ is defined by

$$y\left(x\right)={\displaystyle \sum _{i=0}^{\infty }}{a}_i{(x-{\alpha }_0)}^{q\left(i\right)+r\left(i\right)}{(x-{\alpha }_1)}^{q\left(i\right)},$$

where $a_0$, $a_1$ are given in (39), and for $i\ge 2$, the coefficients $a_i$ are defined by (38), presenting a solution of the problems (34) and (35). Moreover, it is the unique solution which can be represented as a Newton interpolating series at ${\left\{{\alpha }_k\right\}}_{k\ge 0}$, with ${\alpha }_k={\alpha }_{r\left(k\right)}$.

6. Conclusions

If K is a topological field and $D\subset K$ is an open set such that $\overline{D}$ is compact, by means of generalized divided differences, we studied the interpolation of an m times continuously differentiable function $f:\overline{D}\to K$. In the case of valued fields, where the Weierstrass theorem holds, the proof of Theorem 1 presents a method to construct polynomials which gives simultaneous Hermite interpolation and approximation of a function $f\in C^m\left(\overline{D}\right)$.

Newton analytic series are used in the case of an infinite number of conditions of interpolation. Theorem 2 shows that in the case of p-adic numbers, for D an open subset of the set ${\mathbb{Z}}_p$ (i.e., the set p-adic integers), every infinitely differentiable function $f:\overline{D}\to {\mathbb{Z}}_p$ and all its derivatives can be interpolated at a suitable purely periodic sequence ${\left\{{\alpha }_i\right\}}_{i\ge 0}$ of period p by an infinitely differentiable function, which is the sum of a uniformly convergent Newton interpolating series.

Applications to numerical approximation of variational problems, solution of a functional equation and, in the case of p-adic fields, representation of solutions of a boundary value problem for an equation of the Fuchsian type illustrate the efficiency of the theoretical results. We consider that these applications represent only the first step for extending this study.