Design and Operation of Multipurpose Production Facilities Using Solar Energy Sources for Heat Integration Sustainable Strategies
Abstract
:1. Introduction
Background
2. Modelling Approach
- i.
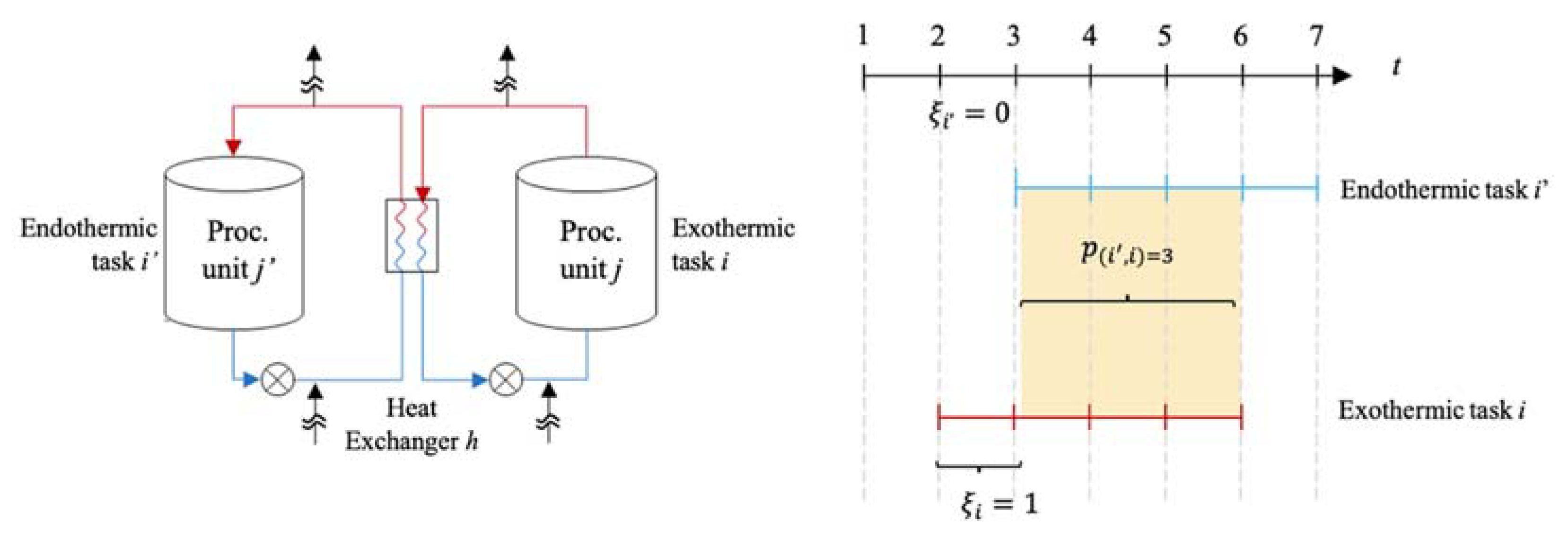
- Direct heat integration is performed if the heat exchange conditions between the streams of an exothermic and endothermic task i are satisfied, and their scheduling overlaps, as shown in Figure 1. During the overlap period, p(i′,i), the heat exchange requires an exchange unit. To reach the heat exchange condition, an offset time, , may be considered before the heat integration starts. An external heat source h may be required if the heat exchanged is not enough.
- ii.
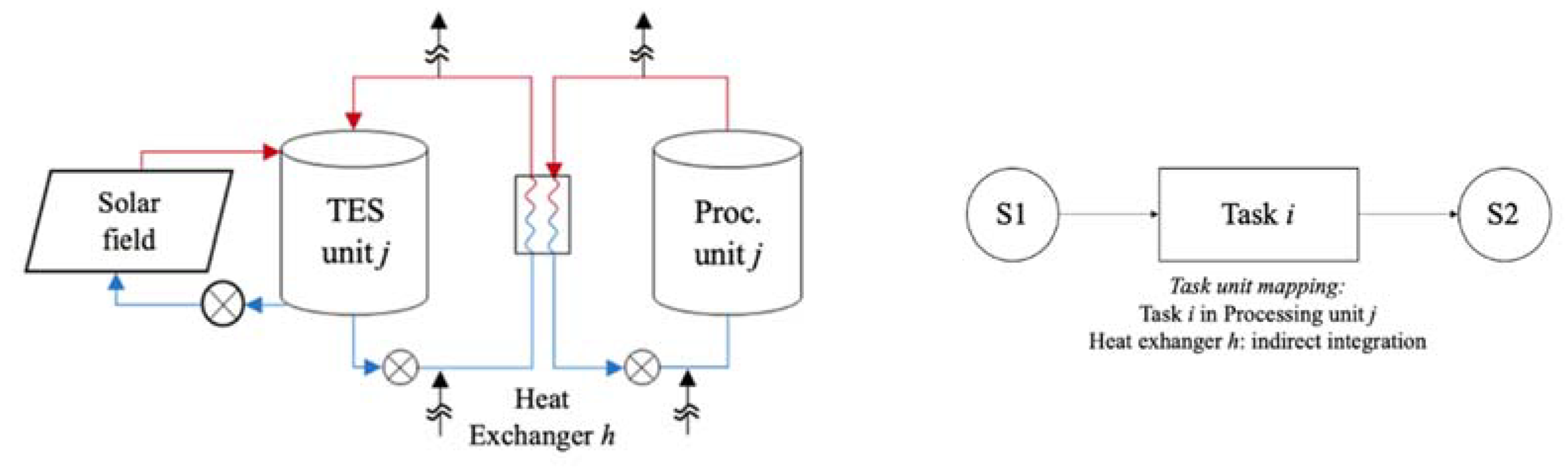
- Indirect heat integration is performed through a TES unit, combining (a) the TES unit that collects heat from the solar field or from an exothermic task, Figure 2, or (b) the TES unit that provides heat for an endothermic task.
- The solar field is characterised by parallel flat plates with a set of properties in which each solar field is connected to one TES unit;
- The solar panels composing a solar field have the same inlet/outlet temperature;
- During time t, the inlet temperature of a solar field is the same as the average temperature of the respective TES unit;
- The TES unit exchanges heat with only one processing task at a time, but may receive heat from the solar field and simultaneously exchange heat with a processing task;
- Once the TES unit starts to exchange heat, no pre-emptive action is allowed;
- The heat exchange only occurs if a minimum temperature difference () between tasks is verified;
- The temperature decay in the TES is based on its thermal resistance ;
- No phase change is assumed in the TES heat medium.
Problem Statement
- Product recipes according to STN representation;
- Production requirements and time horizon;
- Units’ suitability to perform the process/storage tasks and max./min. capacities;
- Task operating temperature and time;
- Utility requirements, heat integration options, and min. temperature differences;
- Operating and capital costs for each unit and task;
- Solar irradiation profile and collector data: type of collector, optical and heat loss performance coefficients, and concentrating ratio.
- The optimal plant topology and design: number and type of processing units, thermal energy storage units, heat exchange units and heat transfer area, number of solar panels and storage vessel collectors;
- Optimal production schedule, with storage policies and batch size characterisation;
- Products and utility profiles, with corresponding heat transfer strategies.
3. Mathematical Formulation
3.1. Process Constraints
3.2. Direct Heat Integration Constraints
3.3. Indirect Heat Integration Constraints
3.4. Solar Energy Constraints
3.5. Objective Function
4. Illustrative Examples
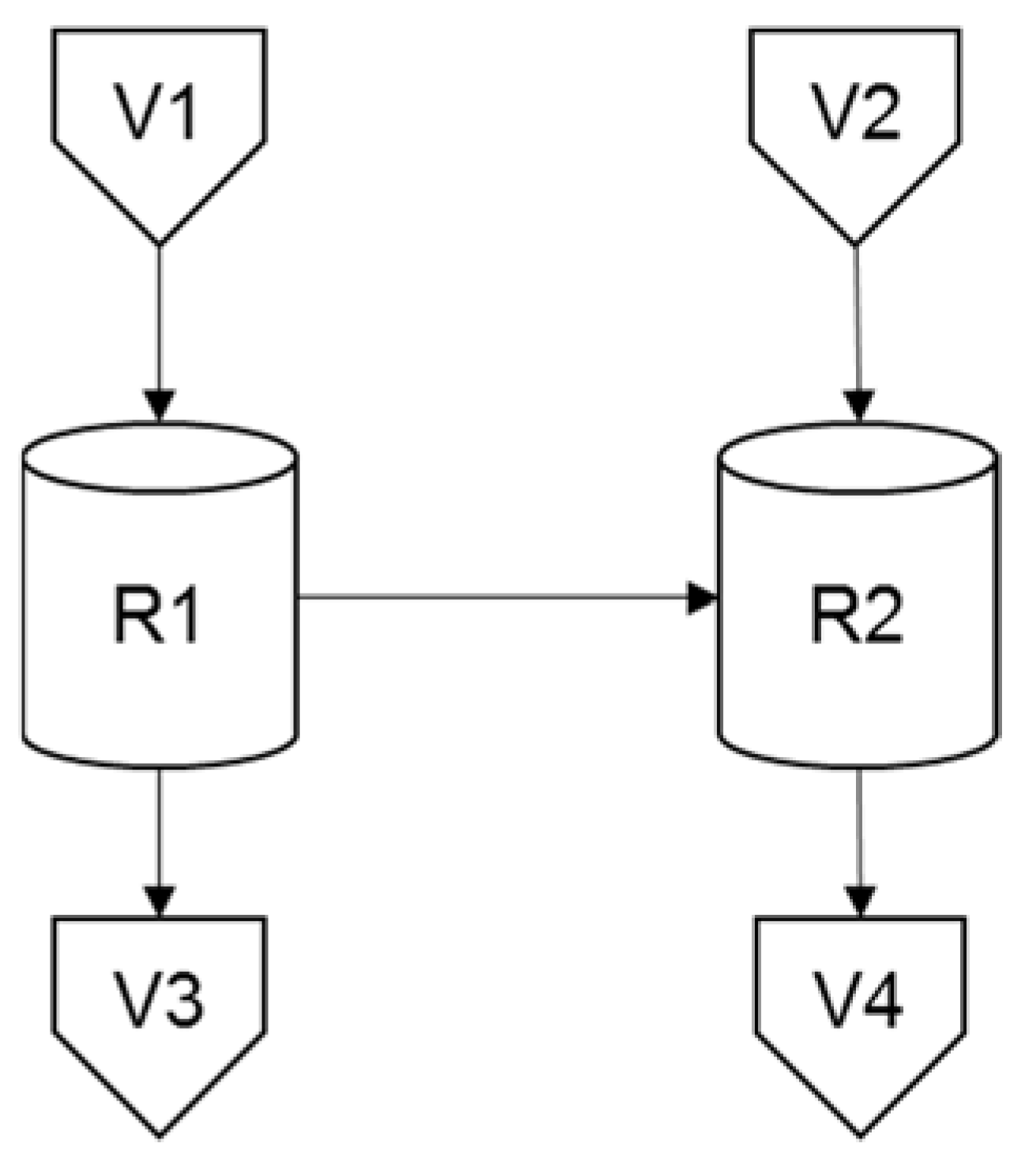
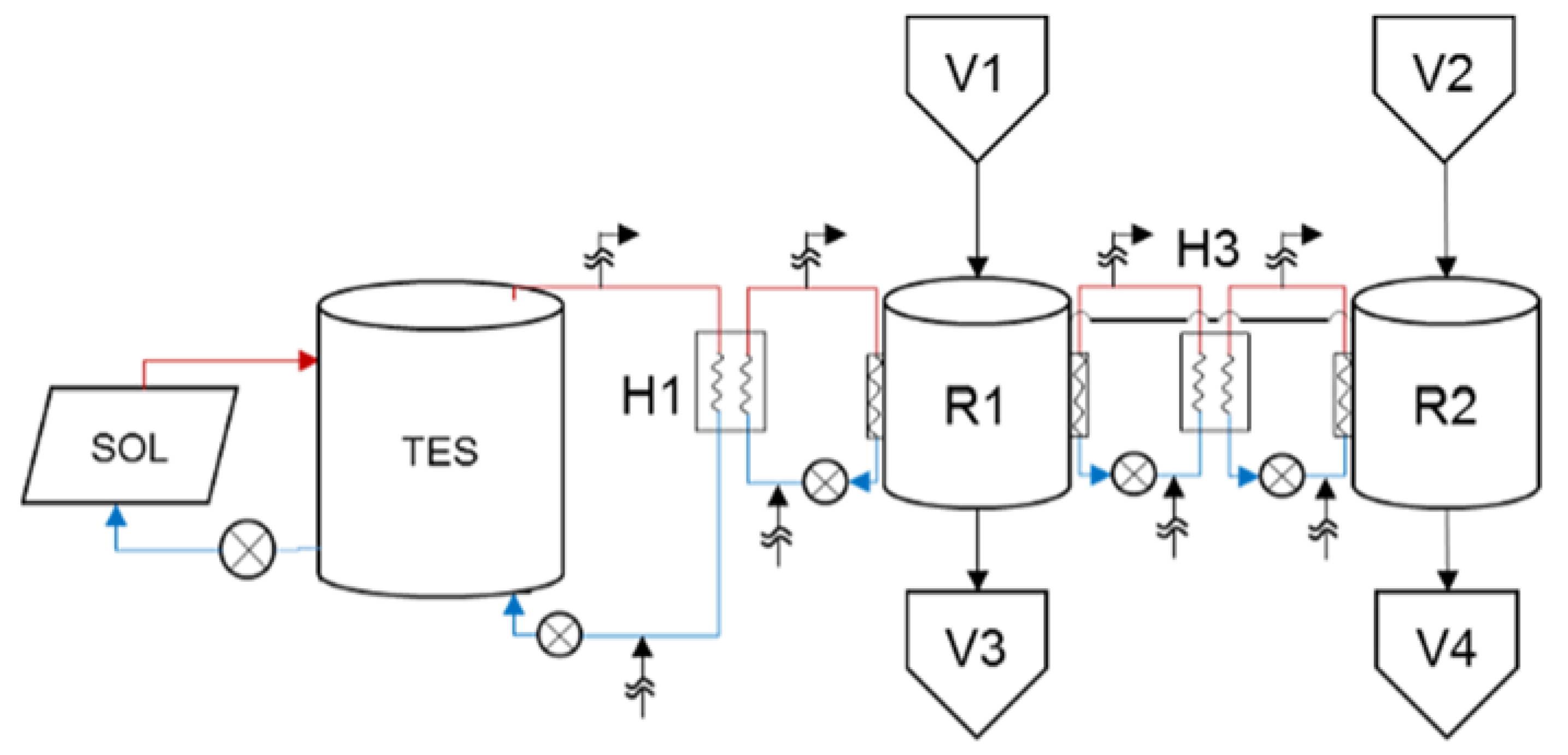
4.1. Example I
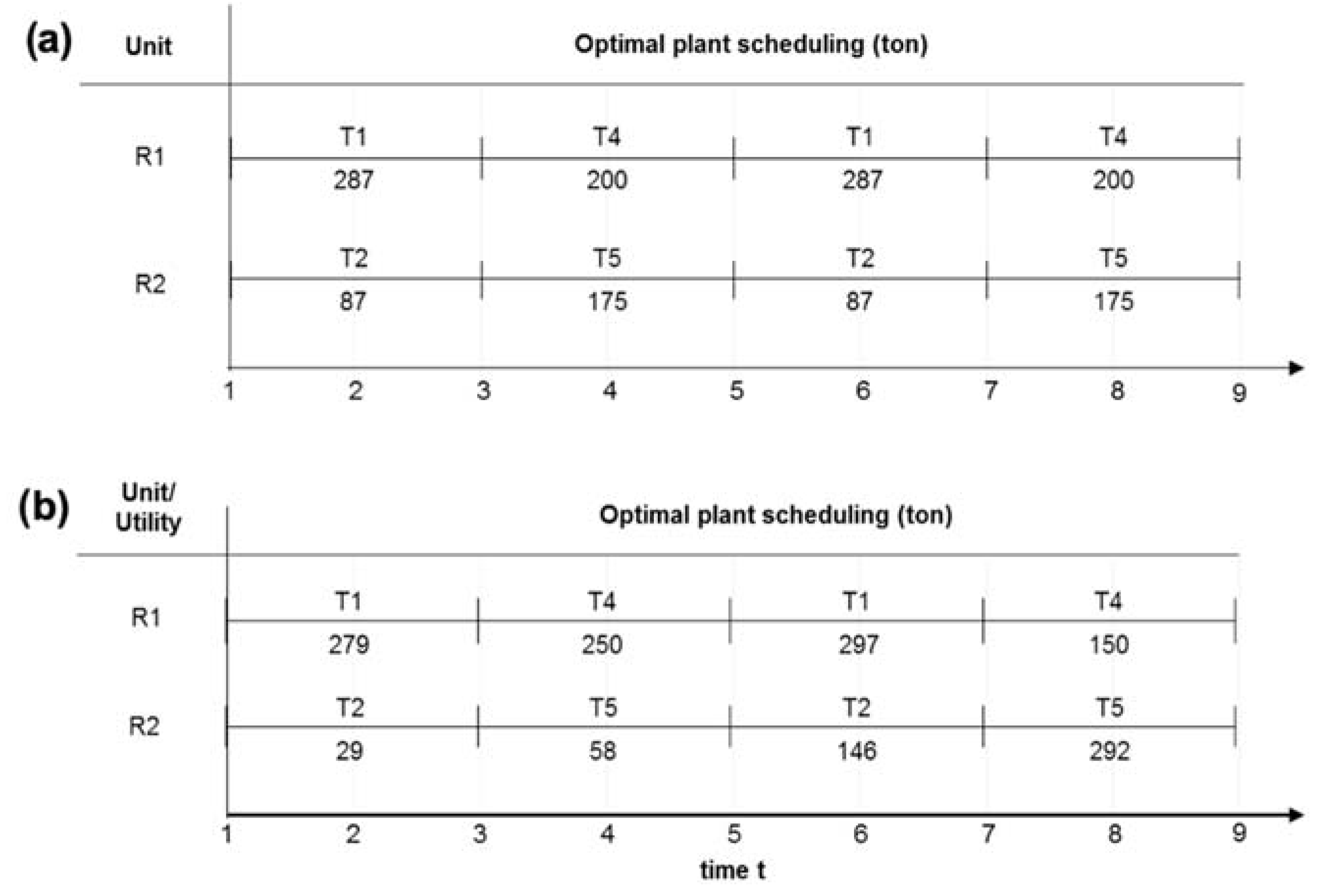
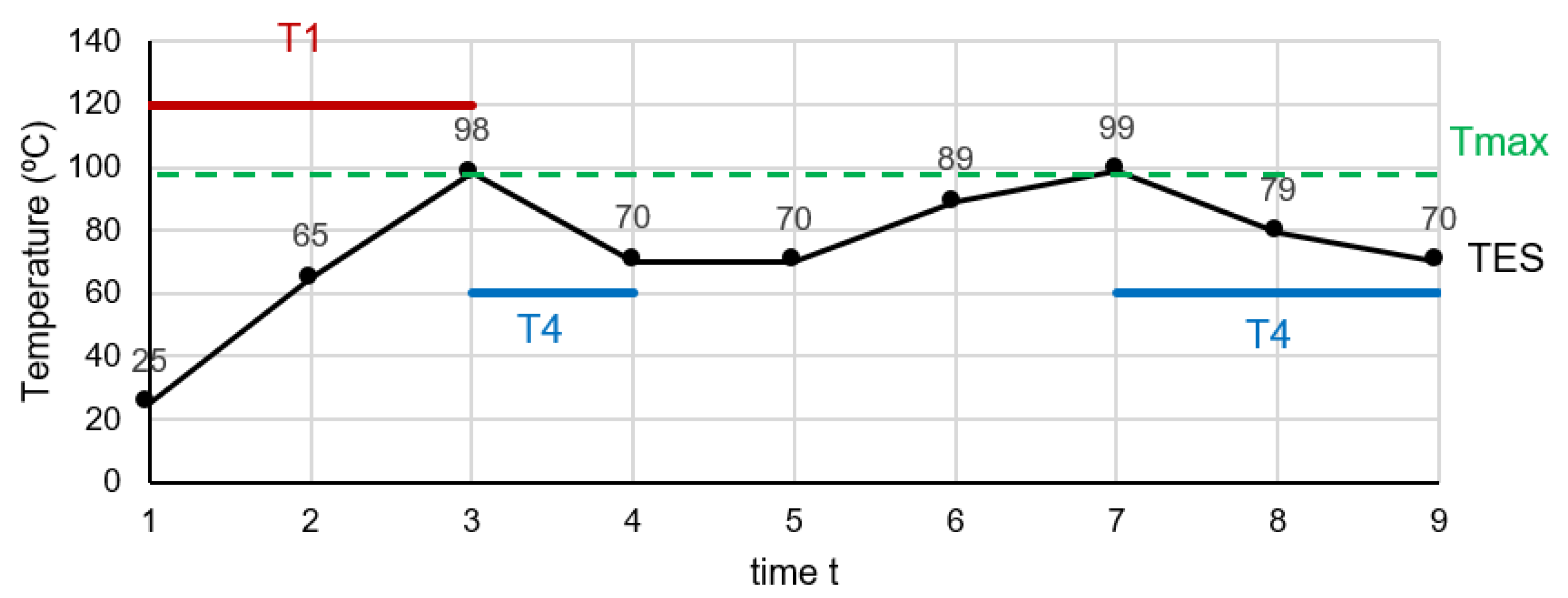
Results and Discussion: Scenario (a) vs. Scenario (b)
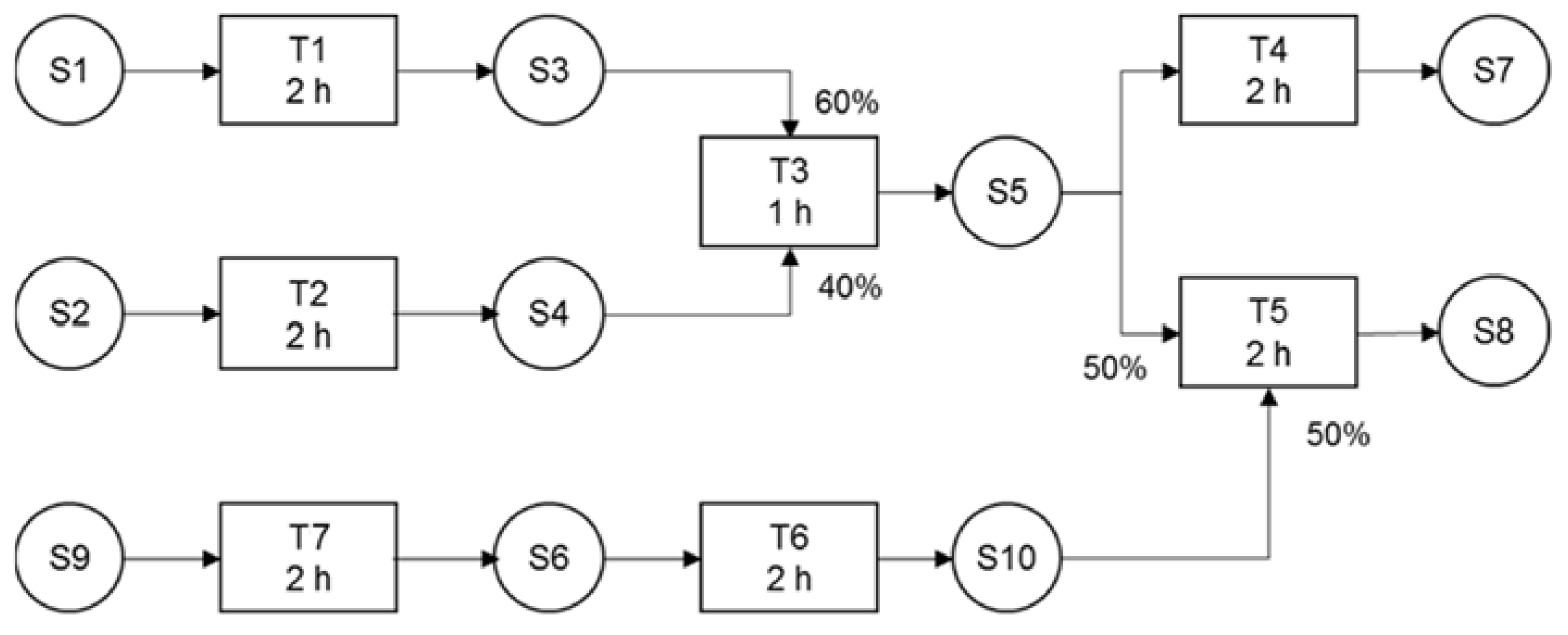
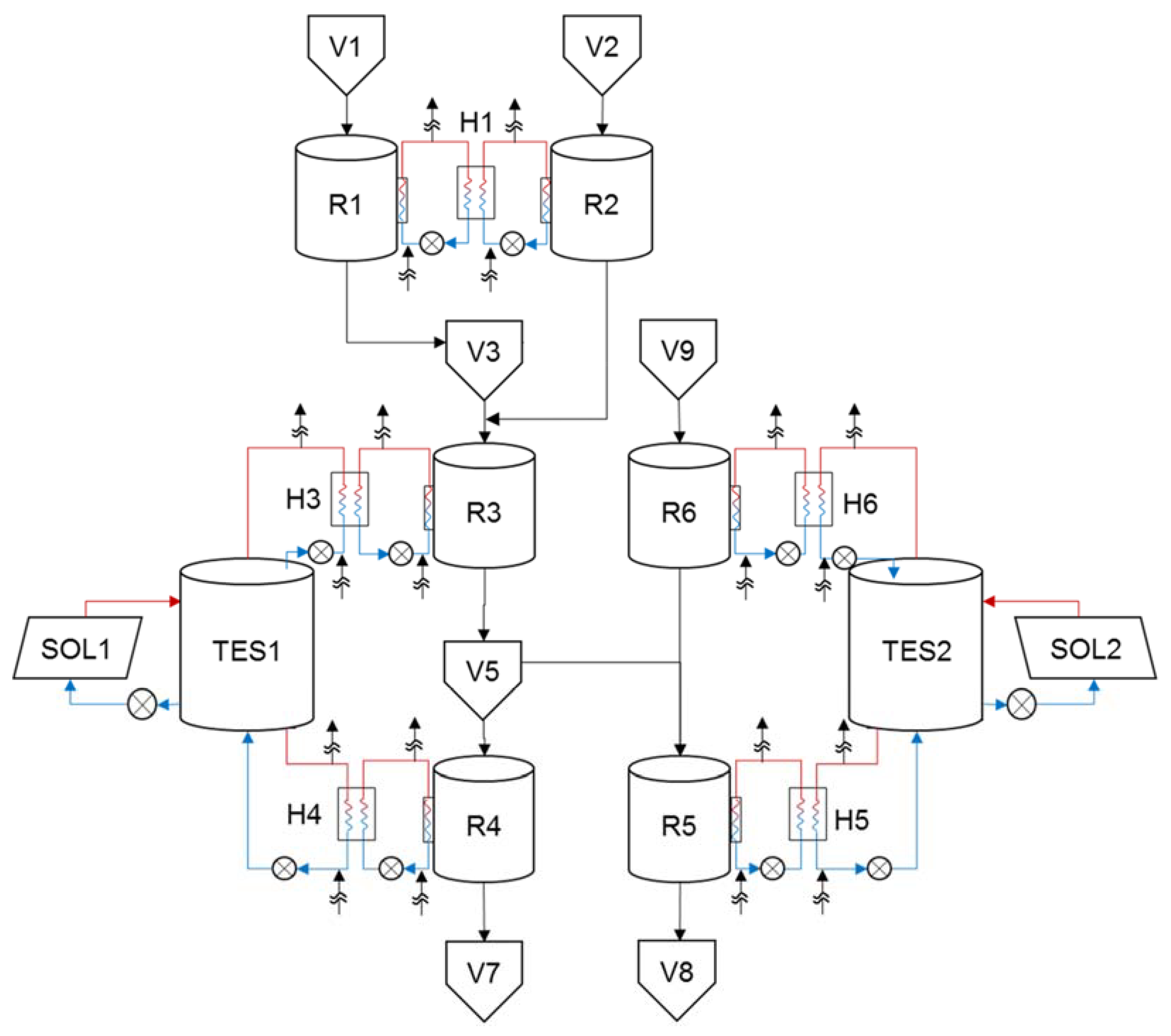
4.2. Example II
Results and Discussion: Scenario (a) vs. Scenario (b)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Sets: | |
| processing and material storage tasks i | |
| processing, material storage, and Thermal Energy Storage (TES) units j | |
| product states s | |
| processing tasks i | |
| processing units j | |
| dedicated material storage units j | |
| dedicated storage units suitable for storing state s | |
| set of k types of unit j | |
| i tasks which can be performed in unit j | |
| j units suitable for task i | |
| i tasks producing/receiving material to state s | |
| initial/final states s | |
| h units suitable to transfer heat | |
| utilities u | |
| h units suitable to transfer heat between tasks | |
| i tasks that can use utility u | |
| u utilities suitable for task i | |
| i tasks that produce heat | |
| i tasks that require heat | |
| i tasks that charge TES unit, | |
| i tasks that discharge TES unit, | |
| TES units j | |
| heat integrated tasks | |
| volume discretisation for TES unit | |
| number of solar panels connected to TES unit | |
| Parameters: | |
| H | Time horizon (discretised with fixed duration ) |
| M | big number |
| processing time of task i | |
| proportion of material of state, s entering/leaving task i | |
| maximum/minimum utilisation factor of task i in unit j | |
| maximum/minimum capacity of unit j of type k/overall max value | |
| minimum/maximum production requirements of material | |
| maximum availability of utility u at time t | |
| heat capacity of utility u | |
| temperature difference for utility u | |
| time offset of task i | |
| fixed/variable heat demand factor of task i at processing time θ | |
| maximum/minimum heat transfer area of unit h | |
| integration time of tasks | |
| mean fluid logarithmic temperature difference in unit h per-forming tasks | |
| overall heat transfer coefficient of unit h | |
| heat capacity of storage fluid w | |
| processing temperature of task i | |
| maximum/minimum TES temperature | |
| volume of TES unit for | |
| thermal resistance of TES unit for | |
| density of storage fluid w | |
| minimum thermal driving force for integration | |
| ambient temperature | |
| hourly solar radiation | |
| solar collector optical efficiency | |
| solar collector 1st order heat loss coefficient | |
| surface area of one solar collector | |
| maximum/minimum flowrate inside solar collector k | |
| number of solar collectors | |
| temperature variation inside the solar collector | |
| number of annual working hours | |
| CCF | capital charge factor |
| value/price of state s | |
| operating cost of dedicated storage of state s | |
| batch size-dependent operational cost of utility u | |
| fixed/variable operating cost of task i, in unit j | |
| fixed/variable capital cost of unit j of type k | |
| fixed/variable operational cost of solar task | |
| fixed/variable capital costs of TES unit | |
| fixed/variable capital costs of heat transfer unit h | |
| Binary variables | |
| 1 if unit j (of type k) is installed, 0 otherwise | |
| 1 if heat transfer unit h is installed, 0 otherwise | |
| 1 if TES unit with volume is installed, 0 otherwise | |
| 1 if the number of solar collectors of option is connected to TES unit, , 0 otherwise | |
| 1 if unit j is performing task i Iint at the time t, 0 otherwise | |
| 1 if heat transfer unit h is performing heat integration of tasks , at the time t, 0 otherwise | |
| Continuous variables: | |
| batch of task i, in unit j, at instant t | |
| capacity of processing unit j | |
| amount of material in the state s, at period t | |
| amount of material s, delivered at period t | |
| amount of material s received at period t | |
| batch of external utility u, required by task i, at period t | |
| heat supplied to task i, by external utility u, at period t | |
| heat transfer area of unit h | |
| heat required by processing task during time t | |
| heat transferred between tasks , using unit h, at period t | |
| energy lost from TES unit during time t | |
| energy stored in TES unit at the beginning of time t | |
| temperature of TES unit at the beginning of time t | |
| temperature of TES unit j, with z volume at the beginning of time t | |
| efficiency of solar collector connected to TES unit at time t | |
| average fluid temperature inside solar collector connected to TES unit at time t | |
| solar collector inlet fluid temperature coming from TES unit at time t | |
| solar collector outlet fluid temperature going to TES unit at time t | |
| mass flow rate supplied to the solar field at time t, connected to TES unit | |
| solar heat charged to TES unit at time t | |
| volume capacity and temperature of TES unit (linearisation) |
References
- Chung, B.D.; Kim, S.I.; Lee, J.S. Dynamic supply chain design and operations plan for connected smart factories with additive manufacturing. Appl. Sci. 2018, 8, 583. [Google Scholar] [CrossRef] [Green Version]
- Han, X.; Li, R.; Wang, J.; Ding, G.; Qin, S. A systematic literature review of product platform design under uncertainty. J. Eng. Des. 2020, 31, 266–296. [Google Scholar] [CrossRef]
- Vieira, M.; Paulo, H.; Pinto-Varela, T.; Barbosa-Póvoa, A.P. Assessment of financial risk in the design and scheduling of multipurpose plants under demand uncertainty. Int. J. Prod. Res. 2021, 59, 6125–6145. [Google Scholar] [CrossRef]
- Woolway, M.; Majozi, T. A novel metaheuristic framework for the scheduling of multipurpose batch plants. Chem. Eng. Sci. 2018, 192, 678–687. [Google Scholar] [CrossRef]
- Harjunkoski, I.; Maravelias, C.T.; Bongers, P.; Castro, P.M.; Engell, S.; Grossmann, I.E.; Hooker, J.; Méndez, C.; Sand, G.; Wassick, J. Scope for industrial applications of production scheduling models and solution methods. Comput. Chem. Eng. 2014, 62, 161–193. [Google Scholar] [CrossRef] [Green Version]
- Seid, E.R.; Majozi, T. Optimization of energy and water use in multipurpose batch plants using an improved mathematical formulation. Chem. Eng. Sci. 2014, 111, 335–349. [Google Scholar] [CrossRef]
- Abdelhady, F.; Bamufleh, H.; El-Halwagi, M.M.; Ponce-Ortega, J.M. Optimal design and integration of solar thermal collection, storage, and dispatch with process cogeneration systems. Chem. Eng. Sci. 2015, 136, 158–167. [Google Scholar] [CrossRef]
- Harik, R.; El Hachem, W.; Medini, K.; Bernard, A. Towards a holistic sustainability index for measuring sustainability of manufacturing companies. Int. J. Prod. Res. 2015, 53, 4117–4139. [Google Scholar] [CrossRef]
- Trianni, A.; Cagno, E.; Neri, A.; Howard, M. Measuring industrial sustainability performance: Empirical evidence from Italian and German manufacturing small and medium enterprises. J. Clean. Prod. 2019, 229, 1355–1376. [Google Scholar] [CrossRef]
- Li, Z.; Ierapetritou, M.G. Integrated production planning and scheduling using a decomposition framework. Chem. Eng. Sci. 2009, 64, 3585–3597. [Google Scholar] [CrossRef]
- Vázquez, D.; Guillén-Gosálbez, G. Process design within planetary boundaries: Application to CO2 based methanol production. Chem. Eng. Sci. 2021, 246, 116891. [Google Scholar] [CrossRef]
- Pinto, T.; Novais, A.Q.; Barbosa-Póvoa, A.P.F. Optimal design of heat-integrated multipurpose batch facilities with economic savings in utilities: A mixed integer mathematical formulation. Ann. Oper. Res. 2003, 120, 201–230. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Seid, E.R.; Majozi, T. Heat integration of intermittently available continuous streams in multipurpose batch plants. Comput. Chem. Eng. 2015, 74, 100–114. [Google Scholar] [CrossRef]
- Castro, P.M.; Custódio, B.; Matos, H.A. Optimal scheduling of single stage batch plants with direct heat integration. Comput. Chem. Eng. 2015, 82, 172–185. [Google Scholar] [CrossRef]
- Sebelebele, N.; Majozi, T. Heat integration of multipurpose batch plants through multiple heat storage vessels. Comput. Chem. Eng. 2017, 106, 269–285. [Google Scholar] [CrossRef]
- Chaturvedi, N.D.; Manan, Z.A.; Alwi, S.R.W. A mathematical model for energy targeting of a batch process with flexible schedule. J. Clean. Prod. 2017, 167, 1060–1067. [Google Scholar] [CrossRef]
- Stamp, J.D.; Majozi, T. Long-term heat integration in multipurpose batch plants using heat storage. J. Clean. Prod. 2017, 142, 1492–1509. [Google Scholar] [CrossRef]
- Vooradi, R.; Mummana, S.S. Cyclic scheduling and heat integration of batch process: Design of heat storage vessels. Chem. Eng. Res. Des. 2022, 179, 130–142. [Google Scholar] [CrossRef]
- Boix, M.; Montastruc, L.; Azzaro-Pantel, C.; Domenech, S. Optimization methods applied to the design of eco-industrial parks: A literature review. J. Clean. Prod. 2015, 87, 303–317. [Google Scholar] [CrossRef] [Green Version]
- Aziz, E.A.; Alwi, S.R.W.; Lim, J.S.; Manan, Z.A.; Klemeš, J.J. An integrated Pinch Analysis framework for low CO2 emissions industrial site planning. J. Clean. Prod. 2017, 146, 125–138. [Google Scholar] [CrossRef]
- Toimil, D.; Gómez, A. Review of metaheuristics applied to heat exchanger network design. Int. Trans. Oper. Res. 2017, 24, 7–26. [Google Scholar] [CrossRef]
- Muster-Slawitsch, B.; Brunner, C.; Padinger, R.; Schnitzer, H. Methodology for batch heat integration and storage system design for ideal integration of solar process heat. Chem. Eng. Trans. 2011, 25, 887–892. [Google Scholar]
- Nemet, A.; Klemeš, J.J.; Varbanov, P.S.; Kravanja, Z. Methodology for maximising the use of renewables with variable availability. Energy 2012, 44, 29–37. [Google Scholar] [CrossRef]
- Wallerand, A.S.; Kermani, M.; Voillat, R.; Kantor, I.; Maréchal, F. Optimal design of solar-assisted industrial processes considering heat pumping: Case study of a dairy. Renew. Energy 2018, 128, 565–585. [Google Scholar] [CrossRef] [Green Version]
- Baniassadi, A.; Momen, M.; Amidpour, M.; Pourali, O. Modeling and design of solar heat integration in process industries with heat storage. J. Clean. Prod. 2018, 170, 522–534. [Google Scholar] [CrossRef]
- Rashid, K.; Safdarnejad, S.M.; Powell, K.M. Process intensification of solar thermal power using hybridization, flexible heat integration, and real-time optimization. Chem. Eng. Processing-Process Intensif. 2019, 139, 155–171. [Google Scholar] [CrossRef] [Green Version]
- Schoeneberger, C.A.; McMillan, C.A.; Kurup, P.; Akar, S.; Margolis, R.; Masanet, E. Solar for industrial process heat: A review of technologies, analysis approaches, and potential applications in the United States. Energy 2020, 206, 118083. [Google Scholar] [CrossRef]
- Kondili, E.; Pantelides, C.C.; Sargent, R.W. A general algorithm for short-term scheduling of batch operations—I. MILP formulation. Comput. Chem. Eng. 1993, 17, 211–227. [Google Scholar] [CrossRef]
- Atkins, M.J.; Walmsley, M.R.; Morrison, A.S. Integration of solar thermal for improved energy efficiency in low-temperature-pinch industrial processes. Energy 2010, 35, 1867–1873. [Google Scholar] [CrossRef]







| Authors | Design | Scheduling | Objective | Direct Heat Integration | Indirect Heat Integration | Time Grid |
|---|---|---|---|---|---|---|
| Pinto et al. (2003) [12] | Yes | Yes | Minimisation of economic indicator | Yes | No | Discrete |
| Seid and Majozi (2014) [6] | Yes | Yes | Minimisation of wastewater generation and energy utility usage | Yes | Yes | Continuous |
| Lee et al. (2015) [13] | No | Yes | Maximisation of heat recovery from process streams | Yes | No | Continuous |
| Castro et al. (2015) [14] | No | Yes | Bi-objective: makespan and utility consumption minimisation | Yes | No | Continuous |
| Sebelebele and Majozi (2017) [15] | Yes | Yes | Minimisation of energy consumption | Yes | Yes | Continuous |
| Chaturvedi et al. (2017) [16] | No | Yes | Minimisation of energy targets | Yes | Yes | Continuous |
| Stamp and Majozi (2017) [17] | Yes | Yes | Makespan minimisation | Yes | Yes | Continuous |
| Vooradi and Mummana (2022) [18] | Yes | Yes | Makespan minimisation | Yes | Yes | Continuous |
| Unit | Suitability | Capacity Min:Max | Costs Fix:Var (103 c.u.) |
|---|---|---|---|
| R1 | Task T1/T4 | 40:300 m3 | 5:0.05 |
| R2 | Task T2/T5 | 70:300 m3 | 5:0.05 |
| V1 | Store S1 | Unlim. | 3:0.01 |
| V2 | Store S2 | Unlim. | 3:0.01 |
| V3 | Store S3 | 0:450 m3 | 3:0.01 |
| V4 | Store S4 | 0:450 m3 | 3:0.01 |
| H3 | Transfer heat R1-R2 | 0:15 m2 | 5:1 |
| H1 | Transfer heat R1-TES1 | 0:15 m2 | 5:1 |
| H2 | Transfer heat TES1-R2 | 0:15 m2 | 5:1 |
| TES1 | Perform task C1/D1 | 1:9 m2 | 5:1 |
| SOL1 | Connect to TES1 | 10:400 units | 5:1 |
| Task | Type | Heating/Cooling Fix + Var (kWh) | Utility | Operating Temp. (°C) |
|---|---|---|---|---|
| T1 | Exothermic | 7 + 0.5 B | Water | 120 |
| T2 | Endothermic | 4 + 0.3 B | Steam | 100 |
| T4 | Endothermic | 8 + 0.9 B | Steam | 60 |
| T5 | Endothermic | 6 + 0.4 B | Steam | 70 |
| C1/D1 | Charge/Discharge | - | 25–100 |
| Unit | Scenario (a) Capacity | Scenario (b) Capacity | |
|---|---|---|---|
| R1 | +3% | 287 m3 | 297 m3 |
| R2 | +67% | 175 m3 | 292 m3 |
| V3 | 0 | 350 m3 | 350 m3 |
| V4 | 0 | 400 m3 | 400 m3 |
| H1 | - | - | 6.5 m2 |
| H3 | - | - | 1.3 m2 |
| TES1 | - | - | 4.8 m3 |
| SOL1 | - | - | 400 un. |
| Scenario (a) | Scenario (b) | ||
|---|---|---|---|
| Profit (c.u. 10³) | +11% | 21,830 | 24,297 |
| External utilities | |||
| Water (kWh) | −67% | 604 | 194 |
| Steam (kWh) | −52% | 1178 | 564 |
| Model statistics | |||
| CPU time (s) | 0.2 | 9.1 | |
| Int. Variables | 56 | 184 | |
| Constraints | 336 | 1696 |
| Unit | Suitability | Capacity Min:Max | Costs Fix:Var (103 c.u.) |
|---|---|---|---|
| R1 | Task T1 | 0:150 m3 | 5:0.05 |
| R2 | Task T2 | 0:150 m3 | 5:0.05 |
| R3 | Task T3/T6 | 0:400 m3 | 5:0.05 |
| R4 | Task T4 | 0:150 m3 | 5:0.05 |
| R5 | Task T5 | 0:150 m3 | 5:0.05 |
| R6 | Task T6/T7 | 0:200 m3 | 5:0.05 |
| V1 | Store S1 | Unlim. | 3:0.01 |
| V2 | Store S2 | Unlim. | 3:0.01 |
| V3 | Store S3 | Unlim. | 3:0.01 |
| V4 | Store S4 | Unlim. | 3:0.01 |
| V7 | Store S7 | 0:450 m3 | 3:0.01 |
| V8 | Store S8 | 0:450 m3 | 3:0.01 |
| V9 | Store S9 | 0:450 m3 | 3:0.01 |
| V10 | Store S10 | Unlim. | 3:0.01 |
| H1 | Transfer heat R1-R2 | 0:15 m2 | 5:1 |
| H3 | Transfer heat R3-TES1 | 0:15 m2 | 5:1 |
| H4 | Transfer heat R4-TES1 | 0:15 m2 | 5:1 |
| H5 | Transfer heat R5-TES2 | 0:15 m2 | 5:1 |
| H6 | Transfer heat R6-TES2 | 0:15 m2 | 5:1 |
| TES1 | Perform task C1/D1 | 1:8 m3 | 5:1 |
| TES2 | Perform task C2/D2 | 1:9 m3 | 5:1 |
| SOL1 | Connect to TES1 | 10:400 un. | 5:2 |
| SOL2 | Connect to TES2 | 10:400 un. | 5:2 |
| Task | Type | Heating/Cooling Fix + Var (kWh) | Operating Temp. (°C) |
|---|---|---|---|
| T1 | Exothermic | 7 + 0.5 B | 80 |
| T2 | Endothermic | 4 + 0.6 B | 70 |
| T3 | Exothermic | 9 + 1.3 B | 120 |
| T4 | Endothermic | 8 + 0.9 B | 60 |
| T5 | Endothermic | 6 + 0.8 B | 70 |
| T6 | Exothermic | 9 + 0.9 B | 150 |
| T7 | Endothermic | 2 + 0.2 B | 80 |
| C1 | TES1 charge | - | 25–100 |
| D1 | TES1 discharge | - | 25–100 |
| C2 | TES2 charge | - | 25–100 |
| D2 | TES2 discharge | - | 25–100 |
| Unit | Capacity | Unit | Capacity |
|---|---|---|---|
| R1 | 128 m3 | H1 | 0.55 m2 |
| R2 | 85 m3 | H3 | 2.07 m2 |
| R3 | 225 m3 | H4 | 1.43 m2 |
| R4 | 150 m3 | H5 | 1.26 m2 |
| R5 | 150 m3 | H6 | 1.67 m2 |
| R6 | 199 m3 | TES1 | 5.8 m3 |
| V7 | 300 m3 | TES1 | 9 m3 |
| V8 | 250 m3 | SOL1 | 260 units |
| V10 | 250 m3 | SOL2 | 390 units |
| No Heat- Integration | With Heat- Integration | ||
|---|---|---|---|
| Profit (c.u. 103) | +19% | 21,009 | 24,890 |
| External utilities | |||
| Water (kWh) | −61% | 1565 | 609 |
| Steam (kWh) | −77% | 1674 | 387 |
| Model statistics | |||
| CPU time (s) | 0.62 | 180 | |
| Int. Variables | 95 | 324 | |
| Constraints | 628 | 3333 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simão, P.; Vieira, M.; Pinto, T.; Pinto-Varela, T. Design and Operation of Multipurpose Production Facilities Using Solar Energy Sources for Heat Integration Sustainable Strategies. Mathematics 2022, 10, 1941. https://doi.org/10.3390/math10111941
Simão P, Vieira M, Pinto T, Pinto-Varela T. Design and Operation of Multipurpose Production Facilities Using Solar Energy Sources for Heat Integration Sustainable Strategies. Mathematics. 2022; 10(11):1941. https://doi.org/10.3390/math10111941
Chicago/Turabian StyleSimão, Pedro, Miguel Vieira, Telmo Pinto, and Tânia Pinto-Varela. 2022. "Design and Operation of Multipurpose Production Facilities Using Solar Energy Sources for Heat Integration Sustainable Strategies" Mathematics 10, no. 11: 1941. https://doi.org/10.3390/math10111941
APA StyleSimão, P., Vieira, M., Pinto, T., & Pinto-Varela, T. (2022). Design and Operation of Multipurpose Production Facilities Using Solar Energy Sources for Heat Integration Sustainable Strategies. Mathematics, 10(11), 1941. https://doi.org/10.3390/math10111941







