Towards the Sign Function Best Approximation for Secure Outsourced Computations and Control
Abstract
:1. Introduction
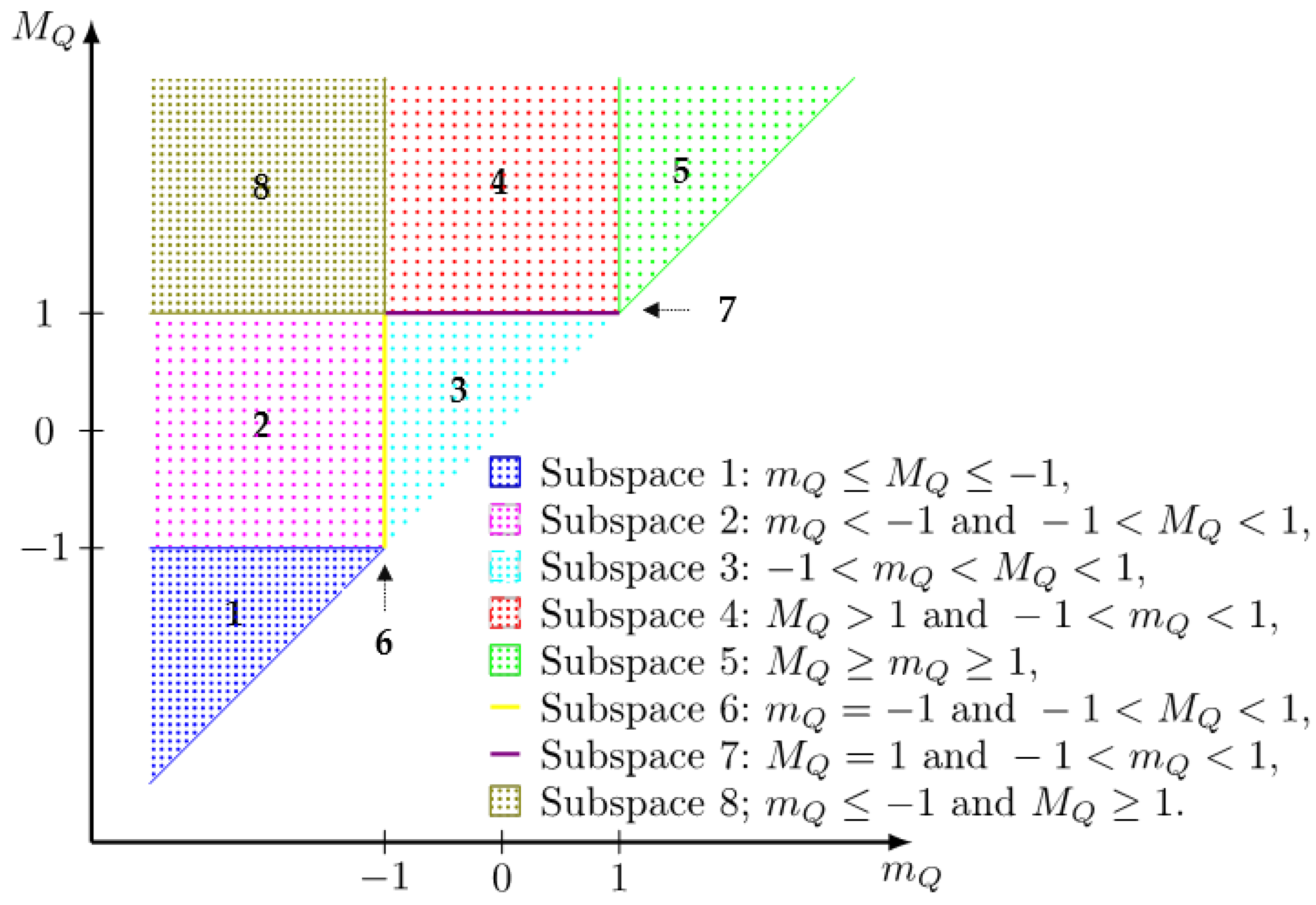
2. Norm and Its Properties
- (a)
- Calculate; if, then.
- (b)
- Calculate; if, then.
3. Approximation of the Sign Function by Bernstein Polynomials
4. Properties of the PBAS
5. The Number of PBAS Odd Functions
6. The Number of PBAS of the Neither Function
- 1.
- Ifis an odd number, then there is no PBAS.
- 2.
- Ifis an even number, then there is an infinite number of PBAS.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cheon, J.H.; Kim, D.; Kim, D.; Lee, H.H.; Lee, K. Numerical Method for Comparison on Homomorphically Encrypted Numbers. Lect. Notes Comput. Sci. 2019, 11922, 415–445. [Google Scholar] [CrossRef]
- Cheon, J.H.; Kim, D.; Kim, D. Efficient Homomorphic Comparison Methods with Optimal Complexity. Lect. Notes Comput. Sci. 2020, 12492, 221–256. [Google Scholar]
- Chen, H.; Chillotti, I.; Song, Y. Improved Bootstrapping for Approximate Homomorphic Encryption. Lect. Notes Comput. Sci. 2019, 11477, 34–54. [Google Scholar]
- Han, K.; Ki, D. Better bootstrapping for approximate homomorphic encryption. Lect. Notes Comput. Sci. 2020, 12006, 364–390. [Google Scholar] [CrossRef]
- Boura, C.; Gama, N.; Georgieva, M. Chimera: A unified framework for B/FV, TFHE and HEAAN fully homomorphic encryption and predictions for deep learning. IACR Cryptol. ePrint Arch. 2018, 2018, 758. [Google Scholar]
- Gilad-Bachrach, R.; Dowlin, N.; Laine, K.; Lauter, K.; Naehrig, M.; Wernsing, J. Cryptonets: Applying neural networks to encrypted data with high throughput and accuracy. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; Volume 48, pp. 201–210. Available online: http://proceedings.mlr.press/v48/gilad-bachrach16.pdf (accessed on 10 April 2022).
- Kim, M.; Song, Y.; Wang, S.; Xia, Y.; Jiang, X. Secure logistic regression based on homomorphic encryption: Design and evaluation. JMIR Med. Inform. 2018, 6, e19. [Google Scholar] [CrossRef] [PubMed]
- Bonte, C.; Vercauteren, F. Privacy-preserving logistic regression training. BMC Med. Genom. 2018, 11, 86. [Google Scholar] [CrossRef] [PubMed]
- Kim, A.; Song, Y.; Kim, M.; Lee, K.; Cheon, J.H. Logistic regression model training based on the approximate homomorphic encryption. BMC Med. Genom. 2018, 11, 83. [Google Scholar] [CrossRef] [PubMed]
- Bajard, J.-C.; Martins, P.; Sousa, L.; Zucca, V. Improving the Efficiency of SVM Classification with FHE. IEEE Trans. Inf. Forensics Secur. 2019, 15, 1709–1722. [Google Scholar] [CrossRef]
- Bakhvalov, N.S.; Zhidkov, N.P.; Kobelkov, G.M. Numerical Methods; Nauka: Moscow, Russia, 1987; p. 600. [Google Scholar]
- Korkine, A.; Zolotareff, G. Sur un certain minimum. Nouv. Ann. Mathématiques J. Candidats Écoles Polytech. Norm. 1873, 12, 337–355. Available online: http://www.numdam.org/item/NAM_1873_2_12__337_0/ (accessed on 7 November 2019).
- Zygmund, A. Trigonometric Series; Cambridge University Press: New York, NY, USA, 2002; Volume 1, p. 375. [Google Scholar]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics; Addison-Wesley Publishing Company: Reading, MA, USA, 1994; p. 625. [Google Scholar]
- Tchernykh, A.; Babenko, M.; Chervyakov, N.; Miranda-Lopez, V.; Avetisyan, A.; Drozdov, A.Y.; Rivera-Rodriguez, R.; Radchenko, G.; Du, Z. Scalable Data Storage Design for Nonstationary IoT Environment with Adaptive Security and Reliability. IEEE Internet Things J. 2020, 7, 10171–10188. [Google Scholar] [CrossRef]
- Pulido-Gaytan, B.; Tchernykh, A.; Cortés-Mendoza, J.M.; Babenko, M.; Radchenko, G.; Avetisyan, A.; Drozdov, A.Y. Privacy-preserving neural networks with Homomorphic encryption: Challenges and opportunities. Peer-to-Peer Netw. Appl. 2021, 14, 1666–1691. [Google Scholar] [CrossRef]
- Babenko, M.; Tchernykh, A.; Chervyakov, N.; Kuchukov, V.; Miranda-López, V.; Rivera-Rodriguez, R.; Du, Z.; Talbi, E.-G. Positional Characteristics for Efficient Number Comparison over the Homomorphic Encryption. Program. Comput. Softw. 2019, 45, 532–543. [Google Scholar] [CrossRef]
- Cortes-Mendoza, J.M.; Radchenko, G.; Tchernykh, A.; Pulido-Gaytan, B.; Babenko, M.; Avetisyan, A.; Bouvry, P.; Zomaya, A. LR-GD-RNS: Enhanced Privacy-Preserving Logistic Regression Algorithms for Secure Deployment in Untrusted Environments. In Proceedings of the 2021 IEEE/ACM 21st International Symposium on Cluster, Cloud and Internet Computing (CCGrid), Melbourne, Australia, 10–13 May 2021; IEEE: Melbourne, Australia, 2021; pp. 770–775. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babenko, M.; Tchernykh, A.; Pulido-Gaytan, B.; Avetisyan, A.; Nesmachnow, S.; Wang, X.; Granelli, F. Towards the Sign Function Best Approximation for Secure Outsourced Computations and Control. Mathematics 2022, 10, 2006. https://doi.org/10.3390/math10122006
Babenko M, Tchernykh A, Pulido-Gaytan B, Avetisyan A, Nesmachnow S, Wang X, Granelli F. Towards the Sign Function Best Approximation for Secure Outsourced Computations and Control. Mathematics. 2022; 10(12):2006. https://doi.org/10.3390/math10122006
Chicago/Turabian StyleBabenko, Mikhail, Andrei Tchernykh, Bernardo Pulido-Gaytan, Arutyun Avetisyan, Sergio Nesmachnow, Xinheng Wang, and Fabrizio Granelli. 2022. "Towards the Sign Function Best Approximation for Secure Outsourced Computations and Control" Mathematics 10, no. 12: 2006. https://doi.org/10.3390/math10122006
APA StyleBabenko, M., Tchernykh, A., Pulido-Gaytan, B., Avetisyan, A., Nesmachnow, S., Wang, X., & Granelli, F. (2022). Towards the Sign Function Best Approximation for Secure Outsourced Computations and Control. Mathematics, 10(12), 2006. https://doi.org/10.3390/math10122006









