Modified SHARK Cipher and Duffing Map-Based Cryptosystem
Abstract
:1. Introduction
1.1. Literature Review
1.2. Contribution
- Introducing an efficient cryptosystem based on a mix of chaos and a modified SHARK cipher encryption.
- The proposed system uses a structure of SPN with plaintext-dependent random keys generated from the duffing chaotic map.
- The technique employs numerous phases to achieve extremely random sequencing with minimal correlation.
- Examining and comparing several present state-of-the-art procedures with the offered cryptosystem.
- The proposed scheme is investigated thoroughly using various tests, i.e., histogram, information entropy, peak signal to noise ratio (PSNR), mean squared error (MSE), unified average changing intensity (UACI), number of pixels changing rate (NPCR), National Institute of Standard and Technology (NIST), chi-square analysis, correlation coefficient, and computational complexity analysis.
2. Modified SHARK Algorithm
- Confusion Layer.
- Diffusion Layer.
- Key generation for each round.
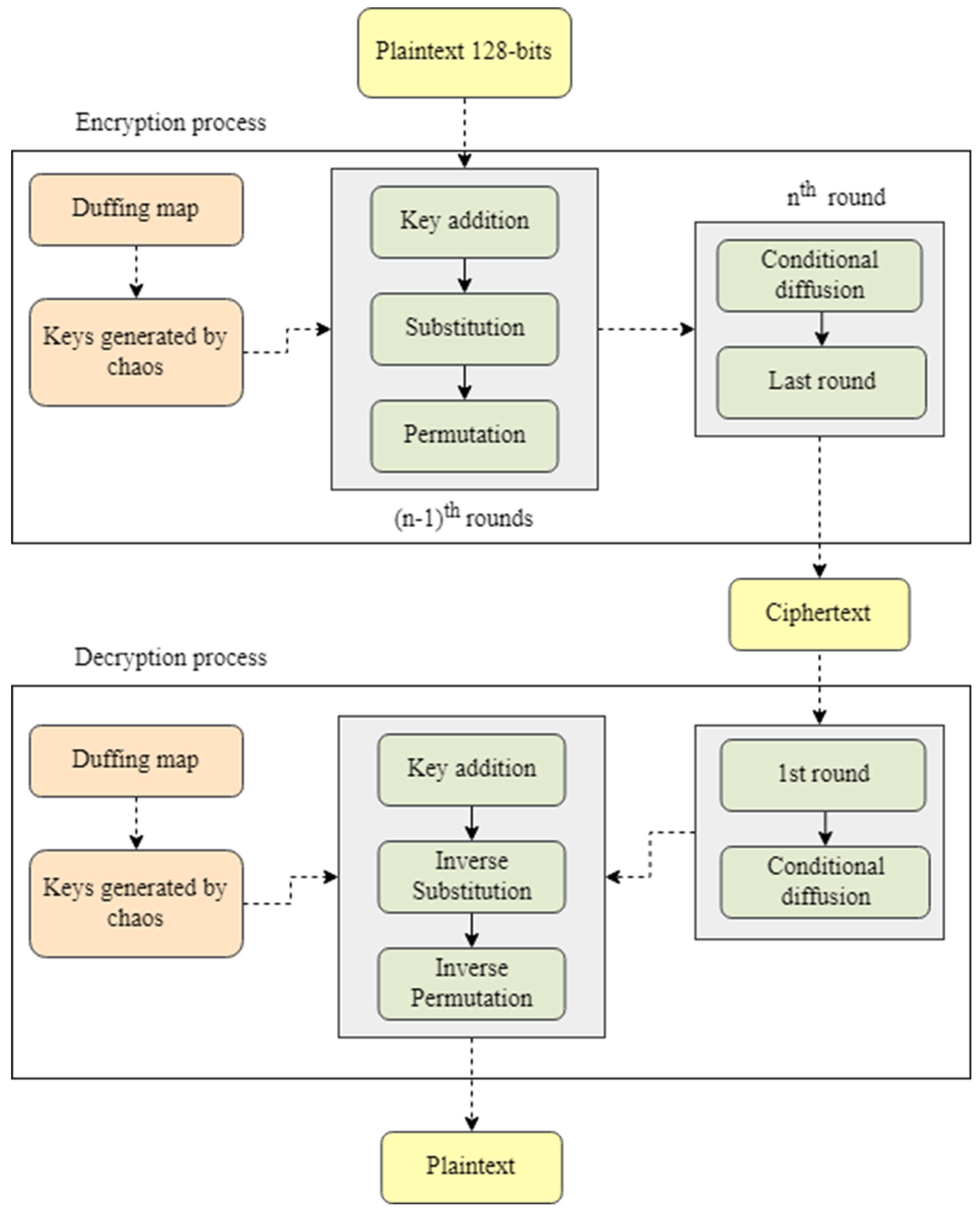
3. Offered Encryption Algorithm
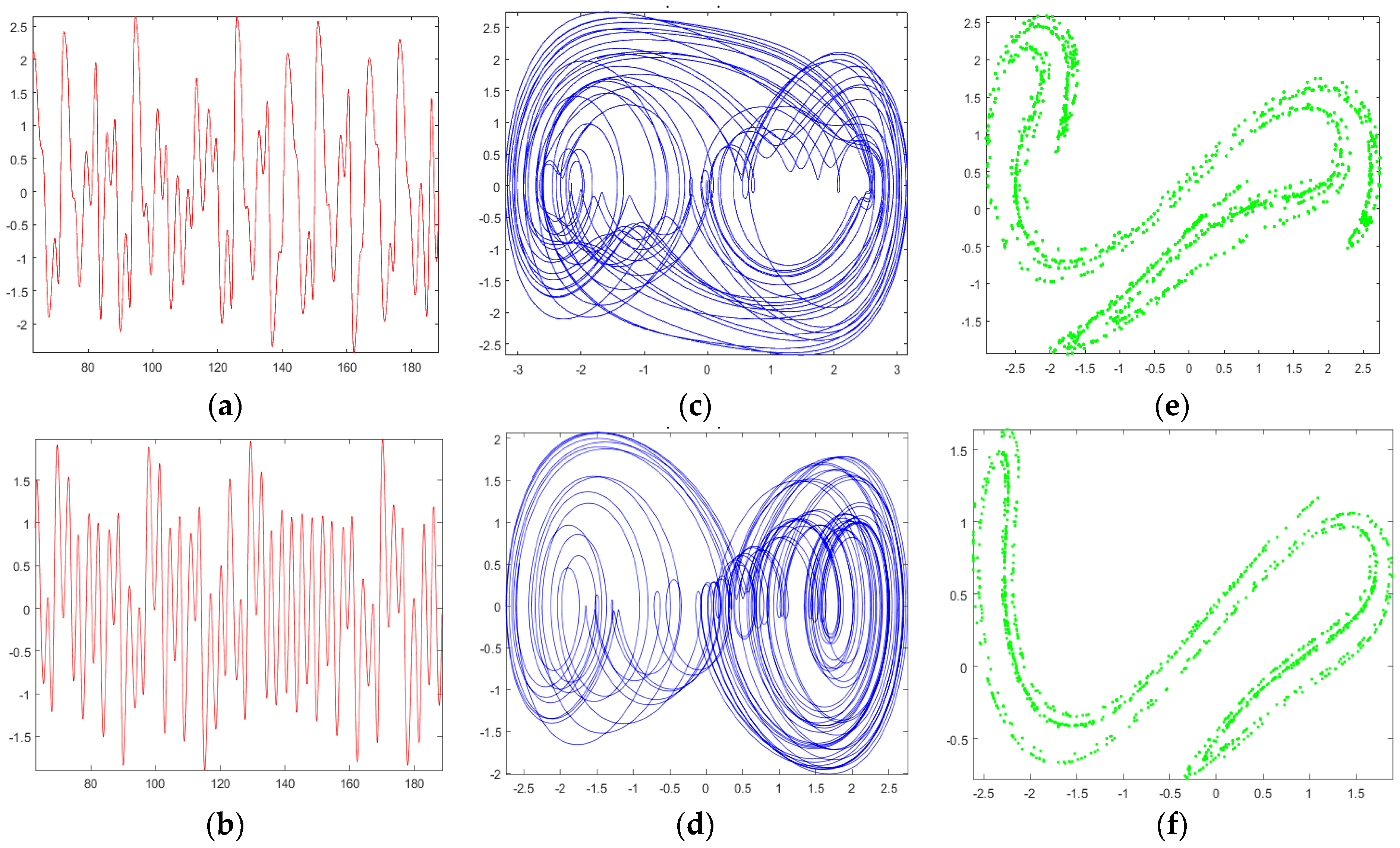
3.1. Key Generation
3.2. Encryption Procedure
- Step 1
- The data matrix of the plaintext image is signified by , and it is read to be encrypted. The image size, which is the number of pixel rows and the number of pixel columns , is obtained. There are pixels in the first row and pixels in the first column, hence is equal to the sum of these values, .
- Step 2
- The initial keys of the duffing map are constructed by seeding the input image in Equations (1) and (2). Then after getting , the private keys of the encryption algorithm are generated from the duffing map.
- Step 3
- The modified SHARK algorithm with the SPN (Substitution Permutation Network) structure is applied to the input data. The first (n − 1) rounds are kept the same as the original SHARK cipher with a different encryption key.
- Step 4
- Before the last round of the modified SHARK cipher, a conditional diffusion algorithm is applied as:where is the encrypted matrix obtained after (n − 1) rounds of the modified SHARK cipher, and and are the substitution and permutation keys of the system, respectively.
- Step 5
- The last round of the SHARK cipher is applied on the cipher image obtained from step 4 and then complied as the encrypted image.
3.3. Decryption Procedure
- Step 1
- The inverse of the last round of SHARK cipher is applied to the encrypted image, which includes inverse permutations, inverse substitution, and key XOR.
- Step 2
- The image data obtained from step 1 is then passed from the conditional shift algorithm in which the key used for encryption is utilized to decrypt whether it is or , where the selection of these keys is entirely made by using Equation (4).
- Step 3
- The next (n − 1) rounds are implemented on the image attained from step 2. The inverse of each operation, permutation, substitution, and key addition are utilized for (n − 1) times to get the original data.
4. Security Analysis and Numerical Results
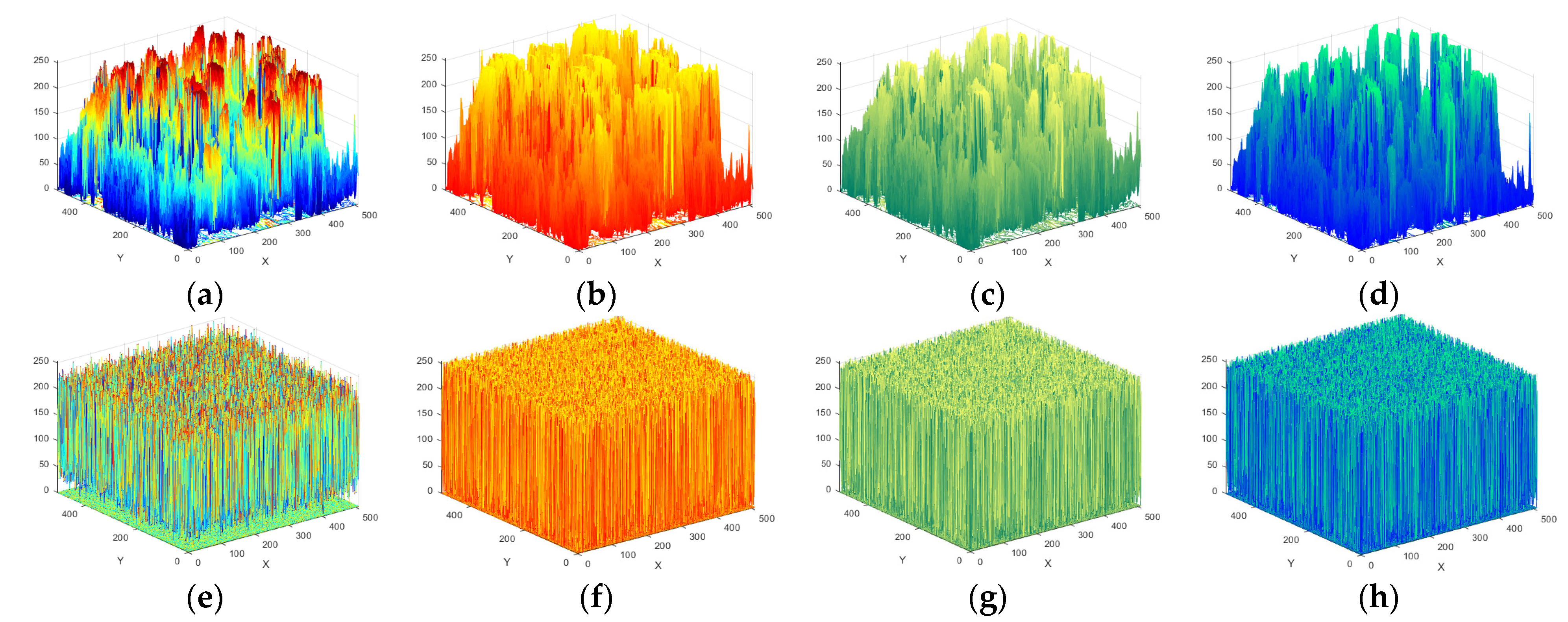
4.1. Histogram Analysis
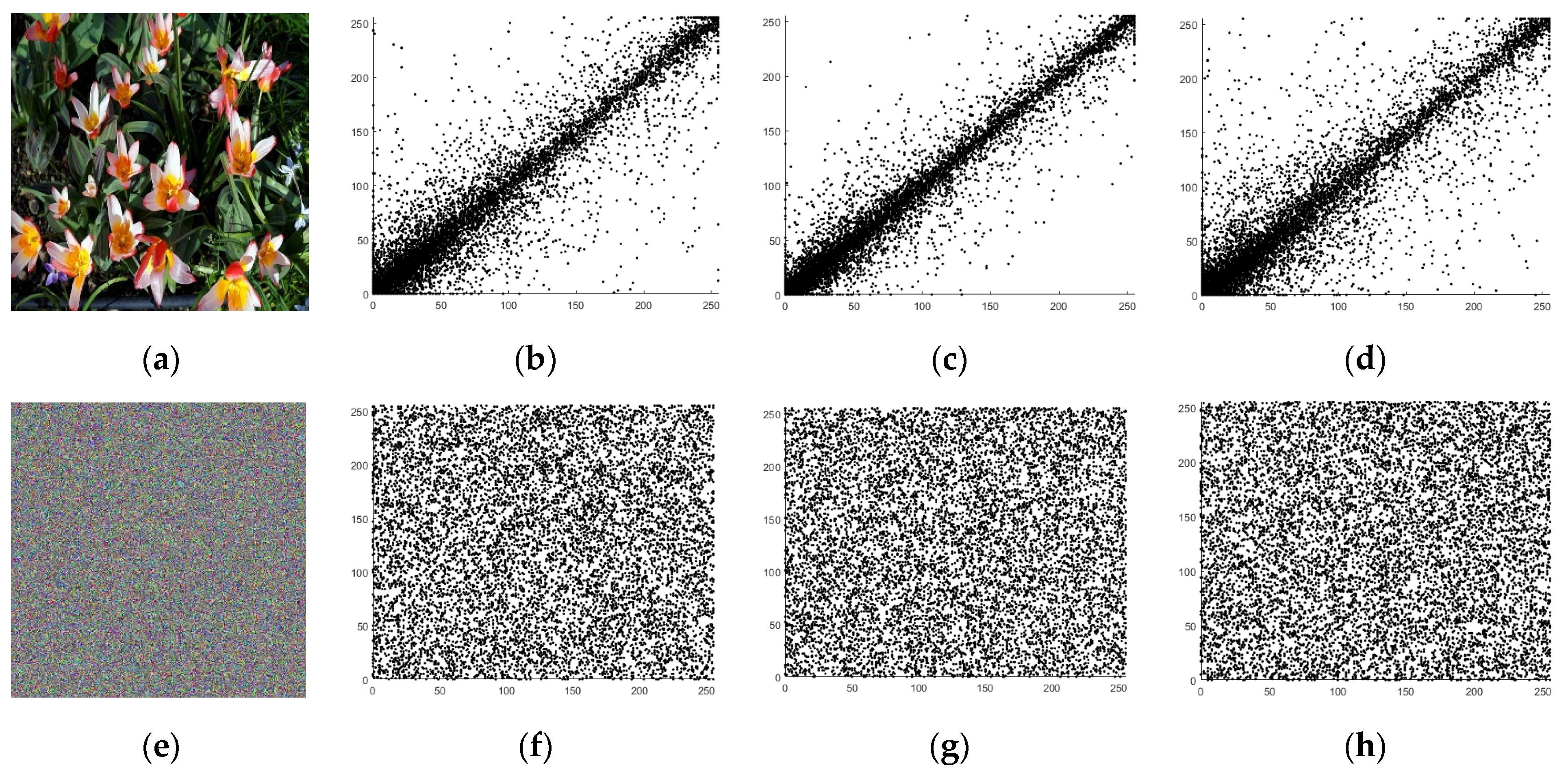
4.2. Correlation
4.3. Entropy
4.4. Ciphertext Sensitivity Analysis
4.5. Mean Squared Error and Peak Signal to Noise Ratio
4.6. NIST
4.7. Security against Brute Force Attack
4.8. Cropped Attack
4.9. Execution Time Analysis
4.10. Classical Cryptanalysis Attacks
5. Comparative Analysis
6. Conclusions and Future Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Advanced Encryption Standard (AES). Federal Information Processing Standards. 26 November 2001. Available online: https://www.nist.gov/publications/advanced-encryption-standard-aes (accessed on 25 May 2022). [CrossRef]
- Tuchman, W. A brief history of the data encryption standard. In Internet Besieged: Countering Cyberspace Scofflaws; ACM Press/Addison-Wesley Publishing Co.: New York, NY, USA, 1997; pp. 275–280. [Google Scholar]
- Rivest, R.; Shamir, A.; Adleman, L. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Pareek, N.K.; Patidar, V.; Sud, K.K. Image encryption using chaotic logistic map. Image. Vis. Comput. 2006, 24, 926–934. [Google Scholar] [CrossRef]
- Gao, Z.; Chen, D.; Zhang, W.; Cai, S. Colour image encryption algorithm using one-time key and FrFT. IET Image Process. 2018, 12, 472–478. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Zhang, Y.; Luo, C. A one-time pad color image cryptosystem based on SHA-3 and multiple chaotic systems. Opt. Lasers Eng. 2018, 103, 1–8. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Pun, C.M.; Chen, C.P. 2D Sine Logistic modulation map for image encryption. Inf. Sci. 2015, 297, 80–94. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, Y.; Song, Y. 2D logistic-modulated-sine-coupling-logistic chaotic map for image encryption. IEEE Access 2019, 7, 14081–14098. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.; Wang, N.; Zhu, L.; Chen, M.; Bao, B. Initials-Boosted Coexisting Chaos in a 2D Sine Map and Its Hardware Implementation. IEEE Trans. Ind. Inform. 2020, 17, 1132–1140. [Google Scholar] [CrossRef]
- Gao, X. A color image encryption algorithm based on an improved Hénon map. Phys. Scr. 2021, 96, 065203. [Google Scholar] [CrossRef]
- Assad, S.E.; Farajallah, M. A New chaos-based image encryption system. Signal Process. Image Commun. 2016, 41, 144–157. [Google Scholar] [CrossRef]
- Li, C.; Luo, G.; Qin, K.; Li, C. An image encryption scheme based on chaotic tent map. Nonlinear Dyn. 2017, 87, 127–133. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X. Multiple-image encryption algorithm based on mixed image element and chaos. Comput. Electr. Eng. 2017, 62, 401–413. [Google Scholar] [CrossRef]
- Li, C.; Lin, D.; Feng, B.; Lü, J.; Hao, F. Cryptanalysis of a Chaotic Image Encryption Algorithm Based on Information Entropy. IEEE Access 2018, 6, 75834–75842. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, G.; Sun, K. Improved Cryptanalysis and Enhancements of an Image Encryption Scheme Using Combined 1D Chaotic Maps. Entropy 2018, 20, 843. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.; Quan, C.; Tay, C.J. Multiple image encryption scheme based on pixel exchange operation and vector decomposition. Opt. Lasers Eng. 2018, 101, 113–121. [Google Scholar] [CrossRef]
- Mishra, D.C.; Sharma, R.K.; Suman, S.; Prasad, A. Multi-layer security of color image based on chaotic system combined with RP2DFRFT and Arnold Transform. J. Inf. Secur. Appl. 2017, 37, 65–90. [Google Scholar] [CrossRef]
- Chai, X. An image encryption algorithm based on bit level Brownian motion and new chaotic systems. Multi. Tools Apps. 2015, 76, 1159–1175. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S. A new image encryption algorithm based on logistic chaotic map with varying parameter. SpringerPlus 2016, 5, 289. [Google Scholar] [CrossRef]
- Ye, G.; Huang, X. A secure image encryption algorithm based on chaotic maps and SHA-3. Secur. Commun. Networks 2016, 9, 2015–2023. [Google Scholar] [CrossRef]
- Lian, S. Efficient image or video encryption based on spatiotemporal chaos system. Chaos Solitons Fractals 2009, 40, 2509–2519. [Google Scholar] [CrossRef]
- Ye, G.; Huang, X. An efficient symmetric image encryption algorithm based on an intertwining logistic map. Neurocomputing 2017, 251, 45–53. [Google Scholar] [CrossRef]
- Ye, G.; Pan, C.; Huang, X.; Zhao, Z.; He, J. A Chaotic Image Encryption Algorithm Based on Information Entropy. Int. J. Bifurc. Chaos 2018, 28, 1850010. [Google Scholar] [CrossRef]
- Solak, E.; Çokal, C.; Yildiz, O.T.; Bíyíkoglu, T. Cryptanalysis of Fridrich’s Chaotic Image Encryption. Int. J. Bifurc. Chaos 2010, 20, 1405–1413. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Huang, H. Cosine-transform-based chaotic system for image encryption. Inf. Sci. 2019, 480, 403–419. [Google Scholar] [CrossRef]
- Kumar, C.M.; Vidhya, R.; Brindha, M. An efficient chaos based image encryption algorithm using enhanced thorp shuffle and chaotic convolution function. Appl. Intell. 2022, 52, 2556–2585. [Google Scholar] [CrossRef]
- Xiao, S.; Yu, Z.; Deng, Y. Design and Analysis of a Novel Chaos-Based Image Encryption Algorithm via Switch Control Mechanism. Secur. Commun. Netw. 2020, 2020, 7913061. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C.; Tan, W.; Li, L. A Novel Chaos-Based Image Encryption Scheme by Using Randomly DNA Encode and Plaintext Related Permutation. Appl. Sci. 2020, 10, 7469. [Google Scholar] [CrossRef]
- Arif, J.; Khan, M.A.; Ghaleb, B.; Ahmad, J.; Munir, A.; Rashid, U.; Al-Dubai, A. A Novel Chaotic Permutation-Substitution Image Encryption Scheme Based on Logistic Map and Random Substitution. IEEE Access 2022, 10, 12966–12982. [Google Scholar] [CrossRef]
- Rijmen, V.; Daemen, J.; Preneel, B.; Bosselaers, A.; Win, E.D. The Cipher SHARK. In Fast Software Encryption, Proceedings of the 3rd International Workshop on Fast Software Encryption (FSE ‘96), Cambridge, UK, 21–23 February 1996; Springer: Berlin/Heidelberg, Germany, 1996; pp. 99–111. [Google Scholar]
- Jakobsen, T.P.; Knudsen, L.R. The Interpolation Attack on Block Ciphers. In Fast Software Encryption, Proceedings of the 4th International Workshop on Fast Software Encryption (FSE ‘97), Haifa, Israel, 20–22 January 2017; Springer: Berlin/Heidelberg, Germany, 1997; pp. 28–40. [Google Scholar]
- Alexan, W.; ElBeltagy, M.; Aboshousha, A. RGB Image Encryption through Cellular Automata, S-Box and the Lorenz System. Symmetry 2022, 14, 443. [Google Scholar] [CrossRef]
- Abduljabbar, Z.A.; Abduljaleel, I.Q.; Ma, J.; Sibahee, M.A.; Nyangaresi, V.O.; Honi, D.G.; Abdulsada, A.I.; Jiao, X. Provably Secure and Fast Color Image Encryption Algorithm Based on S-Boxes and Hyperchaotic Map. IEEE Access 2022, 10, 26257–26270. [Google Scholar] [CrossRef]
- Al-Mashhadi, H.M.; Abduljaleel, I.Q. Color image encryption using chaotic maps, triangular scrambling, with DNA sequences. In Proceedings of the 2017 International Conference on Current Research in Computer Science and Information Technology (ICCIT), Sulaymaniyah, Iraq, 26–27 April 2017; pp. 93–98. [Google Scholar]
- Wang, X.; Su, Y.; Luo, C.; Nian, F.; Teng, L. Color image encryption algorithm based on hyperchaotic system and improved quantum revolving gate. Multim. Tools Appl. 2022, 81, 13845–13865. [Google Scholar] [CrossRef]


| p Values for Each Chaotic Sequences | Status | |||
|---|---|---|---|---|
| Analysis | X | Y | Z | |
| Frequency | 0.1153 | 0.5961 | 0.1174 | √ |
| Block-frequency | 0.9631 | 0.8963 | 0.9654 | √ |
| Runs | 0.6884 | 0.1547 | 0.0947 | √ |
| Universal | 0.9974 | 0.5187 | 0.3349 | √ |
| Block-frequency | 0.0101 | 0.9962 | 0.8585 | √ |
| Overlapping | 0.8114 | 0.8114 | 0.8114 | √ |
| Spectral DFT | 0.0114 | 0.4477 | 0.1593 | √ |
| No overlapping | 0.8962 | 0.7954 | 0.7426 | √ |
| Universal | 0.9901 | 0.9987 | 0.9963 | √ |
| Cumulative sums forward | 0.0036 | 0.0147 | 0.0852 | √ |
| Approximate entropy | 0.5253 | 0.4468 | 0.8991 | √ |
| Cumulative sums reverse | 0.7845 | 0.6650 | 0.6701 | √ |
| Original Image | Enciphered Image | |||||
|---|---|---|---|---|---|---|
| Image | Horizontal | Vertical | Diagonal | Horizontal | Vertical | Diagonal |
| Splash | 0.9674 | 0.9559 | 0.9793 | 0.0002 | 0.0090 | −0.0010 |
| Baboon | 0.9514 | 0.9221 | 0.8704 | −0.0014 | −0.0038 | 0.0007 |
| Parrots | 0.9985 | 0.9561 | 0.8991 | −0.0016 | −0.0009 | −0.0027 |
| Peppers | 0.8974 | 0.7354 | 0.6358 | −0.0008 | 0.0015 | −0.0011 |
| Tulips | 0.9325 | 0.7892 | 0.8967 | 0.0010 | −0.0011 | −0.0138 |
| Image | Layers | Original | Encrypted |
|---|---|---|---|
| Splash | Red | 6.9481 | 7.9986 |
| Green | 6.8845 | 7.9991 | |
| Blue | 6.1265 | 7.9998 | |
| Baboon | Red | 7.7379 | 7.9989 |
| Green | 7.4608 | 7.9994 | |
| Blue | 7.7683 | 7.9998 | |
| Parrots | Red | 7.5458 | 7.9999 |
| Green | 7.5669 | 7.9987 | |
| Blue | 7.3757 | 7.9998 | |
| Peppers | Red | 7.3388 | 7.9997 |
| Green | 7.4963 | 7.9988 | |
| Blue | 7.0583 | 7.9996 | |
| Tulips | Red | 7.4734 | 7.9991 |
| Green | 7.6001 | 7.9978 | |
| Blue | 6.8581 | 7.9997 |
| Test | Image | Result |
|---|---|---|
| NPCR | Splash | 99.6374 |
| Baboon | 99.5815 | |
| Parrots | 99.6016 | |
| Peppers | 99.6125 | |
| Tulips | 99.5925 | |
| UACI | Splash | 33.3478 |
| Baboon | 33.1709 | |
| Parrots | 33.8935 | |
| Peppers | 33.0369 | |
| Tulips | 33.5048 |
| Image | Layers | MSE | PSNR |
|---|---|---|---|
| Splash | Red | 8096.03 | 7.8521 |
| Green | 11,141.62 | 9.5126 | |
| Blue | 9110.45 | 8.5963 | |
| Baboon | Red | 9099.58 | 7.6363 |
| Green | 7048.36 | 7.5541 | |
| Blue | 8948.70 | 7.6999 | |
| Parrots | Red | 9945.10 | 8.9597 |
| Green | 10,635.56 | 8.9632 | |
| Blue | 8267.22 | 9.6358 | |
| Peppers | Red | 8578.69 | 8.9657 |
| Green | 7995.11 | 7.5294 | |
| Blue | 8328.01 | 8.4007 | |
| Tulips | Red | 9336.17 | 9.1148 |
| Green | 11,014.77 | 9.6557 | |
| Blue | 10,478.50 | 7.0041 |
| p Values for Each Layer of the Enciphered Image | Status | |||
|---|---|---|---|---|
| Analysis | R | G | B | |
| Frequency | 0.0035 | 0.2563 | 0.0745 | √ |
| Block-frequency | 0.0895 | 0.0579 | 0.3405 | √ |
| Runs | 0.7985 | 0.1029 | 0.3636 | √ |
| Long runs of ones | 0.0357 | 0.0357 | 0.0357 | √ |
| Universal | 0.9952 | 0.9978 | 0.9951 | √ |
| Block-frequency | 0.0895 | 0.0579 | 0.3405 | √ |
| Overlapping | 0.8114 | 0.8114 | 0.8114 | √ |
| Rank | 0.2919 | 0.2919 | 0.2919 | √ |
| Spectral DFT | 0.9383 | 0.0014 | 0.5742 | √ |
| No overlapping | 0.9963 | 0.9810 | 0.9983 | √ |
| Universal | 0.9952 | 0.9978 | 0.9951 | √ |
| Cumulative sums forward | 0.0369 | 0.2099 | 0.2274 | √ |
| Approximate entropy | 0.9630 | 0.9547 | 0.8770 | √ |
| Cumulative sums reverse | 0.8911 | 0.6010 | 0.8312 | √ |
| Image Size | Execution Time |
|---|---|
| 0.5211 | |
| 1.0084 | |
| 2.9961 | |
| 5.0018 |
| Analysis | Proposed | Ref. [32] | Ref. [33] | Ref. [34] | Ref. [35] |
|---|---|---|---|---|---|
| Keyspace | - | ||||
| NPCR | 99.612 | 99.59360 | 99.60937 | 99.63 | 99.5174 |
| UACI | 33.063 | 32.17523 | 33.83490 | 30.51 | 33.4682 |
| Entropy | 7.9993 | 7.99877 | 7.99890 | 7.95264 | 7.9965 |
| MSE | 8300.6 | 10,092.3 | - | - | 10,869.73 |
| PSNR | 8.2986 | 8.09089 | - | - | 7.7677 |
| Correlation | |||||
| Horizontal | 0.0015 | −0.00063 | −0.0020 | 0.0040 | −0.0015 |
| Diagonal | −0.0008 | −0.00003 | 0.00008 | −0.0016 | 0.0037 |
| Vertical | −0.0011 | −0.00102 | −0.0064 | −0.0015 | 0.0030 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabie, O.; Ahmad, J.; Alghazzawi, D. Modified SHARK Cipher and Duffing Map-Based Cryptosystem. Mathematics 2022, 10, 2034. https://doi.org/10.3390/math10122034
Rabie O, Ahmad J, Alghazzawi D. Modified SHARK Cipher and Duffing Map-Based Cryptosystem. Mathematics. 2022; 10(12):2034. https://doi.org/10.3390/math10122034
Chicago/Turabian StyleRabie, Osama, Jawad Ahmad, and Daniyal Alghazzawi. 2022. "Modified SHARK Cipher and Duffing Map-Based Cryptosystem" Mathematics 10, no. 12: 2034. https://doi.org/10.3390/math10122034
APA StyleRabie, O., Ahmad, J., & Alghazzawi, D. (2022). Modified SHARK Cipher and Duffing Map-Based Cryptosystem. Mathematics, 10(12), 2034. https://doi.org/10.3390/math10122034








