Wiener Process Effects on the Solutions of the Fractional (2 + 1)-Dimensional Heisenberg Ferromagnetic Spin Chain Equation
Abstract
:1. Introduction
2. Preliminaries
- is a continuous function for ,
- For is independent,
- has a normal distribution with variance and mean 0.
- ,
3. The Wave Equation of the SFSHFSCE
4. Analytical Solutions of the SFSHFSCE
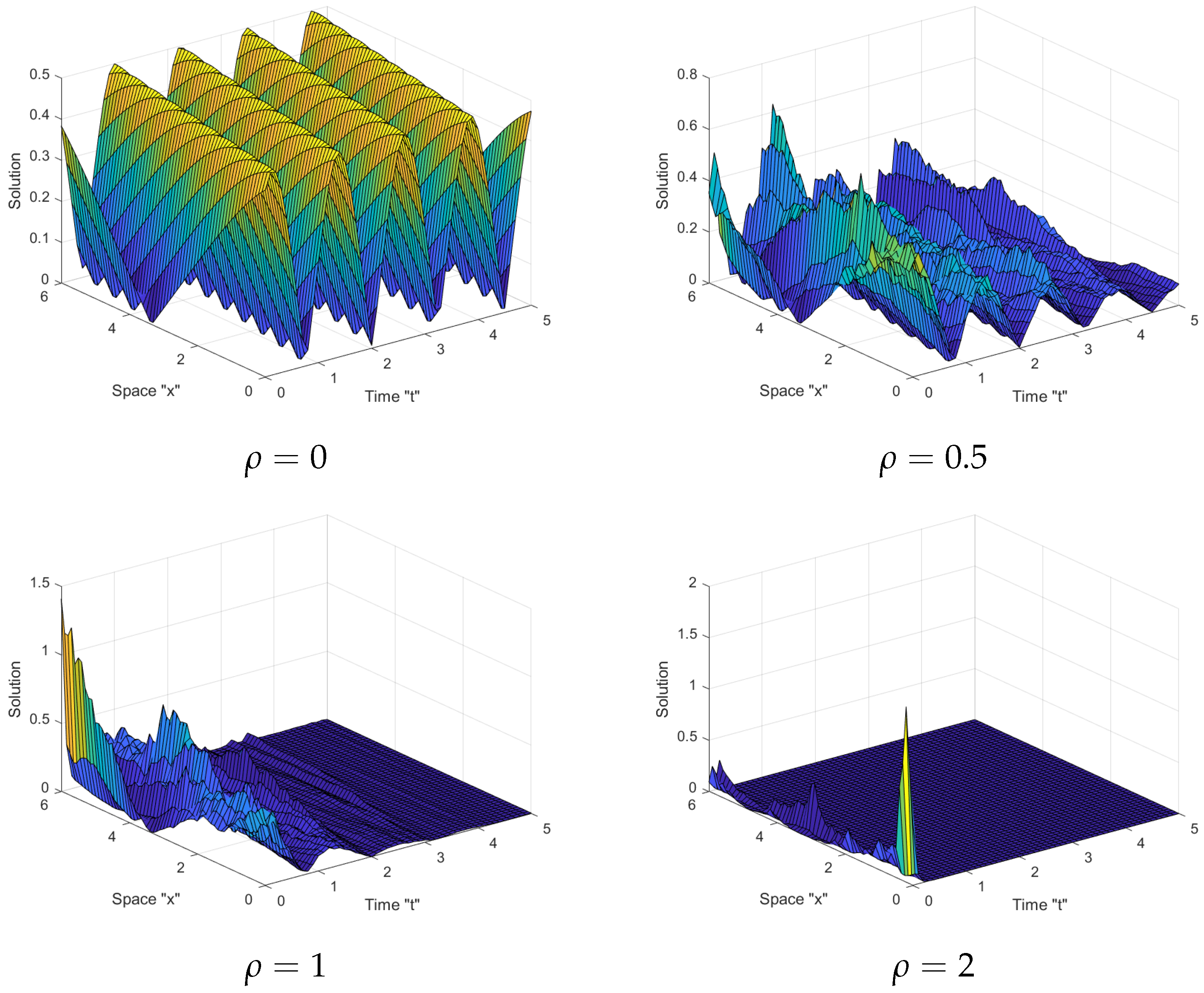
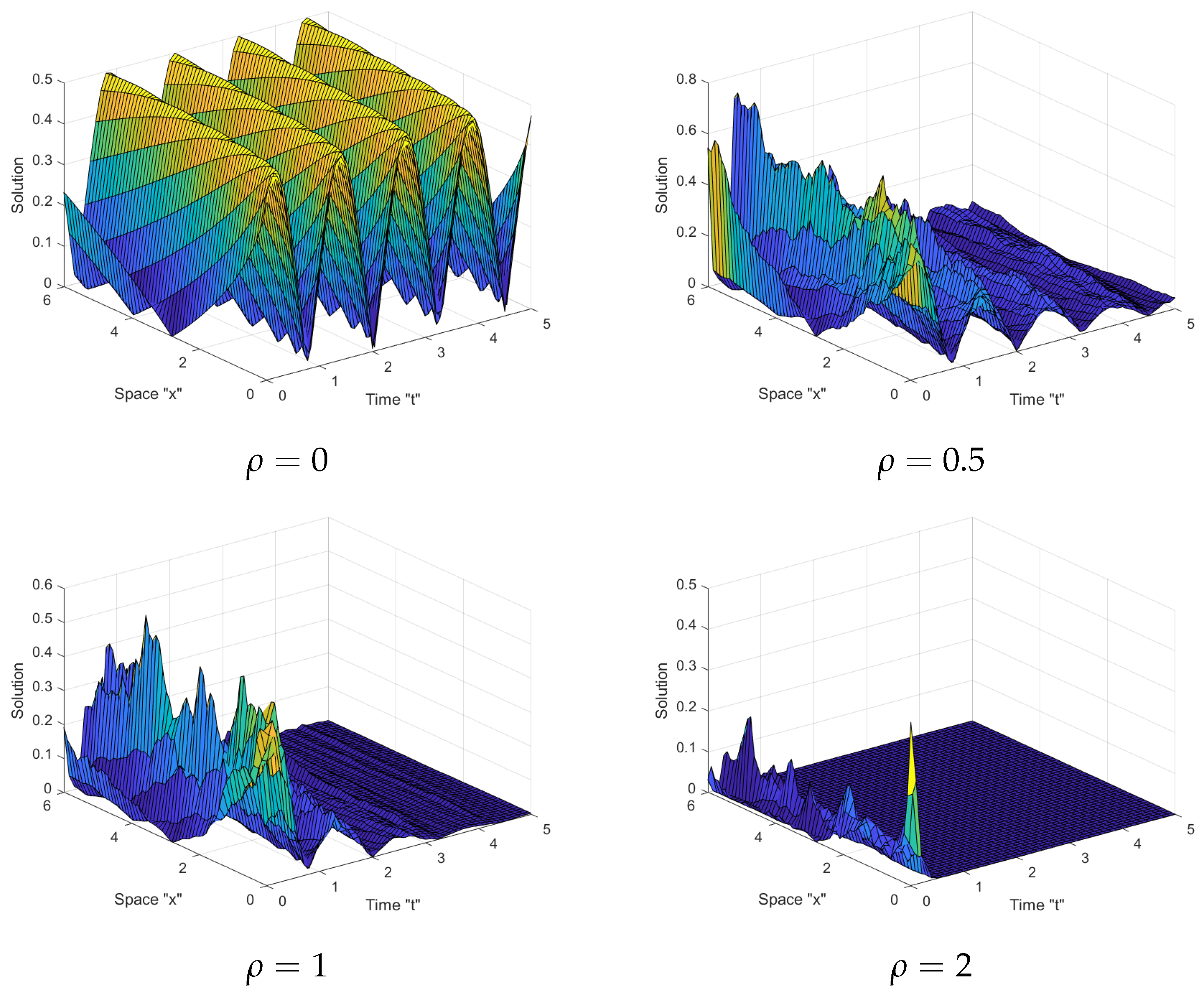
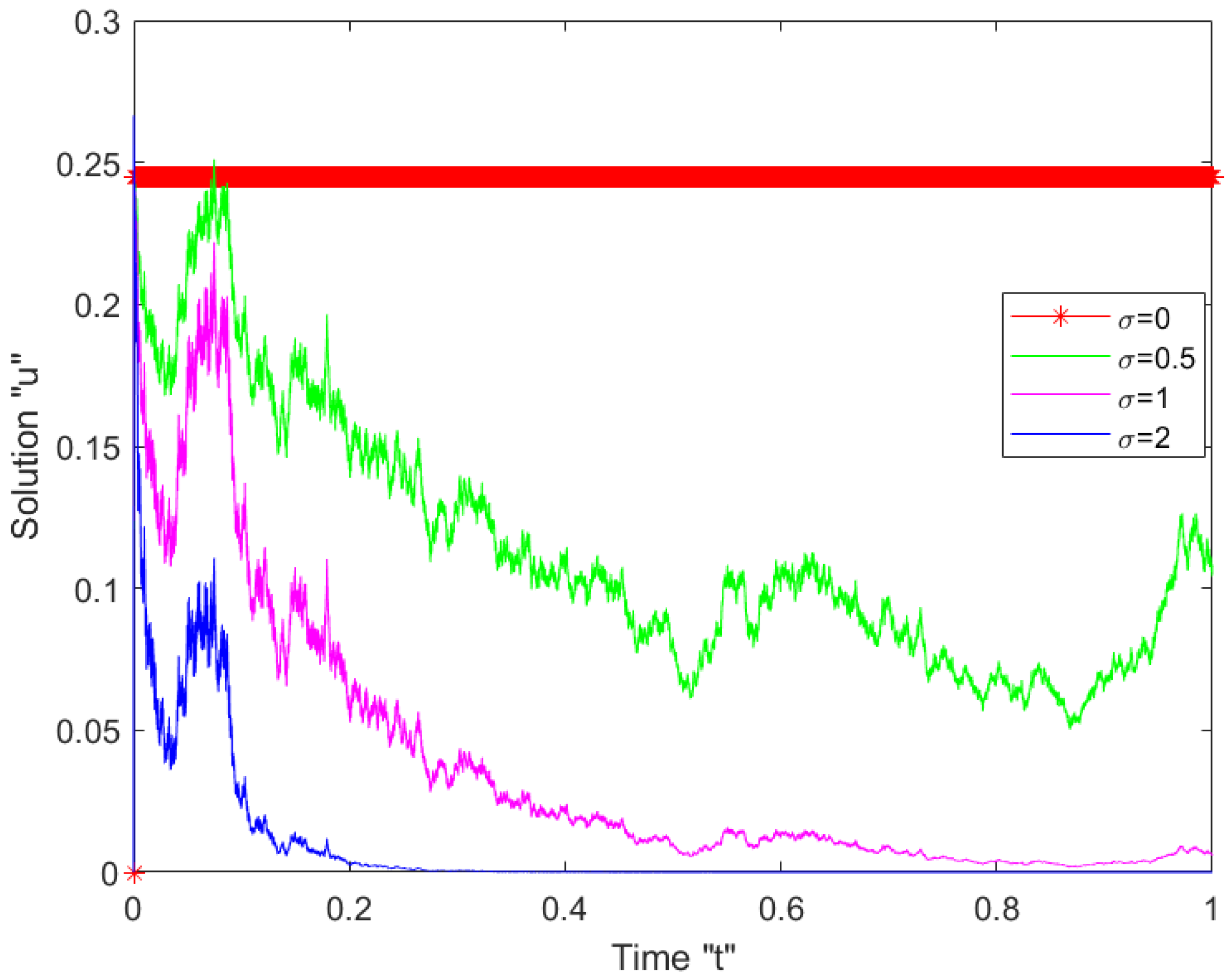
5. The Impact of Noise on the SFSHFSCE Solutions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, X.-F.; Deng, Z.-C.; Wei, Y. A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv. Differ. Equ. 2015, 1, 117. [Google Scholar] [CrossRef] [Green Version]
- Elmandouh, A.A. Bifurcation and new traveling wave solutions for the 2D Ginzburg–Landau equation. Eur. Phys. J. Plus 2020, 135, 648. [Google Scholar] [CrossRef]
- Elbrolosy, M.E.; Elmandouh, A.A. Bifurcation and new traveling wave solutions for (2 + 1)-dimensional nonlinear Nizhnik–Novikov–Veselov dynamical equation. Eur. Phys. J. Plus 2020, 135, 533. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. The tanh method: Exact solutions of the sine-Gordon and the sinh-Gordon equations. Appl. Math. Comput. 2005, 167, 1196–1210. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Mohammed, W.W.; Albalahi, A.M.; El-Morshedy, M. The Impact of the Wiener process on the analytical solutions of the stochastic (2 + 1)-dimensional breaking soliton equation by using tanh-coth method. Mathematics 2022, 10, 817. [Google Scholar] [CrossRef]
- Yan, Z.L. Abunbant families of Jacobi elliptic function solutions of the-dimensional integrable Davey-Stewartson-type equation via a new method. Chaos Solitons Fractals 2003, 18, 299–309. [Google Scholar] [CrossRef]
- Hirota, R. Exact Solution of the Korteweg-de Vries Equation for Multiple Collisions of Solitons. Phys. Rev. Lett. 1971, 27, 1192–1194. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M.A. The exp(-φ(ς))-expansion method for finding travelling wave solutions of Vakhnenko-Parkes equation. Int. J. Dyn. Syst. Differ. Equ. 2014, 5, 72–83. [Google Scholar]
- Mohammed, W.W. Fast-Diffusion Limit for Reaction–Diffusion Equations with Degenerate Multiplicative and Additive Noise. J. Dyn. Differ. Equ. 2020, 33, 577–592. [Google Scholar] [CrossRef]
- Mohammed, W.W. Approximate solutions for stochastic time-fractional reaction–diffusion equations with multiplicative noise. Math. Methods Appl. Sci. 2021, 44, 2140–2157. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Iqbal, N. Impact of the same degenerate additive noise on a coupled system of fractional space diffusion equations. Fractals 2022, 30, 2240033. [Google Scholar] [CrossRef]
- Wang, M.L.; Li, X.Z.; Zhang, J.L. The ()-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Zhang, H. New application of the ()-expansion method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3220–3225. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Alesemi, M.; Albosaily, S.; Iqbal, N.; El-Morshedy, M. The exact solutions of stochastic fractional-space Kuramoto-Sivashinsky equation by Using ()-expansion method. Mathematics 2021, 9, 2712. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A sine-cosine method for handling nonlinear wave equations. Math. Comput. Model. 2004, 40, 499–508. [Google Scholar] [CrossRef]
- Yan, C. The influence of noise on the solutions of fractional stochastic bogoyavlenskii equation. Fractal Fract. 2022, 6, 156. [Google Scholar]
- Seadawy, A.R.; Nasreen, N.; Lu, D.; Arshad, M. Arising wave propagation in nonlinear media for the (2 + 1)-dimensional Heisenberg ferromagnetic spin chain dynamical model. Phys. A 2020, 538, 122846. [Google Scholar] [CrossRef]
- Bulut, H.; Sulaiman, T.A.; Baskonus, H.M. Dark, bright and other soliton solutions to the Heisenberg ferromagnetic spin chain equation. Supperlatt. Microstruct. 2018, 123, 12–19. [Google Scholar] [CrossRef]
- Ma, Y.-L.; Li, B.-Q.; Fu, Y.-Y. A series of the solutions for the Heisenberg ferromagnetic spin chain equation. Math. Methods Appl. Sci. 2018, 41, 3316–3322. [Google Scholar] [CrossRef]
- Ling, L.M.; Liu, Q.P. Darboux transformation for a two-component derivative nonlinear schrödinger equation. J. Phys. A 2010, 43, 434023. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; He, J. Darboux transformation and positons of the inhomogeneous Hirota and the Maxwell-Bloch equation. Sci. China Ser. G Phys. Mech. Astron. 2014, 57, 898–907. [Google Scholar] [CrossRef]
- Ma, W.-X.; Zhang, Y.-J. Darboux transformations of integrable couplings and applications. Rev. Math. Phys. 2018, 30, 1850003. [Google Scholar] [CrossRef]
- Liu, D.Y.; Tian, B.; Jiang, Y.; Xie, X.Y.; Wu, X.Y. Analytic study on a (2 + 1)-dimensional nonlinear Schrödinger equation in the Heisenberg ferromagnetism. Comput. Math. Appl. 2016, 71, 2001–2007. [Google Scholar] [CrossRef]
- Zhao, X.H.; Tian, B.; Liu, D.Y.; Wu, X.Y.; Chai, J.; Guo, Y.J. Dark solitons interaction for a (2 +1)-dimensional nonlinear Schrödinger equation in the Heisenberg ferromagnetic spin chain. Supperlatt. Microstruct. 2016, 100, 587–595. [Google Scholar] [CrossRef]
- Wang, Q.M.; Gao, Y.T.; Su, C.Q.; Mao, B.Q.; Gao, Z.; Yang, J.W. Dark solitonic interaction and conservation laws for a higher-order (2 +1)-dimensional nonlinear Schrödinger-type equation in a Heisenberg ferromagnetic spin chain with bilinear and biquadratic interaction. Ann. Phys. 2015, 363, 440–456. [Google Scholar] [CrossRef]
- Osman, M.S.; Tariq, K.U.; Bekir, A.; Elmoasry, A.; Elazab, N.S.; Younis, M.; Abdel-Aty, M. Investigation of soliton solutions with different wave structures to the (2 + 1)-dimensional Heisenberg ferromagnetic spin chain equation. Commun. Theor. Phys. 2020, 72, 035002. [Google Scholar] [CrossRef]
- Triki, H.; Wazwaz, A.-M. New solitons and periodic wave solutions for the (2 + 1)-dimensional Heisenberg ferromagnetic spin chain equation. J. Electromagn. Waves Appl. 2016, 30, 788–794. [Google Scholar] [CrossRef]
- Rani, M.; Ahmed, N.; Dragomir, S.S.; Mohyud-Din, S.T. New travelling wave solutions to (2 + 1)-Heisenberg ferromagnetic spin chain equation using Atangana’s conformable derivative. Phys. Scr. 2021, 96, 094007. [Google Scholar] [CrossRef]
- Han, T.; Wen, J.; Li, Z.; Yuan, J. New traveling wave solutions for the (2 + 1)-dimensional Heisenberg ferromagnetic spin chain equation. Math. Probl. Eng. 2022, 2022, 1312181. [Google Scholar] [CrossRef]
- Hosseini, K.; Kaur, L.; Mirzazadeh, M.; Baskonus, H.M. 1-Soliton solutions of the (2 + 1)-dimensional Heisenberg ferromagnetic spin chain model with the beta time derivative. Opt. Quant. Electron. 2021, 53, 125. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Yasmeen, A.; Raza, N.; Althobaiti, S. Novel solitary waves for fractional (2 + 1)-dimensional Heisenberg ferromagnetic model via new extended generalized Kudryashov method. Phys. Scr. 2021, 96, 125240. [Google Scholar] [CrossRef]
- Hosseini, K.; Salahshour, S.; Mirzazadeh, M.; Ahmadian, A.; Baleanu, D.; Khoshrang, A. The (2 + 1)-dimensional Heisenberg ferromagnetic spin chain equation: Its solitons and Jacobi elliptic function solutions. Eur. Phys. J. Plus 2021, 136, 206. [Google Scholar] [CrossRef]
- Bashar, H.; Islam, S.R.; Kumar, D. Construction of traveling wave solutions of the (2 + 1)-dimensional Heisenberg ferromagnetic spin chain equation. Partial Differ. Equ. Appl. Math. 2021, 4, 100040. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: New York, NY, USA, 1995. [Google Scholar]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Higham, D.J. An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C.; Botmart, T.; El-Morshedy, M. Wiener Process Effects on the Solutions of the Fractional (2 + 1)-Dimensional Heisenberg Ferromagnetic Spin Chain Equation. Mathematics 2022, 10, 2043. https://doi.org/10.3390/math10122043
Mohammed WW, Al-Askar FM, Cesarano C, Botmart T, El-Morshedy M. Wiener Process Effects on the Solutions of the Fractional (2 + 1)-Dimensional Heisenberg Ferromagnetic Spin Chain Equation. Mathematics. 2022; 10(12):2043. https://doi.org/10.3390/math10122043
Chicago/Turabian StyleMohammed, Wael W., Farah M. Al-Askar, Clemente Cesarano, Thongchai Botmart, and M. El-Morshedy. 2022. "Wiener Process Effects on the Solutions of the Fractional (2 + 1)-Dimensional Heisenberg Ferromagnetic Spin Chain Equation" Mathematics 10, no. 12: 2043. https://doi.org/10.3390/math10122043
APA StyleMohammed, W. W., Al-Askar, F. M., Cesarano, C., Botmart, T., & El-Morshedy, M. (2022). Wiener Process Effects on the Solutions of the Fractional (2 + 1)-Dimensional Heisenberg Ferromagnetic Spin Chain Equation. Mathematics, 10(12), 2043. https://doi.org/10.3390/math10122043







