Fuzzy Fusion of Stereo Vision, Odometer, and GPS for Tracking Land Vehicles
Abstract
:1. Introduction
2. Materials and Methods
2.1. General Structure of Fuzzy Tracking System
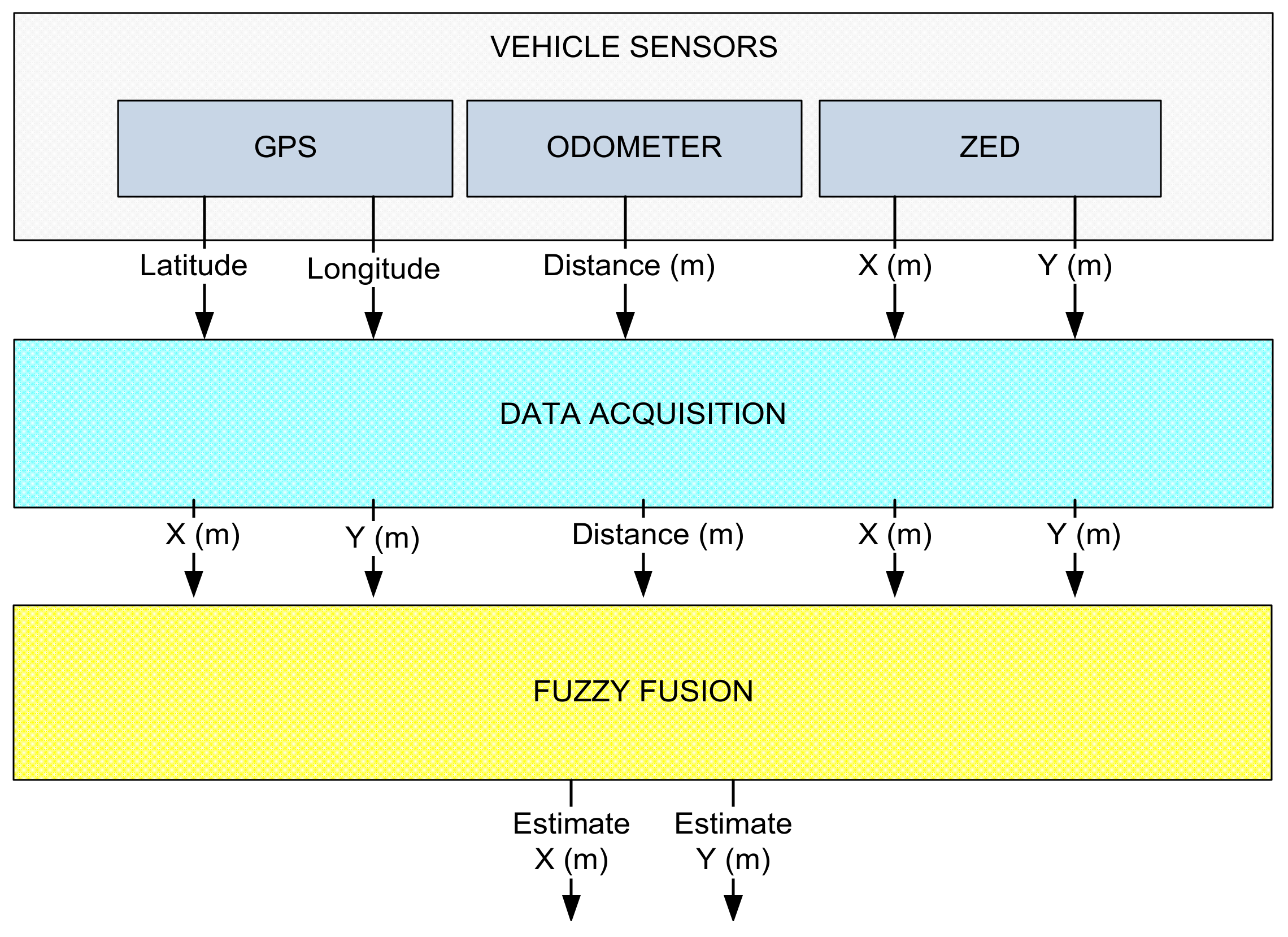
2.2. Signals Acquisition
2.3. Fuzzy Fusion
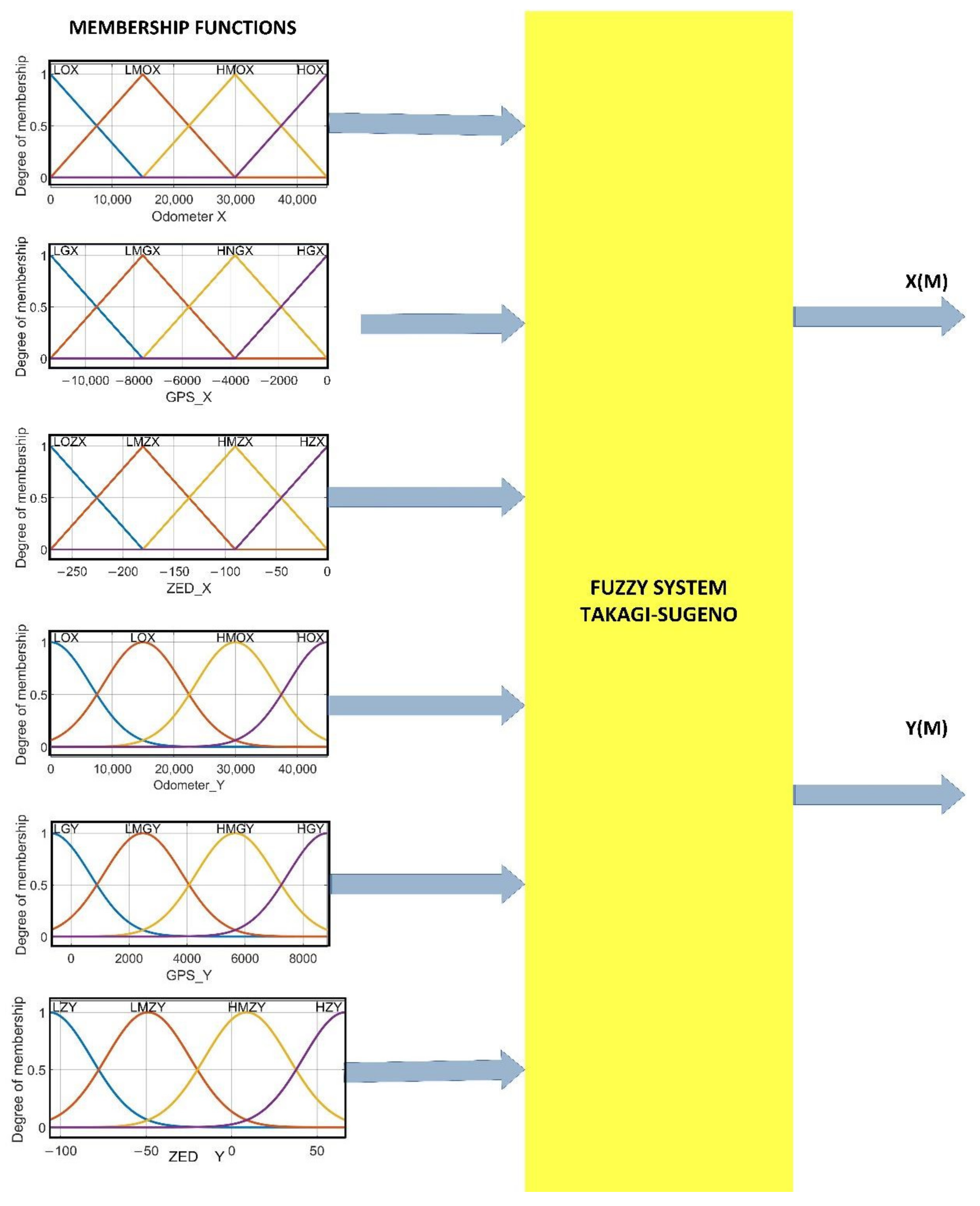
2.4. Fuzzification
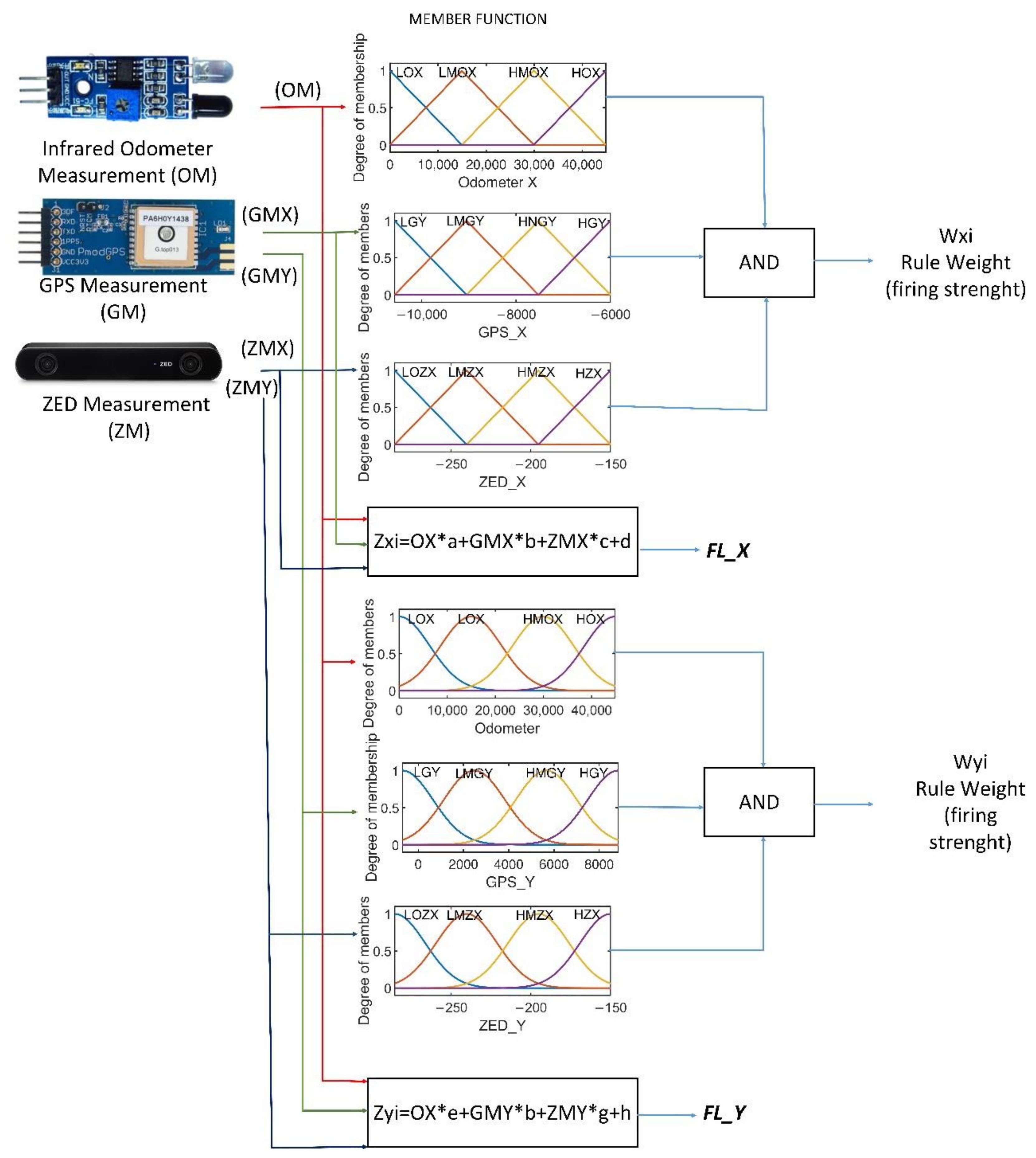
2.5. Inference
- if (odometer is LOX) and (GPSX is LGX) and (ZEDX is LOZX) then (Wx1)
- if (odometer is LOX) and (GPSY is LGY) and (ZEDY is LZY) then (Wy1)
2.6. Defuzzification
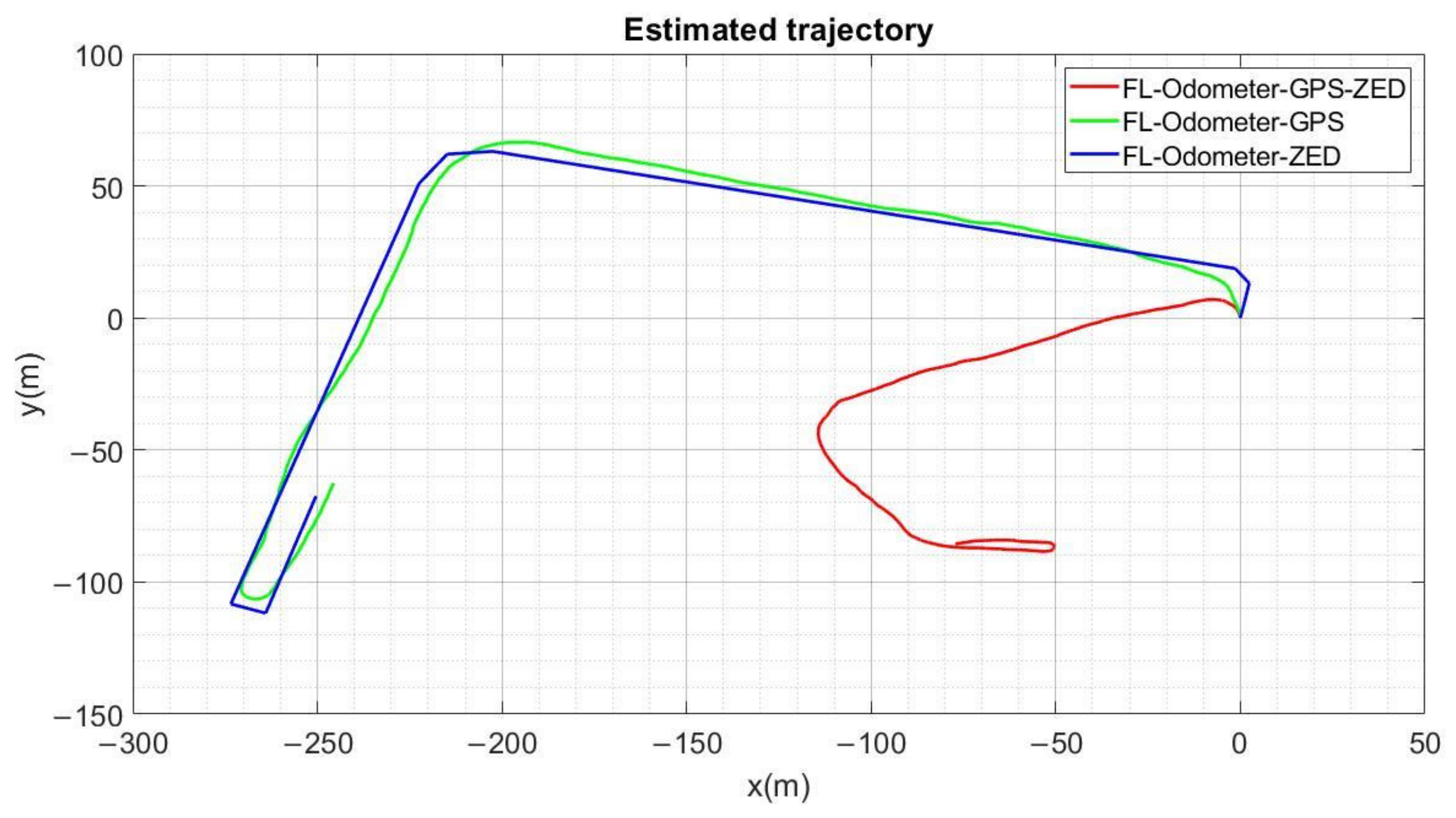
3. Results
Statistical Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Kenney, J.B. Dedicated short-range communications (DSRC) standards in the United States. Proc. IEEE 2011, 99, 1162–1182. [Google Scholar] [CrossRef]
- Dobrev, Y.; Christmann, M.; Bilous, I.; Gulden, P. Steady delivery: Wireless local positioning systems for tracking and autonomous navigation of transport vehicles and mobile robots. IEEE Microw. Mag. 2017, 18, 26–37. [Google Scholar] [CrossRef]
- Tomita, H.; Iotake, Y.; Sugawara, S.; Nomura, T.; Kudo, H. High-precision Satellite Positioning Technique and Service for Next-generation Mobility. Hitachi Rev. 2019, 68, 1–8. [Google Scholar]
- Ho, V.; Rauf, K.; Passchier, I.; Rijks, F.; Witsenboer, T. Accuracy assessment of RTK GNSS based positioning systems for automated driving. In Proceedings of the 2018 15th Workshop on Positioning, Navigation and Communications (WPNC), Bremen, Germany, 25–26 October 2018. [Google Scholar]
- Ordóñez-Hurtado, R.H.; Crisostomi, E.; Shorten, R.N. An assessment on the use of stationary vehicles to support cooperative positioning systems. Int. J. Control 2018, 91, 608–621. [Google Scholar] [CrossRef]
- Somogyi, H.; Soumelidis, A. Comparison of High-Precision GNSS systems for development of an autonomous localization system. In Proceedings of the 2020 23rd International Symposium on Measurement and Control in Robotics (ISMCR), Budapest, Hungary, 15–17 October 2020. [Google Scholar]
- Crowley, J.L.; Demazeau, Y. Principles and techniques for sensor data fusion. Signal Process. 1993, 32, 5–27. [Google Scholar] [CrossRef] [Green Version]
- Rosique, F.; Navarro, P.J.; Padilla, A. A systematic review of perception system and simulators for autonomous vehicles research. Sensors 2019, 19, 648. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, R.; Yang, N.; Stückler, J.; Cremers, D. DirectShape: Direct Photometric Alignment of Shape Priors for Visual Vehicle Pose and Shape Estimation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Esfahani, M.A.; Wang, H.; Wu, K.; Yuan, S. AbolDeepIO: A novel deep inertial odometry network for autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1941–1950. [Google Scholar] [CrossRef]
- Nguyen, T.; Mann, G.K.; Vardy, A.; Gosine, R.G. Developing computationally efficient nonlinear cubature Kalman filtering for visual inertial odometry. J. Dyn. Syst. Meas. Control 2019, 141, 081012. [Google Scholar] [CrossRef]
- Forster, F.; Pizzoli, P.; Scaramuzza, D. SVO: Fast semi-direct monocular visual odometry. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014. [Google Scholar]
- Zhang, Y.; Liu, Z.; Liu, T.; Peng, B.; Li, X. An efficient generation network for 3D object reconstruction from a single image. IEEE Access 2019, 7, 57539–57549. [Google Scholar] [CrossRef]
- Riegler, G.; Liao, Y.; Donne, S.; Koltun, V.; Geiger, G. Connecting the Dots: Learning Representations for Active Monocular Depth Estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Rau, A.; Edwards, P.J.; Ahmad, O.F.; Riordan, P.; Janatka, M.; Lovat, L.B.; Stoyanov, D. Implicit domain adaptation with conditional generative adversarial networks for depth prediction in endoscopy. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 1167–1176. [Google Scholar] [CrossRef] [Green Version]
- Ran, L.; Zhang, Y.; Zhang, Z.; Yang, T. Convolutional neural network-based robot navigation using uncalibrated spherical images. Sensors 2017, 17, 1341. [Google Scholar] [CrossRef] [PubMed]
- Shokry, K.; Alhawary, M. MonoSLAM: A Single Camera SLAM. Univ. Twente Stud. J. Biom. Comput. Vis. 2017, 1, 1–8. [Google Scholar]
- Zhou, K.; Wang, X.; Wang, Z.; Wei, H.; Yin, L. Complete initial solutions for iterative pose estimation from planar objects. IEEE Access 2018, 6, 22257–22266. [Google Scholar] [CrossRef]
- Nilwong, S.; Hossain, D.; Kaneko, S.; Capi, G. Deep learning-based landmark detection for mobile robot outdoor localization. Machines 2019, 7, 25. [Google Scholar] [CrossRef] [Green Version]
- Woo, R.; Yang, E.-J.; Seo, D.-W. DA fuzzy-innovation-based adaptive kalman filter for enhanced Vehicle positioning in dense urban environments. Sensors 2019, 19, 1142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nourmohammadi, H.; Keighobadi, J. Fuzzy adaptive integration scheme for low-cost SINS/GPS navigation system. MSSP 2018, 99, 434–449. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, H.; Tang, G. Predictor-corrector guidance for entry vehicle based on fuzzy logic. Proc. Inst. Mech. Eng. G. 2019, 233, 472–482. [Google Scholar] [CrossRef]
- Teodorescu, H.-N.L. Fuzzy logic system linearization for sensors. In Proceedings of the 2017 International Symposium on Signals, Iasi, Romania, 13–14 July 2017. [Google Scholar]
- Cappetti, N.; Naddeo, A.; Villecco, F. Fuzzy approach to measures correction on Coordinate Measuring Machines: The case of hole-diameter verification. Measurement 2019, 93, 41–47. [Google Scholar] [CrossRef]
- Chaudhary, D.R.; Chaudhari, D.F. Study on Coriolis Mass Flow Meter for Error Correction through Two-phase Fluid Using Fuzzy Logic. In Proceedings of the International Conference on Innovative Advancement in Engineering and Technology (IAET-2020), Jaipur, India, 21–22 February 2020. [Google Scholar]
- Villaseñor-Aguilar, M.J.; Botello-Álvarez, J.E.; Pérez-Pinal, F.J.; Cano-Lara, M.; León-Galván, M.F.; Bravo-Sánchez, M.G.; Bravo- Sánchez, M.G.; Barranco-Gutiérrez, A.I. Fuzzy Classification of the Maturity of the Tomato Using a Vision System. J. Sens. 2019, 2019, 3175848. [Google Scholar] [CrossRef]
- Villaseñor-Aguilar, M.J.; Bravo-Sánchez, M.G.; Padilla-Medina, J.A.; Vázquez-Vera, J.L.; Guevara-González, R.G.; García- Rodríguez, F.J.; Barranco-Gutiérrez, A.I. A maturity estimation of bell pepper (Capsicum annuum L.) by artificial vision system for quality control. J. Sens. 2020, 10, 5097. [Google Scholar] [CrossRef]
- Pena-Aguirre, J.C.; Barranco-Gutierrez, A.I.; Padilla-Medina, J.A.; Espinosa-Calderon, A.; Perez-Pinal, F.J. Fuzzy Logic Power Management Strategy for a Residential DC-Microgrid. IEEE Access 2020, 8, 116733–116743. [Google Scholar] [CrossRef]
- Wang, X. A driverless vehicle vision path planning algorithm for sensor fusion. In Proceedings of the 2019 IEEE 2nd International Conference on Automation, Electronics and Electrical Engineering (AUTEEE), Shenyang, China, 22–24 November 2019. [Google Scholar]




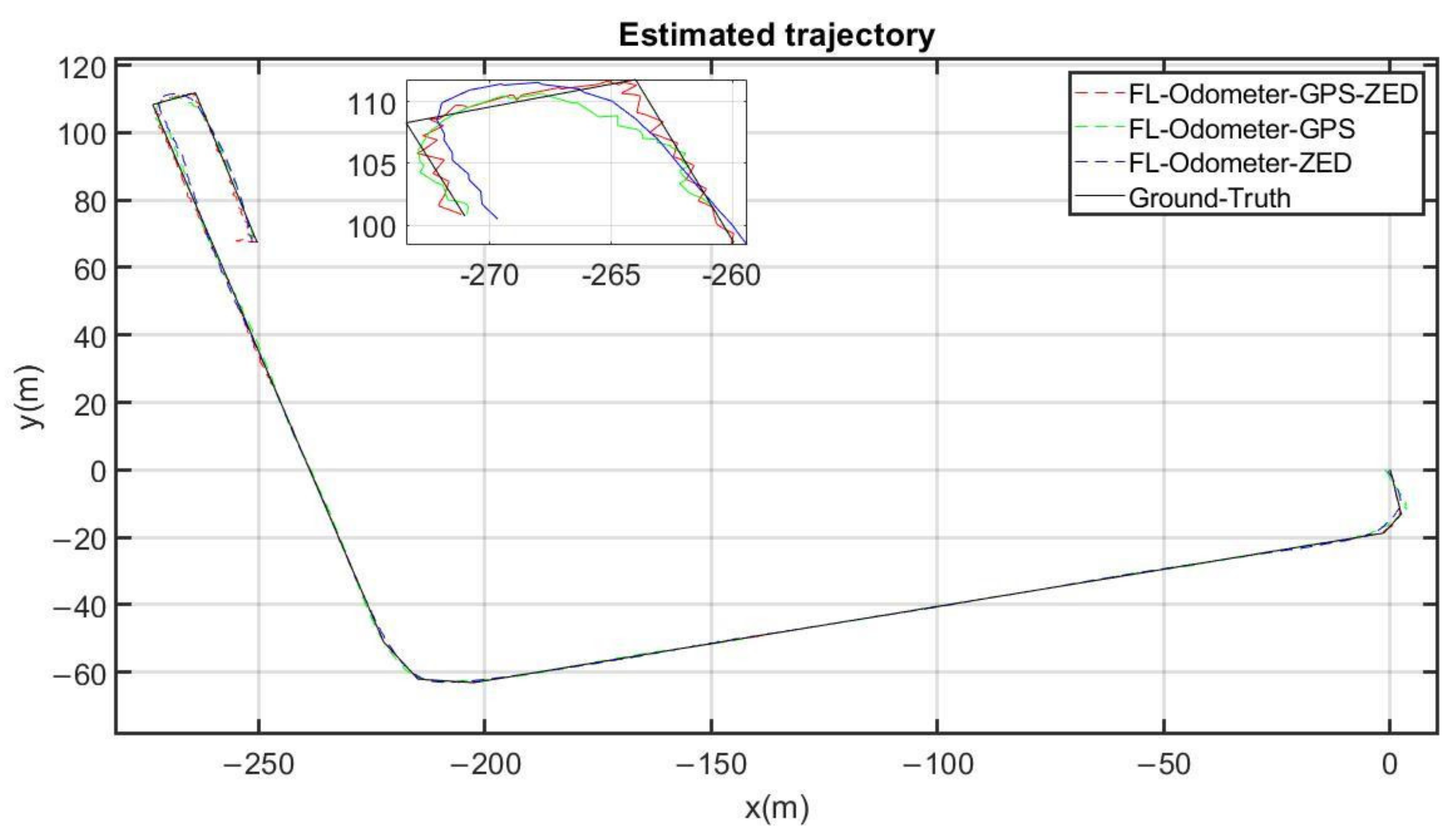
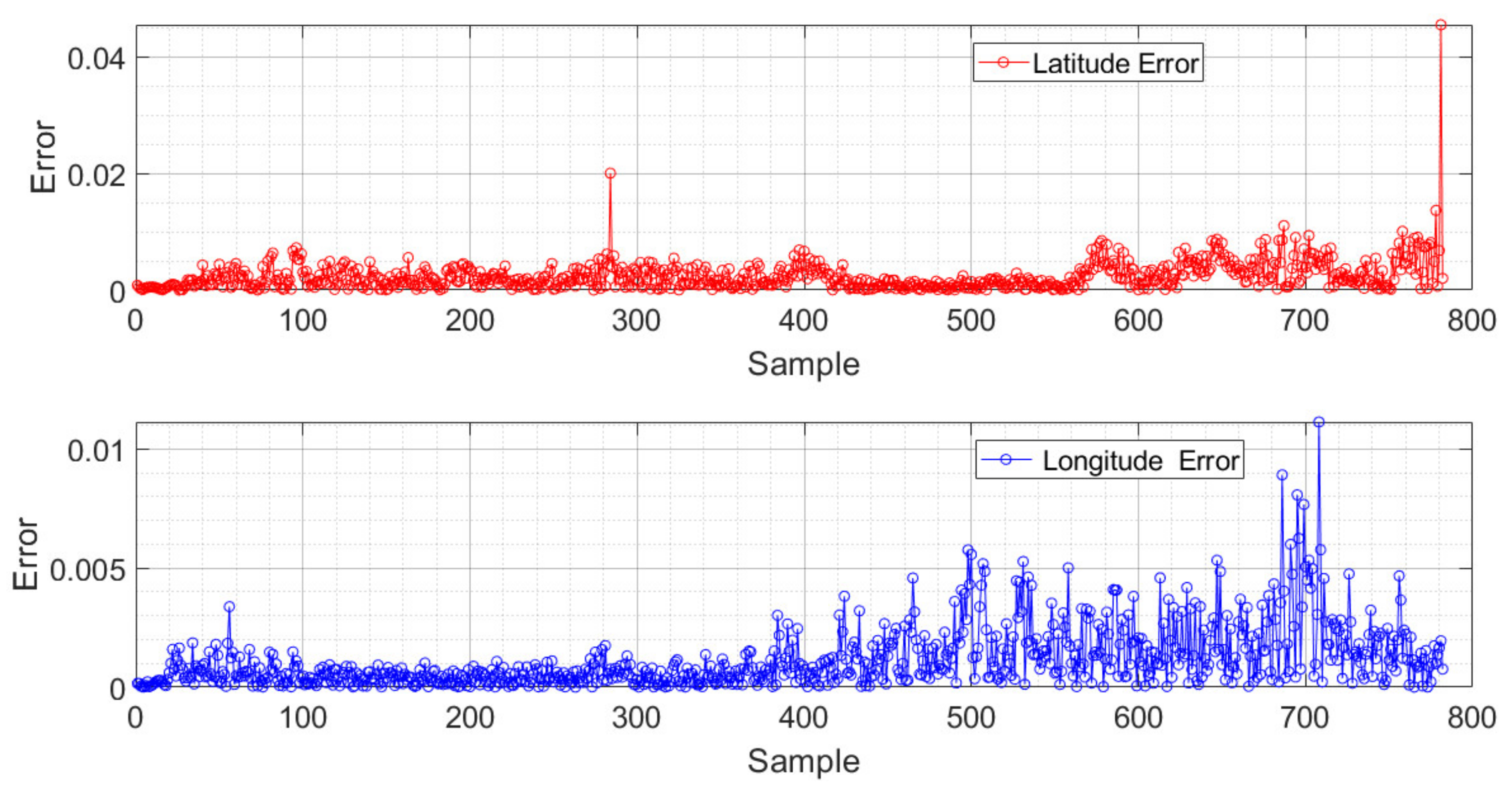
| Models | Input | MF | Outputs | MSE (5 Epochs) |
|---|---|---|---|---|
| 1 | Odometer, GPS X, GPS Y, ZED X, and ZED Y | 20 | X (m) and Y (m) | 0.0335 |
| 2 | Odometer, ZED X, and ZED Y | 12 | X (m) and Y (m) | 0.1042 |
| 3 | Odometer, GPS X, and GPS Y | 12 | X (m) and Y (m) | 0.1382 |
| 4 | ZED X and ZED Y | 12 | X (m) and Y (m) | 0.0765 |
| Number of Inputs | Type of Membership Functions | MSE Latitude | MSE Longitude |
|---|---|---|---|
| 6 | trimf | 0.001267 | 0.000634 |
| 6 | trapmf | 0.004761 | 0.000482 |
| 6 | gbellmf | 0.001637 | 0.000714 |
| 6 | gaussmf | 0.002035 | 0.000304 |
| 6 | gauss2mf | 0.022466 | 0.001828 |
| 6 | pimf | 0.02704 | 0.000729 |
| 6 | dsigmf | 0.012521 | 0.006350 |
| 6 | psigmf | 0.03409 | 0.001283 |
| Triangular Memberships | ||
|---|---|---|
| Infrared Odometer | GPS Latitude | Zed X |
| LOX = (−14952.15, −1.5131 × 10−7, 14952.15) | LGX = ([−15243.013, −11432.26, −7621.5) | LZX = (−15243.013, −11432.26, −7621.507) |
| LMOX = (−1.795 × 10−7, 14952.15, 29904.3) | LMGX = (−11432.259, −7621.507, −3810.753) | LMZX = (−11432.259, −7621.507, −3810.753) |
| HMOX = (14952.15, 29904.299, 44856.449) | HMGX = (−7621.507, −3810.753, −1.638 × 10−8) | HMZX = (−7621.507, −3810.753, −1.6386 × 10−8) |
| HOX = (29904.299, 44856.449, 59808.6) | HGX = (−3810.753, −4.8414 × 10−8, 3810.753) | HZX = (−3810.753, −4.841 × 10−8, 3810.753) |
| Gaussian | ||
|---|---|---|
| Infrared Odometer | GPS Longitude | Zed Y |
| LOX = (6349.59, 0) | LGY = (1350.42, −699.77) | LZY = (38.31, −270.69) |
| LMOX = (6349.59, 14952.15) | LMGY = (1350.42, 2480.24) | LMZY = (38.31, −180.45) |
| HMOX = (6349.59, 29904.3) | HMGY = (1350.42, 5660.25) | HMZY = (38.31, −90.22) |
| HOX = (6349.59, 44856.45) | HGY = (1350.42, 8840.26) | HZY = (38.31, 0.012) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villaseñor-Aguilar, M.J.; Peralta-López, J.E.; Lázaro-Mata, D.; García-Alcalá, C.E.; Padilla-Medina, J.A.; Perez-Pinal, F.J.; Vázquez-López, J.A.; Barranco-Gutiérrez, A.I. Fuzzy Fusion of Stereo Vision, Odometer, and GPS for Tracking Land Vehicles. Mathematics 2022, 10, 2052. https://doi.org/10.3390/math10122052
Villaseñor-Aguilar MJ, Peralta-López JE, Lázaro-Mata D, García-Alcalá CE, Padilla-Medina JA, Perez-Pinal FJ, Vázquez-López JA, Barranco-Gutiérrez AI. Fuzzy Fusion of Stereo Vision, Odometer, and GPS for Tracking Land Vehicles. Mathematics. 2022; 10(12):2052. https://doi.org/10.3390/math10122052
Chicago/Turabian StyleVillaseñor-Aguilar, Marcos J., José E. Peralta-López, David Lázaro-Mata, Carlos E. García-Alcalá, José A. Padilla-Medina, Francisco J. Perez-Pinal, José A. Vázquez-López, and Alejandro I. Barranco-Gutiérrez. 2022. "Fuzzy Fusion of Stereo Vision, Odometer, and GPS for Tracking Land Vehicles" Mathematics 10, no. 12: 2052. https://doi.org/10.3390/math10122052
APA StyleVillaseñor-Aguilar, M. J., Peralta-López, J. E., Lázaro-Mata, D., García-Alcalá, C. E., Padilla-Medina, J. A., Perez-Pinal, F. J., Vázquez-López, J. A., & Barranco-Gutiérrez, A. I. (2022). Fuzzy Fusion of Stereo Vision, Odometer, and GPS for Tracking Land Vehicles. Mathematics, 10(12), 2052. https://doi.org/10.3390/math10122052









