Effect of Particle Size Distribution on the Dynamic Mechanical Properties and Fractal Characteristics of Cemented Rock Strata
Abstract
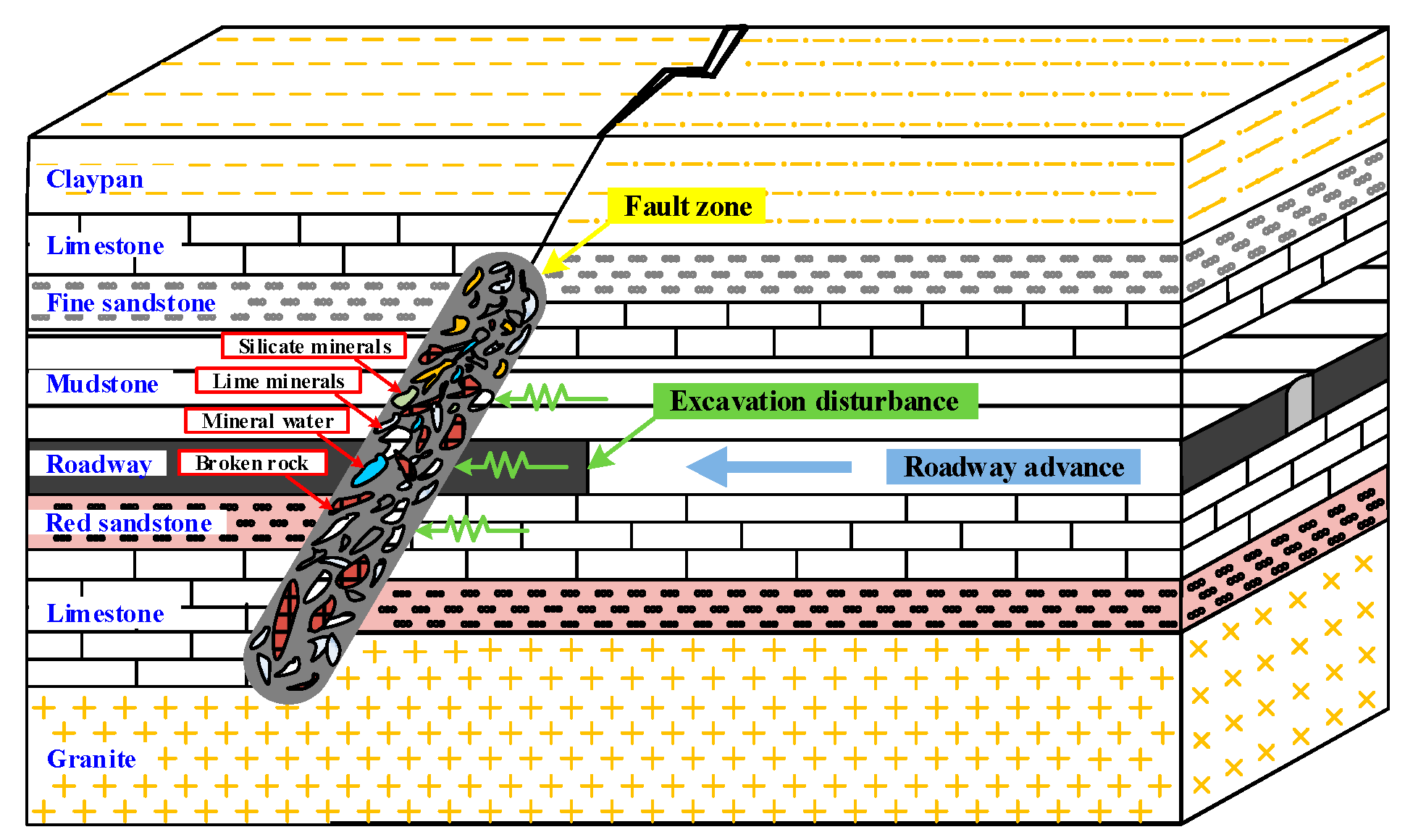
:1. Introduction
2. Materials and Scheme
2.1. Materials
2.2. Test Scheme
3. Test System and Measurement Principles
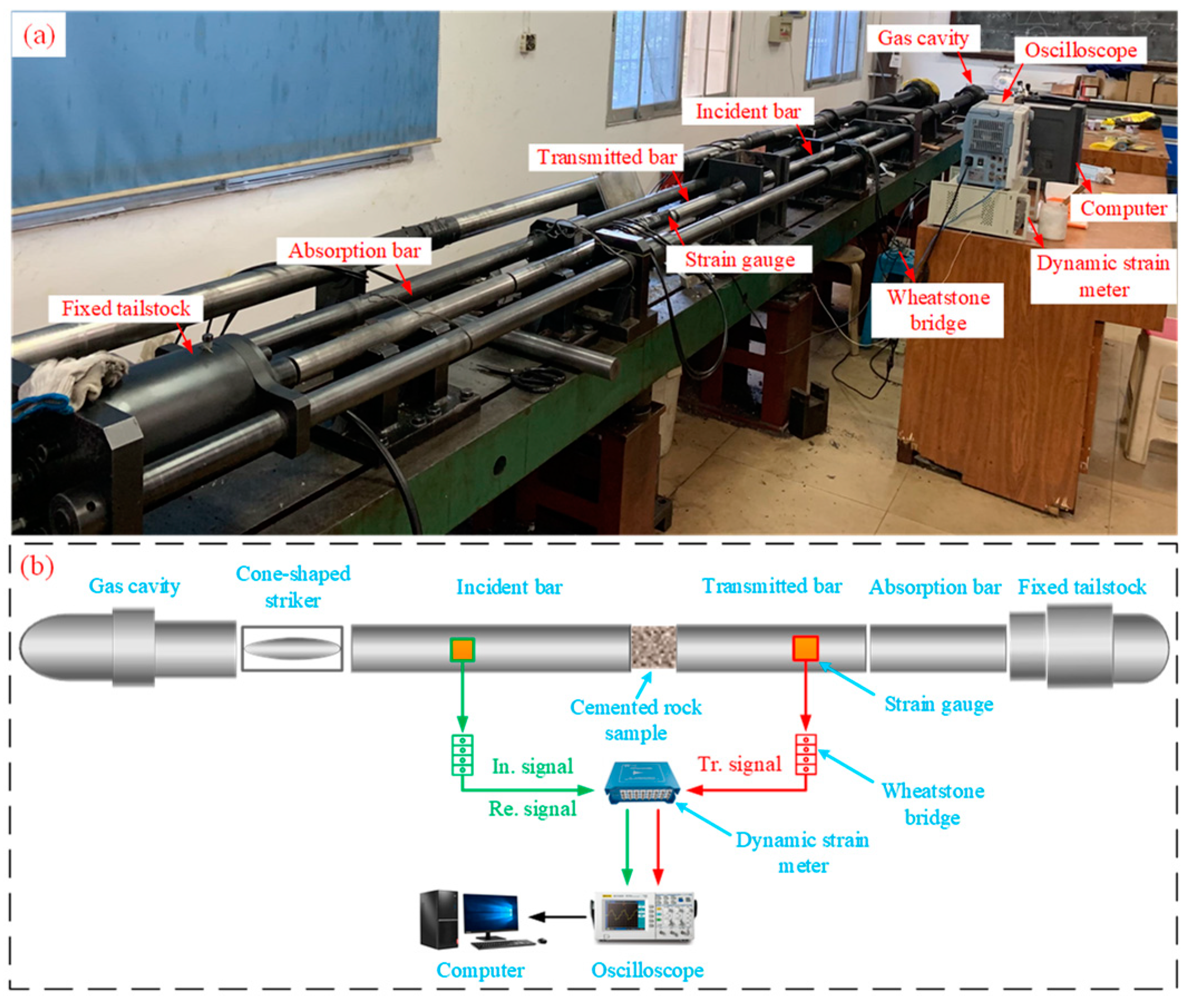
3.1. SHPB Experimental Setup
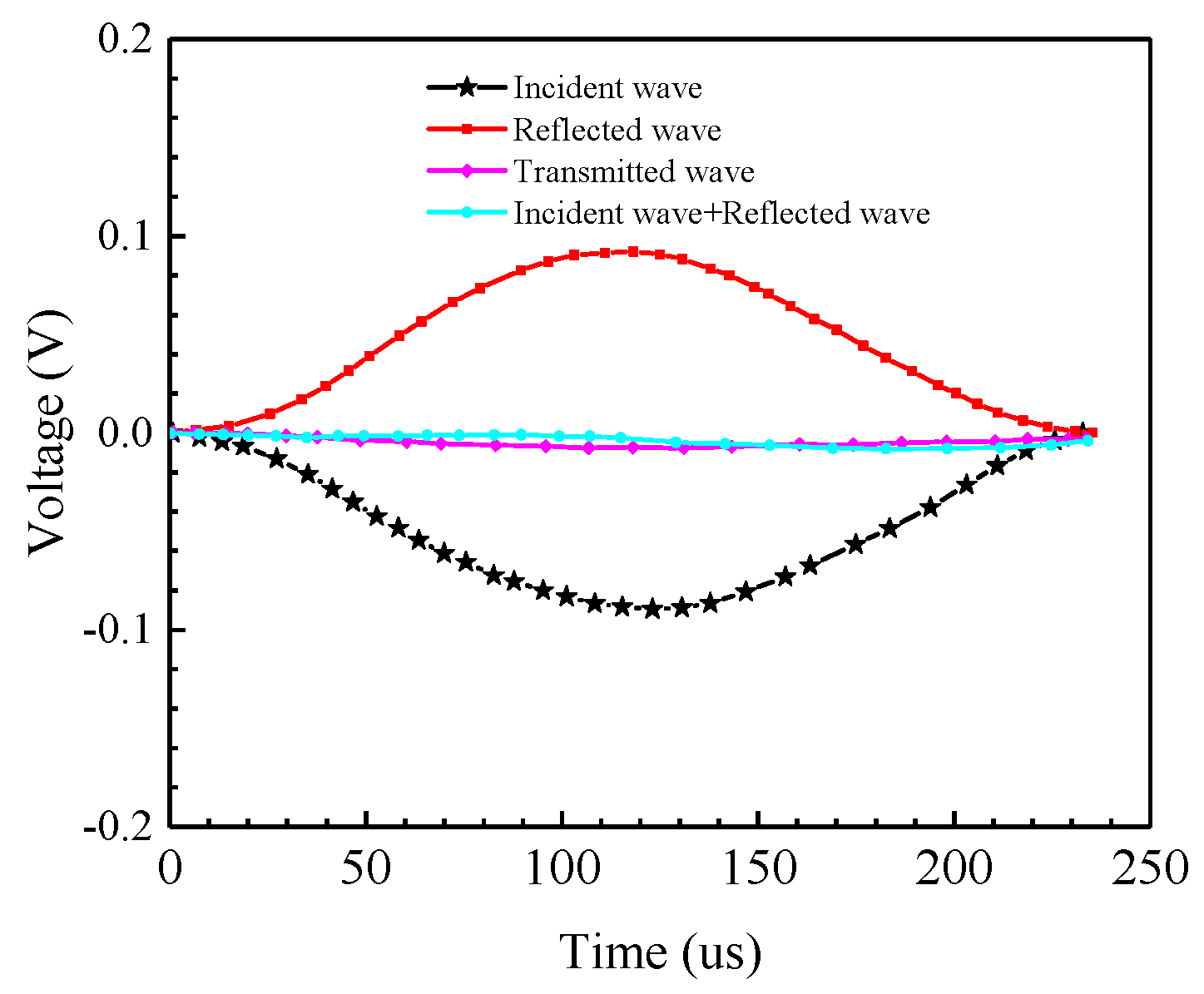
3.2. Measurement Principles
3.2.1. Fractal Dimension
3.2.2. Crushing Ratio
4. Test Results
4.1. Dynamic Mechanical Characteristics
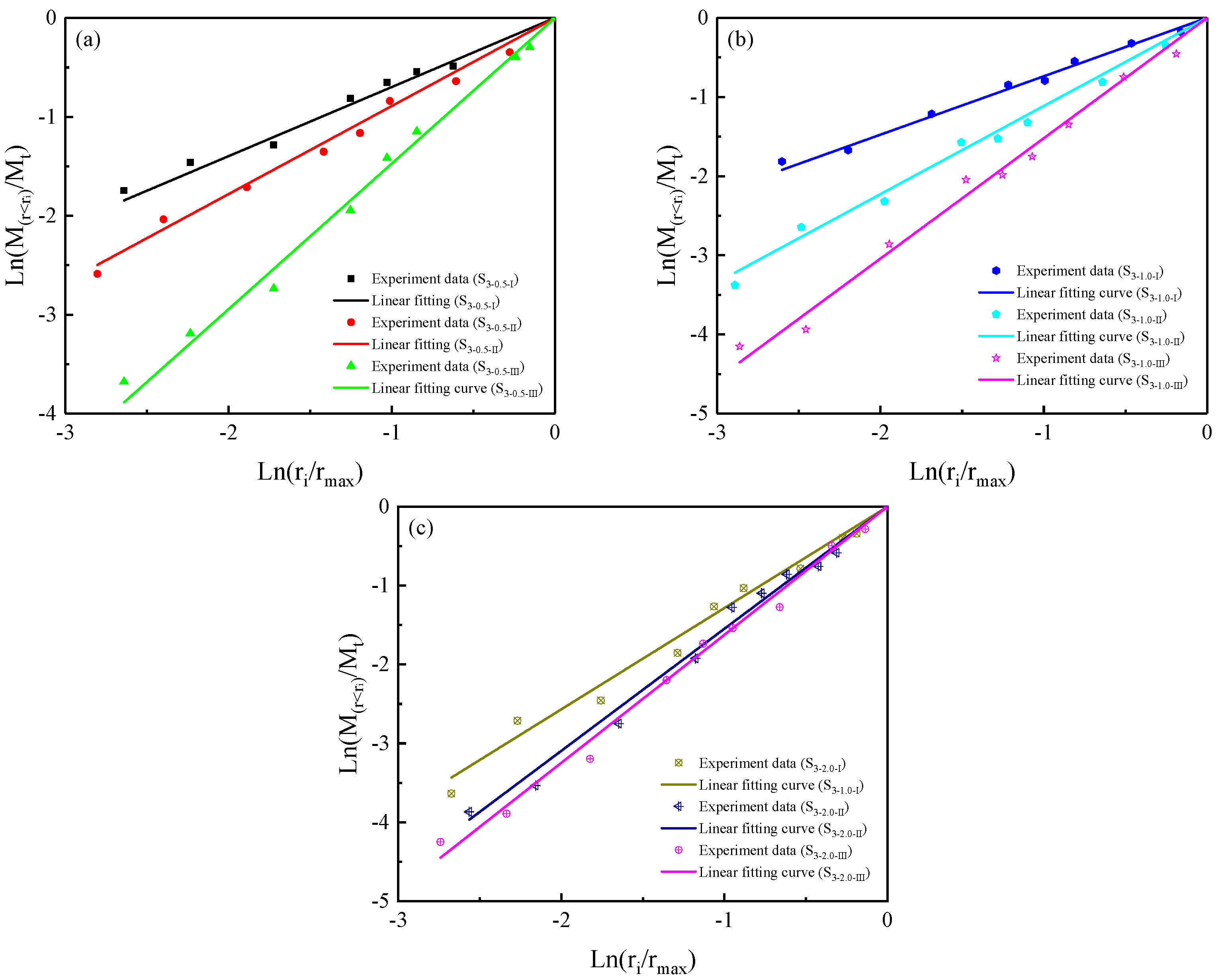
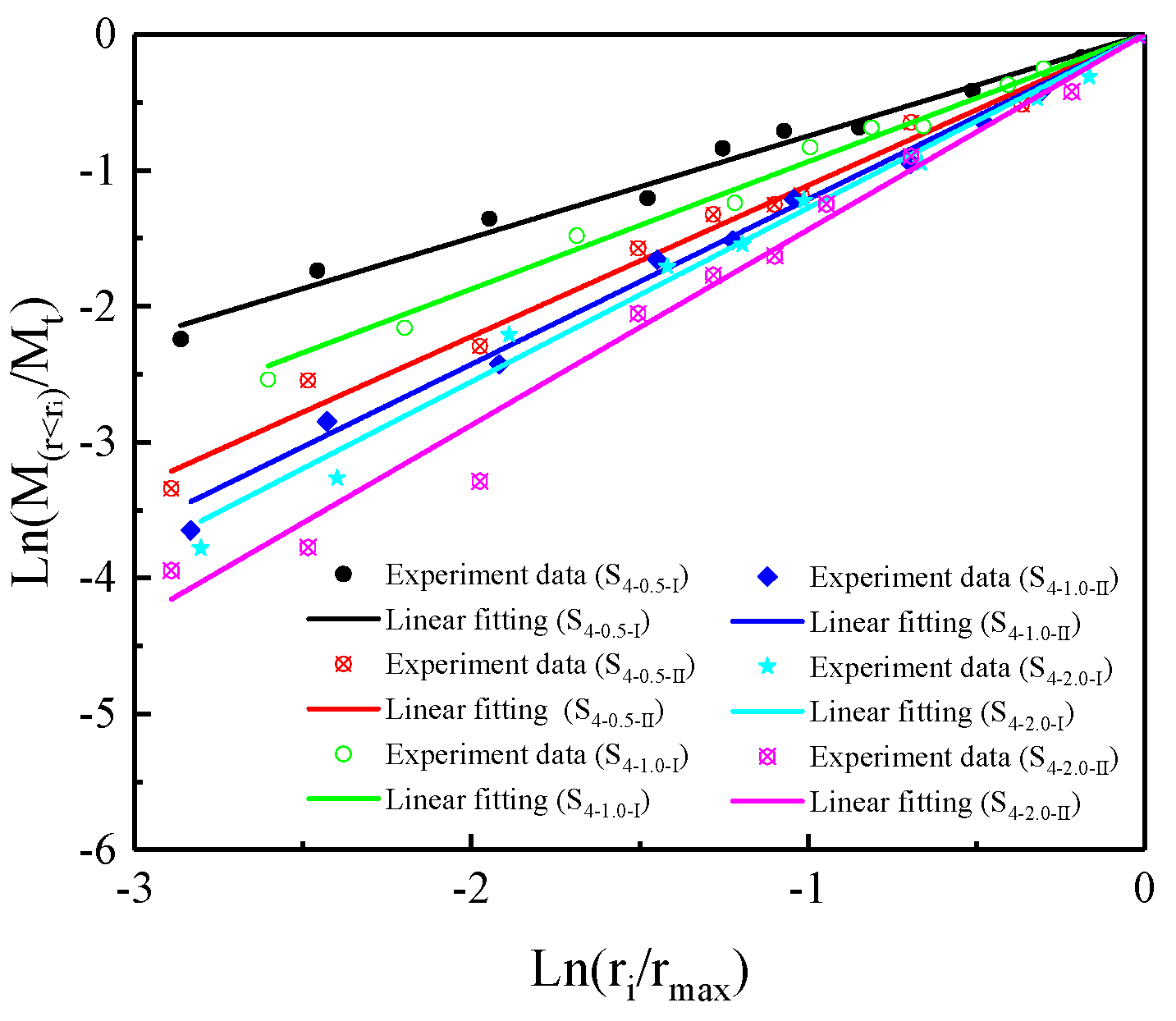
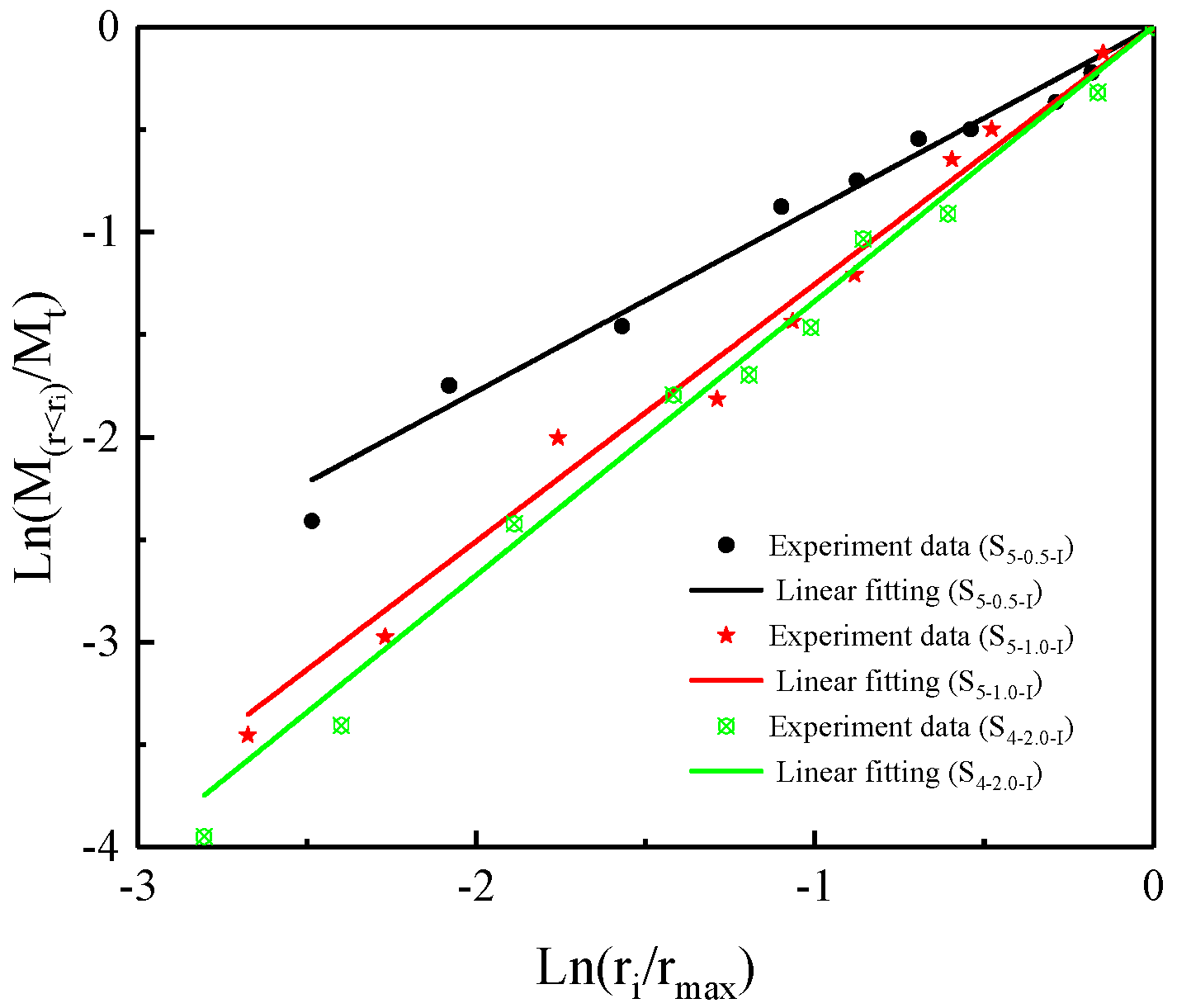
4.2. Variation of Fractal Characteristics of Cemented Rock Samples
4.3. Variation of Breakage Ratio of Cemented Rock Samples
5. Discussion
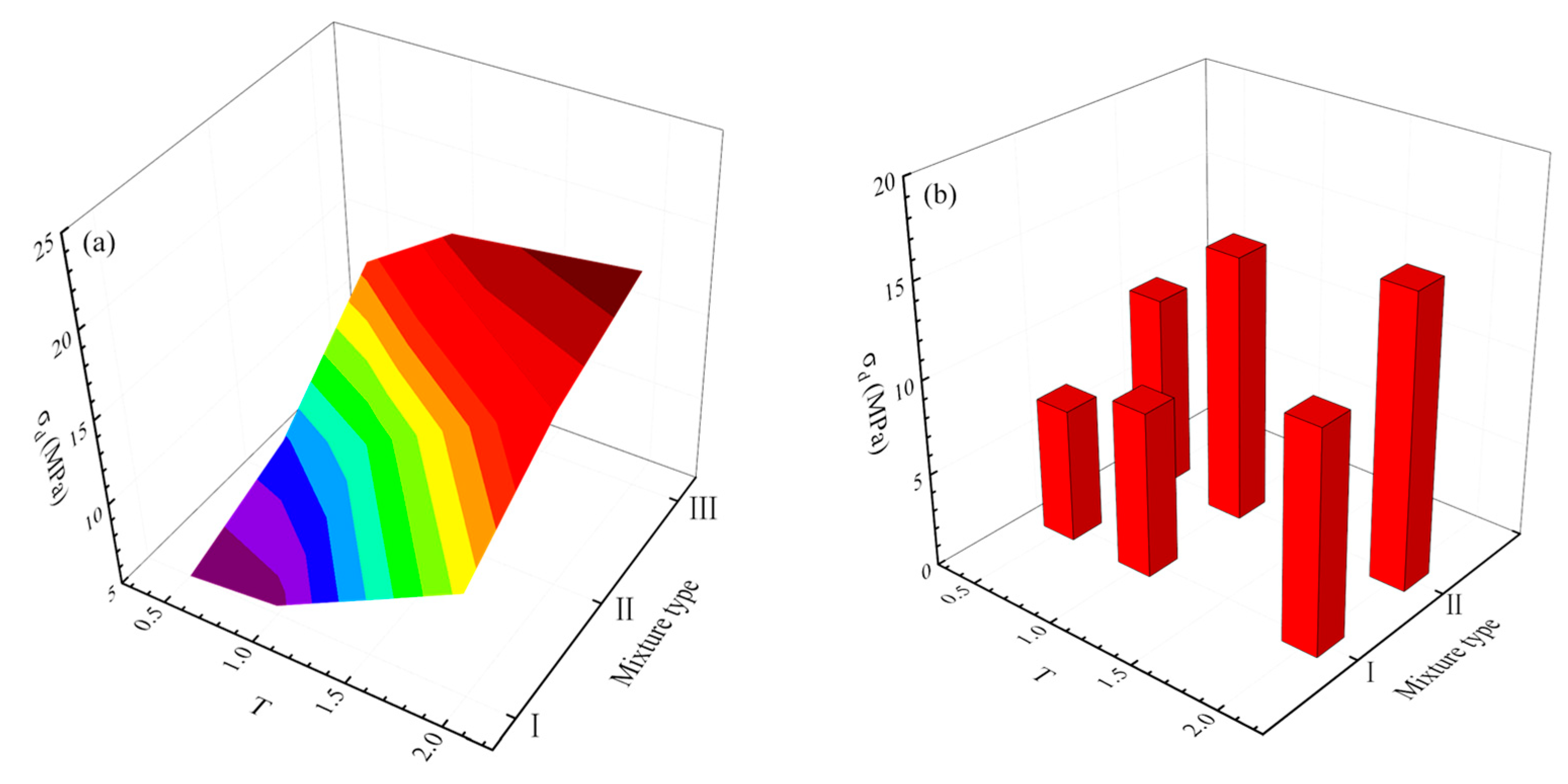
5.1. Effects of PSD and Strain Rate on Dynamic Strength
5.1.1. Effect of PSD on Dynamic Strength
5.1.2. Effect of Strain Rate on Dynamic Strength
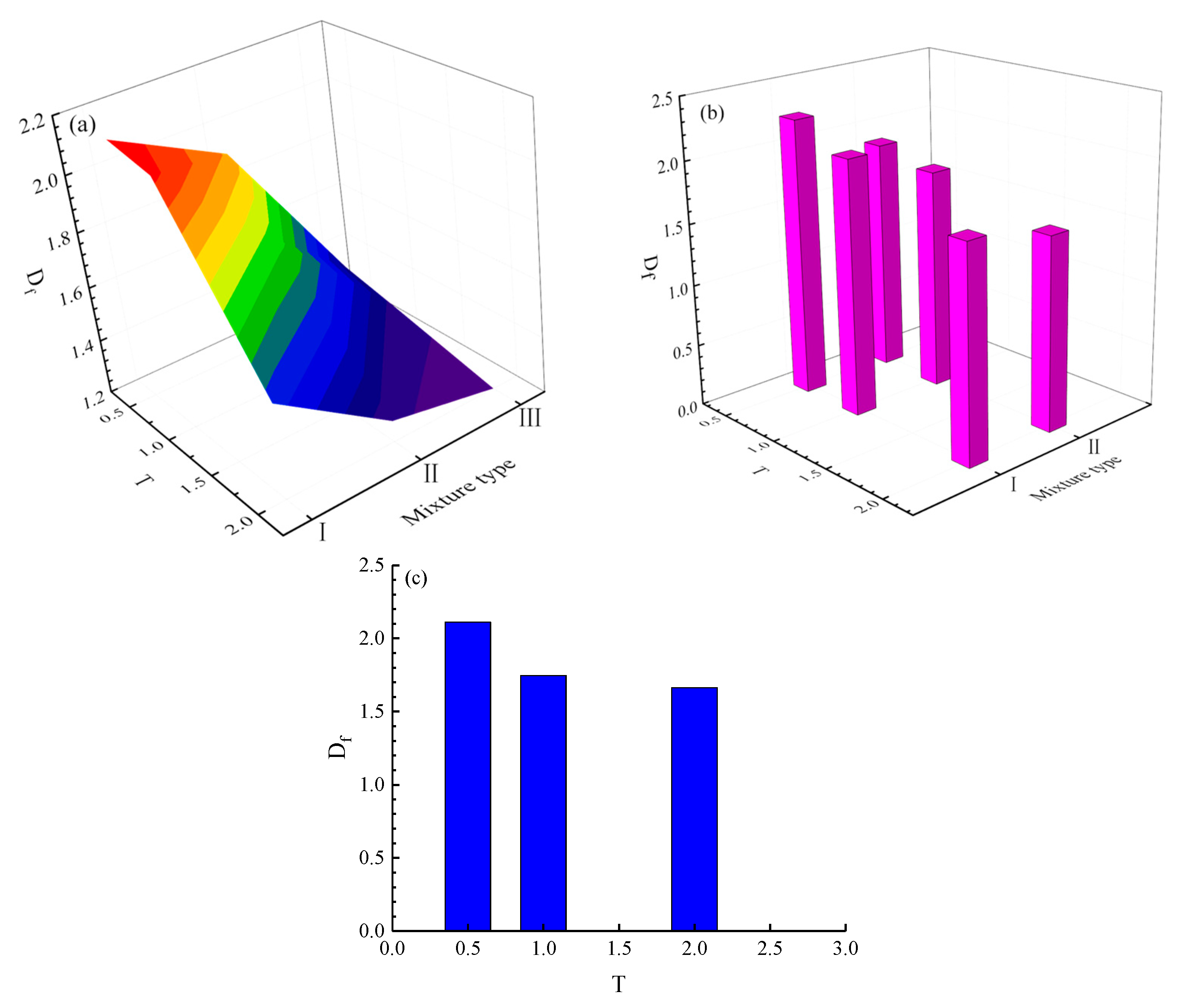
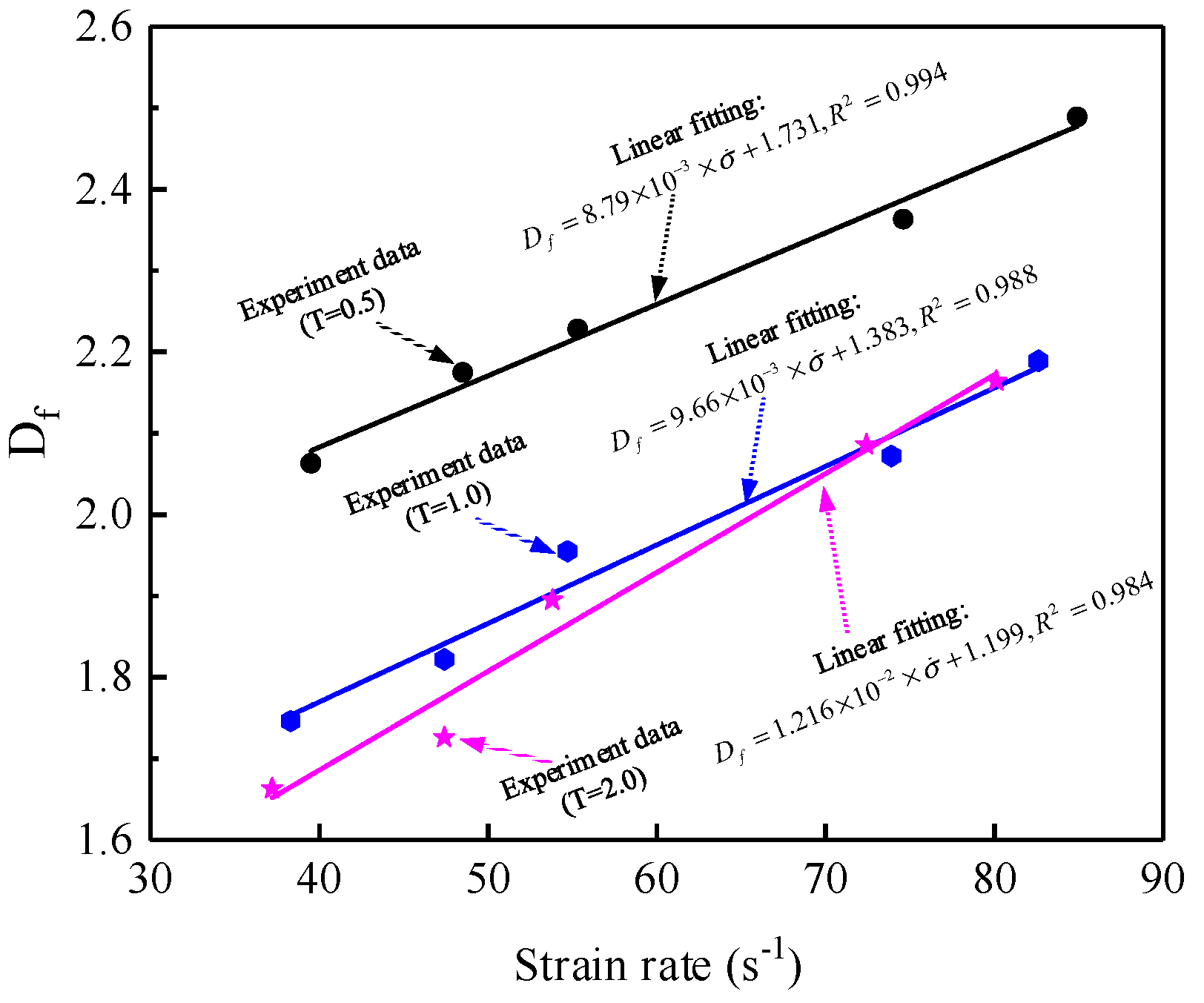
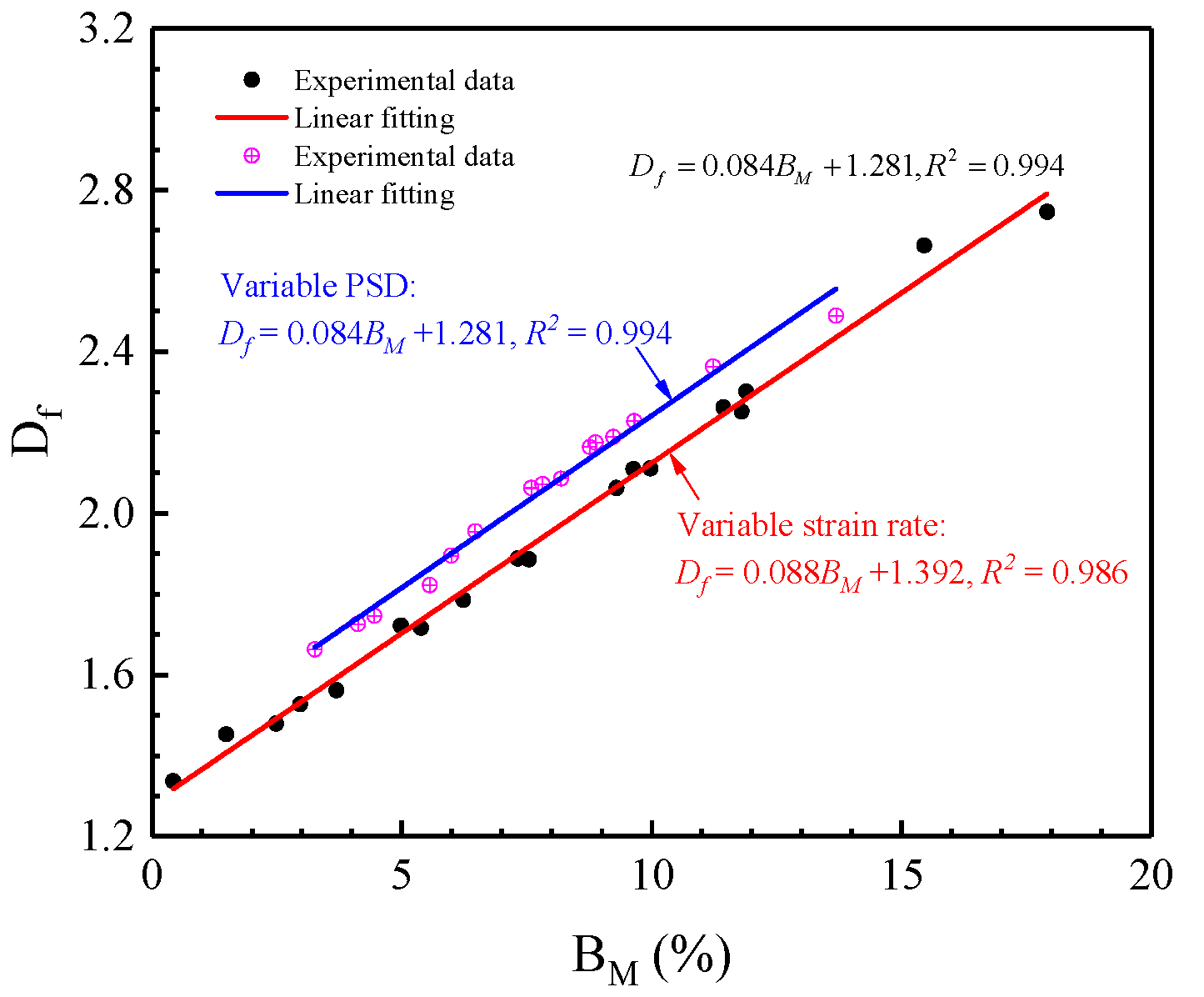
5.2. Effects of PSD and Strain Rate on Fractal Characteristics
5.2.1. Effects of PSD on Fractal Dimension
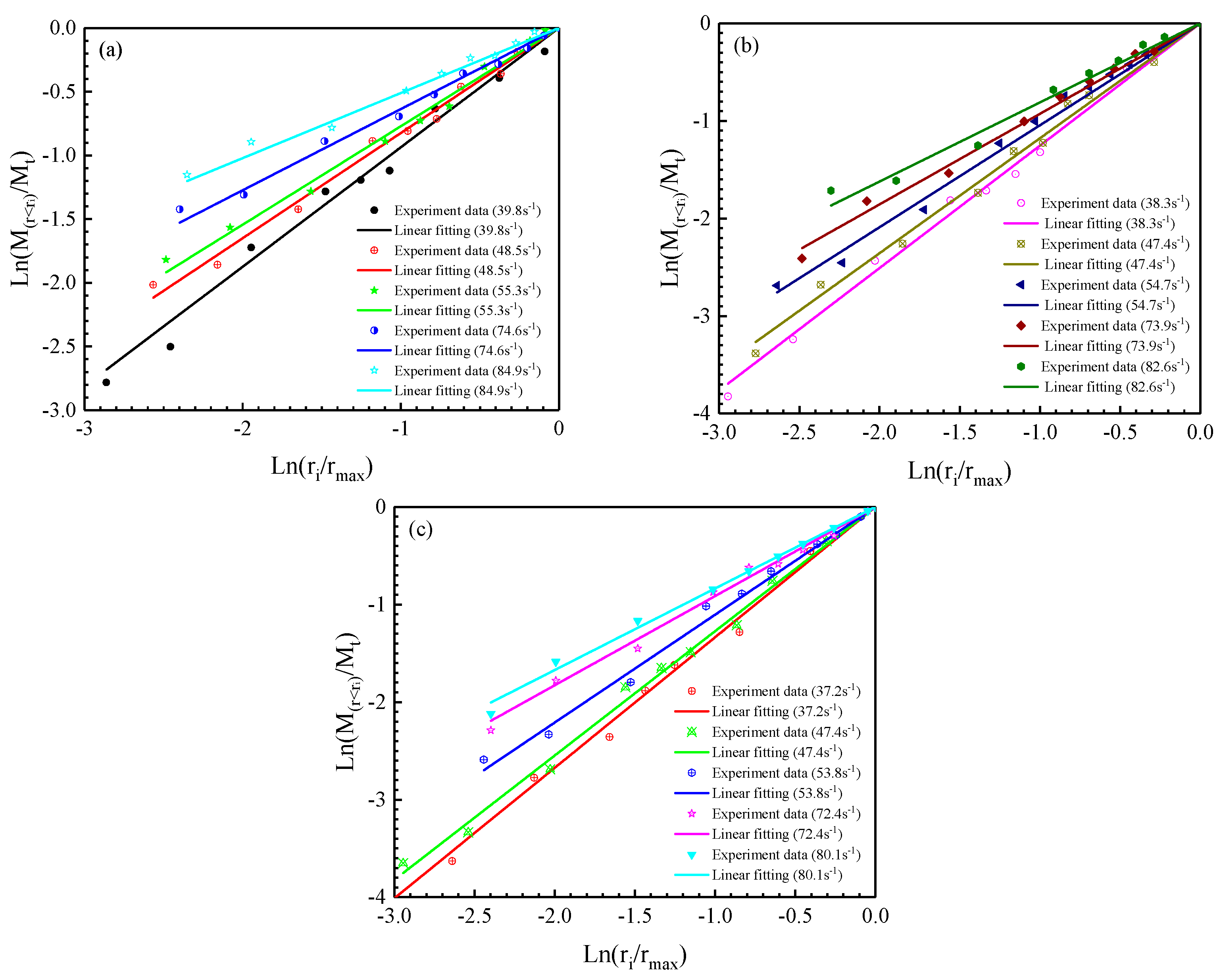
5.2.2. Effect of Strain Rate on Fractal Dimension
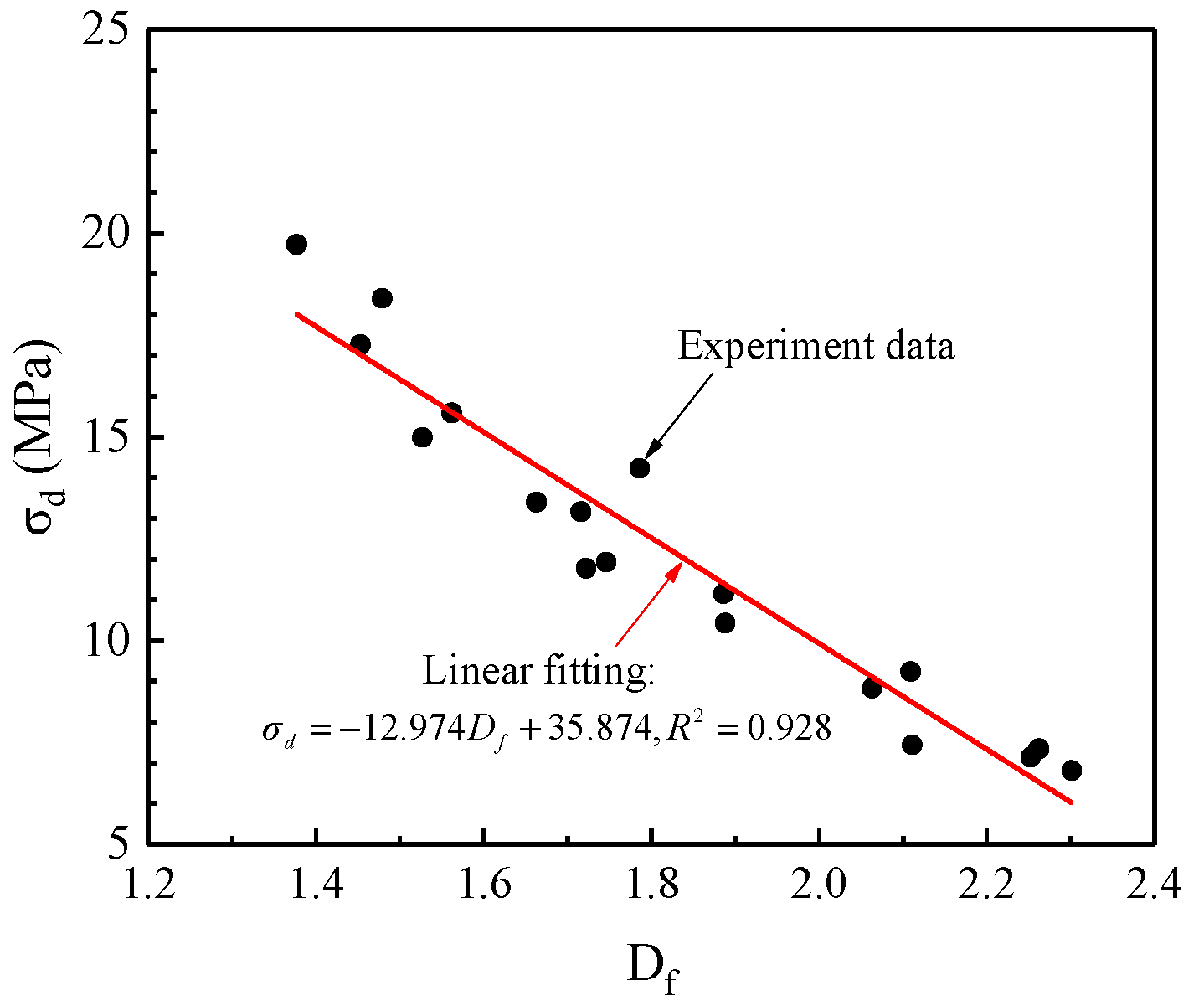
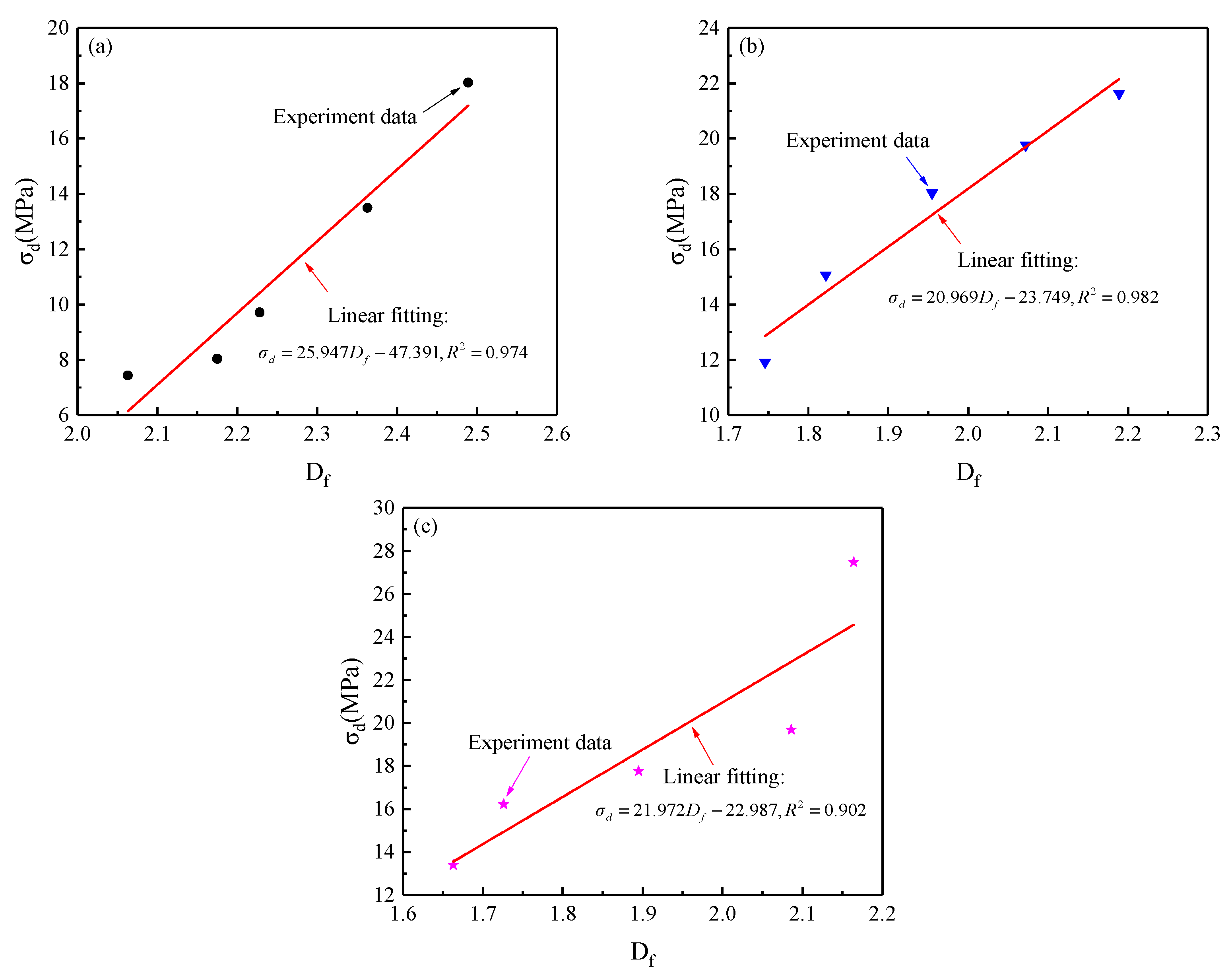
5.3. Relationship between Dynamic Strength and Fractal Dimension
5.3.1. Relationship between Crush Ratio and Fractal Dimension
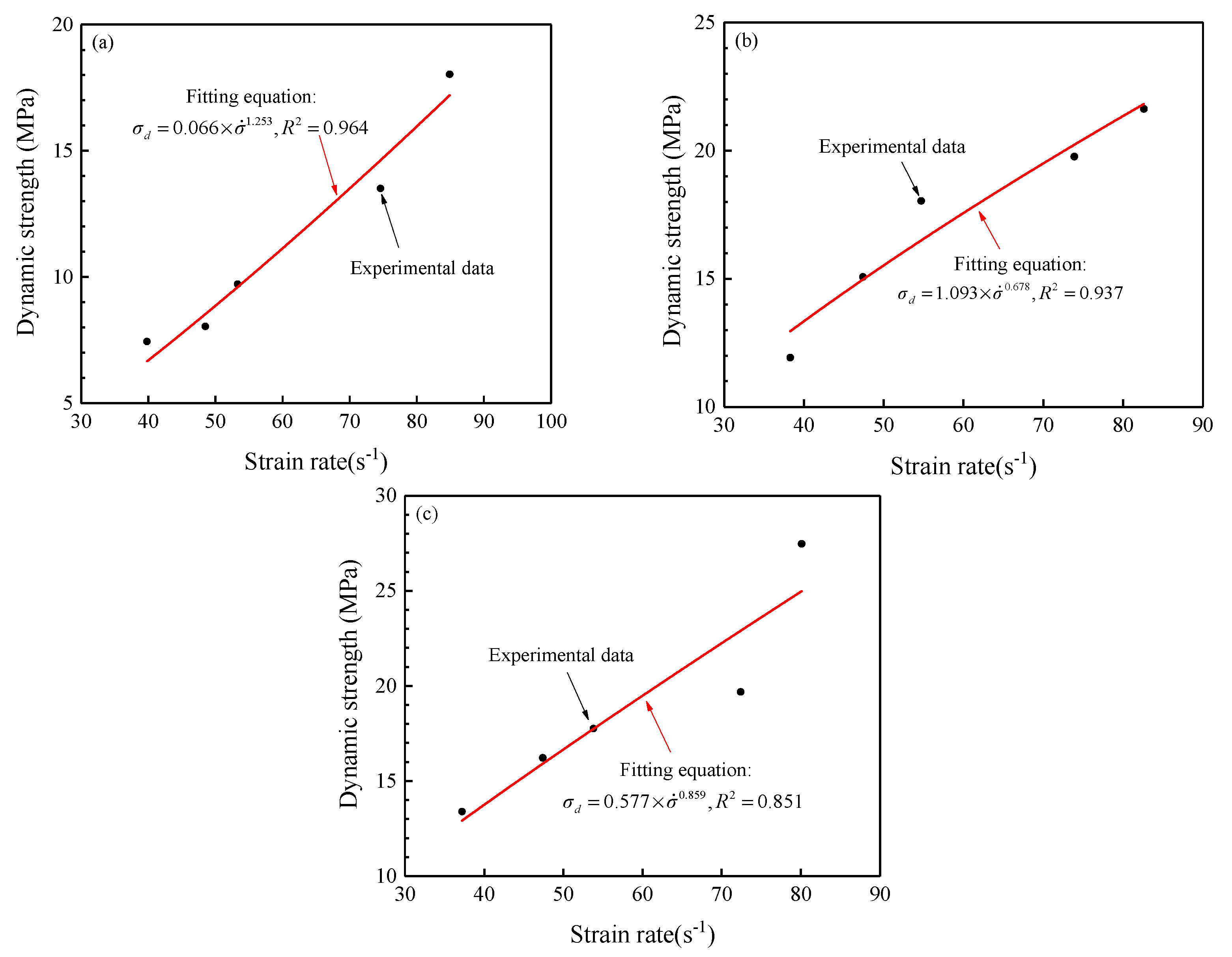
5.3.2. Relationship between Dynamic Strength and Fractal Dimension
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Islam, M.R.; Shinjo, R. Mining-induced fault reactivation associated with the main conveyor belt roadway and safety of the Barapukuria Coal Mine in Bangladesh: Constraints from BEM simulations. Int. J. Coal Geol. 2009, 79, 115–130. [Google Scholar] [CrossRef]
- Wang, H.; Xue, S.; Shi, R.; Jiang, Y.; Gong, W.; Mao, L. Investigation of Fault Displacement Evolution During Extraction in Longwall Panel in an Underground Coal Mine. Rock Mech. Rock Eng. 2020, 53, 1809–1826. [Google Scholar] [CrossRef]
- Ma, D.; Kong, S.; Li, Z.; Zhang, Q.; Wang, Z.; Zhou, Z. Effect of wetting-drying cycle on hydraulic and mechanical properties of cemented paste backfill of the recycled solid wastes. Chemosphere 2021, 282, 131163. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Li, W.; Chen, J. Application of Various Nonlinear Models to Predict the Uniaxial Compressive Strength of Weakly Cemented Jurassic Rocks. Nat. Resour. Res. 2022, 31, 371–384. [Google Scholar] [CrossRef]
- Demirdag, S. Effects of freezing-thawing and thermal shock cycles on physical and mechanical properties of filled and unfilled travertines. Constr. Build. Mater. 2013, 47, 1395–1401. [Google Scholar] [CrossRef]
- Yin, Q.; Jing, H.; Su, H.; Zhao, H. Experimental Study on Mechanical Properties and Anchorage Performances of Rock Mass in the Fault Fracture Zone. Int. J. Geomech. 2018, 18, 04018067. [Google Scholar] [CrossRef]
- Zhu, W.; Hughes, J.J.; Bicanic, N.; Pearce, C.J. Nanoindentation mapping of mechanical properties of cement paste and natural rocks. Mater. Charact. 2007, 58, 1189–1198. [Google Scholar] [CrossRef]
- Huang, L.; Guo, Y.; Li, X. Failure characteristics of shale after being subjected to high temperatures under uniaxial compression. Bull. Eng. Geol. Environ. 2021, 81, 33. [Google Scholar] [CrossRef]
- Wang, J.; Ma, D.; Li, Z.; Huang, Y.; Du, F. Experimental investigation of damage evolution and failure criterion on hollow cylindrical rock samples with different bore diameters. Eng. Fract. Mech. 2022, 260, 108182. [Google Scholar] [CrossRef]
- Fu, J.-X.; Song, W.-D.; Tan, Y.-Y. Study on Microstructural Evolution and Strength Growth and Fracture Mechanism of Cemented Paste Backfill. Adv. Mater. Sci. Eng. 2016, 2016, 8792817. [Google Scholar] [CrossRef] [Green Version]
- Fall, M.; Benzaazoua, M.; Ouellet, S. Experimental characterization of the influence of tailings fineness and density on the quality of cemented paste backfill. Miner. Eng. 2005, 18, 41–44. [Google Scholar] [CrossRef]
- Jiang, H.; Fall, M. Yield stress and strength of saline cemented tailings materials in sub-zero environments: Slag-paste backfill. J. Sustain. Cem.-Based Mater. 2017, 6, 314–331. [Google Scholar] [CrossRef]
- Xu, W.-b.; Liu, B.; Wu, W.-l. Strength and deformation behaviors of cemented tailings backfill under triaxial compression. J. Cent. South Univ. 2020, 27, 3531–3543. [Google Scholar] [CrossRef]
- Weilv, W.; Xu, W.; Jianpin, Z. Effect of inclined interface angle on shear strength and deformation response of cemented paste backfill-rock under triaxial compression. Constr. Build. Mater. 2021, 279, 122478. [Google Scholar] [CrossRef]
- Yu, X.; Kemeny, J.; Li, J.; Song, W.; Tan, Y. 3D Observations of Fracturing in Rock-Backfill Composite Specimens Under Triaxial Loading. Rock Mech. Rock Eng. 2021, 54, 6009–6022. [Google Scholar] [CrossRef]
- Yin, S.; Wu, A.; Hu, K.; Wang, Y.; Zhang, Y. The effect of solid components on the rheological and mechanical properties of cemented paste backfill. Miner. Eng. 2012, 35, 61–66. [Google Scholar] [CrossRef]
- Fang, K.; Fall, M. Chemically Induced Changes in the Shear Behaviour of Interface Between Rock and Tailings Backfill Undergoing Cementation. Rock Mech. Rock Eng. 2019, 52, 3047–3062. [Google Scholar] [CrossRef]
- Zhou, N.; Zhang, J.; Ouyang, S.; Deng, X.; Dong, C.; Du, E. Feasibility study and performance optimization of sand-based cemented paste backfill materials. J. Clean. Prod. 2020, 259, 120798. [Google Scholar] [CrossRef]
- Zhou, X.; Hu, S.; Zhang, G.; Li, J.; Xuan, D.; Gao, W. Experimental investigation and mathematical strength model study on the mechanical properties of cemented paste backfill. Constr. Build. Mater. 2019, 226, 524–533. [Google Scholar] [CrossRef]
- Lu, G.; Fall, M. Modeling Postblasting Stress and Pore Pressure Distribution in Hydrating Fill Mass at an Early Age. Int. J. Geomech. 2018, 18, 04018090. [Google Scholar] [CrossRef]
- Liu, Z.-y.; Gan, D.-q.; Gan, Z. Dynamic regimes of cemented backfill at early-age. J. Cent. South Univ. 2021, 28, 2079–2090. [Google Scholar] [CrossRef]
- Dikonda, R.K.; Mbonimpa, M.; Belem, T. Specific Mixing Energy of Cemented Paste Backfill, Part II: Influence on the Rheological and Mechanical Properties and Practical Applications. Minerals 2021, 11, 1159. [Google Scholar] [CrossRef]
- Cao, S.; Yilmaz, E.; Song, W.; Yilmaz, E.; Xue, G. Loading rate effect on uniaxial compressive strength behavior and acoustic emission properties of cemented tailings backfill. Constr. Build. Mater. 2019, 213, 313–324. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, L.; Li, X.; Guo, Y.; Liu, H.; Wang, J. Effects of Strain Rate and Temperature on Physical Mechanical Properties and Energy Dissipation Features of Granite. Mathematics 2022, 10, 1521. [Google Scholar] [CrossRef]
- Cao, S.; Xue, G.; Song, W.; Teng, Q. Strain rate effect on dynamic mechanical properties and microstructure of cemented tailings composites. Constr. Build. Mater. 2020, 247, 118537. [Google Scholar] [CrossRef]
- Tan, Y.-y.; Yu, X.; Elmo, D.; Xu, L.-h.; Song, W.-d. Experimental study on dynamic mechanical property of cemented tailings backfill under SHPB impact loading. Int. J. Miner. Metall. Mater. 2019, 26, 404–416. [Google Scholar] [CrossRef]
- Xue, G.; Yilmaz, E.; Feng, G.; Cao, S.; Sun, L. Reinforcement effect of polypropylene fiber on dynamic properties of cemented tailings backfill under SHPB impact loading. Constr. Build. Mater. 2021, 279, 122417. [Google Scholar] [CrossRef]
- Yang, L.; Xu, W.; Yilmaz, E.; Wang, Q.; Qiu, J. A combined experimental and numerical study on the triaxial and dynamic compression behavior of cemented tailings backfill. Eng. Struct. 2020, 219, 110957. [Google Scholar] [CrossRef]
- Xu, S.; Suorineni, F.T.; Li, K.; Li, Y. Evaluation of the strength and ultrasonic properties of foam-cemented paste backfill. Int. J. Min. Reclam. Environ. 2017, 31, 544–557. [Google Scholar] [CrossRef]
- Chen, X.; Shi, X.; Zhou, J.; Li, E.; Qiu, P.; Gou, Y. High strain rate compressive strength behavior of cemented paste backfill using split Hopkinson pressure bar. Int. J. Min. Sci. Technol. 2021, 31, 387–399. [Google Scholar] [CrossRef]
- Nasir, O.; Fall, M. Shear behaviour of cemented pastefill-rock interfaces. Eng. Geol. 2008, 101, 146–153. [Google Scholar] [CrossRef]
- Zheng, D.; Song, W.; Cao, S.; Li, J.; Sun, L. Investigation on Dynamical Mechanics, Energy Dissipation, and Microstructural Characteristics of Cemented Tailings Backfill under SHPB Tests. Minerals 2021, 11, 542. [Google Scholar] [CrossRef]
- Wang, C.-l.; Ren, Z.-z.; Huo, Z.-k.; Zheng, Y.-c.; Tian, X.-p.; Zhang, K.-f.; Zhao, G.-f. Properties and hydration characteristics of mine cemented paste backfill material containing secondary smelting water-granulated nickel slag. Alex. Eng. J. 2021, 60, 4961–4971. [Google Scholar] [CrossRef]
- Wu, J.; Yin, Q.; Gao, Y.; Meng, B.; Jing, H. Particle size distribution of aggregates effects on mesoscopic structural evolution of cemented waste rock backfill. Environ. Sci. Pollut. Res. 2021, 28, 16589–16601. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Zhou, N.; Guo, Y.; Li, B.; Yan, H.; Deng, X. Investigation of spatial stratified heterogeneity of cemented paste backfill characteristics in construction demolition waste recycled aggregates. J. Clean. Prod. 2020, 249, 119332. [Google Scholar] [CrossRef]
- Ma, D.; Duan, H.; Li, X.; Li, Z.; Zhou, Z.; Li, T. Effects of seepage-induced erosion on nonlinear hydraulic properties of broken red sandstones. Tunn. Undergr. Space Technol. 2019, 91, 102993. [Google Scholar] [CrossRef]
- Li, X.B.; Lok, T.S.; Zhao, J. Dynamic Characteristics of Granite Subjected to Intermediate Loading Rate. Rock Mech. Rock Eng. 2005, 38, 21–39. [Google Scholar] [CrossRef]
- Li, X.; Zhou, T.; Li, D. Dynamic Strength and Fracturing Behavior of Single-Flawed Prismatic Marble Specimens Under Impact Loading with a Split-Hopkinson Pressure Bar. Rock Mech. Rock Eng. 2017, 50, 29–44. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and fragmentation. J. Geophys. Res. Solid Earth 1986, 91, 1921–1926. [Google Scholar] [CrossRef]
- Deng, Y.; Chen, M.; Jin, Y.; Zou, D. Theoretical analysis and experimental research on the energy dissipation of rock crushing based on fractal theory. J. Nat. Gas Sci. Eng. 2016, 33, 231–239. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhou, T.; Li, D.; Wang, Z. Experimental and Numerical Investigations on Feasibility and Validity of Prismatic Rock Specimen in SHPB. Shock. Vib. 2016, 2016, 7198980. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Gu, H.; Tao, M.; Peng, K.; Cao, W.; Li, Q. Failure characteristics and meso-deterioration mechanism of pre-stressed coal subjected to different dynamic loads. Theor. Appl. Fract. Mech. 2021, 115, 103061. [Google Scholar] [CrossRef]
- Huang, L.-q.; Wang, J.; Momeni, A.; Wang, S.-f. Spalling fracture mechanism of granite subjected to dynamic tensile loading. Trans. Nonferrous Met. Soc. China 2021, 31, 2116–2127. [Google Scholar] [CrossRef]
- Li, X.; Zou, Y.; Zhou, Z. Numerical Simulation of the Rock SHPB Test with a Special Shape Striker Based on the Discrete Element Method. Rock Mech. Rock Eng. 2014, 47, 1693–1709. [Google Scholar] [CrossRef]

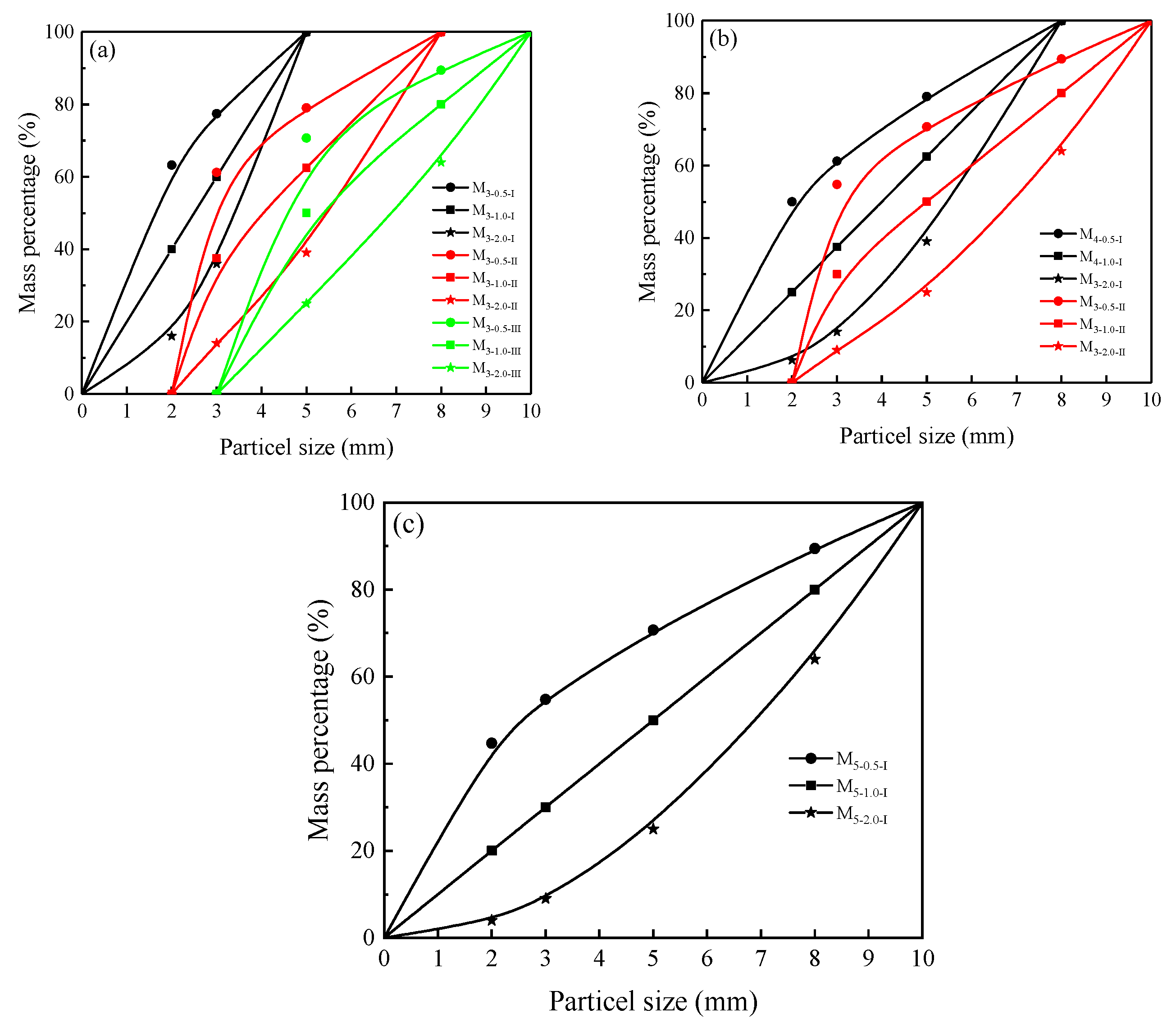





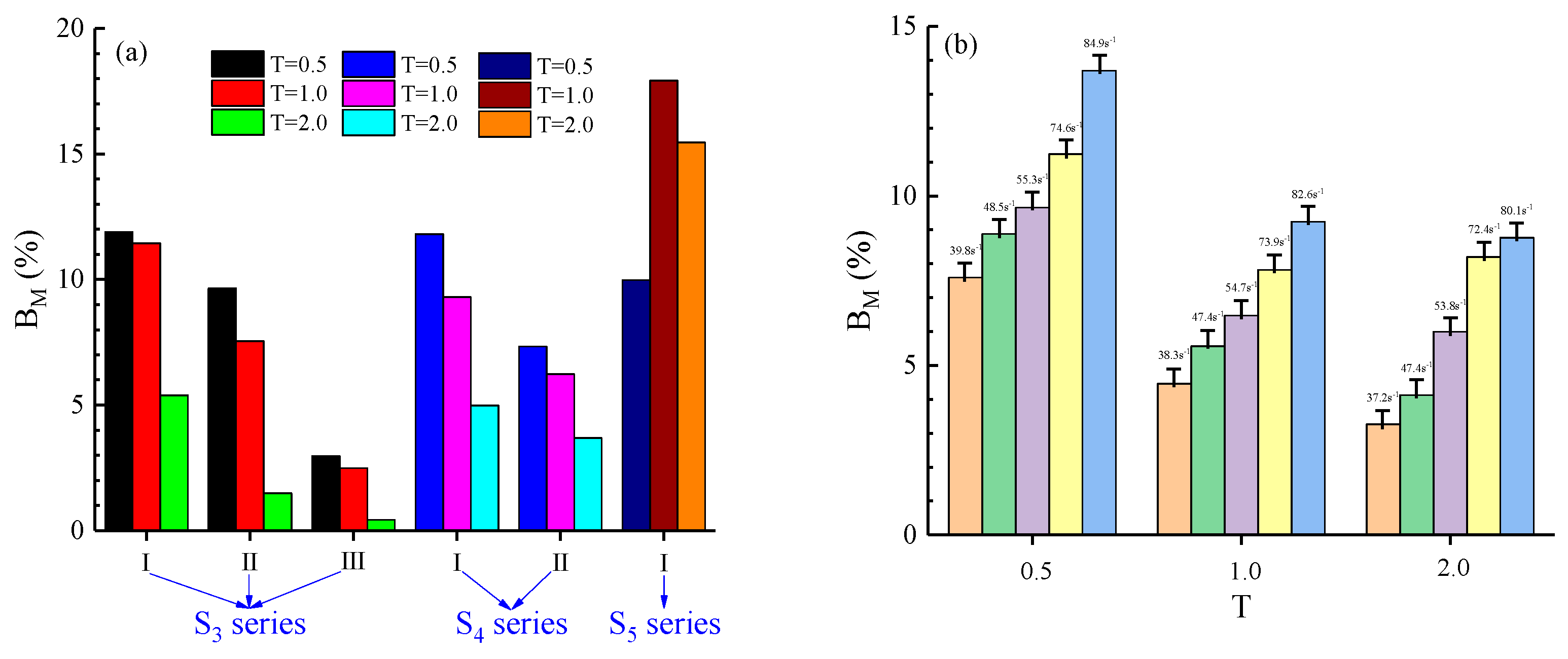

| Sample Number | Talbot Index T | Particle Mass (g) | Total Mass (g) | ||||
|---|---|---|---|---|---|---|---|
| 0–2 mm | 2–3 mm | 3–5 mm | 5–8 mm | 8–10 mm | |||
| S3–0.5-I | 0.5 | 44.27 | 9.95 | 15.78 | / | / | 70.00 |
| S3–0.5-II | / | 42.87 | 12.47 | 14.66 | / | 70.00 | |
| S3–0.5-III | / | / | 49.50 | 13.11 | 7.39 | 70.00 | |
| S3–1.0-I | 1.0 | 28.00 | 14.00 | 28.00 | / | / | 70.00 |
| S3–1.0-II | / | 26.25 | 17.50 | 26.25 | / | 70.00 | |
| S3–1.0-III | / | / | 35.00 | 21.00 | 14.00 | 70.00 | |
| S3–2.0-I | 2.0 | 11.20 | 14.00 | 44.80 | / | / | 70.00 |
| S3–2.0-II | / | 9.84 | 17.50 | 42.66 | / | 70.00 | |
| S3–2.0-III | / | / | 17.50 | 27.30 | 25.20 | 70.00 | |
| S4–0.5-I | 0.5 | 35.00 | 7.87 | 12.47 | 14.66 | / | 70.00 |
| S4–0.5-II | / | 38.34 | 11.16 | 13.11 | 7.39 | 70.00 | |
| S4–1.0-I | 1.0 | 17.50 | 8.75 | 17.50 | 26.25 | / | 70.00 |
| S4–1.0-II | / | 21.00 | 14.00 | 21.00 | 14.00 | 70.00 | |
| S4–2.0-I | 2.0 | 4.38 | 5.47 | 17.50 | 42.65 | / | 70.00 |
| S4–2.0-II | / | 6.30 | 11.20 | 27.30 | 25.20 | 70.00 | |
| S5–0.5-I | 0.5 | 31.30 | 7.04 | 11.16 | 13.11 | 7.39 | 70.00 |
| S5–1.0-I | 1.0 | 14.00 | 7.00 | 14.00 | 21.00 | 14.00 | 70.00 |
| S5–2.0-I | 2.0 | 2.80 | 3.50 | 11.20 | 27.30 | 25.20 | 70.00 |
| Sample No. | Linear Fitting Formula | R2 |
|---|---|---|
| S3–0.5-I | 0.901 | |
| S3–0.5-II | 0.913 | |
| S3–0.5-III | 0.924 | |
| S3–1.0-I | 0.935 | |
| S3–1.0-II | 0.927 | |
| S3–1.0-III | 0.906 | |
| S3–2.0-I | 0.918 | |
| S3–2.0-II | 0.904 | |
| S3–2.0-III | 0.911 | |
| S4–0.5-I | 0.935 | |
| S4–0.5-II | 0.907 | |
| S4–1.0-I | 0.929 | |
| S4–1.0-II | 0.956 | |
| S4–2.0-I | 0.919 | |
| S4–2.0-II | 0.922 | |
| S5–0.5-I | 0.914 | |
| S5–1.0-I | 0.903 | |
| S5–2.0-I | 0.917 |
| Sample No. | Strain Rate | Linear Fitting Formula | R2 |
|---|---|---|---|
| S5–0.5-I | 39.5 s−1 | 0.934 | |
| 48.5 s−1 | 0.921 | ||
| 55.3 s−1 | 0.925 | ||
| 74.6 s−1 | 0.902 | ||
| 84.9 s−1 | 0.945 | ||
| S5–1.0-I | 38.3 s−1 | 0.925 | |
| 47.4 s−1 | 0.931 | ||
| 54.7 s−1 | 0.951 | ||
| 73.9 s−1 | 0.916 | ||
| 82.6 s−1 | 0.912 | ||
| S5–2.0-I | 37.2 s−1 | 0.925 | |
| 47.4 s−1 | 0.933 | ||
| 53.8 s−1 | 0.904 | ||
| 72.4 s−1 | 0.926 | ||
| 80.1 s−1 | 0.938 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Huang, L.; Li, X.; Wu, Y.; Liu, H. Effect of Particle Size Distribution on the Dynamic Mechanical Properties and Fractal Characteristics of Cemented Rock Strata. Mathematics 2022, 10, 2078. https://doi.org/10.3390/math10122078
Wang J, Huang L, Li X, Wu Y, Liu H. Effect of Particle Size Distribution on the Dynamic Mechanical Properties and Fractal Characteristics of Cemented Rock Strata. Mathematics. 2022; 10(12):2078. https://doi.org/10.3390/math10122078
Chicago/Turabian StyleWang, Jiajun, Linqi Huang, Xibing Li, Yangchun Wu, and Huilin Liu. 2022. "Effect of Particle Size Distribution on the Dynamic Mechanical Properties and Fractal Characteristics of Cemented Rock Strata" Mathematics 10, no. 12: 2078. https://doi.org/10.3390/math10122078
APA StyleWang, J., Huang, L., Li, X., Wu, Y., & Liu, H. (2022). Effect of Particle Size Distribution on the Dynamic Mechanical Properties and Fractal Characteristics of Cemented Rock Strata. Mathematics, 10(12), 2078. https://doi.org/10.3390/math10122078







