Observer-Based Finite-Time H_∞ Control of the Blood Gases System in Extracorporeal Circulation via the T-S Fuzzy Model

Abstract

This paper studies the problem of the finite-time $H_{\infty }$ control of the blood gases system, presented as a T-S fuzzy model with bounded disturbance during extracorporeal circulation. The aim was to design an observer-based fuzzy controller to ensure that the closed-loop system was finite-time bounded with the $H_{\infty }$ performance. Firstly, different from the existing results, the T-S fuzzy model of a blood gas control system was developed and a new method was given to process the time derivatives of the membership functions. Secondly, based on the fuzzy Lyapunov function, sufficient conditions for the $H_{\infty }$ finite-time boundedness of the system were obtained by using Finsler’s lemma and matrix decoupling techniques. Simulation results are provided to demonstrate the effectiveness of the proposed methodology.

1. Introduction

Extracorporeal circulation (ECC), mainly consisting of an artificial heart, artificial lungs, thermostats, pipelines, filters, consoles, and electronic instruments, is an important technique in clinical medicine. It is receiving more attention, especially pertaining to major vascular surgery and life support for patients with heart failure, e.g., regarding blood utilization or artificial heart control [1,2,3,4]. In some results, i.e., robust control [5] and finite-time control [6], factors in the blood gas control (BGC) system, such as the flow rate and arterial partial pressure, should be controlled in a finite-time interval, and the transient performance of the system needs to be guaranteed, otherwise, it might cause metabolic alkalosis or acidosis for the patient, or even endanger the patient’s life. Hence, how to control the flow rate and arterial partial pressure of blood gases is an issue. Due to external and internal influences, the BGC during the ECC process, which contains nonlinearity, is complicated. For convenience, the linear state-space model of the BGC system in [5] was given by using standard linearization methods. Although it unavoidably led to larger deviations for the BGC system with nonlinearity, this model—as a research basis—could be improved further by considering the R-C circuit under pulsed operation. To our knowledge, the T-S fuzzy model, since it has better approximation properties, consists of a set of linear models and membership functions (MFs) and can represent a nonlinear system, such as a stochastic system [7] or the inverted pendulum system [8]. In addition, the type-2 fuzzy model [9] is more complex than T-S, and can deal with uncertainty and disturbance. Therefore, it is worthy to consider establishing a T-S fuzzy model of the BGC system.

On the one hand, the analysis and synthesis of the fuzzy system have been diffusely investigated, such as stability analysis, controller design [10,11,12,13], filter design [14,15,16], observer design [17,18,19], etc. Most of the improved methods to reduce conservatism generally focus on designing Lyapunov functions (LFs), analyzing MFs, and introducing slack variables. For nonlinear complex systems, non-quadratic LFs (NQLFs) in [20] (also called fuzzy LFs, multiple fuzzy sums) were designed to overcome the shortcoming of quadratic LFs. Significantly, the derivatives of NQLFs normally include the derivatives of MFs to be dealt with. Some conditions restricting time derivatives of MFs were provided in [21,22,23,24]. On the other hand, different from asymptotic stability based on the Lyapunov stability theory, other concepts, such as finite-time stability (FTS) [25] and finite-time boundedness (FTB) [26,27], were introduced to study the dynamic characteristics of linear and nonlinear systems in finite-time intervals. Moreover, the results on finite-time control were further improved in [28,29,30,31] and the references therein. In recent decades, although the notion of FTB has been extended to various fields, there are few works about FTB in the BGC system. For instance, the resilient controller in [6] was designed to maintain the levels of blood gases. The $H_{\infty }$ finite-time contractive boundedness was proposed in [32] by designing a non-fragile controller. Therefore, it is worth noting that the FTB has good application prospects in the BGC system, combined with the fuzzy control theory.

Inspired by the above discussions, in this paper, we designed an observer-based fuzzy controller for the BGC system via the T-S fuzzy model, such that the closed-loop system is $H_{\infty }$ FTB. The contributions of this paper are listed as follows:

•

The T-S fuzzy model of the blood gas control system, different from the existing results [5,6,32], was built by using the local approximation approach; an observer-based state feedback controller (depending on MFs) was designed.

•

A new method, different from [33], which reduces the redundant restrictive conditions, is proposed in the form of LMIs (to deal with the time derivatives of MFs).

•

Based on non-quadratic LFs, new sufficient conditions for the $H_{\infty }$ FTB of the system were obtained by using the Finsler lemma and matrix decoupling techniques, which include some existing results in [6] as a special case.

Notation: $H^T$ is the transpose of H, the sign $trp\left(H\right)=H+H^T$, $H_h={\sum }_{i=1}^r{h}_i{H}_i$, $H_{hh}={\sum }_{i=1}^r{\sum }_{j=1}^r{h}_i{h}_j{H}_{ij}$. ’*’ in the matrix indicates the transpose of its symmetric term.

2. Preliminaries

2.1. The T-S Fuzzy Model of the BGC System

Based on the complex BGC system shown in [5], the flow rates of gases (O₂ and CO₂) and their arterial partial pressures are considered. The actual control flow is illustrated in Figure 1, where the control inputs $u\left(t\right)$ are the flow rates of O₂ and CO₂, and the arterial partial pressure is the measured output $y\left(t\right)$. Since there are always uncertainties, such as artificial disturbances, the changes in patient physiology, considering the nonlinear BGC system, are as follows:

$$\left\{\begin{array}{c}\dot{x}=f_1(x\left(t\right),u\left(t\right),\omega \left(t\right))\hfill \\ y=f_2(x\left(t\right),u\left(t\right))\hfill \end{array}\right.$$

(1)

where $x\left(t\right)\in {\mathbb{R}}^4,u\left(t\right)\in {\mathbb{R}}^2,y\left(t\right)\in {\mathbb{R}}^2$, and $\omega \left(t\right)\in {\mathbb{R}}^2$ are the actual system state, actual control input, measured output, and disturbances, respectively.

Based on the linear model shown in [5], we established the T-S fuzzy model of the BGC system (1) by applying the local approximation method in [34] as follows:

$$\left\{\begin{array}{cc}\hfill \dot{x}\left(t\right)& =A_{h}x\left(t\right)+B_{h}u\left(t\right)+{\mathsf{\Gamma }}_h\omega \left(t\right)\hfill \\ \hfill z\left(t\right)& =G_{h}x\left(t\right)+D_{h}u\left(t\right)+{\mathsf{\Phi }}_h\omega \left(t\right)\hfill \\ \hfill y\left(t\right)& =C_{h}x\left(t\right)\hfill \end{array}\right.$$

(2)

where $A_h={\sum }_{i=1}^r{h}_i\left(x\right)A_i$, $B_h={\sum }_{i=1}^r{h}_i\left(x\right)B_i$, $C_h={\sum }_{i=1}^r{h}_i\left(x\right)C_i$, $D_h={\sum }_{i=1}^r{h}_i\left(x\right)D_i$, $G_h={\sum }_{i=1}^r{h}_i\left(x\right)G_i$, ${\mathsf{\Gamma }}_h={\sum }_{i=1}^r{h}_i\left(x\right){\mathsf{\Gamma }}_i$, ${\mathsf{\Phi }}_h={\sum }_{i=1}^r{h}_i\left(x\right){\mathsf{\Phi }}_i$, $x\left(t\right)={\left[\begin{array}{cccc}{x}_1\left(t\right)& x_2\left(t\right)& x_3\left(t\right)& x_4\left(t\right)\end{array}\right]}^T$$\in {\mathbb{G}}_1=\left\{\begin{array}{c}x:\left|\begin{array}{c}{x}_k\end{array}\right|\le {\phi }_{1k},k=1,2,3,4\end{array}\right\}$ including the flow rates of O₂ and CO₂ and their arterial partial pressure; $u\left(t\right)={\left[\begin{array}{cc}{u}_1\left(t\right)& u_2\left(t\right)\end{array}\right]}^T$, including the commanded flow rates of O₂ and CO₂; $z\left(t\right)\in {\mathbb{R}}^2$, is the controlled output; $\omega \left(t\right)$ is the external bounded disturbance satisfying ${\omega }^T\omega \le {\sigma }^2$, ${\int }_0^{T_{\tau }}{w}^T\left(t\right)w\left(t\right)dt\le a^2$ for the given actual time $T_{\tau }$, and $h_i\left(x\left(t\right)\right)$ is the normalized MF satisfying the convex sum properties ${\sum }_{i=1}^r{h}_i\left(x\left(t\right)\right)=1$, $0\le h_i\left(x\right)\le 1,i=1,2,\cdots ,r$.

Different from [35], we designed a fuzzy full-dimensional state observer as follows:

$$\left\{\begin{array}{cc}\hfill \dot{\widehat{x}}\left(t\right)& =A_h\widehat{x}\left(t\right)+B_{h}u\left(t\right)+{\mathsf{\Gamma }}_h\omega \left(t\right)+K\left(h\right)(y\left(t\right)-\widehat{y}\left(t\right))\hfill \\ \hfill \widehat{y}\left(t\right)& =C_h\widehat{x}\left(t\right)\hfill \\ \hfill u\left(t\right)& =F\left(h\right)\widehat{x}\left(t\right)\hfill \end{array}\right.$$

(3)

where $\widehat{x}\left(t\right)\in {\mathbb{G}}_2=\left\{\begin{array}{c}\widehat{x}:\left|\begin{array}{c}{\widehat{x}}_k\end{array}\right|\le {\phi }_{2k},k=1,2,3,4\end{array}\right\}$, $K\left(h\right)$, and $F\left(h\right)$ are the observer and controller gains to be designed, and

$$\begin{array}{c}F\left(h\right)=X_{Fh}^{-1}{Y}_{Fh}={\left(\sum _{i=1}^r{h}_i{X}_{Fi}\right)}^{-1}\left(\sum _{i=1}^r{h}_i{Y}_{Fi}\right),\\ K\left(h\right)=X_{Kh}^{-1}{Y}_{Kh}={\left(\sum _{i=1}^r{h}_i{X}_{Ki}\right)}^{-1}\left(\sum _{i=1}^r{h}_i{Y}_{Ki}\right).\end{array}$$

For the sake of brevity, the following parts ignore the time symbol t.

Merging (3) and (2), we have

$$\left\{\begin{array}{c}{\dot{x}}_d=A_d{x}_d+B_d\omega \\ z=C_d{x}_d+D_d\omega \end{array}\right.$$

(4)

where $x_d=\left[\begin{array}{c}x\\ x-\widehat{x}\end{array}\right]$, $A_d=\left[\begin{array}{cc}{A}_h+B_{h}F\left(h\right)& -B_{h}F\left(h\right)\\ 0& A_h-K\left(h\right)C_h\end{array}\right]$, $B_d=\left[\begin{array}{c}{\mathsf{\Gamma }}_h\\ 0\end{array}\right]$, $D_d={\mathsf{\Phi }}_h$, $C_d=\left[\begin{array}{cc}{G}_h+D_{h}F\left(h\right)& -D_{h}F\left(h\right)\end{array}\right]$.

Remark 1.

Effectively, due to physical and external influence, it is reasonable to bound the states in the BGC system. Therefore, the BGC system is signified by the T-S fuzzy model, which is valid in region ${\mathbb{G}}_1$. Similarly, the estimations of the system states need to be bounded.

Definition 1.

Ref. [27]: the system (4) is FTB with respect to $(T_{\tau },a,R,c_1,c_2)$, where $0<c_1<c_2$, $t\in \left[\begin{array}{c}0,T_{\tau }\end{array}\right],R\in {\mathbb{R}}^{n\times n}$ and $R>0$, if $\omega \left(t\right)$ satisfy ${\int }_0^{T_{\tau }}{w}^T\left(t\right)w\left(t\right)dt\le a^2$ and

$$\begin{array}{c}\hfill x_d^T\left(0\right)R{x}_d\left(0\right)\le c_1^2\Rightarrow x_d^T\left(t\right)R{x}_d\left(t\right)<c_2^2\end{array}$$

(5)

Definition 2.

Ref. [35]: the system (4) is $H_{\infty }$ FTB, with respect to $(\gamma ,T_{\tau },R,a,c_1,c_2)$, $\gamma >0$, if system (4) is FTB and under $x\left(0\right)=0$, the output $z\left(t\right)$ satisfies

$${\int }_0^{T_{\tau }}{z}^T\left(t\right)z\left(t\right)dt<{\gamma }^2{\int }_0^{T_{\tau }}{\omega }^T\left(t\right)\omega \left(t\right)dt$$

(6)

for any nonzero $\omega \left(t\right)$.

The aim of this paper was to design $F\left(h\right)$ and $K\left(h\right)$, guaranteeing that system (4) is FTB and the $H_{\infty }$ performance is guaranteed for $T_{\tau }>0$.

2.2. Properties

Property 1.

Ref. [36]: There exists $\rho >0$ and matrices X, $L_i$, $M_i$, and $N_i(i=1,\dots p)$, if

$$\left[\begin{array}{ccccc}X& L_1+\rho M_1& L_2+\rho M_2& \cdots & L_p+\rho M_p\\ *& -\rho N_1-\rho N_1^T& 0& \cdots & 0\\ *& *& -\rho N_2-\rho N_2^T& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ *& *& *& \cdots & -\rho N_p-\rho N_p^T\end{array}\right]<0,$$

then,

$$X+\sum _{i=1}^p[\left(L_i{N}_i^{-1}{M}_i^T\right)+{\left(L_i{N}_i^{-1}{M}_i^T\right)}^T]<0.$$

Property 2.

Ref. [37]: given matrices ${\mathsf{\Omega }}_{ij}$ with suitable dimensions, then, ${\sum }_{i=1}^r{\sum }_{j=1}^r{h}_i{h}_j{\mathsf{\Omega }}_{ij}<0$ holds if

$$\left\{\begin{array}{c}{\mathsf{\Omega }}_{ii}<0,\hfill \\ \frac{2}{r-1}{\mathsf{\Omega }}_{ii}+{\mathsf{\Omega }}_{ij}+{\mathsf{\Omega }}_{ji}<0,i\ne j.\hfill \end{array}\right.$$

Property 3.

Ref. [8]: If matrices M, N, and $Q>0$ have proper dimensions, then,

$$M^{T}N+N^{T}M<M^{T}QM+N^T{Q}^{-1}N.$$

3. Main Results

Different from [35], we designed the fuzzy Lyapunov function

$$V\left(x_d\right)=x_d^T{P}_h{x}_d=x_d^T(\sum _{i=1}^r{h}_i\left(x\right)P_i)x_d.$$

(7)

Then, we have

$$\begin{array}{cc}\hfill \dot{V}\left(x_d\right)& ={\dot{x}}_d^T{P}_h{x}_d+x_d^T{P}_h{\dot{x}}_d+x_d^T{\dot{P}}_h{x}_d\hfill \\ \hfill & =x_d^T(trp\left(P_h{A}_d\right)+{\dot{P}}_h)x_d+2x_d^T{P}_h{B}_d\omega \hfill \end{array}$$

(8)

and

$$\begin{array}{c}\hfill {\dot{P}}_h=\sum _{i=1}^r{\dot{h}}_i{P}_i=\sum _{i=1}^r{(\frac{\partial h_i}{\partial x})}^Tϵ\dot{x}{P}_i=\sum _{i=1}^r\left({\zeta }_i^Tϵ(\mathsf{\Pi }{x}_d+{\mathsf{\Gamma }}_h\omega )\right)P_i,\end{array}$$

(9)

where ${\zeta }_i=\frac{\partial h_i}{\partial x},\mathsf{\Pi }=\left[\begin{array}{cc}{A}_h+B_{h}F\left(h\right)& -B_{h}F\left(h\right)\end{array}\right]$.

Remark 2.

Owing to $h_k$, depending on state x, if $h_k$ depends on all elements of the state, then ϵ is the unit matrix. If $h_k$ depends on the partial state, for example, $h_k$ depends only on $x_3$, then $ϵ=diag\left\{\begin{array}{c}0,0,1,0\end{array}\right\}$.

Based on [33], considering $|{\dot{h}}_k|\le {\mu }_k$$(k=1,2,\cdots ,r)$; that is,

$$\left|{\zeta }_k^Tϵ(\mathsf{\Pi }{x}_d+{\mathsf{\Gamma }}_h\omega )\right|\le {\mu }_k.$$

(10)

Lemma 1.

Expression (10) holds if given $∥\begin{array}{c}{x}_d\end{array}∥\le g$, $∥\begin{array}{c}\frac{\partial h_k}{\partial x}\end{array}∥\le l_k$, $∥\begin{array}{c}\omega \end{array}∥\le \sigma$ and ${\rho }_1>0$, $p=1,2$, there exist $Q_{ij}=Q_{ij}^T$$(i,j=1,2,\cdots ,r)$, such that

$$\left\{\begin{array}{c}{\mathsf{\Omega }}_{ii}^{\left(p\right)}<0,\hfill \\ \frac{2}{r-1}{\mathsf{\Omega }}_{ii}^{\left(p\right)}+{\mathsf{\Omega }}_{ij}^{\left(p\right)}+{\mathsf{\Omega }}_{ji}^{\left(p\right)}<0,i\ne j,\hfill \end{array}\right.$$

(11)

where ${\beta }_k=\frac{2{\mu }_k}{l_k^2+g^2+{\sigma }^2}$, ${\mathsf{\Omega }}_{ij}^{\left(1\right)}=Q_{ij}-{\beta }_{k}I$,

$\begin{array}{c}{\mathsf{\Omega }}_{ij}^{\left(2\right)}=\left[\begin{array}{ccccc}-{\beta }_{k}I& ϵA_i+ϵB_i{Y}_{Fj}& -ϵB_i{Y}_{Fj}& ϵ{\mathsf{\Gamma }}_i& -ϵB_i{X}_{Fj}+ϵB_i\\ *& -Q_{ij}^{11}& -Q_{ij}^{12}& -Q_{ij}^{13}& {\rho }_1{Y}_{Fi}^T\\ *& *& -Q_{ij}^{22}& -Q_{ij}^{23}& -{\rho }_1{Y}_{Fi}^T\\ *& *& *& -Q_{ij}^{33}& 0\\ *& *& *& *& -trp\left({\rho }_1{X}_{Fi}\right)\end{array}\right]\hfill \end{array}$,

$Q_{ij}=\left[\begin{array}{ccc}{Q}_{ij}^{11}& Q_{ij}^{12}& Q_{ij}^{13}\\ *& Q_{ij}^{22}& Q_{ij}^{23}\\ *& *& Q_{ij}^{33}\end{array}\right]$.

Proof. 

Write (10) simply as

$$\left|\begin{array}{c}{\zeta }_k^T\mathsf{\Lambda }\delta \end{array}\right|\le {\mu }_k,$$

(12)

where ${\zeta }_k=\frac{\partial h_k}{\partial x}$, $\mathsf{\Lambda }=\left[\begin{array}{cc}ϵ\mathsf{\Pi }& ϵ{\mathsf{\Gamma }}_h\end{array}\right]$, $\delta =\left[\begin{array}{c}{x}_d\\ \omega \end{array}\right]$.

Expression (12) is equivalent to

$$\left|\begin{array}{c}{\zeta }_k^T\mathsf{\Lambda }\delta \end{array}\right|+\left|\begin{array}{c}{\delta }^T{\mathsf{\Lambda }}^T{\zeta }_k\end{array}\right|\le 2{\mu }_k$$

(13)

By Property 3, there exists a positive definite matrix $Q_{hh}$, such that (13) is deduced by

$${\zeta }_k^T\mathsf{\Lambda }{Q}_{hh}^{-1}{\mathsf{\Lambda }}^T{\zeta }_k+{\delta }^T{Q}_{hh}\delta \le 2{\mu }_k.$$

(14)

Given $∥\begin{array}{c}{x}_d\end{array}∥\le g$, $∥\begin{array}{c}\frac{\partial h_k}{\partial x}\end{array}∥\le l_k$, $∥\begin{array}{c}\omega \end{array}∥\le \sigma$, then

$$\frac{2{\mu }_k}{l_k^2+g^2+{\sigma }^2}({∥\begin{array}{c}{\zeta }_k\end{array}∥}^2+{∥\begin{array}{c}{x}_d\end{array}∥}^2+{∥\begin{array}{c}\omega \end{array}∥}^2)\le 2{\mu }_k.$$

(15)

It can be seen that (14) holds, if (16) holds

$${\begin{array}{c}\left[\begin{array}{c}{\zeta }_k\\ \delta \end{array}\right]\hfill \end{array}}^T\left[\begin{array}{cc}\mathsf{\Lambda }{Q}_{hh}^{-1}{\mathsf{\Lambda }}^T& 0\\ 0& Q_{hh}\end{array}\right]\left[\begin{array}{c}{\zeta }_k\\ \delta \end{array}\right]\le \frac{2{\mu }_k}{l_k^2+g^2+{\sigma }^2}{\begin{array}{c}\left[\begin{array}{c}{\zeta }_k\\ \delta \end{array}\right]\hfill \end{array}}^T\begin{array}{c}\left[\begin{array}{c}{\zeta }_k\\ \delta \end{array}\right]\hfill \end{array}.$$

(16)

Let ${\beta }_k=\frac{2{\mu }_k}{l_k^2+g^2+{\sigma }^2}$, (16) can be ensured by (17) and (18)

$$\mathsf{\Lambda }{Q}_{hh}^{-1}{\mathsf{\Lambda }}^T-{\beta }_{k}I\le 0,$$

(17)

$$Q_{hh}-{\beta }_{k}I\le 0.$$

(18)

Let $Q_{hh}=\left[\begin{array}{ccc}{Q}_{hh}^{11}& Q_{hh}^{12}& Q_{hh}^{13}\\ *& Q_{hh}^{22}& Q_{hh}^{23}\\ *& *& Q_{hh}^{33}\end{array}\right]>0$, by the Schur complement, (17) is equivalent to

$$\left[\begin{array}{cccc}-{\beta }_{k}I& ϵA_h+ϵB_h{X}_{Fh}^{-1}{Y}_{Fh}& -ϵB_h{X}_{Fh}^{-1}{Y}_{Fh}& ϵ{\mathsf{\Gamma }}_h\\ *& -Q_{hh}^{11}& -Q_{hh}^{12}& -Q_{hh}^{13}\\ *& *& -Q_{hh}^{22}& -Q_{hh}^{23}\\ *& *& *& -Q_{hh}^{33}\end{array}\right]\le 0.$$

(19)

Due to

$$ϵB_h{X}_{Fh}^{-1}{Y}_{Fh}=ϵB_h{Y}_{Fh}+(-ϵB_h{X}_{Fh}+ϵB_h)X_{Fh}^{-1}{Y}_{Fh},$$

(20)

then, (19) is decomposed into

$${\mathsf{\Pi }}_1+trp\left(\left[\begin{array}{c}-ϵB_h{X}_{Fh}+ϵB_h\\ 0\\ 0\\ 0\end{array}\right]X_{Fh}^{-1}\left[\begin{array}{cccc}0& Y_{Fh}& -Y_{Fh}& 0\end{array}\right]\right)\le 0,$$

(21)

where

$${\mathsf{\Pi }}_1=\left[\begin{array}{cccc}-{\beta }_{k}I& ϵA_h+ϵB_h{Y}_{Fh}& -ϵB_h{Y}_{Fh}& ϵ{\mathsf{\Gamma }}_h\\ *& -Q_{hh}^{11}& -Q_{hh}^{12}& -Q_{hh}^{13}\\ *& *& -Q_{hh}^{22}& -Q_{hh}^{23}\\ *& *& *& -Q_{hh}^{33}\end{array}\right].$$

By Property 1, (21) is guaranteed by

$${\mathsf{\Omega }}_{hh}^{\left(2\right)}=\begin{array}{c}\left[\begin{array}{ccccc}-{\beta }_{k}I& ϵA_h+ϵB_h{Y}_{Fh}& -ϵB_h{Y}_{Fh}& ϵ{\mathsf{\Gamma }}_h& -ϵB_h{X}_{Fh}+ϵB_h\\ *& -Q_{hh}^{11}& -Q_{hh}^{12}& -Q_{hh}^{13}& {\rho }_1{Y}_{Fh}^T\\ *& *& -Q_{hh}^{22}& -Q_{hh}^{23}& -{\rho }_1{Y}_{Fh}^T\\ *& *& *& -Q_{hh}^{33}& 0\\ *& *& *& *& -trp\left({\rho }_1{X}_{Fh}\right)\end{array}\right]\le 0.\hfill \end{array}$$

(22)

So (22) can be ensured by (11) with ${\mathsf{\Omega }}_{ij}^{\left(2\right)}$.

In addition, (11) with ${\mathsf{\Omega }}_{ij}^{\left(1\right)}$ also guarantees (18). Therefore, (10) holds. □

Remark 3.

To reduce the conservatism, Ref. [33] introduced many unknown parameters to be searched, but it is time-consuming. This paper reduces the introduction of parameters by applying the equivalence transformation.

Theorem 1.

The BGC system (4) is $H_{\infty }$ FTB with respect to $(c_1,c_2,T_{\tau },R,\gamma ,a)$ under the observer-based fuzzy controller (3) if given matrix $R>0$ and positive scalars g, $l_k$, σ, ${\rho }_1$, ${\rho }_2$, α, $T_{\tau }$, $c_1$, a, there exist matrices $P_i>0$, $X_{Ki}$, $X_{Fi}$, $Y_{Ki}$, $Y_{Fi}$, $M_{ij}$ ($i,j=1,2,\dots ,r$) and $\eta >0$, $c_2>0$, $\gamma >0$, such that the LMIs (11) with ${\mathsf{\Omega }}_{ij}^{\left(p\right)}$($p=1,2,3,4$) and (23), (24) hold

$$R<P_i<\eta R,$$

(23)

$$e^{\alpha T_{\tau }}\eta c_1^2+{\gamma }^2{a}^2-c_2^2<0,$$

(24)

where

$$\begin{array}{c}{\mathsf{\Omega }}_{ij}^{\left(3\right)}=\left[\begin{array}{ccccc}{\mathsf{\Xi }}_{ij}^{11}& P_i{\overline{\mathsf{\Gamma }}}_j& {\mathsf{\Xi }}_{ij}^{13}& {\mathsf{\Xi }}_{ij}^{14}& {\mathsf{\Xi }}_{ij}^{15}\\ *& -{\gamma }^2{e}^{-\alpha T_{\tau }}& {\mathsf{\Phi }}_i^T& 0& 0\\ *& *& -I& {\mathsf{\Xi }}_{ij}^{34}& 0\\ *& *& *& {\mathsf{\Xi }}_i^{44}& 0\\ *& *& *& *& {\mathsf{\Xi }}_i^{55}\end{array}\right],\hfill \end{array}$$

$${\mathsf{\Omega }}_{ij}^{\left(4\right)}=M_{ij}+P_k,k=1,2,\cdots ,r,$$

${\mathsf{\Xi }}_{ij}^{11}=trp(P_i{\overline{A}}_j+{\overline{B}}_i{Y}_{Fj}{I}_1+I_2{Y}_{Ki}{\overline{C}}_j)-\alpha P_i+{\sum }_{k=1}^r{\mu }_k(P_k+M_{ij})$, ${\mathsf{\Xi }}_{ij}^{13}={\overline{G}}_i^T+I_1^T{Y}_{Fj}^T{D}_i^T$, ${\mathsf{\Xi }}_{ij}^{14}=-{\overline{B}}_i{X}_{Fj}+P_i{\overline{B}}_j+{\rho }_1{I}_1^T{Y}_{Fi}^T$, ${\mathsf{\Xi }}_{ij}^{15}=-I_2{X}_{Ki}+P_i{I}_2+{\rho }_1{\overline{C}}_i^T{Y}_{Fj}^T$, ${\mathsf{\Xi }}_{ij}^{34}=-D_i{X}_{Fj}+D_i$, ${\mathsf{\Xi }}_i^{44}=-{\rho }_2{X}_{Fi}-{\rho }_2{X}_{Fi}^T$, ${\mathsf{\Xi }}_i^{55}=-{\rho }_2{X}_{Ki}-{\rho }_2{X}_{Ki}^T$.

Proof. 

Let $\mathbf{J}=\dot{V}\left(x_d\left(t\right)\right)-\alpha V\left(x_d\left(t\right)\right)-{\gamma }^2{e}^{-\alpha T_{\tau }}{\omega }^T\omega +z^{T}z$, then $\mathbf{J}<0$ is ensured by

$${\delta }^T({\mathsf{\Theta }}_1+{\left[\begin{array}{cc}{C}_d& D_d\end{array}\right]}^T\left[\begin{array}{cc}{C}_d& D_d\end{array}\right])\delta <0,$$

(25)

where $\delta =\left[\begin{array}{c}{x}_d\\ \omega \end{array}\right],{\mathsf{\Theta }}_1=\left[\begin{array}{cc}trp\left(P_h{A}_d\right)-\alpha P_h+{\dot{P}}_h& P_h{B}_d\\ *& -{\gamma }^2{e}^{-\alpha T_{\tau }}\end{array}\right]$.

For convenience, considering matrices ${\overline{A}}_h=\left[\begin{array}{cc}{A}_h& 0\\ 0& A_h\end{array}\right]$, ${\overline{B}}_h=\left[\begin{array}{c}{B}_h\\ 0\end{array}\right]$, ${\overline{C}}_h=\left[\begin{array}{cc}0& C_h\end{array}\right]$, ${\overline{G}}_h=\left[\begin{array}{cc}{G}_h& 0\end{array}\right]$, ${\overline{\mathsf{\Gamma }}}_h=\left[\begin{array}{c}{\mathsf{\Gamma }}_h\\ 0\end{array}\right]$, $I_1=\left[\begin{array}{cc}I& -I\end{array}\right]$, $I_2=\left[\begin{array}{c}0\\ -I\end{array}\right]$, then $A_d={\overline{A}}_h+{\overline{B}}_h{X}_{Fh}^{-1}{Y}_{Fh}{I}_1+I_2{X}_{Kh}^{-1}{Y}_{Kh}{\overline{C}}_h$, $B_d={\overline{\mathsf{\Gamma }}}_h$, $C_d={\overline{G}}_h+D_h{X}_{Fh}^{-1}{Y}_{Fh}{I}_1$, $D_d={\mathsf{\Phi }}_h$, $P_h{A}_d=P_h{\overline{A}}_h+P_h{\overline{B}}_h{X}_{Fh}^{-1}{Y}_{Fh}{I}_1+P_h{I}_2{X}_{Kh}^{-1}{Y}_{Kh}{\overline{C}}_h$ and $P_h{B}_d=P_h{\overline{\mathsf{\Gamma }}}_h$.

By the Schur complement, (25) is equivalent to

$$\left[\begin{array}{ccc}{\mathsf{\Delta }}_1& P_h{\overline{\mathsf{\Gamma }}}_h& {({\overline{G}}_h+D_h{X}_{Fh}^{-1}{Y}_{Fh}{I}_1)}^T\\ *& -{\gamma }^2{e}^{-\alpha T_{\tau }}& {\mathsf{\Phi }}_h^T\\ *& *& -I\end{array}\right]<0,$$

(26)

where ${\mathsf{\Delta }}_1=trp(P_h{\overline{A}}_h+P_h{\overline{B}}_h{X}_{Fh}^{-1}{Y}_{Fh}{I}_1+P_h{I}_2{X}_{Kh}^{-1}{Y}_{Kh}{\overline{C}}_h)-\alpha P_h+{\dot{P}}_h$.

Due to ${\sum }_{i=1}^r{\dot{h}}_i=0$, there exits a symmetric matrix $M_{hh}={\sum }_{i=1}^r{\sum }_{j=1}^r{h}_i{h}_j{M}_{ij}$ with proper dimensions, and ${\sum }_{i=1}^r{\dot{h}}_i{M}_{hh}=0$, such that

$$P_i+M_{hh}\ge 0,i=1,2,\cdots ,r.$$

(27)

Obviously, (27) can be guaranteed by (11) with ${\mathsf{\Omega }}_{ij}^{\left(4\right)}$.

Owing to $|{\dot{h}}_k|\le {\mu }_k$, then

$$\begin{array}{cc}\hfill {\dot{P}}_h& =\sum _{k=1}^r{\dot{h}}_k(P_k+M_{hh})\hfill \\ \hfill & \le \sum _{k=1}^r{\mu }_k(P_k+M_{hh}).\hfill \end{array}$$

(28)

Expression (26) holds if (29) holds

$$\left[\begin{array}{ccc}{\mathsf{\Delta }}_2& P_h{\overline{\mathsf{\Gamma }}}_h& {({\overline{G}}_h+D_h{X}_{Fh}^{-1}{Y}_{Fh}{I}_1)}^T\\ *& -{\gamma }^2{e}^{-\alpha T_{\tau }}& {\mathsf{\Phi }}_h^T\\ *& *& -I\end{array}\right]<0,$$

(29)

where ${\mathsf{\Delta }}_2=trp(P_h{\overline{A}}_h+P_h{\overline{B}}_h{X}_{Fh}^{-1}{Y}_{Fh}{I}_1+P_h{I}_2{X}_{Kh}^{-1}{Y}_{Kh}{\overline{C}}_h)-\alpha P_h+{\sum }_{k=1}^r{\mu }_k(P_k+M_{hh})$.

By using a similar process to (20) and (21), (29) is equivalent to

$${\mathsf{\Theta }}_2+trp\left(\left[\begin{array}{c}-{\overline{B}}_h{X}_{Fh}+P_h{\overline{B}}_h\\ 0\\ -D_h{X}_{Fh}+D_h\end{array}\right]X_{Fh}^{-1}\left[\begin{array}{ccc}{Y}_{Fh}{I}_1& 0& 0\end{array}\right]\right)<0,$$

(30)

where

$${\mathsf{\Theta }}_2=\left[\begin{array}{ccc}{\mathsf{\Xi }}_{hh}^{11}& P_h{\overline{\mathsf{\Gamma }}}_h& {({\overline{G}}_h+D_h{Y}_{Fh}{I}_1)}^T\\ *& -{\gamma }^2{e}^{-\alpha T_{\tau }}& {\mathsf{\Phi }}_h^T\\ *& *& -I\end{array}\right],$$

${\mathsf{\Xi }}_{hh}^{11}=trp(P_h{\overline{A}}_h+{\overline{B}}_h{Y}_{Fh}{I}_1+I_2{Y}_{Kh}{\overline{C}}_h)-\alpha P_h+{\sum }_{k=1}^r{\mu }_k(P_k+M_{hh})$.

By Property 1, we know that (30) holds if (31) holds

$$\left[\begin{array}{ccccc}{\mathsf{\Xi }}_{hh}^{11}& P_h{\overline{\mathsf{\Gamma }}}_h& {\mathsf{\Xi }}_{hh}^{13}& {\mathsf{\Xi }}_{hh}^{14}& {\mathsf{\Xi }}_{hh}^{15}\\ *& -{\gamma }^2{e}^{-\alpha T_{\tau }}& {\mathsf{\Phi }}_h^T& 0& 0\\ *& *& -I& {\mathsf{\Xi }}_{hh}^{34}& 0\\ *& *& *& {\mathsf{\Xi }}_h^{44}& 0\\ *& *& *& *& {\mathsf{\Xi }}_h^{55}\end{array}\right]<0,$$

(31)

where ${\mathsf{\Xi }}_{hh}^{13}={\overline{G}}_h^T+I_1^T{Y}_{Fh}^T{D}_h^T$, ${\mathsf{\Xi }}_{hh}^{14}=-{\overline{B}}_h{X}_{Fh}+P_h{\overline{B}}_h+{\rho }_1{I}_1^T{Y}_{Fh}^T$, ${\mathsf{\Xi }}_{hh}^{15}=-I_2{X}_{Kh}+P_h{I}_2+{\rho }_1{\overline{C}}_h^T{Y}_{Fh}^T$, ${\mathsf{\Xi }}_{hh}^{34}=-D_h{X}_{Fh}+D_h$, ${\mathsf{\Xi }}_h^{44}=-{\rho }_2{X}_{Fh}-{\rho }_2{X}_{Fh}^T$, ${\mathsf{\Xi }}_h^{55}=-{\rho }_2{X}_{Kh}-{\rho }_2{X}_{Kh}^T$.

By Property 2, (31) is ensured by (11) with ${\mathsf{\Omega }}_{ij}^{\left(3\right)}$.

On the one hand, (25) implies that

$${\mathsf{\Theta }}_1<0,$$

(32)

which means

$$\begin{array}{c}\hfill \dot{V}\left(x_d\right)<\alpha V\left(x_d\right)+{\gamma }^2{e}^{-\alpha T_{\tau }}{\omega }^T\omega .\end{array}$$

(33)

Multiplying left and right by $e^{-\alpha t}$ and integrating from 0 to t with $t\in [0,T_{\tau }]$, (33) turns into

$$V\left(x_d\left(t\right)\right)<e^{\alpha t}V\left(x_d\left(0\right)\right)+{\gamma }^2{e}^{-\alpha T_{\tau }}{\int }_0^t{e}^{\alpha (t-\varphi )}{w}^T\left(\varphi \right)w\left(\varphi \right)d\varphi .$$

(34)

Given $\alpha >0,0\le t\le T_{\tau }$, then $e^{\alpha t}\le e^{\alpha T_{\tau }}$. So (34) implies

$$\begin{array}{c}\hfill V\left(x_d\left(t\right)\right)<e^{\alpha T_{\tau }}\left(x_d^T\left(0\right)P_h{x}_d\left(0\right)\right)+{\gamma }^2{\int }_0^{T_{\tau }}{\omega }^T\left(t\right)\omega \left(t\right)dt.\end{array}$$

(35)

(23) guarantees

$$R<P_h<\eta R.$$

(36)

By (24), (35) and (36), we have

$$x_d^{T}R{x}_d<V\left(x_d\right)<e^{\alpha T_{\tau }}\eta c_1^2+{\gamma }^2{a}^2<c_2^2.$$

(37)

Therefore, by Definition 1, system (4) is FTB.

On the other hand, under $V\left(x_d\left(0\right)\right)=0$, both sides of $\mathbf{J}<0$ are multiplied by $e^{-\alpha t}$ and integrated from 0 to $T_{\tau }$ to have

$$\begin{array}{c}\hfill V\left(x_d\left(T_{\tau }\right)\right)<{\gamma }^2{\int }_0^{T_{\tau }}{e}^{-\alpha t}{\omega }^T\left(t\right)\omega \left(t\right)dt-e^{\alpha T_{\tau }}{\int }_0^{T_{\tau }}{e}^{-\alpha t}{z}^T\left(t\right)z\left(t\right)dt.\end{array}$$

(38)

Due to $0<V\left(x_d\left(T_{\tau }\right)\right)$ and $0\le t\le T_{\tau }$, then $1\ge e^{-\alpha t}\ge e^{-\alpha T_{\tau }}$, from (38) we have

$${\int }_0^{T_{\tau }}{z}^T\left(t\right)z\left(t\right)dt<{\gamma }^2{\int }_0^{T_{\tau }}{\omega }^T\left(t\right)\omega \left(t\right)dt.$$

(39)

Thus, by Definition 2, the BGC system (4) is $H_{\infty }$ FTB. □

Remark 4.

To obtain and easily solve LMI conditions, Ref. [18] designed the LF matrices with diagonal structures (which might lead to conservatism). However, this paper rids itself of this restriction.

Remark 5.

Based on the linearized state-space model in [6], if Theorem 1 is adapted to $P_i=P$, $X_{Ki}=X_L$, $X_{Fi}=X_K$, $Y_{Ki}=Y_L$, $Y_{Fi}=Y_K$, the results of Corollary 1 in [6] will be obtained. Therefore, Theorem 1 contains Corollary 1 in [6] as a special case.

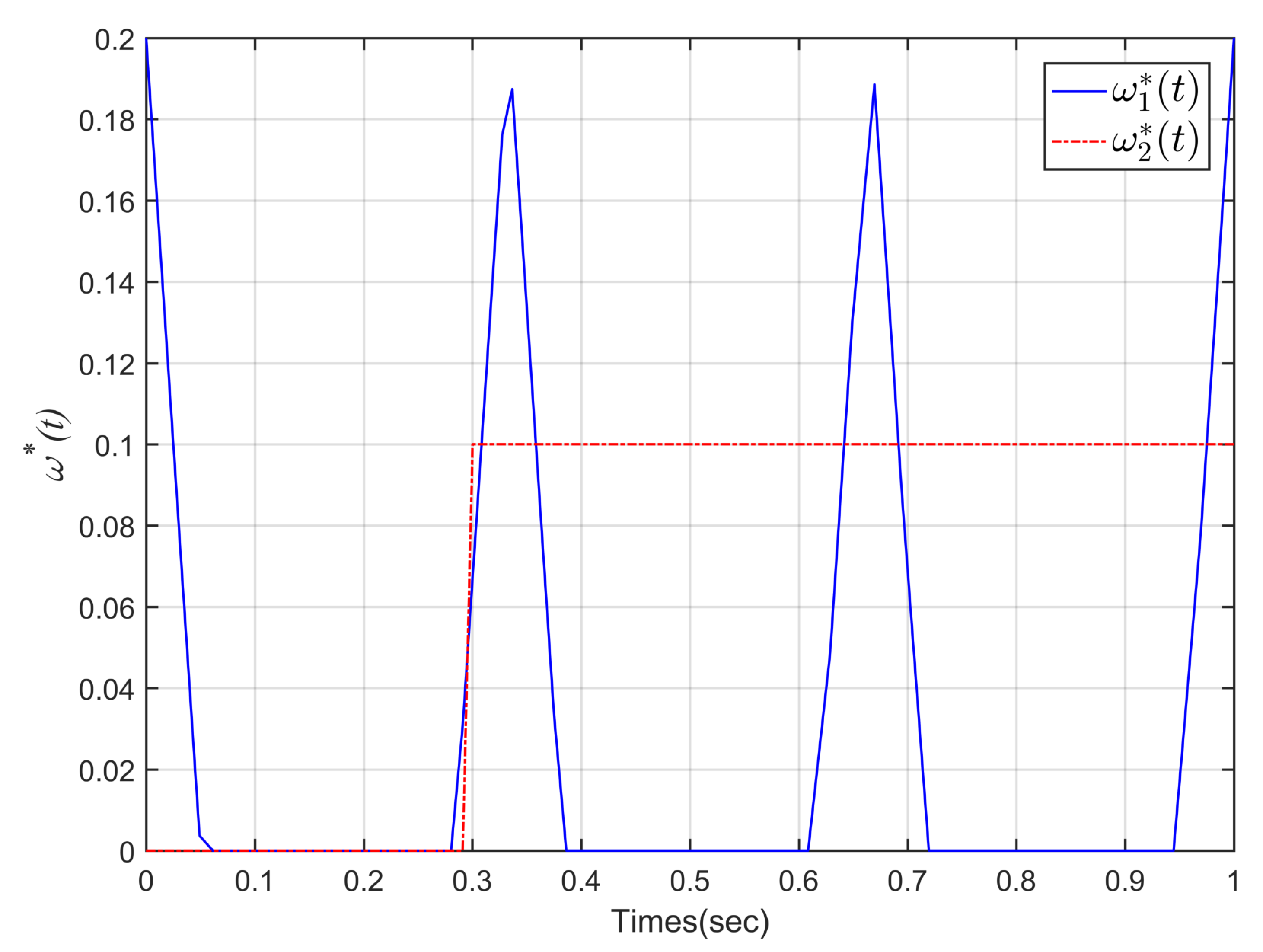
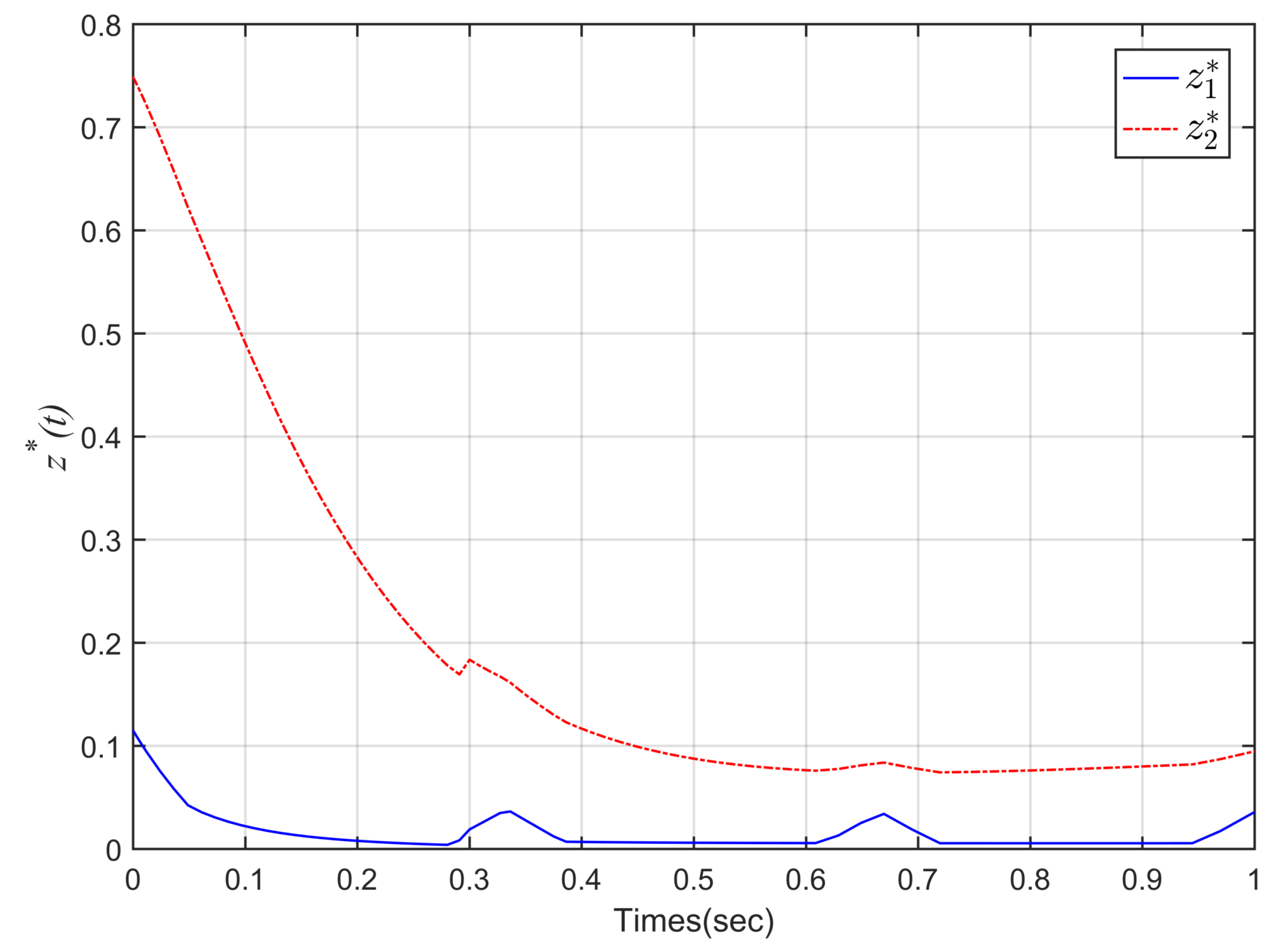
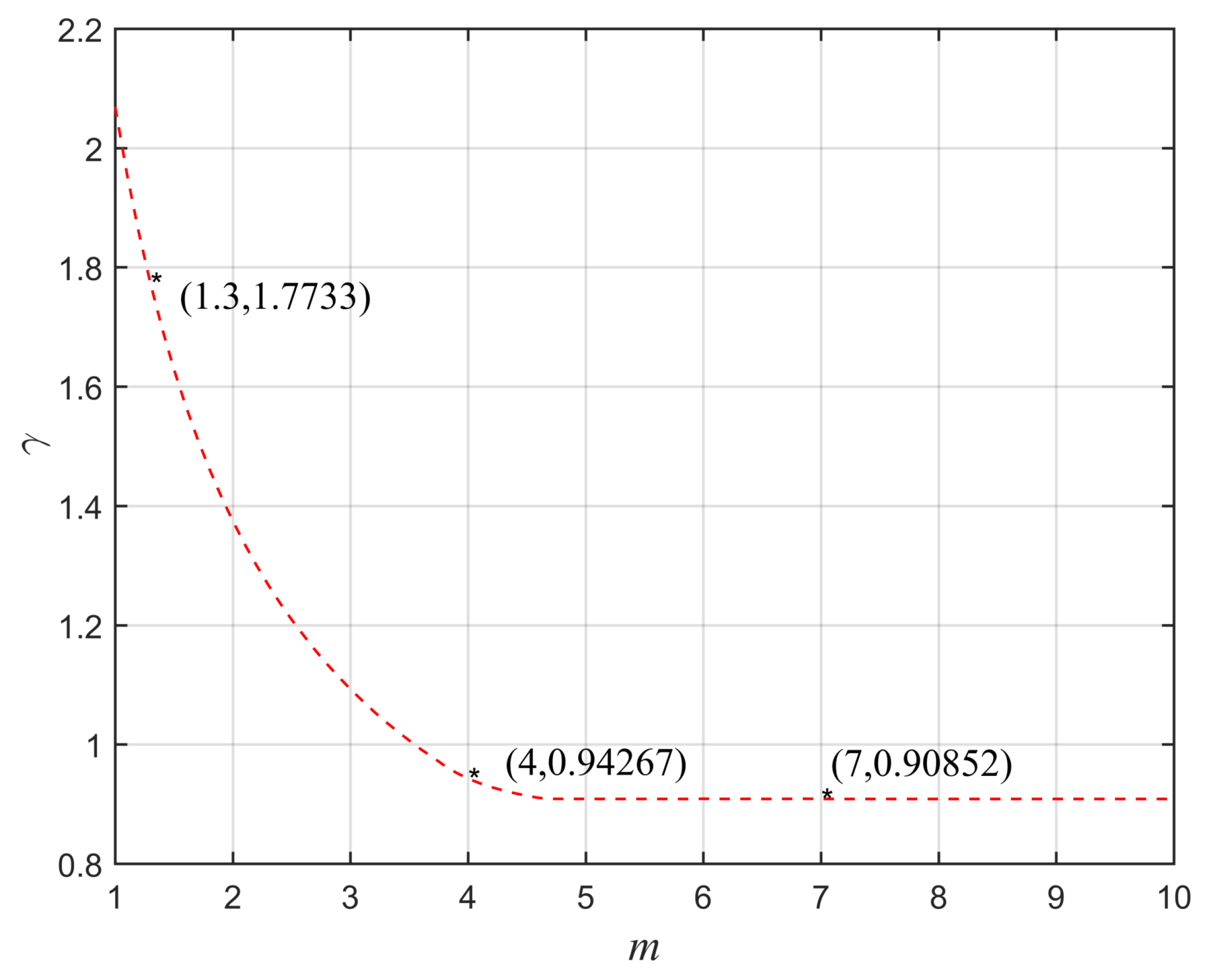
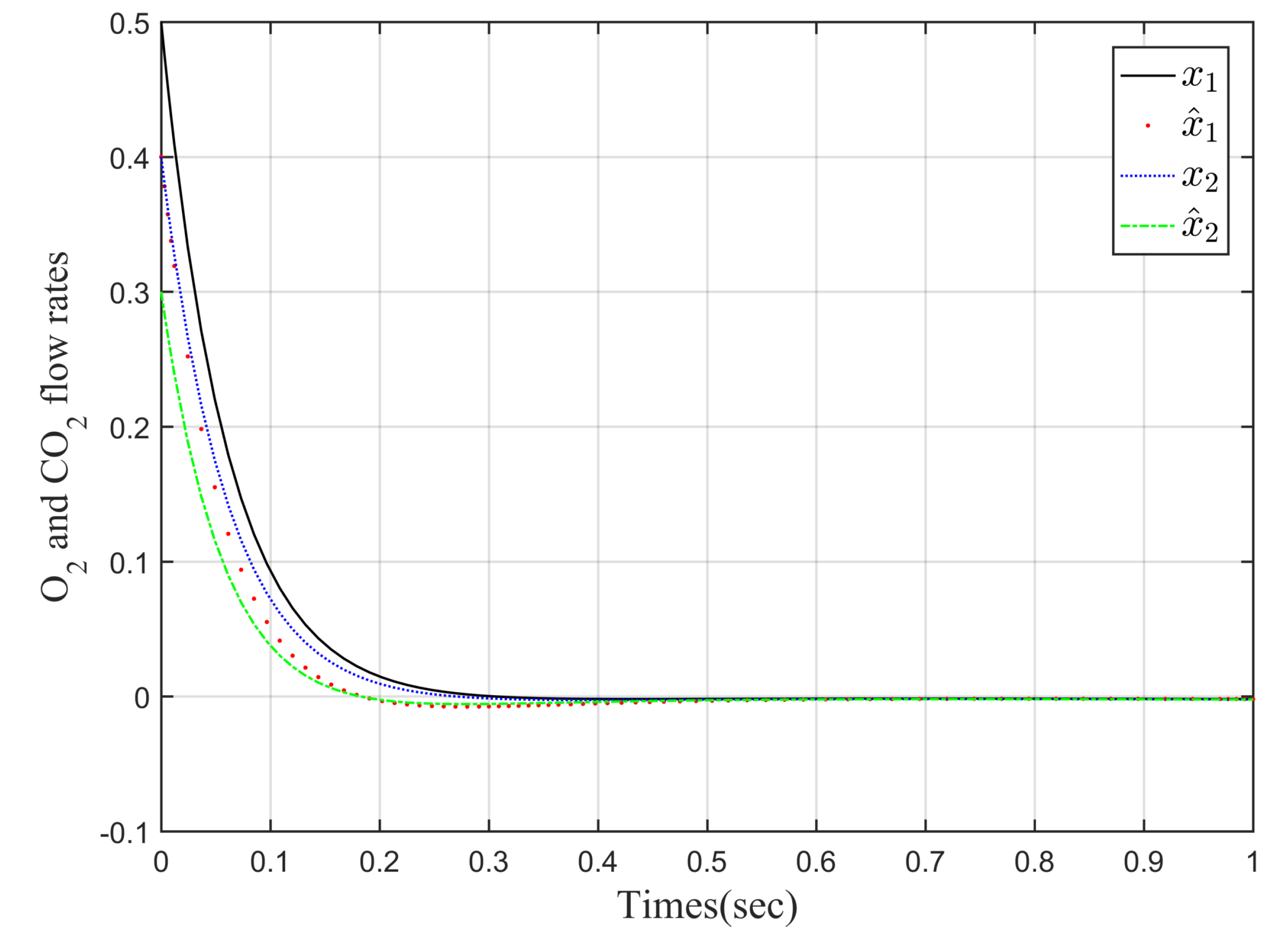
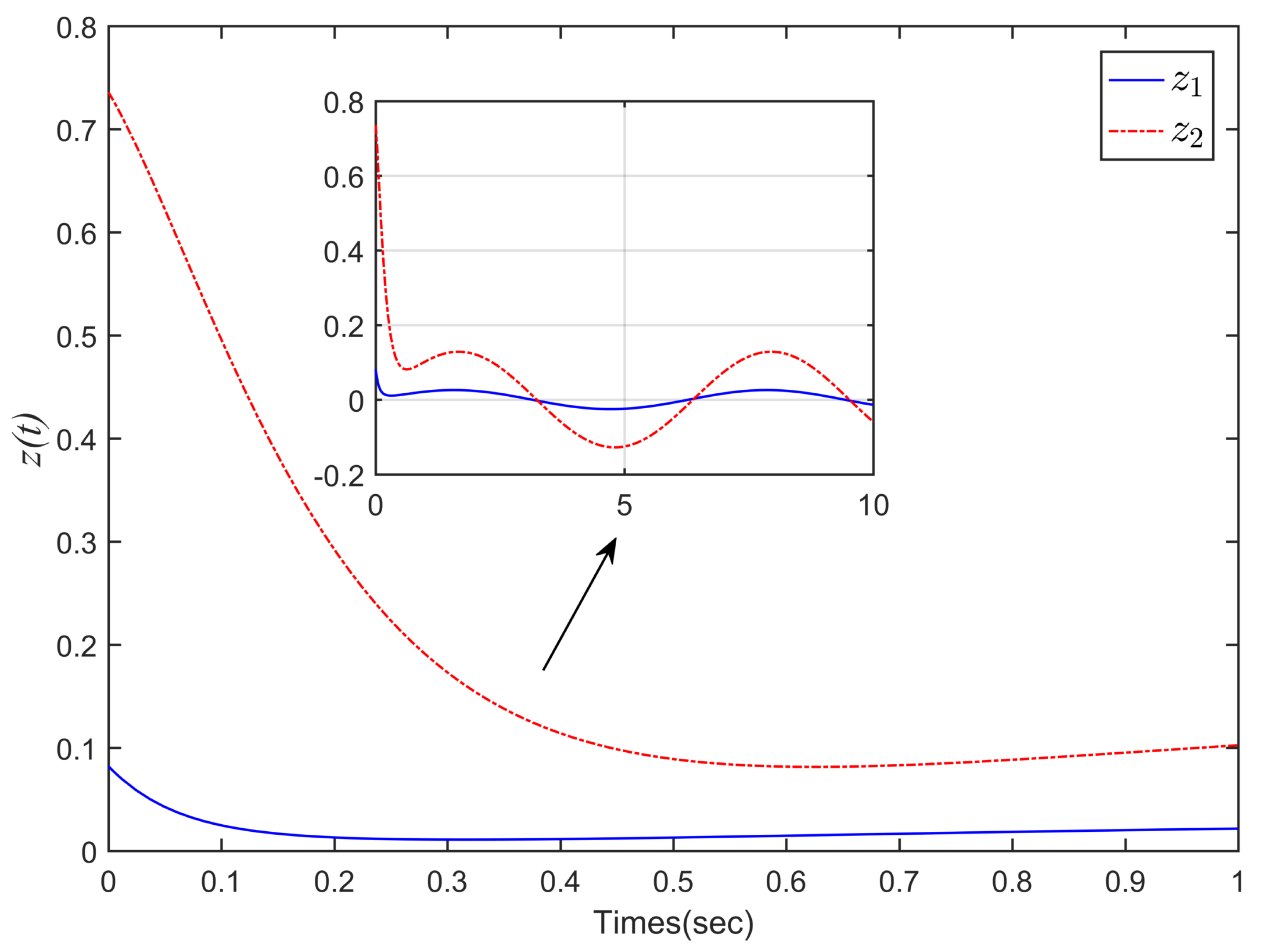
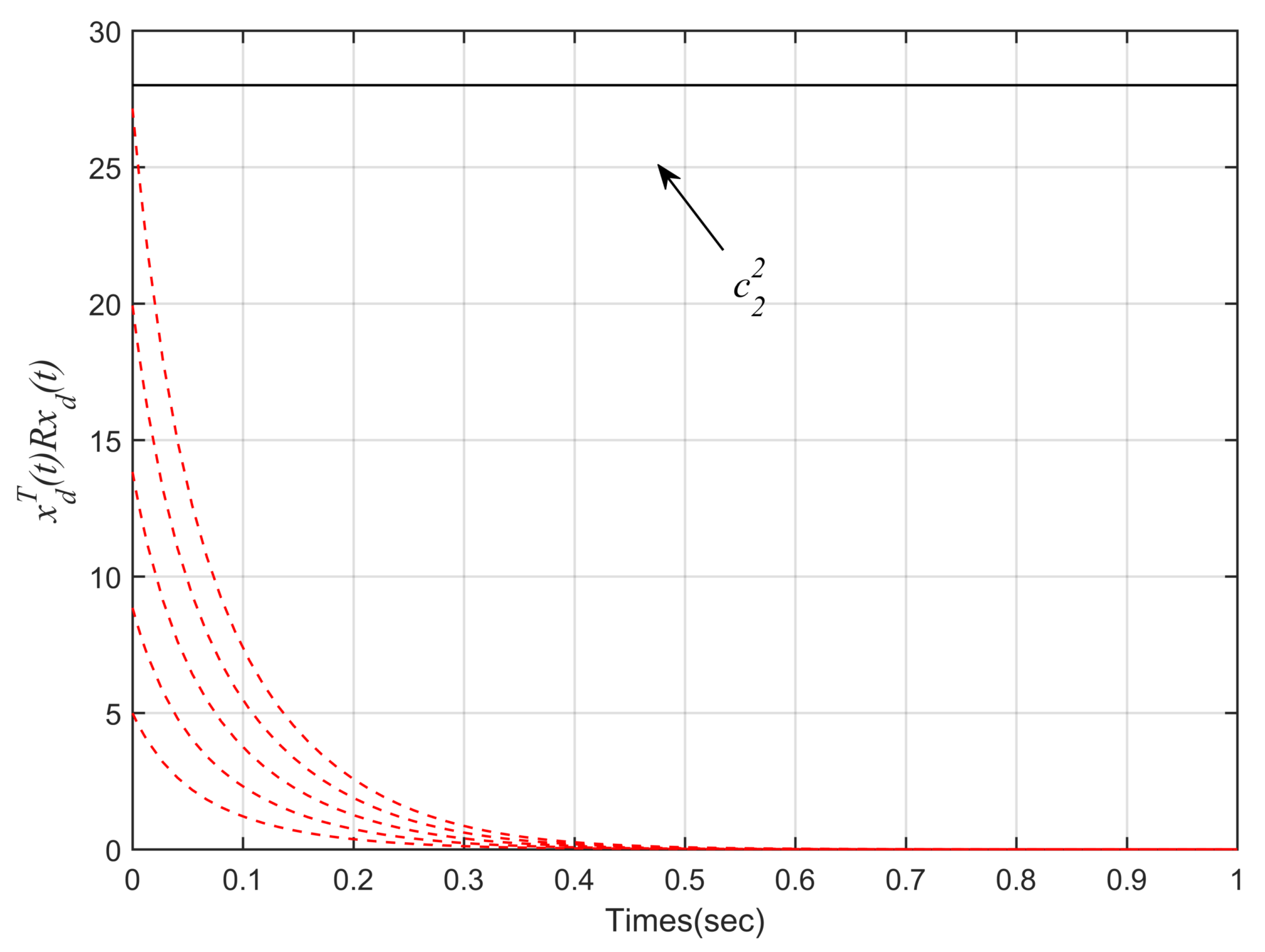
4. Simulation Example

Based on the reasonable nominal data in [38], by using the local approximation method of fuzzy control, we consider (2) with

$A_1=\left[\begin{array}{cccc}-10.045& 0.002& 0.003& 0.001\\ 0.001& -9.989& 0.001& 0.001\\ 6.045& -3.002& -4.997& 0.001\\ 0.002& 0.505& 0.001& -5.002\end{array}\right]$, $A_2=\left[\begin{array}{cccc}-6.012& 0.003& 0.001& 0.002\\ 0.003& -12.023& 0.002& 0.003\\ 5.234& -4.021& -m& 0.002\\ 0.001& 0.323& 0.003& -7.132\end{array}\right]$,

$B_1=\left[\begin{array}{cc}10& 0\\ 0& 10\\ 0& 0\\ 0& 0\end{array}\right],B_2=\left[\begin{array}{cc}8& 1\\ 2& 9\\ 0& 0\\ 2& 1\end{array}\right],C_1^T=\left[\begin{array}{cc}0& 0\\ 0& 0\\ 0& 1\\ 1& 0\end{array}\right]$, $C_2^T=\left[\begin{array}{cc}0& 0\\ 0& 0\\ 0& 1\\ 1& 0\end{array}\right],{\mathsf{\Gamma }}_1=\left[\begin{array}{cc}0.1& 0\\ 0.1& 0\\ 0& 1\\ 0& 1\end{array}\right],{\mathsf{\Gamma }}_2=\left[\begin{array}{cc}0.1& 0.2\\ 0.1& 0\\ 0& 1\\ 0& 1\end{array}\right]$, $G_1^T=\left[\begin{array}{cc}0.2& 0\\ 0.3& 0\\ 0& 1\\ 0& 1\end{array}\right],G_2^T=\left[\begin{array}{cc}0.1& 0.4\\ 0.1& 0.1\\ 0.1& 0.1\\ 2& 2\end{array}\right],D_1=\left[\begin{array}{cc}0.2& 0.1\\ 0.1& 0.3\end{array}\right]$, $D_2=\left[\begin{array}{cc}0.1& 0.2\\ 0.2& 0.1\end{array}\right],{\mathsf{\Phi }}_1=\left[\begin{array}{cc}0.2& 0.1\\ 0.1& 0.3\end{array}\right],{\mathsf{\Phi }}_2=\left[\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right]$.

Given ${\phi }_{11}=0.5$, ${\phi }_{12}={\phi }_{21}=0.4$, ${\phi }_{13}={\phi }_{14}={\phi }_{22}=0.3$, ${\phi }_{23}={\phi }_{24}=0.2$. Considering $h_1\left(x\left(t\right)\right)=\frac{sin\left(x_3\right)+1}{2}$, $h_2=1-h_1$, then $\frac{\partial h_1}{\partial x}={\left[\begin{array}{cccc}0& 0& \frac{cos\left(x_3\right)}{2}& 0\end{array}\right]}^T$, $\frac{\partial h_2}{\partial x}=-\frac{\partial h_1}{\partial x}$, thus $l_1^2=l_2^2=\frac{1}{4}$. The external disturbance of the system is represented by sine waves, as shown in Figure 2. In order to obtain the dynamic output response of the system under different disturbances, two different disturbance signals, shown in Figure 3, were added; the corresponding responses are shown in Figure 4, from which it can be seen that the $H_{\infty }$ performance of the system is still guaranteed under different disturbances. In Theorem 1, we give $g=1$, $\alpha =0.5$, ${\rho }_1={\rho }_2=1$, $c_1=3$, $T_{\tau }=1$, $R=I$, $a=1$, and ${\sigma }^2=0.05$.

Considering $m\in \left[\begin{array}{c}1,10\end{array}\right]$, it can be seen that $\gamma$ decreases as m increases in Figure 5. However, when m increases to a certain value, $\gamma$ hardly decreases, which demonstrates the rejection of the designed method to changes in the parameters of the system.

When $m=5$, we have $\gamma =0.915$; the observer gains and controller gains are as follows

$X_{K1}=\left[\begin{array}{cccc}3.1291& -0.1299& 1.3003& 0.0074\\ -0.1315& 2.9072& -0.6823& 0.1082\\ -1.3882& 0.7232& 1.9007& 0.0009\\ -0.0060& -0.1181& 0.0008& 1.9077\end{array}\right]\times {10}^4$, $Y_{K1}=\left[\begin{array}{cc}0.0126& 2.6764\\ 0.2287& -1.4003\\ 0.0218& 4.2223\\ 4.6372& 0.0218\end{array}\right]\times {10}^4$, $X_{K2}=\left[\begin{array}{cccc}3.6175& -0.1623& 1.3662& 0.0118\\ -0.1585& 3.3145& -0.7542& 0.0857\\ -1.7459& 0.9348& 2.1909& 0.0004\\ -0.0126& -0.0944& 0.0004& 2.2916\end{array}\right]\times {10}^4$, $Y_{K2}=\left[\begin{array}{cc}0.0250& 3.2595\\ 0.1817& -1.7561\\ 0.0212& 4.0383\\ 3.9390& 0.0212\end{array}\right]\times {10}^4$, $X_{F1}=\left[\begin{array}{cc}4.8604& -6.0459\\ -6.4957& 20.1384\end{array}\right]$, $Y_{F1}=\left[\begin{array}{cccc}-3.6785& 1.4934& -0.7126& 0.6388\\ 0.7056& -5.5814& 0.0612& -2.9655\end{array}\right]$, $X_{F2}=\left[\begin{array}{cc}4.0007& -11.8306\\ -8.8187& 41.9150\end{array}\right]$,  $Y_{F2}=\left[\begin{array}{cccc}-2.2876& 2.4976& -0.6585& 0.0804\\ 2.7176& -8.5638& 1.1232& -2.5295\end{array}\right]$.

Under the fuzzy controller (3) with the above observer gains and controller gains, Figure 6 illustrates the flow rates of O₂ and CO₂ in the BGC system and the values observed by the observer. The arterial partial pressures of O₂ and CO₂ and their observed values are illustrated in Figure 7. The command input is drawn in Figure 8 and the controlled output is drawn in Figure 9. The $x_d^T\left(t\right)R{x}_d\left(t\right)$ responses over a time interval of $[0,1]$ under different initial conditions are illustrated in Figure 10, which proves the system is FTB.

5. Conclusions

This paper studies the finite time $H_{\infty }$ control of the BGC system. By the local approximation method, the T-S fuzzy model was established and an observer-based fuzzy controller was designed. An LMI-based new method was given to bound the derivatives of MFs and sufficient conditions for the $H_{\infty }$ FTB of the system were obtained. Finally, the simulation results show the effectiveness of the designed method.