Dynamic Analytical Solution of a Charged Dilaton Black Hole
Abstract
:1. Introduction
2. Dynamical Equation in Extended Phase Space
2.1. Thermodynamic Equation
2.2. Dynamical Balance Equation
3. Analytical Solution of Dynamics
4. Numerical Comparison
5. Conclusions
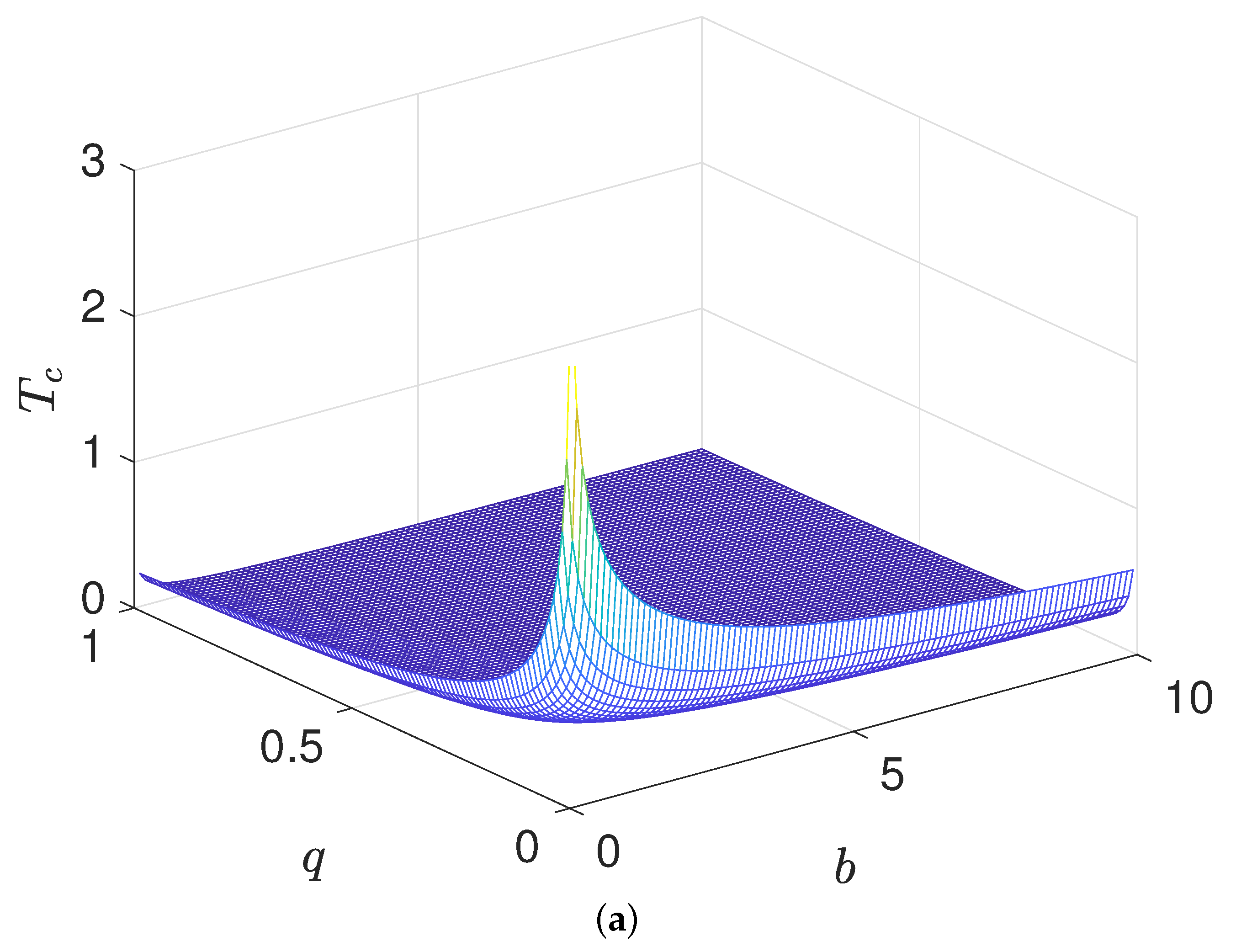
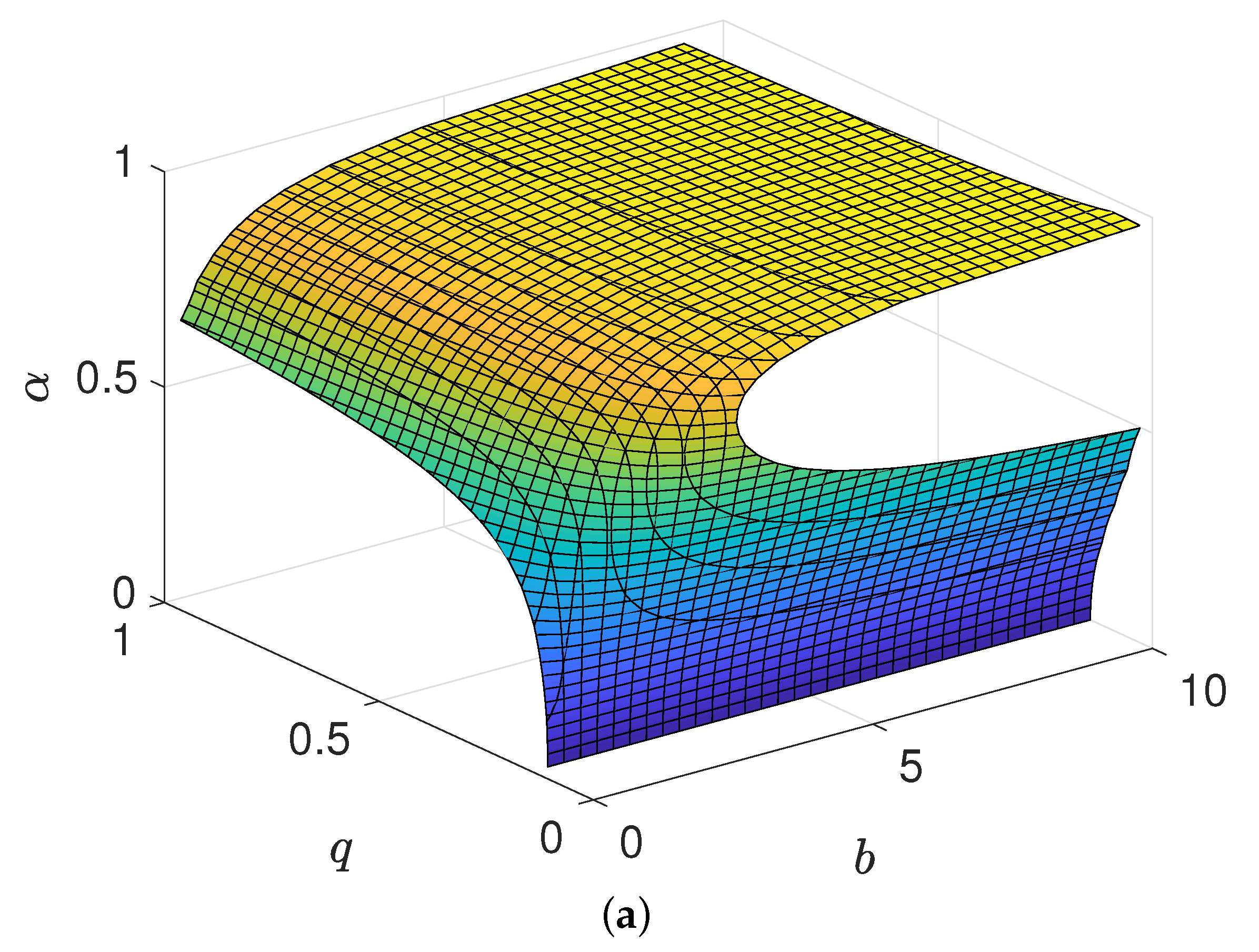
- For a given value of the dilaton parameter, the critical temperature decreases with the increase of the charge;
- For the given value of parameter b, the critical temperature value first decreases and then increases with the increase of the value of the dilaton parameter when the charge is small. On the contrary, the critical temperature value increases with the increase of the dilaton parameter value;
- For a given value of the critical temperature, there is a complicated relationship between the charge and the dilaton parameter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Curiel, E. The many definitions of a black hole. Nat. Astron. 2019, 3, 27–34. [Google Scholar] [CrossRef]
- Pati, S.K.; Nayak, B.; Singh, L.P. Black hole dynamics in power-law based metric f(R) gravity. Gen. Relativ. Gravit. 2020, 52, 78. [Google Scholar] [CrossRef]
- Dehyadegari, A.; Sheykhi, A.; Montakhab, A. Critical behavior and microscopic structure of charged AdS black holes via an alternative phase space. Phys. Lett. 2017, 768, 235–240. [Google Scholar] [CrossRef]
- Yazdikarimi, H.; Sheykhi, A.; Dayyani, Z. Critical behavior of Gauss-Bonnet black holes via an alternative phase space. Phys. Rev. 2019, 99, 124017. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.C.; Ma, M.S.; Zhao, H.H.; Zhao, R. Thermodynamics of phase transition in higher-dimensional Reissner-Nordström-de Sitter black hole. Eur. Phys. J. 2014, 74, 3052. [Google Scholar] [CrossRef] [Green Version]
- Dehghani, M. Three-dimensional scalar-tensor black holes with conformally invariant electrodynamics. Phys. Rev. 2019, 100, 084019. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, D.V.; Ghosh, S.G. D-dimensional Bardeen-AdS black holes in Einstein-Gauss-Bonnet theory. Eur. Phys. J. 2019, 79, 275. [Google Scholar] [CrossRef] [Green Version]
- Dehghani, M.H.; Hendi, S.H.; Sheykhi, A.; Rastegar Sedehi, H. Thermodynamics of rotating black branes in Einstein-Born-Infeld-dilaton gravity. J. Cosmol. Astropart. Phys. 2007, 2, 020. [Google Scholar] [CrossRef]
- Ghosh, S.G.; Singh, D.V.; Maharaj, S.D. Regular black holes in Einstein-Gauss-Bonnet gravity. Phys. Rev. D 2018, 97, 104050. [Google Scholar] [CrossRef]
- Wang, P.; Wu, H.W.; Yang, H.T. Thermodynamics and phase transition of a nonlinear electrodynamics black hole in a cavity. J. High Energy Phys. 2019, 2019, 2. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Wu, H.W.; Yang, H.T. Thermodynamics and phase transitions of nonlinear electrodynamics black holes in an extended phase space. J. Cosmol. Astropart. Phys. 2019, 2019, 052. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.W.; Hu, X.Y.; Lan, M.J. Thermodynamics and weak cosmic censorship conjecture in (2+1)-dimensional regular black hole with nonlinear electrodynamics sources. Eur. Phys. J. Plus 2020, 135, 172. [Google Scholar] [CrossRef] [Green Version]
- Hendi, S.H.; Azari, F.; Rahimi, E.; Elahi, M.; Owjifard, Z.; Armanfard, Z. Thermodynamics and the, phase transition of topological dilatonic Lifshitz-like black holes. Ann. Phys. 2020, 532, 2000162. [Google Scholar] [CrossRef]
- Hendi, S.H.; Panah, B.E.; Panahiyan, S. Thermodynamical structure of AdS black holes in massive gravity with stringy gauge-gravity corrections. Class. Quantum Gravity 2017, 33, 235007. [Google Scholar] [CrossRef] [Green Version]
- Sherkatghanad, Z.; Mirza, B.; Mirzaeyan, Z.; Mansoori, S.A.H. Critical behaviors and phase transitions of black holes in higher order gravities and extended phase spaces. Int. J. Mod. Phys. D 2017, 26, 1750017. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.W.; Xiu, Y.H.; Li, N. Throttling process of the Kerr-Newman-anti-de Sitter black holes in the extended phase space. Phys. Rev. D 2018, 98, 124003. [Google Scholar] [CrossRef] [Green Version]
- Ghaffarnejad, H.; Yaraie, E. Effects of a cloud of strings on the extended phase space of Einstein-Gauss-Bonnet AdS black holes. Phys. Lett. B 2018, 785, 105–111. [Google Scholar] [CrossRef]
- Chen, D.Y. Thermodynamics and weak cosmic censorship conjecture in extended phase spaces of anti-de Sitter black holes with particles’ absorption. Eur. Phys. J. C 2019, 79, 353. [Google Scholar] [CrossRef]
- Qian, W.L.; Lin, K.; Wu, J.P.; Zhang, M.; Yang, Z.Y.; Zou, D.C.; Xu, W.; Yue, R.H. P-V criticality of AdS black hole in the Einstein-Maxwell-power-Yang-Mills gravity. Gen. Relativ. Gravit. 2014, 47, 14. [Google Scholar]
- Nam, C.H. Extended phase space thermodynamics of regular charged AdS black hole in Gauss-Bonnet gravity. Gen. Relativ. Gravit. 2019, 51, 100. [Google Scholar] [CrossRef]
- Hu, Y.P.; Zeng, H.A.; Jiang, Z.M.; Zhang, H. P-V criticality in the extended phase space of black holes in Einstein-Horndeski gravity. Phys. Rev. D 2019, 100, 084004. [Google Scholar] [CrossRef] [Green Version]
- Dehghani, M. Thermal fluctuations of AdS black holes in three-dimensional rainbow gravity. Phys. Lett. B 2019, 793, 234–239. [Google Scholar] [CrossRef]
- Singh, B.K.; Singh, R.P.; Singh, D.V. Extended phase space thermodynamics of Bardeen black hole in massive gravity. Eur. Phys. J. Plus 2020, 135, 862. [Google Scholar] [CrossRef]
- Singh, B.K.; Singh, R.P.; Singh, D.V. P-v criticality, phase structure and extended thermodynamics of AdS ABG black holes. Eur. Phys. J. Plus 2021, 136, 575. [Google Scholar] [CrossRef]
- Singh, D.V.; Siwach, S. Thermodynamics and P-v criticality of Bardeen-AdS Black Hole in 4-D Einstein-Gauss-Bonnet Gravity. Phys. Lett. B 2020, 808, 135658. [Google Scholar] [CrossRef]
- Emparan, R. Higher-dimensional black hole solutions, approximate methods. Gen. Relativ. Gravit. 2014, 46, 1686. [Google Scholar] [CrossRef]
- Huang, H.; Fan, Z.Y.; Lü, H. Static and dynamic charged black holes. Eur. Phys. J. C 2019, 79, 975. [Google Scholar] [CrossRef]
- Dehghani, M. Thermodynamic properties of novel black hole solutions in the Einstein-Born-Infeld-dilaton gravity theory. Eur. Phys. J. C 2020, 80, 996. [Google Scholar] [CrossRef]
- Toshmatov, B.; Ahmedov, B.; Abdujabbarov, A.; Stuchlík, Z. Rotating regular black hole solution. Phys. Rev. D 2014, 89, 104017. [Google Scholar] [CrossRef] [Green Version]
- Hendi, S.H.; Dehghani, A. Criticality and extended phase space thermodynamics of AdS black holes in higher curvature massive gravity. Eur. Phys. J. C 2019, 79, 227. [Google Scholar] [CrossRef]
- Dehghani, M. Nonlinearly charged AdS black hole solutions in three-dimensional massive gravity’s rainbow. Phys. Lett. B 2020, 803, 135335. [Google Scholar] [CrossRef]
- Hendi, S.H. Asymptotic charged BTZ black hole solutions. J. High Energy Phys. 2012, 2012, 065. [Google Scholar] [CrossRef] [Green Version]
- Bazeia, D.; Brito, F.A.; Costa, F.G. Two-dimensional Hořava-Lifshitz black hole solutions. Phys. Rev. D 2015, 91, 044026. [Google Scholar] [CrossRef] [Green Version]
- Abishev, M.E.; Boshkayev, K.A.; Dzhunushaliev, V.D.; Ivashchuk, V.D. Dilatonic dyon black hole solutions. Class. Quantum Gravity 2015, 32, 165010. [Google Scholar] [CrossRef] [Green Version]
- Xu, W. Exact anyon black hole solutions. Eur. Phys. J. C 2018, 78, 871. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.; Gao, C. Exact black hole solutions with nonlinear electrodynamic field. Int. J. Mod. Phys. D 2020, 29, 20500327. [Google Scholar] [CrossRef] [Green Version]
- Ayón-Beato, E.; García, A. Four-parametric regular black hole solution. Gen. Relativ. Gravit. 2005, 37, 635–641. [Google Scholar] [CrossRef]
- Sheykhi, A.; Allahverdizadeh, M. Higher dimensional charged rotating dilaton black holes. Gen. Relativ. Gravit. 2010, 42, 367–379. [Google Scholar] [CrossRef] [Green Version]
- Sheykhi, A.; Kazemi, A. Higher dimensional dilaton black holes in the presence of exponential nonlinear electrodynamics. Phys. Rev. D 2014, 90, 044028. [Google Scholar] [CrossRef] [Green Version]
- Sheykhi, A.; Hajkhalili, S. Dilaton black holes coupled to nonlinear electrodynamic field. Phys. Rev. D 2014, 89, 104019. [Google Scholar] [CrossRef] [Green Version]
- Sheykhi, A. Charged rotating dilaton black strings in (A)dS spaces. Phys. Rev. D 2008, 78, 064055. [Google Scholar] [CrossRef] [Green Version]
- Sheykhi, A. Magnetic dilaton strings in anti-de Sitter spaces. Phys. Lett. B 2009, 672, 101–105. [Google Scholar] [CrossRef]
- Sheykhi, A. Rotating black holes in Einstein-Maxwell-dilaton gravity. Phys. Rev. D 2008, 77, 104022. [Google Scholar] [CrossRef] [Green Version]
- Lessa, L.A.; Silva, J.E.G.; Maluf, R.V.; Almeida, C.A.S. Modified black hole solution with a background Kalb-Ramond field. Eur. Phys. J. C 2020, 80, 335. [Google Scholar] [CrossRef] [Green Version]
- Dimakis, N.; Leon, G.; Paliathanasis, A. Exact black hole solutions in Einstein-aether scalar field theory. Phys. Rev. D 2021, 103, 044001. [Google Scholar] [CrossRef]
- Poshteh, M.B.J.; Riazi, N. Phase transition and thermodynamic stability in extended phase space and charged Hořava-Lifshitz black holes. Gen. Relativ. Gravit. 2017, 49, 64. [Google Scholar] [CrossRef] [Green Version]
- Hendi, S.H.; Panah, B.E.; Panahiyan, S.; Liu, H.; Meng, X. Black holes in massive gravity as heat engines. Phys. Lett. B 2018, 781, 40–47. [Google Scholar] [CrossRef]
- Chabab, M.; El Moumni, H.; Iraoui, S.; Masmar, K. Phase transitions and geothermodynamics of black holes in dRGT massive gravity. Eur. Phys. J. C 2019, 79, 342. [Google Scholar] [CrossRef]
- Khan, I.A.; Ali, F.; Islam, S.; Khan, A.S. The role of the cosmological constant in dynamics of the particle in the Schwarzschild black hole. Phys. Scr. 2020, 95, 065003. [Google Scholar] [CrossRef]
- Sharif, M.; Shahzadi, M. Particle dynamics near Kerr-MOG black hole. Eur. Phys. J. C 2017, 77, 363. [Google Scholar] [CrossRef]
- Rácz, I. Can we prescribe the physical parameters of multiple black holes? Mathematics 2021, 9, 3170. [Google Scholar] [CrossRef]
- Qian, W.L.; Lin, K.; Wu, J.P.; Wang, B.; Yue, R.H. On quasinormal frequencies of black hole perturbations with an external source. Eur. Phys. J. C 2020, 80, 959. [Google Scholar] [CrossRef]
- Charmousis, C.; Crisostomi, M.; Langlois, D.; Noui, K. Perturbations of a rotating black hole in DHOST theories. Class. Quantum Gravity 2019, 36, 235008. [Google Scholar] [CrossRef] [Green Version]
- Rham, C.D.; Zhang, J. Perturbations of stealth black holes in degenerate higher-order scalar-tensor theories. Phys. Rev. D 2019, 100, 124023. [Google Scholar] [CrossRef] [Green Version]
- Shafiq, S.; Hussain, S.; Ozair, M.; Aslam, A.; Hussain, T. Charged particle dynamics in the surrounding of Schwarzschild anti-de Sitter black hole with topological defect immersed in an external magnetic field. Eur. Phys. J. C 2020, 80, 744. [Google Scholar] [CrossRef]
- Wang, R.F.; Gao, F.B. Analytical solution and quasi-periodic behavior of a charged dilaton black hole. Universe 2021, 7, 377. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Wei, S.W.; Liu, Y.X. Spinning test particle in four-dimensional Einstein-Gauss-Bonnet black holes. Universe 2020, 6, 103. [Google Scholar] [CrossRef]
- Deng, X.M. Periodic orbits around brane-world black holes. Eur. Phys. J. C 2020, 80, 489. [Google Scholar] [CrossRef]
- Jawad, A.; Ali, F.; Shahzad, M.U.; Abbas, G. Dynamics of particles around time conformal Schwarzschild black hole. Eur. Phys. J. C 2016, 76, 586. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Iftikhar, S. Dynamics of particles near black hole with higher dimensions. Eur. Phys. J. C 2016, 76, 404. [Google Scholar] [CrossRef] [Green Version]
- Wei, S.W.; Yang, J.; Liu, Y.X. Geodesics and periodic orbits in Kehagias-Sfetsos black holes in deformed Hořava-Lifshitz gravity. Phys. Rev. D 2019, 99, 104016. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.B.; Llibre, J. Global dynamics of Hořava-Lifshitz cosmology with non-zero curvature and a wide range of potentials. Eur. Phys. J. C 2020, 80, 137. [Google Scholar] [CrossRef]
- Gao, F.B.; Llibre, J. Global dynamics of the Hořava-Lifshitz cosmological system. Gen. Relativ. Gravit. 2019, 51, 152. [Google Scholar] [CrossRef]
- Liu, C.Q.; Ding, C.K.; Jing, J.L. Periodic orbits around Kerr Sen black holes. Commun. Theor. Phys. 2019, 12, 1461–1468. [Google Scholar] [CrossRef] [Green Version]
- Ingram, A.R.; Motta, S.E. A review of quasi-periodic oscillations from black hole X-ray binaries, Observation and theory. New Astron. Rev. 2019, 85, 101524. [Google Scholar] [CrossRef] [Green Version]
- Kolo, M.; Shahzadi, M.; Stuchlík, Z. Quasi-periodic oscillations around Kerr-MOG black holes. Eur. Phys. J. C 2020, 80, 133. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Wiley-VCH: Hoboken, NJ, USA, 1995. [Google Scholar]
- Dai, C.Q.; Chen, S.B.; Jing, J.L. Thermal chaos of a charged dilaton-AdS black hole in the extended phase space. Eur. Phys. J. C 2020, 80, 245. [Google Scholar] [CrossRef]
- Sheykhi, A. Thermodynamics of charged topological dilaton black holes. Phys. Rev. D 2007, 76, 124025. [Google Scholar] [CrossRef] [Green Version]
- Sheykhi, A. Topological Born-Infeld-dilaton black holes. Phys. Lett. B 2008, 662, 7–13. [Google Scholar] [CrossRef] [Green Version]
- Dehyadegari, A.; Sheykhi, A.; Montakhab, A. Novel phase transition in charged dilaton black holes. Phys. Rev. D 2017, 96, 084012. [Google Scholar] [CrossRef] [Green Version]
- Dehghani, M.H.; Kamrani, S.; Sheykhi, A. P-V criticality of charged dilatonic black holes. Phys. Rev. D 2014, 90, 104020. [Google Scholar] [CrossRef] [Green Version]
- Dehyadegari, A.; Sheykhi, A. Critical behavior of charged dilaton black holes in AdS space. Phys. Rev. D 2020, 102, 064021. [Google Scholar] [CrossRef]
- Li, A.C.; Shi, H.Q.; Zeng, D.F. Phase structure and quasinormal modes of a charged AdS dilaton black hole. Phys. Rev. D 2018, 97, 026014. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Li, H.T.; Zhang, S.J. Chaos in Born-Infeld-AdS black hole within extended phase space. Gen. Relativ. Gravit. 2019, 51, 134. [Google Scholar] [CrossRef] [Green Version]
- Chabab, M.; Moumni, H.E.; Iraoui, S.; Masmar, K.; Zhizeh, S. Chaos in charged AdS black hole extended phase space. Phys. Lett. B 2018, 78, 316–321. [Google Scholar] [CrossRef]
- Mahish, S.; Bhamidipati, C. Chaos in charged Gauss-Bonnet AdS black holes in extended phase space. Phys. Rev. D 2019, 99, 106012. [Google Scholar] [CrossRef] [Green Version]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Liu, J.; Gao, F. Dynamic Analytical Solution of a Charged Dilaton Black Hole. Mathematics 2022, 10, 2113. https://doi.org/10.3390/math10122113
Wang R, Liu J, Gao F. Dynamic Analytical Solution of a Charged Dilaton Black Hole. Mathematics. 2022; 10(12):2113. https://doi.org/10.3390/math10122113
Chicago/Turabian StyleWang, Ruifang, Jianwen Liu, and Fabao Gao. 2022. "Dynamic Analytical Solution of a Charged Dilaton Black Hole" Mathematics 10, no. 12: 2113. https://doi.org/10.3390/math10122113
APA StyleWang, R., Liu, J., & Gao, F. (2022). Dynamic Analytical Solution of a Charged Dilaton Black Hole. Mathematics, 10(12), 2113. https://doi.org/10.3390/math10122113





