A Novel Inverse Time–Frequency Domain Approach to Identify Random Forces
Abstract
:1. Introduction
2. Random Forces Identification
2.1. Equation of Motion
2.2. Random Forces Identification
2.3. Summary of the Time–Frequency Method
- (1)
- Obtain the random responses Z(t) by the Newmark’s method.
- (2)
- Give the weighting matrix W and calculate the matrix .
- (3)
- Perform the truncated singular value decomposition of the matrix .
- (4)
- Select the proper regularization parameter by using the GCV function.
- (5)
- Compute the identified random forces .
- (6)
- Obtain the PSD of the identified random forces
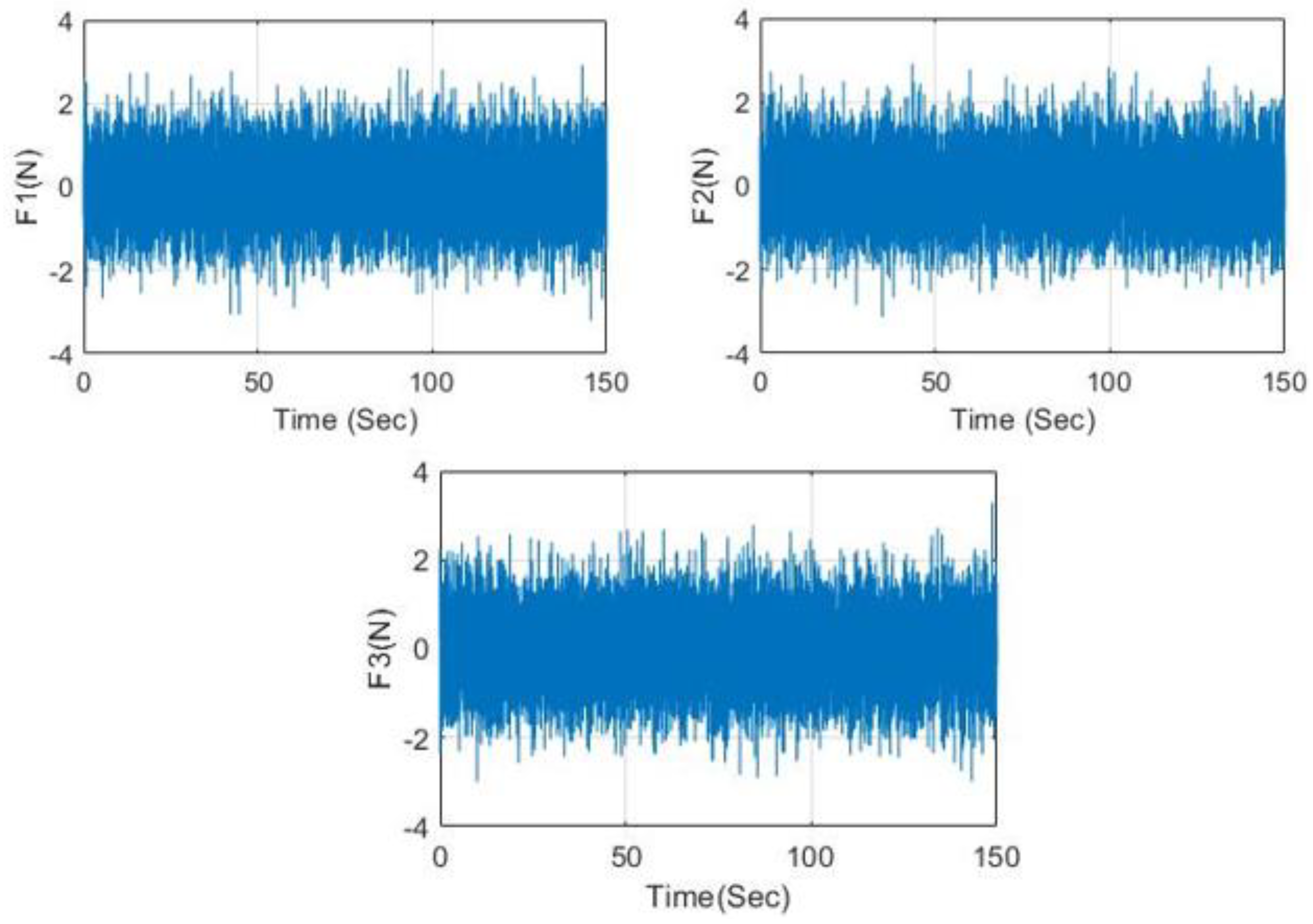
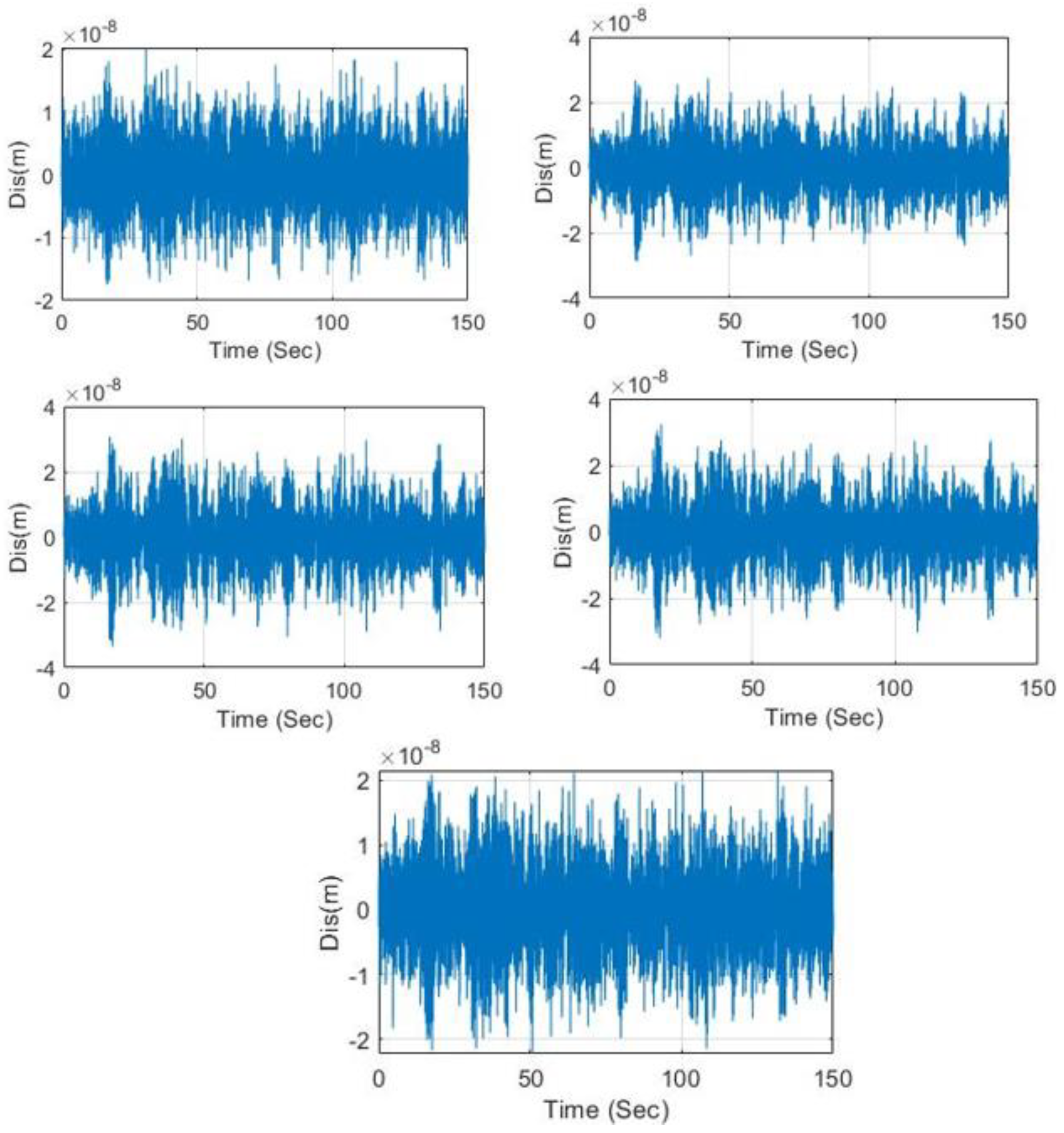
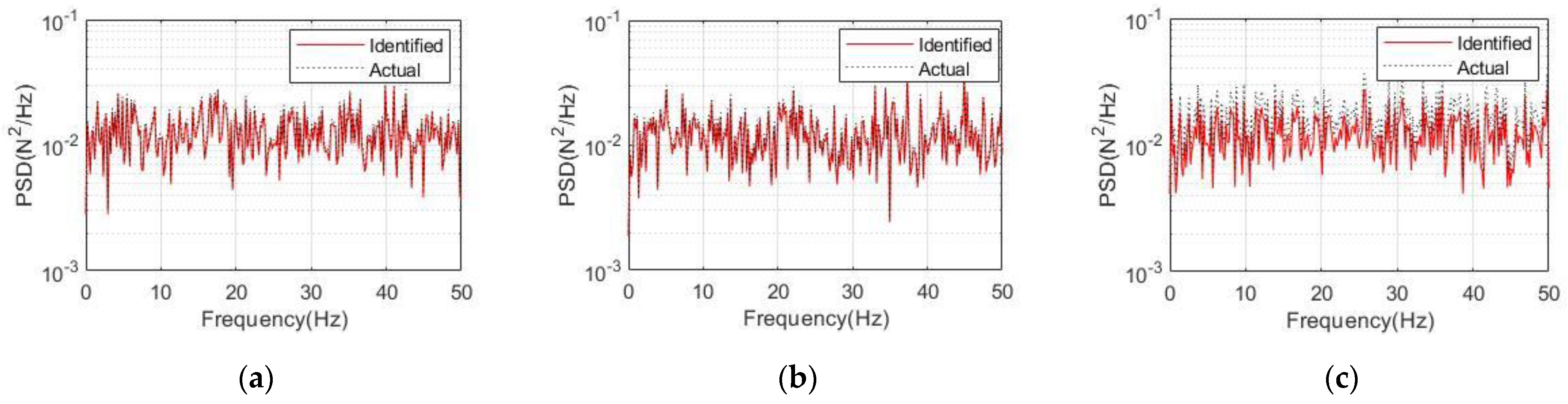
3. Numerical Validation
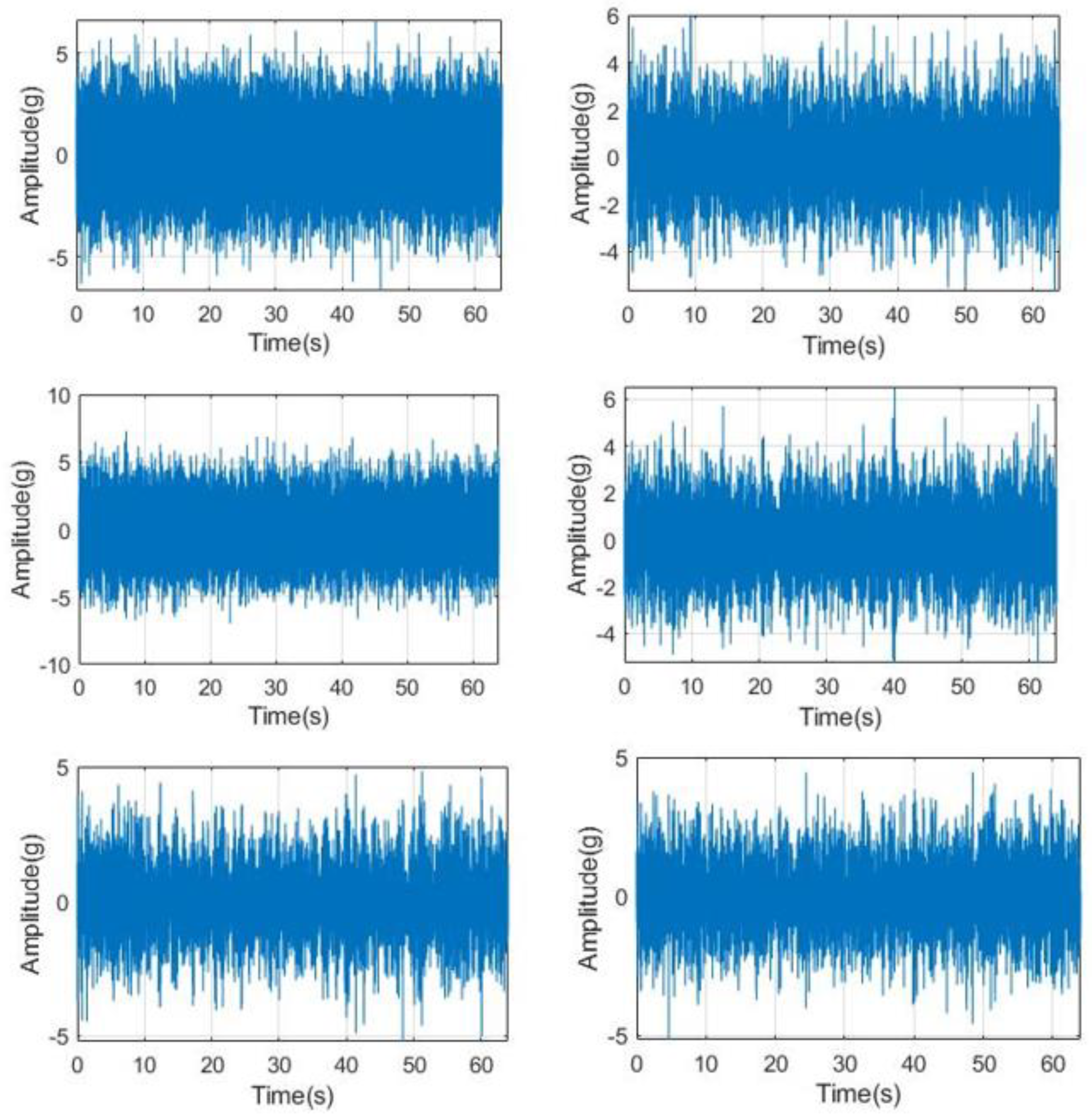
4. Experimental Verification
5. Conclusions
- (1)
- The results show that the time–frequency inverse method is able to correctly identify the random forces acting on engineering structures. It was also found that large errors mainly occurred at the beginning of the analysis.
- (2)
- The weighted regularization method can significantly improve the accuracy of load identification.
- (3)
- The format of the weighting matrix is not unique and can be optimized to improve the effectiveness of the method.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, H.; Park, Y. Error analysis of indirect force determination and a regularization method to reduce force determination error. Mech. Syst. Signal Process. 1995, 9, 615–633. [Google Scholar] [CrossRef]
- O’Callahan, J.; Piergentili, F. Force estimation using operational data. In Proceedings of the 14th International Modal Analysis Conference, Dearborn, MI, USA, 12–15 February 1995; SPIE: Bellingham, WA, USA, 1996; Volume 2768, pp. 1586–1592. [Google Scholar]
- Tikhonov, A.N.; Arsenin, V.Y. Solutions of Ill-Posed Problems, 1st ed.; Wiley: New York, NY, USA, 1977; pp. 84–102. [Google Scholar]
- Jia, Y.; Yang, Z.C.; Song, Q.Z. Experimental study of random dynamic loads identification based on weighted regularization method. J. Sound Vib. 2015, 342, 113–123. [Google Scholar] [CrossRef]
- Jia, Y.; Yang, Z.C.; Guo, N.; Wang, L. Random dynamic load identification based on error analysis and weighted total least squares method. J. Sound Vib. 2015, 358, 111–123. [Google Scholar] [CrossRef]
- Liu, J.; Li, K. Sparse identification of time-space coupled distributed dynamic load. Mech. Syst. Signal Process. 2021, 148, 107177. [Google Scholar] [CrossRef]
- Batou, A.; Soize, C. Identification of stochastic loads applied to a non-linear dynamical system using an uncertain computational model and experimental responses. Comput. Mech. 2009, 43, 559–571. [Google Scholar] [CrossRef]
- Batou, A.; Soize, C. Experimental identification of turbulent fluid forces applied to fuel assemblies using an uncertain model and fretting-wear estimation. Mech. Syst. Signal Process. 2009, 23, 2141–2153. [Google Scholar] [CrossRef] [Green Version]
- Zhang, E.; Antoni, J.; Feissel, P. Bayesian force reconstruction with an uncertain model. J. Sound Vib. 2012, 331, 798–814. [Google Scholar] [CrossRef]
- Li, Q.F.; Lu, Q.H. A hierarchical Bayesian method for vibration-based time domain force reconstruction problems. J. Sound Vib. 2018, 421, 190–204. [Google Scholar] [CrossRef]
- Zhou, J.M.; Dong, L.; Guan, W.; Yan, J. Impact load identification of nonlinear structures using deep recurrent neural network. Mech. Syst. Signal Process. 2019, 133, 106292. [Google Scholar] [CrossRef]
- Feng, W.; Li, Q.; Lu, Q.; Li, C.; Wang, B. Group relevance vector machine for sparse force localization and reconstruction. Mech. Syst. Signal Process. 2021, 161, 107900. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Gu, K.; Li, M. Artificial Neural Network (ANN)—Bayesian Probability Framework (BPF) based method of dynamic force reconstruction under multi-source uncertainties. Knowl. Based Syst. 2022, 237, 107796. [Google Scholar] [CrossRef]
- Cumbo, R.; Tamarozzi, T.; Janssens, K.; Desmet, W. Kalman-based load identification and full-field estimation analysis on industrial test case. Mech. Syst. Signal Process. 2019, 117, 775–781. [Google Scholar] [CrossRef]
- Tang, Q.Z.; Xin, J.Z.; Jiang, Y.; Zhou, J.; Li, S. Novel identification technique of moving loads using the random response power spectral density and deep transfer learning. Measurement 2022, 195, 111120. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to machine learning and deep learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Tran, H.; Inoue, H. Further development and experimental verification of wavelet deconvolution technique for impact force reconstruction. Mech. Syst. Signal Process. 2021, 148, 107165. [Google Scholar] [CrossRef]
- Samagassi, S.; Jacquelin, E.; Khamlichi, A.; Sylla, M. Bayesian sparse regularization for multiple force identification and location in time domain. Inverse Probl. Sci. Eng. 2018, 27, 1221–1262. [Google Scholar] [CrossRef] [Green Version]
- Clough, R.W.; Penzien, J.; Griffin, D.S. Dynamics of structures. J. Appl. Mech. 1977, 44, 366. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Zhao, C.; Yu, H.; Wen, B. Dynamic load identification algorithm based on Newmark-β and self-filtering. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 96–107. [Google Scholar]
- Bendat, J.; Piersol, A. Engineering applications of correlation and spectral analysis. J. Acoust. Soc. Am. 1998, 70, 262–263. [Google Scholar]
- Jia, Y.; Yang, Z.; Liu, E.; Fan, Y.; Yang, X. Prediction of random dynamic loads using second-order blind source identification algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 1720–1732. [Google Scholar] [CrossRef]


| Method | Force 1 | Force 2 |
|---|---|---|
| Actual | 0.5426 | 0.5662 |
| Proposed method | 0.6212 | 0.6108 |
| method [22] | 0.4587 | 0.4369 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Y.; Li, R.; Fan, Y.; Huang, H. A Novel Inverse Time–Frequency Domain Approach to Identify Random Forces. Mathematics 2022, 10, 2331. https://doi.org/10.3390/math10132331
Jia Y, Li R, Fan Y, Huang H. A Novel Inverse Time–Frequency Domain Approach to Identify Random Forces. Mathematics. 2022; 10(13):2331. https://doi.org/10.3390/math10132331
Chicago/Turabian StyleJia, You, Ruikai Li, Yanhong Fan, and Haijie Huang. 2022. "A Novel Inverse Time–Frequency Domain Approach to Identify Random Forces" Mathematics 10, no. 13: 2331. https://doi.org/10.3390/math10132331
APA StyleJia, Y., Li, R., Fan, Y., & Huang, H. (2022). A Novel Inverse Time–Frequency Domain Approach to Identify Random Forces. Mathematics, 10(13), 2331. https://doi.org/10.3390/math10132331





