Computing Frequency-Dependent Hysteresis Loops and Dynamic Energy Losses in Soft Magnetic Alloys via Artificial Neural Networks

Abstract

A neural network model to predict the dynamic hysteresis loops and the energy-loss curves (i.e., the energy versus the amplitude of the magnetic induction) of soft ferromagnetic materials at different operating frequencies is proposed herein. Firstly, an innovative Fe-Si magnetic alloy, grade 35H270, is experimentally characterized via an Epstein frame in a wide range of frequencies, from 1 Hz up to 600 Hz. Parts of the dynamic hysteresis loops obtained through the experiments are involved in the training of a feedforward neural network, while the remaining ones are considered to validate the model. The training procedure is accurately designed to, firstly, identify the optimum network architecture (i.e., the number of hidden layers and the number of neurons per layer), and then, to effectively train the network. The model turns out to be capable of reproducing the magnetization processes and predicting the dynamic energy losses of the examined material in the whole range of inductions and frequencies considered. In addition, its computational and memory efficiency make the model a useful tool in the design stage of electrical machines and magnetic components.

1. Introduction

The macro-scale simulation of the dynamic magnetization processes in soft ferromagnetic materials is still an interesting and promising field of research. Indeed, the optimum design of electrical machines and magnetic components, regardless of the particular area of application, requires an accurate description of the materials used [1,2]. More specifically, the response of the material to the external excitations, together with the geometry of the device, highly influences the final merit factors [2,3,4,5]. Device simulation is typically performed via commercial Computer-Aided Design (CAD) programs based on the Finite-Element Method (FEM), which is not able to account for the material characteristics thoroughly. For instance, hysteresis models embedded into FEM schemes are not yet available in commercial software, and the material is usually represented with a constant value of the magnetic permeability or, in the best cases, with a suitable non-linear anhysteretic function identified from the data provided by the manufacturer. It has to be specified that the FEM analysis carried out using a non-linear anhysteretic material model can only take the material saturation into account, but cannot provide important information related to the coercivity, the remanence, or the phase lag between the magnetic field H(t) and the magnetic induction B(t). In addition, since the curve on the B-H plane does not show any area, it is definitely impossible to predict the loss of energy.

Despite the coupling between FEM and the hysteresis models having been extensively studied, this technique is still limited to specific applications [6,7,8,9], and it is not assessed in a general way. The hysteresis models are well-established and fully applicable only in the case of scalar excitations, whilst for vector problems, many issues are not yet resolved [10]. To further stress this problem, the validation of the available models is demanded in light of the new emerging materials and technologies, such as sintering and 3D printing.

Apart from implementing suitable hysteresis models in FEM programs, the availability of an efficient model able to simulate regime-state hysteresis loops at arbitrary levels of magnetic induction and frequency values could be a valuable tool in the design stage of electrical machines and magnetic components. Indeed, from classic FEM analysis in which the material is modeled by means of non-linear anhysteretic functions, only the amplitudes of both the magnetic field and the magnetic induction can be obtained for any frequency. On the other hand, a dynamic model of hysteresis can be used to simulate hysteresis loops at arbitrary frequency values, giving additional information. First of all, the shape of the frequency-dependent hysteresis loops can be determined for any level of induction, as can the differential permeability. In addition, the dynamic energy loss per unit of volume can be obtained as the area enclosed by the loop in the HB plane.

It turns out that, in conducting ferromagnetic materials, the total dynamic energy loss at the regime state can be expressed as the sum of hysteresis, classic, and excess components [11,12]. The first component is only associated with rate-independent hysteresis, the second one arises from the circulation of macro-eddy currents, and the third one reproduces the micro-eddy current losses caused by the motion of the domain walls.

A suitably identified dynamic model of hysteresis addresses all the three loss components, whilst traditional electromagnetic analysis, like the FEM-based models, does not take into account the excess term, which has to be computed separately [13]. Amongst the approaches available in the literature, the Dynamic Jiles–Atherton model (DJAM) [14,15,16,17] and the Dynamic Preisach Model (DPM) [18,19,20,21] are perhaps the two most popular rate-dependent models of hysteresis.

The DJAM, derived conceptually from the classic static JAM, is developed with the aim of incorporating the effects of both the macro- and micro-eddy currents. However, despite the small computational cost and memory allocation, and despite the interesting features of the computed hysteresis loops—such as their shape and their dependence on frequency—some critical aspects need to be carefully addressed, as discussed in detail in [16]. Nonphysical features, such as the negative values of susceptibility, may occur and require ad hoc corrections. In addition, to improve the model accuracy, several parameters must be varied with respect to the amplitude of the excitation [17], giving rise to a lot of extensions and modifications to the original approach.

Two main rate-dependent generalizations of the classic (static) Preisach model have been proposed in the literature. The first one, developed by Bertotti [18], is based on Preisach operators with a finite rate of change in their output with respect to the applied magnetic field. The rate-dependence only involves the input–output relationship of the operators and does not influence the distribution function. Conversely, Mayergoyz proposed the use of traditional Preisach operators and the application of a suitable rate-dependent distribution function [19]. Most of the subsequent research articles available in the literature dealing with the rate-dependent Preisach model and its applications are based either on the Bertotti [20] or on the Mayergoyz [21,22] extensions. However, despite the abundant studies in the literature concerning the classic Preisach model formulations and applications, very few articles are available about rate-dependent hysteresis. The model validation often involves a narrow interval of frequencies and magnetic inductions, and the comparison is based on other numerical models [21]. From the available studies, it can be concluded that the DPM is, in general, more robust than the DJAM, since it does not suffer any nonphysical features; however, it is also more complex and very cumbersome from the viewpoint of the computational time and the memory requirement.

The principal scope of this research is to give a contribution to the development of the dynamic models of hysteresis for innovative soft ferromagnetic materials, exploiting artificial neural networks (ANNs). Until now, ANNs have been successfully applied in the development of both scalar [23,24,25] and vector models of static hysteresis [26,27,28], but fewer studies also take the rate dependence into account [29,30,31,32]. The main advantages of neural network-based models are related to their cheap memory allocation and high computational speed, especially when implemented at a low level of abstraction. However, they do not have the intrinsic memory-storage mechanism typical of hysteretic systems. For this reason, neural networks are seldom used as standalone methods, but they are generally coupled with other hysteretic models, which provide the past history dependence. This is also a common approach for rate-dependent models based on artificial neural networks. For instance, in [31], the authors developed a dynamic model of a piezoelectric actuator exploiting an artificial neural network coupled with a Nonlinear Autoregressive Moving Average Model with Exogeneous Inputs (NARMAX). In [29], the authors proposed modeling of the frequency-dependent hysteresis loops via an array of feedforward neural networks, each one working on a specific interval of the H field axis, whilst in [30], the fully connected cascade architecture was explored. Both the approaches are, in general, more complex than the ones exploiting a standalone feedforward neural network. Furthermore, the models were tested only on a few hysteresis loops and in a narrow interval of frequencies below 100 Hz. More recently, in [32], another neural-network-based model of dynamic hysteresis was proposed and tested in a wider range of B and f. It was formulated to obtain the magnetic field H as a function of the actual B, with its peak value in the cycle B_pk and the frequency f. The evaluation of the model output disregards the status of the system, which is represented by the values of both the magnetic field and the magnetic induction.

Recently, some authors have proposed a standalone neural-network-based hysteresis model with an intrinsic dependence on past history [25]. The model computes the magnetic permeability as a function of the previous actual and k values of both H and B, thus mimicking the memory storage properties of the hysteretic systems.

In this work, we adopted a similar formulation, applying the excitation frequency as an additional input to the model, with the aim of reproducing the dynamic hysteresis loops under periodic excitation waveforms for an innovative soft ferromagnetic alloy. Furthermore, the neural network was trained directly on the experimental data without exploiting intermediate models and/or data augmentation techniques to generate the training set. However, since the measured data are generally noisier than numerical simulations, it was found that the use of magnetic induction instead of permeability as a model output is more convenient and straightforward.

The ferromagnetic material examined in this work is a Non-Grain-Oriented (NGO) laminated Fe-Si steel, grade 35H270, suitable for the manufacturing of performing electrical machines and magnetic components. Thanks to its small thickness (0.35 mm), the material is particularly suitable for medium- and high-frequency applications, such as those in electric mobility and the avionic environment. For this reason, the alloy has been experimentally characterized up to 600 Hz, covering the typical supply frequencies of aircraft equipment. The experimental measurements were carried out in our laboratory using Epstein apparatus, in agreement with the international standard IEC60404-2, and consist of a family of hysteresis loops with sinusoidal magnetic induction at different amplitudes for each applied frequency. Further details about the experimental analysis are discussed in Section 2.1. The families of hysteresis loops, measured at different frequencies, were divided into a training set, used to identify the dynamic neural-network-based model (DNNM), and a test set, used to assess it. The neural network architecture, the algorithm that implements the model, and the training procedure are described in Section 2.2. To conclude, in Section 3, the training results and the comparison of the predicted frequency-dependent hysteresis loops with the measured ones are shown. The reproduction of the energy losses as a function of both the amplitude of B and the frequency is also investigated, and the results are compared with both the values obtained by the experiments and those provided by the manufacturer. Final technical comments concerning the computational cost of the model are given.

2. Materials and Methods

The material that was experimentally characterized is a commercial Fe-Si laminated alloy with non-oriented grains, grade 35H270, suitable for the manufacturing of magnetic cores for electrical machines and magnetic components. According to the manufacturer’s data sheet, provided by the manufacturer, the main physical and geometrical parameters of the alloy are listed in the table below.

The material turns out to be particularly well suited for a performing electric motor, since the random grain orientation makes the in-plane properties almost independent of the direction. In addition, due to the small thickness, similar to one of the grain-oriented laminations, the behavior of the core loss against the operative frequency allows its application in several fields of power electronics. For instance, filtering inductors for static-energy-conversion systems are usually realized by exploiting these types of magnetic materials [33].

2.1. Experimental Investigation

To experimentally investigate the dynamic magnetization processes for the 35H270 steel, a 30 cm × 30 cm Epstein testing frame was adopted. The strips of ferromagnetic material, with a length 300 ± 0.2 mm and a width of 30 ± 0.2 mm, were prepared via a suitable mechanical cutting process and arranged, eight per side, in the Epstein machine.

The device, realized in agreement with the international standard IEC 60404-2, has two windings, with N = 840 turns each—one for the excitation (the primary) and the other one for the measurement of the induced electromotive force $e_{II}\left(t\right)$. From the current circulating on the primary coil $I_I\left(t\right)$ it is possible to obtain the magnetic field at the surface of the laminations, according to Ampere’s law of circulation. On the other hand, it is possible to calculate the mean magnetic induction inside the laminations from the electromotive force at the secondary coil. The equations used are listed in the following:

$$H\left(t\right)=\frac{N{I}_I\left(t\right)}{l_m}, B\left(t\right)=\frac{1}{NS}{{\displaystyle \int }}_{t_0}^t{e}_{II}\left(t\right)dt$$

(1)

where $l_m=1.08 m$ is the mean magnetic path length (equal to the mean geometrical path length of the Epstein circuit), while $S$ is the total cross-sectional area of the magnetic circuit formed.

The primary winding is fed by a linear, 4-quadrant, programmable power amplifier (PA 100-52—Brockhaus Messtechnik GmbH & Co. KG, Lüdenscheid, Germany) with a maximum output power of 5.0 kW, optimized for resistive–inductive loads. 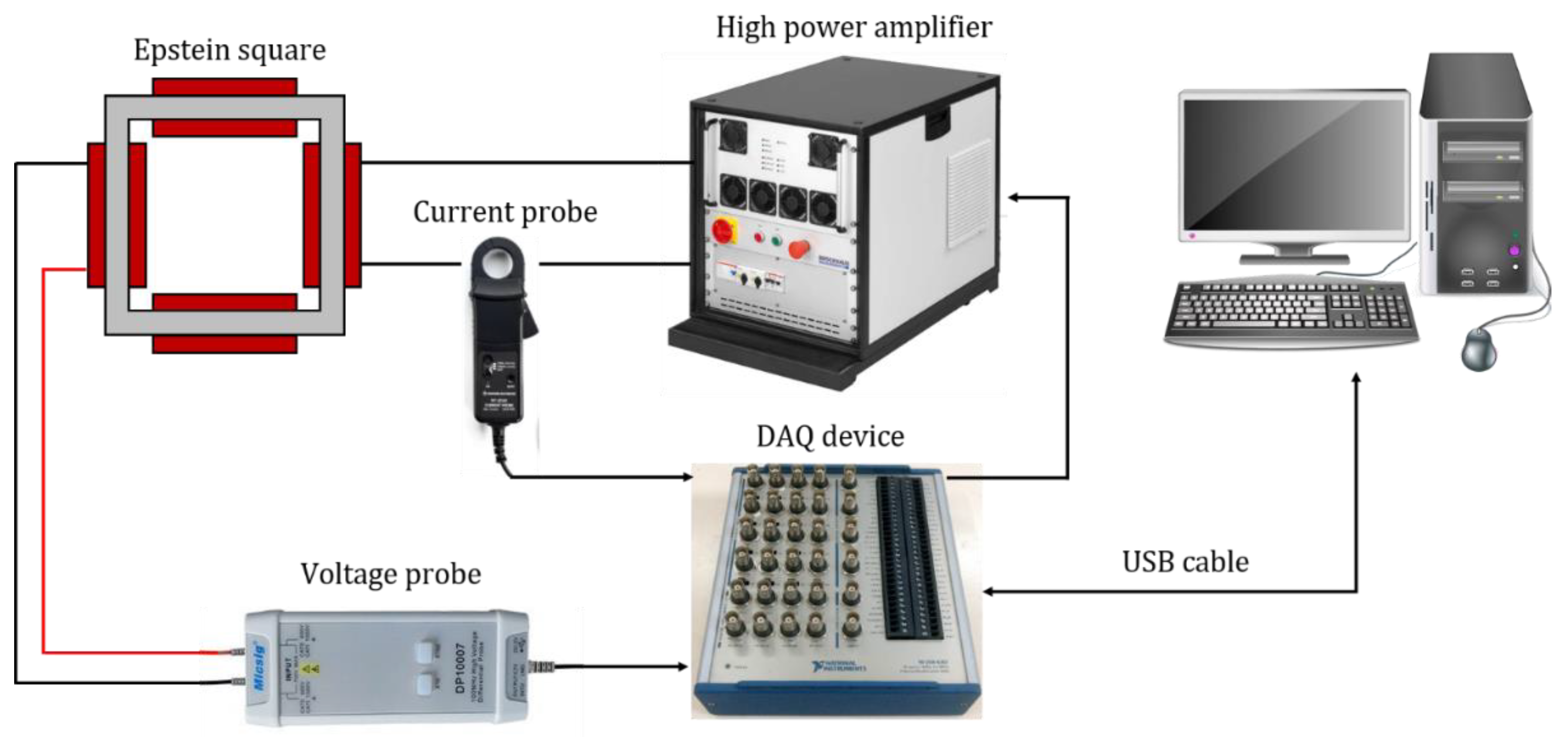The power amplifier is driven by a data generation/acquisition module (NI^® USB 6363-BNC Type) via an analog output port, programmed via PC using the session-based interface available in Matlab^® (version 2021b—The MathWorks, Inc., Natick, CA, USA). The current on the primary coil is detected through a DC—100 MHz active current probe (RT-ZC02—Rohde & Schwarz GmbH & Co. KG). Finally, the electromotive force at the secondary coil is measured using a DC—100 MHz active voltage probe (DP 10013—Shenzhen Micsig Technology Co., Ltd., Shenzhen, China) to increase the signal-to-noise ratio. The current and the voltage probes are connected to opportunely configured analog inputs of the data acquisition/generation module. A scheme of the experimental setup used to measure the dynamic hysteresis loops is shown in Figure 1.

The measurement process is supervised by Matlab^® custom software. The user can specify the settings of the acquisition, such as the sample rate, the channel configuration, the range of the quantizer, and the settings of the analog output ports for the signal generation. The program’s core is a powerful feedback algorithm that allows the control of the magnetic induction waveform.

In this work, according to the specifications reported in the international standard, the measurements were performed using sinusoidal flux densities. The algorithm at each iteration I evaluates the instantaneous difference $∆B\left(t\right)=B_{ref}\left(t\right)-B_{meas}^i\left(t\right)$ between the reference waveform (sinusoidal) and the one measured at iteration i, and the instantaneous difference between their time derivatives $\dot{∆B\left(t\right)}=\dot{B_{ref}\left(t\right)}-\dot{B_{meas}^i\left(t\right)}$. Then, the voltage waveform to be applied at the next iteration $v^{i+1}\left(t\right)$ is computed as a function of the voltage waveform applied at iteration i and a suitable linear combination of the two instantaneous differences:

$$v^{i+1}\left(t\right)=v^i\left(t\right)+\frac{\underset{\mathrm{t}}{\max }\left\{v^i\left(t\right)\right\}}{B_0}\left[\alpha ·∆B\left(t\right)+\left(1-\alpha \right)·\dot{∆B\left(t\right)}\right]$$

(2)

The parameter α by default is equal to 1, but with the capability to be chosen in the range [0, 1] by the user, to optimize and speed up the acquisition process. By reducing α, the new voltage waveform is more susceptible to the derivative of the measured signal, and this may lead to a convergence in a small number of iterations at the expense of a weakening of the feedback stability. Indeed, too-small values of α may cause uncontrollable oscillations.

However, to prevent any damage to the equipment, the amplitude of the current is constantly monitored during the measurement process. The supply of the Epstein frame is disconnected as soon as the current on the primary exceeds 16 A. The feedback algorithm exits if at least one of the following conditions are met:

• The displacement between the form factor computed from the measured flux density and the theoretical one of the sinusoidal waves (1.111) is less than the quantity $dis{p}_{FF}$, specified by the user (1% by default).
• The maximum relative error $\max \left\{∆B\left(t\right)/B_0\right\}$ is less than the quantity $E_M$, specified by the user (0.015 by default).
• The maximum number of iterations (30 by default) is reached.

As a result, to obtain sinusoidal magnetic inductions, the resulting waveforms of the applied magnetic field are somewhat distorted, as one can see in Figure 2.

A family of eight magnetization loops with amplitude $B_0$ = 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, and 1.5 T was measured at each one of the frequencies $f$ = 1, 2, 5, 10, 20, 50, 100, 200, 300, 400, 500, and 600 Hz. A sample rate equal to 250/f was chosen, such that all the hysteresis loops were sampled with the same number of samples per period. In the figure below, the magnetic-field waveforms obtained to acquire the sinusoidal inductions at any amplitude between 0.2 and 1.5 T are shown for f = 1, 50 and 600 Hz.

The loss of energy per unit of volume dissipated in one period is calculated as the area enclosed by the dynamic hysteresis loop on the H-B plane, and it consists of the combined effects of hysteresis, and classic and excess loss components. The obtained values for B = 1.0 and B = 1.5 T at the frequency of 50 Hz are, respectively, 17.6 mJ/kg and 43.0 mJ/kg, in substantial agreement with the ones listed in

Table 1. Declared physical and geometrical properties of the 35H270 NGO steel.

Thickness	Mass Density	Magnetic Induction @ 800 A/m	Core Loss @ 1.0 T and 50 Hz	Core Loss @ 1.5 T and 50 Hz
d [mm]	γ [kg/m3]	B800 [T]	W1.0 [mJ/kg]	W1.5 [mJ/kg]
0.35	7650	1.62	19.8	46.0

. The maximum deviation of 6.5% from the manufacturer’s data is acceptable, since the declared values refer to “typical performances” and are not related to a specific lot fabricated.

2.2. Dynamic Neural Network Model

In the research presented, the reproduction of regime-state dynamic hysteresis loops by means of artificial neural networks is investigated in a wide range of magnetic inductions and frequencies. In particular, thanks to the abundant availability of effective training algorithms and their computational efficiency, the feedforward architecture is considered. The dynamic model, after the individuation of an appropriate formulation and an effective training procedure, both discussed in the following, is then used to simulate the magnetization loops of the investigated material from quasi-DC excitations up to 600 Hz, and to predict the total loss of energy. In addition, being identified directly on the measured dynamic loops, the model accounts for all the energy terms: hysteresis loss, classic eddy current loss, and excess loss.

The inputs and the output of the model are determined to take the status of the magnetic system into account and to guarantee the uniqueness of the solution. Then, the inputs are the current (actual) value of both the magnetic field H(k) and the magnetic induction B(k), plus the frequency of the periodic magnetic field waveform. This set of variables is necessary and sufficient to compute the value of the magnetic induction in the successive (future) step B(k + 1). The calculation of the output, which is performed sample-by-sample, only requires the values of the magnetic field waveform and its fundamental frequency. In contrast, the magnetic induction at each sample step is given by the value previously calculated by the model. For this reason, the model simulation starts from a known initial point on the H-B plane (H(0), B(0)) and is performed in a closed loop.

The model consists of a feedforward neural network with three input neurons and one output neuron, and it is fully characterized by the number of neurons on each hidden layer, described by the vector NPL = [N_h1, …, N_hJ], where J is the number of hidden layers. The authors decided to choose a feedforward neural network because, in our case, there are no important memory effects involved. This kind of neural architecture is sufficient to face the problem under analysis; moreover, it does not need high training and execution times. The activation function of the hidden neurons is the hyperbolic-tangent sigmoid, while the output neuron has a pure linear activation. Indeed, the hyperbolic-tangent sigmoid (called tansig in MATLAB), allows more numerical flexibility for the hidden neurons because its output range is the interval [−1, 1] (unlike the classical sigmoid function that is [0, 1]).

The vector NPL is determined via an optimized training procedure developed by the authors. First of all, the training set is determined from the entire experimental dataset selecting only some hysteresis loops and some frequencies. The amplitudes of the magnetic induction selected for the training are those with B₀ = B_0train = 0.2, 0.6, 1.0, 1.2, and 1.5 T; then, the amplitudes available for the test are B_0test = 0.4, 0.8, and 1.4 T.

The families of 5 dynamic hysteresis loops applied in training are those at the frequencies f_train = 1, 2, 5, 10, 50, 100, 200, 300, 500, and 600 Hz, while the values f_test = 20 and 400 Hz are considered for the test and the model assessment. Actually, two different types of tests can be performed, as will be shown in Section 3:

• TEST 1: simulation of unknown loops with B₀ = B_0test at the known frequencies f_train.
• TEST 2: simulation of unknown loops at the unknown frequencies f_test.

Only the ascending branches of the hysteresis loops are used to train the feedforward neural network because the descending branches can be easily obtained via symmetry. Indeed, let H_asd(k) be the samples of the magnetic field sequence along the ascending branch, and let B_asd(k + 1) = NET(H_asd(k), B_asd(k), f) be the computed values of the magnetic induction; then, the descending branch can be evaluated as: B_des(k + 1) = −NET(–H_asd(k), B_des(k), f). The size of the training set is then equal to 10 × 5 × 125 = 6250 samples and corresponds to 52% of the whole experimental dataset. On the other hand, the total size of the test set is (2 × 8 + 10 × 3) × 125 = 5750 samples, equal to 48% of the total. The sizes of the training and the test sets are rather balanced.

The first step of the developed training procedure aims at the individuation of a suitable NPL vector, and then to define the best network architecture. The main computer program, appositely developed by the authors, iterates both the number of hidden layers and the number of neurons per layer. In particular, for each hidden layer j between 1 and MAX_LENGTH_NPL = 5, the procedure iterates the number i of hidden neurons between 1 and MAX_NEURONS = 25, and for any value of i, a feedforward neural network is configured and trained via a training algorithm, which is the core of the computer program.

The algorithm is implemented as a Matlab^® function that accepts the training method (Levenberg–Marquardt, in our case) and the number of epochs N_ep (6000 by default) as arguments; it returns the trained net object and a struct, named TR, containing some output features, such as the best epoch and the open-loop mean-squared error (MSE_OL). After that, the same training set is simulated in a closed loop by using the function “simul”; it returns the values computed by the network and the closed-loop mean-squared error (MSE_CL), which is our figure of merit for the evaluation of the model performances.

After that, i reaches MAX_NEURONS, and the best value of the number of hidden neurons in layer j is determined as the one with the smallest MSE_CL. However, before adding the optimal number of hidden neurons to the NPL vector at position j, the minimum MSE_CL is compared with the one found in the previous iteration j − 1. If the current minimum MSE_CL is smaller, the length of NPL is increased, and the number of hidden neurons is appended to NPL in the new position j; otherwise, the procedure stops and returns the NPL vector found at the previous iteration j − 1. The Matlab^® script that implements the training algorithm described above is listed in the following (Algorithm 1).

Algorithm 1. NN training

%% MAIN_SCRIPT_TRAINING.m %%

method = ‘trainlm’;    % training method

Nep = 6000;

NPL = [];         % initialization of NPL vector

MAX_LENGTH_NPL = 5;

MAX_NEURONS = 25;

opt_net_found = true;   % optimum net found for the current j

j = 1;

PERF = []; % minimum training error as a function of length(NPL)

while (j <= MAX_LENGTH_NPL && opt_net_found);

MSE_CL = []

for i = 1:1:MAX_NEURONS;

[net,TR] = training_algorithm([NPL, i],method,Nep);

[Y,mse] = simul(net,X);

MSE_CL = [MSE_CL, mse];

end

[min_err, pos_min] = min(MSE_CL);  % find minimum MSE and i

if min_err >= min(PERF);

opt_net_found = false;  % stop the algorithm

else

NPL = [NPL, pos_min];  % update NPL

PERF = [PERF, min_err];  % update PERF vector

end

j = j + 1;

end

After that, the optimal architecture of the feedforward net is determined, and six independent runs of the training algorithm are launched using the same optimal NPL vector.

This final step avoids possible local minima of the MSE_CL function in the parameters space, and the best net is finally saved.

3. Results and Discussion

The training procedure illustrated in Section 2.2 returned a feedforward neural network with three hidden layers and a number of neurons per layer specified by the vector NPL = [10, 5, 5]. The effectiveness of the training procedure is confirmed by the low value of the open-loop mean-squared error returned by the algorithm, which was MSE_OL = 1.85 × 10⁻⁶. On the other hand, the robustness of the identified feedforward net and the stability of the closed-loop calculation are determined by the value of the MSE_CL = 7.02 × 10⁻⁴. The assessment of the neural network requires the analysis of the capability of generalization, i.e., the capability of the dynamic model to predict unknown magnetization loops by generalizing the ones known from the training. The dataset obtained through the experimental investigation allows us to reserve a lot of dynamic magnetization loops for the validation of the model (the ones for TEST 1 and TEST 2, already mentioned in Section 2.2). The hysteresis processes of both TEST 1 and TEST 2 are performed by the trained neural network, applying the measured sequences of the magnetic field directly to the input of the model. The calculation of the magnetic induction is performed sample-by-sample and in a closed loop. Furthermore, both branches of each hysteresis loop are calculated. The reversal is performed by means of a flag variable that switches the signs of the inputs H(k) and B(k), and the sign of the output B(k + 1), as well, in the function of the sign of dH(k) = H(k) − H(k − 1) and the value of H(k) itself.

Let us initially present the simulation results relative to the dynamic hysteresis loops of TEST 1. The frequency values (1, 2, 5, 10, 50, 100, 200, 300, 500, and 600 Hz) were already used to train the neural network, but the magnetic-field waveforms corresponding to the loops with B = 0.4, 0.8, and 1.4 T are entirely “new”. The magnetic induction sequences predicted by the model turned out to reliably reproduce the experimental ones in the entire frequency range. The calculation of the closed-loop mean-squared error on the whole dataset (7500 points) gave a value of 1.45 × 10⁻³, which is about double the one previously obtained by the simulation of the training set. Apparently, the error propagates very slowly, and it is, in any case, sufficiently small to assume that the first test passed successfully. The comparison between the experimental loops (always drawn in a continuous black line) and the simulated ones (drawn in cross-shaped colored markers) is illustrated in Figure 3 for f = 5 and 600 Hz, highlighting the capability of the model to reproduce both the quasi-DC hysteretic curves and the ones obtained at the highest frequency value.

A simulation of the dynamic hysteresis processes of TEST 2 was also performed. Now, both the magnetic field sequences—again, corresponding to the loops at 0.4, 0.8, and 1.4 T, and the frequency values, 20 and 400 Hz—are completely unknown; this further challenges the generalization capability of the dynamic neural network model. Now, the error is slightly increased, reaching a value of 6.29 × 10⁻³ on the 1500 samples processed. Nevertheless, the accuracy, reliability, and stability of the model are not compromised, as one can verify from the comparative analysis against the experimental loops, shown in Figure 4.

In the left panel, where the dynamic hysteresis loops at 20 Hz are reported, the displacement found for the minor loop (0.4 T) appears non-negligible, and it is a significant contribution to the total MSE. When H decreases after the peak value, the differential permeability decreases with less respect to the measured one, as reflected in a wider loop area. As the magnetic induction increases, and the agreement improves sensibly. In the right panel, a comparison between the simulated and measured loops is shown for f = 400 Hz. In this case, a higher accuracy is found for any value of B.

In the final step of our investigation, the prediction of the dynamic energy losses is discussed. It can be demonstrated that the area on the H-B plane enclosed by a hysteresis loop, having a given amplitude B and frequency f, represents the total energy dissipated in the process per unit of volume. It accounts for the hysteresis, and the classic and excess loss components, according to the separation principle. 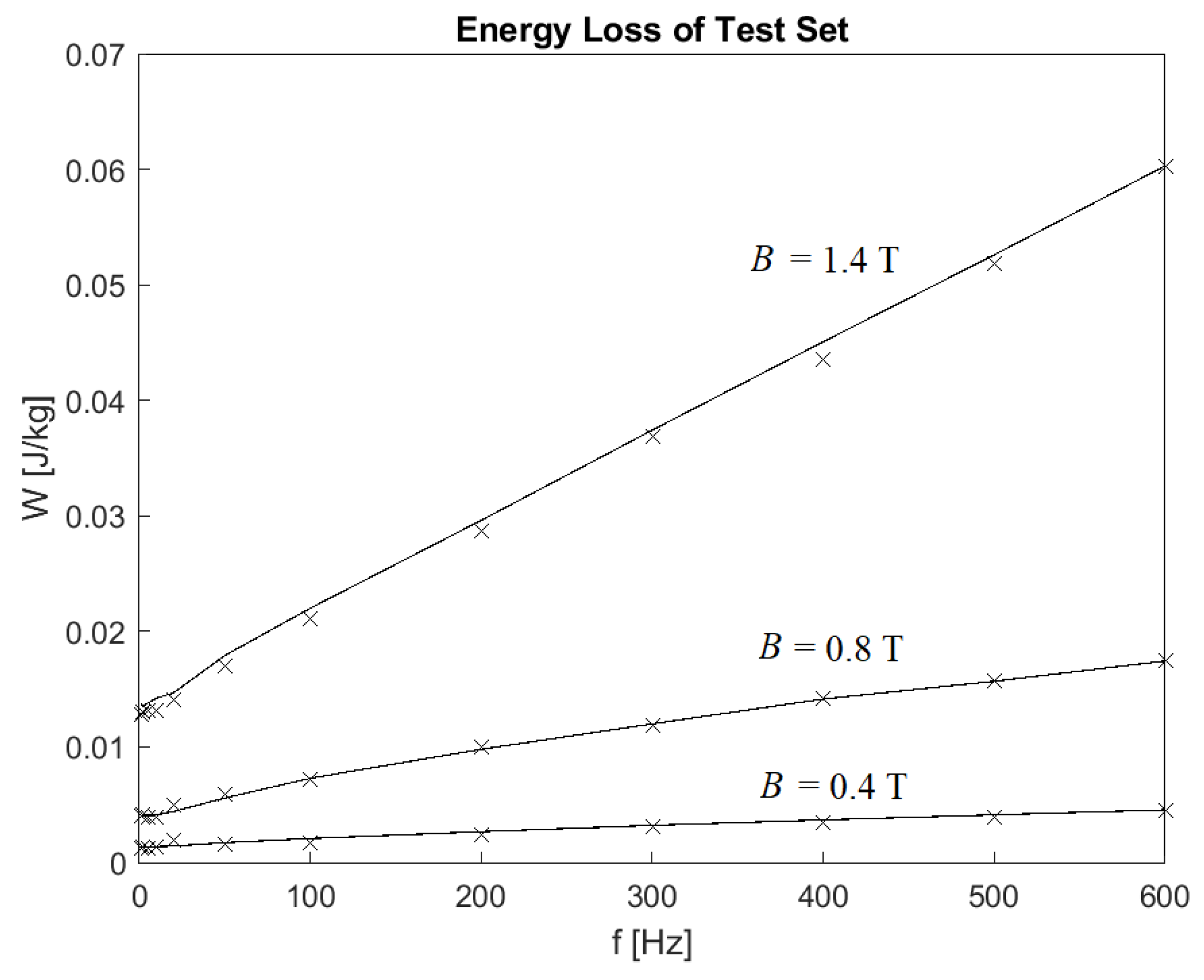Here, the energy losses are calculated numerically for each measured and simulated loop, exploiting the trapezoidal approximation of the function B(H), and are plotted against the frequency for fixed values of the magnetic induction. Since the curves relative to the training set are easily reproduced by the neural network model, the prediction of the energy losses and the comparison with the experimental values are most interesting if performed on the test set. For this reason, Figure 5 shows the behavior of the experimental losses in the frequency interval of interest, together with the ones predicted by the model for B = 0.4 T, B = 0.8 T, and B = 1.4 T. To allow the visualization of the curves in the entire frequency range, the y axis is at a logarithmic scale. In

Table 2. Energy losses [J/kg] in function of frequency, obtained from simulations on amplitudes of B not involved in the training.

	1 Hz	2 Hz	5 Hz	10 Hz	20 Hz	50 Hz	100 Hz	200 Hz	300 Hz	400 Hz	500 Hz	600 Hz
1.4 T	0.0127	0.0130	0.0132	0.0132	0.0141	0.0171	0.0211	0.0287	0.0368	0.0436	0.0518	0.0602
0.8 T	0.0040	0.0041	0.0040	0.0039	0.0049	0.0058	0.0072	0.0100	0.0119	0.0142	0.0157	0.0174
0.4 T	0.0013	0.0013	0.0013	0.0014	0.0019	0.0016	0.0017	0.0024	0.0031	0.0034	0.0040	0.0045

, the results of Figure 5 are shown in numerical form.

From the comparison, the effectiveness of the model in simulating the dynamic hysteresis for the magnetic material examined can, again, be highlighted. The largest deviation, as expected, is found for B = 0.4 T and f = 20 Hz (minor loop shown in the left panel of Figure 4). In this case, the neural network model tends to overestimate the energy loss by an amount of 6.35 J/m³.

The curve traced with B = 0.4 T, after the overestimation of the energy loss for f = 20 Hz, shows a slight underestimation for f in the range of [50–300 Hz], but the absolute displacement is smaller than 3 J/kg. For any other value of B and f, the difference between the predicted values and the experimental ones is not appreciable and can be neglected. Figure 6 and Figure 7 show the percentage error and mean-squared error, respectively, related to the energy loss (Figure 5) on the test set.

To conveniently exploit the high computational and memory efficiency of the neural network, the model was implemented at a low level of abstraction in Matlab^®. The solution of a single value of the output, requires the calculation of three matrix operations of “multiply and add”, in the form [w_l][x_l] + [b_l], where: [w_l] is the weight matrix of the neurons in the layer l; [b_l] is their biases; and [x_l] is the inputs to the layer l, plus three calls to the activation function f_act, since [x_l+1] = f_act([w_l][x_l] + [b_l]). In the Matlab^® environment, the typical calculation speed [25] for feedforward neural networks with tens of neurons is some kSample/s on a conventional computer. In this work, the simulations were performed on the same PC, equipped with a CPU Intel^® Core™ i7 @ 2.20 GHz, with 8 GB of RAM memory and a 64-bit operating system, and we reached 5.0 kSample/s. The memory intrinsically occupied by the model is very small: 110 weights and 21 biases stored as floating-point variables.

4. Conclusions and Future Research

We proposed a performing model of dynamic hysteresis based on a standalone feedforward neural network for the simulation of regime-state hysteresis loops under periodic magnetic-field waveforms. To simulate the dynamic magnetization processes of a given material—35H270, in the present work—the model needs to be identified on a large set of measurements; then, a thorough experimental investigation has to be preliminarily carried out in a wide range of magnetic inductions and frequencies. The measured data can then be subdivided into training and test sets.

A dedicated procedure allows the individuation of the optimal network architecture before effective training. The model assessment via simulation of the dynamic hysteresis loops of the test set indicated that both curves on the H-B plane and the energy losses could be reproduced with good accuracy up to saturation, and in a wide frequency interval. In particular, both quasi-DC hysteresis loops (f ≤ 5 Hz) and dynamic ones up to 600 Hz were correctly replicated by the neural network, covering the range of supply frequencies of the magnetic components for the avionic environment. The high computational speed, coupled with the low memory requirements, makes the proposed approach a powerful tool for the simulation of dynamic hysteresis processes in soft ferromagnetic materials; we are confident that it could help in the optimum design of electrical machines and magnetic components.

The model described herein reproduces, with high accuracy, regime-state magnetization processes under periodic magnetic field sequences; the development of a neural network model in the time domain for transient simulations is one of the main research activities on which the group is currently focused.