An Epidemic Model with Time Delay Determined by the Disease Duration
Abstract
:1. Introduction
2. Model Formulation
2.1. Model with Distributed Parameters
2.2. Reduction to SIR Model
2.3. Delay Model
3. Epidemic Characteristics
3.1. Basic Reproduction Number
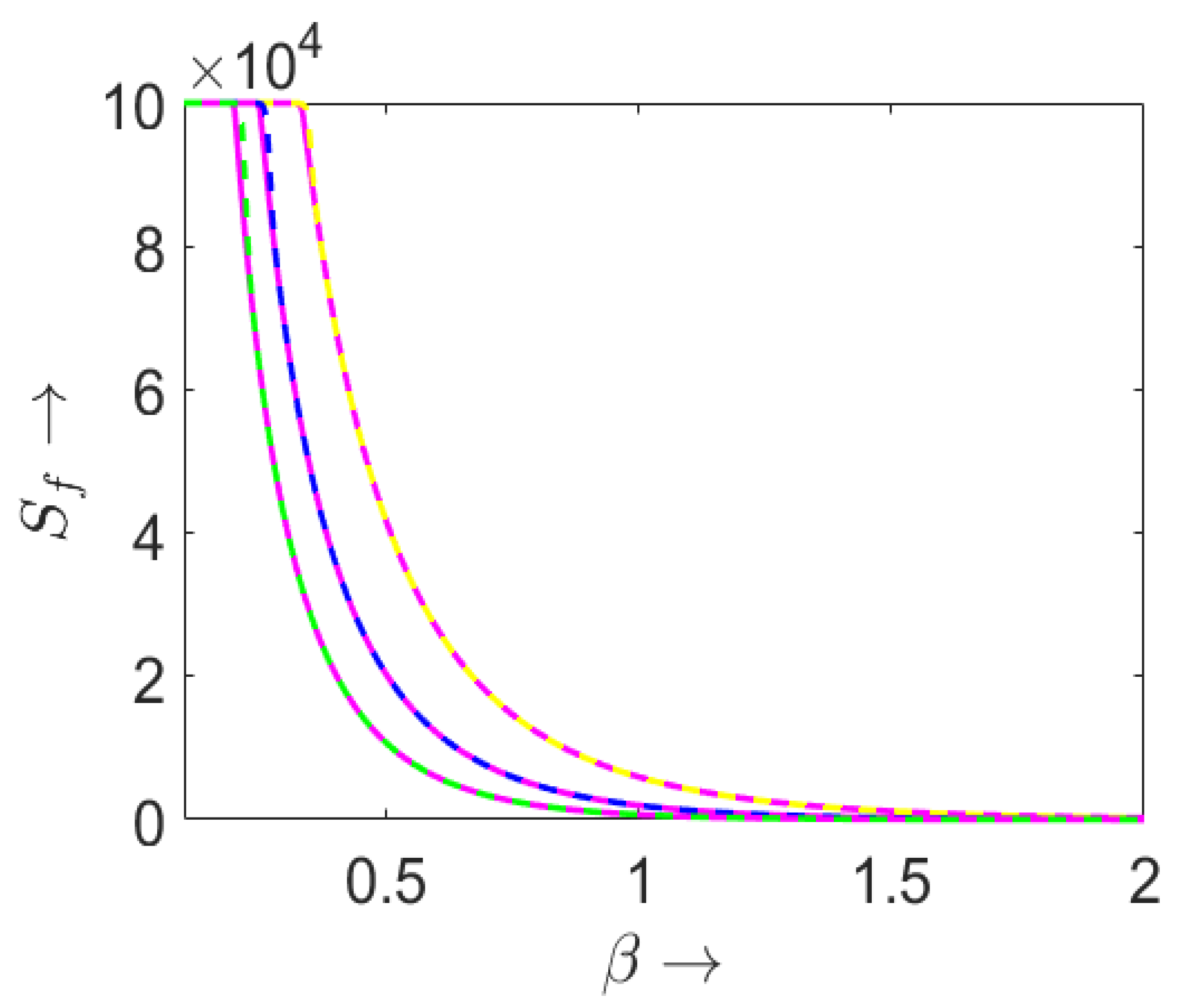
3.2. Final Size of the Epidemic
3.3. Maximum Number of Infected Individuals
4. Comparison of Models (3) and (9) and SIR (4)
5. Determination of Disease Duration from Data
6. Model Validation with Epidemiological Data
7. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Review of Delay Models
Appendix B. Positiveness of the Delay Model (9)
Appendix C. Gamma Distributions for Recovery and Death Rates

References
- Hoch, S.P.F.; Hutwagner, L. Opportunistic candidiasis: An epidemic of the 1980s. Clin. Infect. Dis. 1995, 21, 897–904. [Google Scholar] [CrossRef] [PubMed]
- Chintu, C.; Athale, U.H.; Patil, P.S. Childhood cancers in Zambia before and after the HIV epidemic. Arch. Dis. Child. 1995, 73, 100–105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anderson, R.M.; Fraser, C.; Ghani, A.C.; Donnelly, C.A.; Riley, S.; Ferguson, N.M.; Leung, G.M.; Lam, T.H.; Hedley, A.J. Epidemiology, transmission dynamics and control of SARS: The 2002–2003 epidemic. Philos. Trans. R. Soc. B: Biol. Sci. 2004, 359, 1091–1105. [Google Scholar] [CrossRef] [PubMed]
- Lam, W.K.; Zhong, N.S.; Tan, W.C. Overview on SARS in Asia and the World. Respirology 2003, 8, S2–S5. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Smith, G.J.D.; Li, K.S.; Wang, J.; Fan, X.H.; Rayner, J.M.; Vijaykrishna, D.; Zhang, J.X.; Zhang, L.J.; Guo, C.T.; et al. Establishment of multiple sublineages of H5N1 influenza virus in Asia: Implications for pandemic control. Proc. Natl. Aacd. Sci. USA 2006, 103, 2845–2850. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kilpatrick, A.M.; Chmura, A.A.; Gibbons, D.W.; Fleischer, R.C.; Marra, P.P.; Daszak, P. Predicting the global spread of H5N1 avian influenza. Proc. Natl. Aacd. Sci. USA 2006, 103, 19368–19373. [Google Scholar] [CrossRef] [Green Version]
- Jain, S.; Kamimoto, L.; Bramley, A.M.; Schmitz, A.M.; Benoit, S.R.; Louie, J.; Sugerman, D.E.; Druckenmiller, J.K.; Ritger, K.A.; Chugh, R.; et al. Hospitalized Patients with 2009 H1N1 Influenza in the United States, April–June 2009. N. Engl. J. Med. 2009, 361, 1935–1944. [Google Scholar] [CrossRef] [Green Version]
- Girard, M.P.; Tam, J.S.; Assossou, O.M.; Kieny, M.P. The 2009 A (H1N1) influenza virus pandemic: A review. Vaccine 2010, 28, 4895–4902. [Google Scholar] [CrossRef]
- Frieden, T.R.; Damon, I.; Bell, B.P.; Kenyon, T.; Nichol, S. Ebola 2014—New challenges, new global response and responsibility. N. Engl. J. Med. 2014, 371, 1177–1180. [Google Scholar] [CrossRef] [Green Version]
- WHO Ebola Response Team. Ebola Virus Disease in West Africa — The First 9 Months of the Epidemic and Forward Projections. N. Engl. J. Med. 2014, 371, 1481–1495. [Google Scholar] [CrossRef] [Green Version]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. A Lond 1927, 115, 700–721. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics. II. —The problem of endemicity. Proc. R. Soc. A Lond 1932, 138, 55–83. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics. III.—Further studies of the problem of endemicity. Proc. R. Soc. A Lond 1933, 141, 94–122. [Google Scholar]
- Sharma, S.; Volpert, V.; Banerjee, M. Extended SEIQR type model for COVID-19 epidemic and data analysis. Math. Biosci. Eng. 2020, 17, 7562–7604. [Google Scholar] [CrossRef]
- Khan, M.A.; Atangana, A. Mathematical modeling and analysis of COVID-19: A study of new variant Omicron. Physica A 2022, 599, 127452. [Google Scholar] [CrossRef]
- Brauer, F. Compartmental Models in Epidemiology. In Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2008; pp. 19–79. [Google Scholar]
- d’Onofrio, A.; Banerjee, M.; Manfredi, P. Spatial behavioural responses to the spread of an infectious disease can suppress Turing and Turing–Hopf patterning of the disease. Phys. A Stat. Mech. Appl. 2020, 545, 123773. [Google Scholar] [CrossRef]
- Sun, G.-Q.; Jin, Z.; Liu, Q.-X.; Li, L. Chaos induced by breakup of waves in a spatial epidemic model with nonlinear incidence rate. J. Stat. Mech. Theory Exp. 2008, P08011, 2008. [Google Scholar] [CrossRef]
- Bichara, D.; Iggidr, A. Multi-patch and multi-group epidemic models: A new framework. J. Math. Biol. 2018, 77, 107–134. [Google Scholar] [CrossRef] [Green Version]
- Lahodny, G.E.; Allen, L.J.S. Probability of a disease outbreak in stochastic multipatch epidemic models. Bull. Math. Biol. 2013, 75, 1157–1180. [Google Scholar] [CrossRef]
- McCormack, R.K.; Allen, L.J.S. Multi-patch deterministic and stochastic models for wildlife diseases. J. Biol. Dyn. 2007, 1, 63–85. [Google Scholar] [CrossRef]
- Elbasha, E.H.; Gumel, A.B. Vaccination and herd immunity thresholds in heterogeneous populations. J. Math. Biol. 2021, 83, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Aniţa, S.; Banerjee, M.; Ghosh, S.; Volpert, V. Vaccination in a two-group epidemic model. Appl. Math. Lett. 2021, 119, 107197. [Google Scholar] [CrossRef]
- Faniran, T.S.; Ali, A.; Al-Hazmi, N.E.; Asamoah, J.K.K.; Nofal, T.A.; Adewole, M.O. New Variant of SARS-CoV-2 Dynamics with Imperfect Vaccine. Complexity 2022, 2022, 1062180. [Google Scholar] [CrossRef]
- Ahmed, N.; Wei, Z.; Baleanu, D.; Rafiq, M.; Rehman, M.A. Spatio-temporal numerical modeling of reaction-diffusion measles epidemic system. Chaos 2019, 29, 103101. [Google Scholar] [CrossRef]
- Filipe, J.A.N.; Maule, M.M. Effects of dispersal mechanisms on spatio-temporal development of epidemics. J. Theor. Biol. 2004, 226, 125–141. [Google Scholar] [CrossRef]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2015; Volume 61. [Google Scholar]
- Brauer, F.; Chavez, C.C.; Feng, Z. Mathematical Models in Epidemiology; Springer: Berlin/Heidelberg, Germany, 2019; Volume 32. [Google Scholar]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef] [Green Version]
- Hurd, H.S.; Kaneene, J.B. The application of simulation models and systems analysis in epidemiology: A review. Prev. Vet. Med. 1993, 15, 81–99. [Google Scholar] [CrossRef]
- Ghosh, S.; Volpert, V.; Banerjee, M. An epidemic model with time-distributed recovery and death rates. Bull. Math. Biol. 2022, 84, 78. [Google Scholar] [CrossRef]
- Ghosh, S.; Banerjee, M.; Volpert, V. Immuno-epidemiological model-based prediction of further COVID-19 epidemic outbreaks due to immunity waning. Math. Model. Nat. Phenom. 2022, 17, 9. [Google Scholar] [CrossRef]
- Volpert, V.; Banerjee, M.; Petrovskii, S. On a quarantine model of coronavirus infection and data analysis. Math. Model. Nat. Phenom. 2020, 15, 24. [Google Scholar] [CrossRef]
- Paul, S.; Lorin, E. Estimation of COVID-19 recovery and decease periods in Canada using delay model. Sci. Rep. 2021, 11, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.worldometers.info/coronavirus/ (accessed on 8 May 2022).
- Verity, R.; Okell, L.C.; Dorigatti, I.; Winskill, P.; Whittaker, C.; Imai, N.; Dannenburg, G.C.; Thompson, H.; Walker, P.G.T.; Fu, H.; et al. Estimates of the severity of coronavirus disease 2019: A model-based analysis. Lancet Infect. Dis. 2020, 20, 669–677. [Google Scholar] [CrossRef]
- Arino, J.; Portet, S. A simple model for COVID-19. Infect. Dis. Model. 2020, 5, 309–315. [Google Scholar] [CrossRef] [PubMed]
- Nishiura, H.; Kobayashi, T.; Miyama, T.; Suzuki, A.; Jung, S.; Hayashi, K.; Kinoshita, R.; Yang, Y.; Yuan, B.; Akhmetzhanov, A.R.; et al. Estimation of the asymptomatic ratio of novel coronavirus infections (COVID-19). Int. J. Infect. Dis. 2020, 94, 154–155. [Google Scholar] [CrossRef] [PubMed]
- Mizumoto, K.; Kagaya, K.; Zarebski, A.; Chowell, G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Eurosurveillance 2020, 25, 2000180. [Google Scholar] [CrossRef] [Green Version]
- Sentis, C.; Billaud, G.; Bal, A.; Frobert, E.; Bouscambert, M.; Destras, G.; Josset, L.; Lina, B.; Morfin, F.; Gaymard, A.; et al. SARS-CoV-2 Omicron Variant, Lineage BA.1, Is Associated with Lower Viral Load in Nasopharyngeal Samples Compared to Delta Variant. Viruses 2022, 14, 919. [Google Scholar] [CrossRef]
- Huang, G.; Takeuchi, Y.; Ma, W.; Wei, D. Global Stability for Delay SIR and SEIR Epidemic Models with Nonlinear Incidence Rate. Bull. Math. Biol. 2010, 72, 1192–1207. [Google Scholar] [CrossRef] [Green Version]
- Mehdaoui, M. A review of commonly used compartmental models in epidemiology. arXiv 2021, arXiv:2110.09642. [Google Scholar] [CrossRef]
- Cooke, K.; Driessche, P.V.d.; Zou, X. Interaction of maturation delay and nonlinear birth in population and epidemic models. J. Math. Biol. 1999, 39, 332–352. [Google Scholar] [CrossRef]
- Lou, Y.; Zhao, X.-Q. Threshold dynamics in a time-delayed periodic SIS epidemic model. Discrete Contin. Dyn. Syst. B 2009, 12, 169. [Google Scholar] [CrossRef]






| Parameters | Estimated Value | 95% Confidence Interval |
|---|---|---|
| 8.06275 | [6.15314, 10.565] | |
| 2.2140 | [1.67523, 2.92623] | |
| 6.00014 | [3.69566, 9.74161] | |
| 2.19887 | [1.32639, 3.64526] |
| Country | Estimated Value | Estimated Value | Estimated Value | Estimated Value |
|---|---|---|---|---|
| of (in Days) | of (in Days) | of (in Days) | of (in Days) | |
| during Peak 1 | during Peak 2 | during Peak 3 | during Peak 4 | |
| Italy | 19 (April 2020) | 20 (November 2020) | 14 (March 2021) | 11 (January 2022) |
| Russia | 25 (May 2020) | 24 (January 2021) | 26 (November 2021) | 9 (February 2022) |
| China | 16 (February 2020) | - | - | - |
| Romania | 16 (November 2020) | 14 (March 2021) | 18 (October 2021) | 12 (February 2022) |
| Sweden | 20 (July 2020) | 20 (December 2020) | 19 (April 2021) | 14 (February 2022) |
| Iran | 14 (December 2020) | 24 (May 2021) | 28 (August 2021) | 10 (February 2022) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghosh, S.; Volpert, V.; Banerjee, M. An Epidemic Model with Time Delay Determined by the Disease Duration. Mathematics 2022, 10, 2561. https://doi.org/10.3390/math10152561
Ghosh S, Volpert V, Banerjee M. An Epidemic Model with Time Delay Determined by the Disease Duration. Mathematics. 2022; 10(15):2561. https://doi.org/10.3390/math10152561
Chicago/Turabian StyleGhosh, Samiran, Vitaly Volpert, and Malay Banerjee. 2022. "An Epidemic Model with Time Delay Determined by the Disease Duration" Mathematics 10, no. 15: 2561. https://doi.org/10.3390/math10152561
APA StyleGhosh, S., Volpert, V., & Banerjee, M. (2022). An Epidemic Model with Time Delay Determined by the Disease Duration. Mathematics, 10(15), 2561. https://doi.org/10.3390/math10152561








