Some Important Points of the Josephson Effect via Two Superconductors in Complex Bases
Abstract
:1. Introduction
2. Theoretical Analysis of Scheme
3. Applications
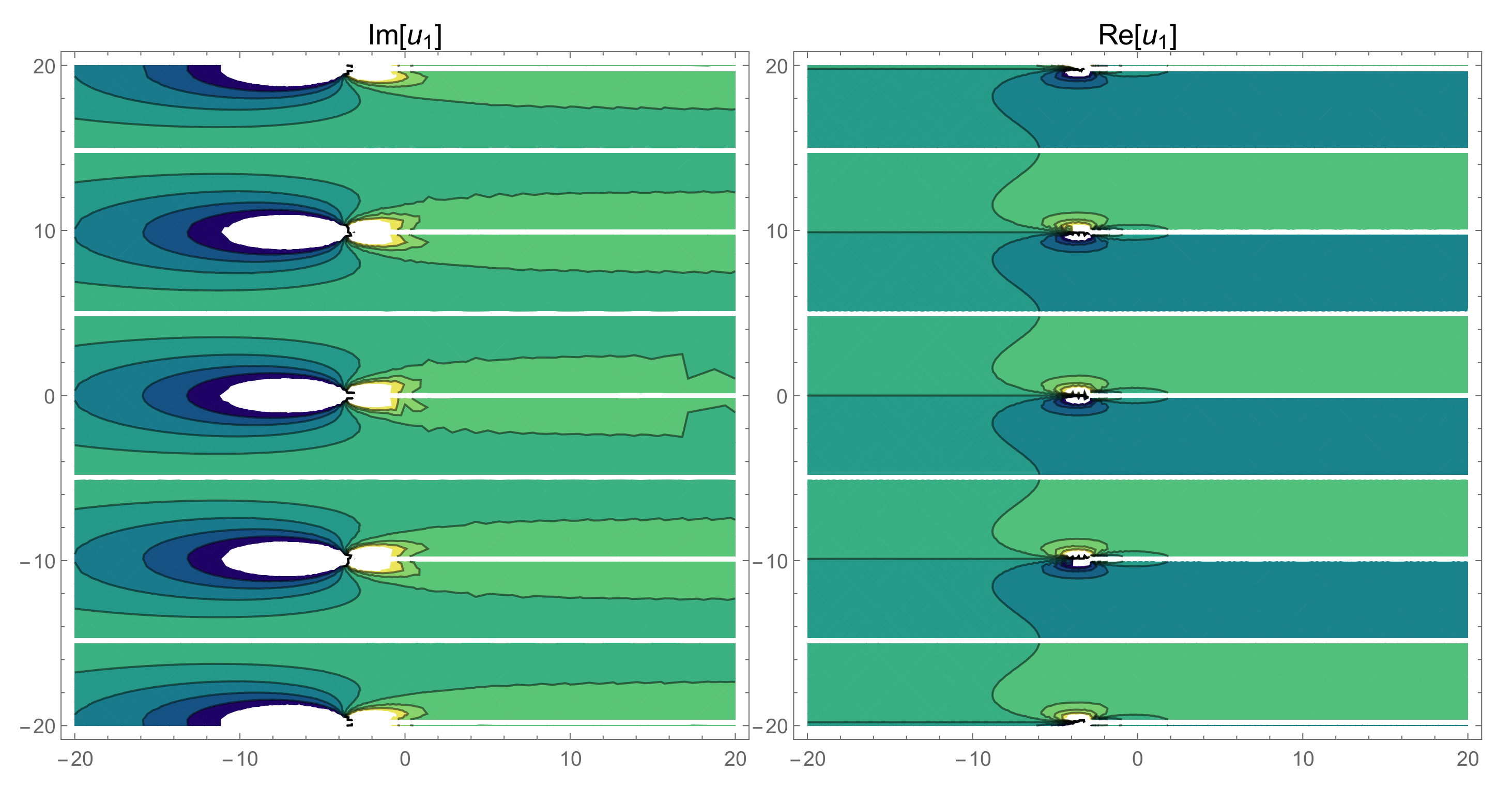
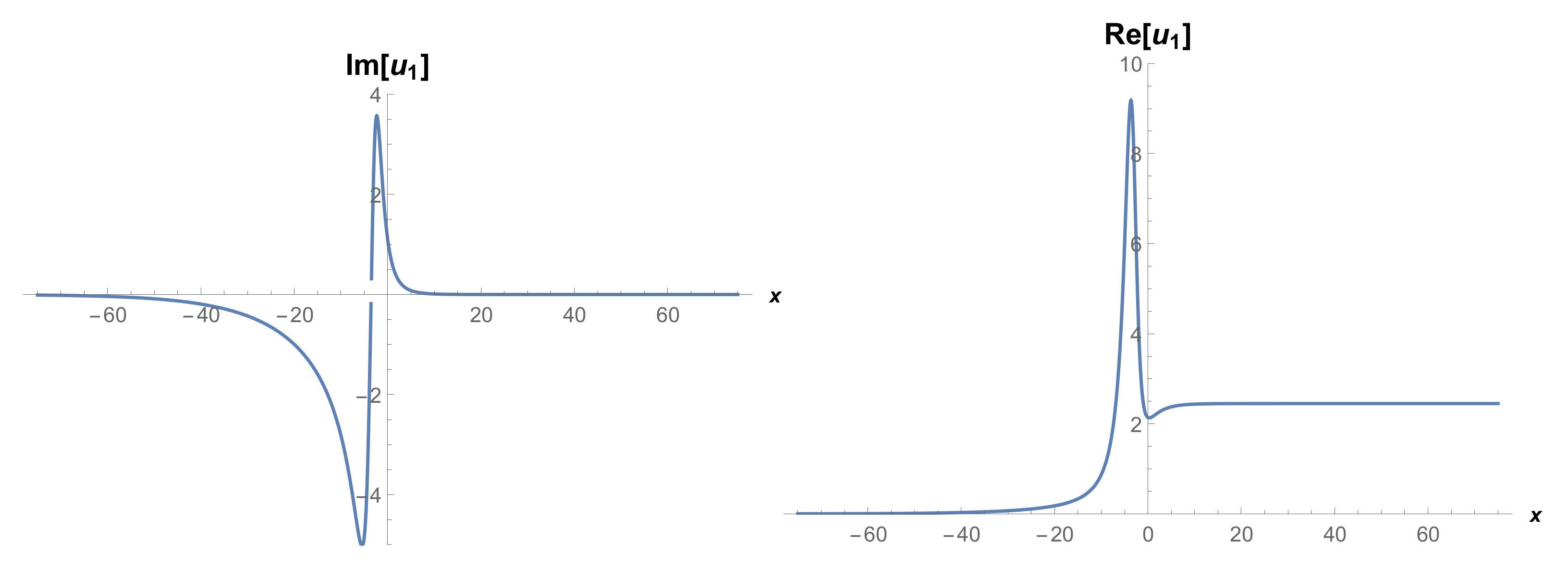
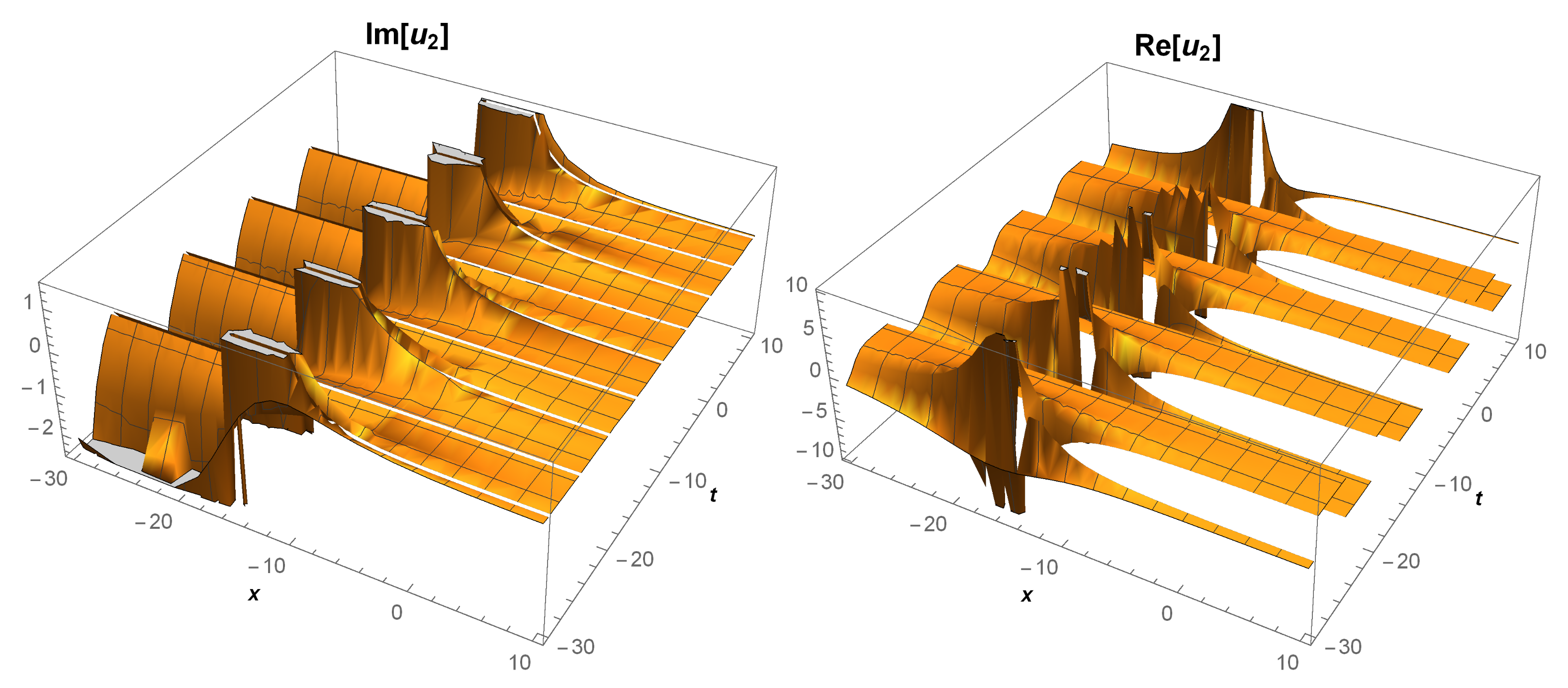
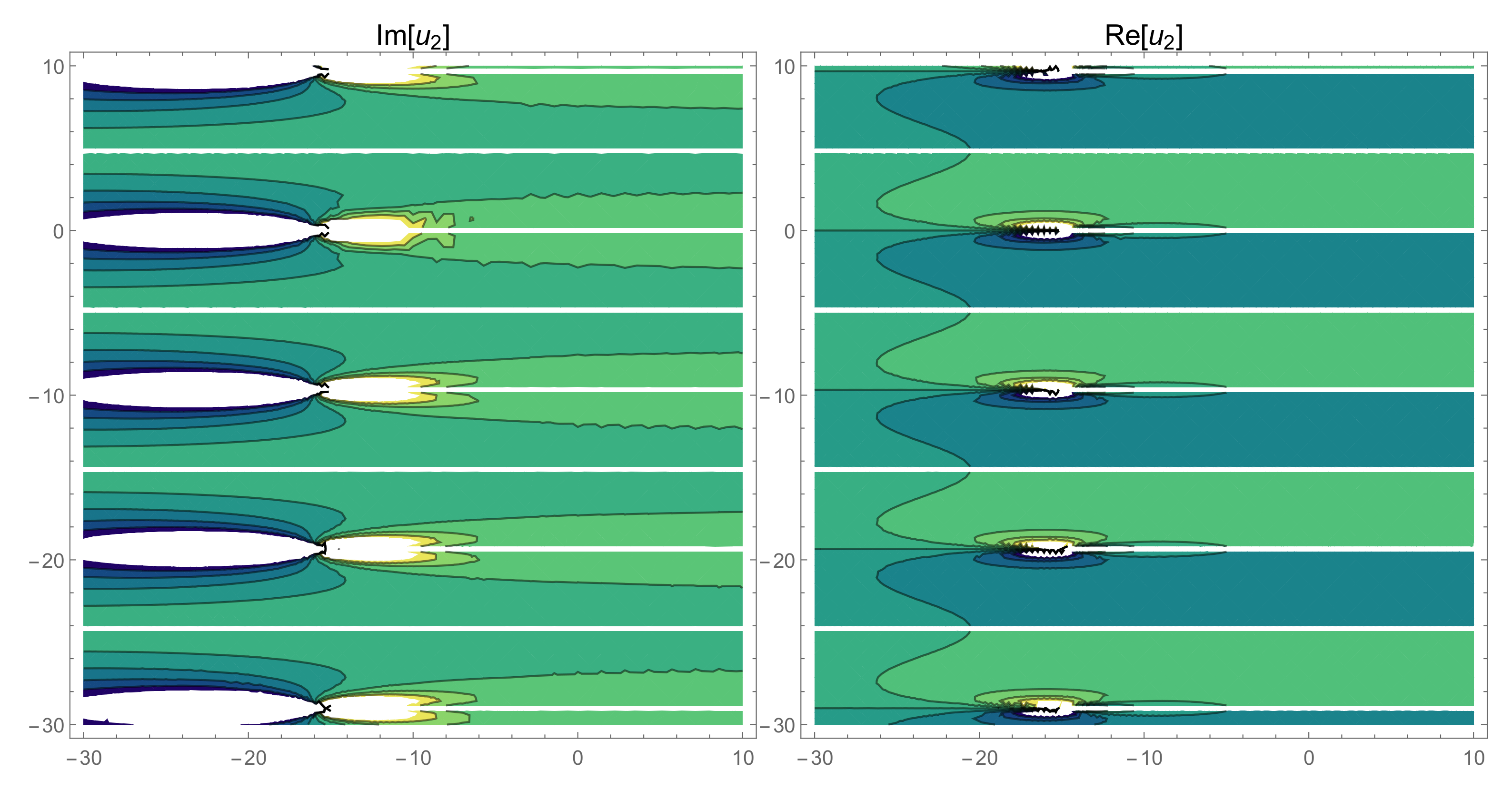
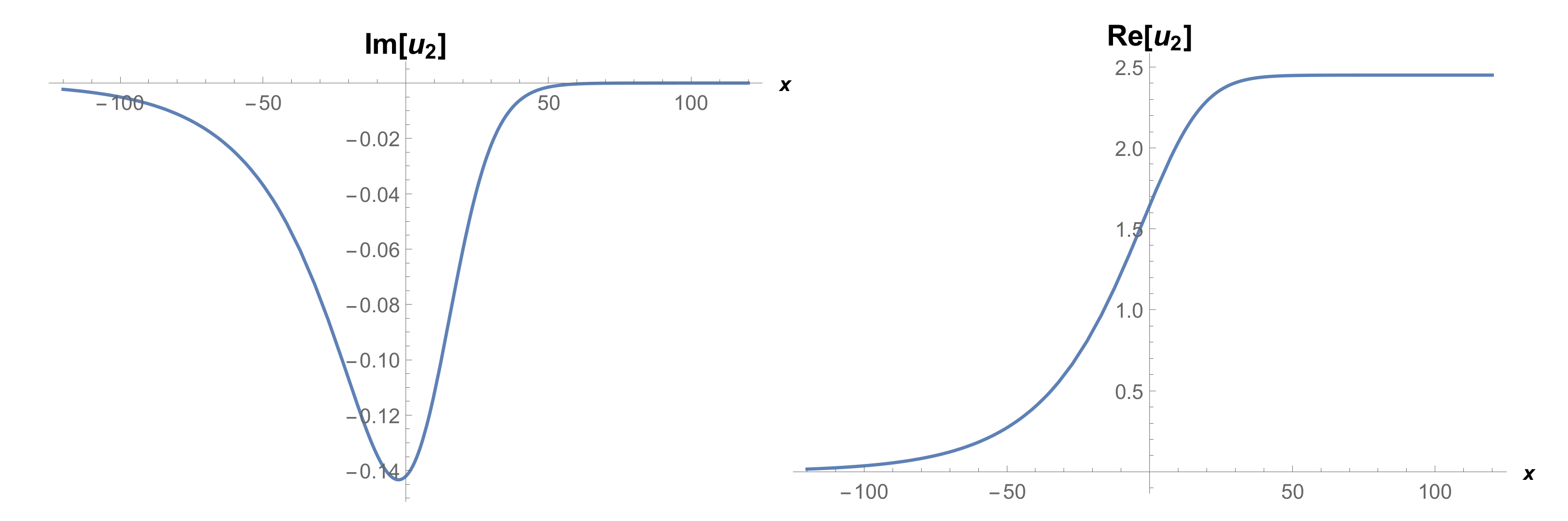
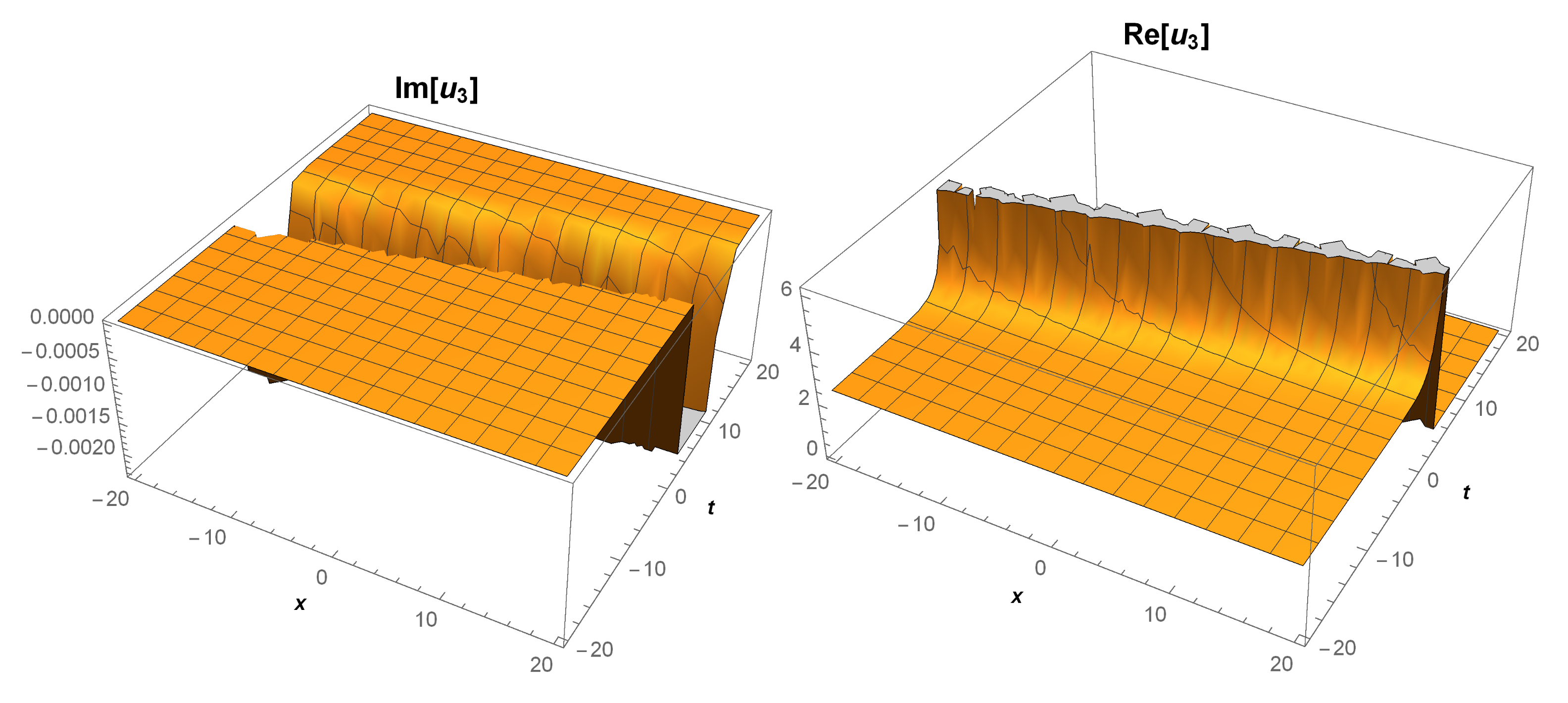
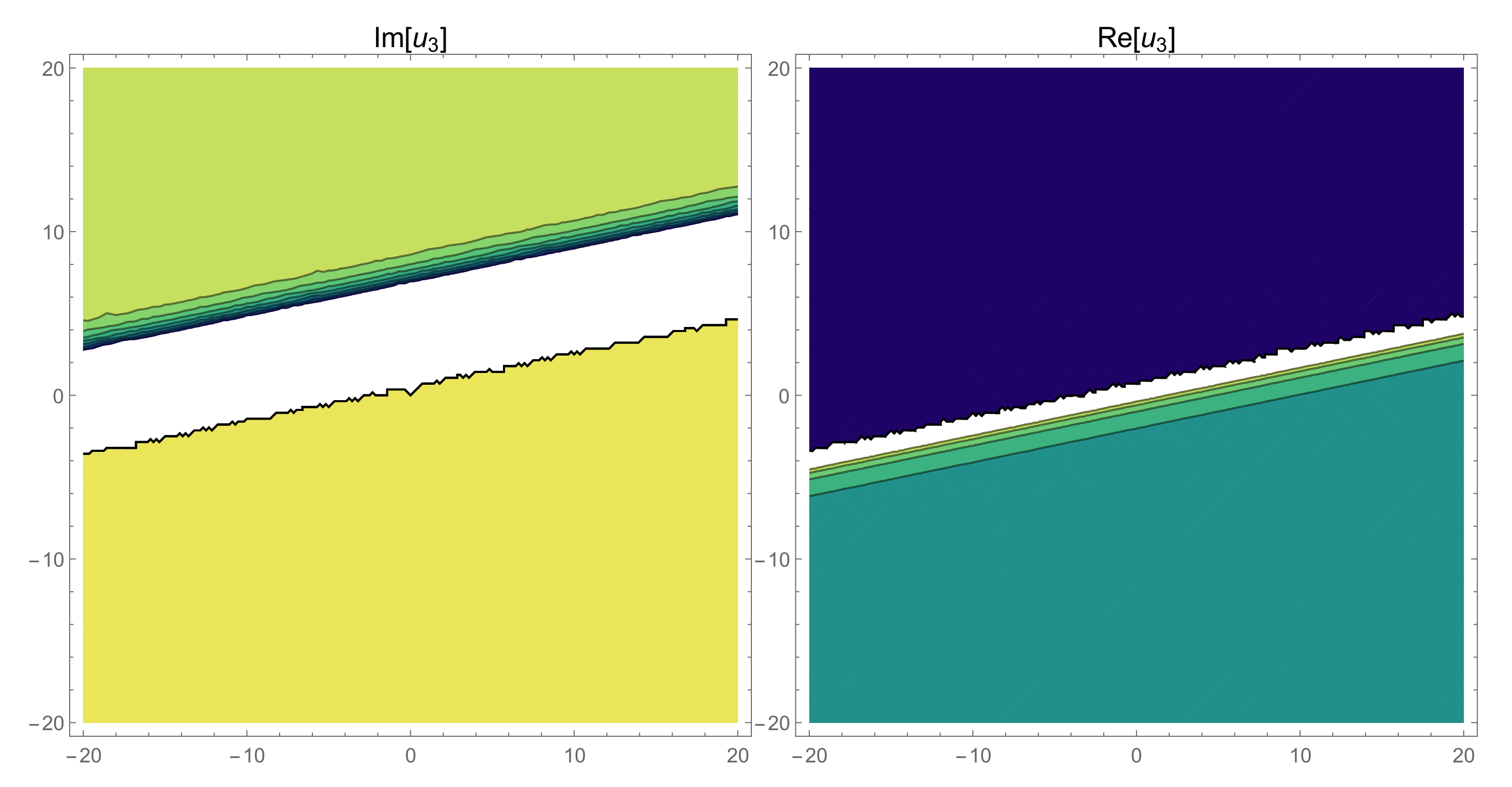
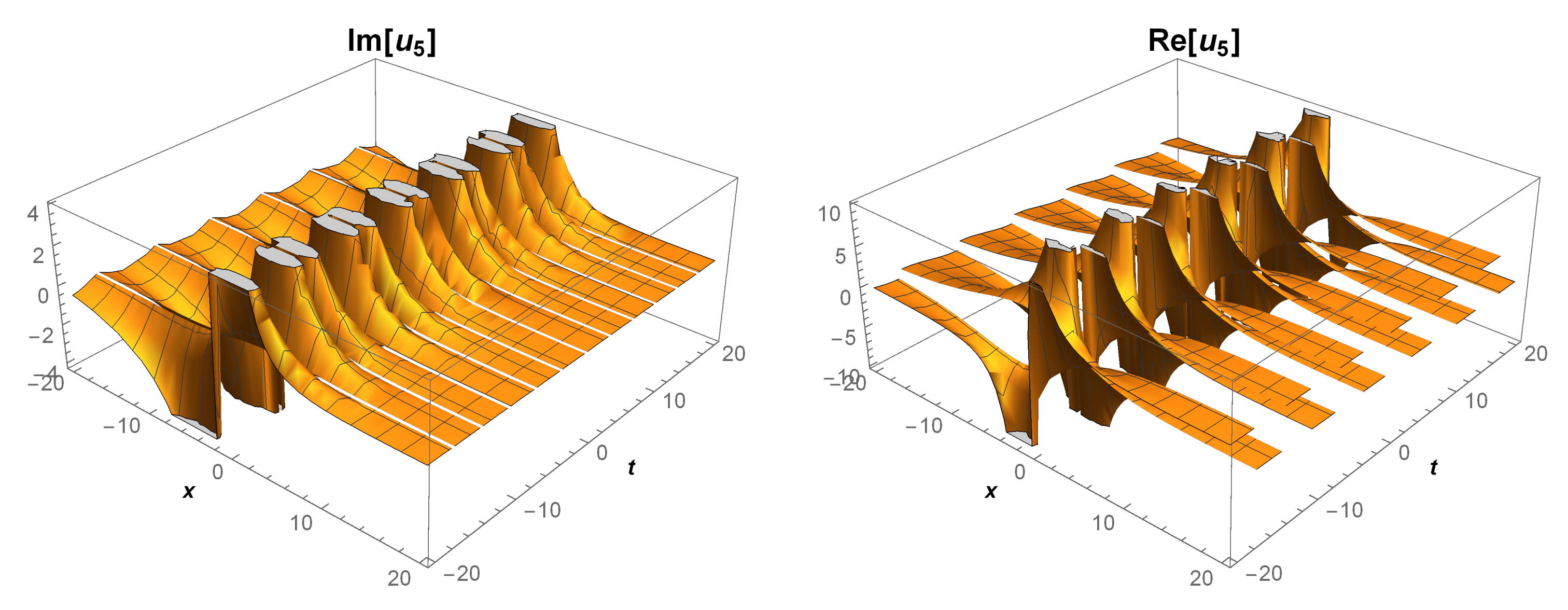
4. The Physical Properties
5. Some Remarks and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Josephson, B.D. Possible new effects in superconductive tunnelling. Phys. Lett. 1962, 1, 251–253. [Google Scholar] [CrossRef]
- Josephson, B.D. The discovery of tunnelling supercurrents. Rev. Mod. Phys. 1974, 46, 251–254. [Google Scholar] [CrossRef] [Green Version]
- Available online: https://www.britannica.com/biography/Brian-Josephson (accessed on 1 January 2020).
- Anderson, P.W.; Rowell, J.M. Probable Observation of the Josephson Tunnel Effect. Phys. Rev. Lett. 1963, 10, 230. [Google Scholar] [CrossRef]
- Zharkov, G.F. The Josephson Tunneling Effect In Superconductors. Soviet Physics Uspekhi 1966, 9, 1–13. [Google Scholar] [CrossRef]
- Pankratov, A.L.; Sobolev, A.S.; Koshelets, V.P.; Mygind, J. Influence of surface losses and the self-pumping effect on current-voltage characteristics of a long Josephson junction. Phys. Rev. B 2007, 75, 184516. [Google Scholar] [CrossRef] [Green Version]
- Pankratov, A.L. Long Josephson junctions with spatially inhomogeneous driving. Phys. Rev. B 2002, 66, 134526. [Google Scholar] [CrossRef] [Green Version]
- Pankratov, A.L. Noise self-pumping in long Josephson junctions. Phys. Rev. B 2008, 78, 024515. [Google Scholar] [CrossRef]
- Ha, J.; Nakagiri, S.I. Identification of constant parameters in perturbed sine-Gordon equations. J. Korean Math. Soc. 2006, 43, 931–950. [Google Scholar] [CrossRef] [Green Version]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Barone, A.; Paternò, G. Physics and Applications of the Josephson Effect; John Wiley and Sons, Inc.: New York, NY, USA, 1982. [Google Scholar]
- Scott, A.C.; Chu, F.Y.F.; Reible, S.A. Magnetic flux propagation on a Josephson transmission line. J. Appl. Phys. 1976, 47, 3272–3286. [Google Scholar] [CrossRef]
- Derks, G.; Doelman, A.; van Gils, S.A.; Visser, T. Travelling waves in a singularly perturbed sine-Gordon equation. Physica D 2003, 180, 40–70. [Google Scholar] [CrossRef] [Green Version]
- Kivshar, Y.S.; Malomed, B.A. Many-particle effects in nearly integrable systems. Physica D 1987, 24, 125–154. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Malomed, B.A. Dynamics of solitons in nearly integrable systems. Rev. Mod. Phys. 1989, 61, 763–915. [Google Scholar] [CrossRef]
- Ha, J.H.; Nagiri, S. Identification problems of damped sine-gordon equations with constant parameters. J. Korean Math. Soc. 2002, 39, 509–524. [Google Scholar] [CrossRef]
- Lions, J.L.; Magenes, E. Non-Homogeneous Boundary Value Problems and Applications; Springer: New York, NY, USA; Heildelberg, Germany, 1972; Volume II. [Google Scholar]
- Sasaki, A.; Ikegaya, S.; Habe, T.; Golubov, A.A.; Asano, Y. Josephson effect in two-band superconductors. Phys. Rev. B 2020, 101, 184501. [Google Scholar] [CrossRef]
- Pagano, S. Introduction to Weak Superconductivity Josephson Effect: Physics and Applications; Lecture Notes; Springer: New York, NY, USA, 2020. [Google Scholar]
- Seidel, P. 8-High-Tc Josephson junctions. High-Temp. Supercond. 2011, 317–369. [Google Scholar] [CrossRef]
- Couëdo, F.; Amari, P.; Palma, C.F.; Ulysse, C.; Rivastava, Y.K.S.; Singh, R.; Bergeal, N.; Lesueur, J. Dynamic properties of high-Tc superconducting nano-junctions made with a focused helium ion beam. Sci. Rep. 2020, 10, 10256. [Google Scholar] [CrossRef]
- Zheng, B. Application of A Generalized Bernoulli Sub-ODE Method For Finding Traveling Solutions of Some Nonlinear Equations. WSEAS Trans. Math. 2012, 7, 618–626. [Google Scholar]
- Baskonus, H.M.; Mahmud, A.A.; Muhamad, K.A.; Tanriverdi, T. A study on Coudrey-Dodd-Gibbon-Sawada-Kotera partial differential equation. Math. Methods Appl. Sci. 2022. [Google Scholar] [CrossRef]
- Gao, W.; Baskonus, H.M.; Mahmud, A.A.; Muhamad, K.A.; Tanriverdi, T. Studing on kudryashov-sinelshchıkov dynamical equation arising in mixtures liquid and gas bubbles. Therm. Sci. 2022, 26, 1229–1244. [Google Scholar]
- Weisstein, E.W. Concise Encyclopedia of Mathematics, 2nd ed.; CRC Press: New York, NY, USA, 2002. [Google Scholar]
- Wang, K.J. Abundant exact soliton solutions to the Fokas system. Optik 2022, 249, 168265. [Google Scholar] [CrossRef]
- Wang, K.J. Abundant analytical solutions to the new coupled Konno-Oono equation arising in magnetic field. Results Phys. 2021, 31, 104931. [Google Scholar] [CrossRef]
- Wang, K.J.; Wang, G. Exact traveling wave solutions for the system of the ion sound and Langmuir waves by using three effective methods. Results Phys. 2022, 35, 105390. [Google Scholar] [CrossRef]
- Wang, K.J.; Wang, G. Variational theory and new abundant solutions to the (1+2)-dimensional chiral nonlinear Schrödinger equation in optics. Phys. Lett. A 2021, 412, 127588. [Google Scholar] [CrossRef]
- Wang, K.J. Jing Si, Investigation into the Explicit Solutions of the Integrable (2+1)-Dimensional Maccari System via the Variational Approach. Axioms 2022, 11, 234. [Google Scholar] [CrossRef]
- Wang, K.J.; Shi, F.; Liu, J.H.; Si, J. Application of the extended F-expansion method for solving the fractional Gardner equation with conformable fractional derivative. Fractal 2022. [Google Scholar] [CrossRef]
- Wang, K.J. Traveling wave solutions of the Gardner equation in dusty plasmas. Results Phys. 2022, 33, 105207. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. On the exact solutions to some system of complex nonlinear models. Appl. Math. Nonlinear Sci. 2020, 6, 29–42. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H.; Sulaiman, T.A. New Complex Hyperbolic Structures to the Lonngren-Wave Equation by Using Sine-Gordon Expansion Method. Appl. Math. Nonlinear Sci. 2019, 4, 141–150. [Google Scholar] [CrossRef] [Green Version]
- Frassu, S.; Viglialoro, G. Boundedness criteria for a class of indirect (and direct) chemotaxis-consumption models in high dimensions. Appl. Math. Lett. 2022, 132, 108108. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Kayan, M. Regarding new wave distributions of the nonlinear integro-partial ITO differential and fifth-order integrable equations. Appl. Math. Nonlinear Sci. 2021, 1–20. [Google Scholar] [CrossRef]
- Yu, X.Q.; Kong, S. Travelling wave solutions to the proximate equations for LWSW. Appl. Math. Nonlinear Sci. 2021, 6, 335–346. [Google Scholar] [CrossRef]
- Gao, W.; Ismael, H.F.; Husien, A.M.; Bulut, H.; Baskonus, H.M. Optical Soliton solutions of the Nonlinear Schrodinger and Resonant Nonlinear Schrodinger Equation with Parabolic Law. Appl. Sci. 2020, 10, 219. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Viglialoro, G. Boundedness for a nonlocal reaction chemotaxis model even in the attraction-dominated regime. Diff. Int. Equ. 2021, 34, 315–336. [Google Scholar]
- Uddin, M.F.; Hafez, M.G.; Hammouch, Z.; Rezazadeh, H.; Baleanu, D. Traveling wave with beta derivative spatial-temporal evolution for describing the nonlinear directional couplers with metamaterials via two distinct methods. Alex. Eng. J. 2021, 60, 1055–1065. [Google Scholar] [CrossRef]
- Uddin, M.F.; Hafez, M.G.; Hammouch, Z.; Baleanu, D. Periodic and rogue waves for Heisenberg models of ferromagnetic spin chains with fractional beta derivative evolution and obliqueness. Waves Random Complex Media 2020, 31, 2135–2149. [Google Scholar] [CrossRef]
- Greco, A.; Viglialoro, G. Existence and Uniqueness for a Two-Dimensional Ventcel Problem Modeling the Equilibrium of a Prestressed Membrane. Appl. Math. 2022. [Google Scholar] [CrossRef]
- Bulut, H.; Akkilic, A.N.; Khalid, B.J. Soliton solutions of Hirota equation and Hirota-Maccari system by the (m+1/G’)-expansion method. Adv. Math. Model. Appl. 2021, 6, 22–30. [Google Scholar]
- Xu, L.; Aouad, M. Application of Lane-Emden differential equation numerical method in fair value analysis of financial accounting. Appl. Math. Nonlinear Sci. 2022. [Google Scholar] [CrossRef]
- Ciancio, A.; Ciancio, V.; Onofrio, A.; Flora, B.F.F. A Fractional Model of Complex Permittivity of Conductor Media with Relaxation: Theory vs. Experiments. Fractal Fract. 2022, 6, 390. [Google Scholar] [CrossRef]
- Ciancio, A.; Ciancio, V.; Franccesso, F. Wave propagation in media obeying a thermoviscoanelastic model. U.P.B. Sci. Bull. Ser. A 2007, 69, 69–79. [Google Scholar]
- Ciancio, A.; Yel, G.; Kumar, A.; Baskonus, H.M.; Ilhan, E. On the complex mixed dark-bright wave distributions to some conformable nonlinear integrable models. Fractals 2022, 30, 2240018. [Google Scholar] [CrossRef]
- Ramos, H.; Rufai, M.A. An adaptive one-point second-derivative Lobatto-type hybrid method for solving efficiently differential systems. Int. J. Comput. Math. 2022, 99, 1687–1705. [Google Scholar] [CrossRef]
- Duromola, M.K.; Momoh, A.L.; Rufai, M.A.; Animasaun, I.L. Insight into 2-step continuous block method for solving mixture model and SIR model. Int. J. Comput. Sci. Math. 2021, 14, 347–356. [Google Scholar] [CrossRef]

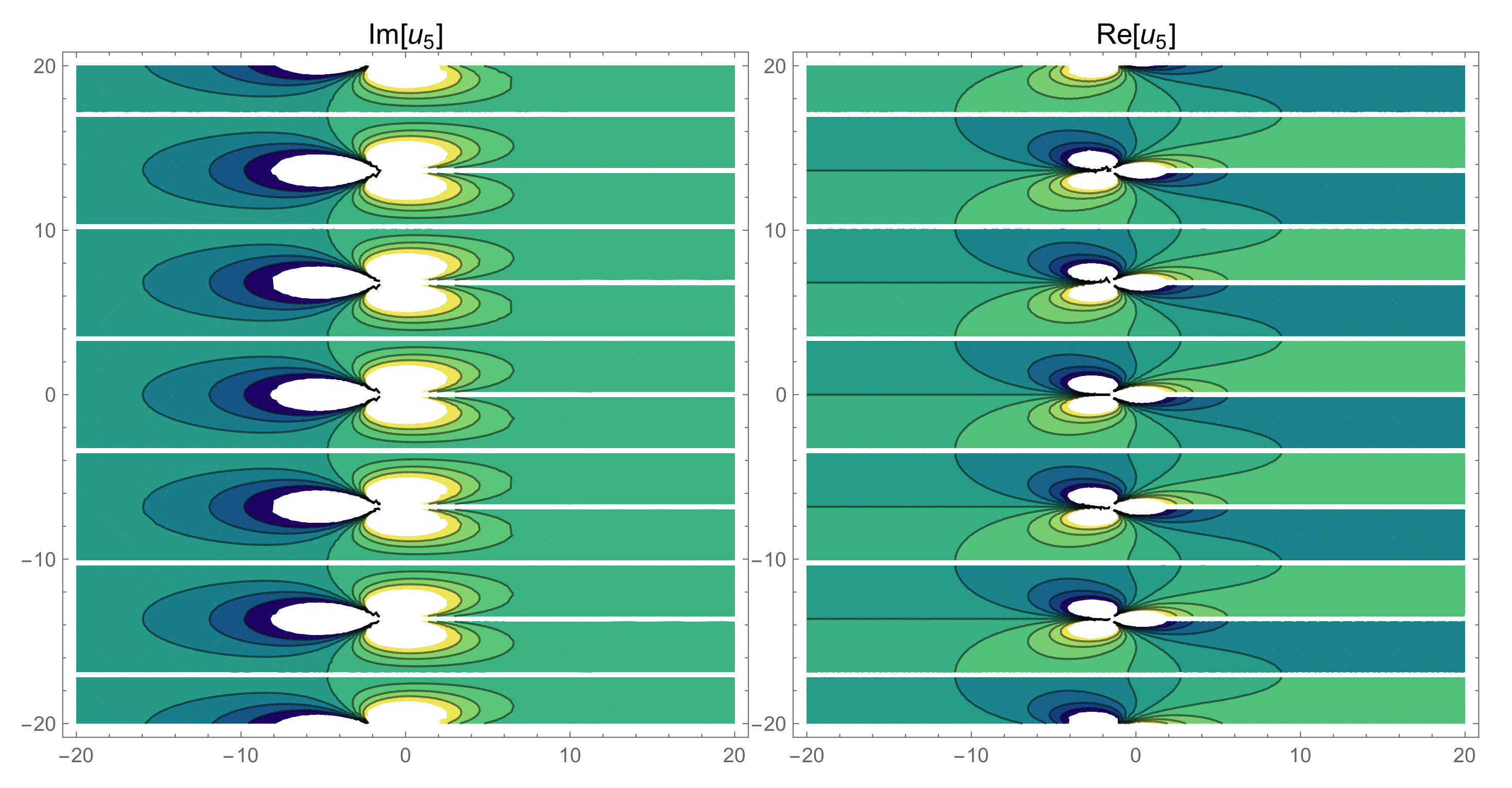
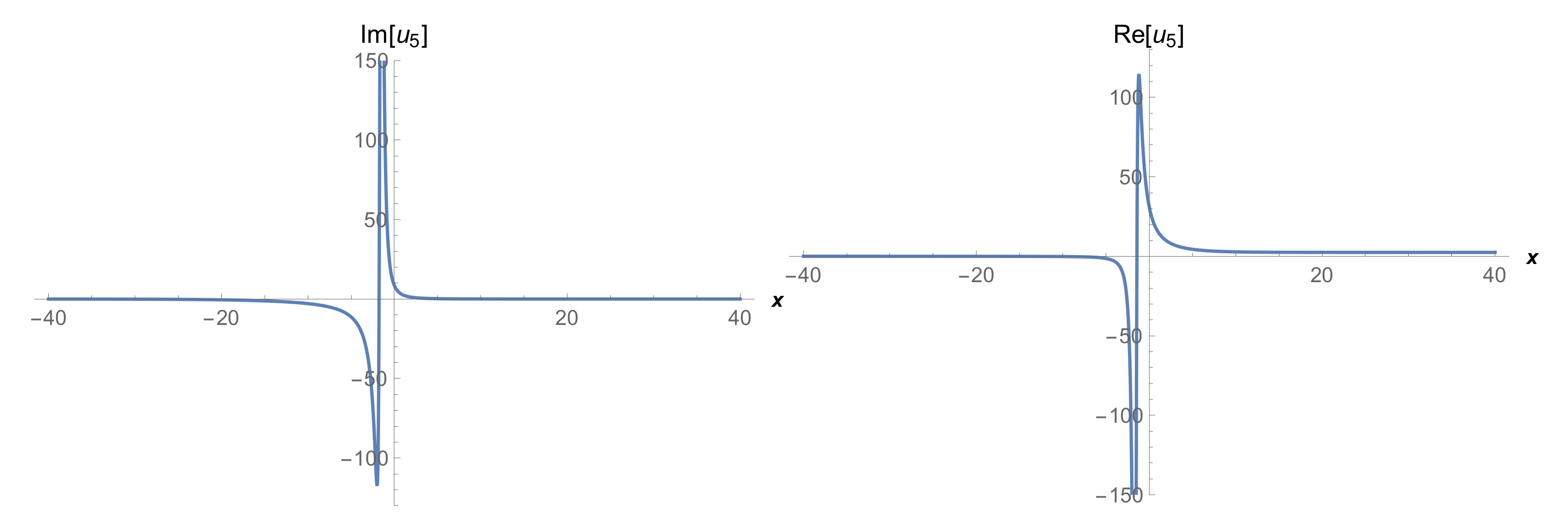
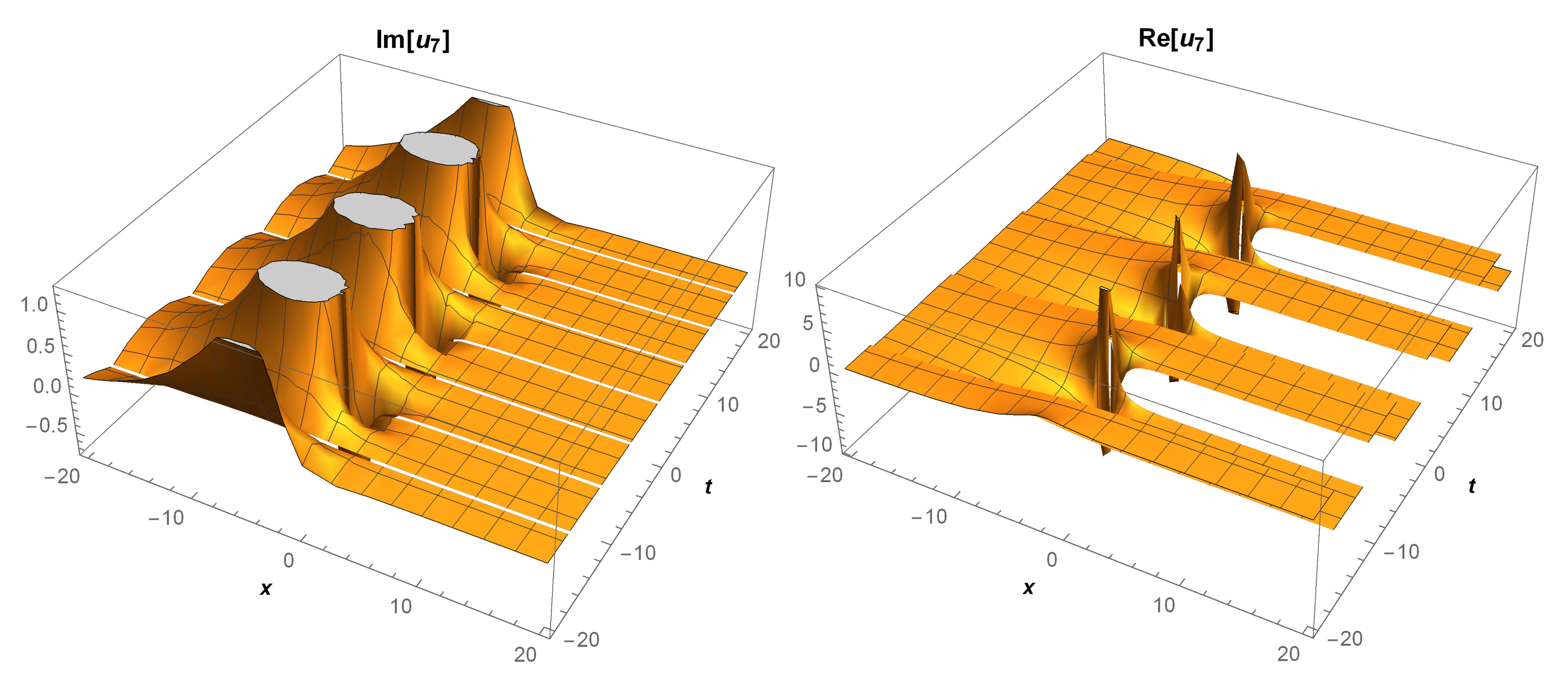
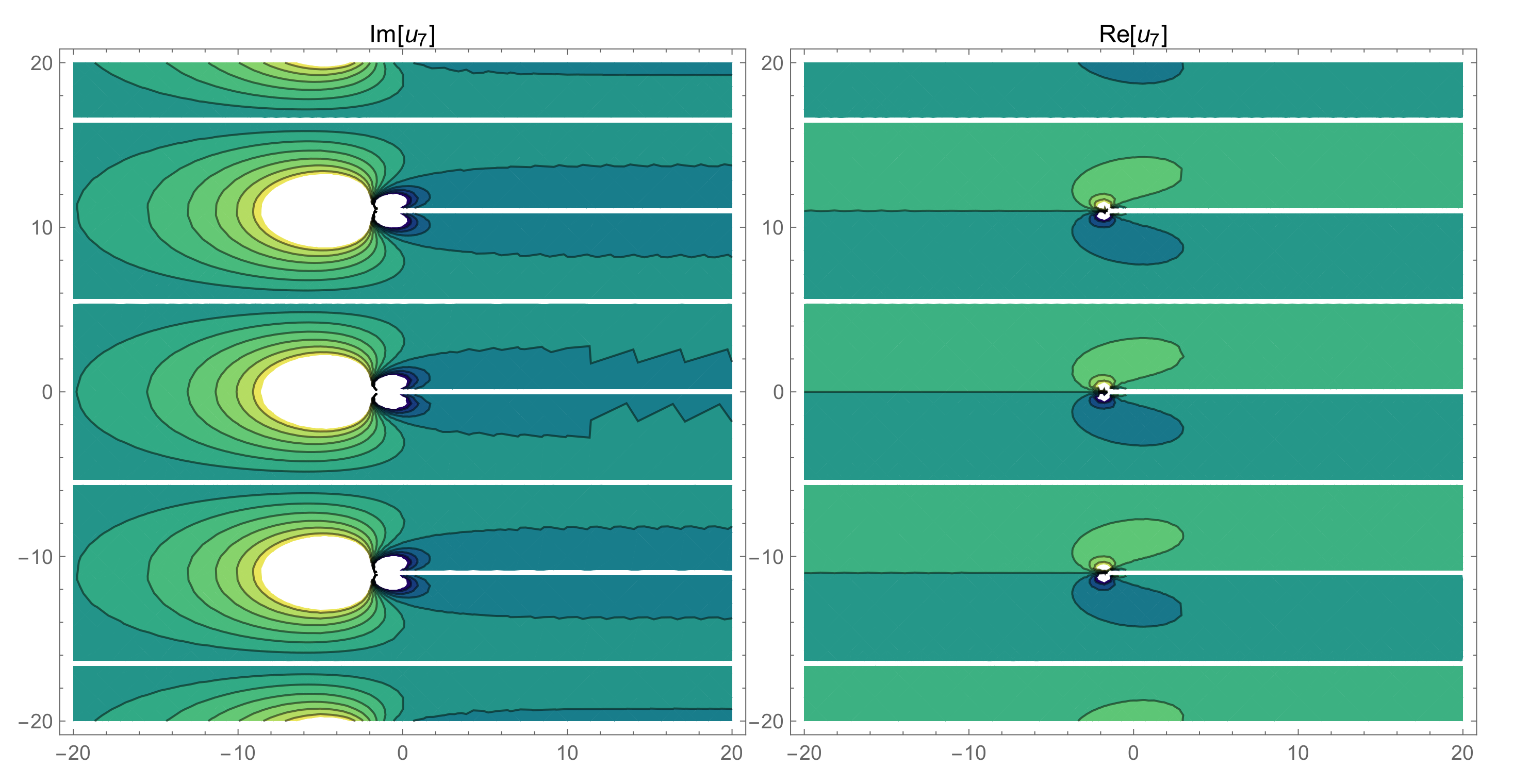

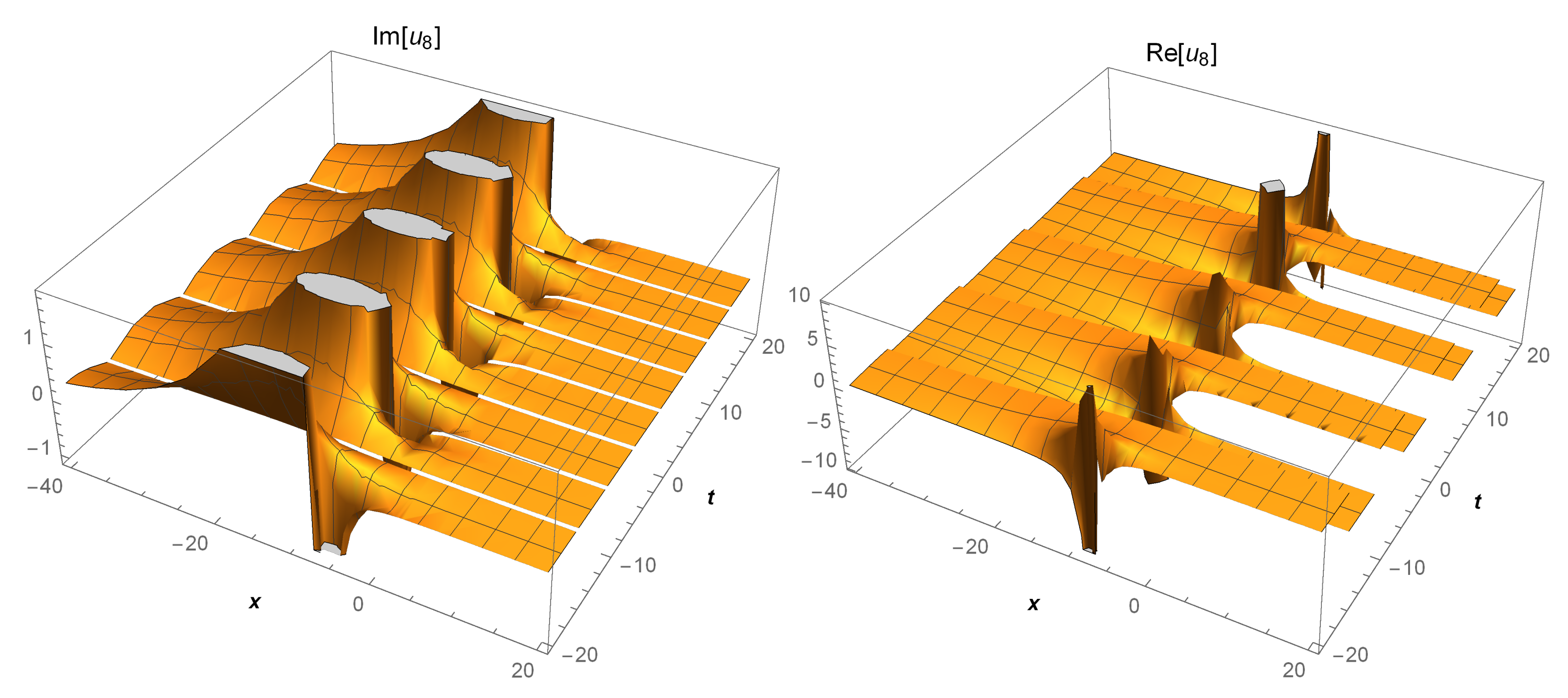
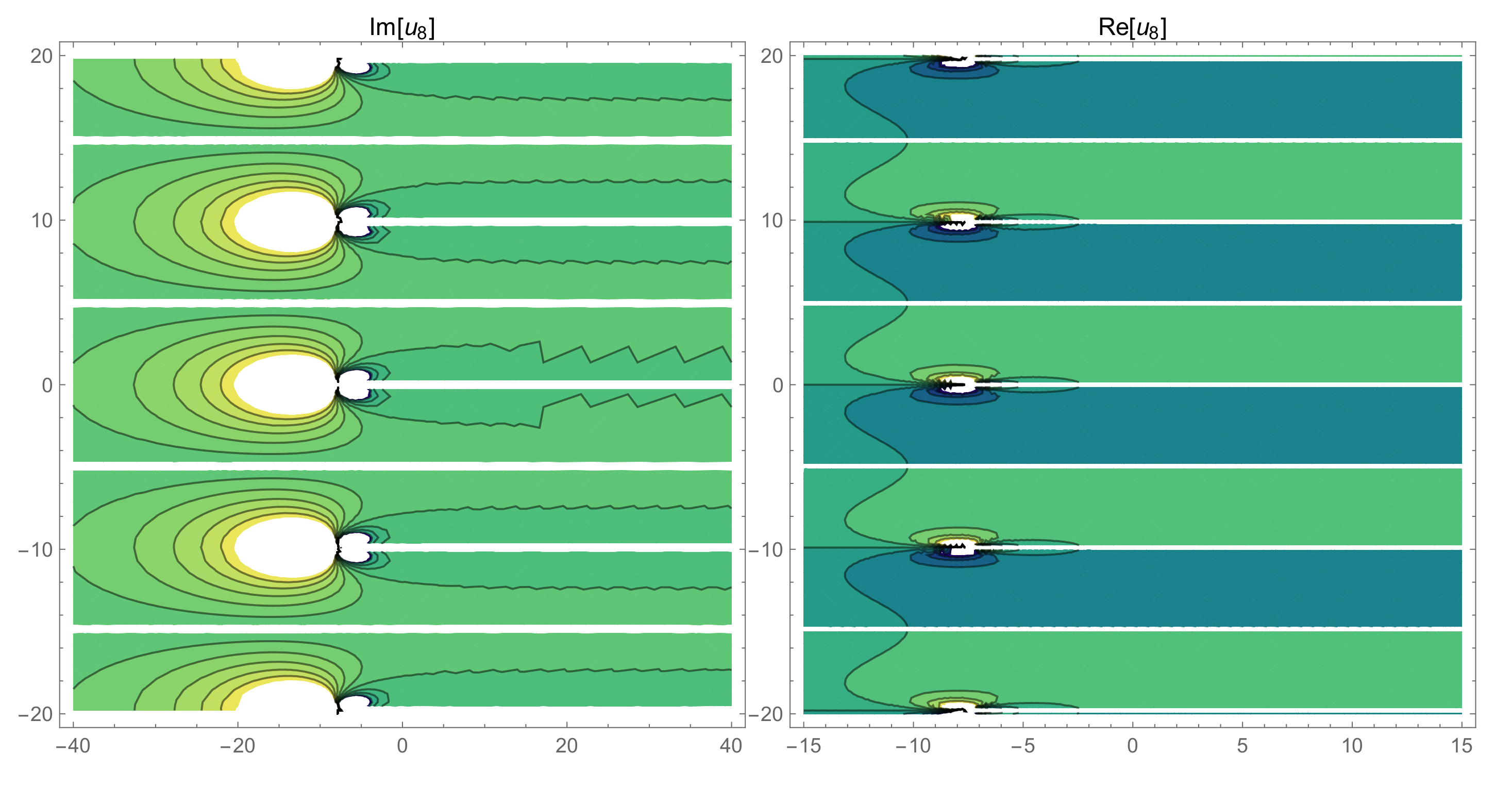
| Parameters | Meanings |
|---|---|
| The applied bias current | |
| The ohmic losses term | |
| The surface losses term | |
| The term for definiteness |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Causanilles, F.S.V.; Baskonus, H.M.; Guirao, J.L.G.; Bermúdez, G.R. Some Important Points of the Josephson Effect via Two Superconductors in Complex Bases. Mathematics 2022, 10, 2591. https://doi.org/10.3390/math10152591
Causanilles FSV, Baskonus HM, Guirao JLG, Bermúdez GR. Some Important Points of the Josephson Effect via Two Superconductors in Complex Bases. Mathematics. 2022; 10(15):2591. https://doi.org/10.3390/math10152591
Chicago/Turabian StyleCausanilles, Fernando S. Vidal, Haci Mehmet Baskonus, Juan Luis García Guirao, and Germán Rodríguez Bermúdez. 2022. "Some Important Points of the Josephson Effect via Two Superconductors in Complex Bases" Mathematics 10, no. 15: 2591. https://doi.org/10.3390/math10152591
APA StyleCausanilles, F. S. V., Baskonus, H. M., Guirao, J. L. G., & Bermúdez, G. R. (2022). Some Important Points of the Josephson Effect via Two Superconductors in Complex Bases. Mathematics, 10(15), 2591. https://doi.org/10.3390/math10152591








