Research on Dynamic Properties of Deep Marble Influenced by High Temperature
Abstract
:1. Introduction
2. Specimen Preparation and Test Procedures
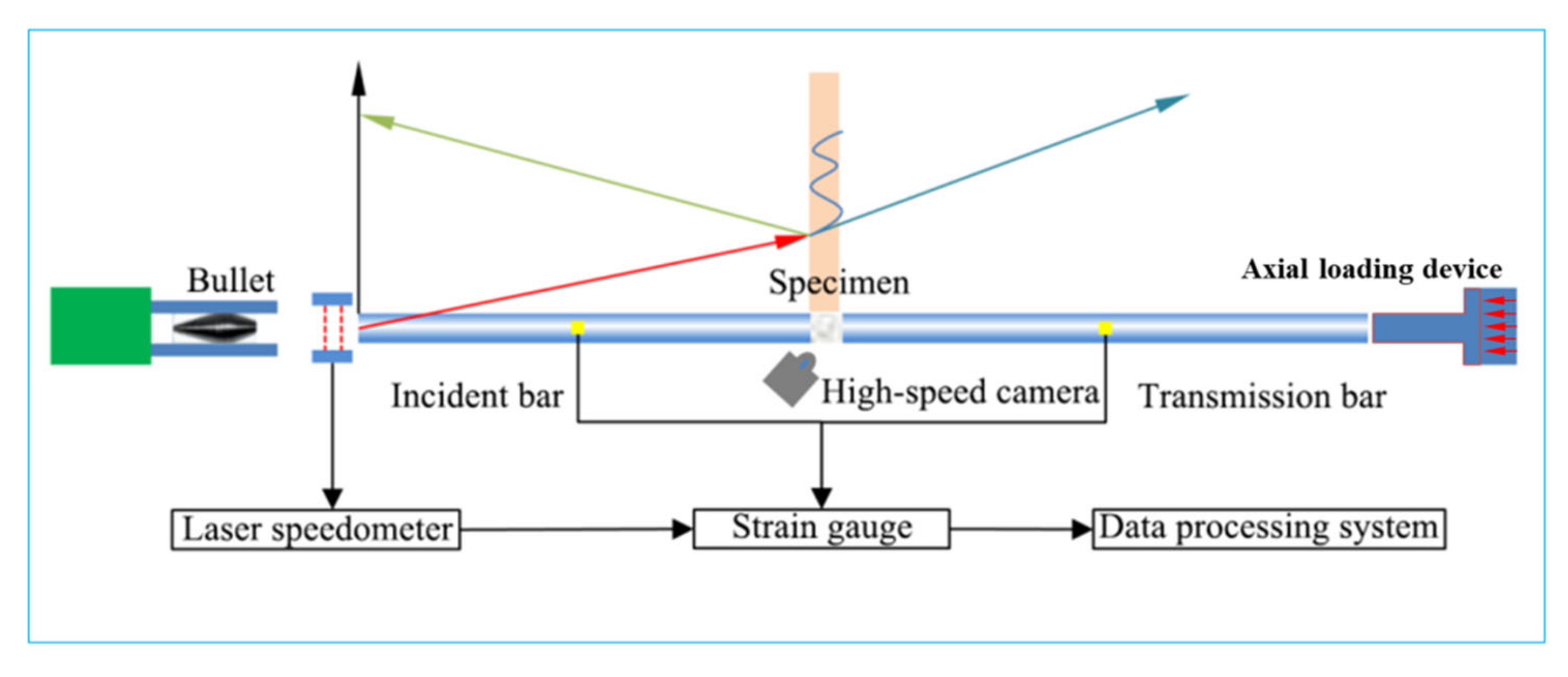
2.1. Experimental System and Experimental Principle
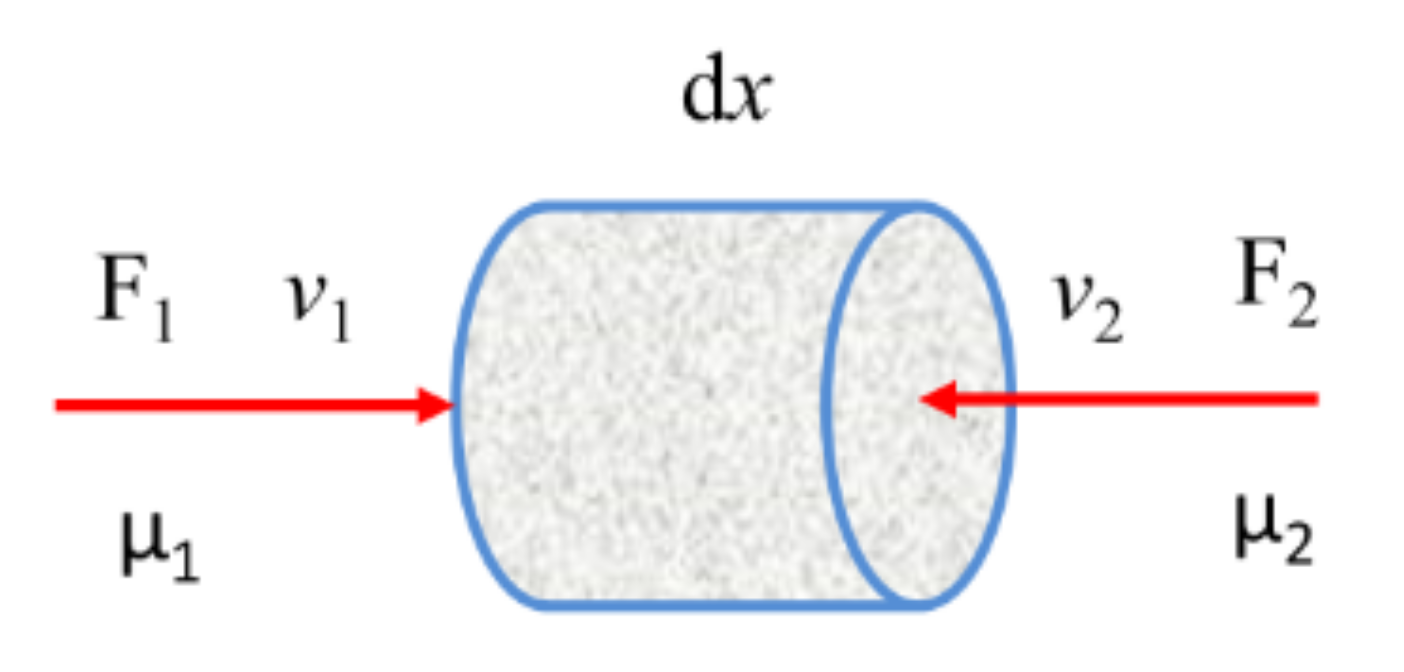
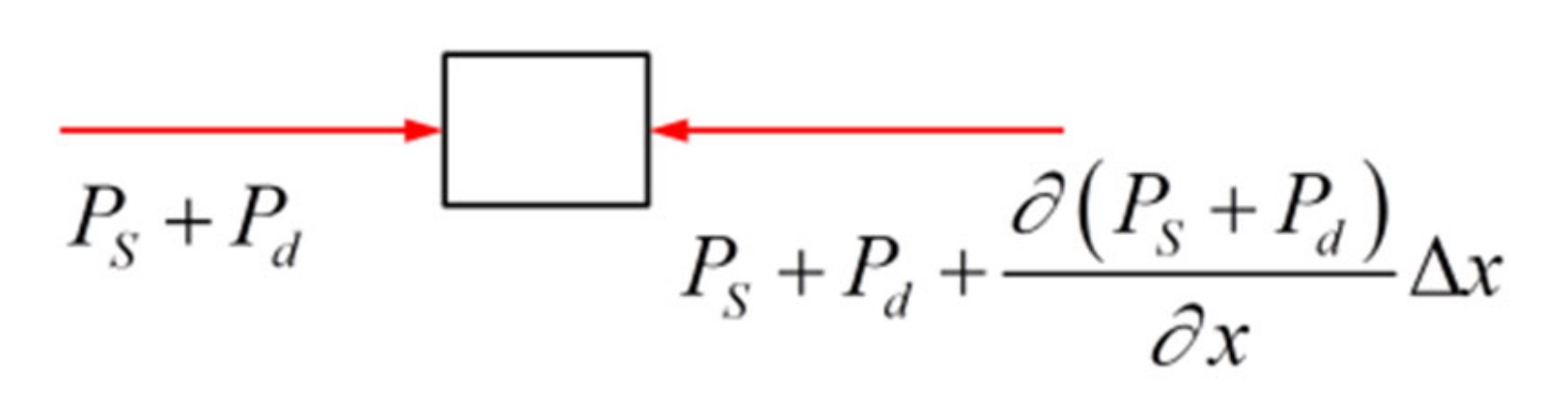
2.2. Model and Principle of One-Dimensional Static and Dynamic Combination Loading
2.3. Experimental Procedure
3. Physical Properties of Marble before and after High Temperature
3.1. Apparent Morphological Characteristics of Specimens before and after High Temperature
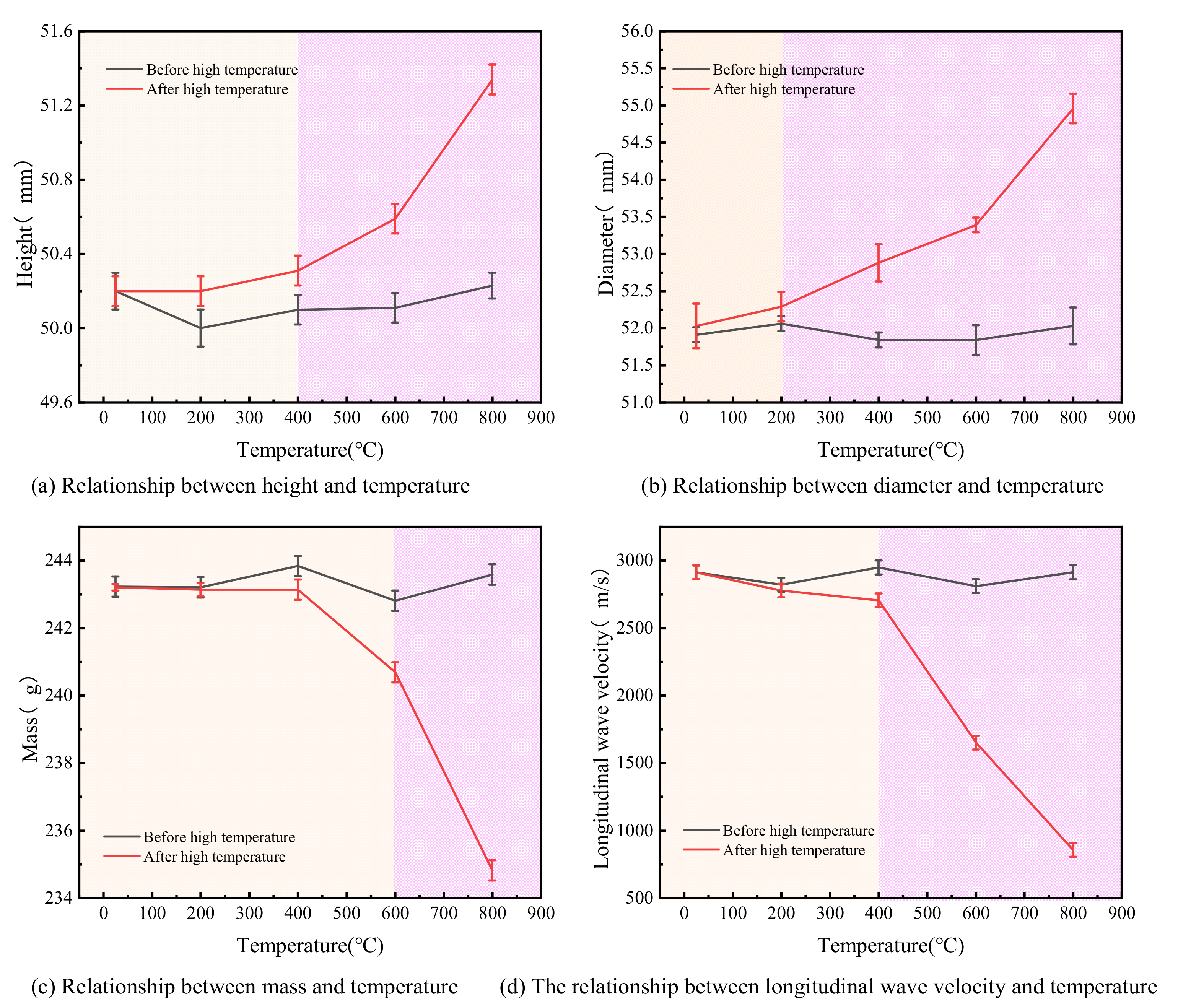
3.2. Variation in Specimen Mass and Longitudinal Wave Velocity
3.3. Influence of High Temperature on the Microstructure of Marble
4. Dynamic Compressive Mechanical Properties of Marble after High Temperature
4.1. Stress–Strain Properties
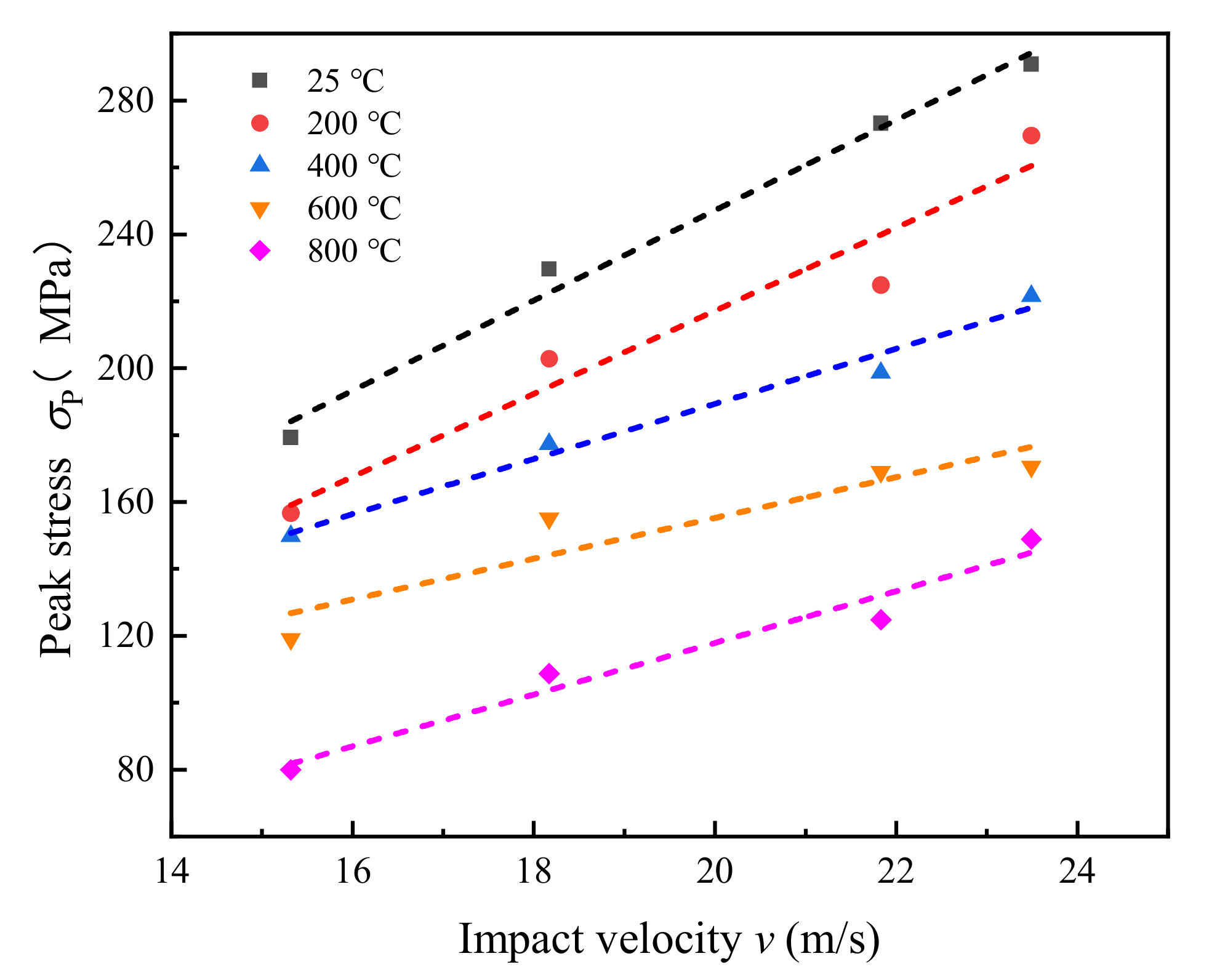
4.2. The Variation Pattern of Peak Stress
4.3. Crack Extension Process and Damage Mode
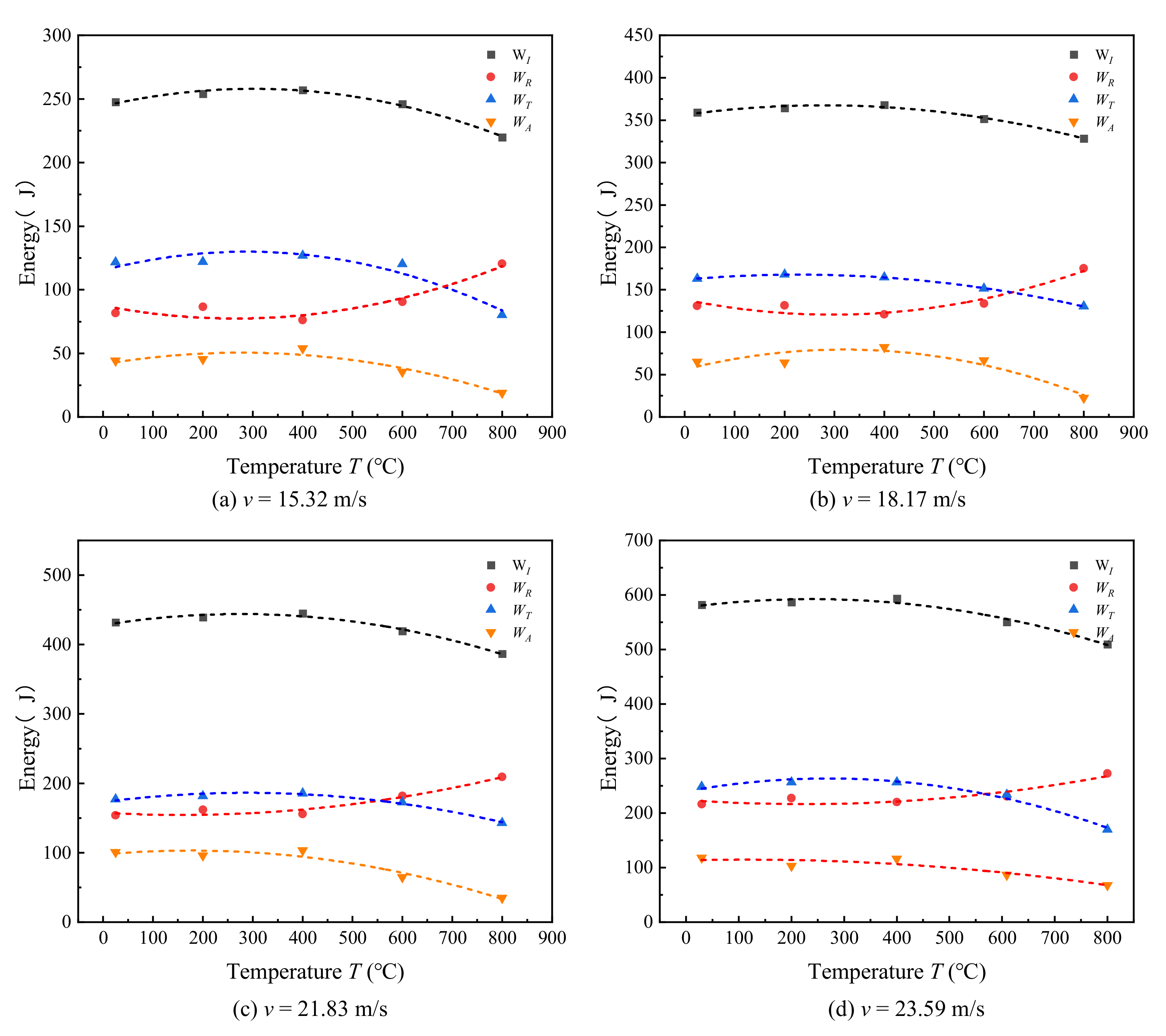
4.4. Energy Analysis of Rocks under Combined Dynamic and Static Loading
5. Conclusions
- (1)
- Temperature has a great influence on the physical properties and geometric size of marble. As the temperature increases, the color of marble specimens gradually changes from light gray to milky white. The length and diameter of marble samples increase with the increase of temperature, while the mass and longitudinal wave velocity decrease with the increase of temperature. From room temperature to 200 °C, the change of physical properties and geometric size of marble is not obvious, but the change is more obvious at 400~800 °C. The higher the temperature, the more obvious the change.
- (2)
- At the same temperature, the stress-strain curves of marble specimens under different impact velocities are similar. When the impact velocity is constant, with the increase of temperature, the curve gradually shifts to the right, the brittleness of the specimen decreases and the plasticity increases.
- (3)
- The crack propagation of the specimen is completed within 200 μs, and the failure mode is tensile stress splitting failure. Temperature has significant influence on the failure mechanism of specimens. In general, when the impact velocity is constant, when 25 °C ≤ T ≤ 400 °C, the crushing degree of the specimen is higher than 600 °C ≤ T ≤ 800 °C. When the temperature is constant, the crushing degree increases with the increase of impact velocity, the crushing size decreases gradually, and the particles tend to be uniform.
- (4)
- When the impact velocity is constant, with the increase of temperature, the changes of incident energy, transmission energy and absorption energy of the specimen are similar, and all increase first and then decrease with the increase of temperature. The relationship between the above energy and temperature is a quadratic function of opening upward. The transmitted energy decreases first and then increases with the increase of temperature, and there is a quadratic function relationship between them.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, M.C.; Xie, H.P.; Peng, S.P.; Jiang, Y.D. Study on rock mechanics in deep mining engineering. Chin. J. Rock Mech. Eng. 2005, 24, 2803–2813. [Google Scholar]
- Xie, H.P.; Gao, F.; Ju, Y. Research and development of rock mechanics in deep ground engineering. Chin. J. Rock Mech. Eng. 2015, 34, 2161–2178. [Google Scholar]
- Xie, H.P. Research review of the state key research development program of China: Deep rock mechanics and mining theory. J. China Coal Soc. 2019, 44, 1283–1305. [Google Scholar]
- Wang, S.F.; Tang, Y.; Wang, S.Y. Influence of brittleness and confining stress on rock cuttability based on rock indentation tests. J. Cent. South Univ. 2021, 28, 2786–2800. [Google Scholar] [CrossRef]
- Xie, H.P.; Gao, M.Z.; Zhang, R.; Peng, G.; Wang, W.; Li, A. Study on the mechanical properties and mechanical response of coal mining at 1000 m or deeper. Rock Mech. Rock Eng. 2019, 52, 1475–1490. [Google Scholar] [CrossRef]
- Wang, S.F.; Tang, Y.; Li, X.B.; Kun, D.U. Analyses and predictions of rock cuttabilities under different confining stresses and rock properties based on rock indentation tests by conical pick. Trans. Nonferr. Met. Soc. China 2021, 31, 1766–1783. [Google Scholar] [CrossRef]
- Wang, S.F.; Li, X.B.; Yao, J.R.; Gong, F.; Li, X.; Du, K.; Tao, M.; Huang, L.; Du, S. Experimental investigation of rock breakage by a conical pick and its application to non-explosive mechanized mining in deep hard rock. Int. J. Rock Mech. Min. Sci. 2019, 21, 104063. [Google Scholar] [CrossRef]
- Wang, S.F.; Sun, L.C.; Li, X.B.; Wang, S.; Du, K.; Li, X.; Feng, F. Experimental investigation of cuttability improvement for hard rock fragmentation using conical cutter. Int. J. Geomech. 2021, 21, 06020039. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, Z.Y.; Meng, J.L.; Huang, Y.; Li, H.; Wang, J. Research on Deep-Hole Cutting Blasting Efficiency in Blind Shafting with High In-Situ Stress Environment Using the Method of SPH. Mathematics 2021, 9, 3242. [Google Scholar] [CrossRef]
- Somani, A.; Nandi, T.K.; Pal, S.K.; Majumder, A.K. Pre-treatment of rocks prior to comminution—A critical review of present practices. Int. J. Min. Sci. Technol. 2017, 27, 339–348. [Google Scholar] [CrossRef]
- Chen, G.F.; Yang, S.Q. Study on failure mechanical behavior of marble after high temperature. Eng. Mech. 2014, 31, 189–196. [Google Scholar] [CrossRef]
- Zhao, H.B.; Yin, G.Z.; Chen, L.J. Experimental study on effect of temperature on sandstone damage. Chin. J. Rock Mech. Eng. 2009, 28, 2784–2788. [Google Scholar]
- Zhai, S.T.; Wu, G.; Sun, H.; Pan, J.H. Acoustic emission characteristics of thermal cracking of marble under uniaxial compression. Chin. J. Rock Mech. Eng. 2012, 31, 1237–1244. [Google Scholar]
- Ni, X.H.; Li, X.J.; Huang, D.W. Uniaxial compression tests on mechanical properties of marble after undergoing different numbers of temperature cycling. J. Hydroelectr. Eng. 2016, 35, 95–100. [Google Scholar]
- Huang, Z.P.; Zhang, Y.; Wu, W.D. Analysis of mechanics and fluctuation characteristics of high temperature marble cooled by water. Rock Soil Mech. 2016, 37, 367–375. [Google Scholar]
- Zeng, Y.J.; Rong, G.; Peng, J.; Sha, S. Experimental study of crack propagation of marble after high temperature cycling. Rock Soil Mech. 2018, 39, 220–226. [Google Scholar]
- Li, Q.S.; Yang, S.Q.; Chen, G.F. Strength and deformation properties of post-high-temperature joint sandstone. J. China Coal Soc. 2014, 39, 1283–1305. [Google Scholar]
- Zhang, Z.Z.; Gao, F.; Liu, Z.J. Research on rockburst proneness and its microcosmic mechanism of granite considering temperature effect. Chin. J. Rock Mech. Eng. 2010, 29, 1591–1602. [Google Scholar]
- Xu, J.Y.; Liu, S. Effect of impact velocity on dynamic mechanical behaviors of marble after high temperatures. Chin. J. Geotech. Eng. 2013, 35, 879–883. [Google Scholar]
- Yin, T.B.; Li, X.B.; Yin, Z.Q.; Zhou, Z.L.; Liu, X.L. Study and comparison of mechanical properties of sandstone under static and dynamic loadings after high temperature. J. Rock Mech. Eng. 2012, 31, 273–279. [Google Scholar]
- Ping, Q.; Su, H.P.; Ma, D.D.; Zhang, H.; Ma, C.L. Experimental study on physical and dynamic mechanical properties of limestone after different high temperature treatments. Rock Soil Mech. 2021, 42, 932–942. [Google Scholar]
- Yin, T.B.; Li, X.B.; Ye, Z.Y.; Gong, F.Q.; Zhou, Z.L. Energy dissipation of rock fracture under thermo- mechanical coupling and dynamic disturbances. J. Rock Mech. Eng. 2013, 32, 1197–1202. [Google Scholar]
- Liu, L.; Li, R.; Qin, H.; Liu, Y. Dynamic mechanical properties and microscopic damage characteristics of deep skarn after high-temperature treatment. Chin. J. Geotech. Eng. 2022, 44, 1166–1174. [Google Scholar]
- Li, M.; Mao, X.B.; Cao, L.L.; Mao, R.R.; Tao, J. Experimental study of mechanical properties on strain rate effect of sandstones after high temperature. Rock Soil Mech. 2014, 35, 3479–3488. [Google Scholar]
- Zhang, R.R.; Jing, L.W. The relationship between the fracture degree of deep sandstone and energy dissipation after high and low temperature in the SHPB test. J. China Coal Soc. 2018, 43, 1884–1892. [Google Scholar]
- Li, X.B.; Yin, T.B.; Zhou, Z.L.; Hong, L.; Gao, K. Study of dynamic properties of siltstone under coupling effects of temperature and pressure. Chin. J. Rock Mech. Eng. 2010, 29, 2377–2384. [Google Scholar]
- Kraut, E.A. Advances in the theory of anisotropic elastic wave propagation. Rev. Geophys. 1962, 1, 401–448. [Google Scholar] [CrossRef]
- Wang, Y.B.; Wen, Z.J.; Liu, G.Q.; Wang, J.; Bao, Z.; Lu, K.; Wang, D.; Wang, B. Explosion propagation and characteristics of rock damage in decoupled charge blasting based on computed tomography scanning. Int. J. Rock Mech. Min. Sci. 2020, 136, 104540. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhou, H.G.; Zhong, J.C.; Liu, D. Study on the relation between damage and permeability of sandstone at depth under cyclic loading. Int. J. Coal Sci. Technol. 2019, 6, 479–492. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.B.; Yang, R.S. Study of the dynamic fracture characteristics of coal with a bedding structure based on the NSCB impact test. Eng. Fract. Mech. 2017, 184, 319–338. [Google Scholar] [CrossRef]
- Liu, L.; Dong, L.Z.; An, H.M.; Fan, Y.; Wang, Y. Experimental Study of the Thermal and Dynamic Behaviors of Polypropylene Fiber-Reinforced Concrete. Appl. Sci. 2021, 11, 10757. [Google Scholar] [CrossRef]
- Liu, S.; Xu, J.J.; Bai, E.L.; Zhi, L.P.; Chen, T.F. Experimental study of dynamic tensile behaviors of marble after high temperature. Rock Soil Mech. 2013, 34, 3500–3504. [Google Scholar]
- Liu, L.; Li, R.; Qin, H.; Sun, W. Experimental SHPB Study of Limestone Damage under Confining Pressures after Exposure to Elevated Temperatures. Metals 2021, 11, 1663. [Google Scholar] [CrossRef]
- Xia, X.H.; Lu, Y.P.; Huang, X.H.; Shen, W.P. Experimental research on ultrasonic characteristics of marble under the action of high temperature. J. Shanghai Jiaotong Univ. 2004, 38, 1225–1228. [Google Scholar]
- Yang, R.S.; Wang, Y.B.; Ding, C.X. Laboratory study of wave propagation due to explosion in a jointed medium. Int. J. Rock Mech. Min. Sci. 2016, 81, 70–78. [Google Scholar] [CrossRef]
- Gao, T.; Sun, W.; Liu, Z.; Cheng, H.Y. Cheng, Investigation on fracture characteristics and failure pattern of inclined layered cemented tailings backfill. Constr. Build. Mater. 2022, 343, 128110. [Google Scholar] [CrossRef]
- Zuo, J.P.; Zhou, H.W.; Xie, H.P. Fracture characteristics of sandstone under thermal effects. Eng. Mech. 2008, 25, 124–130. [Google Scholar]
- Zhang, R.R.; Jing, L.W. Analysis on the fragment and energy dissipation of deep sandstone after high/low temperature treatment in SHPB tests. J. China Coal Soc. 2018, 43, 1884–1892. [Google Scholar]



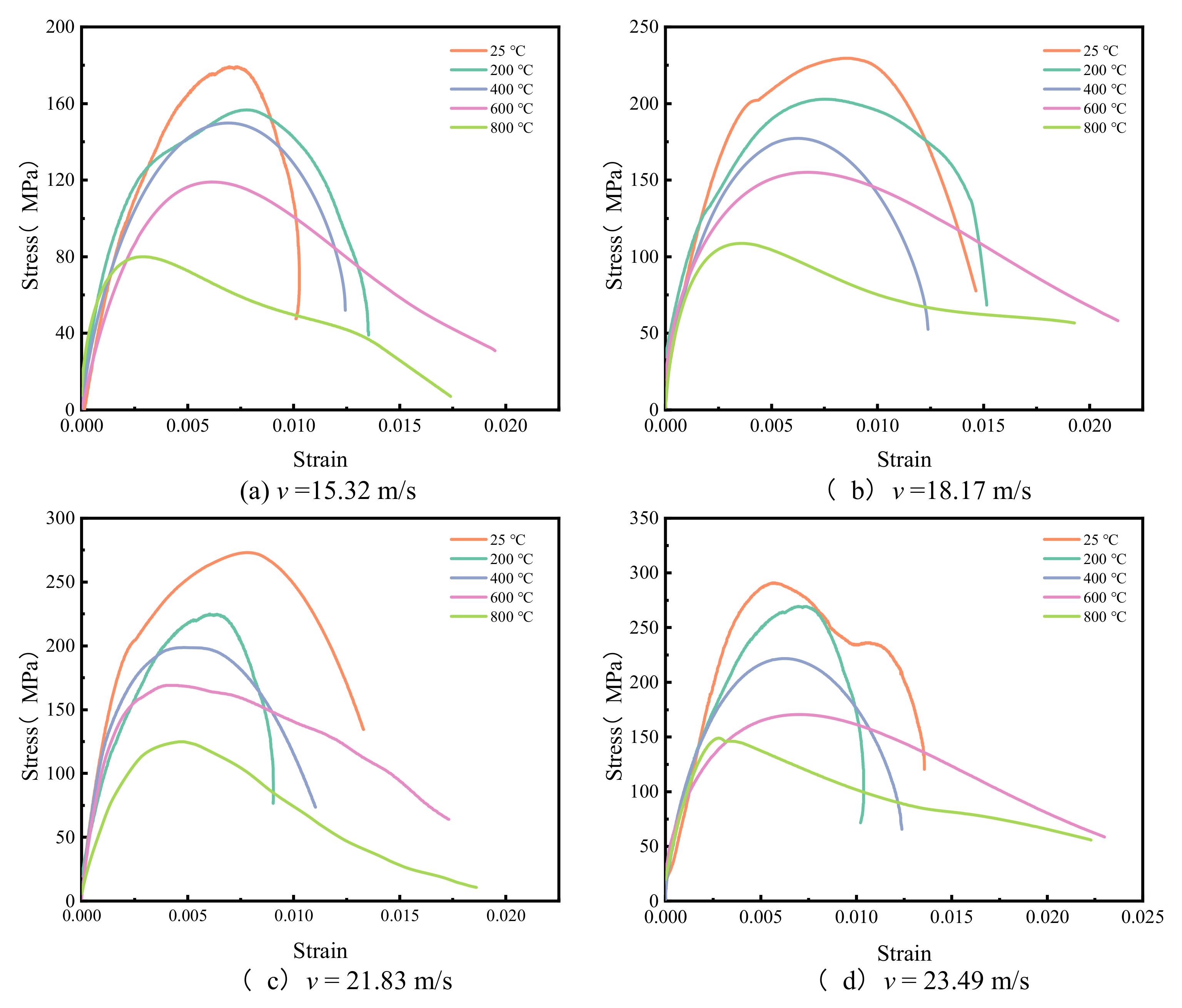


| Temperature T/°C | a | b | R2 |
|---|---|---|---|
| 25 | 13.48 | −22.42 | 0.98 |
| 200 | 12.41 | −31.01 | 0.94 |
| 400 | 8.24 | 24.52 | 0.98 |
| 600 | 6.09 | 33.49 | 0.87 |
| 800 | 7.73 | −36.62 | 0.96 |
| Impact Velocity (m/s) | Fitting Relationship | R2 |
|---|---|---|
| 15.32 | WI = 244.30 + 0.09T − 1.51 × 10−4T2 | 0.98 |
| WR = 87.51 − 0.08T + 1.44 × 10−4T2 | 0.90 | |
| WT = 115.35 + 0.10T − 1.96 × 10−4T2 | 0.91 | |
| WA = 41.43 + 0.07T − 1.18 × 10−4T2 | 0.92 | |
| 18.17 | WI = 356.28 + 0.08T − 1.44 × 10−4T2 | 0.98 |
| WR = 138.41 − 0.12T + 2.03 × 10−4T2 | 0.91 | |
| WT = 161.91 + 0.05T − 1.15 × 10−4T2 | 0.98 | |
| WA = 55.95 + 0.15T − 2.32 × 10−4T2 | 0.88 | |
| 21.83 | WI = 427.99 + 0.12T − 2.10 × 10−4T2 | 0.98 |
| WR = 157.64 − 0.04T + 1.31 × 10−4T2 | 0.95 | |
| WT = 172.91 + 0.09T − 1.62 × 10−4T2 | 0.98 | |
| WA = 97.44 + 0.06T − 1.79 × 10−4T2 | 0.94 | |
| 23.59 | WI = 577.06 + 0.13T − 2.67 × 10−4T2 | 0.95 |
| WR = 223.99 − 0.07T + 1.54 × 10−4T2 | 0.87 | |
| WT = 239.89 + 0.17T − 3.22 × 10−4T2 | 0.99 | |
| WA = 113.18 + 0.02T − 9.95 × 10−4T2 | 0.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wu, Y.; He, L.; Zhang, X.; Wang, J. Research on Dynamic Properties of Deep Marble Influenced by High Temperature. Mathematics 2022, 10, 2603. https://doi.org/10.3390/math10152603
Li X, Wu Y, He L, Zhang X, Wang J. Research on Dynamic Properties of Deep Marble Influenced by High Temperature. Mathematics. 2022; 10(15):2603. https://doi.org/10.3390/math10152603
Chicago/Turabian StyleLi, Xianglong, Yongbo Wu, Lihua He, Xiaohua Zhang, and Jianguo Wang. 2022. "Research on Dynamic Properties of Deep Marble Influenced by High Temperature" Mathematics 10, no. 15: 2603. https://doi.org/10.3390/math10152603
APA StyleLi, X., Wu, Y., He, L., Zhang, X., & Wang, J. (2022). Research on Dynamic Properties of Deep Marble Influenced by High Temperature. Mathematics, 10(15), 2603. https://doi.org/10.3390/math10152603







