Dynamic Analysis of a Piezoelectrically Layered Perforated Nonlocal Strain Gradient Nanobeam with Flexoelectricity
Abstract
:1. Introduction
2. Mathematical Formulation
2.1. Equivalent Geometrical Model
2.2. Kinematic Relations
2.3. The Nonclassical Constitutive Relations
3. Dynamic Equation of Motion
4. Free Vibration Solution
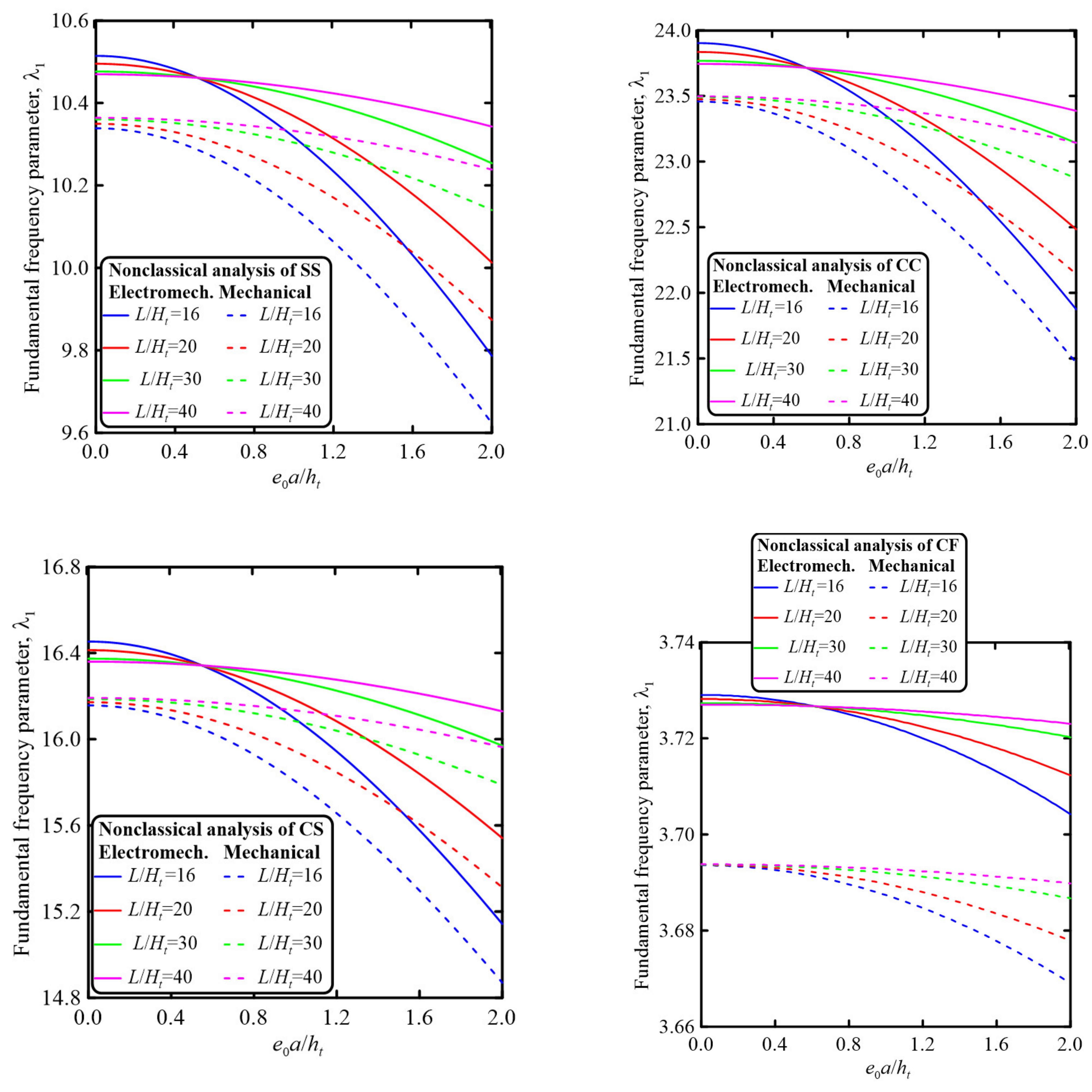
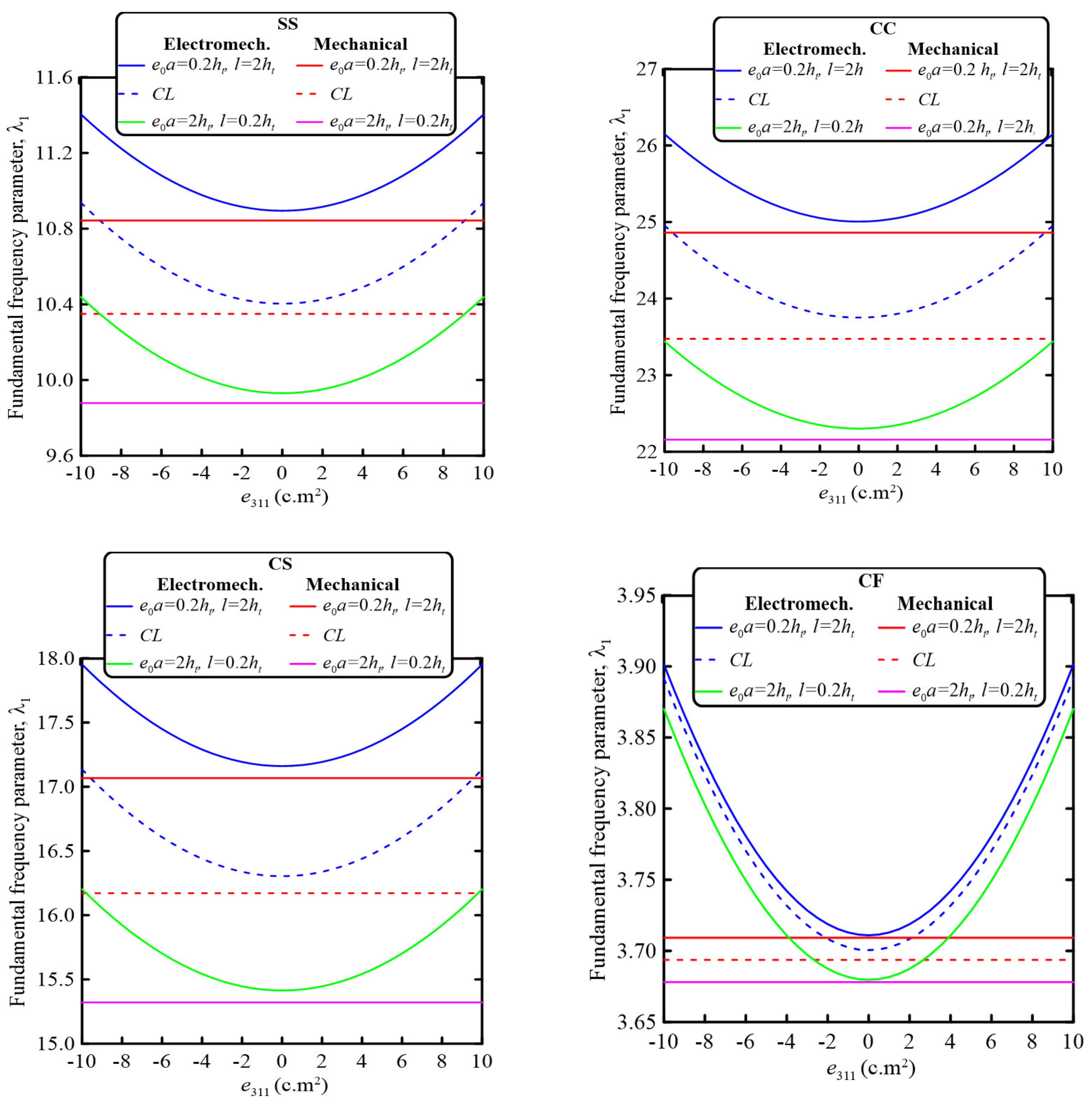
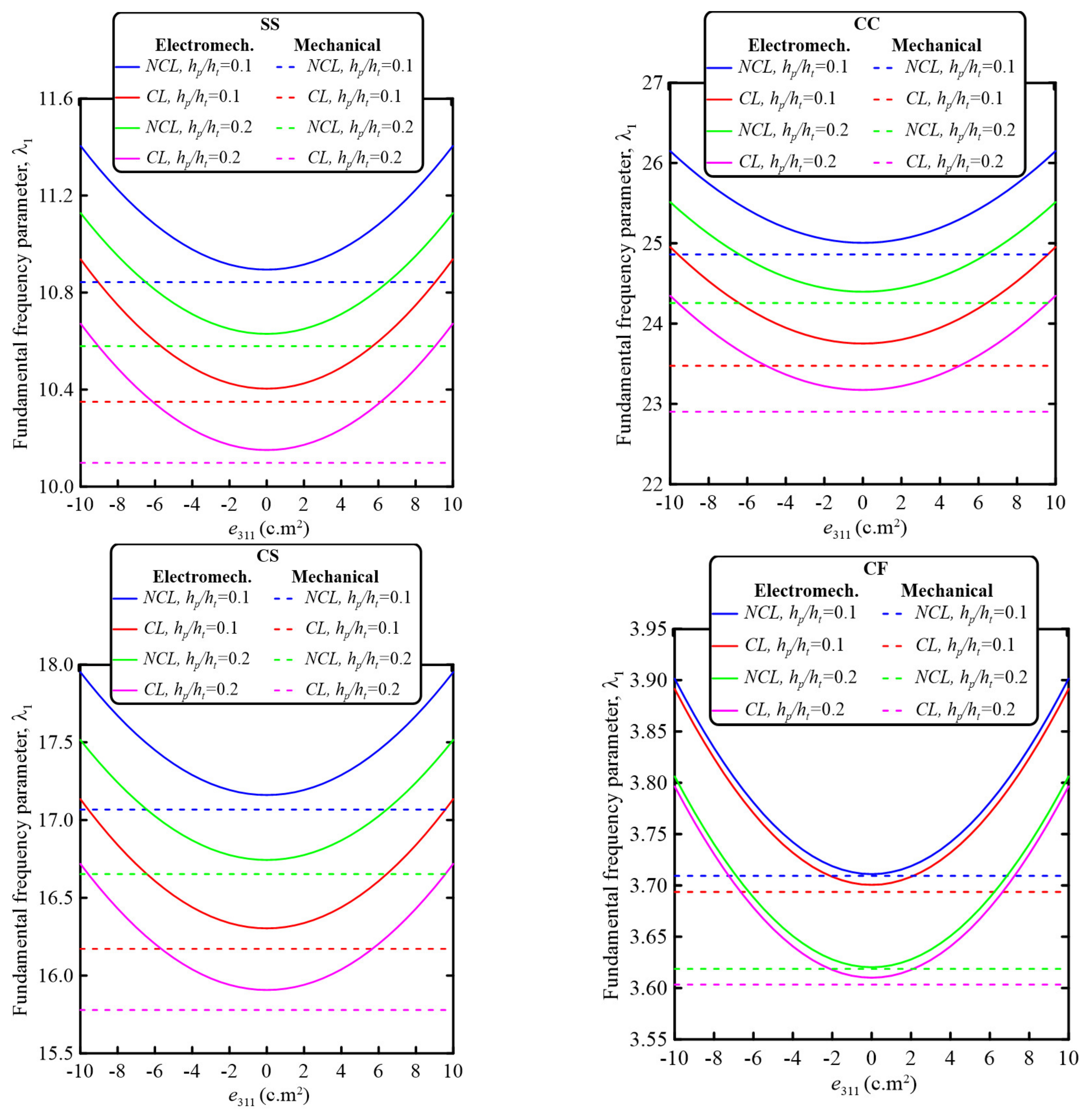
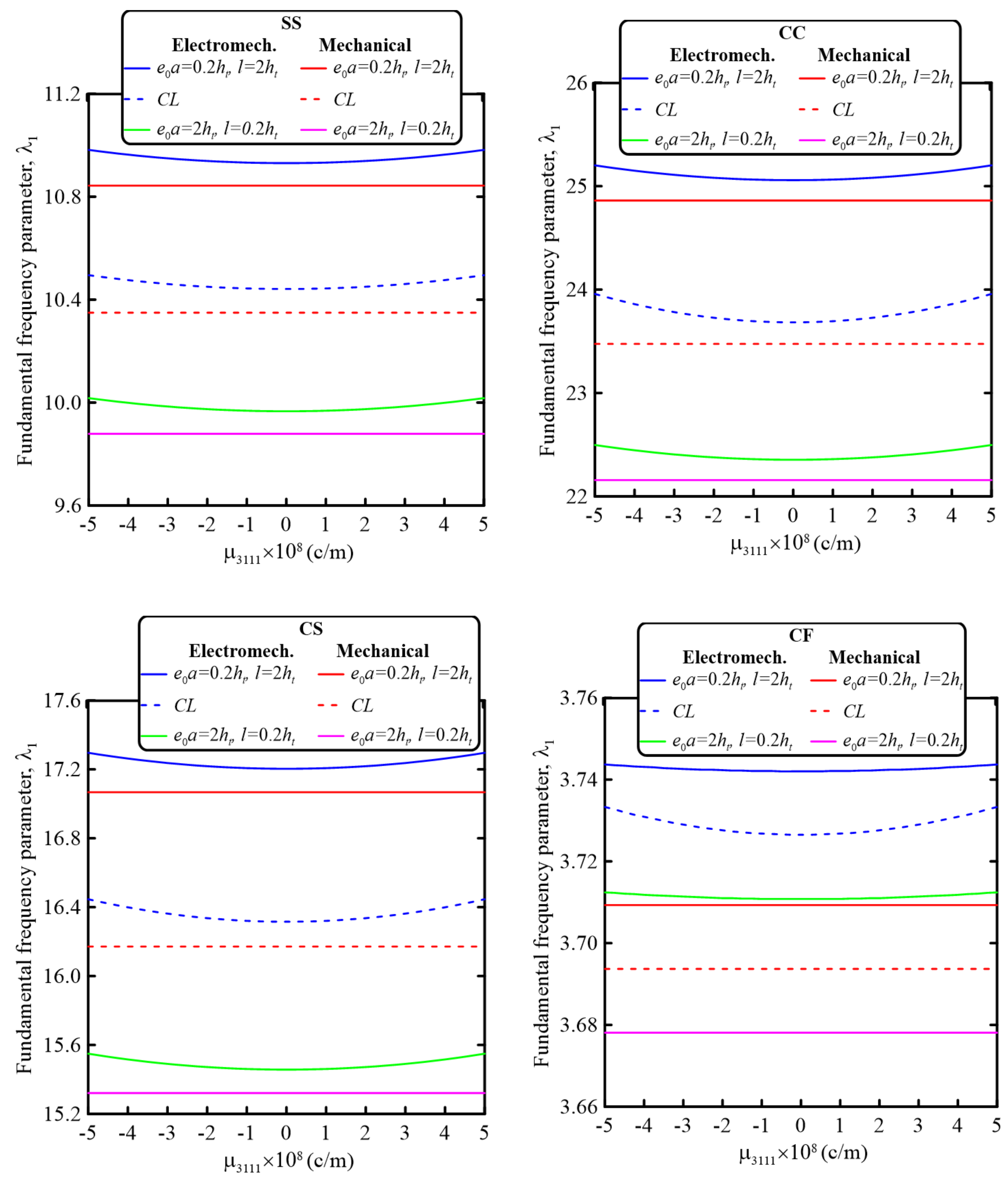
5. Numerical Results and Discussion
5.1. Validation of the Developed Methodology
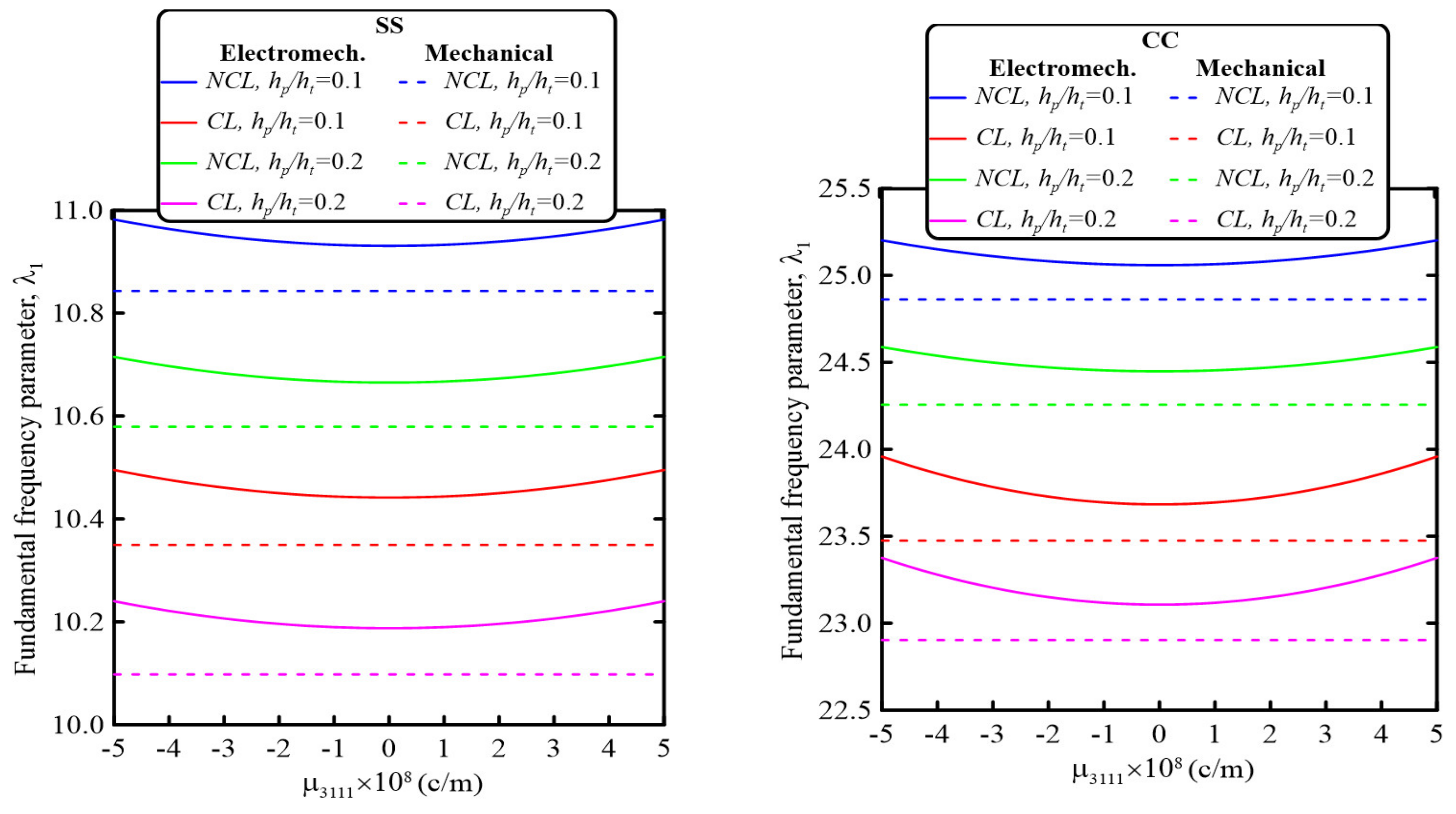
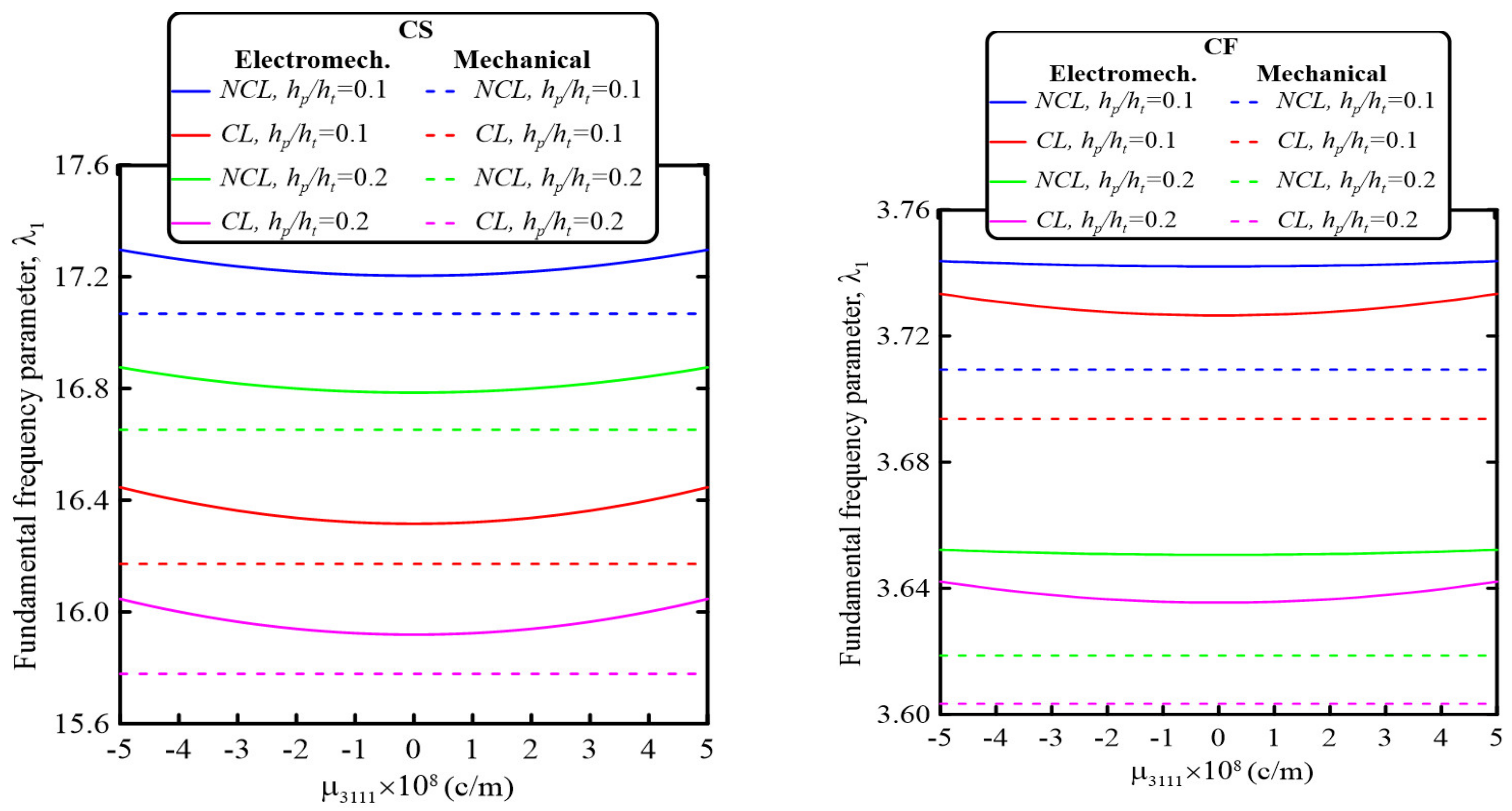
5.2. Parametric Studies
6. Conclusions
- ➢
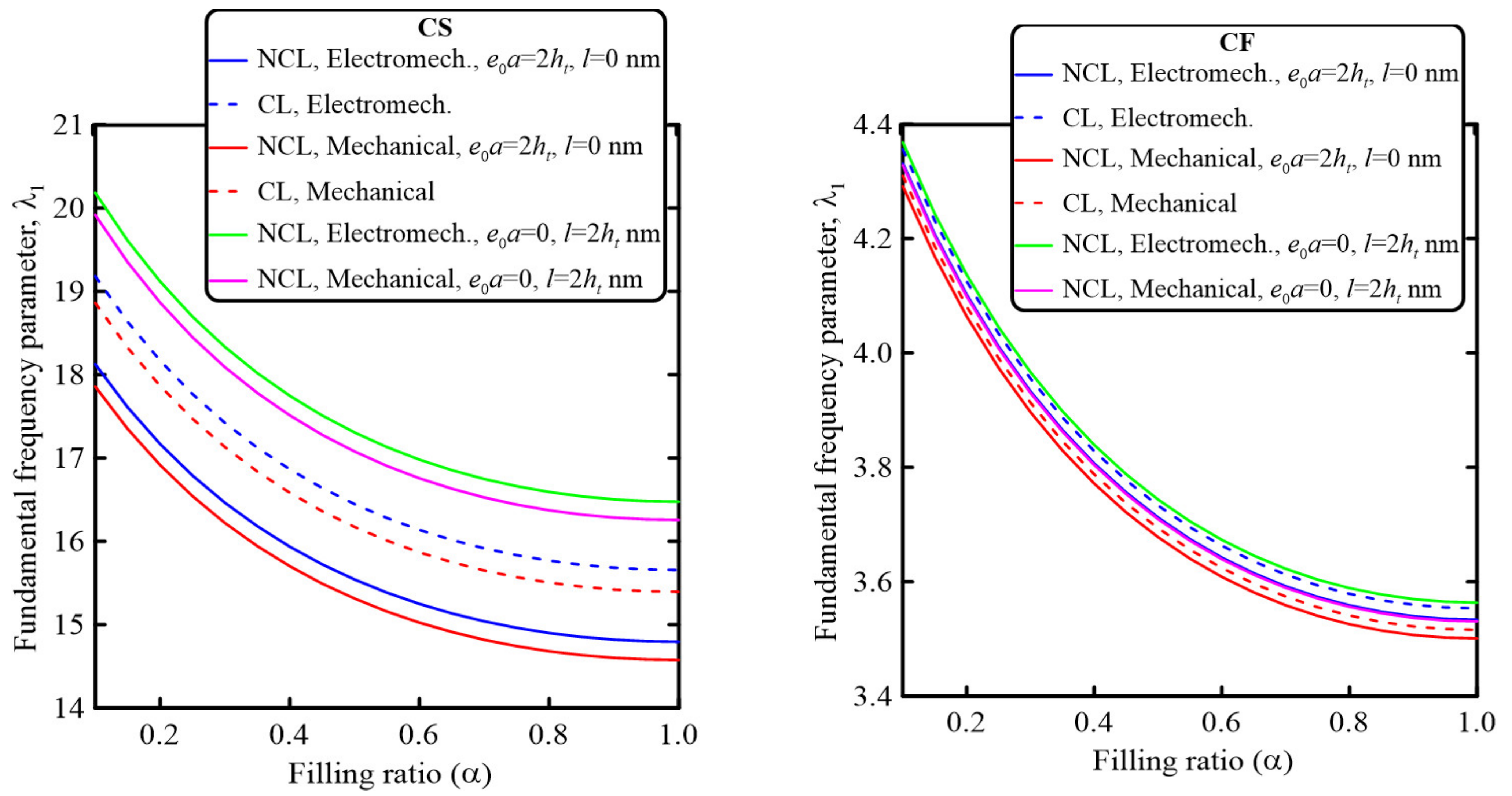
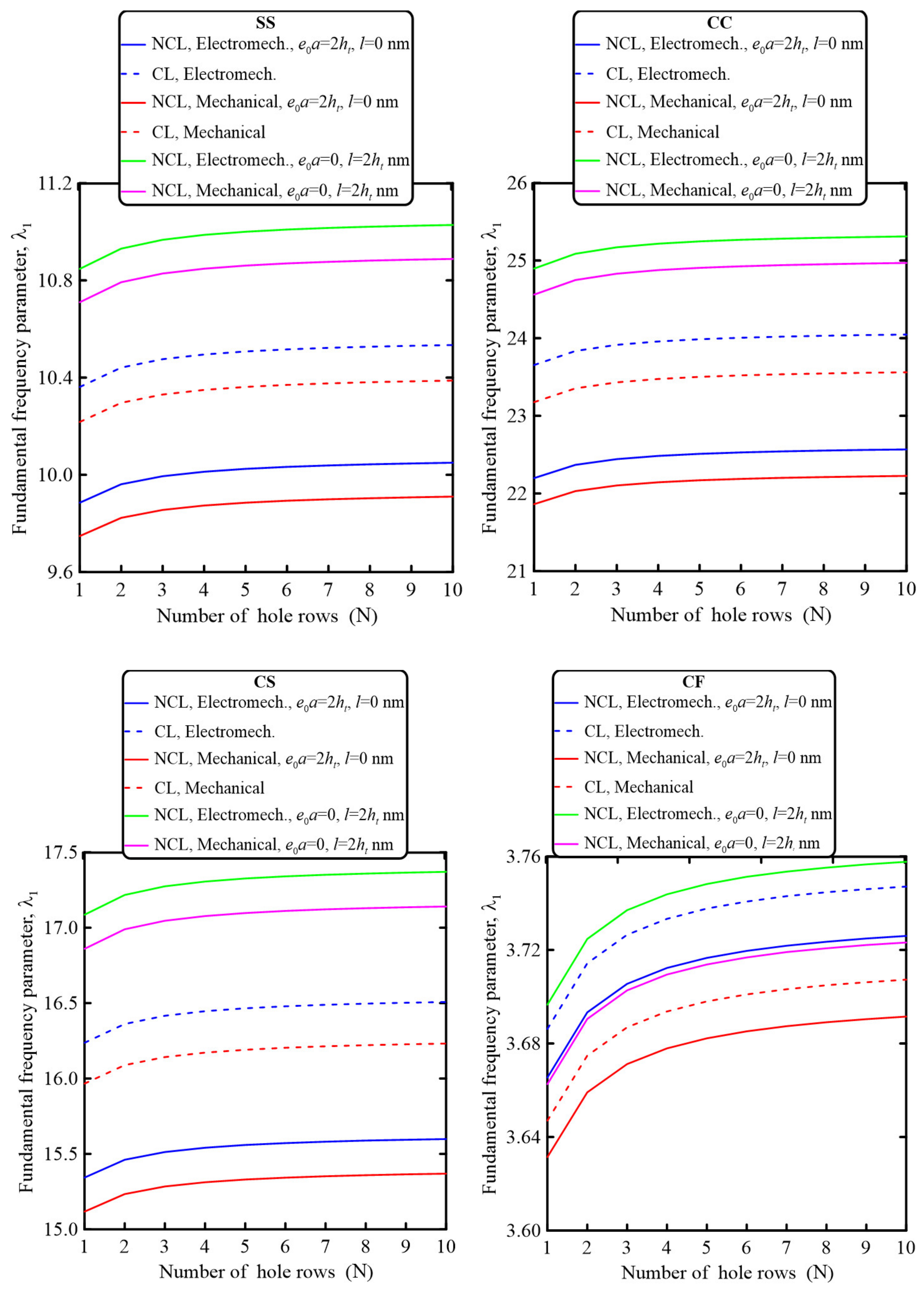
- The perforation parameters significantly affected the electromechanical and mechanical dynamic behavior of the sandwich nanobeams. Based on the selected geometrical and material parameters, increasing the perforation filling ratio decreased the fundamental frequency parameter for all considered beam boundary conditions. On the other hand, increasing the number of hole rows through the beam cross-section increased the fundamental frequency parameters. Thus, both the electromechanical and mechanical dynamic behavior of the perforated sandwich nanobeam could be controlled by careful selection of the perforation parameters.
- ➢
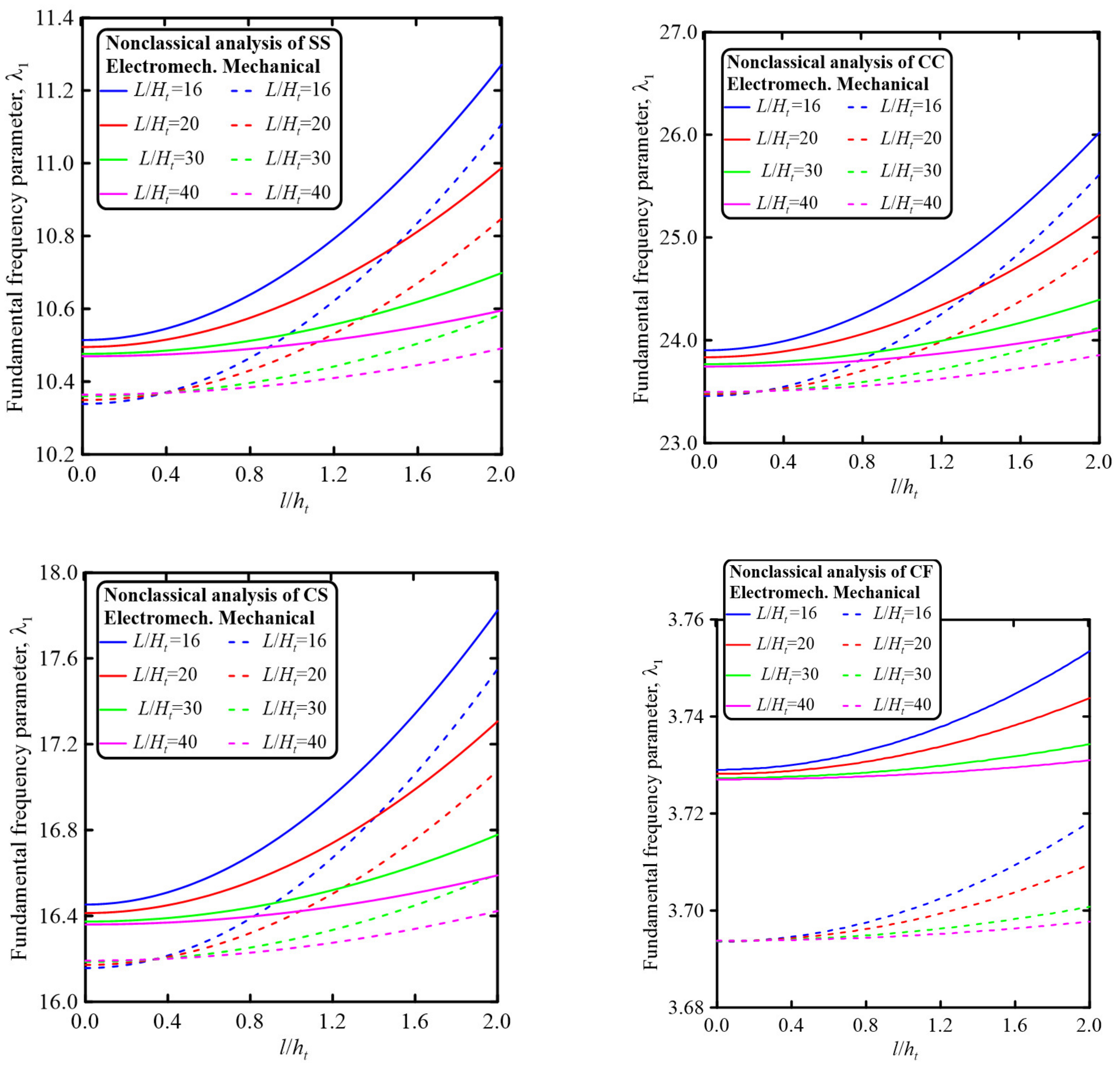
- The electromechanical and mechanical dynamic behavior of the sandwich perforated nanobeam could also be controlled by the size-dependent parameters. The nonlocal strain gradient theory could be used to incorporate either softening or stiffening effects. Increasing the strain gradient parameter resulted in a stiffening effect, while increasing the nonlocal parameter led to a softening effect.
- ➢
- Incorporating the piezoelectricity and flexoelectricity resulted in increasing the frequency parameter. Furthermore, the effects of the flexoelectricity on the dimensionless natural frequency were more noticeable for a smaller nanobeam aspect ratio.
- ➢
- Increasing the piezoelectric layer thickness resulted in decreasing the natural frequency parameter, and thus both the piezoelectric and flexoelectricity effects were more significant for smaller sizes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghobadi, A.; Golestanian, H.; Beni, Y.T.; Żur, K.K. On the size-dependent nonlinear thermo-electro-mechanical free vibration analysis of functionally graded flexoelectric nano-plate. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105585. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.; Bowen, C. Piezoelectric effects and electromechanical theories at the nanoscale. Nanoscale 2014, 6, 13314–13327. [Google Scholar] [CrossRef] [PubMed]
- Eltaher, M.A.; Omar, F.A.; Abdalla, W.S.; Gad, E.H. Bending and vibrational behaviors of piezoelectric nonlocal nanobeam including surface elasticity. Waves Random Complex Media 2019, 29, 264–280. [Google Scholar] [CrossRef]
- Attia, M.A. On the mechanics of functionally graded nanobeams with the account of surface elasticity. Int. J. Eng. Sci. 2017, 115, 73–101. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.; Li, X. Longitudinal vibration of size-dependent rods via nonlocal strain gradient theory. Int. J. Mech. Sci. 2016, 115, 135–144. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Faghidian, S.A.; Luciano, R.; De Sciarra, F.M. Free vibrations of elastic beams by modifiednonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 133, 99–108. [Google Scholar] [CrossRef]
- Esfahani, S.; Khadem, S.E.; Mamaghani, A.E. Nonlinear vibration analysis of an electrostatic functionally graded nano-resonator with surface effects based on nonlocal strain gradient theory. Int. J. Mech. Sci. 2019, 151, 508–522. [Google Scholar] [CrossRef]
- Fakher, M.; Hosseini-Hashemi, S. On the vibration of nanobeams with consistent two-phase nonlocal strain gradient theory: Exact solution and integral nonlocal finite-element model. Eng. Comput. 2022, 38, 2361–2384. [Google Scholar] [CrossRef]
- Abdelrahman, A.A.; Esen, I.; Özarpa, C.; Eltaher, M.A. Dynamics of perforated nanobeams subject to moving mass using the nonlocal strain gradient theory. Appl. Math. Model. 2021, 96, 215–235. [Google Scholar] [CrossRef]
- Abdelrahman, A.A.; Esen, I.; Ozarpa, C.; Shaltout, R.; Eltaher, M.A.; Assie, A.E. Dynamics of perforated higher order nanobeams subject to moving load using the nonlocal strain gradient theory. Smart Struct. Syst. 2021, 28, 515–533. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Esen, I.; Abdelrahman, A.A.; Abdraboh, A.M.; Eltaher, M.A. Dynamic analysis of functionally graded (FG) nonlocal strain gradient nanobeams under thermo-magnetic fields and moving load. Adv. Nano Res. 2022, 12, 231–251. [Google Scholar] [CrossRef]
- Daikh, A.A.; Houari, M.S.A.; Eltaher, M.A. A novel nonlocal strain gradient Quasi-3D bending analysis of sigmoid functionally graded sandwich nanoplates. Compos. Struct. 2021, 262, 113347. [Google Scholar] [CrossRef]
- Daikh, A.A.; Houari, M.S.A.; Belarbi, M.O.; Mohamed, S.A.; Eltaher, M.A. Static and dynamic stability responses of multilayer functionally graded carbon nanotubes reinforced composite nanoplates via quasi 3D nonlocal strain gradient theory. Def. Technol. 2021; in press. [Google Scholar] [CrossRef]
- Shariati, M.; Azizi, B.; Hosseini, M.; Shishesaz, M. On the calibration of size parameters related to non-classical continuum theories using molecular dynamics simulations. Int. J. Eng. Sci. 2021, 168, 103544. [Google Scholar] [CrossRef]
- Esen, I.; Abdelrhmaan, A.A.; Eltaher, M.A. Free vibration and buckling stability of FG nanobeams exposed to magnetic and thermal fields. Eng. Comput. 2021, 1–20. [Google Scholar] [CrossRef]
- Esen, I.; Abdelrahman, A.A.; Eltaher, M.A. On vibration of sigmoid/symmetric functionally graded nonlocal strain gradient nanobeams under moving load. Int. J. Mech. Mater. Des. 2021, 17, 721–742. [Google Scholar] [CrossRef]
- Esen, I.; Daikh, A.A.; Eltaher, M.A. Dynamic response of nonlocal strain gradient FG nanobeam reinforced by carbon nanotubes under moving point load. Eur. Phys. J. Plus 2021, 136, 1–22. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, W. On the thermal buckling and postbuckling responses of temperature-dependent graphene platelets reinforced porous nanocomposite beams. Compos. Struct. 2022, 296, 115880. [Google Scholar] [CrossRef]
- Hamidi, B.A.; Hosseini, S.A.; Hayati, H. Forced torsional vibration of nanobeam via nonlocal strain gradient theory and surface energy effects under moving harmonic torque. Waves Random Complex Media 2022, 32, 318–333. [Google Scholar] [CrossRef]
- Nuhu, A.A.; Safaei, B. State-of-the-Art of Vibration Analysis of Small-Sized Structures by using Nonclassical Continuum Theories of Elasticity. Arch. Comput. Methods Eng. 2022, 1–189. [Google Scholar] [CrossRef]
- Anton, S.R.; Sodano, H.A. A review of power harvesting using piezoelectric materials (2003–2006). Smart Mater. Struct. 2007, 16, R1. [Google Scholar] [CrossRef]
- Ke, L.L.; Wang, Y.S.; Wang, Z.D. Nonlinear vibration of the piezoelectric nanobeams based on the nonlocal theory. Compos. Struct. 2012, 94, 2038–2047. [Google Scholar] [CrossRef]
- Arani, A.G.; Kolahchi, R.; Mortazavi, S.A. Nonlocal piezoelasticity based wave propagation of bonded double-piezoelectric nanobeam-systems. Int. J. Mech. Mater. Des. 2014, 10, 179–191. [Google Scholar] [CrossRef]
- Liang, X.; Hu, S.L.; Shen, S.P. Effects of surface and flexoelectricity on a piezoelectric nanobeam. Smart Mater. Struct. 2014, 23, 035020. [Google Scholar] [CrossRef]
- Arani, A.G.; Abdollahian, M.; Kolahchi, R. Nonlinear vibration of a nanobeam elastically bonded with a piezoelectric nanobeam via strain gradient theory. Int. J. Mech. Sci. 2015, 100, 32–40. [Google Scholar] [CrossRef]
- Li, A.; Zhou, S.; Qi, L.; Chen, X. A reformulated flexoelectric theory for isotropic dielectrics. J. Phys. D: Appl. Phys. 2015, 48, 465502. [Google Scholar] [CrossRef]
- Mehralian, F.; Beni, Y.T. Vibration analysis of size-dependent bimorph functionally graded piezoelectric cylindrical shell based on nonlocal strain gradient theory. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 1–15. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Omar, F.A.; Abdalla, W.S.; Kabeel, A.M.; Alshorbagy, A.E. Mechanical analysis of cutout piezoelectric nonlocal nanobeam including surface energy effects. Struct. Eng. Mech. 2020, 76, 141–151. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Omar, F.A.; Abdraboh, A.M.; Abdalla, W.S.; Alshorbagy, A.E. Mechanical behaviors of piezoelectric nonlocal nanobeam with cutouts. Smart Struct. Syst. 2020, 25, 219–228. [Google Scholar] [CrossRef]
- Kachapi, H.S.H. Nonlinear vibration and stability analysis of piezo-harmo-electrostatic nanoresonator based on surface/interface and nonlocal strain gradient effects. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–28. [Google Scholar]
- Ali, I.A.; Alazwari, M.A.; Eltaher, M.A.; Abdelrahman, A.A. Effects of viscoelastic bonding layer on performance of piezoelectric actuator attached to elastic structure. Mater. Res. Express 2022, 9, 045701. [Google Scholar] [CrossRef]
- Mechkour, H. Two-scale homogenization of piezoelectric perforated structures. Mathematics 2022, 10, 1455. [Google Scholar] [CrossRef]
- Saeed, T. Hybrid Finite Element Method to Thermo-Elastic Interactions in a Piezo-Thermo-Elastic Medium under a Fractional Time Derivative Model. Mathematics 2022, 10, 650. [Google Scholar] [CrossRef]
- Qi, L.; Zhou, S.; Li, A. Size-dependent bending of an electro-elastic bilayer nanobeam due to flexoelectricity and strain gradient elastic effect. Compos. Struct. 2016, 135, 167–175. [Google Scholar] [CrossRef]
- Ray, M.C. Analysis of smart nanobeams integrated with a flexoelectric nano actuator layer. Smart Mater. Struct. 2016, 25, 055011. [Google Scholar] [CrossRef]
- Sidhardh, S.; Ray, M.C. Effect of nonlocal elasticity on the performance of a flexoelectric layer as a distributed actuator of nanobeams. Int. J. Mech. Mater. Des. 2018, 14, 297–311. [Google Scholar] [CrossRef]
- Shu, L.; Liang, R.; Rao, Z.; Fei, L.; Ke, S.; Wang, Y. Flexoelectric materials and their related applications: A focused review. J. Adv. Ceram. 2019, 8, 153–173. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi, F.; Haghi, P.; Dabbagh, A. Analytical wave dispersion modeling in advanced piezoelectric double-layered nanobeam systems. Struct. Eng. Mech. 2018, 67, 175–183. [Google Scholar] [CrossRef]
- Wang, K.F.; Wang, B.L.; Zeng, S. Analysis of an array of flexoelectric layered nanobeams for vibration energy harvesting. Compos. Struct. 2018, 187, 48–57. [Google Scholar] [CrossRef]
- Sobamowo, M.G. Analysis of Nonlinear Vibration of Piezoelectric Nanobeam Embedded in Multiple Layers Elastic Media in a Thermo-Magnetic Environment Using Iteration Perturbation Method. J. Solid Mech. 2022, 14, 221–251. [Google Scholar] [CrossRef]
- Luschi, L.; Pieri, F. An analytical model for the determination of resonance frequencies of perforated beams. J. Micromech. Microeng. 2014, 24, 055004. [Google Scholar] [CrossRef]
- Abdelrahman, A.A.; Eltaher, M.A. On bending and buckling responses of perforated nanobeams including surface energy for different beams theories. Eng. Comput. 2022, 38, 2385–2411. [Google Scholar] [CrossRef]
- Zeng, S.; Wang, K.; Wang, B.; Wu, J. Vibration analysis of piezoelectric sandwich nanobeam with flexoelectricity based on nonlocal strain gradient theory. Appl. Math. Mech. 2020, 41, 859–880. [Google Scholar] [CrossRef]
- Eftekhari, S.A.; Toghraie, D. Vibration and dynamic analysis of a cantilever sandwich microbeam integrated with piezoelectric layers based on strain gradient theory and surface effects. Appl. Math. Comput. 2022, 419, 126867. [Google Scholar] [CrossRef]
- Kaghazian, A.; Hajnayeb, A.; Foruzande, H. Free vibration analysis of a piezoelectric nanobeam using nonlocal elasticity theory. Struct. Eng. Mech. 2017, 61, 617–624. [Google Scholar] [CrossRef]
- Chu, L.; Dui, G.; Ju, C. Flexoelectric effect on the bending and vibration responses of functionally graded piezoelectric nanobeams based on general modified strain gradient theory. Compos. Struct. 2018, 186, 39–49. [Google Scholar] [CrossRef]
- Chanthanumataporn, S.; Watanabe, N. Free vibration of a light sandwich beam accounting for ambient air. J. Vib. Control 2018, 24, 3658–3675. [Google Scholar] [CrossRef]
- Lu, L.; Guo, X.; Zhao, J. Size-dependent vibration analysis of nanobeams based on the nonlocal strain gradient theory. Int. J. Eng. Sci. 2017, 116, 12–24. [Google Scholar] [CrossRef]
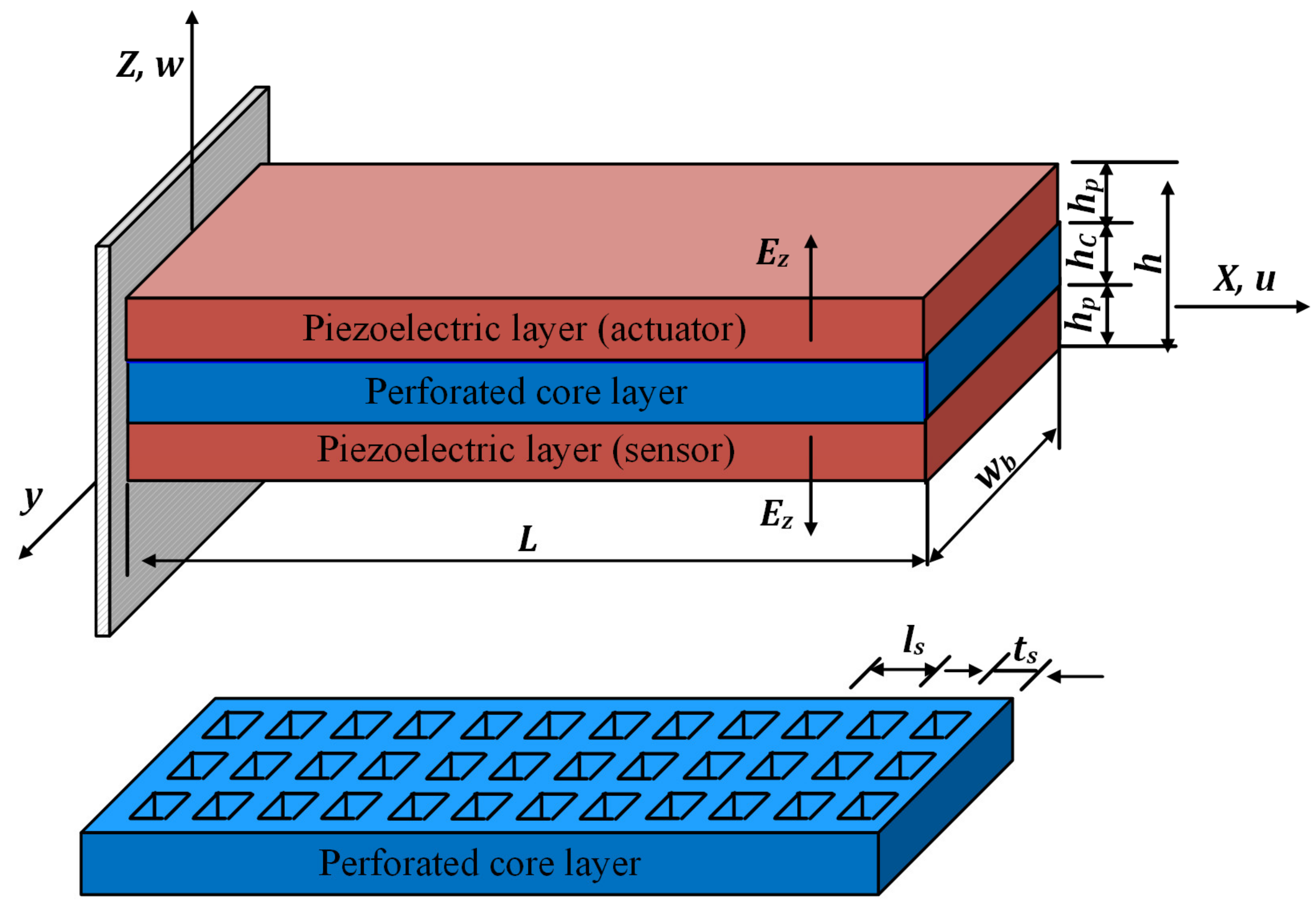

| BCs. | at X = 0 | at X = 1 | |
|---|---|---|---|
| SS | |||
| CF | |||
| CC | |||
| CS |
| n | CF | CC | CS | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.8751 | 0.7341 | 0.2441 | 4.730 | 0.9825 | 0.5499 | 3.9266 | 1.0008 | 0.7467 |
| 2 | 4.6941 | 1.0185 | 0.6033 | 7.8532 | 1.0008 | 0.7467 | 7.0686 | 1.0000 | 0.8585 |
| 3 | 7.8548 | 0.9992 | 0.7440 | 10.9956 | 0.9999 | 0.8181 | 10.2102 | 1.0000 | 0.9021 |
| 4 | 10.9955 | 1.0000 | 0.8181 | 14.1372 | 1.0000 | 0.8585 | 13.3518 | 1.0000 | 0.9251 |
| 5 | 14.1372 | 0.9999 | 0.8585 | 17.2788 | 1.0000 | 0.8843 | 16.4934 | 1.0000 | 0.9394 |
| 6 | 17.2788 | 1.0000 | 0.8843 | 20.4204 | 1.0000 | 0.9021 | 19.6350 | 1.0000 | 0.9491 |
| 7 | 20.4204 | 1.0000 | 0.9021 | 23.5620 | 1.0000 | 0.9151 | 22.7765 | 1.0000 | 0.9561 |
| 8 | 23.5620 | 1.0000 | 0.9151 | 26.7035 | 1.0000 | 0.9251 | 25.9181 | 1.0000 | 0.9614 |
| 9 | 26.7035 | 1.0000 | 0.9251 | 29.8451 | 1.0000 | 0.9330 | 29.0597 | 1.0000 | 0.9656 |
| 10 | 29.8451 | 1.0000 | 0.9330 | 32.9867 | 1.0000 | 0.9706 | 32.2013 | 1.0000 | 0.9688 |
| Mode | Present Model | [44] Analytical | [48] FE | [48] Analytical | % Error with [44] |
|---|---|---|---|---|---|
| 1 | 20.0667 | 19.9436 | 19.946 | 19.902 | 0.6172 |
| 2 | 80.2513 | 79.7746 | 79.784 | 79.083 | 0.5976 |
| 3 | 180.5081 | 179.4928 | 176.023 | 179.513 | 0.5656 |
| 4 | 320.7608 | 319.0984 | 308.349 | 319.135 | 0.5210 |
| 5 | 500.9028 | 498.5912 | 473.037 | 498.648 | 0.4636 |
| 6 | 720.7976 | 717.9713 | 666.657 | 718.053 | 0.3937 |
| 7 | 980.2793 | 977.2387 | 885.597 | 977.349 | 0.3111 |
| 8 | 1279.1529 | 1276.3934 | 1126.269 | 1276.538 | 0.2162 |
| Method of Analysis | First Vibration Mode (λ1) | Second Vibration Mode (λ2) | |||||
|---|---|---|---|---|---|---|---|
| Strain Gradient Parameter (l) | Strain Gradient Parameter (l) | ||||||
| 0 | 0.5 ht | ht | 0 | 0.5 ht | ht | ||
| 0 | [40] | 9.8293 | 9.9498 | 10.3029 | 38.8446 | 40.7164 | 45.8759 |
| Present | 9.8291 | 9.9496 | 10.3027 | 38.8415 | 40.7132 | 45.8722 | |
| [37] | 9.8293 | 9.9498 | 10.3029 | 38.8446 | 40.7164 | 45.8759 | |
| % Error | 0.0020 | 0.0020 | 0.0019 | 0.0080 | 0.0079 | 0.0081 | |
| 0.5 | [40] | 9.7102 | 9.8293 | 10.1781 | 37.0589 | 38.844 6 | 43.7669 |
| Present | 9.710 | 9.8291 | 10.1779 | 37.0559 | 38.8415 | 43.7634 | |
| [37] | 9.7102 | 9.8293 | 10.1781 | 37.0589 | 38.8446 | 43.7669 | |
| % Error | 0.0021 | 0.0020 | 0.0020 | 0.0081 | 0.0080 | 0.0080 | |
| 1.0 | [40] | 9.3774 | 9.4924 | 9.8293 | 32.8910 | 34.4759 | 38.8446 |
| Present | 9.3772 | 9.4922 | 9.8291 | 32.8884 | 34.4732 | 38.8415 | |
| [37] | 9.3774 | 9.4924 | 9.8293 | 32.8910 | 34.4759 | 38.8446 | |
| % Error | 0.0021 | 0.0021 | 0.0020 | 0.0079 | 0.0078 | 0.0080 | |
| 1.5 | [40] | 8.8915 | 9.000 5 | 9.319 9 | 28.2683 | 29.6305 | 33.3851 |
| Present | 8.8913 | 9.0003 | 9.3197 | 28.266 | 29.6281 | 33.3825 | |
| [37] | 8.8915 | 9.0005 | 9.3199 | 28.2683 | 29.6305 | 33.3851 | |
| % Error | 0.0022 | 0.0022 | 0.0021 | 0.0081 | 0.0081 | 0.0078 | |
| 2.0 | [40] | 8.3228 | 8.4248 | 8.7238 | 24.1877 | 25.3532 | 28.5659 |
| Present | 8.3226 | 8.4246 | 8.7236 | 24.1857 | 25.3512 | 28.5636 | |
| [37] | 8.3228 | 8.4248 | 8.7238 | 24.187 7 | 25.3532 | 28.5659 | |
| % Error | 0.0024 | 0.0024 | 0.0023 | 0.0083 | 0.0079 | 0.0081 | |
| L/ht | SS | CC | CS | CF | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Present | [23] | [44] | % Error | Present | [44] | % Error | Present | [23] | [44] | % Error | Present | [44] | % Error | |
| 6 | 0.4519 | 0.4570 | 0.4571 | 1.1376 | 1.0149 | 1.0245 | 0.9370 | 0.7012 | 0.7077 | 0.7087 | 1.0583 | 0.1699 | 0.1714 | 0.8751 |
| 8 | 0.3406 | 0.3428 | 0.3428 | 0.6418 | 0.7644 | 0.7684 | 0.5206 | 0.5284 | 0.5310 | 0.5315 | 0.5833 | 0.1274 | 0.1285 | 0.8560 |
| 10 | 0.2731 | 0.2742 | 0.2742 | 0.4012 | 0.6127 | 0.6167 | 0.6486 | 0.4236 | 0.4250 | 0.4252 | 0.3763 | 0.1020 | 0.1028 | 0.7782 |
| 16 | 0.1711 | 0.1714 | 0.1714 | 0.1750 | 0.3838 | 0.3842 | 0.1041 | 0.2654 | 0.2658 | 0.2658 | 0.1505 | 0.0637 | 0.0643 | 0.9331 |
| 20 | 0.1370 | 0.1371 | 0.1371 | 0.0729 | 0.3072 | 0.3073 | 0.0325 | 0.2124 | 0.2127 | 0.2126 | 0.0941 | 0.0510 | 0.0514 | 0.7782 |
| 30 | 0.0914 | 0.0914 | 0.0914 | 0 | 0.2049 | 0.2049 | 0 | 0.1417 | 0.1420 | 0.1417 | 0 | 0.0340 | 0.0343 | 0.8746 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melaibari, A.; Abdelrahman, A.A.; Hamed, M.A.; Abdalla, A.W.; Eltaher, M.A. Dynamic Analysis of a Piezoelectrically Layered Perforated Nonlocal Strain Gradient Nanobeam with Flexoelectricity. Mathematics 2022, 10, 2614. https://doi.org/10.3390/math10152614
Melaibari A, Abdelrahman AA, Hamed MA, Abdalla AW, Eltaher MA. Dynamic Analysis of a Piezoelectrically Layered Perforated Nonlocal Strain Gradient Nanobeam with Flexoelectricity. Mathematics. 2022; 10(15):2614. https://doi.org/10.3390/math10152614
Chicago/Turabian StyleMelaibari, Ammar, Alaa A. Abdelrahman, Mostafa A. Hamed, Ahmed W. Abdalla, and Mohamed A. Eltaher. 2022. "Dynamic Analysis of a Piezoelectrically Layered Perforated Nonlocal Strain Gradient Nanobeam with Flexoelectricity" Mathematics 10, no. 15: 2614. https://doi.org/10.3390/math10152614
APA StyleMelaibari, A., Abdelrahman, A. A., Hamed, M. A., Abdalla, A. W., & Eltaher, M. A. (2022). Dynamic Analysis of a Piezoelectrically Layered Perforated Nonlocal Strain Gradient Nanobeam with Flexoelectricity. Mathematics, 10(15), 2614. https://doi.org/10.3390/math10152614






