1. Introduction
Information security and identification have become a crucial part of everyday life. Traditionally secured systems are not reliable enough and are vulnerable to brute force attacks. Instead of these conventional mechanisms, biometric physical or behavioral characteristics are used for personal identification or in security systems. Although biometrics-based identification is a complex task, its use is increasingly widespread. There are several well-known biometric parameters related to physiological characteristics, such as DNA, face recognition, iris, retina, hand geometry, palm print, fingerprint, palm vein, finger vein and dorsal hand vein, or behavioral characteristics such as voice style, typing rhythm, signature and its dynamics.
Blood vessel segmentation is a topic of great interest in medical image segmentation because it can help in establishing the correct diagnosis, identifying adequate treatment and planning the execution of surgery. In the literature, the most widespread vein segmentation systems are applied on retinal vessel segmentation [
1], liver vessel segmentation [
2], coronary vessel from angiogram images [
3] or brain vessels [
4]. The purpose of this paper is not human identification, but the accurate segmentation of dorsal hand veins. These veins are under the subcutaneous fat and are very difficult to detect, with only some parts of the veins being located under the skin at a distance of approximately 3–5 mm. Observation and, thereby, automatic detection of the vessels presents great difficulties, especially in the obese. The veins on the surface can be better visualized in infrared light at a wavelength of 700–1000 nm due to the differences in the absorption capacity of hemoglobin in vessels compared to other surrounding tissues.
The aim of this paper is to propose and implement a robust dorsal hand vein segmentation system that combines unsupervised traditional segmentation used as labels in subsequent steps that boost the labels obtained initially with different U-Net-based CNN methods. Currently, there are extremely few researchers [
5,
6] in the medical field concentrating on dorsal hand vein segmentation due to the lack of an expert-annotated database.
The role of the automatic segmentation of dorsal hand veins would assist nurses and doctors in determining the precise placement of a needle for injection, a butterfly needle for perfusion or a catheter. Automatic non-contact insertion of the needle would not only eliminate multiple misplaced needle pricks, but also possible infection with contagious diseases.
The main contribution of this article is an automatic segmentation of dorsal hand vein NIR images from the NCUT [
7] database. In every computer vision application, the results obtained are greatly influenced by the quality and quantity of the images used. In our work, we propose a two-phase automatic segmentation system that does not require manual labeling. The creation of an overall accepted ground truth manually labeled by experts is a demanding and time-consuming task, and still not perfect. In our paper, we combine unsupervised traditional image processing techniques with supervised CNN segmentation. In the first phase, we implement automatic segmentation using different geometric image processing steps to detect the veins. This segmentation result is designated Label I. It is known that more annotators can improve the quality and accuracy of annotation. Thus, we wanted to improve the segmentation first obtained using supervised segmentation. In the second phase, we apply an ensemble of different CNN networks adapted for vein segmentation. The ensemble model obtained by supervised learning based on Label I substantially corrects the initial labels. This result constitutes Label II. The improvement between Label I and Label II is experimentally demonstrated by training the ResNet–UNet model in the same way on both labels. The performance obtained shows an improvement of approximately 5%, from a Dice score of 90.65% to 95.11%.
To the best of our knowledge, there are only two research papers in the field of dorsal hand vein segmentation that apply CNNs. The two articles report a mIoU of 78.12% [
5] and a Dice score of 78.21% [
6], both using other proprietary datasets instead of NCUT. All the other papers in the literature neglect the rigorous segmentation of the veins; rather, they concentrate on human biometric identification based on veins. Instead of segmentation performance (overlap: mIoU, Dice score), they measure human identification parameters: FAR (false acceptance rate), impostor acceptance of or FRR (false rejection rate) rejection of authentic matching. Our segmentation results are not comparable to authentication errors.
The rest of the paper is organized as follows: after a short review of the currently known dorsal hand vein authentication systems in the literature, the methods applied are presented. First, an unsupervised vein extraction method is proposed, which is further improved by two-phase supervised CNN segmentation. Finally, we describe our experiments and results on the networks studied and adapted for dorsal vein segmentation. Here, we are able to experimentally prove the effect of the two-phase boosting of labels used in training. The article ends with the discussion and conclusions.
2. Related Work
There are several state-of-the-art vein recognition methods that involve the steps of image acquisition, preprocessing, feature extraction and classification. In the domain of biometric identification, the most used methods are based on shape or texture.
Shape-based methods extract the topological structures of the vessels, extracting segments, bifurcation and endpoints. This kind of local shape can be described using LBP [
8], PLBP [
9], BGM [
10] and the Width Skeleton Model [
11]. In [
8], the authors propose to combine global and local shape representations using several techniques, such as the cross-sectional profile of the veins, Gaussian matched filter, extraction of extreme points, skeletonization, binary coding (BC)-based local binary pattern (LBP) and factorized graph matching (FGM). Ref. [
9] introduces partition local binary patterns (PLBP), where the image is divided into subregions and partial LBPs are computed to extract uniform pattern features. In [
10], Biometric Graph Matching (BGM) is used to compare graph-like templates; this method includes registration to the template, graph matching and distance computation. The final identification is done using the k-Nearest Neighbors method. The Width Skeleton Model (WSM) [
11] is also a graph model that takes both the topology of the vessels and their width into account.
The most important texture-based methods use various types of texture descriptors, such as Gabor features [
12], SIFT [
13] or local keypoint matching features, such as Oriented Gradient Maps (OGM) [
14] or Centroid-Based Circular Keypoint Grid (CCKG) and fine-grained matching [
15]. Ref. [
13] uses Contrast-Limited Adaptive Histogram Equalization (CLAHE), Harris–Laplace corner detector and Scale Invariant Feature Transform (SIFT). In [
16], the distinctiveness of vein patterns and the surrounding textures is measured using OGMs, and final matching is done through SIFT keypoint matching.
From the perspective of classification, the most widely used classifiers were unsupervised methods such as k-NN [
10] or its weighted variants and SVM [
17] until the most recent advances in the field of CNNs.
The convolutional neural network approach is not very widespread in this domain. The CNNs known in the literature are used especially for hand vein-based recognition and authentication, but not for segmentation. The reason is the lack of an annotated vein database required for segmentation. All of the following articles use CNNs for personal authentication with the NCUT [
7] or other proprietary databases. Wang et al. [
18] present a four-layered (one conv. layer) RCNN and test the identification accuracy on a self-made database. Li et al. [
11] compare AlexNet, VGG-16 and GoogleNet for personal identification. Wan et al. [
19] describe a VGG-based and an ensemble CNN made up of a combination of four SqueezeNet layers. Deep Hashing Networks (DHN) were first introduced in [
20] and used for dorsal hand vein-based feature extraction and matching with a simplified CNN implementation [
21]. In [
22], the authors describe an identification system based on palm and dorsal hand vein features using DHN and BGM or finger vein + fingerprint + face.
In recent years, deep learning, i.e., convolutional neural networks, has been used with great success in medical image segmentation compared to traditional methods. The CNNs used for object detection or localization, such as AlexNet, VGG, Inception, ResNet, MobileNet and others, were not suitable for image segmentation. Fully convolutional (FCN) networks were adaptations containing two major parts, which are downconvolution (encoder) and upconvolution (decoder). These types of networks can aggregate context features, capturing, in each stage, a reduced resolution of the original image. In this way, a pixelwise segmentation of the whole test image can be obtained over a single pass through the trained network. The most important drawback in this case is the loss of information during each convolution and pooling. The loss of detail leads to incorrect margins and rough segmentations. The most widely used network in pixelwise segmentation is U-Net, introduced in [
23]. U-Net introduced so-called skip connections, which refined the features in the upsampling part by concatenating the corresponding encoder feature map with its decoder pair. Different types of U-Nets have been used to segment different organs or tumors. U-Net is also applied in several engineering applications, such as manufacturing defects [
24], fringe pattern denoising [
25], concrete crack detection [
26] and fluid dynamics [
27]. V-Net [
28] was initially proposed for prostate segmentation, while 3D U-Net [
29] was aimed at kidney segmentation. The weighted Res-UNet [
30] was proposed first for retinal vessel segmentation; Recurrent Residual U-Net [
31] was applied in lung segmentation, skin cancer and retinal vessel segmentation; and H-DenseUNet [
32] was used in liver and tumor segmentation.
Recently, participants in the Medical Segmentation Decathlon Challenge [
33] have proposed general methods that test different types of architectures and different parametrization schemes that can generally be applied in several segmentation tasks. AutoML [
34] and nnU-Net [
35] have the great advantage of not needing manual fine-tuning of the CNN or its hyperparameters. They perform computations and set the parameter search space based on the data (resolution), and test some of the extant CNN architectures and produce a segmentation result based on the best ensemble obtained. This automated process is extremely long-lasting.
The segmentation of vessels via convolutional neural networks is a computationally complex problem. The above-mentioned CNN architectures can be applied only in supervised learning, where not only the original image but the expert gold-standard segmentation is also provided. For retinal vessel segmentation [
36], the DRIVE [
37] and CHASE DB1 [
38] databases are the most widely used, containing 40 and 28 expert-segmented images, respectively. Several architectural variants have been evaluated; for instance, U-Net is used in [
39]. The authors of [
40] propose a pyramid self-attention-module, and Guo et al. [
41] segment the retinal vessels with a Residual Spatial Attention Network.
The subcutaneous veins (finger [
42,
43], palm [
44] or dorsal-hand [
7]) are usually obtained from near-infrared images. The publicly available images used in the literature have low contrast and low resolution, and only the superficial parts of the vein can be seen and detected. They are not expert-annotated, and thus the segmentation with CNNs is only possible through a combination of manual segmentation and traditional geometrical feature extraction. In other cases, the original images and their annotations are self-acquired and not available publicly for further comparison [
43]. In palm print and palm vein recognition, research is focused only on the distinction between impostor and genuine [
45] or personal identification [
44].
In the domain of dorsal hand vein identification, traditional methods are the most widespread, even nowadays. There are only a few systems that propose dorsal hand vein recognition based on deep learning solutions. This article proposes AlexNet and VGG combined with logistic regression for this purpose [
19]. A fine-tuned VGG16 network was proposed for human identification in [
46]. A deep biometric hash learning framework has been proposed for palm vein, palm print or dorsal hand vein recognition [
47].
To the best of our knowledge, there are only two convolutional neural network approaches for the segmentation of dorsal hand veins, due to the lack of a corresponding vein annotation database.
In [
6], the authors propose a GAN network for obtaining dorsal hand vein image segmentation. The generative part is a U-Net network, and no architecture for the two discriminators is specified, only their inputs. One has input pairs of the original image
x and the segmentation
y, requiring
to be minimized. The other discriminator has input pairs of the original image and the generated image
, where the
has to be maximized. The article says nothing about the 50 images used in the training set and the 20 images in the test set. It similarly gives no information on how they obtained the labels used in the generator network. It is probably a proprietary database with manual labeling. The results of this article are compared with our experiments.
The authors of [
5] propose a modified U-Net architecture for dorsal hand vein segmentation. They describe a self-labeled, publicly unavailable database of 116 subjects and 1439 images. They obtain the labeling by hand, marking the vein part pixel by pixel. The proposed architecture uses VGGNet as the backbone for feature extraction, an attention mechanism made up of matrix multiplication and three bottleneck
layers, as well as a U-Netup layer that combines feature outputs 4 and 5 in VGGNet. The results obtained in this article are the best in the literature so far, and they are also compared with our results.
4. Experiments and Results
In this work, we propose to create a fully automated system for dorsal hand vein segmentation for NIR images. The main contribution of this paper is the boosting of the labels obtained using geometry-based image processing methods and correcting them via multiple U-Net networks. The boosted labels facilitate better segmentation via CNN training. The novelty of this paper is a two-stage CNN-based segmentation. First, multiple networks were trained on labels obtained without supervision. In this step, we have chosen the U-Net, U-Net++ and U-Net3+ networks with different loss types to reevaluate labels and decide on new labels. Secondly, the ResNet–UNet network was chosen to be trained on both labels. The more accurate Dice scores demonstrate the relevancy of boosting the labels. The method presented is useful, especially in the absence of precisely annotated ground truth labels made by experts. However, the pixelwise annotation of medical data, particularly vein images, is very tiresome and requires accurate pixelwise annotation from expert physicians.
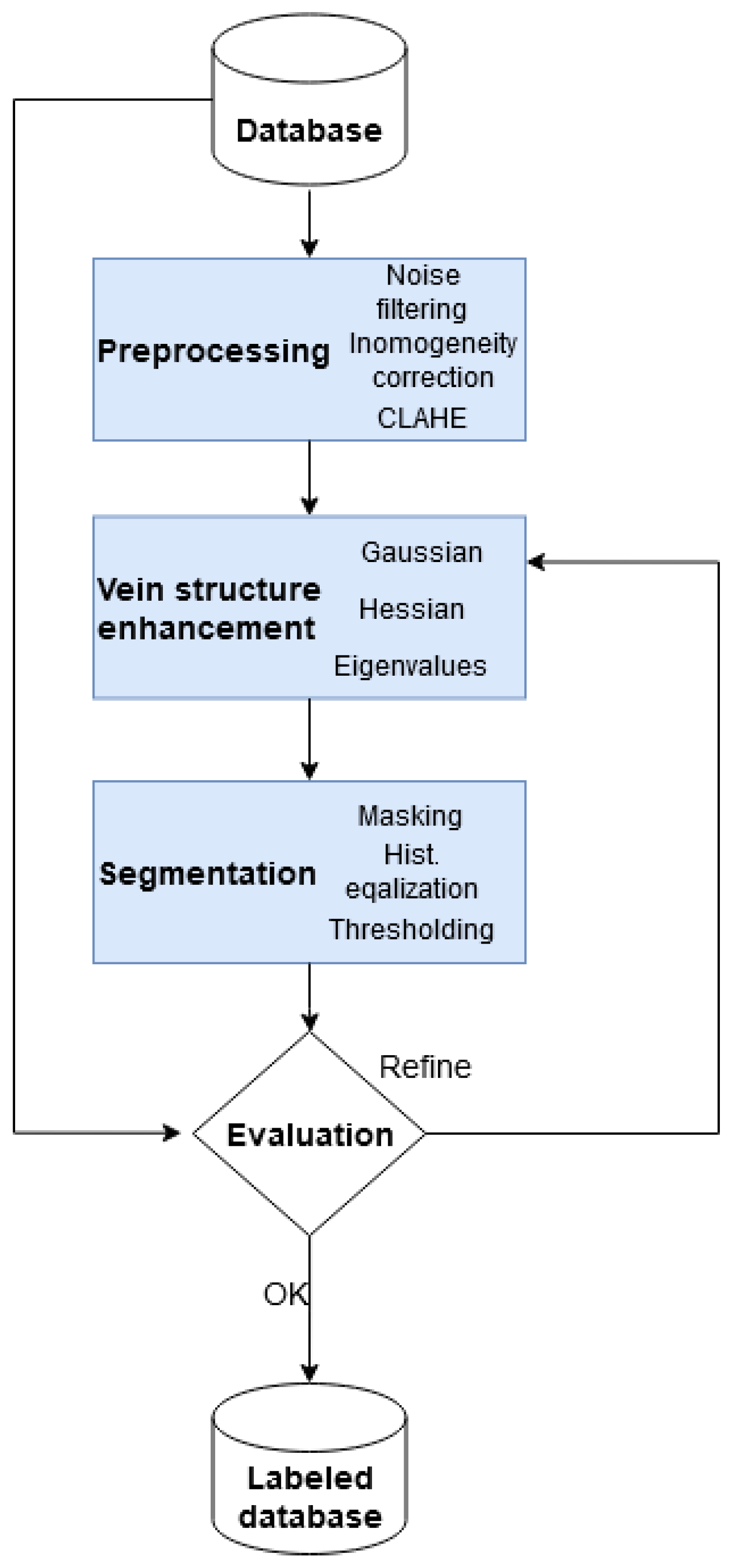
The pipeline (
Figure 11) of our boosted segmentation method is as follows.
Phase 1 (upper part of our pipeline) represents the training and evaluation of different types of segmentation networks to determine which is best suited for vein segmentation. The segmentation performance of the networks studied is evaluated and measured, comparing them to the labeled images described in
Section 3.2. These labels are denoted Label I.
In phase 2, the labels obtained before are boosted using an experimentally defined group of networks that proves to be sufficiently accurate and has a more complex architecture with better generalization properties. The segmentation thus obtained is named Label II. The best networks not included in the creation of Label II are trained for these more accurate labels, and their segmentation performance is measured and compared to the same networks, but trained on Label I instead.
In our experiments, the original training dataset from NCUT [
7] was augmented using well-known augmentation steps. From every image, we generated 10 other augmented images, applying a random scale between 80 and 120%, a crop and padding to the original size, a translation of 5–10%, horizontal and vertical flipping with a probability of 50% and 20%, respectively, a rotation of
and shearing of
. Each image was augmented using different and randomly selected methods. In this way, we obtained a total of
20,400 vein images.
The datasets obtained in this manner were split into training, validation and test sets in a proportion of 60%, 20% and 20%. We tried both two-class segmentation considering vein and background and three-class segmentation, taking into account vein, hand and background separately, motivated by the different grayscale levels of hand and background. The hand is usually light gray and the background black or masked into black. For both two-class and three-class segmentation, we computed the masks for all the images and annotations. The masking process was described in detail in
Section 3.2.
Figure 12 shows a sequence of the augmented original images and their pairs of augmented segmentations.
During our experiments, we compared different variants of segmentation networks fine-tuned and adapted for dorsal hand vein segmentation. The role of creating different types of segmentation architectures was to determine the architecture and hyperparameters of the networks that are suitable for vein segmentation. All these networks were trained on the labels annotated with no supervision (Label I) and proved to have a high capacity for generalization. The first set of networks that were trained were VGG–UNet, FCN32, FCN8 and the ResNet–UNet architectures. Out of these architectures, we determined the most suitable network for our purpose of vein segmentation. The second set of networks that were trained were U-Net, U-Net++ and U-Net3+. The role of these networks was to build an ensemble segmentor.
The components of a single CNN training process are shown in
Figure 13.
Our first group of experiments compared four CNN networks adapted and trained for vein segmentation: FCN32, FCN8, VGG–UNet and ResNet–UNet. All four architectures were trained on the NCUT augmented dataset, with 12,240 images in the training set, 4080 images in the validation and 4080 images in the test set, respectively. The training process ran for 100 epochs, with a batch size of 16. The optimization algorithm was Adadelta, set to an initial learning rate of 0.1 and a decay rate of 0.95. Adadelta is an extended and more robust version of Adagrad. Instead of considering all past gradients, it considers the moving average of the previous gradients. In this way, it adapts its learning rate by considering a fixed-size moving window. With this type of optimization, Adadelta continues to learn, even after many update steps in iterations and epochs. The networks were optimized on the weighted DSC loss with a weight of 93/100 for the vein pixels 7/100 for the background pixels.
The Dice similarity score (DSC) measures the overlap similarity between the result and the target label. In our case, it measures the similarity between the segmentation obtained via CNN supervised learning and the unsupervised labels. The DSC is computed in every epoch and for each of the 765 iterations per epoch. It is computed for every image in the 16-sized batch:
The Dice loss is computed from the mean Dice score (Equation (
8)), and the mean Dice score is the mean over all images.
The Dice loss is
. We have trained one of the networks studied both on weighted and unweighted Dice loss. The introduction of weights into the loss computation improves the training process considerably. The role of minimizing the CNN architecture on the weighted Dice loss is to balance the quite unbalanced NCUT dataset. On average, the total number of vein points was 6.8% of the image. This consideration led to us introducing a weight of 93/100 for vein pixels and 7/100 for the background (skin and black background pixels in total).
In the case of weighted Dice loss, the formula can be written as:
Figure 14 and
Table 1 show the accuracy of ResNet–UNet trained with unweighted and weighted Dice loss. It is clear that the unweighted loss performs 4–5% worse. The results only refer to the test set.
After setting the most suitable hyperparameters for all the networks, the four segmentor networks that were compared were the FCN32, FCN8, VGG–UNet and ResNet–UNet, all with weighted Dice loss.
Figure 15 illustrates the training process. As can be seen, FCN8 and FCN32 are slightly worse in training than VGG–UNet and ResNet–UNet. The training and validation accuracies for all four networks are presented in
Table 2 and
Figure 15 and
Figure 16.
We compared not only the losses during the training and validation processes, but the segmentation performance of these four networks as well, which we deemed the most important. We can draw the following conclusions based on the Dice scores, sensitivities and specificities measured on the test tests: FCN32 is the worst network in this case, with a Dice score of only 0.8024, followed by FCN8 (Dice = 0.8271) and VGG–UNet (0.8594). The best segmentor network out of the four shown is ResNet–UNet (Dice = 0.9065). We measured the Dice score, sensitivity (TPR = true positive rate) and specificity (TNR = true negative rate) for our segmentations for further comparison (
Table 3 and
Figure 17).
Figure 18 shows a segmentation result from these four networks.
Based on the segmentation results and training time, we decided to continue our experiments with the best network obtained only, namely ResNet–UNet, having the best Dice score of 0.9065.
By analyzing the segmentation results visually, we observed that the best networks detected supplementary veins or connected discontinuous regions by joining them, or even eliminated incorrect patches considered noise in Label I. We drew the conclusion that Label I obtained without supervision should be over-evaluated via training some other good networks and computing their ensemble response. In this second group of experiments, we considered three different CNN architectures (U-Net, U-Net++, U-Net3+) not used in the first experiment, and for each one, three different loss functions (BCE loss, Dice loss and focal loss) were computed in the optimization phase.
Figure 19 shows an example of the segmentation obtained by the three network architectures with Dice loss.
We have chosen these architectures for relabeling because they are even more complex than the FCN or VGG–UNet networks. U-Net++ and U-Net3+ have a greater capacity for generalization and similar performance on Label I compared to ResNet–UNet. The advantage of these architectures, selected to obtain the ensemble network, is the multiple interconnectivity between layers to consider more complex feature maps at each stage, leading to accurate segmentation.
In this way, we have created nine differently trained architectures. The segmentation responses from these networks were used to create the ensemble. The final response of the ensemble is considered as the new labeling of veins (Label II).
The hyperparameters of the U-Net, U-Net++ and U-Net3+ architectures are: a learning rate of 0.001, the Adadelta optimizer, 100 epochs and different losses—BCE, Dice or focal losses. For the focal loss, the learning rate had to be changed to 0.0002. The batch size is 8 for U-Net, 4 for U-Net++ and 2 for U-Net3+.
The comparison of the different loss functions can be seen in
Figure 20, showing the Dice scores, sensitivity and specificity of every network from each of the nine architectures. The last box gives the performance of the ensemble network.
According to the Dice scores, sensitivities and specificities, focal loss is the best loss out of the three losses studied. The progress of focal loss on the three architectures during the validation process is shown in
Figure 21. All three networks perform visibly well, but the best validation performance is given by U-Net3+.
The majority voting of the ensemble of nine networks was what defined the new label, namely Label II.
Figure 22 shows an example of differences between the original label (Label I) and the new label (Label II). The Dice coefficient between the old labels and the new labels is 0.8872. Clearly, all three networks detect more vein regions, especially at the borders, and furthermore, U-Net2+ and U-Net3+ also detect continuous vein regions, linking perhaps discontinuous vein parts in Label I. The first row in
Figure 22 shows the original image and the segmentation obtained by U-Net, U-Net2+ and U-Net3+. Row 2 shows Label I and the differences in row 1 segmentation to Label I. Row 3 shows the ensemble segmentation (Label II) and the differences in row 1 segmentation to Label II.
Our last group of experiments proves the assumption of this article—namely, that the slightly inaccurate segmentation obtained by unsupervised traditional image processing techniques can be improved by applying an ensemble of multiple CNN networks trained on the labels obtained in previous steps.
We trained our best ResNet–UNet network using the same training parameters and the most common loss function, the Dice loss and the best loss obtained in our previously described experiment, namely the focal loss. All the other hyperparameters were set to the same as previously. The results, as expected, show a 2–5% improvement in the Dice score on Label II compared to Label I.
Table 4 and
Figure 23 show the results on Label I for both Dice and focal losses.
Table 5 and
Figure 24 show the results on Label II for both Dice and focal losses.
Analyzing the boxplots of the corresponding experiments on the same test set, we can see that the segmentation after phase 2 is much better than after phase 1. The boxplots for both losses become flatter, which means that the interquartile range (IQR) is much smaller. For the Dice loss, the IQR is Q3 − Q1 = 0.9233 − 0.8977 = 0.0256, whereas in the second phase, it becomes equal to IQR = 0.9578 − 0.9462 = 0.011, which represents a 2.3-fold improvement. The difference is even better if we consider that the worst segmentation response is 0.7413 (minimum) in phase 1 and 0.9162 (minimum) in phase 2. The segmentation of the worst image improves by 17.49%. Better results are obtained for focal loss as well if we compare the two ResNet–UNet networks trained on the focal loss. The difference between Dice scores here is 2.12%, while the difference between minimums is 12.91%.
Figure 25 shows an image with significant differences between Label I and Label II and ResNet–UNet phase 1 and ResNet–UNet phase 2, both trained with Dice loss.
All our experiments related to CNN training were done on a dual Nvidia Geforce RTX 2080 GPU system with 11 GB memory on each graphics card. Our experiments were run in Keras Tensorflow and Pytorch as well. Each of these deep learning frameworks relies on the Python programming language. The traditional image processing steps were implemented, and the correct workflow was experimentally set up via ImageJ and the ITK image processing software.
5. Discussion
There are very few articles in the literature that describe dorsal hand vein segmentation, due to the lack of expert annotation on dorsal hand or palm vein images. Most dorsal hand vein databases are made not for precise vein segmentation, but rather for personal identification. The papers discussing human identification rely on traditional image processing methods that extract geometrical features such as bifurcation, angel, segment length or certain local or global image features [
15]. The two existing articles in the domain, also mentioned in the state-of-the-art section, are Gao et al. [
5] from 31 December 2021 and Yakno et al. [
6], which appeared in February 2022. Gao et al. present a system based on the U-Net network, introducing the so-called U-Netup that uses an attention module in the U-Net and joins the outputs of conv. layers 4 and 5, called feature 4 and feature 5, followed by two other convolutions to form the output of the CNN. They use a self-made dorsal hand vein database from 116 subjects, totaling 2024 images. The labels used for training are hand-marked, pixel by pixel. As we can see, these initial images are not standardized and the hand-marked labels are not quite accurate in the examples given in their article, with only 1–3 vein sections being marked with a maximum of 1–2 bifurcations. The results reported by the authors are defined as the mean intersection over reunion (mIoU) as a sum of (TP+TN)/2, considering the weights of both classes equal. In general, when computing mIOU, the correct class matches must be weighted by the number of elements in that class over the total number of elements. In this way, the background TN percentage does not have a weight of 1/2 in the final formula. The authors have not considered this, allowing for a straightforward comparison of the mIOU reported in [
5] with our TP (sensitivity) and TN (specificity) values.
Table 6 shows the results of paper [
5] compared to our results.
The most recent article in dorsal hand vein segmentation is [
6]. Yakno et al. present a system that achieves vein segmentation using Vein-Generative Adversarial Network (V-GAN). They use only 50 images for training and 20 for testing. The resolution of the images is
pixels. Based on the single visualization figure from the article and the resolution of the original images, it cannot be excluded that they used a small part of the same NCUT database that we used. The generative part of the GAN is U-Net, but the discriminative part is not specified; only the loss functions of the two discriminators are described, while their exact structure is not detailed at all. They trained the networks on ground truth labels, although their actual origin is not specified. They present two segmentation results, with and without preprocessing. As preprocessing, they applied ROI extraction of
pixels, CLAHE and gamma correction. Their sensitivity, specificity and Dice scores can be compared to ours (
Table 7).
In addition to comparing our results to the articles in the literature, we have studied the same procedure on databases other than only the NCUT. The Sakarya University of Applied Sciences (SUAS) database [
59] consists of 919 vein images from 155 different subjects, measuring
pixels. We have also extracted the veins from these images with the traditional segmentation method proposed and applied the already trained ensemble network to segment these types of images as well.
The results were surprisingly good. The segmentations obtained are shown in
Figure 26. Some post-processing steps of erosion and deleting small unconnected false veins would correct the segmentation. The purpose here was to examine the model obtained trained only on the NCUT with other types of dorsal hand images as well. The veins here are considered wider, influenced by the transition intensity from the vein to the skin that had a greater width in the original database, but that is not the case here.
The same unsupervised vein extraction and CNN testing process was performed on the PUT database [
60] as well. It consists of 1200 wrist images from 50 persons, containing three series of four images each for the left and right hands, meaning 24 images for each person. The resolution of the images is
pixels. Here, the segmentation appears more precise than for the SUAS, but the horizontal line across the wrist introduces horizontal noise, especially in unsupervised segmentation, but in supervised testing as well. The results are shown in
Figure 27.
Considering these two different databases, which were not included in the training process of our model, we can conclude that the veins are being detected, but the segmentation results are noisy. This result can be explained by the different vein acquisition equipment and the lack of an identical acquisition protocol. Some images can be standardized over a series of preprocessing steps, but in certain situations, it is impossible to unify the images acquired by different equipment. To generalize the supervised segmentation, the model should be rebuilt, including these diverse images in the training process. The numerical results were not measured in this case because the entire automatic labeling and training procedure should have been redone from scratch, which was not the goal of this research effort.
6. Conclusions
The lack of ground truth labels of medical images means that the standard segmentation performance measure compares two results between each other and not the results with the gold standard. The ground truth is non-existent both in our case and in many other segmentation applications. In practice, it is essential to define the goal of segmentation and accepted error rates. In this paper, we proposed a novel pipeline for image segmentation, presenting a case study on dorsal hand vein NIR images. However, vein annotation can never be perfect because of the anatomical structure of the veins. The vascular system is arborescent, with many branches and bifurcations. Additionally, the veins become increasingly thinner in the extremities or in different organs. In the images used, vein width was between 4 and 25 pixels, corresponding to 0.6–4 mm, while 1 pixel was 0.15 mm. As a comparison, by applying a morphological operation of erosion or dilatation of only 1 pixel on the segmented images, the results changed by 4% in the Dice score. This is the reason for considering only the detectable, meaning the visible, subcutaneous veins in our labeling process.
The approach combines unsupervised segmentation with supervised learning. The first major step in our system is gross segmentation by applying traditional image processing techniques. The processing steps here include essential steps of image correction, such as inhomogeneity reduction and contrast-limited adaptive histogram equalization, to visualize and analyze the valleys on the horizontal profile image, which is followed by the extraction of tubular structures from the image. The final step in the unsupervised part is the local threshold, for obtaining the binary segmentation used further on as labels.
The second major step of the system proposed was the adaptation, training and fine-tuning of different CNN architectures initially used for object detection or medical image segmentation. These types of networks require supervised training; thus, they require not only the original image, but the ground truth segmentation as well. Lacking expert annotations on any of the publicly available dorsal hand vein images, we had to use the previously obtained segmentations as labels in our CNNs. Surprisingly, during visual verification, some of the CNNs performed even better than the labels given. This observation caused us to decide in favor of the second phase segmentation. An ensemble classifier based on majority voting by nine networks created more accurate image labels. These new labels were considerably better than the initial ones and led to better training and generalization of the initially studied convolutional networks that were not included in the ensemble. By using the second labeled dataset, the ResNet–UNet classifier presented improves the initial Dice score by approximately 4–5% and increases the sensitivity significantly. In this way, we obtained our best Dice score for the test set of 95.11%.
The ResNet–UNet classifier was also tested on two different databases not involved in the training process. The results are promising and are a compelling reason to include other types of images in the training process. It is possible to improve our results even more; we propose to study other CNN networks in the field of medical image segmentation.
The limitations of the paper presented are the restricted selection of geometric image processing segmentation steps used for obtaining Label I. The steps shown may work very well for some datasets and less so for others. This traditional segmentation pipeline needs further fine-tuning and adjustment to obtain the best possible labels for different kinds of vein images. On the other hand, in the second phase, the drawbacks include the general limitations of CNNs due to different stages of downconvolution and upconvolution. The more complex networks presented and applied in our case detect vein contours more precisely, with increasing computational complexity and training time. In addition, the accuracy of the resulting model is highly influenced by the quality, quantity and diversity of input data.
In the future, we intend to analyze networks that can handle the border pixels of the vein region. A more accurate detection of border pixels may lead to a Dice improvement of 1–2%. For this purpose, we will apply attention-guided networks and multi-pathway multi-resolution networks. We also propose to apply SegAN [
61] to generate more images in our dataset and to investigate and train the nnU-Net [
35] model, which is considered a benchmark in medical image segmentation.
At present, there are few research efforts studying dorsal hand vein segmentation in the clinical medical field because of a lack of ground truth images labeled by experts [
5]. This article may be considered a starting point for non-contact injection in the dorsal hand veins to efficiently gain intravenous access, to administer different medications, apply intravenous therapy, perfusion, or to perform several types of blood tests, intravenous cannulation or catheter insertion. Nowadays, especially in hospitals for contagious and infectious diseases, where medical staff have to wear protective equipment such as gloves, goggles, surgery masks, aprons and gowns, the precise determination of the vein for an accurate needle prick is essential.
Furthermore, the pipeline proposed not only solves the problem of dorsal hand vein segmentation, but may also be applied in other vessel segmentation tasks, such as retinal vessel segmentation on fundus images to supplement computer-aided diagnosis and surgery planning for diabetic patients, lung vessel segmentation to detect pulmonary vascular diseases or identifying blocked or narrowed veins in the heart from a coronary angiogram. All these applications require well-acquired and standardized datasets of several thousand images collected thoroughly and according to a well-defined imaging protocol.