Advancing Algebra Achievement Using Affordances of Classroom Connectivity Technology: The Case for Noticing through Discussion

Abstract

This article reports on two aspects of a professional learning (PL) and research study. Twenty-five teachers participated in a two-year PL program that sought to support teachers to implement classroom connectivity technology (CCT) in their Algebra I classrooms. Students in one school who learned Algebra I with CCT outperformed their peers who learned without CCT. Therefore, we explored the classroom practices of one teacher whose students attained higher achievement. There were several aspects of this teacher’s instruction that created the context for noticing and potentially led to the significant difference in Algebra I achievement. First, we describe the foundational components of the classroom context that established the expectations for learning and lesson mini cycles that provided a consistent format for students. We discuss several components of this work that supported student noticing, including connections to prior knowledge, task analysis, and carefully curated lessons. Students’ observations were codified in the conjectures that they developed individually and in groups as well as in the summaries of the classroom engagement in several ways. The implications of these results and future research are discussed.

1. Introduction

Learning is the construction of connected webs of knowledge through activity within social contexts [1,2,3]. Accordingly, for mathematics education, learning occurs when students engage in mathematics while participating in social interaction. The source of knowledge construction within a technology-enhanced classroom is the student’s mathematical behaviors (e.g., exploring, experimenting, conjecturing, and noticing) as they engage with learning objects presented by the teacher. This is particularly the case when learning is facilitated with dynamic algebra software that enables students to manipulate a mathematical object (e.g., the leading coefficient of a quadratic equation) and examines how their manipulations affect the dynamically-linked mathematical object (e.g., changes in the position and shape of the associated parabola). Information and communication technologies, which support visualizing mathematical concepts, solving mathematical problems, and encouraging creativity, can promote meaningful learning in mathematics [4,5]. Furthermore, the effective use of technology during mathematics instruction improves students’ mathematical dispositions (motivation and attitudes) and achievement [6]. Research, however, shows equivocal outcomes for student learning with technology-enhanced instruction [7,8]. For students to effectively learn from their mathematical behaviors within technology-enhanced mathematics classrooms, they need to be taught to notice the relationship between their mathematical behavior and the outcomes of these behaviors [9]. Teaching students to notice the impact of their behaviors is critical for effective technology-enhanced learning.

Student noticing has been defined “as selecting, interpreting, and working with particular mathematical features or regularities when multiple sources of information compete for one’s attention” [9] (p. 809). To learn a mathematical concept, Lobato and colleagues postulated that students must assert “executive attention”, which “involves selecting one dimension or piece of information in the presence of competing sources of information” (p. 811–812). As a distributed process, noticing and thus learning from one’s noticing is a social process through which the learner comes to “centers of focus”, which are the features of the mathematical object to which a learner attends. A teacher may engage the students in interactions that focus their attention toward a specific aspect of a mathematical task. Specifically, support for visualization, such as color in a graph, is typically noticed more readily than textual supports for knowledge construction. Finally, Lobato and colleagues posited the nature of the mathematics activity to be “the participatory organization that establishes the roles governing students’ and teachers’ actions that contributes to the emergence of centers of focus” (p. 814). Research has shown that different individuals notice different aspects of a mathematical object, resulting in different learning outcomes [9] that emerge as a result of the differences in the presentation of a mathematical object [10].

To understand this critical mechanism of noticing, we draw upon the concept of opportunity to learn from a sociocultural perspective [11]. According to Gee, the teacher’s role is to align the learning opportunities, or affordances for learning, with learner capacity and readiness to engage with these learning opportunities, which he named the learners’ effectivities. Gee used the term affordances “to describe the perceived action possibilities posed by objects or features in the environment” or “what the individual can perceive as feasible to, in, on, with, or about the objects or features of that environment” (p. 81). Gee further stated that “a human actor must also have the capacity to transform the affordance into an actual and effective action” (p. 81) and described effectivities as “the set of capacities for action that the individual has for transforming affordances into action” (p. 81). In the example of learning quadratic equations within a technology-enhanced context, the learning opportunities (i.e., affordances, also known as action possibilities) are the different activities or inquiries designed by the teacher to foster learning. Students are only able to engage with these affordances for learning if they are able to enact their effectivities (i.e., capacity for action) for learning from these affordances. In technologically-enhanced instructional contexts, this means that they must be able to effectively engage with the dynamic software and learn from their interactive behaviors with the calculator. We posit that students can only act on the affordance of the calculator if they are supported to notice the relationship between their behaviors with the calculator (e.g., changing the parameters of the coefficient of the quadratic term) and the outcomes of their behaviors on the mathematical object (i.e., the parabola).

Applying Gee’s theory to the mathematics classroom, the teacher’s role is to align the learning opportunities with the learners’ potential for acting upon the learning affordance. To do so, the teacher uses several tools: the teacher’s content knowledge, which enables the teacher to understand, for example, the student’s mathematical thinking; the teacher’s knowledge of student understanding, which is gained through using classroom connectivity technology (CCT, see description below) to project students’ mathematical thinking onto a smartboard or classroom screen; classroom interactional patterns, which enable the teacher to garner student thinking; and, in this case, slowing down student behavior to enable the noticing of the relationship between their behavior and the impact of this behavior on the mathematical object under examination.

1.1. Purpose of the Present Study

This article reports on two aspects of a professional learning (PL) and research study. We examined the achievement on standardized assessments of Algebra I between students who learned Algebra I in a traditional context and students who learned Algebra I in a context using CCT. Then, we explored the classroom practices of one teacher whose students attained higher achievement to understand mechanisms that might have contributed to improved student performance in Algebra I. This research study was focused on two research questions:

• What is the impact of teacher implementation of CCT following professional learning on Algebra I achievement?
• What are the characteristics of classroom instruction that might support Algebra I achievement?

1.2. Classroom Connectivity Technology

In 21st century learning environments, CCT and dynamically-linked Algebra systems are among the tools that teachers can use to facilitate learning within the mathematics classroom. CCT tools are advanced audience response systems (ARS), which provide teachers with instant electronic student learning data while class is in session. For example, students may use a clicker with a remote device that connects with the teacher’s computer to respond to a whole-group prompt or question. Students’ responses are sent to the teacher’s computer, which aggregates the data and projects students’ responses anonymously on a screen for students to examine. The projections of the students’ responses then become objects for whole-class discussion.

Our study explored Algebra I teachers’ use of the Texas Instruments (TI) Nspire Navigator™, an advanced ARS system. The TI-Nspire Navigator™ system includes multiple components. Students use a handheld graphing calculator that remotely communicates with the teacher’s computer to provide instantaneous individual and group-level student responses. Additional components of this system include Quick Poll, Quiz Documents, Screen Capture, and Activity Documents. Each of these functions of the CCT system offers affordances for learning, such as technology-assisted formative feedback and assessment, task documents that focus student learning, and the ability to capture and project students’ mathematical behaviors to stimulate classroom discourse. Quick Poll allows teachers to quickly check students’ understanding using multiple-choice and open-ended questions. The TI-Nspire Navigator™ also allows teachers to send a Quiz Document to the students’ graphing calculators to which students can respond in multiple formats. Both the Quick Poll and the Quiz Document allow the teacher to assess students’ levels of mastery of prior material before facilitating instruction on new content. The Screen Capture function allows the teacher to capture student work on their graphing calculators and view student’s individual screens on the teacher’s computer. The teacher can then use this function to anonymously project students’ work from their graphing calculators to the classroom projection screen to examine within the whole-class discussion. Finally, Activity Documents (aligned with Common Core Standards for Mathematics in the United States [12]) are learning activities to support mathematical conceptual understanding, which the teacher can create on their own or download from TI’s website and adapt for their classroom content (e.g., [13,14]). The ways in which one teacher engaged her students with these documents is the focus of our investigation in the present study.

Prior studies found improvements in students’ Algebra I achievement due to the teachers’ use of several unique functions of this CCT Navigator system [15,16,17,18]. The Navigator system allows for the close integration of dynamically-linked representations (i.e., changes in a graphical representation are linked to changes in its equation or values of points in a table) and publicly displayed representations that provide teachers and students the opportunity for productive classroom discourse [19,20,21,22] or “socially situated interaction and investigation” [23] (p. 183) related to students’ mathematical behaviors. Specifically, through teachers’ projections of the dynamic, synchronous manipulations of the algebraic equations, these graphed representations and manipulations of the concepts become objects of classroom discourse that allow students to collaboratively discover and create mathematical conjectures and hypotheses. Ultimately, the TI-Nspire Navigator™ system provides for bidirectional communication between the teacher’s computer and students’ graphing calculator that can be used to observe student thinking in action while students are individually or collaboratively exploring dynamically-linked graphs of algebraic concepts in a coordinate plane. The affordances in this CCT system can be leveraged to facilitate discourse for social construction of knowledge related to a projected graph.

Studies that examined early versions of ARS resulted in improved enthusiasm for learning but limited gains in learning [24]. When student-centered learning strategies were used with these technologies, improvements in several areas were evidenced, including student attendance and participation (e.g., [25,26]), collaborative learning and student engagement [26,27,28,29,30], student comprehension (e.g., [31,32,33]), and student class satisfaction [24]. For example, Cheng and colleagues [34] found stronger motivation for learning and academic performance among undergraduate students who exhibited greater social presence in classes with ARSs. Further, in a quasi-experimental study of the impact of ARS in middle school mathematics classrooms, Zhu and Urhahne [35] found that teachers with ARSs made more accurate judgments of their students’ understanding than teachers who used diaries or a control classroom. In addition, students in ARS classrooms increased their mathematical understanding when compared to students in the comparison and control classrooms. Finally, in a systematic review of studies reflecting the period from 2006 to 2020, Wood and Shirazi [30] found that ARS impacts engagement by focusing students’ attention on the lecture in anticipation of questions that would be posed to the whole class. This engagement extended to influences on students’ cognitive engagement in the form of greater metacognitive activity. Further, when students’ responses were made public for student review and discussion, the review evidenced deeper interaction in ARS-enhanced classrooms. Finally other benefits included greater questioning and instant feedback leading to greater learning. Thus, over the past two decades, CCT has emerged as a genre of instructional tools that facilitate teacher–student communication and students’ engagement with content. In fact, Hegedus and Penuel pointed out, “James Kaput thought that wireless connectivity ‘inside’ the classroom would change the communicative heart of the mathematics classroom” [36] (p. 171).

The present study follows up an Institute for Education Science (IES) funded project, Classroom Connectivity in Mathematics and Science (CCMS; [15,16,17,18,19]), which was a large, national, randomized control trial that examined the impact of the TI-Nspire Navigator™ on Algebra I achievement. One hundred and twenty-six teachers from 28 U.S. states volunteered to participate. Treatment teachers received professional development and CCT equipment during the first summer, and control teachers received the intervention the second summer of the program. We compared the treatment and control students’ performance on a researcher-created Algebra I achievement test across three years of the program. In Year 1, the comparison reflected the traditional treatment effect (i.e., treatment versus control). In Years 2 and 3, students’ scores for those using the technology were compared versus the Year 1 control students scores. Students in CCT classrooms outperformed their peers in control classrooms during Year 1 with an effect size of 0.30 [18] and continued for three years with CCT classrooms outperforming Year 1 control classrooms with significant effect sizes from 0.19 to 0.37 [15]. An important variable was the formative assessment affordances of the technology, which increased the teachers’ understanding of their students’ comprehension [15,37].

The present study extended the previous study in several ways. First, the PL program extended the model of PL in the CCMS project by including ideas related to both technology-enhanced instruction and traditional pedagogy (e.g., classroom discourse). The PL program was also extended in duration considerably over two years. Second, the present study examined the effect of CCT on a standardized end of course (EOC) Algebra I examination. We compared EOC scores for students whose teacher did and did not implement CCT within one school. Third, the present study extended prior research through an in-depth examination of one successful teacher’s Algebra I instruction using CCT to consider aspects of her instruction with CCT that may have led to improved outcomes for students.

2. Materials and Methods

In the following sections, we describe the professional learning program, participants, materials, data collection, and data analysis of the present study.

2.1. Professional Learning Program

The present study is situated within a PL and research study, which, as stated above, extended the CCMS study by developing more powerful PL opportunities for participating teachers. Specifically, this study providing more in-depth PL related to classroom interactions and effective instruction using CCT based on principles of the effective use of CCT that emerged from this earlier study [17]. It was also aligned with best practices in the field of effective PL programs (e.g., [38,39,40,41,42,43]), which includes active engagement in content-specific activities over an extended period of time (i.e., approximately 15 days over 2 years plus classroom observations), content focused (i.e., Algebra I), coherent, and incorporating collective participation.

The PL program focused on effective technology implementation with the goals of increasing student engagement and achievement. To do this, in addition to the technical training needed to operate the TI-Nspire Navigator™, we encouraged (among other instructional practices) teachers to reveal student thinking through examination of their mathematical constructions; to hold students’ mathematical thinking as objects of discourse; to open the discussion to ways that students arrived at correct and incorrect responses; to engage students with dynamically linked representations that are related to a realistic context; and to engender effort and persistence as norms within the classroom. We met seven times across the school year during the first year of the PL program and eight times across the second year of the program. During each visit, the first author conducted classroom observations on Thursday and Friday; the whole group of teachers met for a day of PL on Saturday; and then the first author visited the teachers again on Monday and Tuesday. Classroom observations were focused on the use of the technology and providing support for implementing the technological and/or pedagogical techniques discussed during our Saturday sessions. The first author provided feedback to the teachers either after the observation or during the Saturday sessions. During the second year of the PL program, the participants engaged in professional learning communities (PLCs), which were intended to create the context for collaborative lesson planning in support of technology-enhanced classroom instruction.

2.2. Participants

Approximately 25 teachers engaged in PL across two school years. The majority of the teacher participants were from one high school (35%) with a group of teachers in one middle school (20%). Fifty-five percent of the participants taught a secondary level mathematics course with 25% teaching Algebra I as their main focus. The remainder of the participants taught middle school mathematics other than Algebra I. The participants were predominantly female (95%) and White (75%) with 25% African American. Fifty percent of the participants pursued undergraduate degrees outside of education, and a smaller percentage (40%) pursued a degree in mathematics or mathematics education. Only 35% of the participants held graduate degrees with several in the process of pursuing their master’s degree at the time of the study. The majority of the participants held a certification in Mathematics Grades 5–9 (50%), with an additional 6 holding certification in Mathematics Grades 6–12. Many of the teachers with Mathematics Grades 5–9 certification also held certification in a secondary area. Six of these participants held an additional certification in Mathematics Grades 6–12; one held certification in Special Education; two held certifications in Elementary Education; and one held certification in Social Studies. Finally, 65% of the participants were veteran teachers and the remaining teachers reported limited experience (less than 5 years). This study is focused on one of the participants, Ms. Joiner (pseudonym), from the larger PL program, whose students outperformed all of the other Algebra I students on the state mandated EOC examination and all three subscales within her school (see analysis below).

Ms. Joiner

Ms. Joiner is a female, white teacher and is currently teaching eighth-grade students in a middle school. She holds a master’s degree in teaching mathematics from a research university in the western region of the United States. Her undergraduate degree is in mathematics from a research university in the southern region of the United States. At the time of data collection, she had three years of teaching experience. During an interview in which we conducted a member check for the present study, Ms. Joiner’s statements reflected the belief that effective teaching requires deep knowledge of mathematics content, curriculum, and students. She also communicated the belief that students learn mathematics through active interaction with mathematical objects to build strong connections between concepts (Personal Communication, 7 March 2022).

2.3. Materials and Data Collection

There were three sources of data within this study. First, all students took the state-mandated Algebra I EOC examination. Second, we video recorded and transcribed five lessons in a unit of instruction related to quadratic equations and their associated graphical representations, the parabola. Third, we interviewed Ms. Joiner to engage in member checking for accuracy of the qualitative themes that arose from our analyses. In addition to serving as a mechanism for member checking the themes that emerged for the research team, these interview data provided the research team with a rich and more nuanced understanding of Ms. Joiners’ background, beliefs, and conceptions of teaching and learning mathematics.

2.3.1. Algebra I End of Course Examination

To examine the impact of CCT on student performance after the second year of teacher participation in the PL program, we compared state EOC examination scores for Algebra I students in treatment (i.e., learning with CCT) and comparison (i.e., learning without CCT) conditions within one school. The school provided de-identified assessment scores for all students in the school with only the treatment (i.e., Ms. Joiner’s students) and control (i.e., all other Algebra I students) identified. The Algebra I EOC assessment measures student achievement as defined within the local state’s curriculum standards. The assessment is given in one 160 min session with a 10 min break after the first 80 min. There are multiple forms of the assessment, with a maximum of 65 items on each test form. Each form of the assessment includes 35–40 multiple-choice and 20–25 fill-in response items. Students receive a scale score that ranges from 325 to 475 [44].

2.3.2. Quadratic Equation Lesson Recordings

As part of the PL program, all teachers were video recorded several times across the two-year program. For Ms. Joiner, we recorded a five-day unit of instruction related to quadratic equations in the spring of the second year prior to the students in the school taking the Algebra I EOC examination. Each lesson was 90 min in duration. Day 1 instruction consisted of an inquiry-based lesson during which students examined the effects of changes in the leading coefficient and constant terms of a quadratic equation on the size, shape, and position of the dynamically-linked parabola. Days 2 and 3 developed the concept of zeros of a quadratic equation by exploring the relationship between the x-intercepts of a parabola and the x-intercepts of the two linear equations that resulted in the quadratic equation when multiplied. The students were able to manipulate the slope and constant terms of the linear equations, resulting in changes to the quadratic equation that resulted from taking the product of these two linear expressions and its dynamically-linked parabola. On day 4, Ms. Joiner engaged her students in further examination of the zeros of a quadratic equation as well as other concepts related to quadratic equations and their graphical representations. Finally, on day 5, Ms. Joiner reviewed the material from the previous days and summarized the intended learning without using the graphing calculator.

2.3.3. Member Check Interviews

The research team met with Ms. Joiner to conduct member checking to ensure the accuracy of our interpretations. This interview was conducted during four 90 min sessions. During the first session, we collected demographic information as well as responses to questions related to Ms. Joiner’s beliefs about effective mathematics teaching and learning. During the first two sessions, we presented Ms. Joiner with selected video clips from her recorded class sessions and asked for her interpretation of these segments. During the third and fourth sessions, we provided Ms. Joiner with our interpretations of her classroom instruction, and she commented on the accuracy of our interpretations.

2.4. Data Analysis

We conducted two analyses to respond to our two research questions. First, we conducted a two-sample t-test to compare means on the Algebra I EOC examination total scale score and subscale scores for the comparison and the treatment groups. Second, we utilized thematic analysis methods to explore the qualitative data from the classroom observation videos for Ms. Joiner’s five quadratic equation lessons. Qualitative analysis is an iterative process that typically involves multiple stages including deep immersion and multiple reviews of the data, generating initial codes, creating themes from codes, peer debriefing, triangulation, and member checking [45,46]. Marshall and Rossman maintain that the qualitative analysis process varies depending upon different researchers’ responses to the data and research questions [45]. During the initial read of the transcripts, the researchers created analytic memos to capture the initial impressions of possible emergent themes. After reading and re-reading the data set, codes were created by each researcher, and then the codes were cross-checked and triangulated during researcher meetings to help illuminate broader themes. The codes were re-examined through deep exposure to the video recordings of the lessons and peer debriefing in numerous meetings amongst the researchers, and then themes were finalized to produce the assertions from the consensus of the iterative data analysis process (cf. [45,47]). Finally, the themes were reviewed with Ms. Joiner during member checking interviews to determine whether our analyses were accurate representations of her work.

3. Results

The results of the study will be presented by the research question. First, we will discuss the outcomes of the statistical analysis, comparing the treatment versus the comparison group achievement on the Algebra I EOC examination. Second, we will present the findings from the qualitative analysis of the video-recorded lessons within one teacher’s classroom to explore the instructional practices that potentially led to differences in student performance on the Algebra I EOC examination.

3.1. Student Achievement

The mean Algebra I EOC scale score for treatment group students (M = 395.09, SD = 25.883) was significantly higher than the comparison group (M = 385.26, SD = 24.081, t = 2.93, p = 0.004) (

Table 1. School A: Algebra I EOC mean scores.

									95% Confidence Interval
		N	Mean	SD	t	df	Sig. (2-Tailed)	Cohen’s d	Lower	Upper
Algebra EOC	Comparison	171	385.26	24.081	2.93	48	0.004	0.399	0.129	0.667
	Treatment	79	395.09	25.883
Functions, Linear Equations, and Inequalities (total items = 31)	Comparison	171	9.06	4.629	3.14	48	0.002	0.427	0.158	0.696
	Treatment	79	11.19	5.655
Polynomials (total items = 10)	Comparison	171	2.32	1.611	3.62	48	<0.001	0.492	0.221	0.762
	Treatment	79	3.23	2.264
Rationals, Radicals, Quadratics, and Discrete Math (total items = 13)	Comparison	171	4.49	2.065	1.94	48	0.054	0.263	−0.05	0.531
	Treatment	79	5.05	2.314

NOTE: EOC = End of Course; N = the number of participants in each group; SD = the standard deviation; t = the t-statistic calculated for the comparison of treatment and comparison groups; df = degrees of freedom; Sig. (2-tailed) = the significance level of the t-statistic; Cohen’s d = the estimated effect size for each comparison; Lower and Upper = the 95% confidence intervals for each of the effect sizes.

). In addition, there were statistically significant differences for two subscales, Functions, Linear Equations, and Inequalities (t = 3.14, p = 0.002) and Polynomials (t = 3.62, p < 0.001), and the third subscale, Rationals, Radicals, Quadratics, and Discrete Mathematics, which approached significance (t = 1.94, p = 0.054). The impact of CCT on academic achievement in algebra was generally positive across the subscales, with an overall effect size of 0.399 (95% CI = [0.129, 0.667]; see Table 1). Among all three subscales, the largest effect size reflected the difference in scores for Polynomials (dPolynomials = 0.492) followed by Functions, Linear Equations and Inequalities (dFLEI = 0.427), and Rationals, Radicals, Quadratics, and Discrete Mathematics (dRRQDM = 0.263); these average effect sizes are all statistically significant, except for Rationals, Radicals, Quadratics, and Discrete Mathematics. Therefore, since Ms. Joiner was the only teacher in her school who used the technology with her students in her Algebra I classroom at the school, we examined her classroom practices during a five-day quadratic equation unit in depth to explore the classroom practices that may have led to these achievement differences.

3.2. Classroom Instruction Using CCT

Based upon the statistical outcomes of Ms. Joiner’s students’ achievement in Algebra I as compared to all the other students in her school, our team conducted a deep analysis of five of her video-recorded class sessions focused on the concept of quadratic equations. This analysis provided evidence of the context for knowledge construction within Mr. Joiner’s classroom as she supported her students’ learning with the CCT and dynamic graphing calculator. Ms. Joiner’s careful curation of learning affordances, or sequential experiences, systematically supported student exploration of mathematics concepts, leading to knowledge construction. The most prominent theme that arose from the data was Ms. Joiner’s establishment of norms and support for noticing. Ms. Joiner took ample time at the beginning of an activity and throughout the activity to conduct a task analysis that slowed down the students’ interaction with the dynamically-linked equations and guided their noticing. She often asked students to look at representations on their calculators or the projection screen and specifically used the word ‘notice’ in discussions of their observations. It was the norm in this class that students were to develop conjectures based on their noticing of the changes that resulted from their manipulations. Ms. Joiner’s classroom context and lesson mini cycles were essential components upon which lessons were constructed. Before we fully delineate Ms. Joiner’s learning affordances to facilitate student noticing, we describe the foundational components of the classroom context and the lesson mini cycles in the following sections. Following this discussion of the classroom and lesson structure, which supported noticing, we explicate the themes that emerged to support noticing, including building connections to prior knowledge, conducting task analysis to focus student noticing, developing conjectures based on student manipulation of mathematical objects, and summarizing the students’ observations and conjectures.

3.2.1. Classroom Context

The classroom emotional climate was established clearly for students. The posters on the walls indicated the expectations for learning, which was further established through the teacher’s focus on learning. The teacher clearly communicated high expectations of all students; Ms. Joiner messaged that they were all in the classroom to learn, which was further supported through her strong rapport with the students. These expectations were communicated in the form of Ms. Joiner’s frequent reminders of the task that students were to accomplish, the expected progress across the lesson, and the skills they possessed to accomplish these tasks. This set the expectation that all students were to be engaged and moving forward. There was also the expectation that students would develop conjectures and hypotheses about the mathematics content from their mathematical behaviors. Ms. Joiner was deliberate in her use of the class time, leaving the students little or no downtime. During these lessons, students were seated in groups at rectangular tables to encourage collaboration. Ms. Joiner expected students to engage with the learning object individually, then collaboratively through talking with peers, and finally as a whole group. Ms. Joiner created this pattern of mini cycles of learning across the 90-minute class session to facilitate high engagement.

3.2.2. Consistent Instructional Mini Cycles

The learning affordances in the classroom were provided within consistent lesson structures. First, the class was conducted in instructional cycles that supported students in their engagement. Each class started with a whole-group warm-up activity, which was presented with the goal of activating prior knowledge. Following the warm-up activity, Ms. Joiner engaged the learners in a task analysis, which emphasized the aspects of the activity on which students should focus their noticing. The second consistent feature of these lessons was the engagement of students in individual thinking, pair or group collaboration, and then whole-group discussion. These groupings provided the social context in which students developed or refined conjectures. Third, the teacher curated the lessons such that there was a repetition of similar activities supporting student conjectures, summarizing multiple times in different formats. These cycles of learning were repeated multiple times throughout the 90-minute period.

3.2.3. Focus on Student Noticing

The main argument we put forth in this analysis is that one reason Ms. Joiner’s students outperformed their peers on the Algebra I EOC examination was the explicit focus on noticing, leading to student-generated conjectures. The teacher set up and conducted the class to support students’ noticing of the effects of their manipulation of mathematical objects using dynamic technology linked to a CCT system. The outcomes of this noticing were conjectures related to the mathematical objects that students manipulated using the dynamic software. The teacher explicitly drew students’ attention to critical elements of the class activity that were devised to support knowledge construction through students’ behaviors with the educational technology. A search of the transcripts for “notic*” yielded 63 occurrences of the term across 5 lessons with 20 of these occurrences during the first day of the five-day unit. Thus, noticing was a critical component of Ms. Joiner’s instructional strategy. Below we discuss several components of this work to support student noticing, including connections to prior knowledge, task analysis, and carefully curated lessons that supported noticing. The students’ noticing was codified in the conjectures that they developed individually and in groups as well as in the summaries of the classroom engagement in several ways. Each of these aspects of Ms. Joiner’s instruction will be explored in the following sections.

Connections to Prior Knowledge

The lessons during each day of the five-day unit of instruction began with a warm-up activity that explicitly elevated students’ prior knowledge upon which they were to construct their new knowledge. These connections were intended to support students’ noticing in relation to the new content. For example, the teacher drew students’ attention to the similar meanings of the leading coefficient of linear equations and quadratic equations, which are both amplifiers (e.g., slope of a line) within their respective equations, several times. A search of the first day’s transcript (21 February) for the word “line” resulted in a total of 23 occurrences despite the focus on quadratic equations. In the following excerpt, we see an example of how Ms. Joiner related the slope of a line and the leading coefficient of the quadratic term:

Ms. J

Ok, so you used the word slope; what do you mean by slope?

S3     

Like the steepness.

Ms. J

Steepness, I totally agree. We can kind of compare this to slope, right? Remember slope was rate of change, how fast something was growing, and the higher the slope we had, the steeper it was, the more up it was. So, you can definitely use that connection. We don’t necessarily have a slope though in a quadratic; it’s not the same as it was in a line but you can definitely use that connection with how it’s growing.

We can see from this example that Ms. Joiner was encouraging and accepting of the ways that the student could contribute to building conceptual understanding that would naturally be an outgrowth of connecting with their prior knowledge and experiences.

Another example of how the teacher created tasks to systematically activate students’ prior knowledge occurred during the warm-up activity on the second day. In this activity, the students were given a handout and asked to match graphs with their equations. The examples were systematically varied to activate prior knowledge about the “a” and “c” values, which were the focus of the previous day’s lesson. Specifically, the graphs and equations were presented in pairs with the parameters systematically varied as shown in

Table 2. Example pairs of warm-up problems.

Example Pairs	Relation of “a” Values across Pairs	Relation of “c” Values across Pairs
(1) and (2)	different	same
(2) and (3)	same	different
(3) and (4)	different	same
(4) and (5)	same	different

. Students were directed to provide two reasons for each match of the graphs and equations.

Focusing students’ noticing on similarities and differences between mathematical objects and discussing these similarities and differences during whole-class discourse supported students in building connections between concepts.

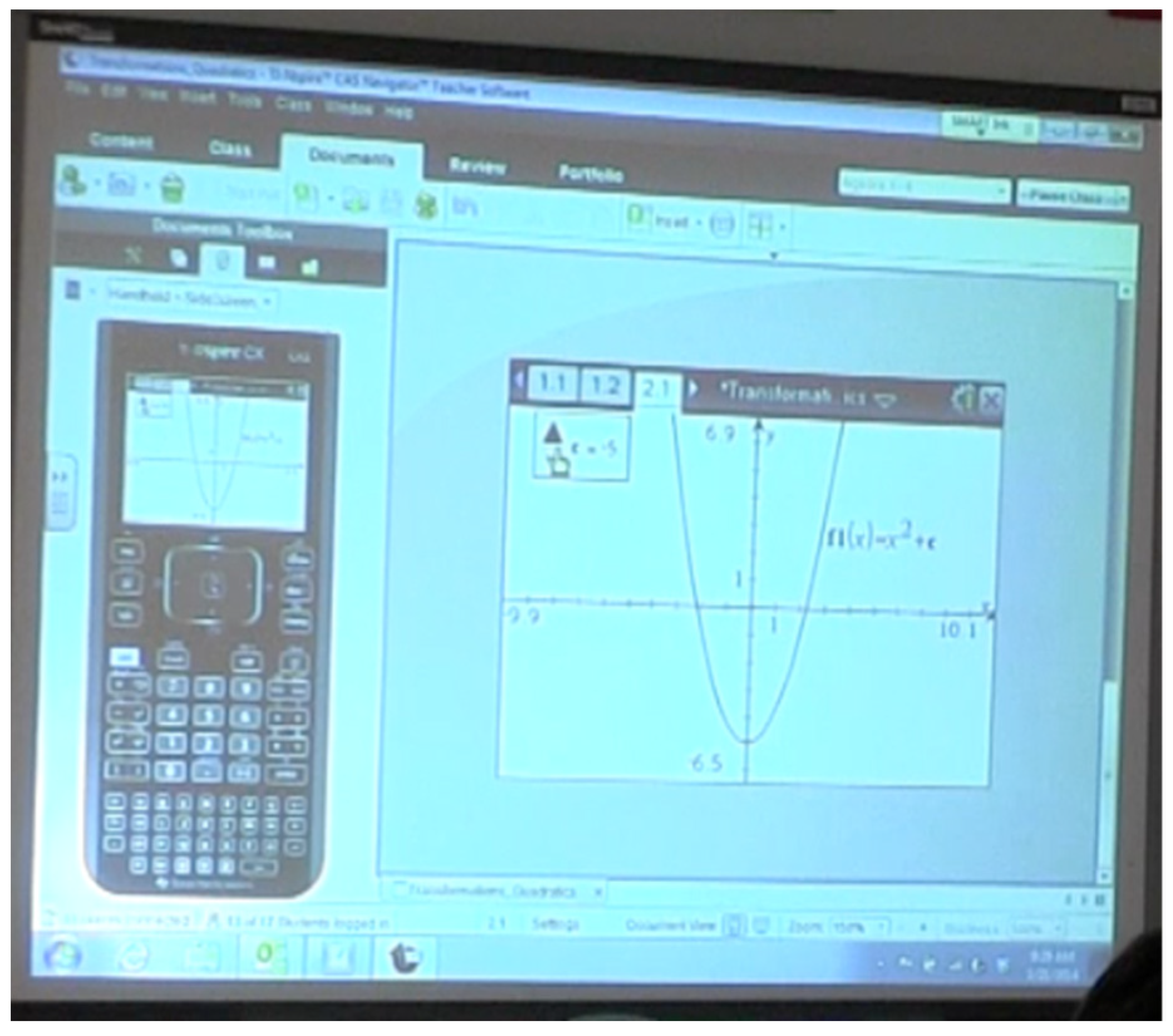
Task Analysis to Focus Student Noticing

Following the warm-up activity, Ms. Joiner typically conducted a whole-class task analysis. Before she sent the students the activity document that was the focus of the day’s learning, she projected the dynamically-linked equation and associated parabola from her computer. Ms. Joiner engaged the students in a discussion of the features of the activity to which they were to attend. This deliberate slowing of the students’ interactions with the activity document enabled their noticing of the relationship between their behaviors and changes in the mathematical objects leading to conjectures. Figure 1 depicts the calculator screen from the first day of the unit [13]. In this figure, we see the pointer (the hand just below 1.1 in the image) that indicates the slider that students manipulated to change the a-value of the quadratic equation.

Students were instructed to pause and notice the changes in the graphical representation at each of the values on the accompanying worksheet. In the following quote, Ms. Joiner provided explicit instructions to draw students attention to notice particular features of the CCT system and the quadratic equation:

Ms. J

So you’re going to use the slider to change the value of the parameter variable and so if you notice right here there’s these up and down arrows? You’re just going to use your mouse to click on them up or down. Don’t do it yet though because it tells you exactly what values to find and notice what letter does it say right there?

S    

A.

Ms. J

A, so what part of this are we changing?

S    

The A.

Ms. J

The A, just the A, only the coefficient of the X squared. That’s what you’re changing right now. Alright so you’re going to move it up and down. Look where it says step two; it tells you the values it wants you to change it to. It wants you to move it to five, one, zero point two, zero, negative zero point two, negative one, and negative five. Do you all see where it says it there? Those are the exact ones it wants you to move it to. You could obviously on the way see different values, but when you get to those values, I want you to pause and really look at it. The first thing you’re going to do is answer those first three questions, numbers one through three and then stop. So go ahead and manipulate that graph and write down what you observed for those three questions. You can work together. You can look at it individually and then share. It’s up to you. I’m going to give you a couple minutes to go through those first three. (21 February, lines 204–221)

Ms. Joiner provided additional explanation later during the activity in the following way:

Ms. J

So you’re going to change these values and something’s going to happen to the graph and you’re going to notice it and then after you change it to those… I want you to go through all those values; there’s a reason they have all those numbers on it and then I want you to answer these three questions based on what you’re noticing is happening. (21 February, lines 236–239)

In Figure 2, we see the projection of the teacher’s computer screen emulating the students’ graphing calculator during the second day of the unit (25 February) [14]. The pointer (arrow, center of screen) indicates one of the four sliders that the students were to manipulate to change the slope or intercept of the linear equations. The graphs included two lines and the parabola that resulted from the product of the linear equations (Figure 2). Each of the equations and their associated graphs were dynamically linked such that changes in the linear equations resulted in changes in the quadratic equation and the associated parabola. Each of the equations and associated graphs were color coded: the quadratic equation and its parabola were red; the two linear equations whose product resulted in the quadratic equation, and their associated graphs were blue and green. These colors were used consistently throughout the lessons to focus students’ noticing on the critical elements of the mathematical task.

In the following excerpt, we see that Ms. Joiner led the task analysis of this activity initially without the students having their calculators in hand to collectively orient the students’ noticing:

Ms. J

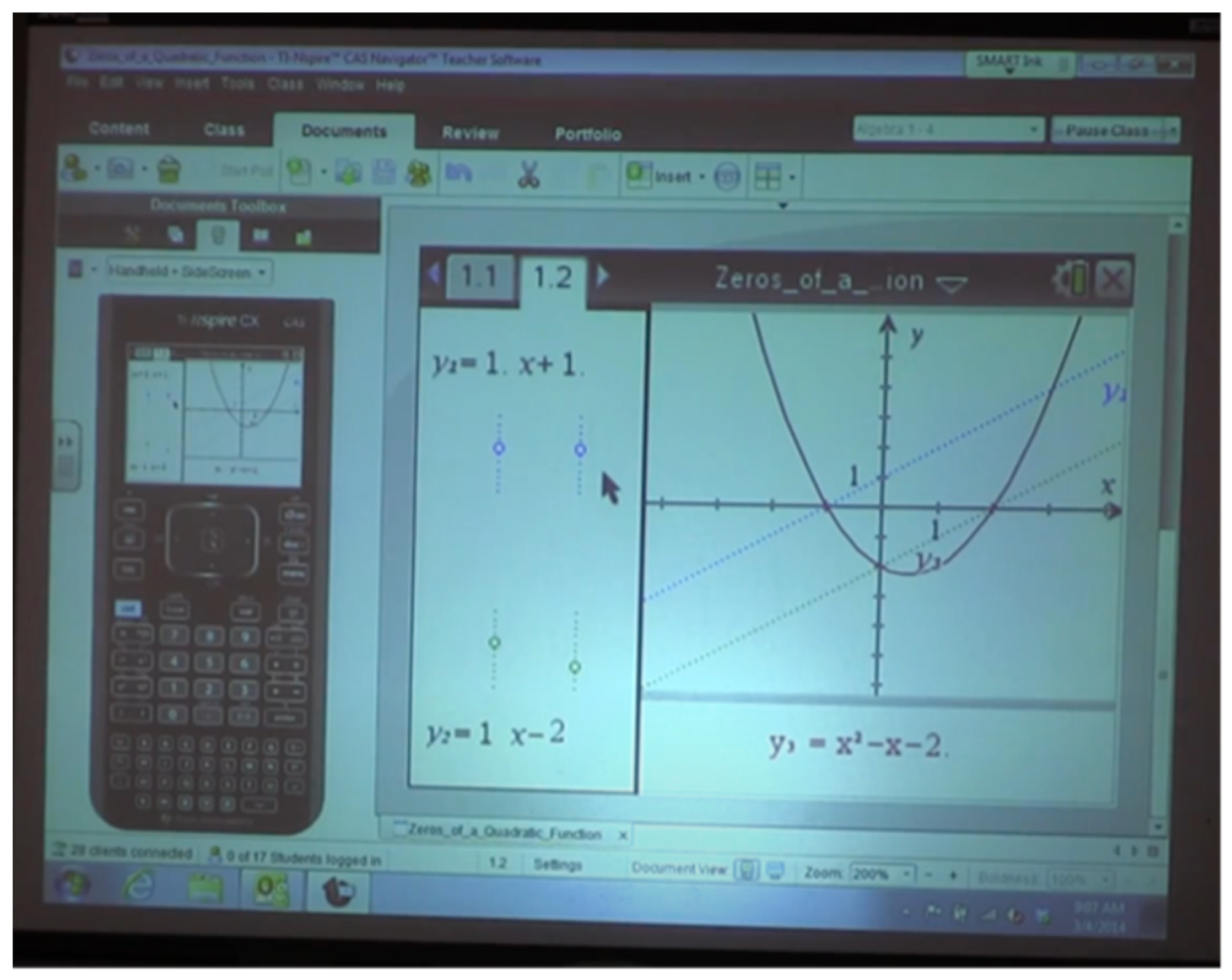
While we’re making sure we get on, let me pass out the sheet you’re going to be writing on today.… You can just set your calculators to the side once you log on because I’m not going to send you anything yet.… I’m going to go ahead and pause the class [within the CCT software] because you don’t need your calculator right now and I want you to look up here. So, this is the document we’re going to be working with; it’s only one screen today, only one screen, and what I want you to do right now on your paper where it says “What do you notice about this graph?”, so it’s number one. I want you to answer that question. Write a couple things that you notice only about the graph. So, we’re only focusing on this part right here. So, write what you see in colors, in shapes, use mathematical terms … however you would describe what you see in this blue box right here. We’re going just [to] write down what we see first before we start talking about it and there’s no right or wrong answer here, just whatever you see. Only on the graph, what do you see there? There’s a lot of things happening. I can see five, six things I would write down. You can talk about the colors, the shapes of the graph… (25 February, lines 369–385)

In the following excerpt, Ms. Joiner then orchestrated an analysis of the task with the students to ensure that they understood the relationships among the elements of the activity document.

Ms. J

What color is this parabola?

S1     

Red.

Ms. J

Red; this is important. Everything we’re doing today that’s red is going to have to do with that parabola. So, I see a parabola. Is there anything else that I see on here? Somebody else, [student]?

S2     

Dashed lines.

Ms. J

Dashed lines and you said it was going through what?

S2     

The parabola.

Ms. J

Going through the parabola. And what color are these lines?

S2     

Blue and green.

Ms. J

Blue and green, so I got blue and green. I really like that you said it’s going through the parabola. Did anybody see where these dashed lines are going through the parabola? (25 February, lines 425–436)

By engaging students in this task analysis, the teacher created the context in which students were able to explore the mathematical affordances provided in the activity document to support their learning. In terms of Gee’s notion of opportunity to learn [11], the teacher created the context and the opportunity for students to engage with the learning opportunities that were carefully constructed within the lesson. With the knowledge of the aspects of the activity to which they were to attend, students were afforded the time to explore one part of the activity at a time. In the excerpts above, Ms. Joiner slowed the students down, specifically asked them to pay attention to the step-by-step directions, and instructed them to make observations.

Developing Conjectures

The task analysis allowed for deep student noticing, which was in the service of building conjectures based on their manipulations of the dynamically-linked equations and changes to the associated graphs. First, students engaged with the activity individually, then compared observations with students in their group. The carefully orchestrated questions within the student documents [13,14] led students to construct conjectures, and Ms. Joiner’s focus on noticing was critical to this process. For example, on the first day of the unit on quadratic equations and parabolas, students first manipulated the coefficient of the quadratic term (i.e., the “a” value in a quadratic equation in standard form) in a systematic way. The students were asked to (a) state their observations in their own words, (b) state a conjecture about the effect of the “a” value on the graph opening (i.e., up or down), and (c) state a conjecture about the effect of the “a” value on the shape of the graph. Following a whole-class discussion of the students’ responses to these three questions for the “a” value, they manipulated the “c” value (i.e., constant term of the quadratic equation) and responded to the same three questions. This second manipulation of the slider for the “c” value was the students’ opportunity to emulate the behaviors and thinking that were modeled by Ms. Joiner during the first part of the lesson.

The questions that the teacher asked the students as she visited with them during individual or group/pair work supported them to make observations by pressing students toward pattern recognition. For example, in the lesson on the first day of the unit (21 February), students were asked to systematically manipulate the value of the coefficient of the quadratic term and the constant term and discover the effect of changes to the quadratic term coefficient in terms of the size, shape, and position of the dynamically-linked parabola in their own words. Following the student manipulation of the coefficient of the “a” and “c” values of the quadratic equation, in the following excerpt, Ms. Joiner asked the students to develop three conjectures in collaborative groups.

Ms. J

What you’re going to do is flip that paper on the back, and I want you to write three conjectures. Anybody know what a conjecture is in math or in science, really anything?

S4     

Never heard of it.

Ms. J

Never heard of it? So, conjecture is kind of like a mathematical hypothesis based on what you have observed. So, based on what you’ve seen so far about a quadratic graph and about A and C I want you to write me three statements, and you can use stuff that you wrote on the other side—any other observations you have. So, I want three statements about graphs of quadratics right now and I want you to talk together, so I kind of want you to come up with these together. I want to hear all you guys talking; share out ideas, what’s the first thing you think of? (21 February, lines 494–504)

Throughout these activities, students were required to provide two reasons as rationale for their conjectures. In addition, the teacher modeled conjectures by revising them to make them more mathematically accurate or stated more precisely. Finally, the teacher pressed students to reveal their reasoning related to these conjectures through questions that served a couple of goals. At times, the teachers’ questions seemed to support students to make connections and build conjectures. Other questions simply sought clarification and therefore resulted in greater clarity in students’ conjectures. Finally, many of her questions were requests for an explanation for students’ responses that focused on reasoning and honed the students’ understanding.

Summaries

The class sessions ended with a summary of the day’s learning, which was explicitly drawn from the student experiences and the conjectures they forwarded from these activities. To co-construct these summaries with her students, Ms. Joiner circulated around the room while students were working, provided individual and group support, and noticed student work that could be used to focus the whole-group discussion. She brought examples and counterexamples from her observations of individuals and pair work to the whole class for discussion that elevated the students’ noticing to be objects of classroom discourse. She used what she heard in the individual and group times to draw out important mathematical points and asked specific students to describe what she had witnessed within their work.

During these summaries, Ms. Joiner refined students’ language as appropriate and lent organization to the summary through her questions and direction of the discussion. Students’ noticings became the objects of whole-classroom discussion as the teacher brought up interesting cases, errors, and mishaps she noticed while visiting with students. She carefully allowed for students’ voice and even mispronounced words (e.g., vortex versus vertex) by eliciting and celebrating their ways of explaining the mathematical ideas they discovered but then carefully and gingerly correcting misstatements. We can see how she artfully brought her own noticings from student discussions to the whole-class discussion in the following excerpts:

Ms. J

Go ahead and stop where you are. As I walked around, I saw a lot of good reasons, really good observations, and I heard some really good answers especially over here at this table. You guys weren’t agreeing very much? (21 February, lines 285–287)

Ms. J

Ok I heard some really interesting things and a lot of really good observations and so tell me… let’s look at this first. What is happening at this vertex, this bottom point… (21 February, lines 460–462)

During these whole-class discussions, Ms. Joiner developed the students’ understanding of mathematics concepts by eliciting their conjectures and their justification for their mathematical conceptions that resulted from their manipulation of the dynamic software. The students and teacher co-constructed the summary of the mathematics concepts. Students stated their conjectures followed by two evidentiary statements. The students and the teacher then co-constructed notes to formalize the mathematics concepts. Throughout this process, Ms. Joiner allowed for student expression of mathematics and honored and celebrated student responses to create a safe environment to explore.

4. Discussion

The significantly higher Algebra I scores for students in Ms. Joiner’s classes and the themes found in her instruction are important for adding to several bodies of literature. These findings support and extend research related to the efficacy of CCT in mathematics [15,16,17,18], Gee’s notions of opportunity to learn [11], and the importance of noticing for developing mathematical knowledge [9].

4.1. Efficacy of Classroom Connectivity Technology

As described earlier, there is a significant history of research that has supported the efficacy of ARS for engaging students in the learning process [25,26,27,28,29,30] as well as student achievement in Algebra I [15,16,17,18]. The present study extends the CCMS project and its findings by showing significant differences on an Algebra I EOC assessment in one school. This school was part of a larger study but became important because Ms. Joiner was the only teacher who taught her students Algebra I. Thus, this study emerged as a natural quasi-experiment within the larger study. As such, it confirmed these earlier findings and led to a more nuanced and in-depth examination of Ms. Joiner’s recorded instruction.

4.2. Gee’s Theory in Action

As described by Gee, it is the teacher’s role to align the learning affordances within a lesson with the students’ potential for acting upon these affordances [11]. Across the two-year PL program, the first author observed many classes in which students would manipulate an equation rapidly without noticing the effect of their behaviors on the dynamically-linked graph. Ms. Joiner’s emphasis on noticing the relationship between their mathematical behaviors and the impact on the mathematical learning object was significant. She helped students utilize the affordances in the CCT system through her methodical lesson mini cycles. She ensured that students were oriented to the various aspects of the CCT system, and she intentionally and slowly focused them on how to engage with the mathematical objects and tasks in the graphing calculators. Students were supported to notice the impact of their mathematical behaviors and to learn mathematics concepts through these behaviors, which is essential when we ask students to use dynamic calculator technology and to build their learning through the manipulation of mathematical objects. From this analysis, we argue that one mechanism for Ms. Joiner’s students’ success was her explicit and careful support for her students to engage their effectivities to act on the affordances within these TI-developed dynamic mathematics tasks [13,14]. This study is unique in its application of Gee’s theory in relation to learning within an Algebra I mathematics context with a CCT system. Future research should continue to examine cases of effective technology use to support student learning such that more teachers may align the affordances of their classroom with the learning potential of their students.

4.3. Using Noticing to Maximize the CCT Affordances

Prior researchers have found that the use of CCT systems with dynamic graphing calculators enhances learning and engagement [15,16,17,18]. Our findings build upon these prior studies by emphasizing the importance of Ms. Joiner’s use of noticing as a central instructional practice to effectively utilize the affordances of the CCT system. As described by Lobato [9], Ms. Joiner consistently worked to create centers of focus for students to attend to specific features of the task, helping the students to pay attention to singular components of the activities. Ms. Joiner curated consistent instructional mini cycles with each lesson beginning with a warm-up to activate prior knowledge followed by careful task analysis that created the context for noticing. Further embodying Lobato’s concepts with the intentional selection and interpretation of mathematics concepts individually and socially [9], students were then asked to explore the mathematical object individually followed by pair or group think, and then whole-group discussion of their conjectures. Students also engaged in consistent activities with similar requests for conjectures and justifications for their conjectures. All these elements, we posit, allowed for the noticing necessary for knowledge construction based on students’ behaviors. Finally, Ms. Joiner co-constructed a summary with her students immediately following an activity by eliciting student responses to the questions on the TI student activity sheet (i.e., [13,14]), by developing conjectures based on these responses, and finally by leading the students to record essential concepts from the session as class notes that all students recorded. Ms. Joiner’s classroom instruction examples provide strong evidence for the potential of classroom technology use through noticing and discussion. Future studies should further explore the various components and strategies involved in focusing students’ attention through noticing in a mathematics classroom with CCT systems.

The focus of this study deeply explored the emergent theme of Ms. Joiner’s use of noticing to maximize the affordances of the dynamic CCT system. Incidentally, another emergent theme that arose from the data analysis was Ms. Joiner’s warm and inclusive classroom context. We hypothesize that her classroom context practices created the foundation for noticing that led to the significant difference in Algebra I EOC scores. In addition to her warmth, Ms. Joiner was explicit in her high expectations for all student learning and engagement. Additionally, the classroom was designed for collaboration following individual activities. We plan to further analyze the relationship between contextual variables of Ms. Joiner’s instructional practice such as classroom climate and the ways that they supported her to develop a culture of noticing in a future study.

5. Conclusions

Too often we put classroom technology in front of students, and even mathematical manipulative materials, and we expect the students to glean knowledge from their actions with technology or manipulative materials. We, educators at all levels, need to support students through the social negotiation of meaning of their manipulations of the mathematical objects. Instead of expecting them to glean knowledge from their actions with mathematical objects, we should learn from Ms. Joiner’s lessons that students’ need to be intentionally focused on aspects of the learning object to which they need to attend as they use the technology or manipulative material to learn a mathematical concept. Like Ms. Joiner, we should then ask students to explore the learning object individually and then to discuss their learning in pairs and as part of whole-group discussion. Through these classroom affordances, students are provided the opportunity to socially construct and negotiate their understandings of their explorations of the mathematical objects. Learning requires social interaction and discussion. Ms. Joiner’s lessons exemplified what Gee [11] and Lobato [9] emphasized as ways of facilitating learning for maximal student discovery and social construction of mathematical knowledge.