Generalized Accelerated Failure Time Models for Recurrent Events
Abstract
:1. Introduction
2. Model
2.1. Accelerated Recurrent Events Time Model
- (C1)
- is non-singular;
- (C2)
- for all .Then,where
2.2. The Recurrent Events Model
2.3. The Proposed Estimation Procedure
2.4. Asymptotic Properties
- (C1’)
- Z and are bounded;
- (C2’)
- (a) is bounded and continuous at , as well as uniform in Z, and (b) is a Lipschitz function of u;
- (C3’)
- (a) each component of is uniformly bound on , where is a neighborhood containing , (b) and is positive definite;
- (C4’)
- for any , where denotes the minimum eigenvalue of a matrix.
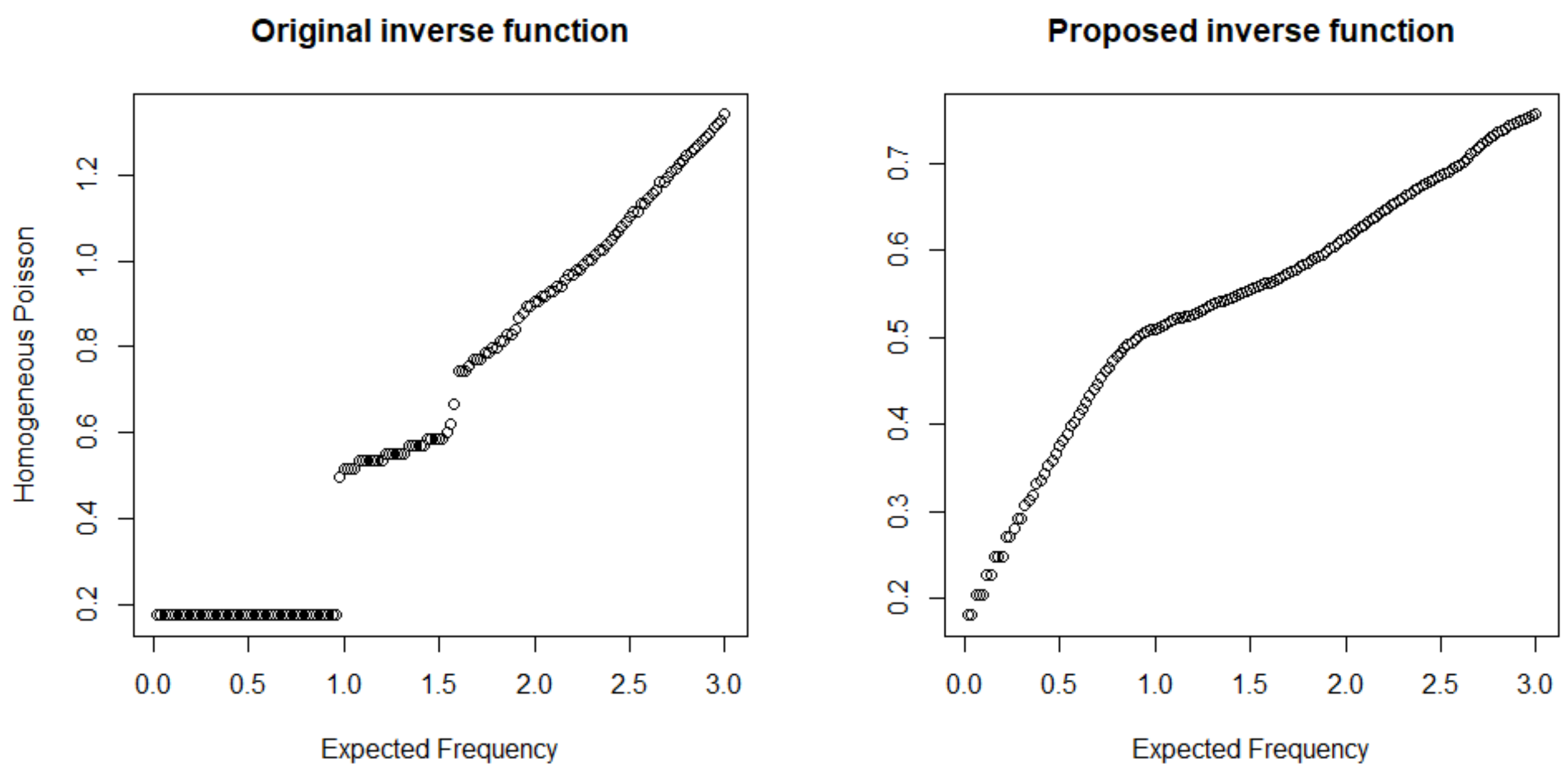
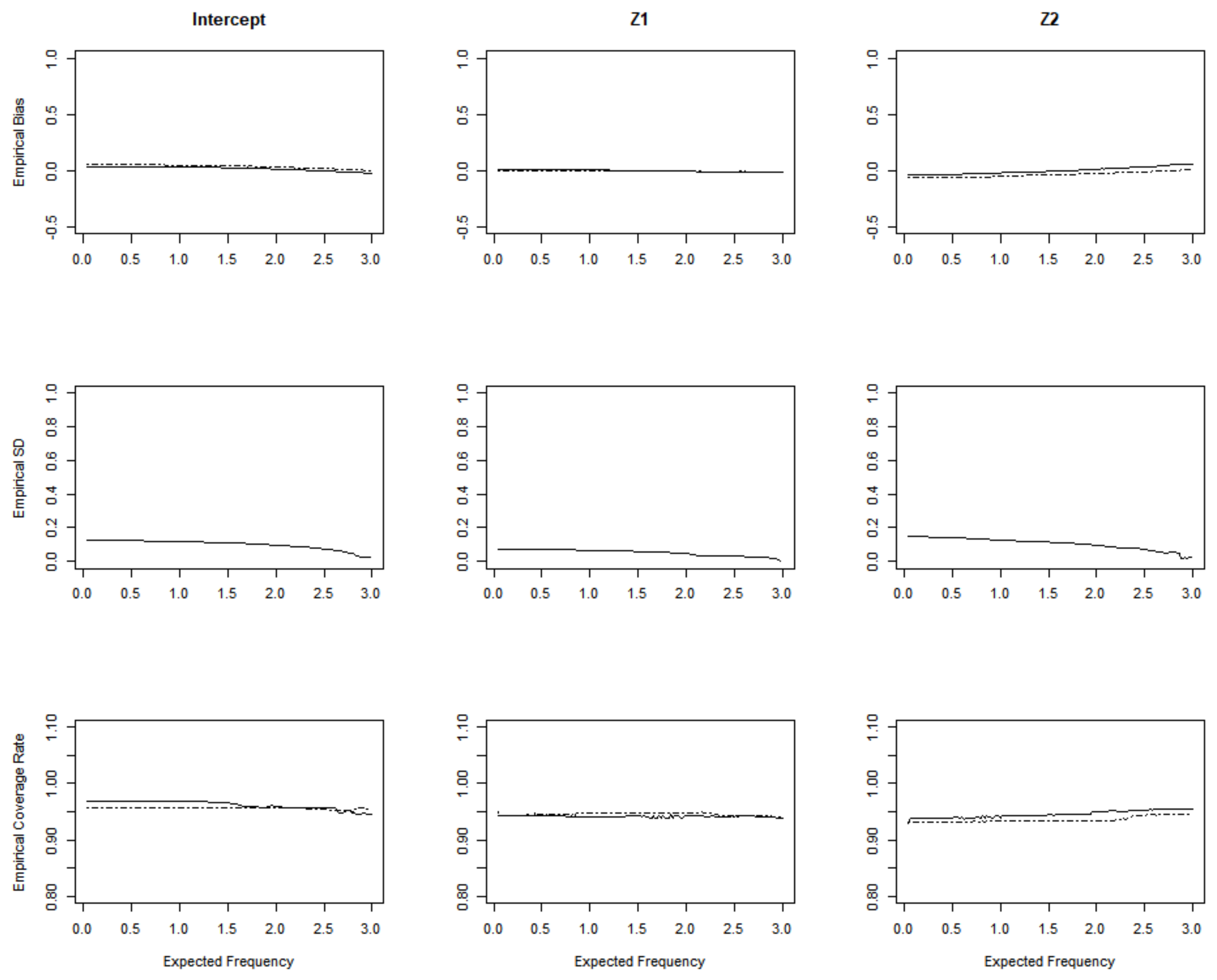
3. Simulation Studies
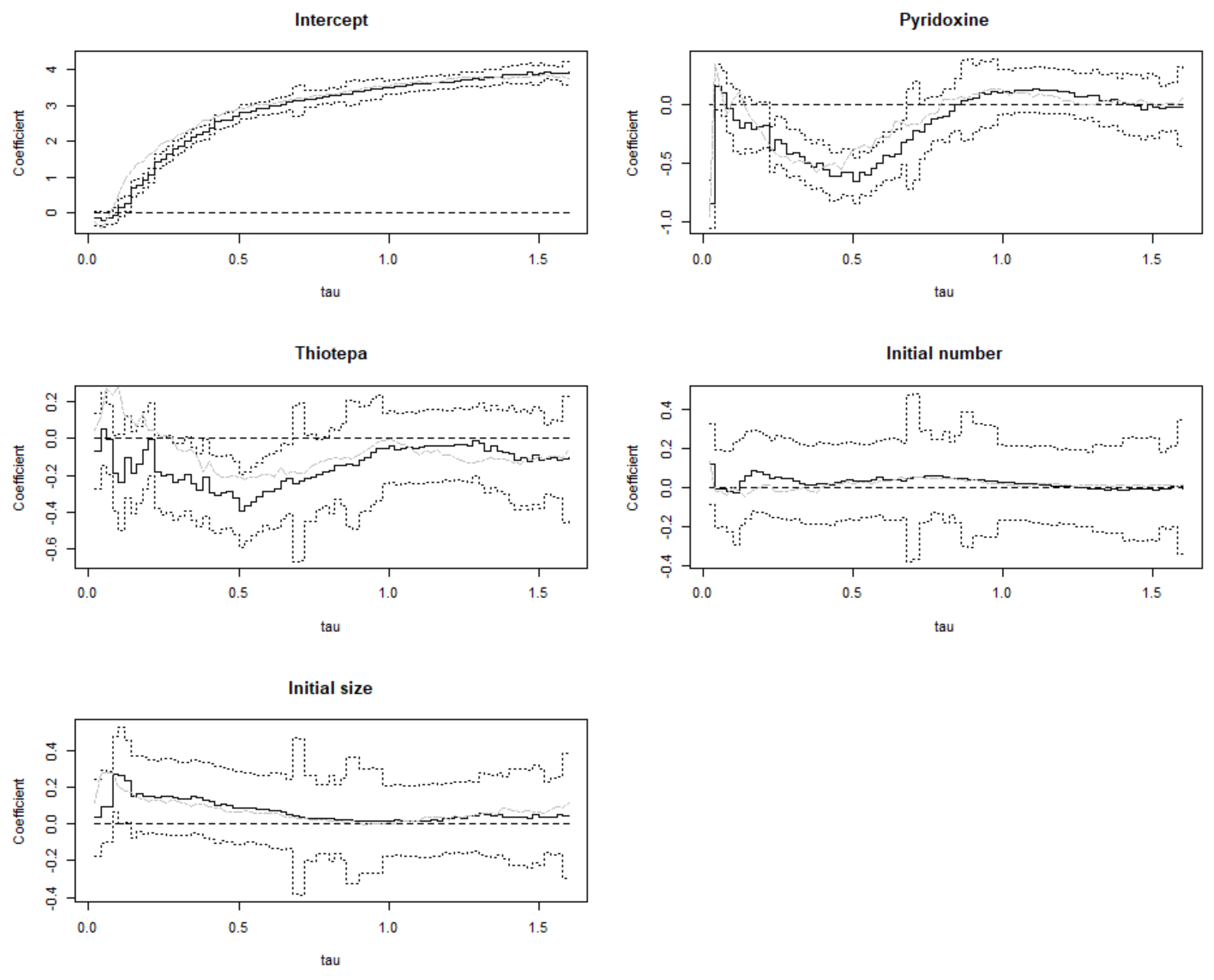
4. Application to the Bladder Tumor Studies
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
- when and ,
- when and ,
- when , since is the unique value that minimizesconsidering the monotonicity of , therefore . By the non-singularity of ,
Recurrent Event Setting
References
- Nelson, W. Hazard plotting for incomplete failure data. J. Qual. Technol. 1969, 1, 27–52. [Google Scholar] [CrossRef]
- Altshuler, B. Theory for the measurement of competing risks in animal experiments. Math. Biosci. 1970, 6, 1–11. [Google Scholar] [CrossRef]
- Lawless, J.F. Regression methods for Poisson process data. J. Am. Stat. Assoc. 1987, 82, 808–815. [Google Scholar] [CrossRef]
- Lin, D.Y.; Wei, L.J.; Yang, I.; Ying, Z. Semiparametric regression for the mean and rate functions of recurrent events. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2000, 62, 711–730. [Google Scholar] [CrossRef] [Green Version]
- Peng, L.; Huang, Y. Survival analysis with quantile regression models. J. Am. Stat. Assoc. 2008, 103, 637–649. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G., Jr. Regression quantiles. Econom. J. Econom. Soc. 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Powell, J.L. Censored regression quantiles. J. Econom. 1986, 32, 143–155. [Google Scholar] [CrossRef]
- Sun, X.; Peng, L.; Huang, Y.; Lai, H.J. Generalizing quantile regression for counting processes with applications to recurrent events. J. Am. Stat. Assoc. 2016, 111, 145–156. [Google Scholar] [CrossRef]
- Wang, H.J.; Wang, L. Locally weighted censored quantile regression. J. Am. Stat. Assoc. 2009, 104, 1117–1128. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.O.; Yang, Y. Semiparametric approach to a random effects quantile regression model. J. Am. Stat. Assoc. 2011, 106, 1405–1417. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andersen, P.K.; Gill, R.D. Cox’s regression model for counting processes: A large sample study. Ann. Stat. 1982, 10, 1100–1120. [Google Scholar] [CrossRef]
- Cox, D.R. Regression models and life-tables. J. R. Stat. Soc. Ser. B (Methodol.) 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Huang, Y.; Peng, L. Accelerated recurrence time models. Scand. J. Stat. 2009, 36, 636–648. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fygenson, M.; Ritov, Y. Monotone estimating equations for censored data. Ann. Stat. 1994, 22, 732–746. [Google Scholar] [CrossRef]
- Byar, D. The veterans administration study of chemoprophylaxis for recurrent stage i bladder tumours: Comparisons of placebo, pyridoxine and topical thiotepa. In Bladder Tumors and Other Topics in Urological Oncology; Springer: Berlin/Heidelberg, Germany, 1980; pp. 363–370. [Google Scholar]
- Vaart, A.V.D.; Wellner, J.A. Weak convergence and empirical processes with applications to statistics. J. R. Stat. Soc.-Ser. A Stat. Soc. 1997, 160, 596–608. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, X.; Xu, J. Generalized Accelerated Failure Time Models for Recurrent Events. Mathematics 2022, 10, 2662. https://doi.org/10.3390/math10152662
Wen X, Xu J. Generalized Accelerated Failure Time Models for Recurrent Events. Mathematics. 2022; 10(15):2662. https://doi.org/10.3390/math10152662
Chicago/Turabian StyleWen, Xiaoyi, and Jinfeng Xu. 2022. "Generalized Accelerated Failure Time Models for Recurrent Events" Mathematics 10, no. 15: 2662. https://doi.org/10.3390/math10152662
APA StyleWen, X., & Xu, J. (2022). Generalized Accelerated Failure Time Models for Recurrent Events. Mathematics, 10(15), 2662. https://doi.org/10.3390/math10152662






