Analytic Matrix Method for Frequency Response Techniques Applied to Nonlinear Dynamical Systems II: Large Amplitude Oscillations
Abstract
:1. Introduction
2. Frequency Response Analysis
3. Analytical Matrix Method
3.1. Motivation
3.2. Proposed Series Solution
4. Study Cases
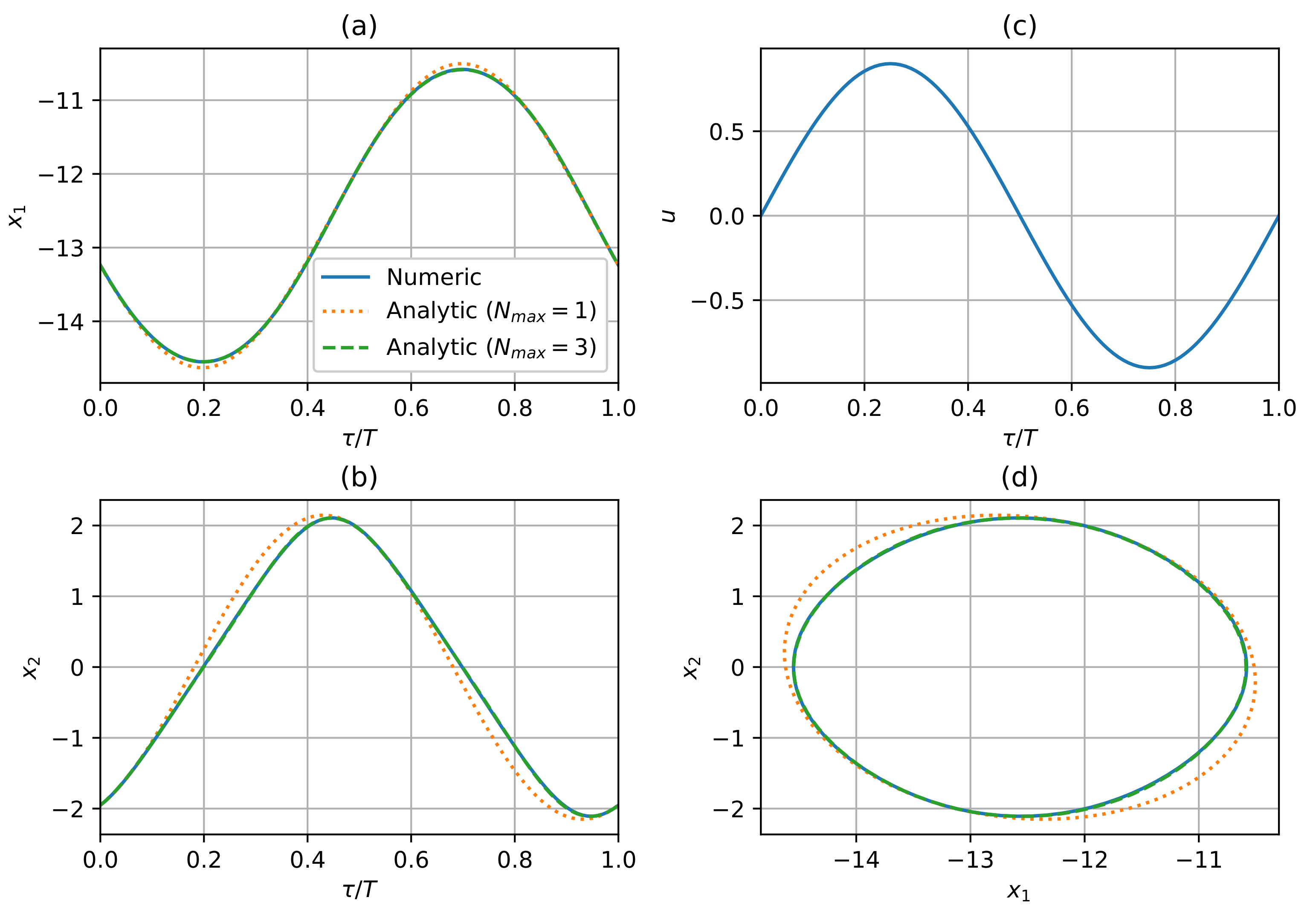
4.1. Series Solutions for a Simple Globally Asymptotically Stable Model
- 1.
- The product iswhere
- 2.
- while the product iswhere
- Coefficient for of Equation (54): ,
- Coefficient for of Equation (55): ,
- Coefficient for of Equation (54): ,
- Coefficient for of Equation (55): .
4.2. Series Solutions for a Simple Pendulum
- For :
- For :
- For :
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FRT | Frequency Response Techniques |
| SAOs | Small Amplitude Oscillations |
| MAOs | Medium Amplitude Oscillations |
| LAOs | Large Amplitude Oscillations |
Appendix A. Series of Cosine
Appendix B. Series Solution for the Pendulum
- Equation (62) for the 0-th term:
- Equation (63) for the 0-th term:
- Equation (64) for the 0-th term:
- Equation (65) for the 0-th term:
- Equation (66) for the 0-th term:
- Equation (67) for the 0-th term:
References
- Pai, P. Time–frequency analysis for parametric and non-parametric identification of nonlinear dynamical systems. Mech. Syst. Signal Process. 2013, 36, 332–353. [Google Scholar] [CrossRef]
- Zhu, Y.; Lang, Z.Q. The effects of linear and nonlinear characteristic parameters on the output frequency responses of nonlinear systems: The associated output frequency response function. Automatica 2018, 93, 422–427. [Google Scholar] [CrossRef]
- Živković, L.A.; Milić, V.; Vidaković-Koch, T.; Petkovska, M. Rapid Multi-Objective Optimization of Periodically Operated Processes Based on the Computer-Aided Nonlinear Frequency Response Method. Processes 2020, 8, 1357. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Lang, Z.; Mao, H.L.; Laalej, H. Nonlinear output frequency response functions: A new evaluation approach and applications to railway and manufacturing systems’ condition monitoring. Mech. Syst. Signal Process. 2022, 163, 108179. [Google Scholar] [CrossRef]
- Azarboni, H.R.; Heidari, H. Nonlinear Primary Frequency Response Analysis of Self-Sustaining NanobeamConsidering Surface Elasticity J. Appl. Comput. Mech. 2022, 8, 1196–1207. [Google Scholar] [CrossRef]
- Dodge, J.S.; Krieger, I.M. Oscillatory shear of nonlinear fluids I. Preliminary investigation. Trans. Soc. Rheol. 1971, 15, 589–601. [Google Scholar] [CrossRef]
- Hyun, K.; Nam, J.G.; Wilhelm, M.; Ahn, K.H.; Lee, S.J. Nonlinear response of complex fluids under LAOS (large amplitude oscillatory shear) flow. Korea-Aust. Rheol. J. 2003, 15, 97–105. [Google Scholar]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Cho, K.S.; Nam, J.G.; Ahn, K.H.; Lee, S.J.; Ewoldt, R.H.; McKinley, G.H. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Prog. Polym. Sci. 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- Hernandez, E.; Manero, O.; Bautista, F.; Garcia-Sandoval, J.P. Analytic Matrix Method for Frequency Response Techniques Applied to Nonlinear Dynamical Systems I: Small and Medium Amplitude Oscillations. Mathematics 2021, 9, 3287. [Google Scholar] [CrossRef]
- Khalil, H. Nonlinear Systems, 3rd ed.; Prentice-Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- Isidori, A. Nonlinear Control Systems II; Springer: London, UK, 1999. [Google Scholar]
- MacFarlane, A.G.J. Frequency-Response Methods in Control Systems; Chapter Part II. The Classical Frequency-Response Techniques; IEEE Press: New York, NY, USA, 1979; pp. 17–139. [Google Scholar]
- Petkovska, M.; Nikolić, D.; Seidel-Morgenstern, A. Nonlinear Frequency Response Method for Evaluating Forced Periodic Operations of Chemical Reactors. Isr. J. Chem. 2018, 58, 663–681. [Google Scholar] [CrossRef]
- Poincaré, H. Les Méthodes Nouvelles de la Mécanique céleste, Tome 3; Gauthier-Villars: Paris, France, 1899; Chapter 26; pp. 140–165. [Google Scholar]
- Kharkongor, D.; Mahato, M.C. Resonance oscillation of a damped driven simple pendulum. Eur. J. Phys. 2018, 39, 065002. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernandez, E.; Manero, O.; Bautista, F.; Garcia-Sandoval, J.P. Analytic Matrix Method for Frequency Response Techniques Applied to Nonlinear Dynamical Systems II: Large Amplitude Oscillations. Mathematics 2022, 10, 2700. https://doi.org/10.3390/math10152700
Hernandez E, Manero O, Bautista F, Garcia-Sandoval JP. Analytic Matrix Method for Frequency Response Techniques Applied to Nonlinear Dynamical Systems II: Large Amplitude Oscillations. Mathematics. 2022; 10(15):2700. https://doi.org/10.3390/math10152700
Chicago/Turabian StyleHernandez, Elena, Octavio Manero, Fernando Bautista, and Juan Paulo Garcia-Sandoval. 2022. "Analytic Matrix Method for Frequency Response Techniques Applied to Nonlinear Dynamical Systems II: Large Amplitude Oscillations" Mathematics 10, no. 15: 2700. https://doi.org/10.3390/math10152700
APA StyleHernandez, E., Manero, O., Bautista, F., & Garcia-Sandoval, J. P. (2022). Analytic Matrix Method for Frequency Response Techniques Applied to Nonlinear Dynamical Systems II: Large Amplitude Oscillations. Mathematics, 10(15), 2700. https://doi.org/10.3390/math10152700





