The Algorithm That Maximizes the Accuracy of k-Classification on the Set of Representatives of the k Equivalence Classes

Abstract

The article formulates the Dictionary Recognition problem, which is relevant for a wide range of applied problems: word recognition in a noisy audio signal for natural language processing tasks or in a noisy electromagnetic signal, recognition of visual patterns in limited visibility, and much more. A Dictionary Recognition problem is finding a set of words from a given set to maximize the classification accuracy of the words in the dictionary without losing semantic representation. The idea of solving the problem is to represent a set of objects (encoded as a sequence of symbols or visual sequences) in the form of a k-partite graph, where each partite of the graph corresponds to a group of objects with a certain common feature (equivalence class). The task is to find such a set of representatives of the k equivalence classes on which the k-classification accuracy by the classifier H meets certain criteria: (1) maximum classification accuracy; (2) maximin accuracy—the binary classification accuracy of every two objects is not lower than a certain value. The proposed Maximin Algorithm provides k-partite cliques with a maximin worst-case classification accuracy and belongs to the P-class. The Maximal Algorithm provides k-partite cliques with the maximum total weight (the problem belongs to the NP-hard class). The presented algorithms select a set of representatives optimally in terms of classification accuracy for the certain classifier and runtime. The algorithms increase classification accuracy when using classical classification methods without additional optimization of the classifiers themselves. We tested the algorithms on simulated data and provide an open-source project on GitHub. The results of the Maximin and Maximal Algorithms give 4-, 8- and 16-classification accuracy close to the best accuracy (obtained by brute-force enumeration) and better than the median accuracy by more than 20% for the support vector machine classifiers. Furthermore, the algorithms increase the selection speed of representatives by five orders of magnitude compared to the brute-force algorithm with a slight loss of accuracy.

1. Introduction

In many applied problems, we are tasked with maximizing the classification accuracy of objects belonging to nonlinearly separable sets. Some of these tasks are of profound practical importance, and their solution can significantly affect the quality of life and the development of society.

Suppose we have a noisy streaming signal in which a human or device has to detect certain sequences (words or visual patterns). For this task, we do not need to recognize natural speech or a wide range of words or patterns, but we need to recognize a particular set of words—a dictionary. It is required to recognize a certain limited set of words (for example, movement commands) and not all possible words from the human vocabulary. Therefore, we can significantly limit the cardinality of the set of words (a dictionary) while maintaining the necessary semantic diversity. It is essential to correctly recognize words and not confuse them with others from the dictionary. For example, correct recognition of a limited set of commands is used by a remotely controlled robotic device that receives control commands through a noisy communication channel (electromagnetic or audio) via any input device and even human–computer interfaces (HCIs) (Figure 1).

Choosing a limited command dictionary is very relevant for the brain–computer interface (BCI) that is used to remotely control a robotic arm by people with movement disorders. This type of HCI perceives and recognizes the patterns of the brain’s electrical activity during thinking and transfers these patterns into the commands, which remote robotic devices or other devices can accept. However, the brain’s electrical activity patterns are similar for words (commands) of similar articulation and semantics. Therefore, classifying the commands from a specific dictionary for the design of input devices using noisy audio or the electromagnetic signal is a serious problem. However, it turns out that 16–20 movement commands are enough for most robotic manipulators, with the greatest recognition accuracy of the selected commands (dictionary) [1,2,3,4,5,6].

Communication with devices or people through recognizers in a noisy environment also does not require an extensive vocabulary [1,6]. However, for the given tasks of communication with remote recognizers in a noisy environment, it is essential to recognize words correctly or correctly classify words (sequences, audio, or visual patterns) from a very modest dictionary. Therefore, the idea came to choose a set of words (sequences) that would be perfectly recognized by the remote recognizer, despite a noisy signal and a low classification accuracy of some words, by choosing the most successful synonyms in terms of classification accuracy. In this case, words should be grouped into semantic subsets (equivalence classes). The recognizer is not required to detect subtle semantic relationships, but to correctly classify these words as belonging to a particular semantic class. For example, to create a device that recognizes the commands of a robotic manipulator, it is crucial to minimize the classification error, while it is not so important which words will be selected as command words for the dictionary. Therefore, the task is to choose a dictionary that would be well classified by the recognizer and would be fully adapted to the required communication.

At the same time, it should be taken into account that, despite the growing computing power, the problem of choosing the optimal dictionary in terms of classification accuracy is resource-intensive. Indeed, this task requires a complete enumeration to find such representatives of equivalence classes (synonyms) so that the classification accuracy of all words in the dictionary is optimal (maximum or not lower than the best of the worst classification accuracies on word representatives). Therefore, we spent the most resources on the classifier training: for each such combination of k representatives, it is was required to train the k-classifier on the existing sample and obtain the accuracy value, which will be decisive when choosing a dictionary (Figure 2). The larger the sample, the more resources are required to train this k-classifier on each combination of representatives.

Most research groups do not follow the path of dictionary selection, but rather increase the sample cardinality to improve the classification accuracy. At the same time, an increase in the sample cardinality does not constantly significantly improve the classification accuracy: there are words (sequences in an audio or the electromagnet signal) that are poorly separated by the classifier [1,2,3,4,5]. With an increase in the sample cardinality of such data (audio recordings of words, a signal from the electrodes of the human–computer interface, visual images), for example, by recruiting new people into the experiments, the signal dispersion in the received distributions of audio or electromagnetic signals corresponding to words increases. As a consequence, the separability problem for poorly chosen word combinations persists. Those scientific groups trying to find a more successful combination of words to solve their task of classifying a dictionary follow the path described above and shown in Figure 2.

In our article, we propose a solution that allows avoiding enumeration and repeatedly training the k-classifier. In our paper, we formulate the problem and also provide a solution to the problem through the representation of the dictionary in the form of a k-partite graph, where representatives of the same equivalence class (synonyms) lie in the same partite. Furthermore, we propose a Maximin Algorithm for finding the close-to-the-optimal dictionary in terms of classification accuracy on word representatives. The proposed Maximin Algorithm provides k-partite cliques with maximin worst-case classification accuracy and belongs to the P-class. We compared the accuracy and runtime of the Maximin Algorithm with the exhaustive search algorithm on simulated data and showed the significant superiority in the runtime of the proposed algorithm over the enumeration with a slight loss of classification accuracy.

Indeed, k-classification is a classic problem in machine learning. However, we looked at the problem not from the view of the classification algorithms, but from the view of the previous step—the choice of the classes. Therefore, the algorithm presented in this paper works one step above the classical classification algorithms, such as naive Bayes classifiers [7], support vector machine (SVM) [8], relevance vector machine (RVM) [9], the k-nearest-neighbors algorithm (k-NN) [10], linear discriminant analysis (LDA) [11], etc. Moreover, all these classification algorithms are applicable after choosing the suitable classes, which is carried out by the presented algorithm. Thus, maximization of the k-classification accuracy begins at the stage of selecting the classes.

The most significant contribution of this work is that the provided algorithm solves the applied problem of maximizing the dictionary k-classification accuracy. Generally speaking, dictionary selection using enumeration cannot be carried out on modern computing power for any extensive dictionary.

The structure of the article has a peculiarity: first, we introduce readers to a formal problem, then we introduce the idea of a solution and the proposed algorithm and draw conclusions about the complexity of the algorithm; further, in the section “Materials and Methods”, we describe the procedure of data simulation, then there are simulation results and a comparison of the Maximin Algorithm with other algorithms on simulated data; then, we finish the article with classic sections with the discussion and conclusion.

2. Theoretical Section

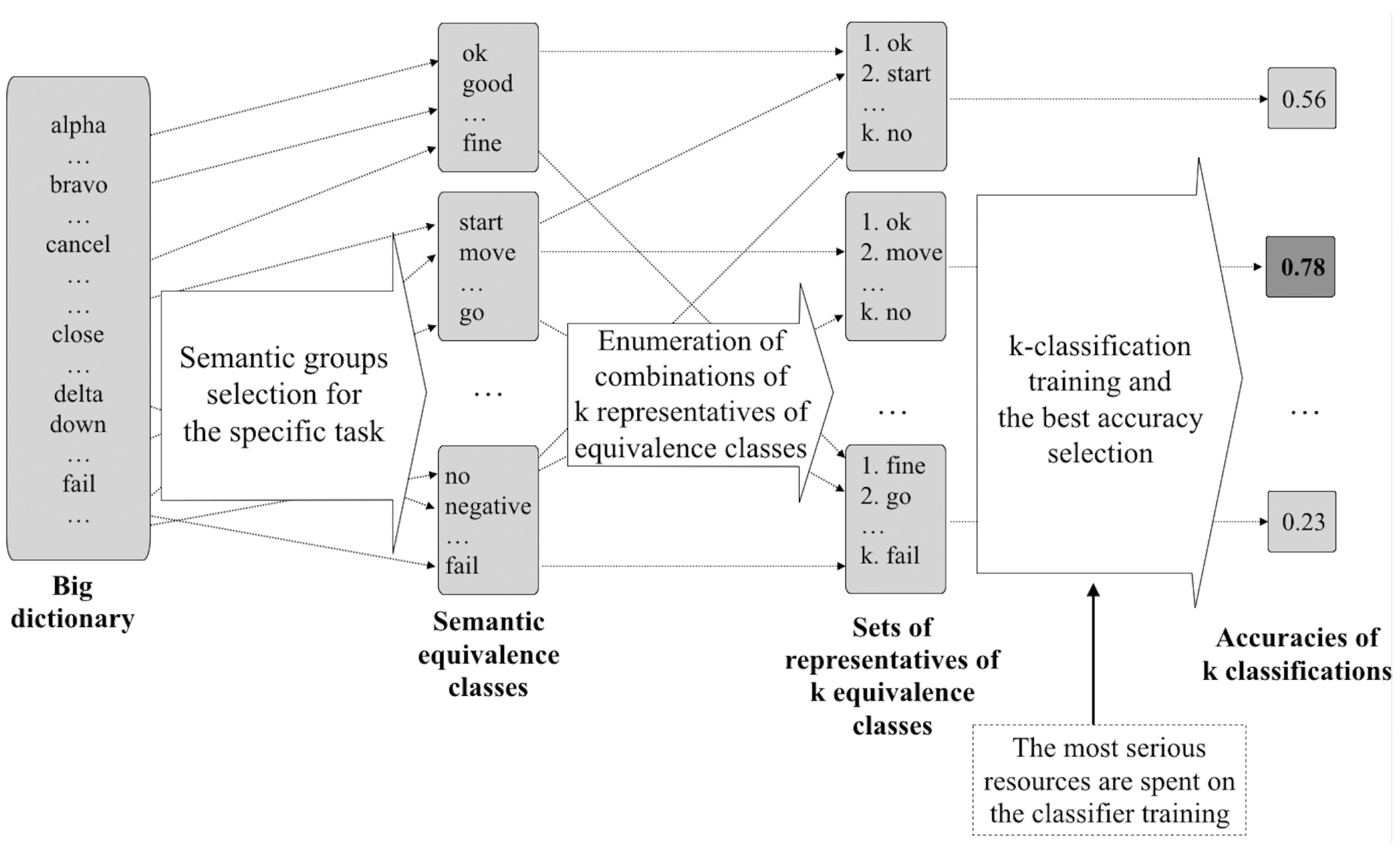
2.1. Formulation of the Problem and Proposed Idea

Suppose there are some sets {$S_0,\cdots ,S_{n-1}$}. Each set is characterized by distribution $D_i$, cardinality $Car{d}_i$, and feature $F_{s_i}$. According to the some criteria of equivalency based on features {$F_{s_0},\cdots ,F_{s_{n-1}}$}, these sets {$S_0,\cdots ,S_{n-1}$} can be grouped into k equivalence classes $\{C_0,\cdots ,C_{k-1}\}$. The relation H is given on representatives from different classes: $H(S_i,S_j),S_i\in C_q,S_j\in C_t,C_q\cap C_t=⌀$ as the binary classification accuracy of the two corresponding distributions. This classifier K may be applicable to classify more than two classes. The main goal is to maximize the accuracy of the k-classification of a given classifier K by selecting k representatives (distributions) from these k equivalence classes $\{C_0,\cdots ,C_{k-1}\}$. Let us formulate the problem.

The problemis to find such a set of representatives of the k equivalence classes $\{C_0,\cdots ,C_{k-1}\}$ on which the k-classification accuracy by the classifier K meets certain criteria: (1) maximum classification accuracy; (2) maximin classification accuracy—the classification accuracy of each of two words is not lower than a certain value.

The idea of solving this problem is in the representation of sets {$S_0,\cdots ,S_{n-1}$} in the form of a k-partite weighted graph G and finding (1) a k-partite clique with maximin worst-case classification accuracy (the minimum weight edge in the clique would have the maximum possible weight) and (2) a k-partite clique with the maximum total weight, where the k-partite clique is a clique, each vertex of which is the only representative of a separate partite of k-partite graph G. The k-partite weighted graph G is built so that synonymous commands fall into the same partite of the graph, and the edges are weighted according to the classification accuracy of the corresponding words (Figure 3).

In this paper, we present the Maximin Algorithm, the main idea of which is to solve the maximin problem of the worst-case classification accuracy between every two sets. We also compared the Maximin Algorithm and Maximal Algorithm, the main idea of which is to find k-partite cliques in the k-partite graph with the maximum total weight. Finally, this paper gives an example of how the algorithms work on simulated data.

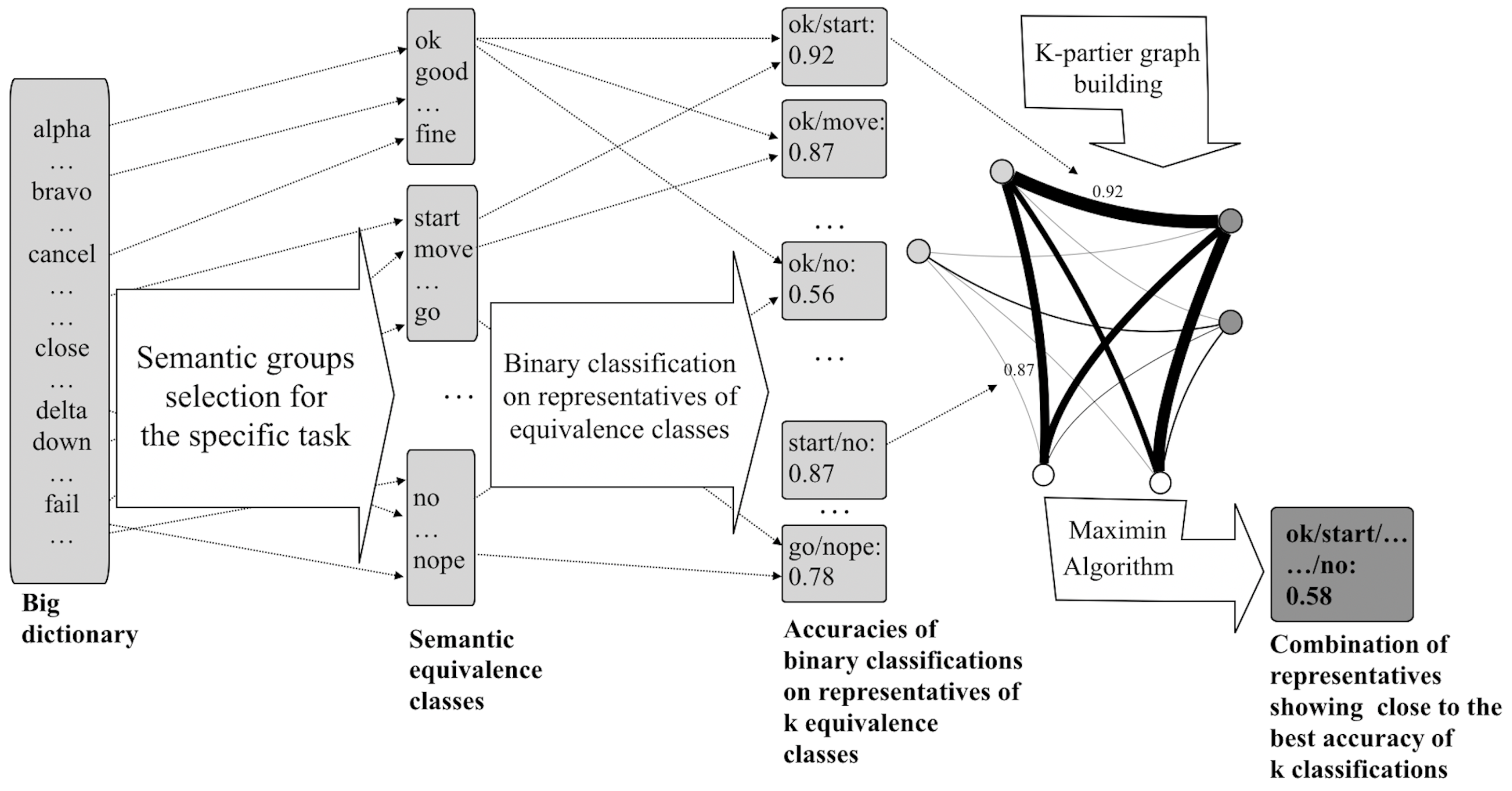
2.2. The Proposed Graph Algorithms

In this paper, we propose two algorithms. Both algorithms solve the k-classification optimization problem by selecting representatives of k equivalence classes.

The first algorithm (Maximin Algorithm) solves the maximin problem of the worst-case classification accuracy of each of two representatives for a set of sets divided into k equivalence classes, where the k-classification is performed on the set of representatives of k equivalence classes.

The second algorithm (Maximal Algorithm) maximizes the k-classification accuracy for representatives of k equivalence classes using binary classifications between representatives.

2.2.1. Maximin Algorithm

See the Maximin Algorithm 1.

Initial state. Suppose that we have n sets of some objects—{$S_0,\cdots ,S_{n-1}$}. According to the samecriterion of equivalency, these sets are grouped into k equivalence classes $\{C_0,\cdots ,C_{k-1}\}$. These k equivalence classes of n sets can be represented as a k-partite weighted graph $G(V,P,E,W),$ where V—set of vertices, $P=\{p_1,p_2,\cdots ,p_k\}$—set of partites, where each partite corresponds to a single equivalence class, E—set of edges, and W—set of edges’ weights. At the initial state, all weights from W are zeroed.

The first step. The binary classifier H is applied one-vs.-one to all possible pairs from {$S_0,\cdots ,S_{n-1}$}, lying in different equivalence classes. Then, to each edge from E of the k-partite graph G, we assign weight $w_{ij},w_{ij}\in W$, equal to the corresponding accuracy obtained by binary classifier H.

The second step. We sort the E set of edges according to the corresponding weights from W in descending order.

The third step. In this step, we find the weight of the edge in the ordered set $E_{ord}$ with index $k(k-1)/2$: $E_{ord}[k(k-1)/2]=w_{initial}$, $w_{initial}$—initial value. We take into account the fact that the necessary number of edges in a graph for at least one k-clique is equal to $k(k-1)/2$.

The forth step. In this step, we remove the edges of the initial k-partite graph G, obtaining graph $G^{\prime }$ from G. We remove only edges with weights lower than $w_{initial}$—the $\left(k\right(k-1)/2-1)$-th of the sorted E set. The $\left(k\right(k-1)/2-1)$ is the number of edges needed for a complete graph with k vertices.

The fifth step. We iteratively copy edges from G to the graph $G^{\prime }$ according to their weight in descending order. First, we add edges with higher weight, meaning those edges correspond to a higher binary classification accuracy of two distributions compared to the rest. At this stage, we consider that to have at least one k-partite clique, each partite of $G^{\prime }$ must contain at least one vertex of $k-1$ or higher power. Therefore, we add edges to the new graph $G^{\prime }$ iteratively until the described necessary condition is satisfied in each partite.

The sixth step with loop. We begin searching for the k-partite clique with the optimal total weight in the graph $G^{\prime }$.

If a k-partite clique is found, then we exit the algorithm.

If no k-partite clique is found, then we add a new edge from the sorted E set to $G^{\prime }$ and launch the search for the k-partite clique again. At this step, we can afford to modify the step and iterate over more than one value. We can iterate according to the certain value of the binary classification accuracy—accuracy $\alpha$. According to this accuracy, we can form the step size (D number)—the number of edges that need to be added to the graph $G^{\prime }$ from the ordered set $E_{ord}$.

Algorithm 1 The Maximin Algorithm.

Initial state: There are n sets of some objects: {$S_0,\cdots ,S_{n-1}$}; each set $S_i$ has an $F_i$ feature, where $i\in \overline{0,n-1}$. These {$S_0,\cdots ,S_{n-1}$} sets are combined into k equivalence classes {$C_0,\cdots ,C_{k-1}$}, according to the {$F_0,\cdots ,F_{n-1}$} features. Set k-partite graph $G(V,P,E,W)$, where $V=\{v_0,\cdots ,v_{n-1}\}$—the set of vertices corresponding to the {$S_0,\cdots ,S_{n-1}$} set, $P=\{p_1,p_2,\cdots ,p_k\}$—the set of k-partites corresponding to the equivalence classes {$C_0,\cdots ,C_{k-1}$}, $E=\{e_0,\cdots ,e_l\}$—the set of edges between vertices from different partites, and $W=\{w_0,\cdots ,w_l\}$—the set of weights, which is initially zeroed. 1: Apply the binary classifier H pairwise to all possible pairs from {$S_0,\cdots ,S_{n-1}$}, lying in different equivalence classes, and assign the resulting classification accuracy to the corresponding weight from W: $\{w_{ij}=H(S_i,S_j)|S_i\in p_l,S_j\in p_h,p_l\cap p_h=⌀,w_{ij}\in W\}$. 2: Organize all the edges E in descending order according to their weights to obtain ordered set $E_{ord}$. 3: Find the weight of the edge in the ordered set $E_{ord}$ with index $k(k-1)/2$: $w_{initial}=w_{k(k-1)/2}$, w—weight of the $e_{k(k-1)/2}$ edge, $e_{k(k-1)/2}\in E_{ord}$. 4: In the initial k-partite graph G, remove all the edges with weights equal to or less than the value $w_{initial}$, and denote the obtained graph as a k-partite graph $G^{\prime }(V^{\prime },P^{\prime },E^{\prime },W^{\prime })$. 5: Moving iteratively along the ordered set $E_{ord}$, add edges with the corresponding weights from the G- to the $G^{\prime }$-graph until each part of the $G^{\prime }$ has at least one vertex of $k-1$ power. 6: Launch the k-partite clique search algorithm in the k-partite graph $G^{\prime }$ 7: ifk-partite clique ∃ then Exit with k-partite clique. 8: else Add the next edge (or D number of edges according to the accuracy $\alpha$ from the ordered set $E_{ord}$) from the ordered set $E_{ord}$ with the corresponding weights from G to $G^{\prime }$. Go to Step 6—launch the k-partite clique search algorithm. 9: end if

This Maximin Algorithm 1 allows finding a clique, each edge of which has a weight, not below a certain value: $min(w_0,w_1,\cdots ,w_{k-1})\ge \alpha$. The presented Maximin Algorithm solves the maximin problem: $Q_{maximin}=\{k$-clique | $w_{mi{n}_q}=max\left(min(w_0,w_1,\cdots ,w_{k-1})\right)\}$, $w_0,\cdots ,w_{k-1}$—weights of the edge of the k-clique in the k-partite graph G, $w_{mi{n}_q}$—the best of the possible worst weights over all k-cliques: $w_{mi{n}_q}=max(w_{mi{n}_{Q_0}},\cdots ,w_{mi{n}_{Q_{n-1}}})$, and $Q_0,\cdots ,Q_{n-1}$—k-cliques in the k-partite graph $G\}$. However, the resulting k-clique may not be the k-clique with the maximum total weight (maximal k-clique) in graph G.

At the same time, for some problems, it may be critical to find a k-clique with the maximum total weight—maximal k-clique. Alternatively, it may be necessary to consider the minimum acceptable edge weight (binary classification accuracy)—the accuracy threshold.

2.2.2. Maximal Algorithm

The Maximal Algorithm maximizes the total accuracy of binary classifications for a set of sets divided into k equivalence classes, where the k-classification is performed on the set of representatives of the equivalence classes. See the Maximal Algorithm 2. The initial state of this Maximal Algorithm is the same as that of the Maximin Algorithm. The essence of the Maximal Algorithm is to enumerate all the maximum cliques, where a maximum clique is a clique with the largest size, to find the clique with the maximum total weight (maximal k-clique).

Algorithm 2 Maximal Algorithm.

1: Initial state: There are n sets of some objects: {$S_0,\cdots ,S_{n-1}$}. Each set $S_i$ has a feature—$F_i$, where $i\in \{0,\cdots ,n-1\}$. These {$S_0,\cdots ,S_{n-1}$} sets are combined into k equivalence classes {$C_0,\cdots ,C_{k-1}$}, according to the {$F_0,\cdots ,F_{n-1}$} features. Set k-partite graph $G(V,P,E,W)$, where $V=\{v_0,\cdots ,v_{n-1}\}$—the set of vertices corresponding to the {$S_0,\cdots ,S_{n-1}$} set, $P=\{p_1,p_2,\cdots ,p_k\}$—the set of k-partites corresponding to the equivalence classes {$C_0,\cdots ,C_{k-1}$}, $E=\{e_0,\cdots ,e_l\}$—the set of edges between vertices from different partites, $W=\{w_0,\cdots ,w_l\}$—the set of weights, which is initially zeroed. 2: Apply the binary classifier H pairwise to all possible pairs of sets from {$S_0,\cdots ,S_{n-1}$}, lying in different equivalence classes, and assign the resulting classification accuracy to the corresponding weight from W: $\{w_{ij}=H(S_i,S_j)|S_i\in p_l,S_j\in p_h,p_l\cap p_h=⌀,w_{ij}\in W\}$. 3: Launch all maximum k-partite cliques in the k-partite graph G search algorithm. 4: Sort all the maximum k-partite cliques according their total weight in descending order. 5: Exit with a certain maximal k-clique with the maximum total weight.

2.2.3. Complexity of the Proposed Maximin and Maximal Algorithms

Estimating the complexity of the proposed algorithms, we can relate the search for k-partite cliques in the k-partite graph to the problem of finding a clique of a given size, which is known as one of Karp’s original 21 NP-complete problems [12]. For a k-partite graph, the size of a maximum clique (clique that has the largest size) is equal to k.

The first k-clique, which appears in graph $G^{\prime }$ during the Maximin Algorithm’s launch, will be the desired clique, which has the maximum of the minimum weights of the clique edges over the possible cliques. From the graph G construction, the accuracy of the binary classification of the two most weak separable sets in combination with a set of representatives is better than in any other combination of representatives.

At the seventh step of the Maximin Algorithm, there is a search for a clique of a certain size (k-clique). It has been published that determining whether the graph has a clique of a given size is known to be NP-complete [12]. However, the Maximin Algorithm solves a different problem. The search for whether or not there is a k-clique that goes over all possible sets of k elements is a polynomial problem. Therefore, the Maximin Algorithm solves a P-class problem.

During the operation of the Maximal Algorithm, several maximum cliques may appear in the graph $G^{\prime }$. In this Maximal Algorithm, we solve the problem of finding all maximum cliques of size k in graph $G^{\prime }$. It is shown that the tight upper bound on the number of maximal k-partite cliques in a k-partite graph with n vertices stays the same as the number of maximal cliques in an arbitrary graph and equals $3^{\frac{n}{3}}$ [13]. Furthermore, what is most important is the theoretical results of the paper, which include the proof of the fact that the problem of enumerating all k-partite cliques in a k-partite graph is NP-hard [13]. Therefore, the Maximal Algorithm that enumerates all k-partite cliques and searches among them for the clique with the maximum total weight is NP-hard. Therefore, detecting all maximum cliques is an NP-complete problem; moreover, finding a clique of a given size of problem is known to be W-complete [13,14].

Therefore, the presented Maximin and Maximal Algorithms belong to the P-class and NP-hard complexity, respectively. However, even NP-hard complexity is not critical in the practical application of dictionary selection. In our work, we show that selecting a dictionary for the task given in the Introduction takes seconds on modern computing devices.

The schema of the algorithms’ application to the dictionary selection task can be seen in Figure 4.

3. Materials and Methods

We provide the open-source project on GitHub (https://github.com/aibern/maximin_k_classification_algorithm accessed on 25 June 2022).

3.1. Data Simulation

For data simulation, we used the NumPy Python library. We ran several experiments on 16, 32, and 64 simulated sets. Each set was characterized by the same cardinality and different normal distribution characteristics in 3D space. The mean and variance were chosen randomly on intervals of [−2, 2] and [0, 2], respectively. The simulated distributions were randomly assigned to different partites of the k-partite graph. To test the proposed algorithms, we fixed the following parameters: cardinality of the sets (40 st) and the number of vertices in one partite of the k-partite graph—that each partite had four vertices. Therefore, we built 4-partite, 8-partite, and 16-partite graphs.

3.2. Data Classification

Support vector machine (SVM) was selected as a method for the binary and k-classification using the scikit-learn 1.0.2 Python library [15]. The following kernel functions of the support vector machine were tested:

• Linear: $(x,x^{\prime })$;
• RBF: $exp(-\gamma ||x-x^{\prime }|{|}^2)$, where $\gamma$ must be greater than 0.

3.3. Proposed Algorithms’ Application and k-Classification Accuracy Comparison

The Maximin and Maximal Algorithms proposed in this article were used to obtain the desired cliques. We obtained the output of the algorithms and compared the k-classification accuracy on the obtained combinations of representatives of k equivalence classes with the best k-classification accuracy on the simulated data—from the brute-force algorithm. The outputs of the Maximin and Maximal Algorithms give sets of representatives on which the k-classification is carried out.

Therefore, we compared three k-classification accuracy values:

• k-classification based on the result of the combination obtained by the Maximin Algorithm (Algorithm 1)—corresponds to a k-clique with the highest lowest weight of the clique edge (the highest worst accuracy of the binary classification);
• k-classification based on the result of the combination obtained by the Maximal Algorithm (Algorithm 2)—the obtained representatives’ combinations based on the k-clique with a maximum total weight;
• The best k-classification accuracy from all possible combinations of representatives for a given simulation—the result of a complete enumeration (the brute-force algorithm).

There are $4^4,4^8,4^{16}$ classifications for 4, 8, 16 classes performed, respectively, in the 3rd case (the brute-force algorithm).

3.4. Runtime of Maximin and Maximal Algorithms and Brute-Force Algorithm

The evaluation of the algorithms’ runtime was carried out on the CPU Intel i5.

The Maximal Algorithm performs a complete enumeration of all combinations of representatives from 4, 8, and 16 equivalence classes (the cardinality of the class set was 4). It searches for the maximum total weight of the clique edges on $4^4,4^8,4^{16}$ variants, respectively. For the Maximal Algorithm, the k-classification was performed once on the data corresponding to the best clique in terms of the maximum total weight (maximum total binary classification).

To obtain the best k-classification accuracy by the brute-force algorithm, we launched $4^4,4^8,4^{16}$ k-classifications using the SVM method (SVM with linear kernel and RBF kernel), respectively.

4. Results

The results of the proposed algorithms on simulated data can be repeated using our open-source projecton GitHub (https://github.com/aibern/maximin_k_classification_algorithm accessed on 25 June 2022).

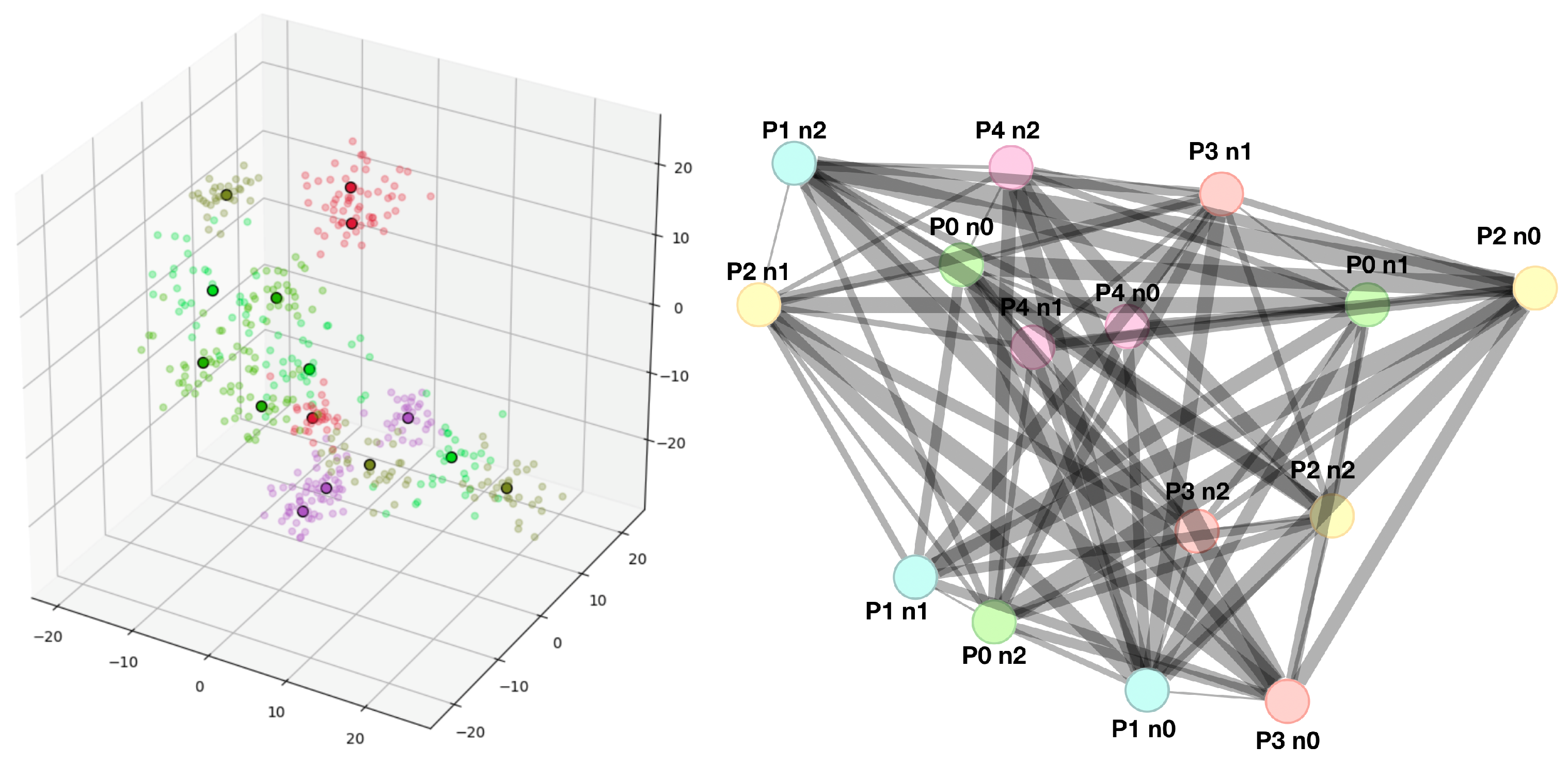
4.1. Data Simulation and Graph Representation

We performed a data simulation of 14 normal distributions with random mean and variance grouped into five equivalence classes (Figure 5). This simulation is for visual demonstration purposes only. The further simulation was carried out for the number of classes, which is a power of two.

4.2. k-Classification Accuracy on Simulated Data Using the Maximin and Maximal Algorithms and the Best k-Classification Accuracy Obtained by the Brute-Force Algorithm

The measurement results of the experiments are shown in

Table 1. k-Classification accuracy obtained on representatives from 16, 32, and 64 normal distributions with random mean and variance grouped into 4, 8, and 16 equivalence classes (5 experiments each) using the Maximin, Maximal, and brute-force algorithms.

Number of Classes	A Set of Distributions Corresponds to the k-Clique from the Maximin Algorithm	A Set of Distributions Corresponds to a Maximal k-Clique from the Maximal Algorithm	The Best k-Classification Accuracy from the Brute-Force Algorithm	Median k-Classification Accuracy	Minimal k-Classification Accuracy
k-classification accuracy (SVM with linear kernel)
	0.93	0.93	0.93	0.72	0.5
	0.98	0.98	0.98	0.75	0.34
4	0.93	0.98	0.98	0.81	0.53
	0.97	0.97	0.97	0.75	0.5
	0.87	0.87	0.97	0.75	0.46
	0.83	0.85	0.89	0.59	0.3
	0.92	0.92	0.92	0.58	0.25
8	0.89	0.85	0.9	0.59	035
	0.68	0.68	0.75	0.54	0.32
	0.76	0.78	0.82	0.55	0.26
	0.64	0.63	0.64	0.50	0.19
16	0.54	0.48	0.54	0.27	0.13
	0.48	0.47	0.50	0.29	0.09
	0.49	0.49	0.49	0.28	0.15
	0.64	0.65	0.66	0.30	0.22
k-classification accuracy (SVM with RBF kernel)
	0.98	0.98	0.98	0.73	0.33
	0.87	0.89	0.92	0.75	0.48
4	0.87	0.87	0.87	0.67	0.42
	0.95	0.95	0.95	0.78	0.48
	0.87	0.87	0.94	0.68	0.41
	0.81	0.78	0.88	0.59	0.33
	0.82	0.88	0.88	0.58	0.33
8	0.9	0.9	0.9	0.6	03
	0.68	0.79	0.8	0.55	0.28
	0.69	0.7	0.75	0.53	0.25
	0.63	0.65	0.66	0.51	0.23
16	0.48	0.48	0.48	0.29	0.14
	0.53	0.47	0.53	0.28	0.12
	0.48	0.47	0.50	0.29	0.09
	0.62	0.64	0.65	0.31	0.23

.

The four-classification accuracy on four representatives obtained at the output of the Maximin Algorithm differs from the best accuracy by 2.7% on average; the eight-classification accuracy on eight representatives differs from the best accuracy (from the brute-force algorithm) by 5.1% on average.

The presented Maximal Algorithm differs in accuracy by 1.1% and 3.6% from the best 4-classification and 8-classification accuracy on average, respectively.

The results of the Maximin and Maximal Algorithms give 4- and 8- classification accuracy close to the best accuracy (obtained during enumeration from the brute-force algorithm) and better than the median accuracy by 20 percent.

4.3. Runtime on Simulated Data Using the Maximin and Maximal Algorithms and Complete Enumeration of the Brute-Force Algorithm

The Maximal Algorithm performs a complete enumeration of all combinations of representatives from 4, 8, and 16 equivalence classes (the cardinality of the class set was four). It searches for the maximum total weight of the clique edges on $4^4,4^8,4^{16}$ variants, respectively.

The measurement results of the experiments can be found in

Table 2. Runtime of the Maximin and Maximal Algorithms and the brute-force algorithm.

	Runtime
Number of Classes	Maximin Algorithm	Maximal Algorithm	Brute-Force Algorithm
4	3 ms	10 ms	700 ms
8	30 ms	300 ms	10 min
16	1200 ms	10 h	160 h

.

The difference in runtime between the Maximin and Maximal Algorithms and brute-force algorithm increases with the number of classes.

5. Discussion

In this paper, we present algorithms that allow us to find a combination of the representatives from a certain number of equivalence classes to improve the classification accuracy. In the search for a better solution, we successfully represented the data in the form of a k-partite graph, where distributions with common properties were defined in one partite.

The ordering of edge weights, which is used in the Maximin Algorithm (Algorithm 1), significantly reduced the load on the calculation, with a slight loss of classification accuracy. Therefore, for four classes, the accuracy of the set obtained by the Maximin Algorithm was less than the best accuracy by only 2.7% on average, while it was better than the median by more than 20%. The eight-classification accuracy on eight representatives differs from the best accuracy by 5.1% on average. The presented Maximal Algorithm differs in accuracy by 1.1% and 3.6% from the best 4-classification and 8-classification accuracy on average, respectively. This loss of accuracy was negligible, especially considering the algorithm’s speed. We see that the classification accuracy on the set represented by the Maximal Algorithm does not generally match the best accuracy from the brute-force algorithm.

The Maximin Algorithm (see Algorithm 1) is particularly important when we compare its runtime with the brute-force algorithm (exhaustive search algorithm). In a small number of classes (4 and 8 classes), the time taken by the algorithms differed slightly. As the number of classes increased, the operation of the Maximin Algorithm gave a significant advantage over the Maximal Algorithm and the brute-force algorithm. When working with 16 classes on simulated data, the Maximin Algorithm completed in a little more than a second, while the exhaustive search algorithm spent more than 5 days on enumeration. The runtime advantage of the Maximin Algorithm was also demonstrated when compared with the Maximal Algorithm. At the same time, the Maximin and Maximal Algorithms’ runtime provides a significant advantage compared with the brute-force search algorithm. However, using the Maximal Algorithm and the brute-force algorithm when working with more than 16 equivalence classes does not seem appropriate.

Brute-force search is a very general problem-solving technique and algorithmic paradigm, which enumerates all possible candidates for the solution and checks whether each candidate satisfies the problem’s statement. If the exhaustive search is not possible, we are looking for algorithms that could bring us closer to the best classification accuracy value. Moreover, it is this possibility that the presented Maximin Algorithm gives us. We realize that if we do not have an optimal algorithm to select an optimal or close to optimal set of words for a dictionary, then the expected classification accuracy should be considered when choosing a random set (random clique). The operation of the Maximin Algorithm makes it possible to increase the accuracy of k-classification accuracy by 20% or more in comparison with a random set, on average.

The algorithms we presented are directly related to the mathematical problem of finding a clique in a graph. Currently, the most widely studied mathematical problems in graph theory include detecting a maximum clique (clique in the graph that has the largest size) or all maximal cliques (the maximal clique is a clique that is not properly contained in another one) in a given graph. However, such algorithmic problems have proven to be among the hardest ones. For example, even determining whether the graph has a clique of a given size is known to be NP-complete [12]. Similarly, detecting a maximum clique and finding all maximal cliques is an NP-complete problem [13]. The NP-hardness of the above problems is the main reason for the recent attempts to develop approximate algorithms. In the case of our research, we need to propose an algorithm for finding a clique consisting of k vertices in a k-partite graph, having exactly one vertex in each of the clusters of the graph. This problem can be treated as a particular case of the above-listed clique problems in graph theory. For instance, one can observe that the required clique is in fact both the maximal and maximum clique in the k-partite graph we are investigating due to the fact that the graph does not contain any intra-partite edges. This implies that any exact or approximate algorithm for solving the above NP-complete problems may also be applied to our case.

Considering the fact that our graph problem is a very special case of the above-mentioned clique detection problems, there does not exist any computationally efficient algorithm for solving it to the best of our knowledge [16,17,18]. Therefore, we suggested algorithms for finding cliques with required conditions and estimating their computational complexity. However, we also noticed that currently known clique detection algorithms may be adapted and applied to our case.

The presented Maximin Algorithm (Algorithm 1) solves the problem of optimizing representatives in terms of finding the best of the worst options for a binary classification through the problem of finding a clique, which is a problem from the P-class. The presented Maximal Algorithm (Algorithm 2) solves the problem belonging to the class of NP-hard complexity. However, the Maximal Algorithm allowed reducing the resources for calculation by several orders of magnitude, which in practice makes it possible to solve the problem computationally efficiently for some dimensions.

The use of this Maximin Algorithm is of great practical importance for developing human–computer interfaces with a specific set of commands for recognition. In addition, this algorithm can be applied to classical NLP tasks that require high recognition accuracy for a particular set of words. We can apply this algorithm to computer vision if we need to select a specific set of visual signs. In general, the algorithm is applicable in areas where we can select some items and we need to optimize the classification accuracy of these items. The presented algorithms were combined with classical classification algorithms (naive Bayes classifiers [7], support vector machine [8], relevance vector machine [9], k-nearest neighbors algorithm [10], linear discriminant analysis [11], etc.), as the algorithms give the optimal set of classes (words) for the selected classifier.

Some researchers may be surprised by the findings on classification accuracy. Nevertheless, the idea of the algorithm was born when solving the problem of choosing a dictionary to control a robotic device using an EEG-based BCI [1,19,20]. Each word (command) was a set of entries from different people in different conditions. On the real data we obtained, the distributions of different words were poorly statistically separated—the words belonged to the same distribution according to the Kolmogorov–Smirnov criterion [1]. Thus, our simulated data (close to real data) were very noisy, which always gives low accuracy values on any classifiers. This is why our new algorithm selects such distributions that classical classifiers, including neural networks, would better separate.

Indeed, there is an essential problem—the Dictionary Recognition problem for non-invasive BCIs, because of the very similar brain signal of different words (commands). Thus, non-invasive EEG-based BCIs recognize only a small number of words. The first works on silent speech recognition were focused on statistical EEG features and the nature of the distribution. In 2009, Charles DaSalla and colleagues proposed an algorithm for two English phonemes’ (/a/ and /u/) recognition with a 78% accuracy [21]. In 2017, researchers from the Birla Institute of Technology and Science (India) used a binary neural network classifier for two English (“yes”, “no”) and two Hindi (“haan”, “na”) words’ recognition with an accuracy of 75.4% [22]. In 2018, there was a publication of an SVM-based algorithm for recognizing 11 phonemes and four English words with an accuracy of 33.33% [3]. In 2019, scientists from India published a method for seven syllables, /iy/, /piy/, /tiy/, /diy/, /uw/, /m/, and /n/, with 57.15% classification accuracy on average [4]. However, the average accuracy for the binary classification of words approached 72% with a maximum accuracy of 85.57%; for the four words, the classification accuracy averaged 59% [3,4,5,21,22,23,24,25,26,27,28,29].

Classification accuracy requirements vary greatly depending on the task. For non-invasive EEG-based BCIs, the claimed accuracy in this paper of the simulated data is impressive given the current progress in classifying EEG-based BCIs [1,2,3,4,5].

Moreover, the Maximin Algorithm is of particular importance in tasks when we need to be able to classify all objects with no worse than a certain accuracy. For such tasks, all objects must be classified approximately equally, and the classification accuracy grows by increasing the size of the training sample.

When collecting data for the BCI dictionary, we cannot afford to produce data for all possible words since this is time- and resource-consuming. Before spending resources on data collection, we must decide which specific words we are ready to spend these resources on. In addition, the very training of the classifier at the time of selecting the optimal dictionary is also very resource-consuming. The presented algorithms allow not only reducing the cost of training and dictionary selection, but, in general, making this task feasible within the limits of human life.

The Maximin Algorithm provides resource advantages over the parallel brute-force enumeration using many CPU/GPU logical cores. The number of required logical cores for the brute-force algorithm grows exponentially with the number of classes: $n^k$, n—the cardinality of the class (number of semantically close words), and k—the number of the classes, whereas the Maximin Algorithm depends on the number of classes polynomially.

In our future work, we plan to generalize the problem of finding representatives. In addition, we plan to apply other classification algorithms, including neural network classification algorithms, and demonstrate the operation of the presented algorithms on the EEG dataset we collected.

6. Conclusions

The presented algorithms (the Maximin and Maximal Algorithms) make it possible to distinguish classes in the context of the Dictionary Recognition problem. The algorithms increase in classification accuracy when using classical classification methods without additional optimization of the classifiers themselves. At the same time, the complexity of choosing a dictionary grows polynomially with the number of classes.

The presented algorithms (the Maximin and Maximal Algorithms) are combined with classical classification algorithms and show practical importance since the algorithms allow finding an approximate accuracy value for a certain classifier that differs from the best accuracy within the error in a practically achievable time. The advantages of the algorithms are the runtime of the practical work with a slight loss of accuracy.

The presented Maximin and Maximal Algorithms belong to the P-class and NP-hard complexity, respectively. The Maximin Algorithm gives resource advantages over parallel enumeration using many CPU/GPU logical cores.

The algorithms make it possible to select a set of representatives on equivalence classes optimally to maximize the classification accuracy (support vector machine) and the runtime of the algorithms. The results of the Maximin and Maximal Algorithms give 4-, 8- and 16-classification accuracy close to the best accuracy (obtained by the brute-force enumeration) and better than the median accuracy by more than 20 percent. The algorithms increase the selection speed of representatives by five orders of magnitude compared to the brute-force algorithm, with a slight loss of accuracy for the support vector machine classifier.