Problem-Based Learning and Applied Mathematics

Abstract

Problem-based learning (PBL) is a teaching method that appeared in the early 1960s and is widely applied in distinct areas nowadays. In the presented manuscript, we describe a PBL methodology use restricted to applied mathematics for problem solving among a group of engineering students in a Portuguese university. In the pandemic context, it was a huge challenge both for the students and for the teacher. Supported by the available literature, the experiment was defined. As it is well known, teachers are not only knowledge transmitters but also designers of teaching initiatives. Thus, teachers and students both have a large role in PBL methodologies, where collaboration, reflection and concepts discussion are essential. In the presented pedagogical challenge, students were devoted to integrating the previous knowledge acquired and the one acquired during the project. This process improved their new competences—both personal and team work. Despite being a recent pedagogical method, PBL is revealed to be an important teaching tool.

1. Introduction

It is well known that the mastery of various skills is increasingly required in order to successfully reach all students. This need is imposed both by the students’ diverse paths and by the need to increase the degrees of freedom of students themselves to be able to build their curricula by combining learning in distinct areas, which has become an emergency during the pandemic in 2020. The scientific community recognizes that problem-based learning (PBL) has been pioneered since the 1960s [1,2]. PBL is a teaching method that focuses on practical and active learning with the goal of investigating and researching/searching for real-world problem solving.

PBL is of particular interest because it appears to be a “popular” method of instruction. It is a method that has been used successfully for many years and is gaining acceptance in a variety of fields, including medicine, engineering, and mathematics, among others. PBL is implemented in a learning environment where problems lead to self-learning. The learning process begins with a problem that must be solved. The problem is designed in such a way that students must learn new information before they can solve it. Students are encouraged to conduct research, integrate theory and practice, and apply knowledge and skills in order to develop a long-term solution to the problem at hand.

The PBL method is based on the premise that learning entails the construction of new knowledge to be acquired through the resolution of the proposed problem, which is supported by cognitive science theory, which states that prior knowledge about something can determine the nature and amount of information that students can process and elaborate in order to be assimilated [3]. Each problem has a challenge, and learning performance is recognized when a student can solve a new problem that is similar to a previous one but the solution is presented in a different way.

2. Problem-Based Learning in Higher Education and Mathematical Modeling

According to [4], PBL is based on Jerome Bruner’s concept of epistemic motivation as an internal force that leads people to better understand the world and John Dewey’s concept of autonomous learning, with an emphasis on learning in response to real-life circumstances. PBL was first used in teacher education at McMaster University’s Faculty of Health Sciences in the mid-1960s. PBL has grown in popularity since then [5,6,7]. Although PBL began in the teaching of medical sciences, it was quickly adopted in the teaching of other disciplines such as engineering [8], business administration, and law [9,10]. In addition, universities such as Rutgers and Wisconsin University have used PBL in teacher education [5,11]. Other PBL applications have been used; Memorial University of Newfoundland has used PBL in the science curriculum [12].

The authors of [13] recently presented a study investigating the effects of PBL in drawing learning models and the creative thinking skills of engineering students from different classes at UNIMED, Indonesia. The findings allowed us to recommend to lecturers that they use this methodology in order to achieve better results. In 2021, the work presented in [14] addresses mathematical problem solving while assessing the pedagogical knowledge of 149 potential participants from a Spanish university. The authors of [15] advocated for a validation study in which a specific case of problem-based learning, real case learning, in which students solve real-world problems using PBL, was evaluated. In four different classes of engineering students at Deusto University in Bilbao, four different types of real case learning were implemented. The findings indicate that students achieved better results when compared to traditional teaching methods. A recent and interesting study comparing PBL methodology to traditional methods of teaching English as a foreign language at a Chinese university can be found in [16]. In contrast to the traditional practice of teaching formal mathematics before practical issues, the authors of [17] present a study in which horizontal mathematization is emphasized. A specific case of PBL, game-case learning, was used with the goal of having the greatest influence on the students. The findings demonstrated that game-case learning is a novel method of teaching mathematics.

In summary, PBL is a strategy that organizes mathematics teaching around problem-solving activities while also providing students with opportunities to think critically, present their own creative ideas, and communicate mathematically with colleagues.

In order to adapt to such a diverse area of knowledge and educational contexts, PBL has taken different formats than the one proposed at McMaster University. The PBL pedagogical model is based on the model developed by Aalborg University in Denmark, which has been recognized globally by universities, researchers, and students as an advanced and efficient learning model. As a result, UNESCO has assigned Aalborg University its sole Danish chair in PBL. Ref. [18] organized the state of the art of the PLB for over 40 years in 2015, and the authors mention that there is still a lack of studies that seek to observe the evolution of scientific production on the subject. To fill this void, the authors conducted a bibliometric study. To fill this void, the authors conducted a bibliometric study using data from the Web of Science database. They found a total of 2551 articles published in 15 countries between 1992 and 2013. The data revealed that PBL research has made significant progress since the end of the twentieth century, with a large volume of the most influential studies being carried out by a group of researchers who are currently or were previously affiliated with Maastricht University. They also noticed that the United States, United Kingdom, Canada, Australia, and the Netherlands account for 64.5% of all publications. As a result of these studies, there has been a geographic (from North America and Europe to Asia) and academic diffusion of scientific production on this teaching methodology [18]. In Portugal, we know that PBL has been used in environmental sciences teaching at the Portuguese Open University since 2009, and it is stated in the 2018 report of the virtual pedagogical model (VPM) of the Portuguese Open University that PBL is an important active learning methodology to use and that it has added value as a methodology to pursue. In addition, on this subject, it is worth noting that some work on the use of PBL approaches was published in 2016 [19] and 2017 [20].

Principles of PBL Methodology

The methods used in PBL and the specific skills to be developed were described in [21] as the ability to think critically, analyze and solve complex real-world problems, identify, evaluate, and use appropriate learning resources, work cooperatively, demonstrate effective communication skills, and use content knowledge and intellectual skills to become lifelong learners.

PBL is an instructional method in which students learn through facilitated problem solving that focuses on a complex problem with no single correct answer. PBL is a student-centered approach that allows them to conduct research, integrate theory and practice, and apply knowledge and skills to develop a viable solution to a given problem. Ref. [22], for example, summarizes the characteristics of PBL in three fundamental aspects:

• The role of the tutor as a facilitator of learning;
• The responsibilities of students to be self-directed and self-regulated in their learning;
• The essential elements in the design of poorly structured learning problems as the driving force for research.

The challenge of implementing a PBL approach is to transition from a teacher as a knowledge provider to a tutor as a manager and facilitator of learning.

Ref. [22] defines, with some modifications, the essential aspects in 2006, based on a detailed list of generic PBL fundamentals proposed by [23]:

• Students must take responsibility for their own learning;
• Problem simulations used in PBL must be poorly structured and allow free interrogation;
• Learning must be integrated from a wide range of disciplines or subjects;
• Collaboration is essential;
• What students learn during their self-directed learning must be applied back to the problem with reanalysis and resolution;
• A final analysis of what has been learned from work with the problem and a discussion of what concepts and principles have been learned are essential;
• Self-assessment and peer review must be carried out at the end of each problem and at the end of each course unit;
• The activities carried out in PBL must be those that are conducive to value the ones in the real world;
• Students exams must measure student progress toward the PBL goals;
• PBL must be the pedagogical base of the curriculum and not be part of a didactic curriculum.

3. Materials and Methods

On this basis, the following research question emerges: how does the PBL methodology focusing on mathematical modeling affect the effectiveness of meaningful calculus content learning when applied to engineering students?

3.1. Modeling the Pedagogical Activity

Three pedagogical challenges were presented to students in the calculus 1 curricular course, with the objective of investigating as well as consolidating certain curriculum contents at various points throughout the academic semester. These topics were previously taught in the traditional manner, i.e., through an explanation of concepts and practice with exercises.

The pedagogical experience associated with one of the challenges is described here. The overarching goal was to comprehend how first-year students in aeronautics, materials and mechanics engineering courses apply mathematical content in problem solving, with the specific goal of comprehending how these students apply aircraft geometry modeling a two-dimensional object by discovering algebraic expressions that model its boundary and calculate its area using simple integrals.

Calculus 1 was a course that covered three subjects: differential calculus, integral calculus, and series. It was finished during the first semester of the school year. The contents of integral calculus, the unit in which this pedagogical challenge is embedded, included anti derivatives and area calculation. Eleven students from the aeronautics engineering, one from materials engineering, and six from mechanics engineering, all in their first year of bachelor’s degree, took part in this challenge.

The pedagogical challenge, here presented, began on 16 November 2021, with a 120-min class in which students: read the course work; paid attention to the part that had been assigned to them; considered using mathematical modeling to solve the problem, specifically by selecting the position of the piece in a 2D Cartesian frame; realized that the boundary lines of the piece corresponded to graphs of functions, the analytical expressions they would have to discover; began using graphic software (“Desmos”) to reproduce the piece graphically; and were able to clear up any misunderstandings with the teacher. Students worked independently from 17 November to 29 November—two weeks. On 30 November, oral presentations and work discussions were held—lasting about 15 min each.

The Pedagogical Challenge (PC) was designed and implemented in four stages: (1) conception by the teacher, (2) presentation of the proposal to the students and its resolution, (3) student presentation to the group class and discussion, and (4) students’ final reflections.

As shown in Figure 1, the teacher graphically sketched some pieces using previously chosen functions (linear, quadratic, circumference equation, constants, and so on).

Far in advance, the teacher cut the pieces out of spongy material, resulting in bidimensional objects, as shown in Figure 2, and presented them to students, enabling them to choose the piece.

The following could be read in the challenge titled “In Search of a Bi-Dimensional Geometric Model”: Consider the object you were given as having negligible thickness. To sketch the graphs, use a support software such as Symbolab Math Solver (for integrals calculus) and the online services provided by Desmos, Inc.—“Desmos” (Graphing Calculator, San Diego, CA, USA).

Consider the following questions:

Q1.

How should the object be placed in a bi-dimensional frame?

Q2.

What are the algebraic expressions of the functions involved (at the boundary of the object)?

Q3.

What is the object’s surface area (in square centimeters’)?

Q4.

A variation on the proposed challenge.

Q4.

Note: Please keep in mind that you can use a ruler.

The table below,

Table 1. Pedagocical Challenge Outline.

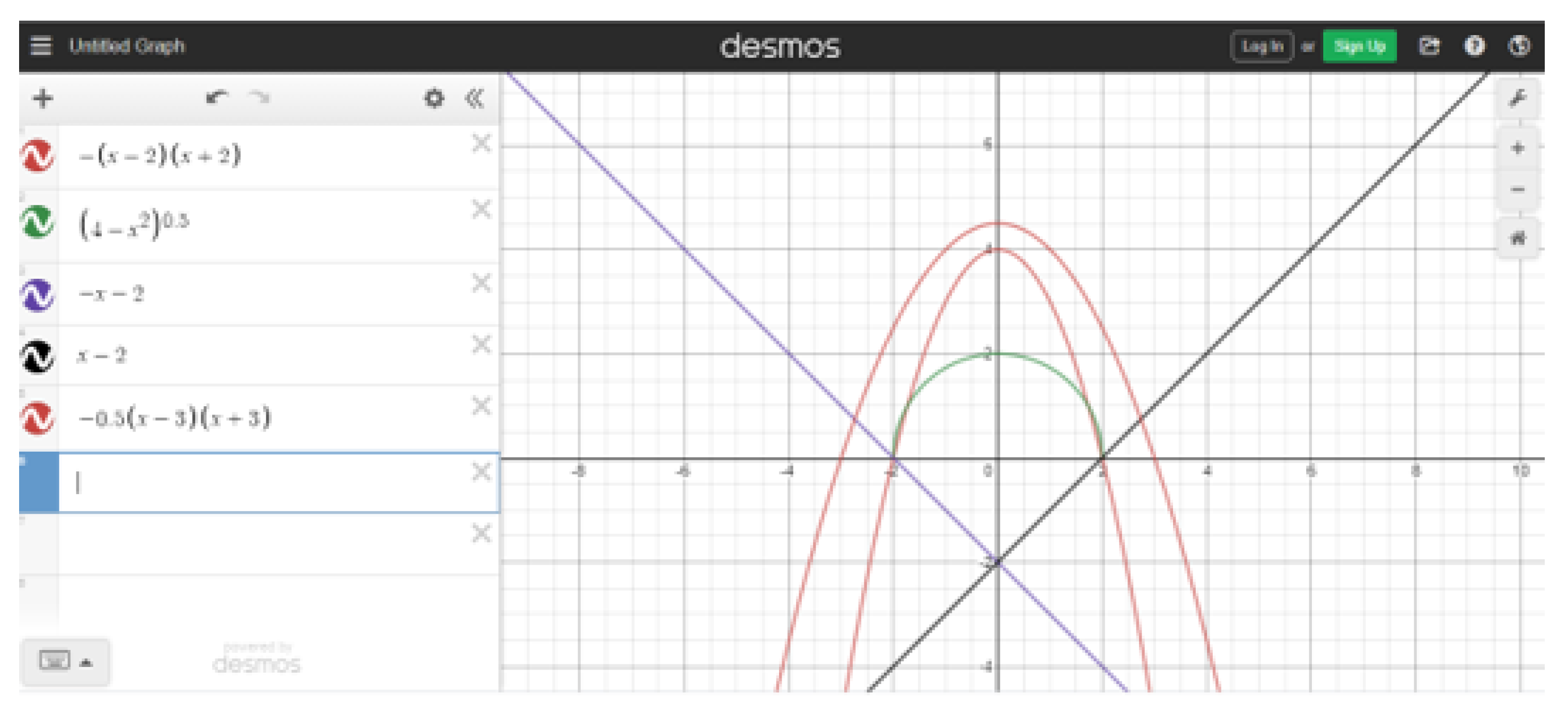
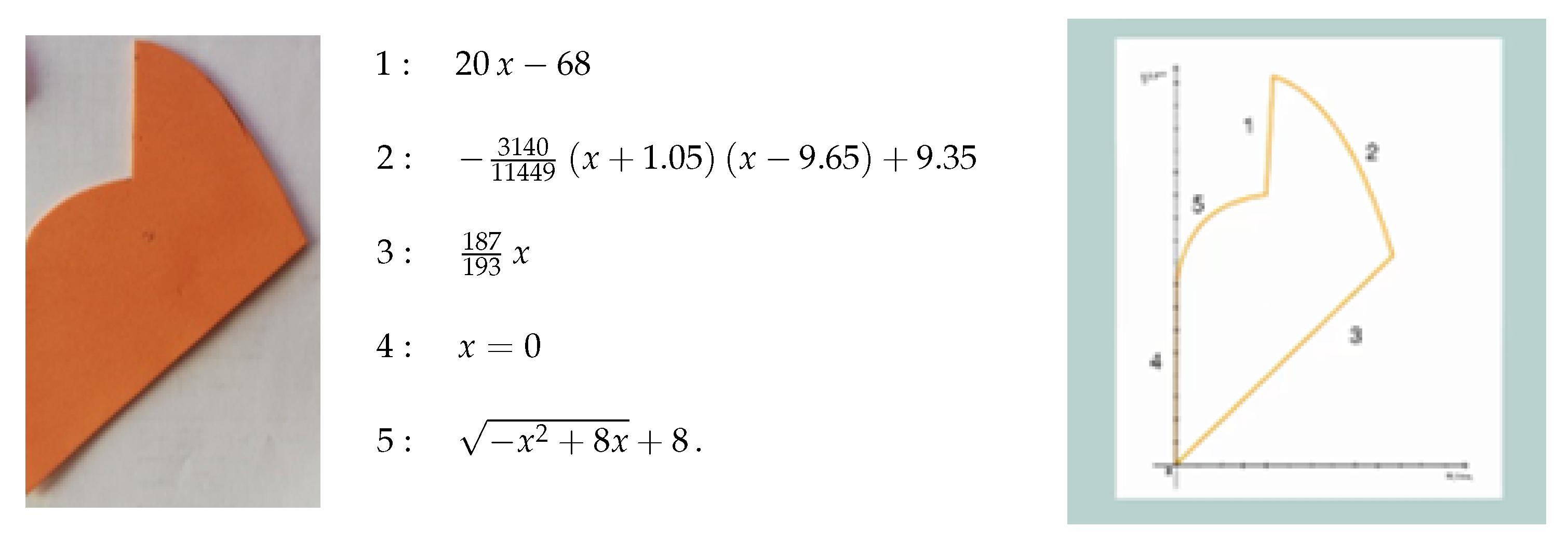
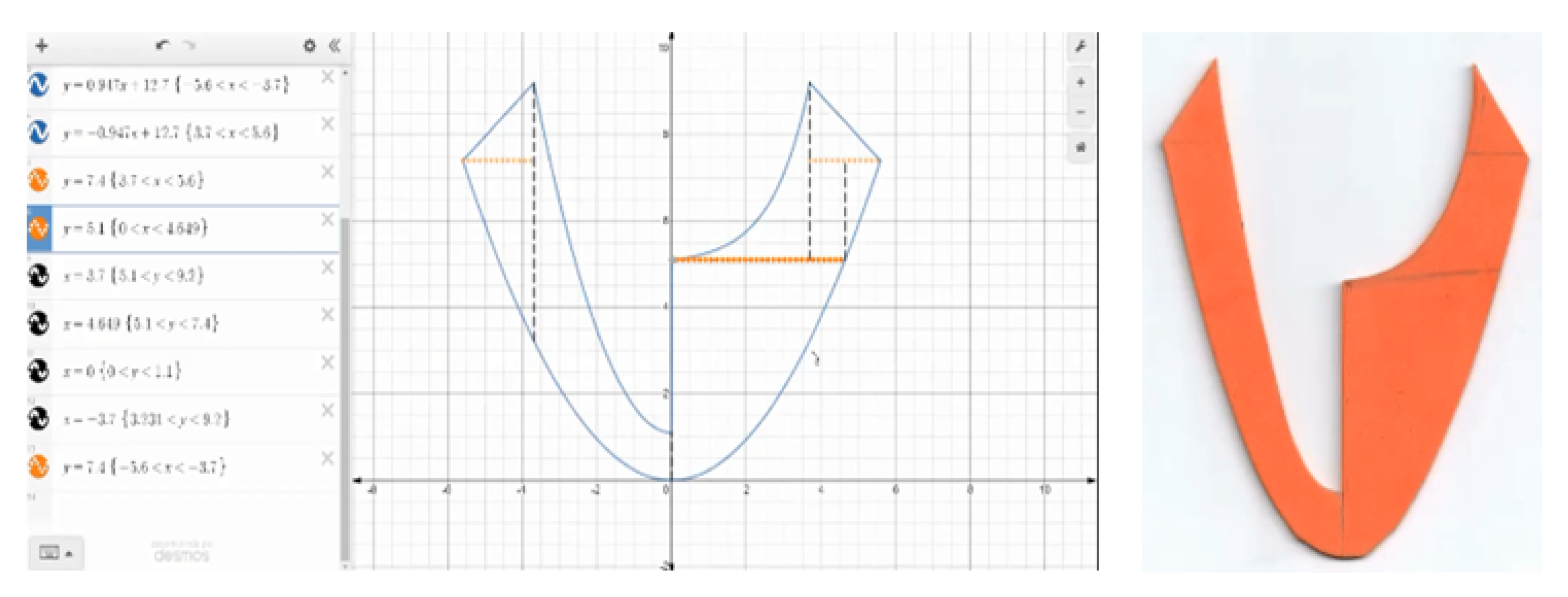
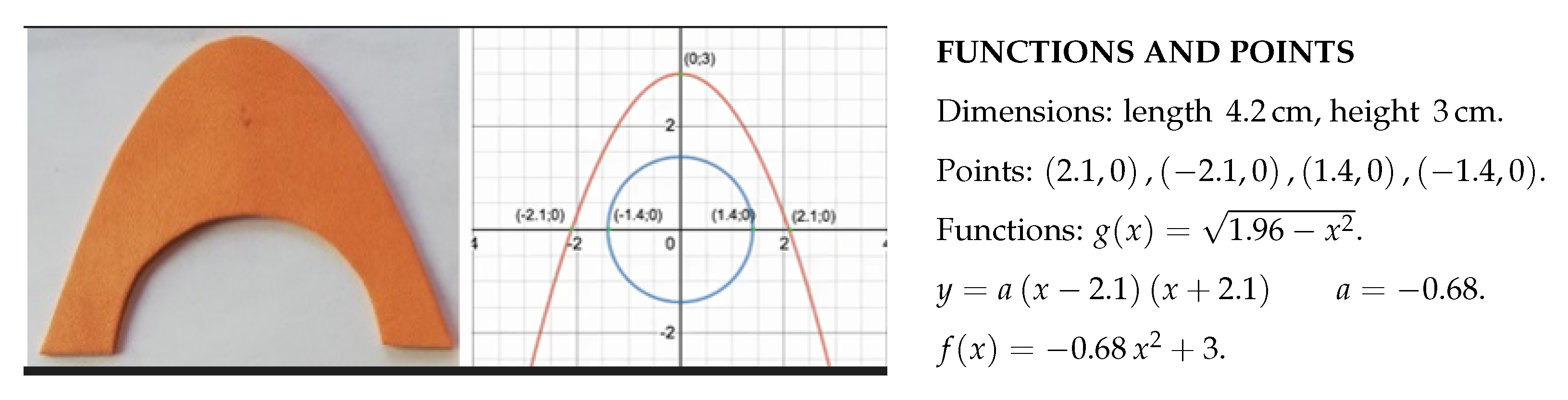
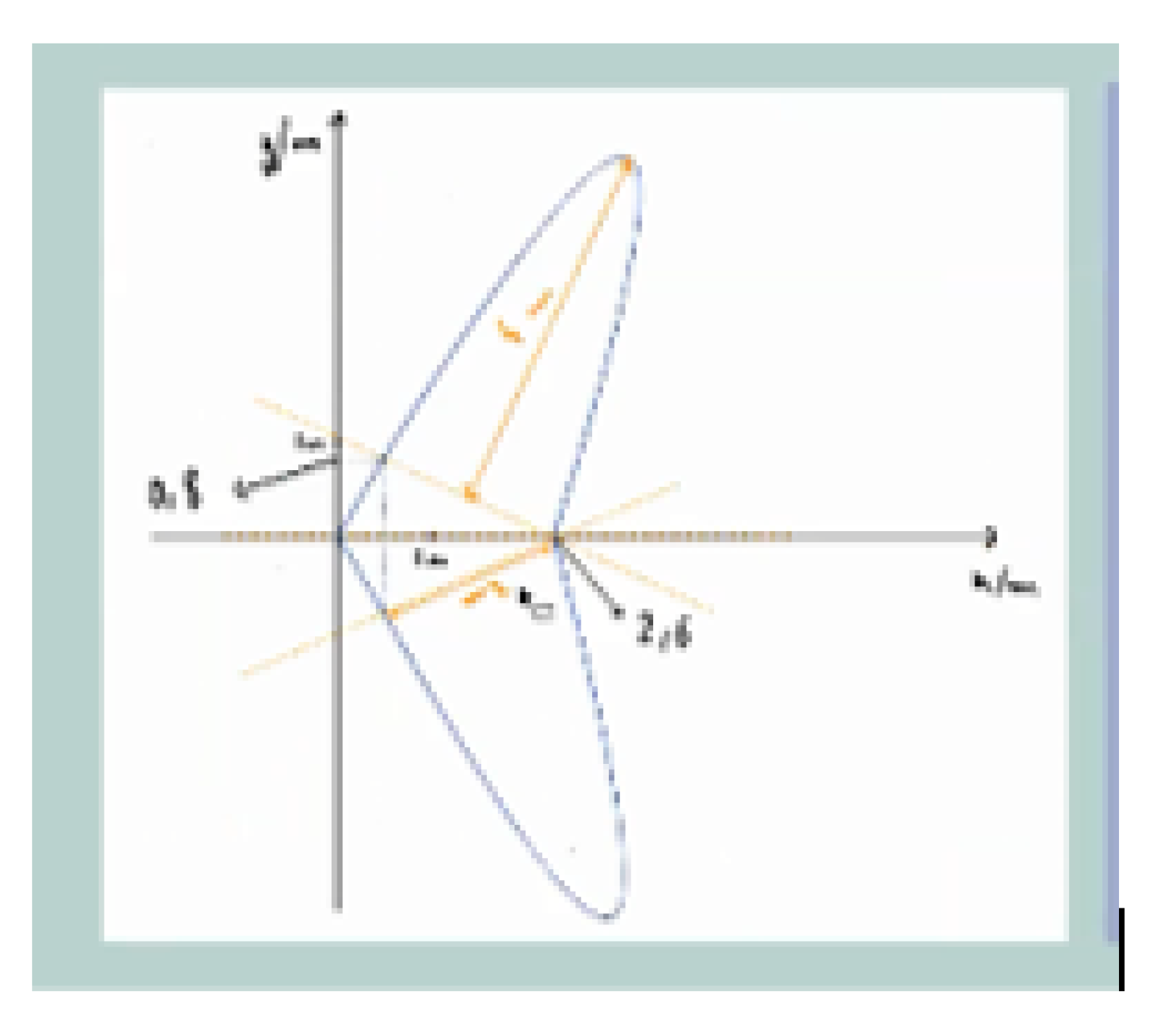
Pedagogical Task	Curricular Contents (to Apply)	Scientific Knowledge (to Discover)	Skills (to Develop)
Pegagogical Challenge	Graphical representation of a function based on its algebraic expression.	The decision to place the piece in a bi-dimensional reference is critical for reducing/increasing the difficulty of algebraic function determination.	Retrieve the piece sketch, use graphical software (Desmos).
In Search of a Bi-Dimensional Geometric Model	Use integral calculus to calculate the area of a surface.	Option to model a surface’s boundary using algebraic expressions of functions.	Extract the numerical calculations, use integral calculus software (Symbolab).
		It is worth noting that some quadratic functions have a graphical representation that is similar to that of a semi circumference.
		Modeling involves some degree of inaccuracy.

, summarizes the curricular contents to be applied as well as the scientific knowledge and skills to be developed in order to complete the proposed activity.

The PC was presented after the curricular contents were taught. Students could work individually or in pedagogical collaboration with colleagues, with the number of group elements ranging from one to four.

The two-hour class on the day of the PC presentation was devoted to tutorial guidance so that students could clearly understand the challenge and how to begin exploring the problem presented. Following that, the work was developed autonomously, with only sporadic doubts. Students were given two weeks to complete the assignment and prepare their presentation.

Students created PowerPoint presentations that included algebraic resolutions, images, and links to digital tools. Presentations lasted about 15 min and had no more than seven slides (forced condition). The presentations explained how the problem was interpreted, how it was solved, how it was extended, and which digital tools were used.

Following the class presentations, students were asked some questions in order to help them understand the effective meaning of solving the proposed problem. The following reflection questions were proposed:

Q1.

What scales were used for the axes? Why?

Q2.

Was it obvious that by defining the figure’s boundary, the graphical representation of the functions and their analytic expressions were obtained?

Q3.

Was Desmos used to confirm the existence of the desired functions?

Q4.

Was the area calculated directly or as the sum/difference of two areas? How did that come across?

Q5.

Are you certain that the functions chosen best approximate the desired surface boundary? Why?

Q6.

Did you mention that by moving the referential, the area obtained remains the same?

Q7.

What effect did the activity have on you? At least three items must be specified.

Thus, after the presentations and group-work class debates, the format of this PBL included a block of four questions in the PC presentation and a block of seven questions for reflection.

3.2. Research Methodology and Tools

The research design in this work employs qualitative methodology, as is common in education and is in fact a case study [24]. It is not intended to be a generalization but rather to highlight the specifics of the presented case. The obtained data were subjected to a thorough, intensive, and in-depth investigation. However, the importance of dealing with a case in which the pedagogical experience encourages students to question and investigate is emphasized.

The observed sample consists of sixteen students who took classes in the curricular required course Calculus 1 during the first semester of their Engineering degree in Aeronautical Sciences, Materials, or Mechanics.

According to [25], the use of small groups is required for the implementation of PBL as a knowledge consolidation tool. In large working groups, each member/student is only responsible for a small portion of the task. In contrast, in groups of two or three elements, all students are responsible for paying attention to details, avoiding obstacles, and becoming more involved in the overall task resolution. The number of elements in each working group in this work ranged from one to four, depending on their preferences.

The following methodological instruments were used in the analysis of results, with the research question in mind: the resolutions of the pedagogical challenges and the students responses to the reflection questions raised by the teacher.

As a result of confinement due to the COVID-19 pandemic, the task was presented in an online class format using the Zoom platform. The students’ resolutions and responses to the reflection questions are described below.

4. Results

4.1. Answers to Questions of the Pedagogical Challenge

Q1. How should the object be placed in a bi-dimensional frame?

The students’ responses are summarized in some fundamental ideas, such as:

• Enable understanding of the values used in the calculation of algebraic expressions of boundary functions;
• The figure is divided in half;
• The OX axis divided the triangle’s semi-circumference (figures identified as being part of the object);
• The bi-dimensional object’s longest side was parallel to one of the axes;
• The parabola is identified as part of the boundary, with an upward concavity.

Q2. What are the algebraic expressions of the functions involved (at the boundary of the object)?

Some students began by tracing the piece and then drawing the axes on paper, see Figure 3. Then, they attempted to deduce what kinds of functions were on the boundary and what algebraic expressions they contained.

Others decided to use Desmos right away, introducing the functions that appeared to be appropriate and having the ability to visualize the graph, see Figure 4, Figure 5, Figure 6 and Figure 7. After that, they took the piece and attempted to superimpose it on the graph, on screen, to see if they were equivalent.

The figures below show how a small group of students approaches the question Q2 using Desmos.

The major difficulty identified at this stage of the challenge was some students’ hesitation to choose a semicircle or a parabola for some boundaries.

Q3. What is the object’s surface area (in square centimeters’)?

Students understood the importance of decomposing the piece into different figures and deciding whether to add or subtract areas. As a result, some decided to define the integrals representing the various sub-areas and calculate them manually or using Desmos, Figure 8.

Q4. A variation on the proposed challenge.

The pedagogical challenge was extended several times, with some students being more creative than others. The most common was the calculation of areas, such as when building a house, but others made a difference. One of the groups attempted to recreate real measurements by graphically recreating the approximate shape of a hang-glider using two parabolas and two triangles and calculating its approximate area in square meters, see Figure 9.

Another group investigated calculating the length of a parabola arc, see Figure 10, and also presented its mathematical formulation,

Table 2. Length of a parabola arc.

$L=\sqrt{{\left(\Delta x_i\right)}^2+{\left(\Delta y_i\right)}^2}$	$f\left(x\right)=-\frac{41}{80}{(x-8)}^2-4.1(x-8)$
$L=\sqrt{1+\left(\frac{\Delta x_i^2}{\Delta y_i^2}\right)}$	$L={\int }_0^8\sqrt{1+f^{\prime }{\left(x\right)}^2}dx$
$L={\int }_a^b\sqrt{1+f^{\prime }{\left(x\right)}^2}dx$	$L\simeq 18.95$.

.

One group proposed using a GoogleMaps photo with an overhead view to calculate the capacity of a swimming pool, specifically the oceanic pool of Oeiras (known as depth value), Figure 11.

Remembering that in high school, students learned to determine the area to obtain the covered distance for a linear representation, as previously mentioned, using a velocity-time graph, Figure 12, and as a result, they can now use any function.

4.2. Answers to the Reflection Questions

The reflection questions were discussed immediately following the work presentations and after being entered into a Google forms survey. The following table,

Table 3. Reflections questions and answers.

Questions	Students Responses
Q1. What scales were used for the axes? Why?	After measuring the dimensions of the object with a ruler, scale in centimeters; Desmos uses a centimeter as a unit of measurement, so it is in square centimeters; Scale in centimeters after noticing that every two squares of a graded sheet measure one centimeter; In the frame, used a one-centimeter scale.
Q2. Was it obvious that by defining the figure’s boundary, the graphical representation of the functions and their analytic expressions were obtained?	Yes, some students said. Others responded no, because it was noticed after observing the piece’s position in the reference frame, not immediately.
Q3. Was Desmos used to confirm the existence of the desired functions?	Only a group of students had not made it. Desmos was mentioned as an important tool for work resolution in general.
Q4. Was the area calculated directly or as the sum/difference of two areas? How did that come across?	The piece position in the axis revealed that the simplest way to calculate area was to sum the areas; A difference in areas necessitated the removal of a portion of the function; A sum of areas, considering the piece’s decomposition as a triangle and a semi-circle; The area was calculated in a straightforward manner; As the sum and difference of two areas. The area of a quarter of a circle was calculated first, and then, it was subtracted from the area of a rectangle (not shown in the figure), and the two areas were added; It was calculated as the sum of areas because it was impossible to compute directly.
Q5. Are you certain that the functions chosen best approximate the desired surface boundary? Why?	Yes, in general, but there were difficulties determining the function part of the figure, which could be a parabola or a circumference.
Q6. Did you mention that by moving the referential, the area obtained remains the same?	With the exception of one group of students, everyone else answered positively.
Q7. What effect did the activity have on you? At least three items must be specified.	By participating in this activity, we were able to answer a persistent question in a practical way: how to calculate the areas of non-rectilinear and flat figures. It was difficult to find the expressions of the lines, but finding the expression of the parabola was even more difficult. It was an intriguing task; I discovered new methods for calculating area, improved my understanding of integrals and anti-derivatives, and became acquainted with useful free software; The ability to apply classroom knowledge to a problem was validated, the ability to recognize and work with functions improved, and this task allowed for better consolidation of the learned contents in order to identify where more time in study was required; Understanding how to decompose a figure and obtain the respective areas, application of area definition through integrals, and resolution of figure areas by integrals are all critical developments; Improved understanding of definite integrals, how to calculate irregular areas of real objects, and how to find function expressions; The discovery of another method for calculating areas aided in integral training; Improved understanding of class material and recognition of potential practical applications.

, summarizes the students’ responses:

5. Data Analysis and Discussion

PBL is based on collaboration, active participation, and interaction with the goal of providing new technical knowledge while also enhancing the schooling process in the acquisition of the defined competencies and boosting behavioral competencies. This is the teacher’s first experience with PBL. On this basis, there are accomplishments to mention as well as new realizations that should be discussed, first and foremost from the student’s perspective, but also from a teaching perspective. The confinement caused by the pandemic situation inspired this research and subsequent teaching experience. Despite the uncertainty of the situation, it was critical to respond quickly.

While acting as a tutor, the teacher who participated in this study was concerned with proposing to students a pedagogical activity that would stimulate their curiosity and pro-activity. Important skills that awaken reflective thinking in students, according to [26], include observation, communication, teamwork, judgment, and decision making. As a result, the PBL methodology was used to foster these abilities. It is also worth noting that the enrolled teacher (co-author of this text) has had a moment of realization to reflect on his own practice in the context of a pandemic.

As [27] points out, teachers are no longer the only carriers of knowledge; they also incorporate teaching initiatives, such as the ability to reflect on their practices, into their classes. The value of teachers and what they can do in the classroom should be acknowledged. According to the literature, the student’s involvement in the process was a clear and anticipated aspect from their point of view. Their availability, whether on the part of the teachers or the students, was critical to the challenge’s success.

After adjusting the obtained results, the students presented solutions to the pedagogical challenge and their responses to the reflection questions both before and after the class presentations, proving that the challenge had been overcome. More than a decade ago, ref. [22] stated that problem-based learning appears to be more than a passing fad in education.

6. Conclusions

It is well understood that in each experience utilizing the PBL approach, both teachers and students must take an active role characterized by both parties commitment and, of course, requiring great responsibility of the involved students. However, it is important to note that there was a common shared environment of learning from many different perspectives in this experiment, which was recognized at the end of the process. This experience arose from the need to teach, stimulate, and encourage students’ learning in distance and online classes. As a result, the first challenge scenario required students to provide a reasonable outline of the entire experience.

According to [28], effective reflection is an important component of quality teaching. A reflective teacher is one who can reflect on their own practices in order to improve their teaching. Students benefit from their increased proclivity to develop and improve their professional learning. In fact, in order to outline the activity to be proposed to the students, the teacher felt compelled to investigate and improve their own teaching practices, aiming to imprint an innovative didactic character that stimulated their students’ scientific curiosity.

The students bear a great deal of responsibility for their contribution to their own learning. Students must be committed and active in the learning processes in order to integrate previous knowledge from other courses with new knowledge gained while developing the project. It entails the development of new skills, whether personal or team-based. This methodology encourages individuals to take responsibility for an approach of investigation and innovation by channeling their creativity into knowledge, productive thought, and a desire to learn and solve problems.

Furthermore, the need to explore new competences arose from this unfortunate context, allowing for not only virtuous but also interesting results with a more comprehensive learning process. Students were able to identify some of the skills they had learned and achievements they had made during the activity, highlighting the following:

• Determined the algebraic expressions for functions;
• Improved their ability to recognize and apply functions;
• Consolidated previously learned material to determine where more study time is needed;
• Learned how to decompose a figure and determine its various areas to improve critical thinking skills;
• Discovered how satellite images are used to calculate area in architecture;
• Determined the irregular areas of real-life objects;
• Recognized and used helpful available software;
• Solved a problem and use concepts learned in class.
• Felt a better understanding of the content and concepts after completing the challenge.

This identification leads us to the conclusion that the learning process increased students’ awareness of the process of acquiring and exploring scientific knowledge. Ref. [22] stated in 2006 that “we do live in interesting times—students can now access massive amounts of information that was unheard of a decade ago, and there are more than enough problems to choose from in a range of disciplines”. Nowadays, it has gained even more authenticity. In conclusion, it is necessary to highlight the remarkable progress that results from the methodology change from separate specific teacher work to a much more multi-part structured one. Although these activities had been carried out during the COVID-19 pandemic, the authors consider they should be implemented in regular academic courses, whether in engineering or other areas of knowledge in which mathematics is part of the academic bachelor’s degree.