Predicting Time SeriesUsing an Automatic New Algorithm of the Kalman Filter
Abstract
:1. Introduction
2. Materials and Methods
2.1. Methods
2.2. Data Analysis
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, K.A.; Spulbar, C.; Pinto, P.; Hawaldar, I.T.; Birau, R.; Joisa, J. Using Econometric Models to Manage the Price Risk of Cocoa Beans: A Case from India. Risks 2022, 10, 115. [Google Scholar] [CrossRef]
- Xu, X. Corn Cash Price Forecasting. Am. J. Agric. Econ. 2020, 102, 1297–1320. [Google Scholar] [CrossRef]
- Bórawski, P.; Bórawski, M.B.; Parzonko, A.; Wicki, L.; Rokicki, T.; Perkowska, A.; Dunn, J.W. Development of Organic Milk Production in Poland on the Background of the EU. Agriculture 2021, 11, 323. [Google Scholar] [CrossRef]
- Bo, Y.; Li, X.; Liu, K.; Wang, S.; Zhang, H.; Gao, X.; Zhang, X. Three Decades of Gross Primary Production (GPP) in China: Variations, Trends, Attributions, and Prediction Inferred from Multiple Datasets and Time Series Modeling. Remote Sens. 2022, 14, 2564. [Google Scholar] [CrossRef]
- Wang, B.; Lu, X.; Ren, Y.; Tao, S.; Gao, W. Prediction Model and Influencing Factors of CO2 Micro/Nanobubble Release Based on ARIMA-BPNN. Agriculture 2022, 12, 323. [Google Scholar] [CrossRef]
- Rathore, R.K.; Mishra, D.; Mehra, P.S.; Pal, O.; HASHIM, A.S.; Shapi’i, A.; Ciano, T.; Shutaywi, M. Real-world model for bitcoin price prediction. Inf. Process. Manag. 2022, 59, 102968. [Google Scholar] [CrossRef]
- Benvenuto, D.; Giovanetti, M.; Vassallo, L.; Angeletti, S.; Ciccozzi, M. Application of the ARIMA model on the COVID-2019 epidemic dataset. Data Brief 2020, 29, 105340. [Google Scholar] [CrossRef]
- Fliessbach, A.; Ihle, R. Cycles in cattle and hog prices in South America. Aust. J. Agric. Resour. Econ. 2020, 64, 1167–1183. [Google Scholar] [CrossRef]
- Nason, J.; Smith, G. Measuring the Slowly Evolving Trend in US Inflation with Professional Forecasts. J. Appl. Econom. 2020, 36, 1–17. [Google Scholar] [CrossRef]
- Wu, J.C.; Xia, F. Negative Interest Rate Policy and the Yield Curve. J. Appl. Econom. 2020, 35, 653–672. [Google Scholar] [CrossRef]
- Beckmann, J.; Koop, G.; Korobilis, D.; Schossler, R.A. Exchange rate predictability and dynamic Bayesian learning. J. Appl. Econom. 2020, 35, 410–421. [Google Scholar] [CrossRef]
- Seetharam, Y. Investigating the low-risk anomaly in South Africa. Rev. Behav. Financ. 2021, 14, 277–295. [Google Scholar] [CrossRef]
- Narci, R.; Delattre, M.; Larédo, C.; Vergu, E. Inference for partially observed epidemic dynamics guided by Kalman filtering techniques. Comput. Stat. Data Anal. 2021, 164, 107319. [Google Scholar] [CrossRef]
- Jutinico, A.L.; Vergara, E.; García, C.E.A.; Palencia, M.A.; non, A.D.O.C. Robust Kalman filter for Tuberculosis Incidence Time Series Forecasting. IFAC Pap. 2021, 54, 424–429. [Google Scholar] [CrossRef]
- Aamir, M.; Shabri, A. Modelling and forecasting monthly crude oil price of Pakistan: A comparative study of ARIMA, GARCH and ARIMA Kalman model. AIP Conf. Proc. 2016, 1750, 060015. [Google Scholar] [CrossRef]
- Xu, D.w.; Wang, Y.d.; Jia, L.m.; Qin, Y.; Dong, H.h. Real-time road traffic state prediction based on ARIMA and Kalman filter. Front. Inf. Technol. Electron. Eng. 2017, 18, 287–302. [Google Scholar] [CrossRef]
- Selvaraj, J.; Arunachalam, V.; Coronado-Franco, K. Time-series modeling of fishery landings in the Colombian Pacific Ocean using an ARIMA model. Reg. Stud. Mar. Sci. 2020, 39, 101477. [Google Scholar] [CrossRef]
- Muhammad, A. Using the Kalman filter with ARIMA for the COVID-19 pandemic dataset of Pakistan. Data Brief 2020, 31, 105854. [Google Scholar] [CrossRef]
- Lagos-Álvareza, B.; Padilla, L.; Mateu, J.; Ferreira, G. A Kalman filter method for estimation and prediction of space-time data with an autoregressive structure. J. Stat. Plan. Inference 2019, 203, 117–130. [Google Scholar] [CrossRef]
- Ewald, C.; Zou, Y. Analytic formulas for futures and options for a linear quadratic jump diffusion model with seasonal stochastic volatility and convenience yield: Do fish jump? Eur. J. Oper. Res. 2021, 294, 801–815. [Google Scholar] [CrossRef]
- Pedregal, D.J. New algorithms for automatic modelling and forecasting of decision support systems. Decis. Support Syst. 2021, 148, 113585. [Google Scholar] [CrossRef]
- Wai Hoh, T.; Adrian, R. Model identification for ARMA time series through convolutional neural networks. Decis. Support Syst. 2021, 146, 113544. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The M4 Competition: 100,000 time series and 61 forecasting methods. Int. J. Forecast. 2020, 36, 54–74. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R.S. Comparing Predictive Accuracy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar] [CrossRef]
- Harvey, D.; Leybourne, S.; Newbold, P. Testing the equality of prediction mean squared errors. Int. J. Forecast. 1997, 13, 281–291. [Google Scholar] [CrossRef]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control, revised ed.; Holden-Day: Cleveland, Australia, 1976. [Google Scholar]
- Hannan, E.; Rissanen, J. Recursive estimation of mixed autoregressive-moving average order. Biometrika 1982, 69, 81–94. [Google Scholar] [CrossRef]
- Monahan, J. A note on enforcing stationarity in autoregressive-moving average models. Biometrika 1984, 71, 403–404. [Google Scholar] [CrossRef]
- Harvey, A.C. Forecasting, Structural Time Series Models and the Kalman Filter; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar] [CrossRef]
- Hamilton, J.D. Handbook of Econometrics. In State-Space Models, 1st ed.; Elsevier: Amsterdam, The Netherlands, 1994; Volume 4, Chapter 5; pp. 3039–3080. [Google Scholar] [CrossRef]
- Singhal, A.; Rafiuddin, A. Role of Bitcoin on Economy. Lect. Notes Eng. Comput. Sci. 2014, 2, 1028–1033. [Google Scholar]
- Seetharaman, A.; Saravanan, A.; Patwa, N.; Mehta, J. Impact of Bitcoin as a World Currency. Account. Financ. Res. 2017, 6, 230. [Google Scholar] [CrossRef]
- Holtmeier, M.; Sandner, P. The Impact of Cryptocurrencies on Developing Countries; FSBC Working Paper; Frankfurt School of Finance & Management: Frankfurt am Main, Germany, 2019. [Google Scholar]
- Yaneva, M.; The Impact of Cryptocurrencies on the Economy. CSIE Working Papers. 2020, pp. 113–118. Available online: https://csei.ase.md/wp/files/issue16/WPIssue16113-118YAN.pdf (accessed on 30 October 2021).
- Guo, H.; Zhang, D.; Liu, S.; Wang, L.; Ding, Y. Bitcoin price forecasting: A perspective of underlying blockchain transactions. Decis. Support Syst. 2021, 151, 113650. [Google Scholar] [CrossRef]
- Chen, W.; Xu, H.; Jia, L.; Gao, Y. Machine learning model for Bitcoin exchange rate prediction using economic and technology determinants. Int. J. Forecast. 2021, 37, 28–43. [Google Scholar] [CrossRef]
- Koo, E.; Kim, G. Prediction of Bitcoin price based on manipulating distribution strategy. Appl. Soft Comput. 2021, 110, 107738. [Google Scholar] [CrossRef]
- Shu, M.; Zhu, W. Real-time prediction of Bitcoin bubble crashes. Phys. A Stat. Mech. Its Appl. 2020, 548, 124477. [Google Scholar] [CrossRef]
- Saba, A.I.; Elsheikh, A.H. Forecasting the prevalence of COVID-19 outbreak in Egypt using nonlinear autoregressive artificial neural networks. Process. Saf. Environ. Prot. 2020, 141, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Khan, F.M.; Gupta, R. ARIMA and NAR based prediction model for time series analysis of COVID-19 cases in India. J. Saf. Sci. Resil. 2020, 1, 12–18. [Google Scholar] [CrossRef]
- Petropoulos, F.; Makridakis, S.; Stylianou, N. COVID-19: Forecasting confirmed cases and deaths with a simple time-series model. Int. J. Forecast. 2020, 38, 439–452. [Google Scholar] [CrossRef]
- Hernandez-Matamoros, A.; Fujita, H.; Hayashi, T.; Perez-Meana, H. Forecasting of COVID19 per regions using ARIMA models and polynomial functions. Appl. Soft Comput. 2020, 96, 106610. [Google Scholar] [CrossRef]
- González-Ramírez, M.; Santoyo-Cortés, V.; Arana-Coronado, J.; Muñoz Rodríguez, M. The insertion of Mexico into the global value chain of berries. World Dev. Perspect. 2020, 20, 100240. [Google Scholar] [CrossRef]
- Yang, H.; O’Connell, J. Short-term carbon emissions forecast for aviation industry in Shanghai. J. Clean. Prod. 2020, 275, 122734. [Google Scholar] [CrossRef]
- Khiem, N.M.; Takahashi, Y.; Dong, K.T.P.; Yasuma, H.; Kimura, N. Predicting the price of Vietnamese shrimp products exported to the US market using machine learning. Soil Tillage Res. 2021, 87, 411–423. [Google Scholar] [CrossRef]
- Maldaner, L.; Corrêdo, L.; Canata, T.; Molin, J. Predicting the sugarcane yield in real-time by harvester engine parameters and machine learning approaches. Comput. Electron. Agric. 2021, 181, 105945. [Google Scholar] [CrossRef]
- Mahto, A.; Alam, M.A.; Biswas, R.; Ahmed, J.; Alam, S.I. Short-Term Forecasting of Agriculture Commodities in Context of Indian Market for Sustainable Agriculture by Using the Artificial Neural Network. J. Food Qual. 2021, 2021, 9939906. [Google Scholar] [CrossRef]
- Yin, H.; Jin, D.; Gu, Y.H.; Park, C.J.; Han, S.K.; Yoo, S.J. STL-ATTLSTM: Vegetable Price Forecasting Using STL and Attention Mechanism-Based LSTM. Agriculture 2020, 10, 2492. [Google Scholar] [CrossRef]
- Ioannidis, J.P.; Cripps, S.; Tanner, M.A. Forecasting for COVID-19 has failed. Int. J. Forecast. 2022, 38, 423–438. [Google Scholar] [CrossRef]
- Taleb, N.N.; Bar-Yam, Y.; Cirillo, P. On single point forecasts for fat-tailed variables. Int. J. Forecast. 2022, 38, 413–422. [Google Scholar] [CrossRef]
- Kongcharoen, C.; Kruangpradit, T. Autoregressive Integrated Moving Average with Explanatory Variable (ARIMAX) Model for Thailand Export. Available online: https://forecasters.org/wp-content/uploads/gravity_forms/7-2a51b93047891f1ec3608bdbd77ca58d/2013/07/Kongcharoen_Chaleampong_ISF2013.pdf (accessed on 3 July 2022).
- Yang, M.; Xie, J.; Mao, P.; Wang, C.; Ye, Z. Application of the ARIMAX Model on Forecasting Freeway Traffic Flow. In CICTP 2017: Transportation Reform and Change—Equity, Inclusiveness, Sharing, and Innovation; American Society of Civil Engineers: Reston, VA, USA, 2018; pp. 593–602. [Google Scholar]
- Wang, Q.; Li, S.; Li, R.; Ma, M. Forecasting U.S. Shale Gas Monthly Production Using a Hybrid ARIMA and Metabolic Nonlinear Grey Model. Energy 2018, 160, 378–387. [Google Scholar] [CrossRef]
- Khan, M.M.H.; Muhammad, N.S.; El-Shafie, A. Wavelet Based Hybrid ANN-ARIMA Models for Meteorological Drought Forecasting. J. Hydrol. 2020, 590, 125380. [Google Scholar] [CrossRef]
- Li, Z.; Han, J.; Song, Y. On the forecasting of high frequency financial time series based on ARIMA model improved by Deep Learning. J. Forecast. 2020, 39, 1081–1097. [Google Scholar] [CrossRef]
- Fang, Y.; Guan, B.; Wu, S.; Heravi, S. Optimal Forecast Combination Based on Ensemble Empirical Mode Decomposition for Agricultural Commodity Futures Prices. J. Forecast. 2020, 39, 877–886. [Google Scholar] [CrossRef]
- Guo, Y.; Huajian, Z.; Zhang, S.; Wang, Y.; Chow, D. Modeling and Optimization of Environment in Agricultural Greenhouses for Improving Cleaner and Sustainable Crop Production. J. Clean. Prod. 2020, 285. [Google Scholar] [CrossRef]
- Hecq, A.; Issler, J.; Telg, S. Mixed Causal? Noncausal Autoregressions with Exogenous Regressors. J. Appl. Econ. 2020, 35. [Google Scholar] [CrossRef]
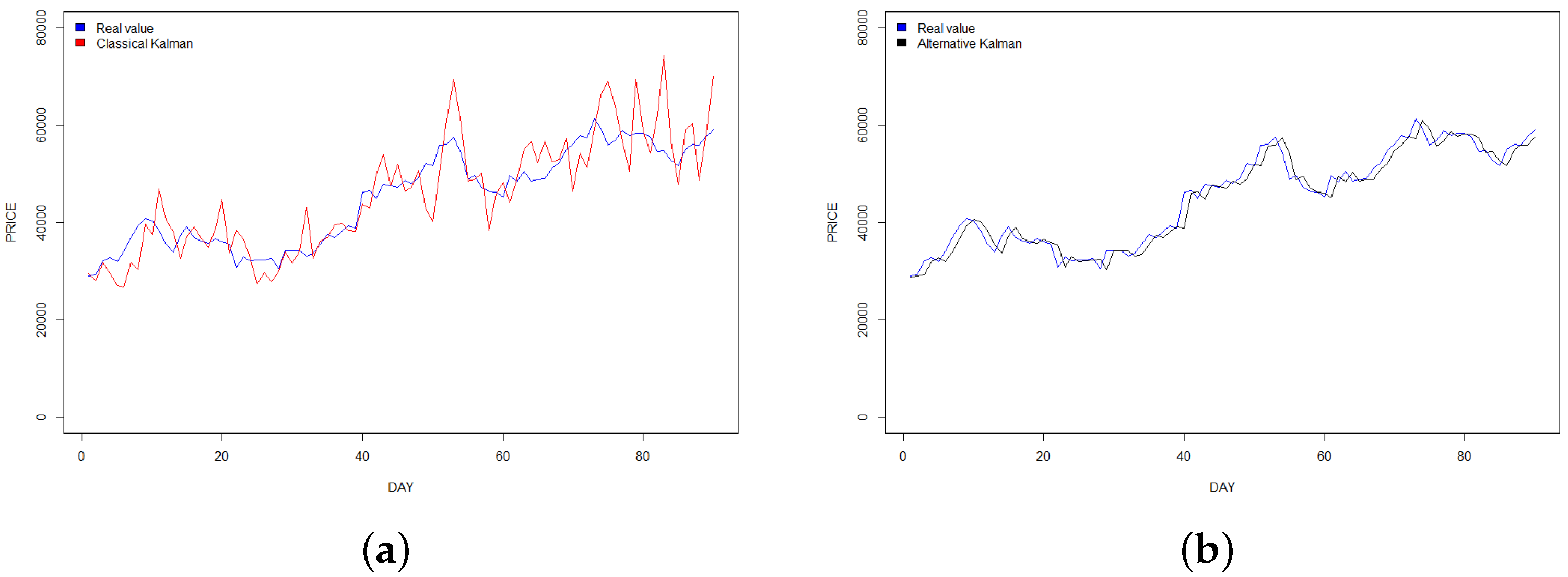

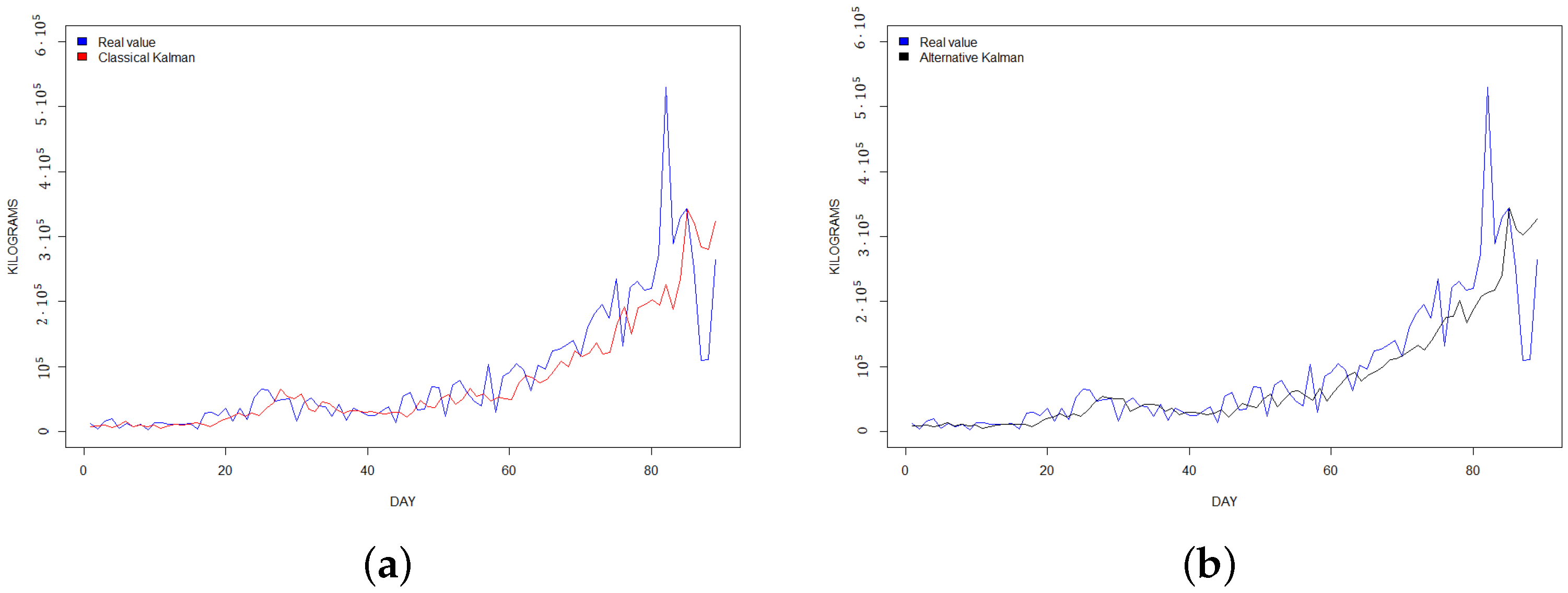
| Bitcoin price | |||||||
| MODEL | AIC | BIC | MAE | RMSE | sMAPE | MASE | |
| Naïve | |||||||
| ARIMA | |||||||
| Classical Kalman | |||||||
| Alternative Kalman | |||||||
| SARS-COV-2 cases | |||||||
| MODEL | AIC | BIC | MAE | RMSE | sMAPE | MASE | |
| Naïve | |||||||
| ARIMA | |||||||
| Classical Kalman | |||||||
| Alternative Kalman | |||||||
| Berry production | |||||||
| MODEL | AIC | BIC | MAE | RMSE | sMAPE | MASE | |
| Naïve | |||||||
| ARIMA | |||||||
| Classical Kalman | |||||||
| Alternative Kalman | |||||||
| Time Series | M-MD Statistic Value (S) | p-Value |
|---|---|---|
| Bitcoin price | × | |
| SARS-COV-2 cases | ||
| Berry production |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borrero, J.D.; Mariscal, J. Predicting Time SeriesUsing an Automatic New Algorithm of the Kalman Filter. Mathematics 2022, 10, 2915. https://doi.org/10.3390/math10162915
Borrero JD, Mariscal J. Predicting Time SeriesUsing an Automatic New Algorithm of the Kalman Filter. Mathematics. 2022; 10(16):2915. https://doi.org/10.3390/math10162915
Chicago/Turabian StyleBorrero, Juan D., and Jesus Mariscal. 2022. "Predicting Time SeriesUsing an Automatic New Algorithm of the Kalman Filter" Mathematics 10, no. 16: 2915. https://doi.org/10.3390/math10162915
APA StyleBorrero, J. D., & Mariscal, J. (2022). Predicting Time SeriesUsing an Automatic New Algorithm of the Kalman Filter. Mathematics, 10(16), 2915. https://doi.org/10.3390/math10162915







