A New Robust and Secure 3-Level Digital Image Watermarking Method Based on G-BAT Hybrid Optimization
Abstract
:1. Introduction
2. Literature Review
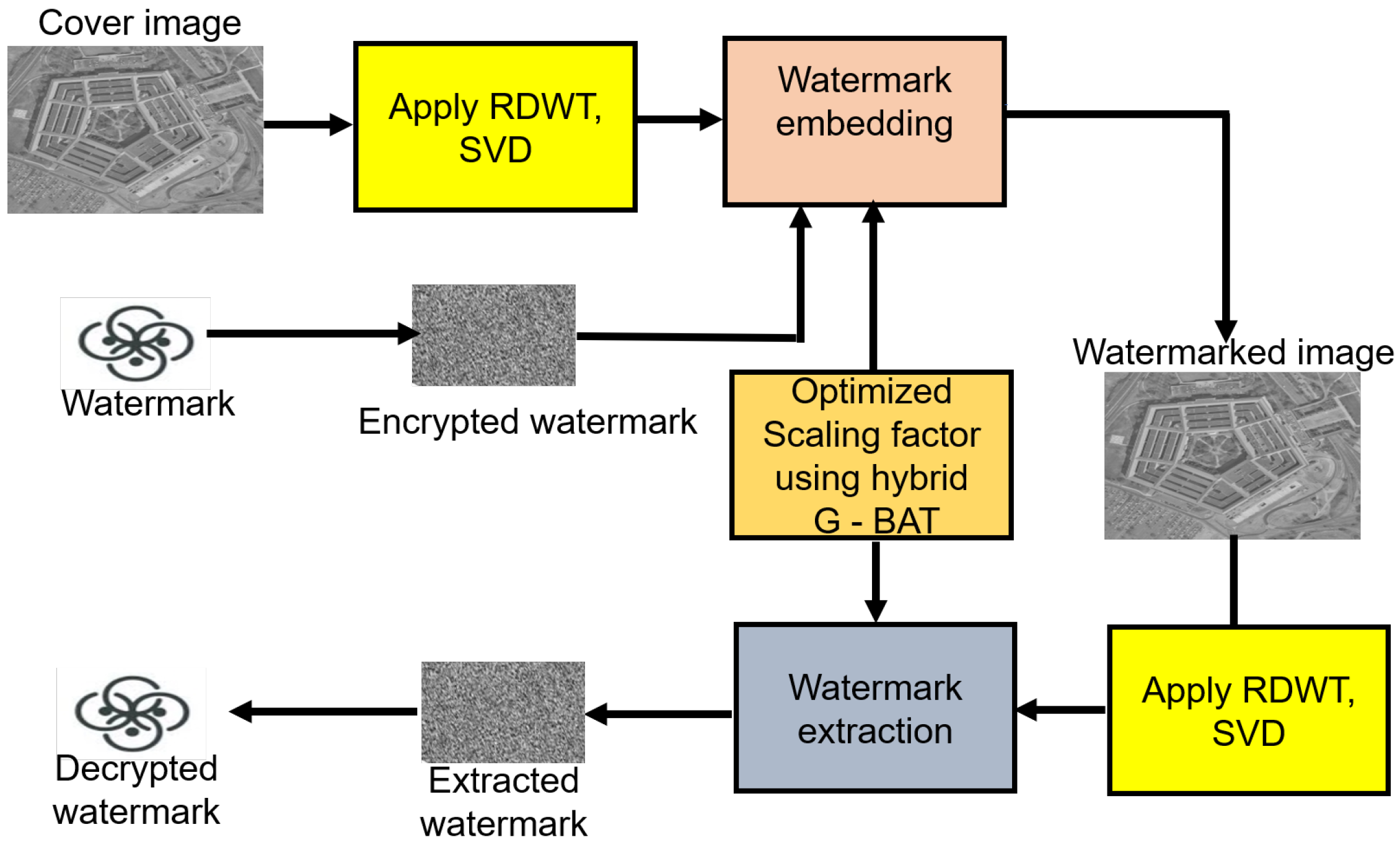
3. Materials and Methods
3.1. Watermark Embedding
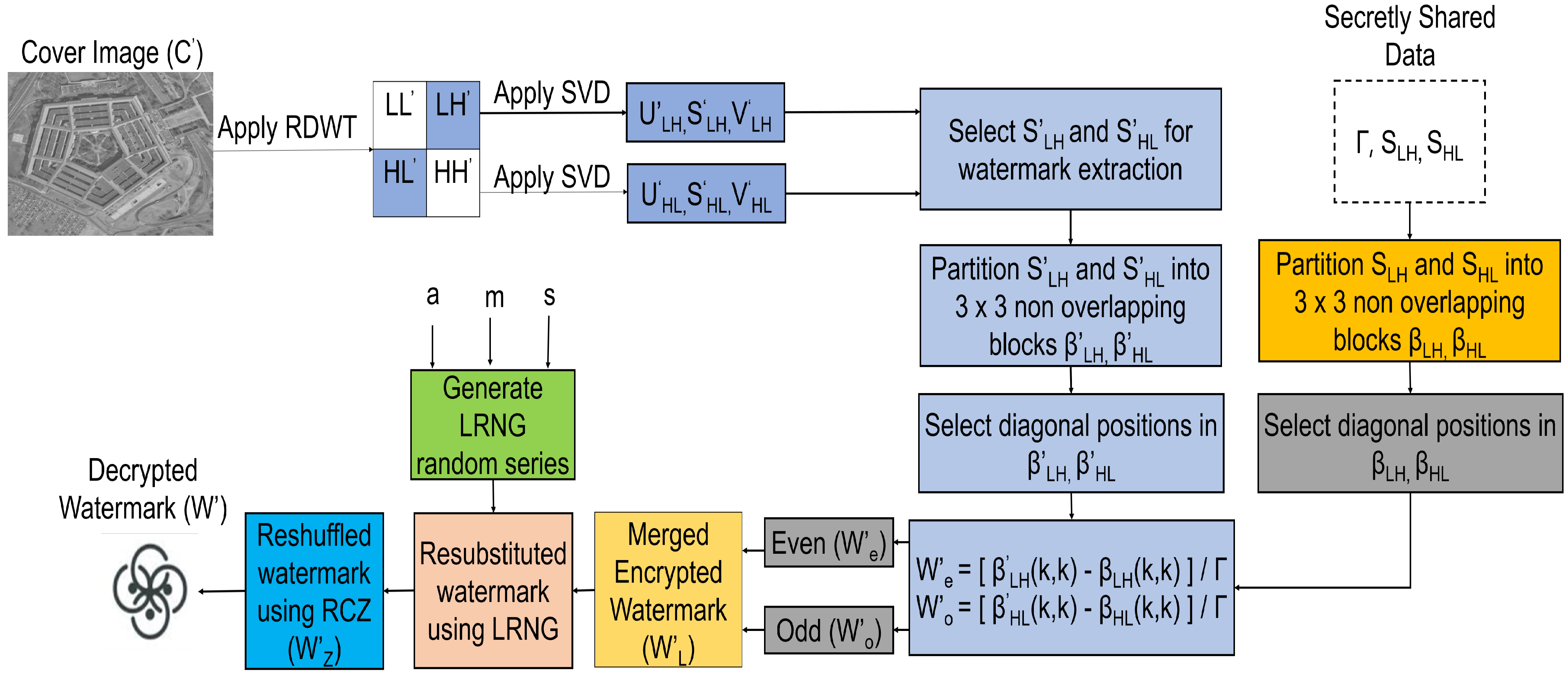
3.2. Watermark Extraction
3.3. Watermark Encryption and Decryption
3.3.1. Watermark Encryption
| Algorithm 1: Algorithm for watermark encryption. |
| Require: Watermark image (W) Ensure: Even () and Odd () watermarks
|
3.3.2. Watermark Decryption
3.4. Scaling Factor Optimization Using Hybrid G-BAT
4. Experimental Results and Discussion
4.1. Imperceptibility Test
4.2. Robustness Test
4.3. Security Test
4.4. Computational Time
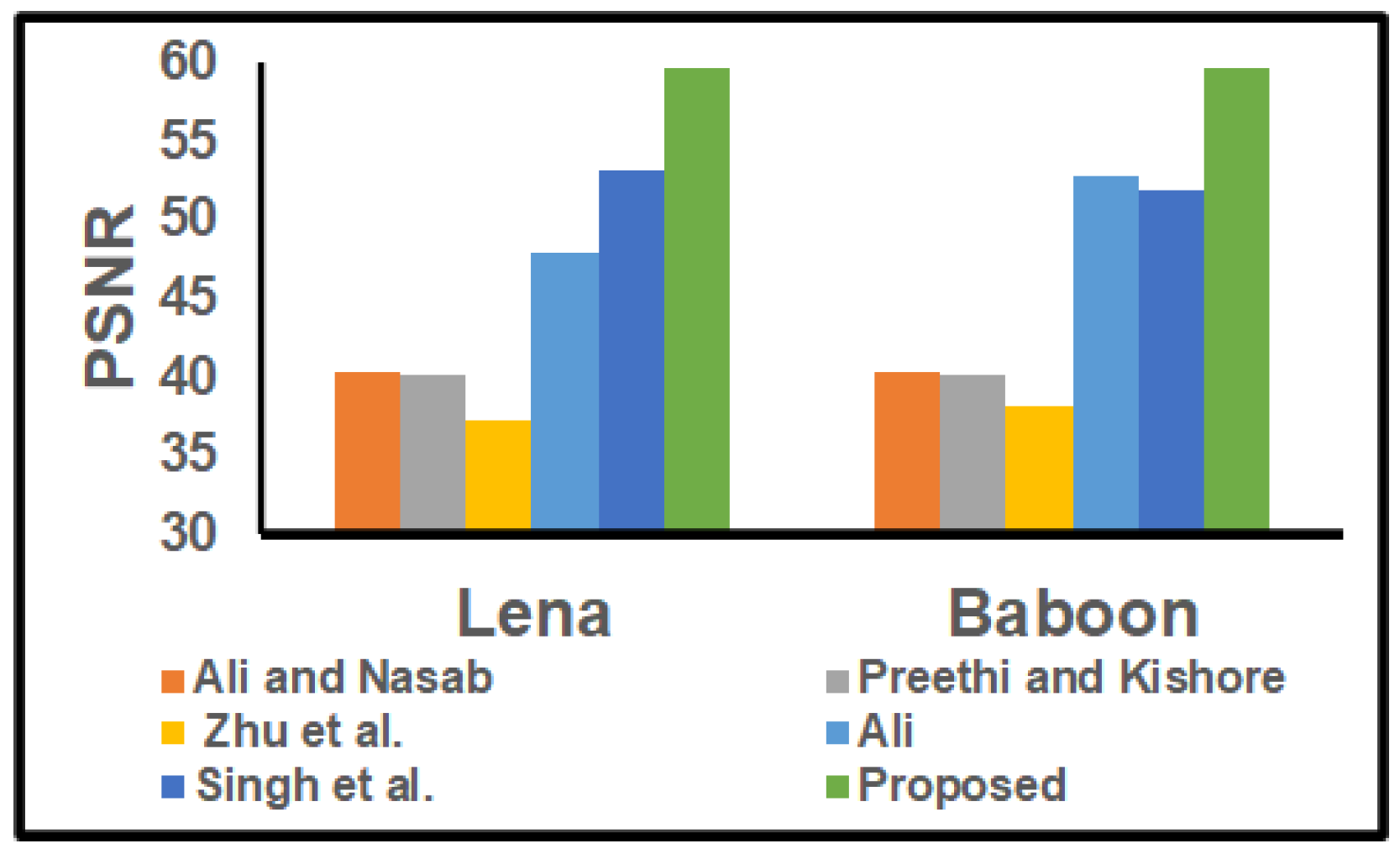
4.5. Comparative Study
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, H.; Peng, M.; Zhong, Y.; Xie, H.; Hao, Z.; Lin, J.; Ma, X.; Hu, X. A Survey on Deep Learning-Based Change Detection from High-Resolution Remote Sensing Images. Remote Sens. 2022, 14, 1552. [Google Scholar] [CrossRef]
- Evsutin, O.; Dzhanashia, K. Watermarking schemes for digital images: Robustness overview. Signal Process. Image Commun. 2022, 100, 116523. [Google Scholar] [CrossRef]
- Zainol, Z.; Teh, J.S.; Alawida, M. Alabdulatif A Hybrid SVD-based image watermarking schemes: A review. IEEE Access 2021, 9, 32931–32968. [Google Scholar]
- Gendreau, M.; Potvin, J.Y. (Eds.) Handbook of Metaheuristics; Springer: New York, NY, USA, 2010; Volume 2.9. [Google Scholar]
- Singh, O.P.; Singh, A.K.; Srivastava, G.; Kumar, N. Image watermarking using soft computing techniques: A comprehensive survey. Multimed. Tools Appl. 2021, 80, 30367–30398. [Google Scholar] [CrossRef]
- Khanduja, N.; Bhushan, B. Recent advances and application of metaheuristic algorithms: A survey (2014–2020). In Metaheuristic and Evolutionary Computation: Algorithms and Applications; Springer: Singapore, 2021; pp. 207–228. [Google Scholar]
- Shankar, R.; Vara Prasad, R.U.; Adiraju, R.V.; Krishna, R.V.; Nandan, D. A Review Paper Based on Image Security Using Watermarking. In Proceedings of the International Conference on Recent Trends in Machine Learning, IoT, Smart Cities and Applications, Hyderabad, India, 28–29 March 2021; Springer: Singapore, 2021; pp. 697–706. [Google Scholar]
- Su, Q.; Liu, D.; Yuan, Z.; Wang, G.; Zhang, X.; Chen, B.; Yao, T. New rapid and robust color image watermarking technique in spatial domain. IEEE Access 2019, 7, 30398–30409. [Google Scholar] [CrossRef]
- Abraham, J.; Paul, V. An imperceptible spatial domain color image watermarking scheme. J. King Saud. Univ.-Comput. Inf. Sci. 2019, 31, 125–133. [Google Scholar] [CrossRef]
- Kunhu, A.; Mansoori, S.A.; Al-Ahmad, H. A Novel Reversible Watermarking Scheme Based on SHA3 for Copyright Protection and Integrity of Satellite Imagery. Int. J. Comput. Sci. Netw. Secur. 2019, 19, 92–102. [Google Scholar]
- Mahmoud, K.; Datta, S.; Flint, J. Frequency Domain Watermarking: An Overview. Int. Arab J. Inf. Technol. 2005, 2, 33–47. [Google Scholar]
- Kang, X.; Chen, Y.; Zhao, F.; Lin, G. Multi-dimensional particle swarm optimization for robust blind image watermarking using intertwining logistic map and hybrid domain. Soft Comput. 2020, 24, 10561–10584. [Google Scholar] [CrossRef]
- Tewari, T.K.; Saxena, V. An improved and robust DCT based digital image watermarking scheme. Int. J. Comput. Appl. 2020, 3, 28–32. [Google Scholar] [CrossRef]
- Pourhadi, A.; Mahdavi-Nasab, H. A robust digital image watermarking scheme based on bat algorithm optimization and SURF detector in SWT domain. Multimed. Tools Appl. 2020, 79, 21653–21677. [Google Scholar] [CrossRef]
- Garg, P.; Kishore, R.R. An efficient and secured blind image watermarking using ABC optimization in DWT and DCT domain. Multimed. Tools Appl. 2021, 1–18. [Google Scholar]
- Zhu, T.; Qu, W.; Cao, W. An optimized image watermarking algorithm based on SVD and IWT. J. Supercomput. 2021, 78, 222–237. [Google Scholar] [CrossRef]
- Alzahrani, A. Enhanced Invisibility and Robustness of Digital Image Watermarking Based on DWT-SVD. Appl. Bionics Biomech. 2022, 2022, 5271600. [Google Scholar] [CrossRef] [PubMed]
- Singh, P.; Devi, K.J.; Thakkar, H.K.; Santamaría, J. Blind and Secured Adaptive Digital Image Watermarking Approach for High Imperceptibility and Robustness. Entropy 2021, 23, 1650. [Google Scholar] [CrossRef]
- Zhu, P.; Jiang, Z.; Zhang, J.; Zhang, Y.; Peng, W. Remote sensing image watermarking based on motion blur degeneration and restoration model. Optik 2021, 248, 168018. [Google Scholar] [CrossRef]
- Yuan, G.; Hao, Q. Digital watermarking secure scheme for remote sensing image protection. China Commun. 2020, 17, 88–98. [Google Scholar] [CrossRef]
- Tong, D.; Ren, N.; Zhu, C. Secure and robust watermarking algorithm for remote sensing images based on compressive sensing. Multimed. Tools Appl. 2019, 78, 16053–16076. [Google Scholar] [CrossRef]
- Mohan, A.; Anand, A.; Singh, A.K.; Dwivedi, R.; Kumar, B. Selective encryption and optimization based watermarking for robust transmission of landslide images. Comput. Electr. Eng. 2021, 95, 107385. [Google Scholar] [CrossRef]
- Hsu, P.H.; Chen, C.C. A robust digital watermarking algorithm for copyright protection of aerial photogrammetric images. Photogramm. Rec. 2016, 31, 51–70. [Google Scholar] [CrossRef]
- Mascagni, M.; Srinivasan, A. Algorithm 806: SPRNG: A scalable library for pseudorandom number generation. ACM Trans. Math. Softw. (TOMS) 2000, 26, 436–461. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper optimisation algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef] [Green Version]
- Ewees, A.A.; Elaziz, M.A.; Houssein, E.H. Improved grasshopper optimization algorithm using opposition-based learning. Expert Syst. Appl. 2018, 112, 156–172. [Google Scholar] [CrossRef]
- Yang, X.-S.; He, X. Bat algorithm: Literature review and applications. Int. J. Bio-Inspired Comput. 2013, 5, 141–149. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. In Nature-Inspired Cooperative Strategies for Optimization (NICSO 2010); Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- The USC-SIPI Image Database. Available online: https:/sipi.usc.edu/database/ (accessed on 20 January 2022).
- The Kaggle Image Database. Available online: https://www.kaggle.com/datasets (accessed on 20 January 2022).
- Rao, Y.R.; Prathapani, N.; Nagabhooshanam, E. Application of normalized cross correlation to image registration. Int. J. Res. Eng. Technol. 2014, 3, 12–16. [Google Scholar]
- Balaska, N.; Ahmida, Z.; Belmeguenai, A.; Boumerdassi, S. Image encryption using a combination of Grain-128a algorithm and Zaslavsky chaotic map. IET Image Process. 2020, 14, 1120–1131. [Google Scholar] [CrossRef]










| Parameter | Initial Value |
|---|---|
| Maximum Number of iterations (MNI) | 30 |
| Swarm size (SZ) | 25 |
| Swarm_minval (min) | 0.001 |
| Swarm_maxval (max) | MNI |
| Swarm generation | SP = min + (max − min) × rand(SZ,1) |
| Termination condition | MNI |
| Loudness (l) | 1 |
| Pulse rate (r0) | 1 |
| Alpha | 0.97 |
| Gamma | 0.1 |
| Freq-min | 0 |
| Freq-max | 2 |
| Gray-Scale Images | ||||||||
|---|---|---|---|---|---|---|---|---|
| Image | With Random = 0.9 | With GO | With BAT | With G-BAT | ||||
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |
| Baboon | 89.03 | 1 | 80.87 | 1 | 79.64 | 1 | 59.74 | 1 |
| Lena | 89.35 | 1 | 75.67 | 1 | 77.92 | 1 | 59.61 | 1 |
| Cameraman | 89.66 | 1 | 81.47 | 1 | 81.03 | 1 | 60.82 | 1 |
| Pirate | 89.21 | 1 | 70.84 | 1 | 66.37 | 1 | 69.26 | 1 |
| Living room | 88.98 | 1 | 73.96 | 1 | 75.82 | 1 | 56.92 | 1 |
| MRI Brain | 89.42 | 1 | 74.29 | 1 | 72.71 | 1 | 62.85 | 1 |
| Color Images | ||||||||
| Image | With Random = 0.9 | With GO | With BAT | With G-BAT | ||||
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |
| Baboon | Inf | 1 | 88.43 | 1 | 85.92 | 1 | 64.27 | 1 |
| Lighthouse | Inf | 1 | 86.45 | 1 | 87.27 | 1 | 71.76 | 1 |
| Peppers | Inf | 1 | 84.23 | 1 | 79.26 | 1 | 59.32 | 1 |
| Splash | Inf | 1 | 81.59 | 1 | 80.75 | 1 | 65.28 | 1 |
| Koala | Inf | 1 | 89.65 | 1 | 88.62 | 1 | 74.24 | 1 |
| Skin | Inf | 1 | 79.27 | 1 | 76.29 | 1 | 58.29 | 1 |
| USC-SIPI [29] Dataset Images | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Image | With Random | With GO | With BAT | With G-BAT | ||||||||||||
| PSNR | SSIM | NC | BER | PSNR | SSIM | NC | BER | PSNR | SSIM | NC | BER | PSNR | SSIM | NC | BER | |
| Img1 | 87.55 | 1 | 0.9789 | 0.0332 | 81.63 | 1 | 0.9919 | 0.0327 | 75.28 | 1 | 0.9931 | 0.0089 | 66.37 | 1 | 0.9996 | 0.0006 |
| Img2 | 87.24 | 1 | 0.9797 | 0.0371 | 80.29 | 1 | 0.9913 | 0.0298 | 76.16 | 1 | 0.9942 | 0.0094 | 68.50 | 1 | 0.9999 | 0.0002 |
| Img3 | 87.32 | 1 | 0.9796 | 0.0374 | 82.82 | 1 | 0.9893 | 0.0301 | 77.13 | 1 | 0.9932 | 0.0085 | 64.35 | 1 | 1 | 0.0002 |
| Img4 | 87.14 | 1 | 0.9798 | 0.0371 | 81.49 | 1 | 0.9903 | 0.0286 | 75.20 | 1 | 0.9949 | 0.0065 | 66.18 | 1 | 0.9998 | 0.0004 |
| Img5 | 87.04 | 1 | 0.9797 | 0.0374 | 79.95 | 1 | 0.9911 | 0.0205 | 68.51 | 1 | 0.9941 | 0.0057 | 62.19 | 1 | 0.9998 | 0.0004 |
| Img6 | 87.17 | 1 | 0.9798 | 0.0371 | 81.63 | 1 | 0.9853 | 0.0302 | 72.61 | 1 | 0.9942 | 0.0085 | 63.28 | 1 | 0.9999 | 0.0002 |
| Img7 | 87.06 | 1 | 0.9799 | 0.0371 | 82.62 | 1 | 0.9868 | 0.0315 | 71.28 | 1 | 0.9921 | 0.0187 | 59.93 | 1 | 0.9999 | 0.0002 |
| Img8 | 87.19 | 1 | 0.9797 | 0.0371 | 78.76 | 1 | 0.9903 | 0.0251 | 76.25 | 1 | 0.9938 | 0.0083 | 60.18 | 1 | 0.9999 | 0.0002 |
| Img9 | 87.08 | 1 | 0.9799 | 0.0371 | 80.61 | 1 | 0.9862 | 0.0253 | 77.51 | 1 | 0.9917 | 0.0176 | 67.92 | 1 | 0.9999 | 0.0002 |
| Img10 | 87.13 | 1 | 0.9798 | 0.0371 | 82.49 | 1 | 0.9827 | 0.0217 | 77.69 | 1 | 0.9929 | 0.0129 | 69.16 | 1 | 0.9999 | 0.0002 |
| Img11 | 86.91 | 1 | 0.9800 | 0.0371 | 79.95 | 1 | 0.9918 | 0.0203 | 76.27 | 1 | 0.9903 | 0.0193 | 64.29 | 1 | 0.9999 | 0 |
| Img12 | 87.09 | 1 | 0.9799 | 0.0371 | 80.62 | 1 | 0.9894 | 0.0296 | 74.18 | 1 | 0.9931 | 0.0153 | 58.93 | 1 | 0.9998 | 0.0004 |
| Img13 | 87.07 | 1 | 0.9799 | 0.0371 | 81.59 | 1 | 0.9905 | 0.0229 | 72.12 | 1 | 0.9941 | 0.0136 | 63.59 | 1 | 0.9999 | 0.0002 |
| Img14 | 87.14 | 1 | 0.9797 | 0.0371 | 78.27 | 1 | 0.9893 | 0.0301 | 74.18 | 1 | 0.9905 | 0.0241 | 61.73 | 1 | 0.9997 | 0.0004 |
| Img15 | 87.09 | 1 | 0.9798 | 0.0371 | 79.27 | 1 | 0.9799 | 0.0298 | 74.14 | 1 | 0.9848 | 0.0253 | 60.37 | 1 | 0.9995 | 0.0012 |
| Kaggle [30] Dataset Images | ||||||||||||||||
| Image | With Random | With GO | With BAT | With G-BAT | ||||||||||||
| PSNR | SSIM | NC | BER | PSNR | SSIM | NC | BER | PSNR | SSIM | NC | BER | PSNR | SSIM | NC | BER | |
| 2.1.08 | Inf | 1 | 0.9692 | 0.0503 | 89.28 | 1 | 0.9819 | 0.0341 | 79.17 | 1 | 0.9925 | 0.0194 | 72.18 | 1 | 0.9997 | 0.0008 |
| 2.1.09 | Inf | 1 | 0.9682 | 0.0503 | 87.18 | 1 | 0.9825 | 0.0361 | 81.28 | 1 | 0.9931 | 0.0162 | 78.92 | 1 | 0.9995 | 0.0012 |
| 2.1.10 | Inf | 1 | 0.9703 | 0.0503 | 88.21 | 1 | 0.9863 | 0.0314 | 83.21 | 1 | 0.9926 | 0.0123 | 74.19 | 1 | 0.9996 | 0.0012 |
| 2.1.11 | Inf | 1 | 0.9720 | 0.0503 | 89.71 | 1 | 0.9827 | 0.0316 | 82.84 | 1 | 0.9916 | 0.0113 | 70.17 | 1 | 0.9995 | 0.0013 |
| 2.1.12 | Inf | 1 | 0.9699 | 0.0503 | 88.61 | 1 | 0.9851 | 0.0381 | 82.81 | 1 | 0.9926 | 0.0202 | 75.72 | 1 | 0.9993 | 0.0018 |
| 2.2.01 | Inf | 1 | 0.9718 | 0.0503 | 87.19 | 1 | 0.9902 | 0.0302 | 81.27 | 1 | 0.9931 | 0.0167 | 72.16 | 1 | 0.9994 | 0.0018 |
| 2.2.02 | Inf | 1 | 0.9655 | 0.0503 | 84.81 | 1 | 0.9852 | 0.0395 | 79.74 | 1 | 0.9918 | 0.0206 | 68.28 | 1 | 0.9992 | 0.0011 |
| 2.2.03 | Inf | 1 | 0.9660 | 0.0503 | 89.71 | 1 | 0.9793 | 0.0426 | 82.65 | 1 | 0.9862 | 0.0184 | 76.13 | 1 | 0.9992 | 0.0010 |
| 2.2.04 | Inf | 1 | 0.9699 | 0.0503 | 88.01 | 1 | 0.9795 | 0.0397 | 81.54 | 1 | 0.9894 | 0.0183 | 78.63 | 1 | 0.9993 | 0.0014 |
| 2.2.05 | Inf | 1 | 0.9718 | 0.0503 | 88.92 | 1 | 0.9804 | 0.0399 | 83.18 | 1 | 0.9875 | 0.0267 | 75.73 | 1 | 0.9993 | 0.0010 |
| 2.2.06 | Inf | 1 | 0.9671 | 0.0503 | 89.90 | 1 | 0.9807 | 0.0403 | 84.28 | 1 | 0.9883 | 0.0204 | 74.82 | 1 | 0.9992 | 0.0012 |
| 2.2.07 | Inf | 1 | 0.9678 | 0.0503 | 85.10 | 1 | 0.9789 | 0.0294 | 79.27 | 1 | 0.9826 | 0.0196 | 71.33 | 1 | 0.9993 | 0.0011 |
| 2.2.08 | Inf | 1 | 0.9717 | 0.0503 | 84.82 | 1 | 0.9821 | 0.0391 | 75.19 | 1 | 0.9904 | 0.0271 | 69.37 | 1 | 0.9994 | 0.0008 |
| 2.2.09 | Inf | 1 | 0.9669 | 0.0503 | 82.64 | 1 | 0.9749 | 0.0396 | 77.26 | 1 | 0.9827 | 0.0292 | 68.65 | 1 | 0.9993 | 0.0012 |
| 2.2.10 | Inf | 1 | 0.9652 | 0.0503 | 81.62 | 1 | 0.9729 | 0.0392 | 79.86 | 1 | 0.9826 | 0.02892 | 72.48 | 1 | 0.9992 | 0.0016 |
| Gray-Scale IMAGES | ||||||||
|---|---|---|---|---|---|---|---|---|
| Image | With Random = 0.9 | With GO | With BAT | With G-BAT | ||||
| NC | BER | NC | BER | NC | BER | NC | BER | |
| Baboon | 0.9208 | 0.1084 | 0.9482 | 0.1062 | 0.9681 | 0.0089 | 0.9993 | 0.0008 |
| Lena | 0.9201 | 0.1116 | 0.9901 | 0.0197 | 0.9902 | 0.1092 | 0.9995 | 0.0012 |
| Cameraman | 0.9275 | 0.1076 | 0.9350 | 0.1051 | 0.9405 | 0.1062 | 0.9894 | 0.0085 |
| Pirate | 0.9205 | 0.1084 | 0.9968 | 0.1079 | 0.9974 | 0.0976 | 0.9994 | 0.0012 |
| Living room | 0.9208 | 0.1087 | 0.9797 | 0.1074 | 0.9683 | 0.1064 | 0.9991 | 0.0010 |
| MRI Brain | 0.9208 | 0.1081 | 0.9873 | 0.1076 | 0.9902 | 0.1062 | 0.9993 | 0.0006 |
| Color Images | ||||||||
| Image | With Random = 0.9 | With GO | With BAT | With G-BAT | ||||
| NC | BER | NC | BER | NC | BER | NC | BER | |
| Baboon | 0.9147 | 0.1182 | 0.9472 | 0.1103 | 0.9527 | 0.1095 | 0.9990 | 0.0042 |
| Lighthouse | 0.9147 | 0.1163 | 0.9381 | 0.1154 | 0.9294 | 0.1183 | 0.9986 | 0.0088 |
| Peppers | 0.9287 | 0.1194 | 0.9328 | 0.1119 | 0.9528 | 0.1104 | 0.9993 | 0.0014 |
| Splash | 0.9261 | 0.1173 | 0.9481 | 0.1103 | 0.9517 | 0.1100 | 0.9992 | 0.0008 |
| Koala | 0.9151 | 0.1160 | 0.9286 | 0.0953 | 0.9319 | 0.0915 | 0.9988 | 0.0086 |
| Skin | 0.9318 | 0.1121 | 0.9528 | 0.1101 | 0.9628 | 0.1086 | 0.9997 | 0.0002 |
| Attack | With Random | With GO | With BAT | With G-BAT | ||||
|---|---|---|---|---|---|---|---|---|
| NC | BER | NC | BER | NC | BER | NC | BER | |
| Sharpening | 0.8895 | 0.2803 | 0.9217 | 0.1281 | 0.9728 | 0.01071 | 0.9892 | 0.0794 |
| Gaussian filter () | 0.9101 | 0.2163 | 0.9382 | 0.1286 | 0.9518 | 0.1082 | 0.9993 | 0.0892 |
| Median filter () | 0.9028 | 0.2518 | 0.9127 | 0.2107 | 0.9219 | 0.1128 | 0.9509 | 0.0228 |
| Average filter () | 0.8182 | 0.3286 | 0.8818 | 0.1729 | 0.9018 | 0.1384 | 0.9493 | 0.0273 |
| Weiner filter () | 0.7825 | 0.3918 | 0.8719 | 0.3017 | 0.8921 | 0.2061 | 0.9785 | 0.0086 |
| Butterworth filter (G = 2, F = 20) | 0.8828 | 0.2821 | 0.9156 | 0.2184 | 0.9418 | 0.0419 | 0.9992 | 0.0012 |
| Salt & pepper (0.0002) | 0.6692 | 0.4182 | 0.6985 | 0.3995 | 0.7928 | 0.2987 | 0.9103 | 0.0698 |
| Gaussian noise | 0.7382 | 0.2981 | 0.8129 | 0.1927 | 0.8528 | 0.1629 | 0.9028 | 0.0518 |
| Speckle noise | 0.7185 | 0.3276 | 0.7219 | 0.2916 | 0.7621 | 0.1986 | 0.8828 | 0.0429 |
| Compression (60%) | 0.8018 | 0.3281 | 0.8291 | 0.2281 | 0.8417 | 0.1192 | 0.9105 | 0.0102 |
| Gamma correction (0.3) | 0.8882 | 0.1719 | 0.9018 | 0.0917 | 0.8827 | 0.0281 | 0.9945 | 0.0061 |
| Histogram equivalent | 0.9592 | 0.2718 | 0.9401 | 0.2418 | 0.9702 | 0.1001 | 0.9991 | 0.0064 |
| Shear | 0.6519 | 0.3998 | 0.7019 | 0.3153 | 0.7663 | 0.1718 | 0.8483 | 0.0615 |
| Row cut (10) | 0.8716 | 0.3641 | 0.8941 | 0.3003 | 0.9142 | 0.1318 | 0.9651 | 0.0063 |
| Column cut (10) | 0.8852 | 0.2164 | 0.8931 | 0.1953 | 0.9172 | 0.0963 | 0.9585 | 0.0084 |
| Rotation () | 0.6318 | 0.4071 | 0.6528 | 0.3821 | 0.6629 | 0.3628 | 0.7027 | 0.3017 |
| Scaling (0.5, 2) | 0.6719 | 0.3715 | 0.6925 | 0.3514 | 0.7016 | 0.3217 | 0.7182 | 0.3012 |
| Translate (0.25, 0.25) | 0.8718 | 0.2614 | 0.8964 | 0.1915 | 0.9012 | 0.1216 | 0.9126 | 0.1174 |
| Cropping | 0.6056 | 0.5123 | 0.6515 | 0.3413 | 0.6414 | 0.3516 | 0.7625 | 0.3016 |
| Attack | With Random | With GO | With BAT | With G-BAT | ||||
|---|---|---|---|---|---|---|---|---|
| NC | BER | NC | BER | NC | BER | NC | BER | |
| Sharpening | 0.8829 | 0.2817 | 0.9161 | 0.1617 | 0.9672 | 0.0176 | 0.9837 | 0.0881 |
| Gaussian filter () | 0.9026 | 0.2185 | 0.9329 | 0.2086 | 0.9629 | 0.1718 | 0.9991 | 0.0995 |
| Median filter () | 0.8827 | 0.3016 | 0.9286 | 0.2894 | 0.9653 | 0.1286 | 0.9931 | 0.0264 |
| Average filter () | 0.8242 | 0.3172 | 0.8931 | 0.1842 | 0.9161 | 0.1281 | 0.9519 | 0.0219 |
| Weiner filter () | 0.7962 | 0.4271 | 0.8871 | 0.2715 | 0.9227 | 0.1852 | 0.9728 | 0.0092 |
| Butterworth filter (G = 2, F = 20) | 0.8731 | 0.2951 | 0.9042 | 0.2615 | 0.9318 | 0.0617 | 0.9991 | 0.0012 |
| Salt & pepper (0.0002) | 0.6318 | 0.5178 | 0.6935 | 0.5071 | 0.7418 | 0.4821 | 0.9065 | 0.0762 |
| Gaussian noise | 0.7194 | 0.3728 | 0.7418 | 0.2618 | 0.7726 | 0.1940 | 0.8986 | 0.0721 |
| Speckle noise | 0.7041 | 0.3718 | 0.7318 | 0.3015 | 0.7821 | 0.2518 | 0.8731 | 0.0528 |
| Compression (60%) | 0.7982 | 0.3517 | 0.8133 | 0.2185 | 0.8374 | 0.1027 | 0.9082 | 0.0124 |
| Gamma correction (0.3) | 0.8832 | 0.1842 | 0.8951 | 0.1372 | 0.9226 | 0.0264 | 0.9921 | 0.0081 |
| Histogram equivalent | 0.9521 | 0.2751 | 0.9427 | 0.2518 | 0.9671 | 0.1052 | 0.9990 | 0.0071 |
| Shear | 0.6417 | 0.4178 | 0.6682 | 0.3194 | 0.7327 | 0.2718 | 0.8381 | 0.0861 |
| Row cut (10) | 0.8618 | 0.3812 | 0.8817 | 0.3027 | 0.9026 | 0.1724 | 0.9528 | 0.0075 |
| Column cut (10) | 0.8863 | 0.2018 | 0.9021 | 0.1862 | 0.9261 | 0.0981 | 0.9692 | 0.0029 |
| Rotation () | 0.6281 | 0.4281 | 0.6381 | 0.4186 | 0.6528 | 0.3919 | 0.7526 | 0.3672 |
| Scaling (0.5, 2) | 0.6682 | 0.3819 | 0.6836 | 0.3729 | 0.6927 | 0.3317 | 0.7091 | 0.3281 |
| Translate (0.25, 0.25) | 0.8662 | 0.2718 | 0.8826 | 0.1829 | 0.8928 | 0.1286 | 0.9071 | 0.1174 |
| Cropping | 0.6219 | 0.4289 | 0.6487 | 0.3718 | 0.6518 | 0.2518 | 0.7729 | 0.2926 |
| Attacks | Img1 | 2.1.01 | 2.1.02 | |||
|---|---|---|---|---|---|---|
| NC | BER | NC | BER | NC | BER | |
| Sharpening | 0.9867 | 0.1418 | 0.9842 | 0.0879 | 0.9921 | 0.0631 |
| Gaussian filter () | 0.9992 | 0.1078 | 0.9994 | 0.0085 | 0.9995 | 0.0064 |
| Median filter () | 0.9429 | 0.02819 | 0.9962 | 0.0221 | 0.9782 | 0.0185 |
| Average filter () | 0.9528 | 0.0221 | 0.9582 | 0.0221 | 0.9642 | 0.0201 |
| Weiner filter () | 0.9885 | 0.0065 | 0.9782 | 0.0069 | 0.9796 | 0.0059 |
| Butterworth filter (G = 2, F = 20) | 0.9991 | 0.0019 | 0.9994 | 0.0010 | 0.9995 | 0.0008 |
| Salt & pepper (0.0002) | 0.8907 | 0.08826 | 0.9105 | 0.0716 | 0.9108 | 0.0685 |
| Gaussian noise | 0.8927 | 0.0818 | 0.9021 | 0.0702 | 0.9281 | 0.0521 |
| Speckle noise | 0.8828 | 0.0796 | 0.8921 | 0.0491 | 0.8985 | 0.0384 |
| Compression (60%) | 0.9192 | 0.0119 | 0.9087 | 0.0131 | 0.9105 | 0.01301 |
| Gamma correction (0.3) | 0.9928 | 0.0069 | 0.9942 | 0.0086 | 0.9962 | 0.0076 |
| Histogram equivalent | 0.9987 | 0.0075 | 0.9986 | 0.0083 | 0.9990 | 0.0075 |
| Shear | 0.8164 | 0.0834 | 0.8291 | 0.0827 | 0.8392 | 0.0792 |
| Row cut (10) | 0.9692 | 0.0063 | 0.9631 | 0.0062 | 0.9684 | 0.0058 |
| Column cut (10) | 0.9719 | 0.0077 | 0.9728 | 0.0063 | 0.9785 | 0.0053 |
| Rotation () | 0.7072 | 0.2918 | 0.6951 | 0.3061 | 0.7051 | 0.2896 |
| Scaling (0.5,2) | 0.7132 | 0.3941 | 0.7095 | 0.3386 | 0.7196 | 0.3172 |
| Translate (0.25,0.25) | 0.9205 | 0.1062 | 0.9077 | 0.1173 | 0.9142 | 0.1023 |
| Cropping | 0.7562 | 0.3613 | 0.7718 | 0.3913 | 0.7821 | 0.3872 |
| Image | CC between W, EW | CC between W, DW | Entropy of W | Entropy of EW | ||||
|---|---|---|---|---|---|---|---|---|
| H | V | D | H | V | D | |||
| Watermark | −0.2838 | −0.2665 | −0.2715 | 1 | 1 | 1 | 0.8930 | 1.0723 |
| Cameraman | −0.5248 | −0.4789 | −0.4750 | 1 | 1 | 1 | 0.9880 | 0.9985 |
| Lena | −0.3430 | −0.2804 | −0.2542 | 1 | 1 | 1 | 0.7194 | 0.9671 |
| Baboon | −0.5231 | −0.5669 | −0.5494 | 1 | 1 | 1 | 0.9960 | 1.8954 |
| MRI Brain | −0.6319 | −0.5724 | −0.5633 | 1 | 1 | 1 | 0.9979 | 1.0276 |
|
Gray-Scale Image | Embedding Time | Extraction Time | Color Image | Embedding Time | Extraction Time |
|---|---|---|---|---|---|
| Lena | 0.150429 | 0.055273 | Baboon | 0.269723 | 0.095462 |
| Cameraman | 0.150136 | 0.065511 | Peppers | 0.240605 | 0.077382 |
| Img1 | 0.156776 | 0.057896 | 2.1.08 | 0.250033 | 0.087393 |
| Img2 | 0.151721 | 0.056821 | 2.1.09 | 0.239758 | 0.075609 |
| Img3 | 0.150708 | 0.055821 | 2.1.10 | 0.241862 | 0.082617 |
| Parameter | Ali and Nasab | Preeti and Kishore | Zhu et al. | Ali | Singh et al. | Proposed |
|---|---|---|---|---|---|---|
| [14] | [15] | [16] | [17] | [18] | ||
| Transformation scheme | SWT+SURF | DWT+DCT | IWT+SVD | DWT+SVD | IWT_ SVD | RDWT+SVD |
| Cover image size | ||||||
| Watermark size | ||||||
| Optimization algorithm | BAT | ABC | GA | NO | GA, ABC, FO | Hybrid G-BAT |
| Security technique | Arnold map | No | Affine transform | NO | Pseudo random key | 3 level security |
| Embedding capacity | 0.0039 | 0.01562 | 0.0039 | 0.25 | 0.01562 | 0.0625 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Devi, K.J.; Singh, P.; Dash, J.K.; Thakkar, H.K.; Santamaría, J.; Krishna, M.V.J.; Romero-Manchado, A. A New Robust and Secure 3-Level Digital Image Watermarking Method Based on G-BAT Hybrid Optimization. Mathematics 2022, 10, 3015. https://doi.org/10.3390/math10163015
Devi KJ, Singh P, Dash JK, Thakkar HK, Santamaría J, Krishna MVJ, Romero-Manchado A. A New Robust and Secure 3-Level Digital Image Watermarking Method Based on G-BAT Hybrid Optimization. Mathematics. 2022; 10(16):3015. https://doi.org/10.3390/math10163015
Chicago/Turabian StyleDevi, Kilari Jyothsna, Priyanka Singh, Jatindra Kumar Dash, Hiren Kumar Thakkar, José Santamaría, Musalreddy Venkata Jayanth Krishna, and Antonio Romero-Manchado. 2022. "A New Robust and Secure 3-Level Digital Image Watermarking Method Based on G-BAT Hybrid Optimization" Mathematics 10, no. 16: 3015. https://doi.org/10.3390/math10163015
APA StyleDevi, K. J., Singh, P., Dash, J. K., Thakkar, H. K., Santamaría, J., Krishna, M. V. J., & Romero-Manchado, A. (2022). A New Robust and Secure 3-Level Digital Image Watermarking Method Based on G-BAT Hybrid Optimization. Mathematics, 10(16), 3015. https://doi.org/10.3390/math10163015








