Dynamics of Eyring–Powell Nanofluids When Bioconvection and Lorentz Forces Are Significant: The Case of a Slender Elastic Sheet of Variable Thickness with Porous Medium
Abstract
:1. Introduction
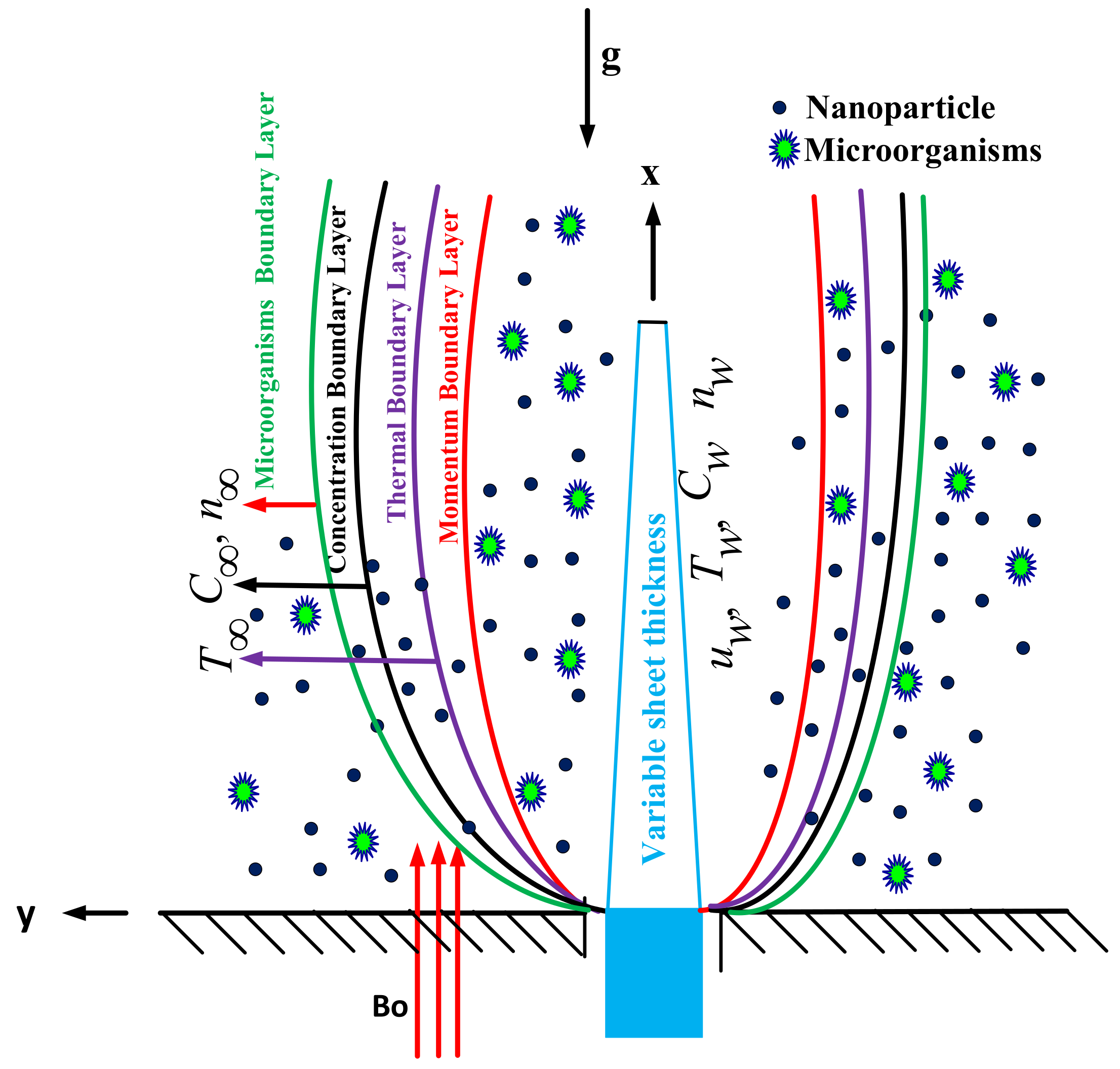
2. Physical Model and Mathematical Formulation
3. Physical Quantities
4. Solution Procedure
5. Results and Discussion
6. Conclusions
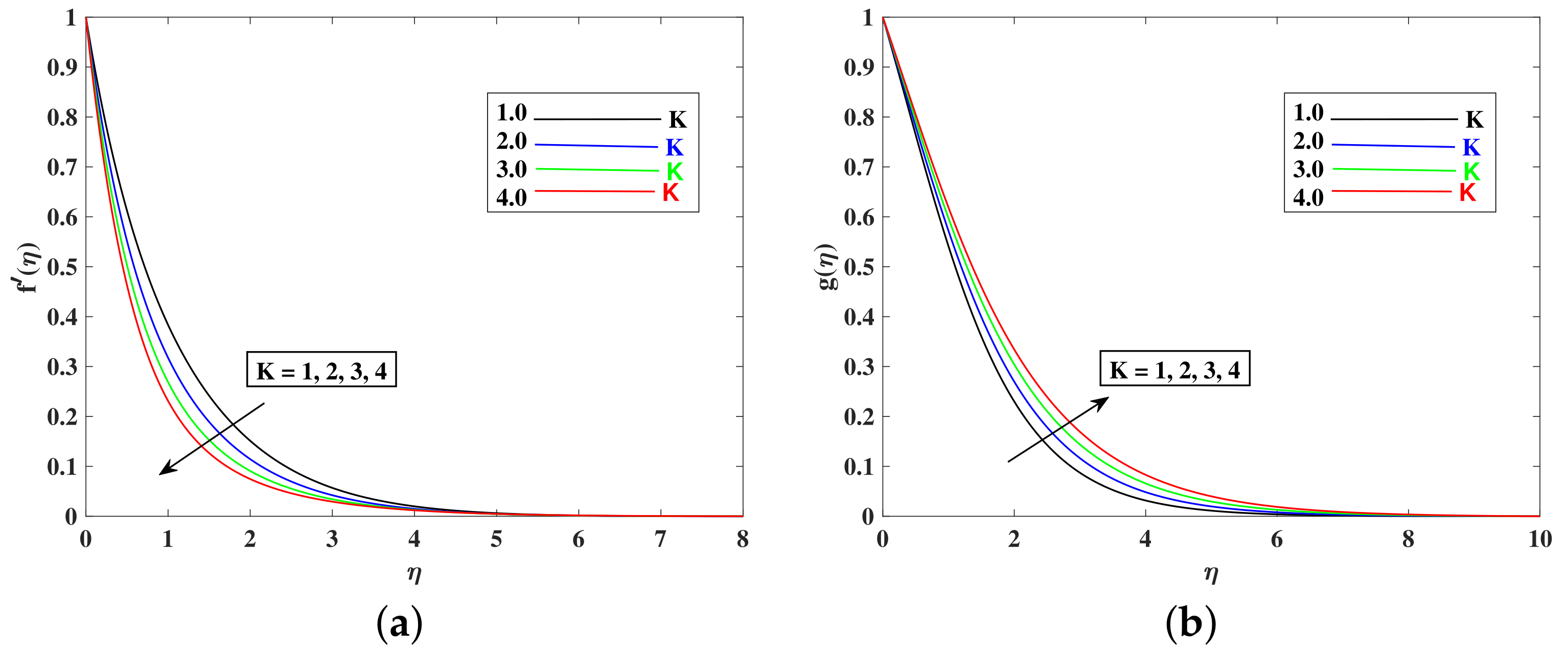
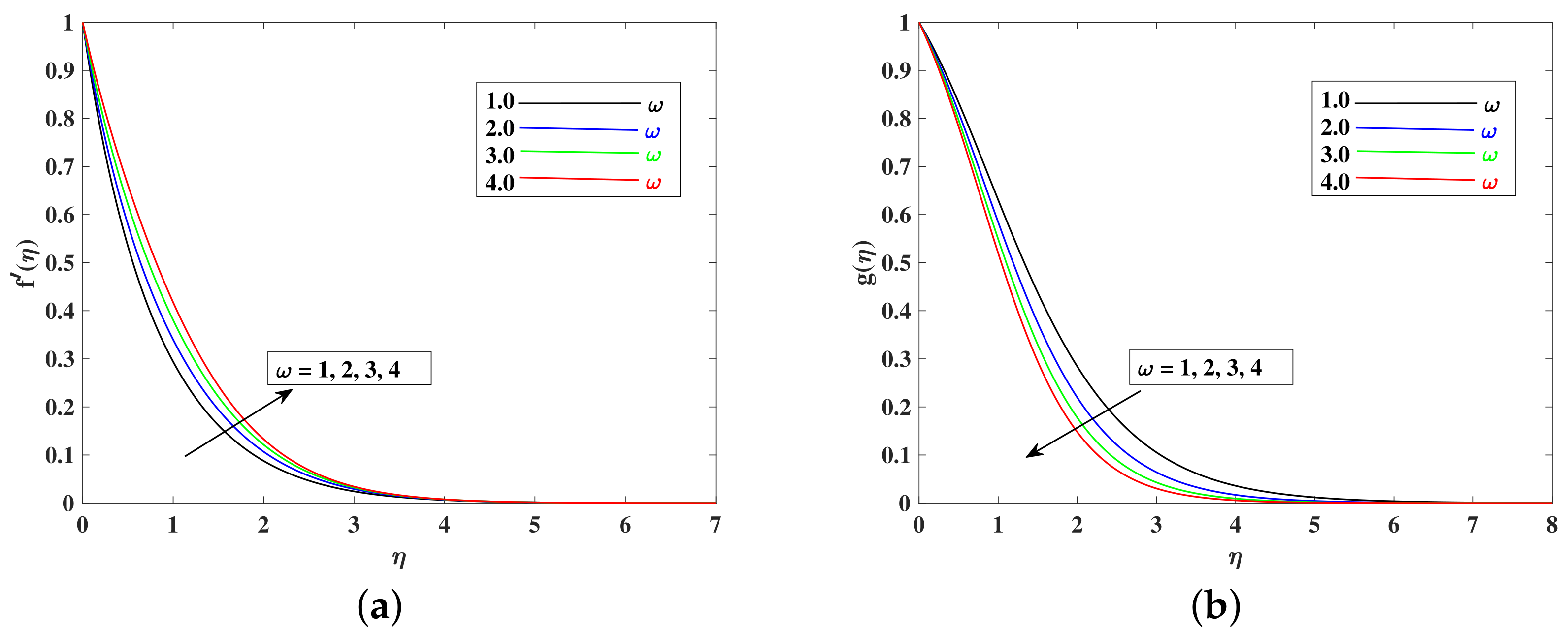
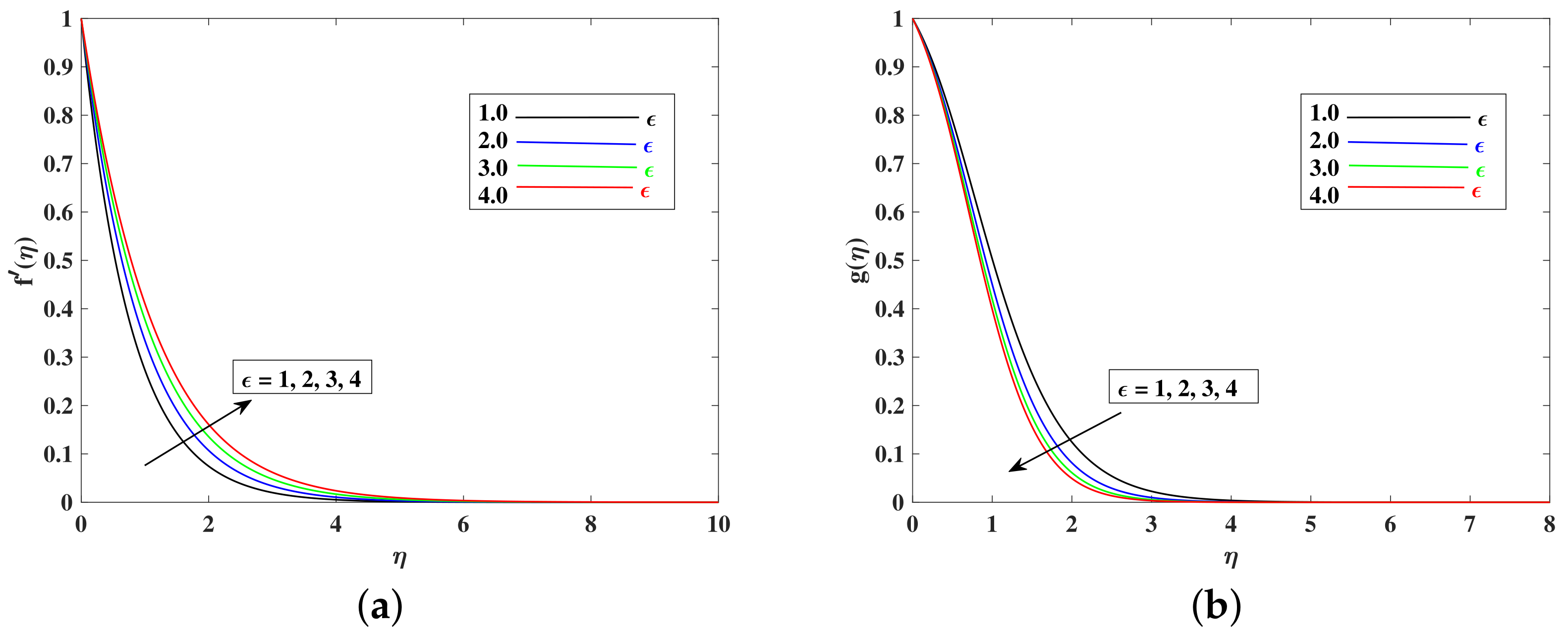
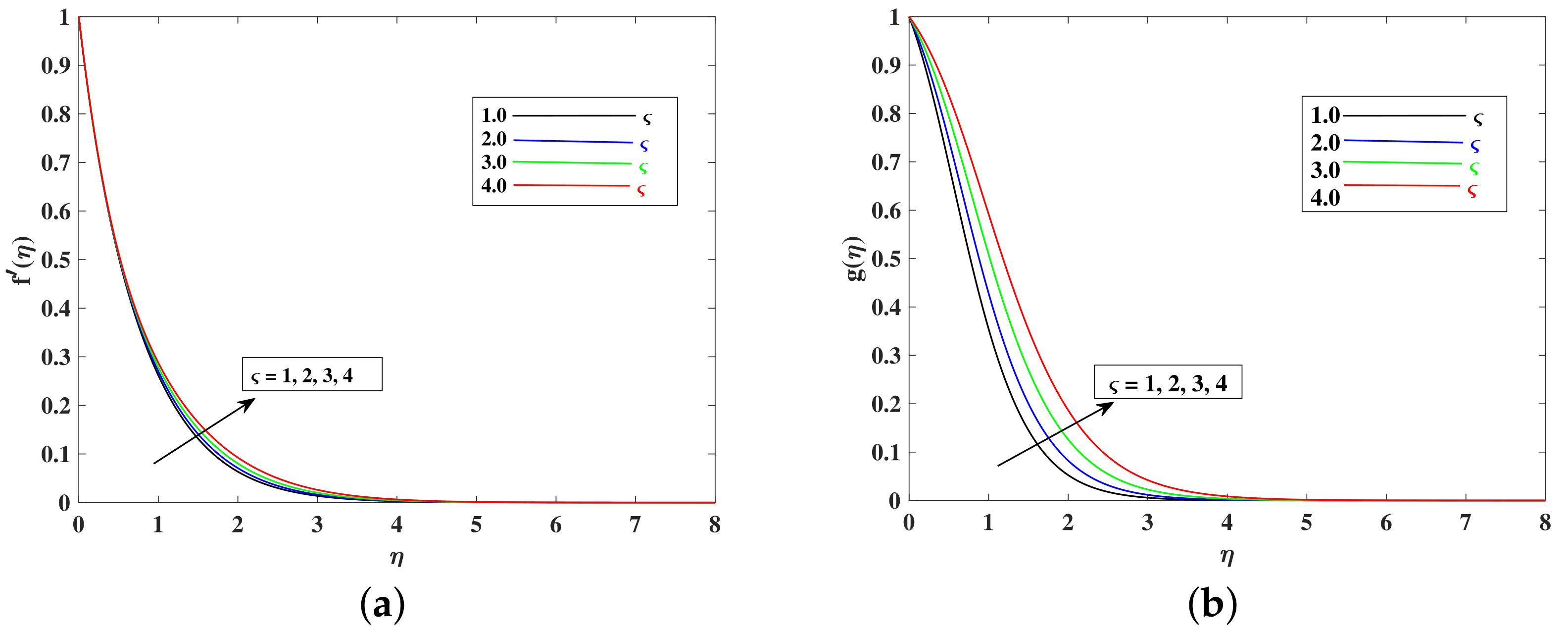
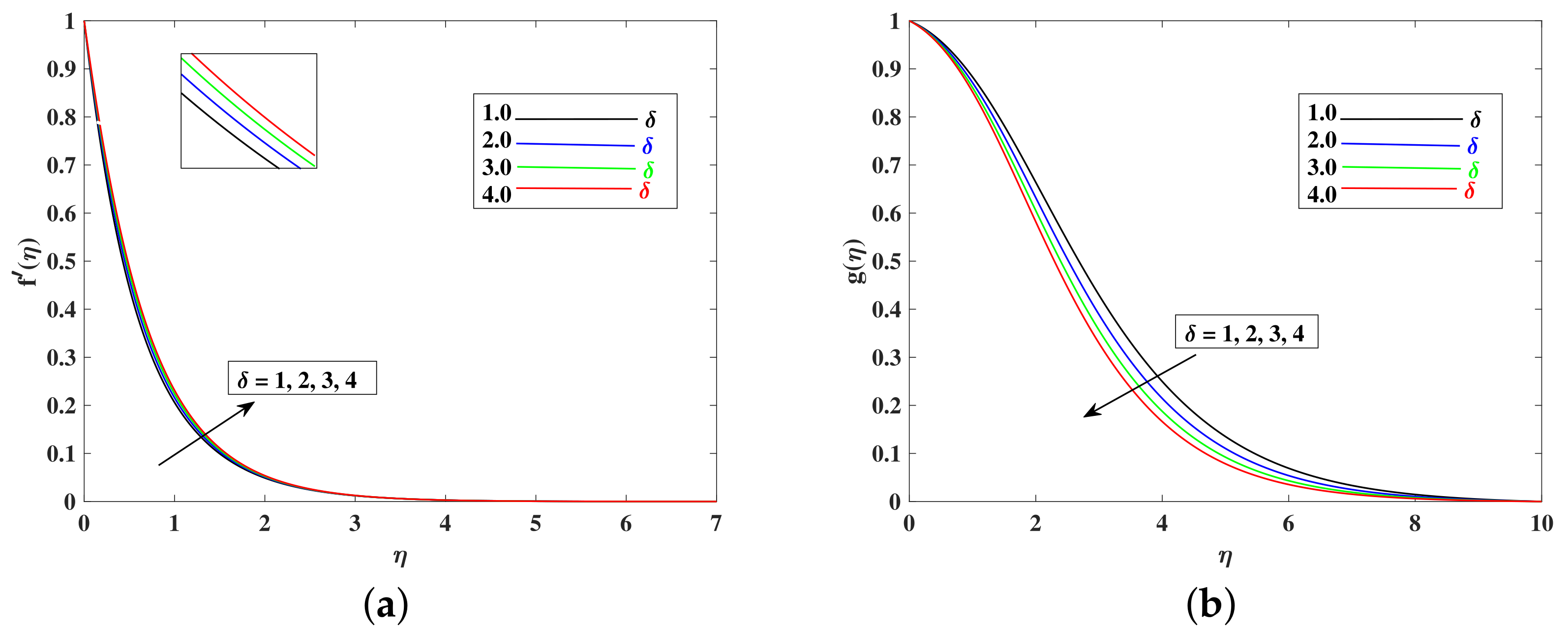
- The fluid’s velocity increases with larger values of the , , , and and it decrease with enhancements in M, K, , and because these parameters are responsible for decelerating the flow.
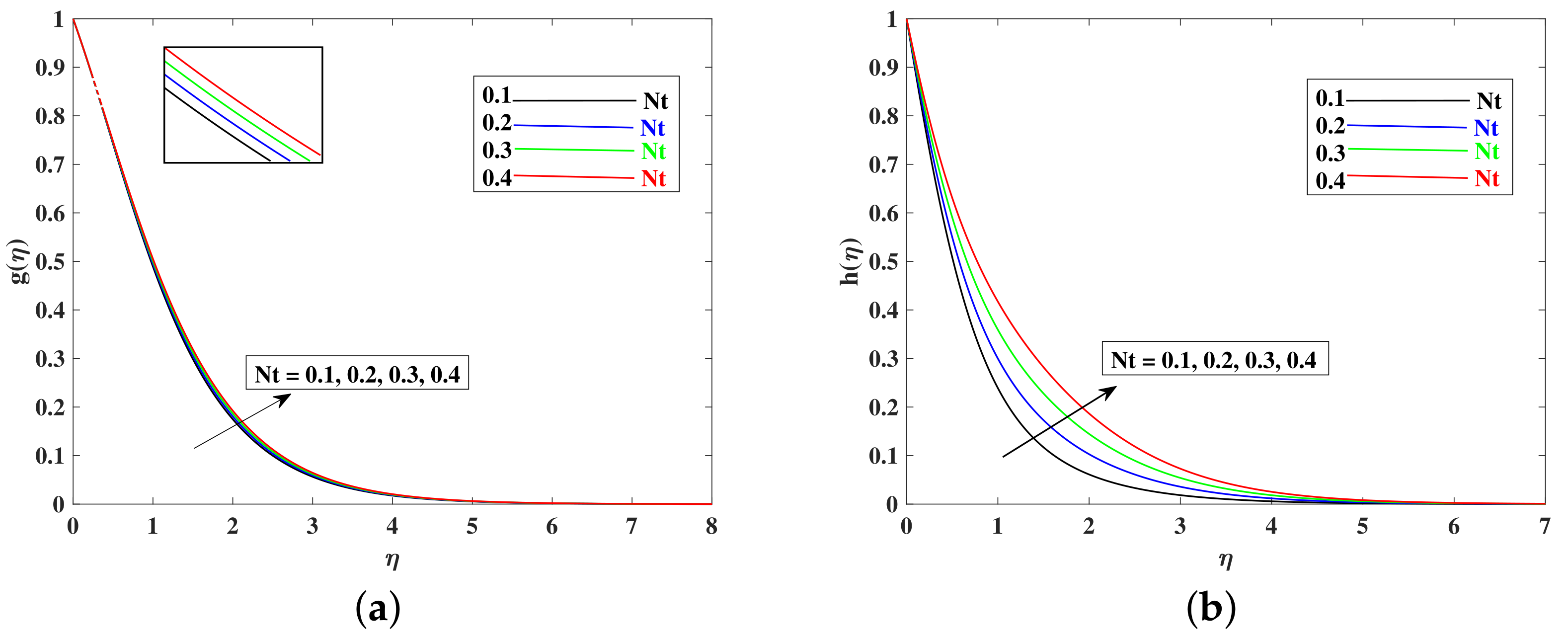
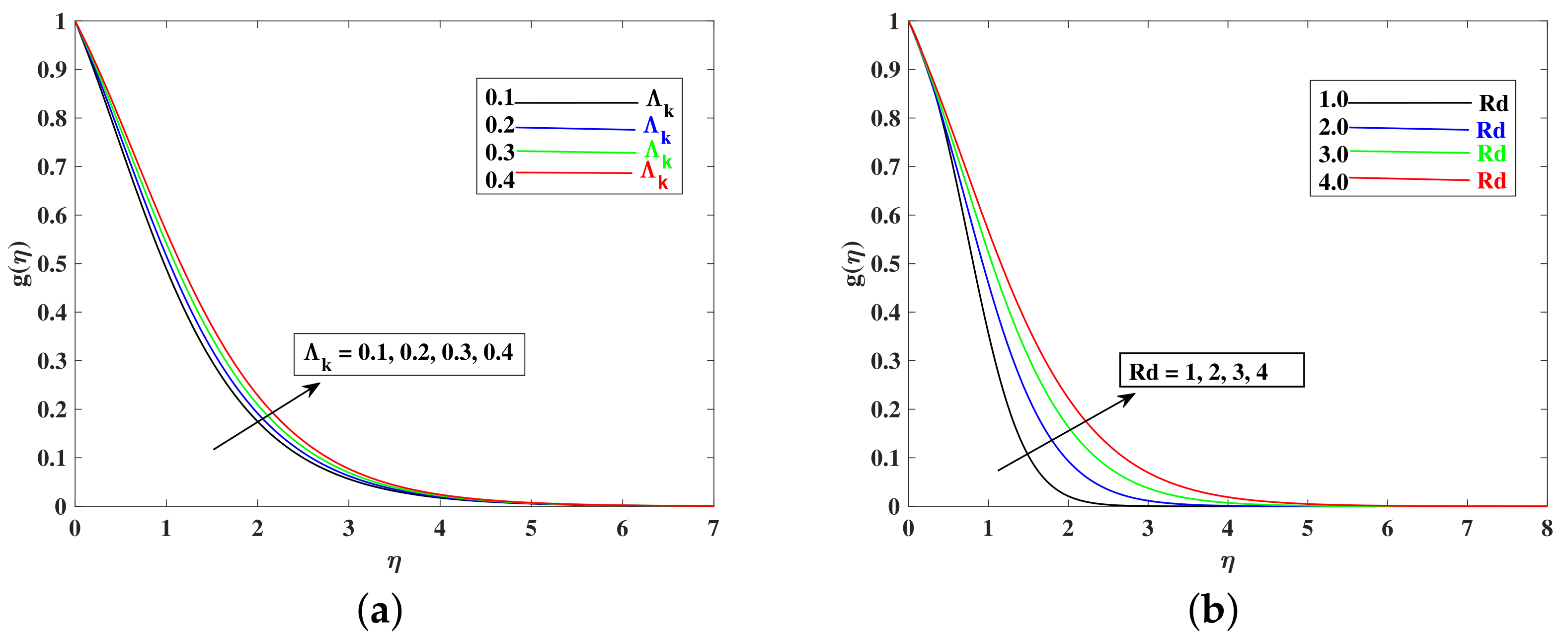
- The temperature profile enhanced with (Brownian motion), (Radiation parameter), and (thermophoretic parameter).
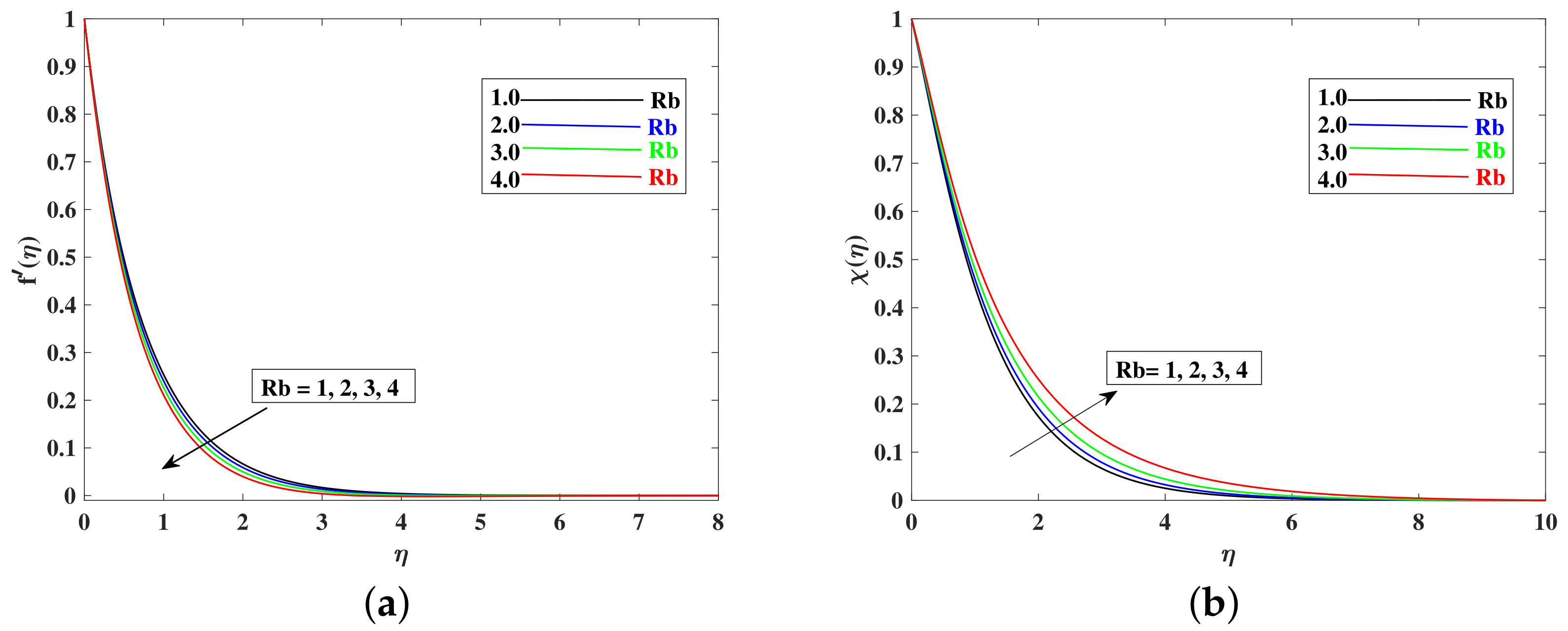
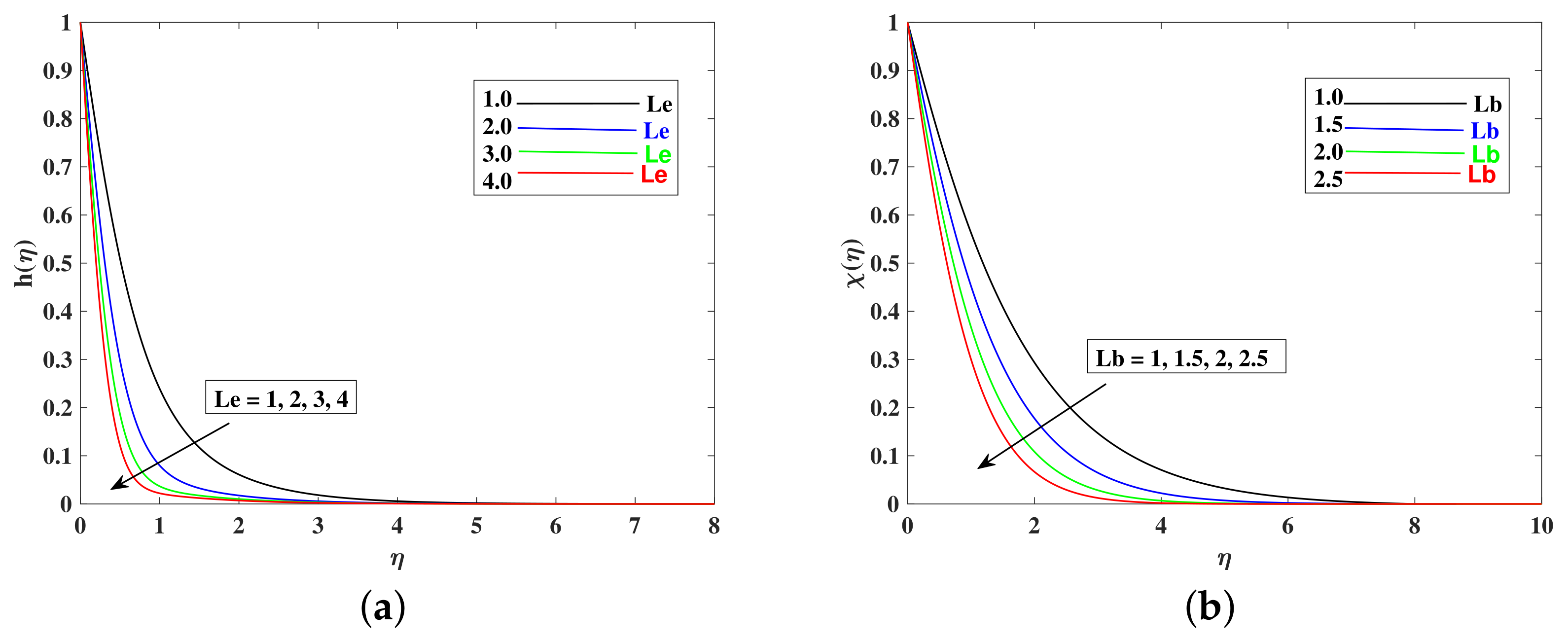
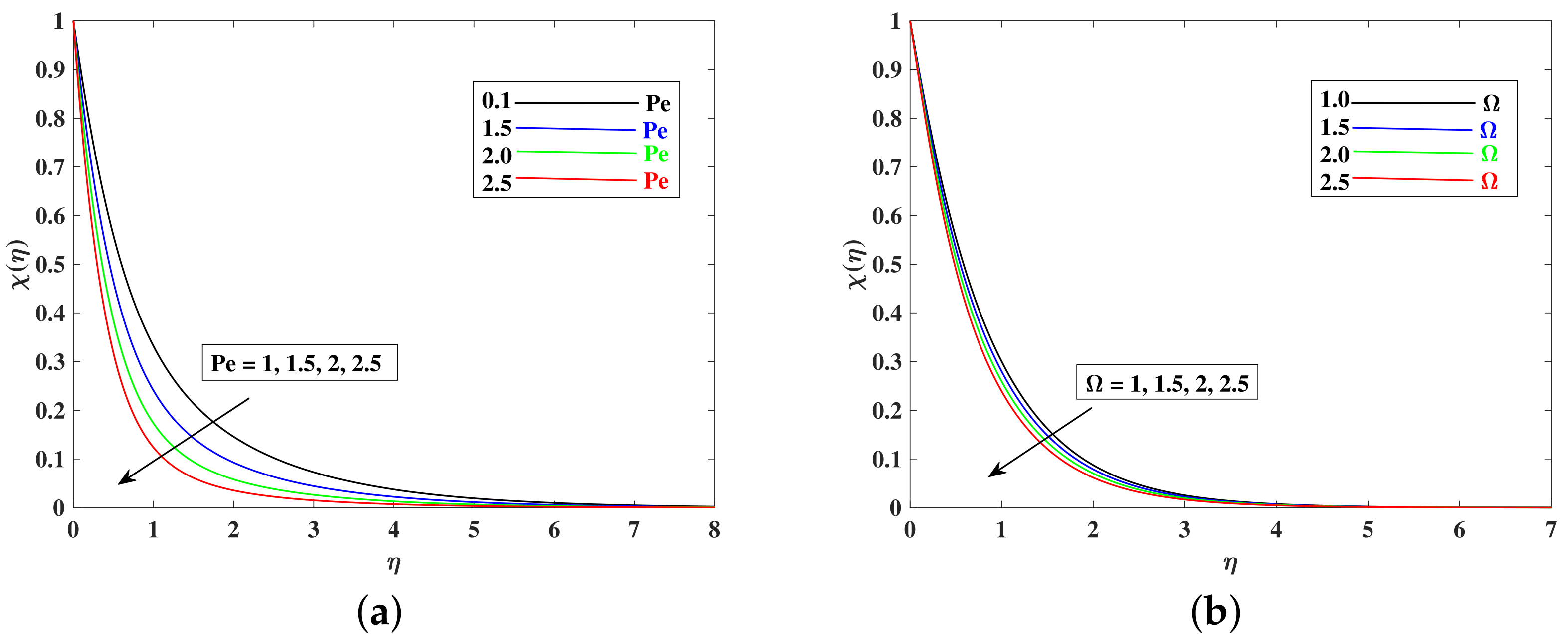
- Nanoparticle concentration increased when Nt is enhanced, and it decreased with the boosted inputs of , , and .
- The bioconvection profile decreased with higher inputs of parameters , , and .
- Skin friction increased with M, K, , , and . However, skin friction increased due to accelerated flows.
- The Nusselt number increased with higher values of , and it decreased when , , , and increased, because these parameters enhanced the temperature distribution relative to the reduced Nusselt number.
- To validate the findings, the current findings are compared to the previous literature.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Ambient motile microorganism | Dynanic viscosity | ||
| Concentration at surface | n | Density of motile microorganism | |
| Brownian diffusion coefficient | Radiative heat flux | ||
| Fluid velocity components along | Fluid velocity components along | ||
| g | Gravitational Acceleration | Heat flux | |
| T | Nanofluid temperature | Average volume of a microorganism | |
| Microorganisms density | Reynolds number | ||
| material liquid parameters of Powell-Eyring model | Electrical conductivity | ||
| Dimensionless velocity profile | Dimensionless nanofluid temperature | ||
| Dimensionless nanofluid concentration | Dimensionless density of motile microorganism | ||
| Mass density of nanoparticles | Thermophoretic diffusion coefficient | ||
| Density ratio of motile microorganisms | Temperature at surface | ||
| Variable viscosity | Kinematic viscosity | ||
| Mean absorption coeffiecient | Density of motile microorganism at surface | ||
| Uniform magnetic field | Ambient temperature | ||
| Fluid parameters | Ambient concentration | ||
| Variable thermal conductivity | Stefan-Boltzman constant | ||
| Specific heat | Linear temperature function | ||
| C | Nanoparticles concentration | Constant maximum cell swimming speed | |
| Variable viscosity | Thermal conductivity | ||
| M | Magnetic parameter | Thermal buoyancy parameter | |
| Thermophoresis parameter | Wall thickness parameter | ||
| Lewis number parameter | Prandtl number | ||
| Bioconvection Lewis number parameter | Peclet number | ||
| Buoyancy ratio parameter | Bioconvection Rayleigh number | ||
| Brownian motion | Radiation parameter | ||
| Mass flux | Motile microorganism flux | ||
| Skin friction coefficient | Nusselt number | ||
| Sherwood number | Density of motile microorganism |
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Technical Report; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Masuda, H.; Ebata, A.; Teramae, K. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Dispersion of Al2O3, SiO2 and TiO2 ultra-fine particles. Netsu Bussei 1993, 7, 227–233. [Google Scholar] [CrossRef]
- Buongiorno, J.; Hu, W. Nanofluid coolants for advanced nuclear power plants. In Proceedings of the ICAPP, Seoul, Korea, 15–19 May 2005; Volume 5, pp. 15–19. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transfer. Mar. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Kuznetsov, A.; Nield, D. Natural convective boundary-layer flow of a nanofluid past a vertical plate. Int. J. Therm. Sci. 2010, 49, 243–247. [Google Scholar] [CrossRef]
- Izadi, A.; Siavashi, M.; Rasam, H.; Xiong, Q. MHD enhanced nanofluid mediated heat transfer in porous metal for CPU cooling. Appl. Therm. Eng. 2020, 168, 114843. [Google Scholar] [CrossRef]
- Raza, J.; Mebarek-Oudina, F.; Ram, P.; Sharma, S. MHD flow of non-Newtonian molybdenum disulfide nanofluid in a converging/diverging channel with Rosseland radiation. Defect Diffus. Forum Trans. Tech. Publ. 2020, 401, 92–106. [Google Scholar] [CrossRef]
- Jamshed, W. Numerical investigation of MHD impact on Maxwell nanofluid. Int. Commun. Heat Mass Transf. 2021, 120, 104973. [Google Scholar] [CrossRef]
- Koriko, O.K.; Shah, N.A.; Saleem, S.; Chung, J.D.; Omowaye, A.J.; Oreyeni, T. Exploration of bioconvection flow of MHD thixotropic nanofluid past a vertical surface coexisting with both nanoparticles and gyrotactic microorganisms. Sci. Rep. 2021, 11, 16627. [Google Scholar] [CrossRef]
- Li, Y.X.; Alshbool, M.H.; Lv, Y.P.; Khan, I.; Khan, M.R.; Issakhov, A. Heat and mass transfer in MHD Williamson nanofluid flow over an exponentially porous stretching surface. Case Stud. Therm. Eng. 2021, 26, 100975. [Google Scholar] [CrossRef]
- Abbas, S.Z.; Khan, M.I.; Kadry, S.; Khan, W.A.; Israr-Ur-Rehman, M.; Waqas, M. Fully developed entropy optimized second order velocity slip MHD nanofluid flow with activation energy. Comput. Methods Programs Biomed. 2020, 190, 105362. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Kumam, P.; Alrabaiah, H.; Khan, W.; Islam, S.; Shaheen, N. Chemically reactive MHD micropolar nanofluid flow with velocity slips and variable heat source/sink. Sci. Rep. 2020, 10, 20926. [Google Scholar] [CrossRef]
- Shi, Q.H.; Hamid, A.; Khan, M.I.; Kumar, R.N.; Gowda, R.; Prasannakumara, B.; Shah, N.A.; Khan, S.U.; Chung, J.D. Numerical study of bio-convection flow of magneto-cross nanofluid containing gyrotactic microorganisms with activation energy. Sci. Rep. 2021, 11, 16030. [Google Scholar] [CrossRef] [PubMed]
- Ashraf, M.Z.; Rehman, S.U.; Farid, S.; Hussein, A.K.; Ali, B.; Shah, N.A.; Weera, W. Insight into Significance of Bioconvection on MHD Tangent Hyperbolic Nanofluid Flow of Irregular Thickness across a Slender Elastic Surface. Mathematics 2022, 10, 2592. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Liu, X.; Iqbal, T.; Zulqarnain, R.M.; Javid, M. A comparative study of unsteady MHD Falkner-Skan wedge flow for non-Newtonian nanofluids considering thermal radiation and activation energy. Chin. J. Phys. 2022, 77, 1625–1638. [Google Scholar] [CrossRef]
- Habib, D.; Salamat, N.; Abdal, S.H.S.; Ali, B. Numerical investigation for MHD Prandtl nanofluid transportation due to a moving wedge: Keller box approach. Int. Commun. Heat Mass Transf. 2022, 135, 106141. [Google Scholar] [CrossRef]
- Wang, J.; Mustafa, Z.; Siddique, I.; Ajmal, M.; Jaradat, M.M.; Rehman, S.U.; Ali, B.; Ali, H.M. Computational Analysis for Bioconvection of Microorganisms in Prandtl Nanofluid Darcy–Forchheimer Flow across an Inclined Sheet. Nanomaterials 2022, 12, 1791. [Google Scholar] [CrossRef]
- Younis, O.; Alizadeh, M.; Kadhim Hussein, A.; Ali, B.; Biswal, U.; Hasani Malekshah, E. MHD Natural Convection and Radiation over a Flame in a Partially Heated Semicircular Cavity Filled with a Nanofluid. Mathematics 2022, 10, 1347. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Liu, X.; Ahmed, S.; Shah, M.A. Analysis of bio-convective MHD Blasius and Sakiadis flow with Cattaneo-Christov heat flux model and chemical reaction. Chin. J. Phys. 2021, 77, 1963–1975. [Google Scholar] [CrossRef]
- Gupta, R.; Sridhar, T. Viscoelastic effects in non-Newtonian flows through porous media. Rheol. Acta 1985, 24, 148–151. [Google Scholar] [CrossRef]
- Subhas, A.; Veena, P. Visco-elastic fluid flow and heat transfer in a porous medium over a stretching sheet. Int. J. Non-Linear Mech. 1998, 33, 531–540. [Google Scholar] [CrossRef]
- Prasad, K.; Abel, M.S.; Khan, S.K. Momentum and heat transfer in visco-elastic fluid flow in a porous medium over a non-isothermal stretching sheet. Int. J. Numer. Methods Heat Fluid Flow 2000, 10, 786–801. [Google Scholar] [CrossRef]
- Seddeek, M.; Salama, F.A. The effects of temperature dependent viscosity and thermal conductivity on unsteady MHD convective heat transfer past a semi-infinite vertical porous moving plate with variable suction. Comput. Mater. Sci. 2007, 40, 186–192. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, C.; Zhang, X.; Zhang, J. Flow and radiation heat transfer of a nanofluid over a stretching sheet with velocity slip and temperature jump in porous medium. J. Frankl. Inst. 2013, 350, 990–1007. [Google Scholar] [CrossRef]
- Dessie, H.; Kishan, N. MHD effects on heat transfer over stretching sheet embedded in porous medium with variable viscosity, viscous dissipation and heat source/sink. Ain Shams Eng. J. 2014, 5, 967–977. [Google Scholar] [CrossRef]
- Mahabaleshwar, U.; Anusha, T.; Hatami, M. The MHD Newtonian hybrid nanofluid flow and mass transfer analysis due to super-linear stretching sheet embedded in porous medium. Sci. Rep. 2021, 11, 22518. [Google Scholar] [CrossRef]
- Vishalakshi, A.; Mahabaleshwar, U.; Sheikhnejad, Y. Impact of MHD and Mass Transpiration on Rivlin–Ericksen Liquid Flow over a Stretching Sheet in a Porous Media with Thermal Communication. Transp. Porous Media 2022, 142, 353–381. [Google Scholar] [CrossRef]
- Kothandapani, M.; Srinivas, S. Peristaltic transport of a Jeffrey fluid under the effect of magnetic field in an asymmetric channel. Int. J. Non-Linear Mech. 2008, 43, 915–924. [Google Scholar] [CrossRef]
- Mekheimer, K.S. Effect of the induced magnetic field on peristaltic flow of a couple stress fluid. Phys. Lett. A 2008, 372, 4271–4278. [Google Scholar] [CrossRef]
- Nadeem, S.; Akbar, N.S. Influence of heat transfer on a peristaltic flow of Johnson Segalman fluid in a non uniform tube. Int. Commun. Heat Mass Transf. 2009, 36, 1050–1059. [Google Scholar] [CrossRef]
- Mekheimer, K.S. Peristaltic flow of a couple stress fluid in an annulus: Application of an endoscope. Phys. A Stat. Mech. Its Appl. 2008, 387, 2403–2415. [Google Scholar] [CrossRef]
- Hayat, T.; Momoniat, E.; Mahomed, F.M. Peristaltic MHD flow of third grade fluid with an endoscope and variable viscosity. J. Nonlinear Math. Phys. 2008, 15, 91–104. [Google Scholar] [CrossRef]
- Srinivas, S.; Gayathri, R.; Kothandapani, M. The influence of slip conditions, wall properties and heat transfer on MHD peristaltic transport. Comput. Phys. Commun. 2009, 180, 2115–2122. [Google Scholar] [CrossRef]
- Bilal, M.; Ashbar, S. Flow and heat transfer analysis of Eyring-Powell fluid over stratified sheet with mixed convection. J. Egypt. Math. Soc. 2020, 28, 40. [Google Scholar] [CrossRef]
- Akbar, N.S.; Ebaid, A.; Khan, Z. Numerical analysis of magnetic field effects on Eyring-Powell fluid flow towards a stretching sheet. J. Magn. Magn. Mater. 2015, 382, 355–358. [Google Scholar] [CrossRef]
- Ibrahim, W.; Anbessa, T. Hall and Ion slip effects on mixed convection flow of Eyring-Powell nanofluid over a stretching surface. Adv. Math. Phys. 2020, 2020. [Google Scholar] [CrossRef]
- Javed, T.; Ali, N.; Abbas, Z.; Sajid, M. Flow of an Eyring-Powell non-Newtonian fluid over a stretching sheet. Chem. Eng. Commun. 2013, 200, 327–336. [Google Scholar] [CrossRef]
- Vishalakshi, A.; Mahabaleshwar, U.; Sarris, I.E. An MHD Fluid Flow over a Porous Stretching/Shrinking Sheet with Slips and Mass Transpiration. Micromachines 2022, 13, 116. [Google Scholar] [CrossRef] [PubMed]
- Saravana, R.; Hemadri Reddy, R.; Narasimha Murthy, K.; Makinde, O. Thermal radiation and diffusion effects in MHD Williamson and Casson fluid flows past a slendering stretching surface. Heat Transfer 2022, 51, 3187–3200. [Google Scholar] [CrossRef]
- Sarada, K.; Gowda, R.J.P.; Sarris, I.E.; Kumar, R.N.; Prasannakumara, B.C. Effect of magnetohydrodynamics on heat transfer behaviour of a non-Newtonian fluid flow over a stretching sheet under local thermal non-equilibrium condition. Fluids 2021, 6, 264. [Google Scholar] [CrossRef]
- Ajeeb, W.; Oliveira, M.S.; Martins, N.; Murshed, S.S. Forced convection heat transfer of non-Newtonian MWCNTs nanofluids in microchannels under laminar flow. Int. Commun. Heat Mass Transf. 2021, 127, 105495. [Google Scholar] [CrossRef]
- Raptis, A.; Perdikis, C.; Takhar, H.S. Effect of thermal radiation on MHD flow. Appl. Math. Comput. 2004, 153, 645–649. [Google Scholar] [CrossRef]
- Hayat, T.; Abbas, Z.; Sajid, M.; Asghar, S. The influence of thermal radiation on MHD flow of a second grade fluid. Int. J. Heat Mass Transf. 2007, 50, 931–941. [Google Scholar] [CrossRef]
- Cortell, R. Effects of viscous dissipation and radiation on the thermal boundary layer over a nonlinearly stretching sheet. Phys. Lett. A 2008, 372, 631–636. [Google Scholar] [CrossRef]
- Rashidi, M.; Ganesh, N.V.; Hakeem, A.A.; Ganga, B. Buoyancy effect on MHD flow of nanofluid over a stretching sheet in the presence of thermal radiation. J. Mol. Liq. 2014, 198, 234–238. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Ghori, M.B. Melting effect on Cattaneo–Christov and thermal radiation features for aligned MHD nanofluid flow comprising microorganisms to leading edge: FEM approach. Comput. Math. Appl. 2022, 109, 260–269. [Google Scholar] [CrossRef]
- Sudarsana Reddy, P.; Sreedevi, P. Impact of chemical reaction and double stratification on heat and mass transfer characteristics of nanofluid flow over porous stretching sheet with thermal radiation. Int. J. Ambient Energy 2022, 43, 1626–1636. [Google Scholar] [CrossRef]
- Childress, S.; Levandowsky, M.; Spiegel, E. Pattern formation in a suspension of swimming microorganisms: Equations and stability theory. J. Fluid Mech. 1975, 69, 591–613. [Google Scholar] [CrossRef]
- Hill, N.; Pedley, T.; Kessler, J.O. Growth of bioconvection patterns in a suspension of gyrotactic in a layer of finite depth. J. Fluid Mech. 1989, 208, 509–543. [Google Scholar] [CrossRef]
- Khan, W.; Makinde, O. MHD nanofluid bioconvection due to gyrotactic microorganisms over a convectively heat stretching sheet. Int. J. Therm. Sci. 2014, 81, 118–124. [Google Scholar] [CrossRef]
- Alqarni, M.; Waqas, H.; Imran, M.; Alghamdi, M.; Muhammad, T. Thermal transport of bio-convection flow of micropolar nanofluid with motile microorganisms and velocity slip effects. Phys. Scr. 2020, 96, 015220. [Google Scholar] [CrossRef]
- Zadeh, S.M.H.; Mehryan, S.; Sheremet, M.A.; Izadi, M.; Ghodrat, M. Numerical study of mixed bio-convection associated with a micropolar fluid. Therm. Sci. Eng. Prog. 2020, 18, 100539. [Google Scholar]
- Chu, Y.M.; Khan, M.I.; Khan, N.B.; Kadry, S.; Khan, S.U.; Tlili, I.; Nayak, M. Significance of activation energy, bio-convection and magnetohydrodynamic in flow of third grade fluid (non-Newtonian) towards stretched surface: A Buongiorno model analysis. Int. Commun. Heat Mass Transf. 2020, 118, 104893. [Google Scholar] [CrossRef]
- Alshomrani, A.S. Numerical investigation for bio-convection flow of viscoelastic nanofluid with magnetic dipole and motile microorganisms. Arab. J. Sci. Eng. 2021, 46, 5945–5956. [Google Scholar] [CrossRef]
- Asjad, M.I.; Ur Rehman, S.; Ahmadian, A.; Salahshour, S.; Salimi, M. First Solution of Fractional Bioconvection with Power Law Kernel for a Vertical Surface. Mathematics 2021, 9, 1366. [Google Scholar] [CrossRef]
- Jawad, M.; Saeed, A.; Khan, A.; Islam, S. MHD bioconvection Darcy-Forchheimer flow of Casson nanofluid over a rotating disk with entropy optimization. Heat Transf. 2021, 50, 2168–2196. [Google Scholar] [CrossRef]
- Khan, M.; Salahuddin, T.; Malik, M.; Alqarni, M.; Alqahtani, A. Numerical modeling and analysis of bioconvection on MHD flow due to an upper paraboloid surface of revolution. Phys. A Stat. Mech. Its Appl. 2020, 553, 124231. [Google Scholar] [CrossRef]
- Ara, A.; Khan, N.A.; Khan, H.; Sultan, F. Radiation effect on boundary layer flow of an Eyring–Powell fluid over an exponentially shrinking sheet. Ain Shams Eng. J. 2014, 5, 1337–1342. [Google Scholar] [CrossRef]
- Wakif, A. A novel numerical procedure for simulating steady MHD convective flows of radiative Casson fluids over a horizontal stretching sheet with irregular geometry under the combined influence of temperature-dependent viscosity and thermal conductivity. Math. Probl. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Hayat, T.; Ullah, I.; Alsaedi, A.; Farooq, M. MHD flow of Powell-Eyring nanofluid over a non-linear stretching sheet with variable thickness. Results Phys. 2017, 7, 189–196. [Google Scholar] [CrossRef]
- Rosseland, S. Astrophysik: Auf Atomtheoretischer Grundlage; Springer: Berlin/Heidelberg, Germany, 2013; Volume 11. [Google Scholar]
- Rehman, S.U.; Mariam, A.; Ullah, A.; Asjad, M.I.; Bajuri, M.Y.; Pansera, B.A.; Ahmadian, A. Numerical computation of buoyancy and radiation effects on MHD micropolar nanofluid flow over a stretching/shrinking sheet with heat source. Case Stud. Therm. Eng. 2021, 25, 100867. [Google Scholar] [CrossRef]
- Wang, F.; Asjad, M.I.; Ur Rehman, S.; Ali, B.; Hussain, S.; Gia, T.N.; Muhammad, T. MHD Williamson Nanofluid Flow over a Slender Elastic Sheet of Irregular Thickness in the Presence of Bioconvection. Nanomaterials 2021, 11, 2297. [Google Scholar] [CrossRef]
- Wei, Y.; Rehman, S.U.; Fatima, N.; Ali, B.; Ali, L.; Chung, J.D.; Shah, N.A. Significance of Dust Particles, Nanoparticles Radius, Coriolis and Lorentz Forces: The Case of Maxwell Dusty Fluid. Nanomaterials 2022, 12, 1512. [Google Scholar] [CrossRef] [PubMed]
- Wang, C. Free convection on a vertical stretching surface. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 1989, 69, 418–420. [Google Scholar] [CrossRef]



| m | Wakif [59] | (Our Results) | ||
|---|---|---|---|---|
| 10 | 1.143320620 | 1.060324666 | 1.143329 | 1.060330 |
| 9.0 | 1.140392519 | 1.058915794 | 1.140397 | 1.058925 |
| 7.0 | 1.132285178 | 1.055044823 | 1.132299 | 1.055048 |
| 5.0 | 1.118590381 | 1.048611306 | 1.118582 | 1.048608 |
| Wang [65] | Wakif [59] | Our Results | |
|---|---|---|---|
| 0.7 | 0.4539 | 0.453916157 | 0.4544 |
| 2.0 | 0.9114 | 0.911357683 | 0.9113 |
| 7.0 | 1.8954 | 1.895403258 | 1.8954 |
| 20 | 3.3539 | 3.353904143 | 3.3539 |
| M | K | |||||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.4 | 0.2 | 0.7 | 0.5 | 1.0 | 0.3 | 0.1 | 1.4350 |
| 0.2 | 1.4788 | |||||||
| 0.3 | 1.5219 | |||||||
| 0.1 | 1.3000 | |||||||
| 0.3 | 1.3907 | |||||||
| 0.4 | 1.4350 | |||||||
| 0.2 | 1.4350 | |||||||
| 0.3 | 1.3887 | |||||||
| 0.4 | 1.3434 | |||||||
| 0.7 | 1.4350 | |||||||
| 0.8 | 1.4879 | |||||||
| 0.9 | 1.5394 | |||||||
| 0.5 | 1.4350 | |||||||
| 0.6 | 1.4382 | |||||||
| 0.7 | 1.4413 | |||||||
| 1.0 | 1.4350 | |||||||
| 1.1 | 1.4478 | |||||||
| 1.2 | 1.4618 | |||||||
| 0.1 | 1.4097 | |||||||
| 0.2 | 1.4224 | |||||||
| 0.3 | 1.4350 | |||||||
| 0.1 | 1.4350 | |||||||
| 0.2 | 1.4502 | |||||||
| 0.3 | 1.4655 |
| 1.1 | 1 | 0.1 | 0.1 | 0.3 | 0.3034 |
| 1.2 | 0.3105 | ||||
| 1.3 | 0.3167 | ||||
| 1.0 | 0.3034 | ||||
| 1.1 | 0.2997 | ||||
| 1.2 | 0.2962 | ||||
| 0.1 | 0.3034 | ||||
| 0.2 | 0.2963 | ||||
| 0.3 | 0.2897 | ||||
| 0.1 | 0.3034 | ||||
| 0.2 | 0.2978 | ||||
| 0.3 | 0.2923 | ||||
| 0.3 | 0.3034 | ||||
| 0.4 | 0.2941 | ||||
| 0.4 | 0.2850 |
| 0.4 | 1.0 | 0.1 | 0.5 | 0.2772 |
| 0.5 | 0.3148 | |||
| 0.6 | 0.3468 | |||
| 1.0 | 0.2772 | |||
| 1.1 | 0.2893 | |||
| 1.2 | 0.3009 | |||
| 0.1 | 0.2772 | |||
| 0.2 | 0.2522 | |||
| 0.3 | 0.2284 | |||
| 0.5 | 0.2772 | |||
| 0.6 | 0.2832 | |||
| 0.7 | 0.2877 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manan, A.; Rehman, S.U.; Fatima, N.; Imran, M.; Ali, B.; Shah, N.A.; Chung, J.D. Dynamics of Eyring–Powell Nanofluids When Bioconvection and Lorentz Forces Are Significant: The Case of a Slender Elastic Sheet of Variable Thickness with Porous Medium. Mathematics 2022, 10, 3039. https://doi.org/10.3390/math10173039
Manan A, Rehman SU, Fatima N, Imran M, Ali B, Shah NA, Chung JD. Dynamics of Eyring–Powell Nanofluids When Bioconvection and Lorentz Forces Are Significant: The Case of a Slender Elastic Sheet of Variable Thickness with Porous Medium. Mathematics. 2022; 10(17):3039. https://doi.org/10.3390/math10173039
Chicago/Turabian StyleManan, Abdul, Saif Ur Rehman, Nageen Fatima, Muhammad Imran, Bagh Ali, Nehad Ali Shah, and Jae Dong Chung. 2022. "Dynamics of Eyring–Powell Nanofluids When Bioconvection and Lorentz Forces Are Significant: The Case of a Slender Elastic Sheet of Variable Thickness with Porous Medium" Mathematics 10, no. 17: 3039. https://doi.org/10.3390/math10173039
APA StyleManan, A., Rehman, S. U., Fatima, N., Imran, M., Ali, B., Shah, N. A., & Chung, J. D. (2022). Dynamics of Eyring–Powell Nanofluids When Bioconvection and Lorentz Forces Are Significant: The Case of a Slender Elastic Sheet of Variable Thickness with Porous Medium. Mathematics, 10(17), 3039. https://doi.org/10.3390/math10173039








